Comparative Study of GPR Acquisition Methods for Shallow Buried Object Detection
Abstract
:1. Introduction
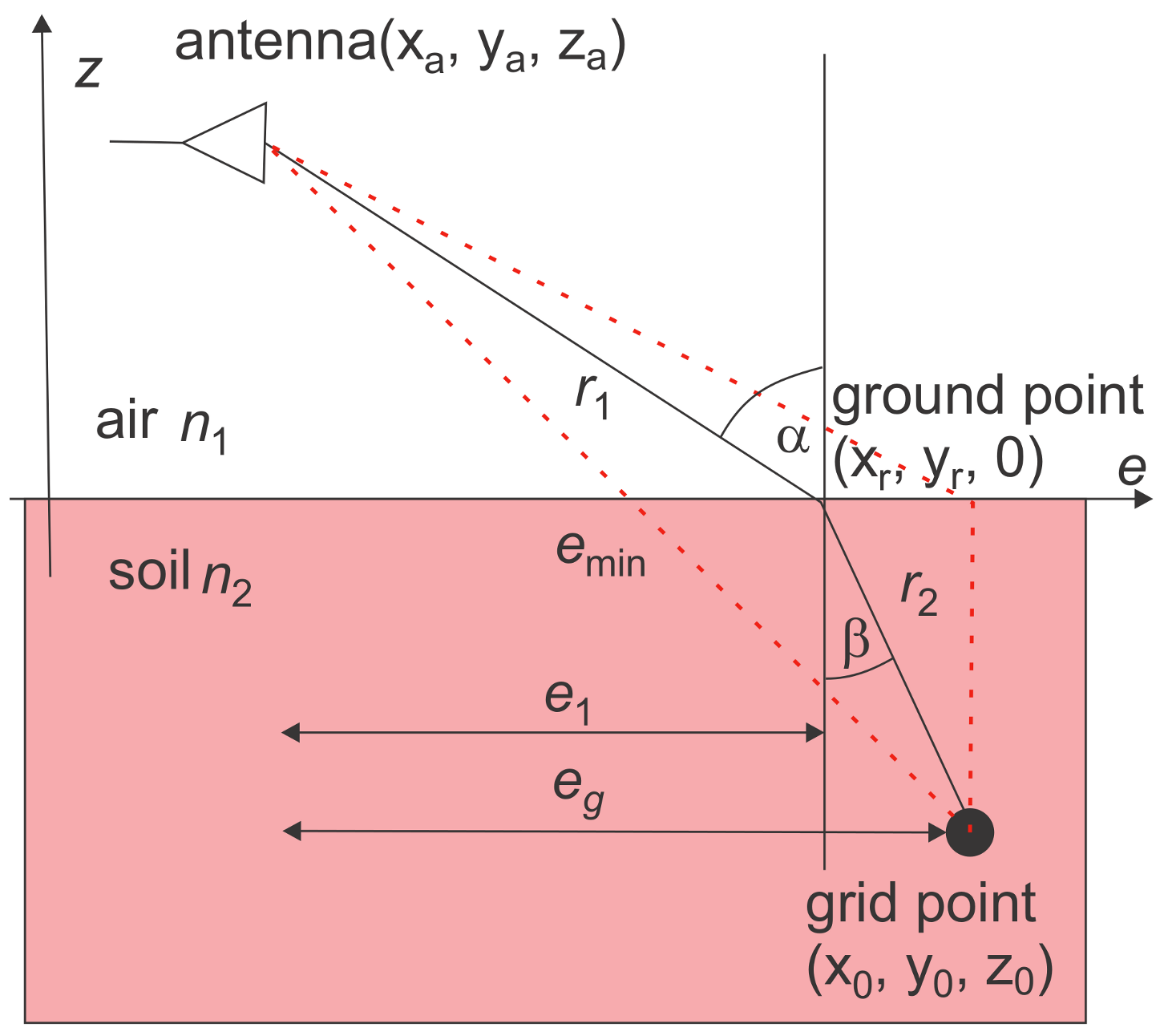
2. Background
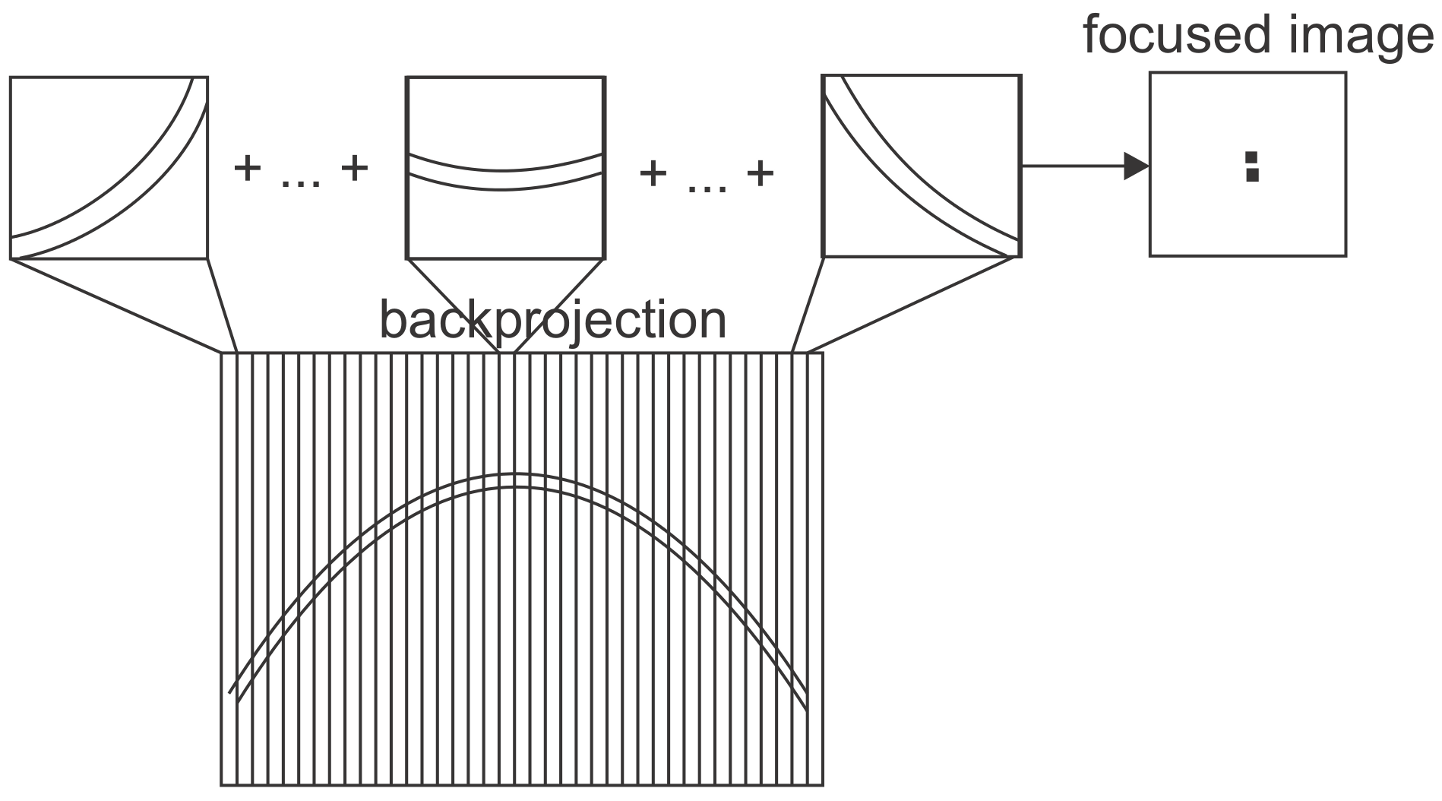
Back Projection Algorithm
3. Methodology
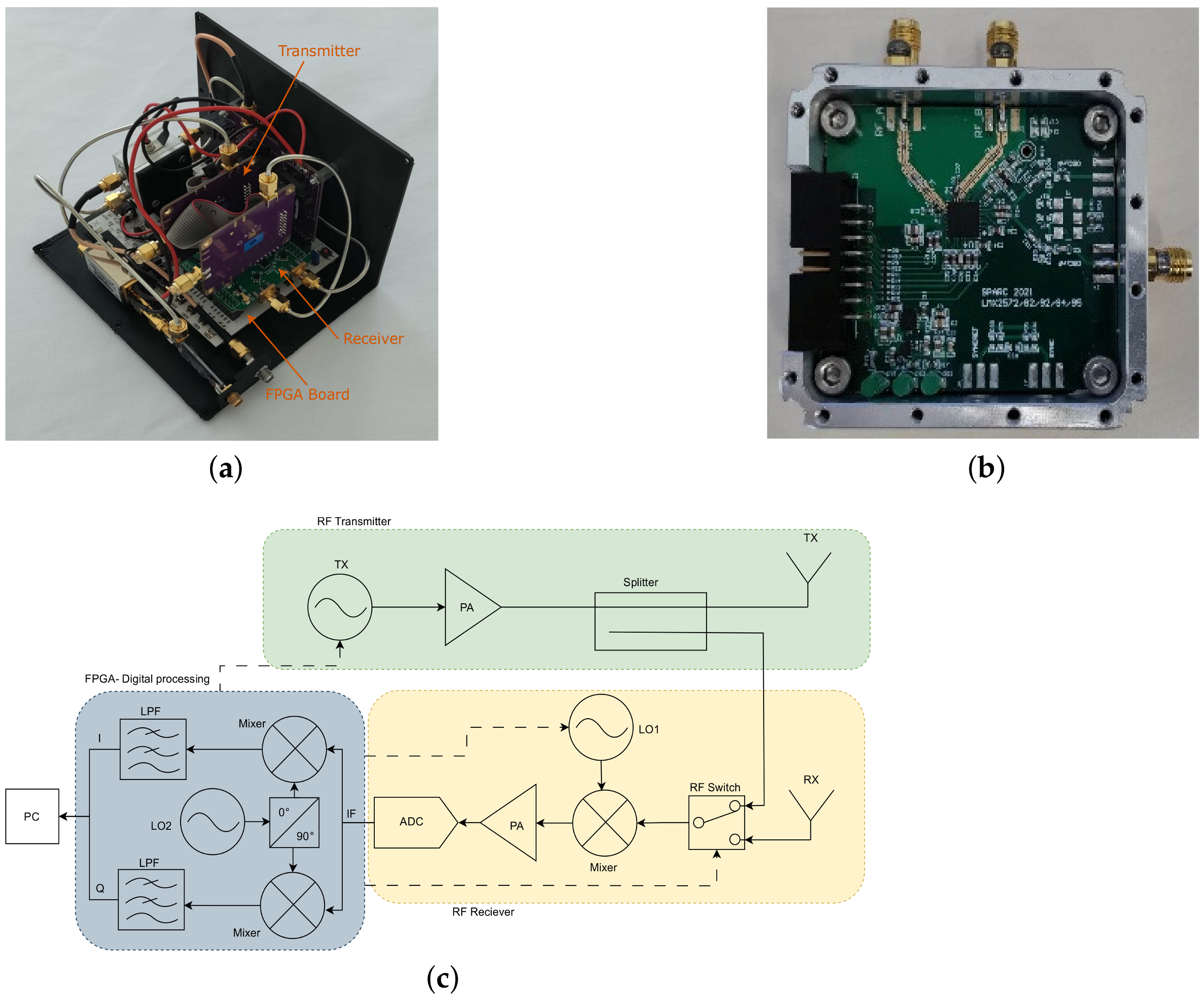
3.1. Radar System Design and Theory
3.2. Experimental Setup
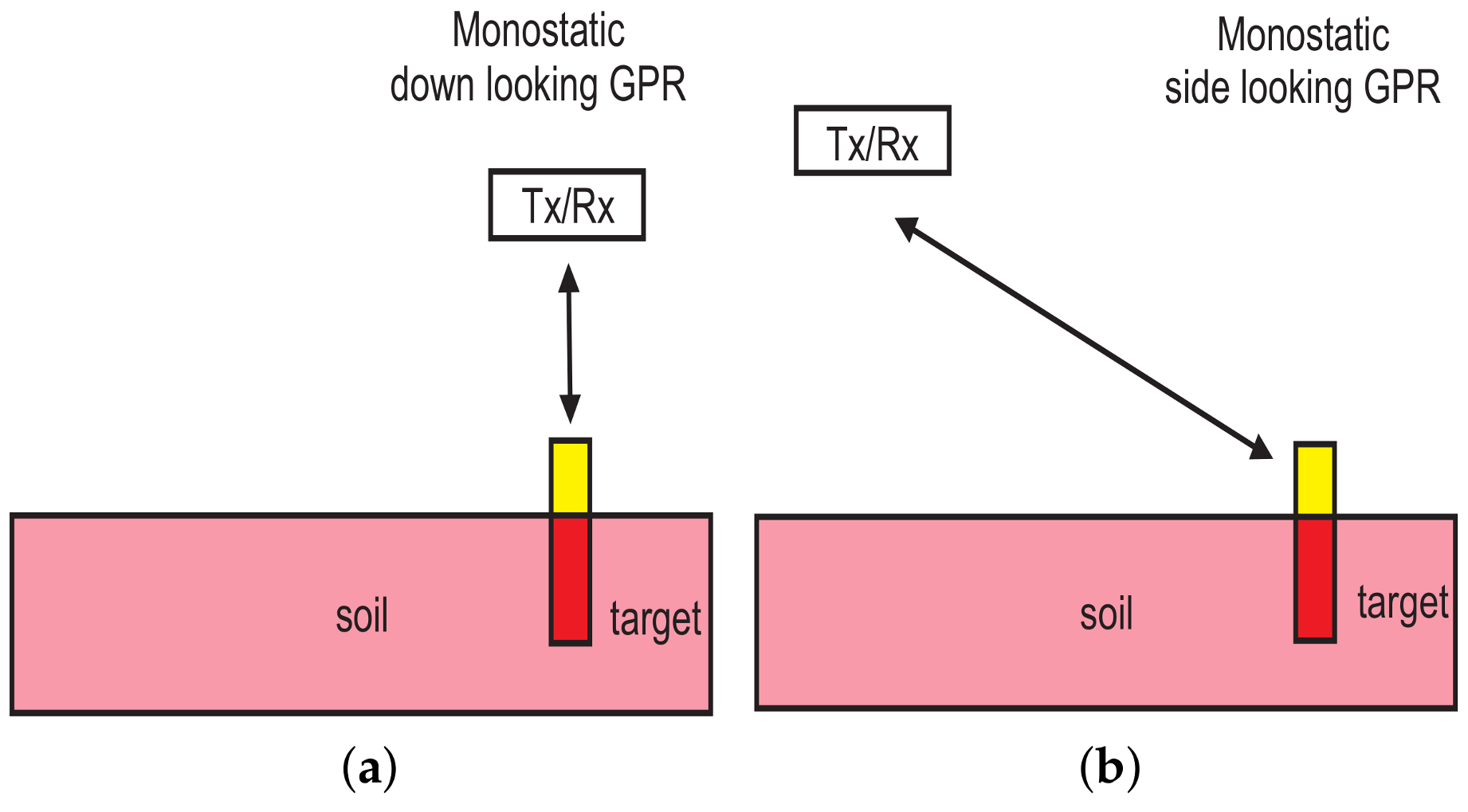
3.2.1. Down-Looking and Side-Looking GPR Configuration
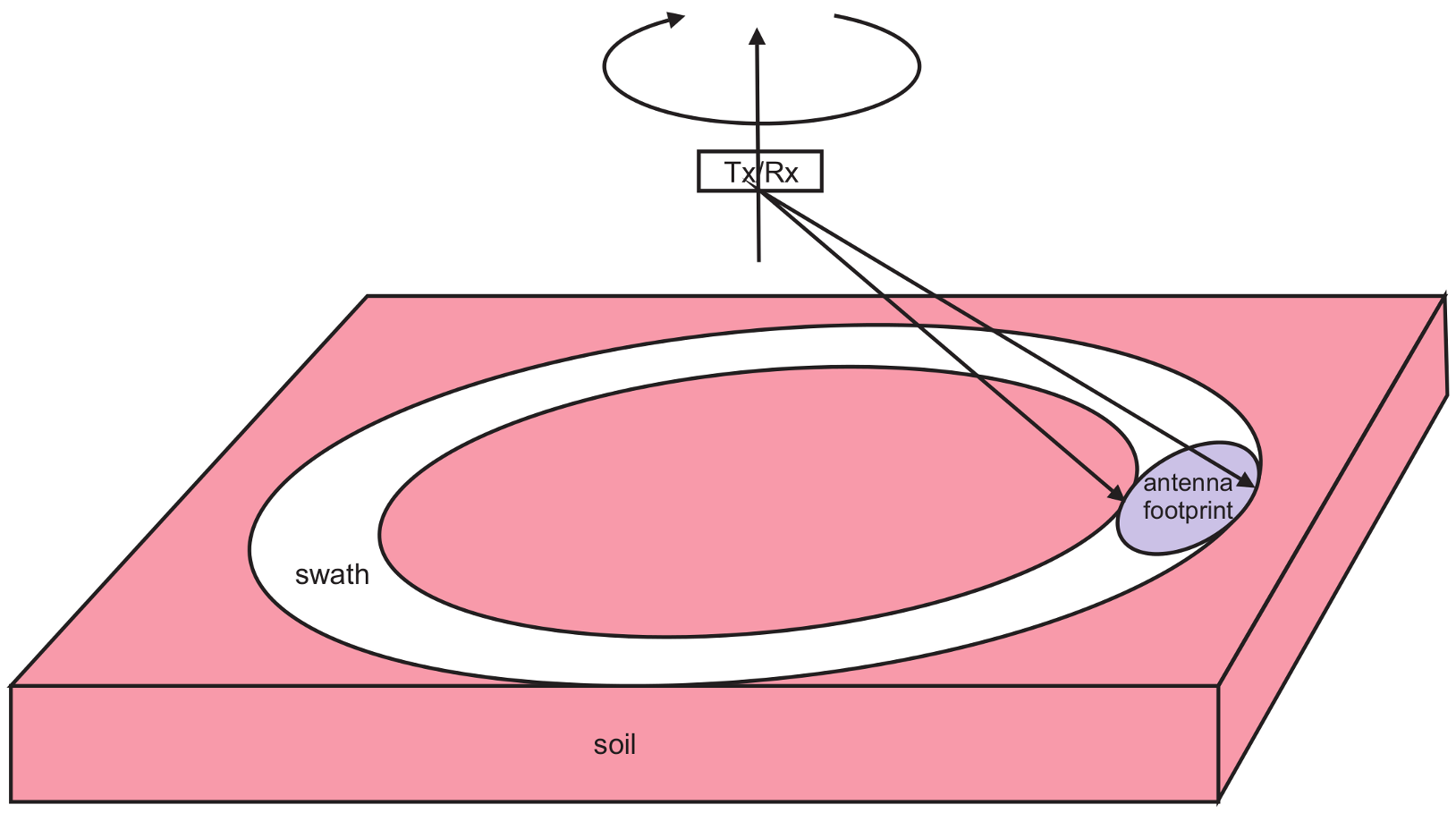
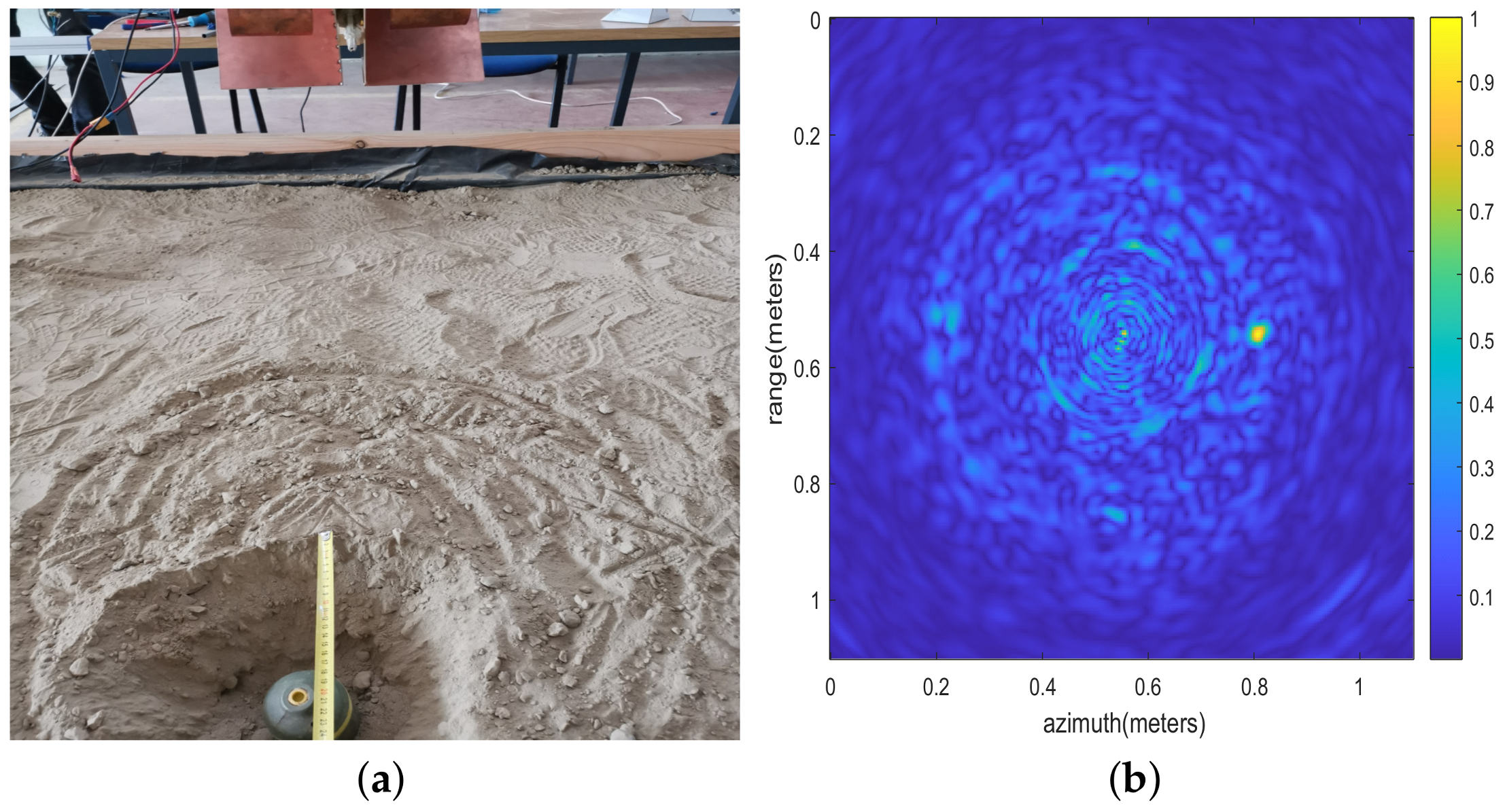
3.2.2. Acquisition Scenarios
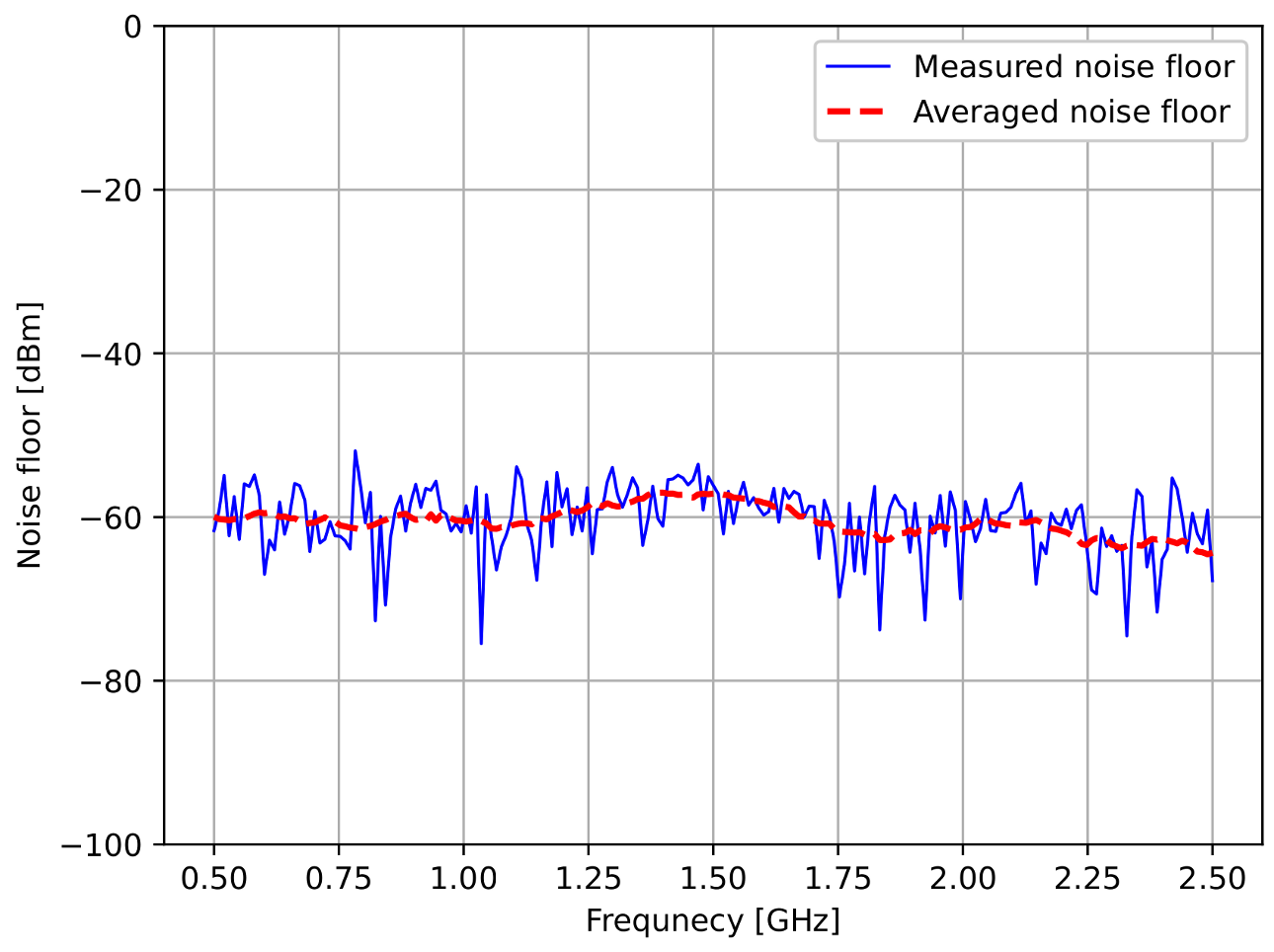
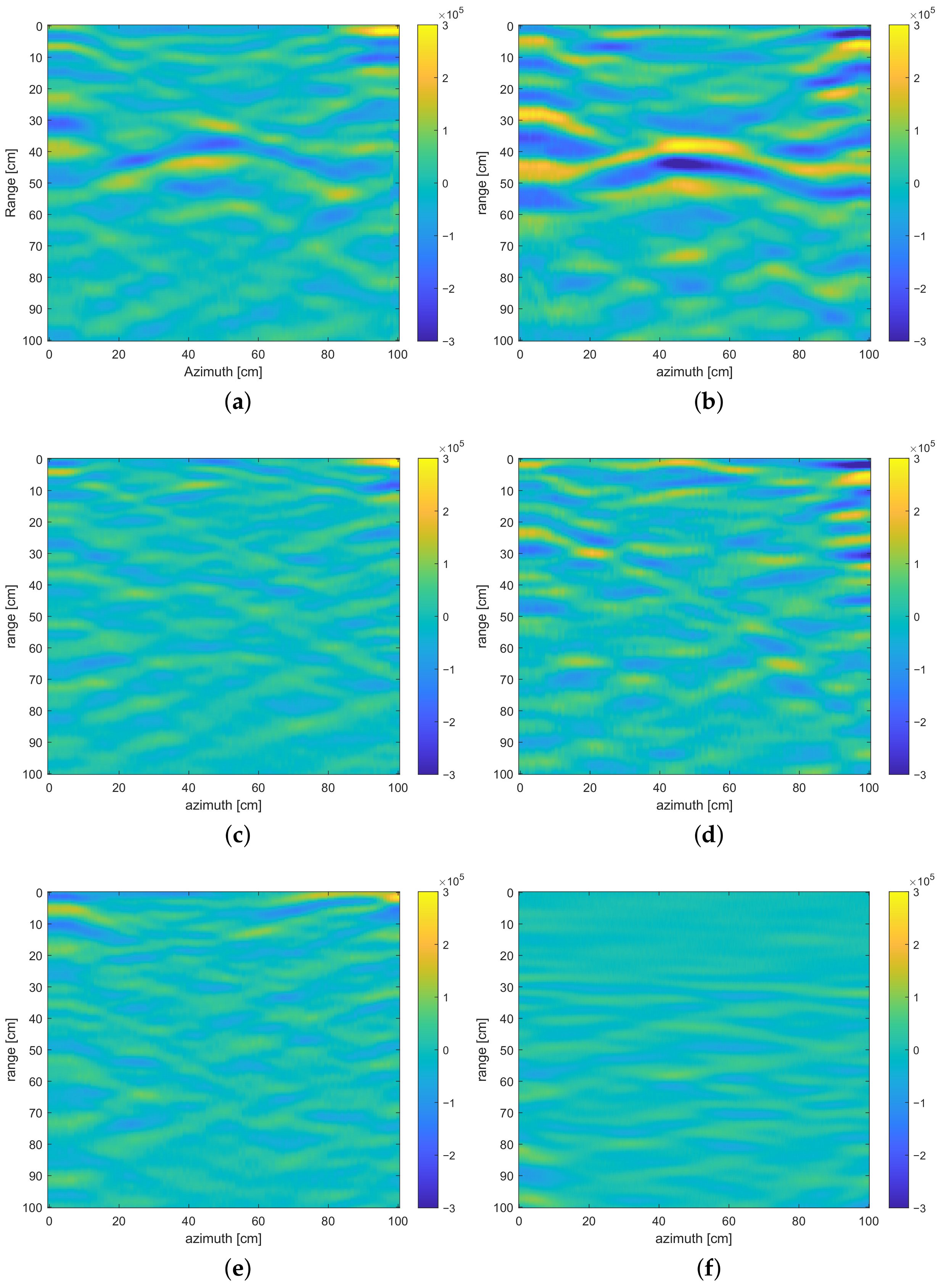
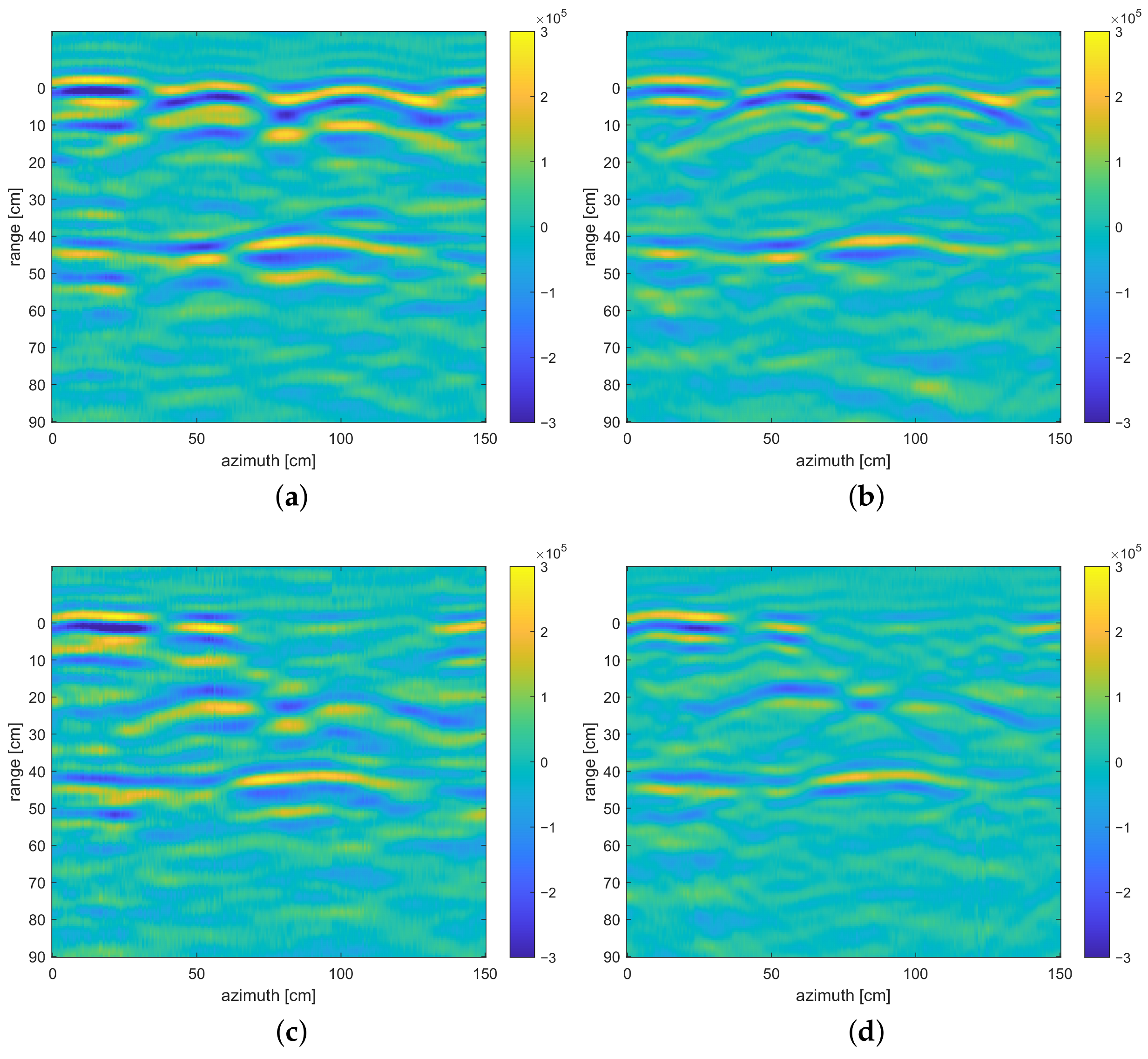
4. Experimental Results
4.1. Monostatic Down-Looking Configuration
4.2. Monostatic Side-Looking Configuration
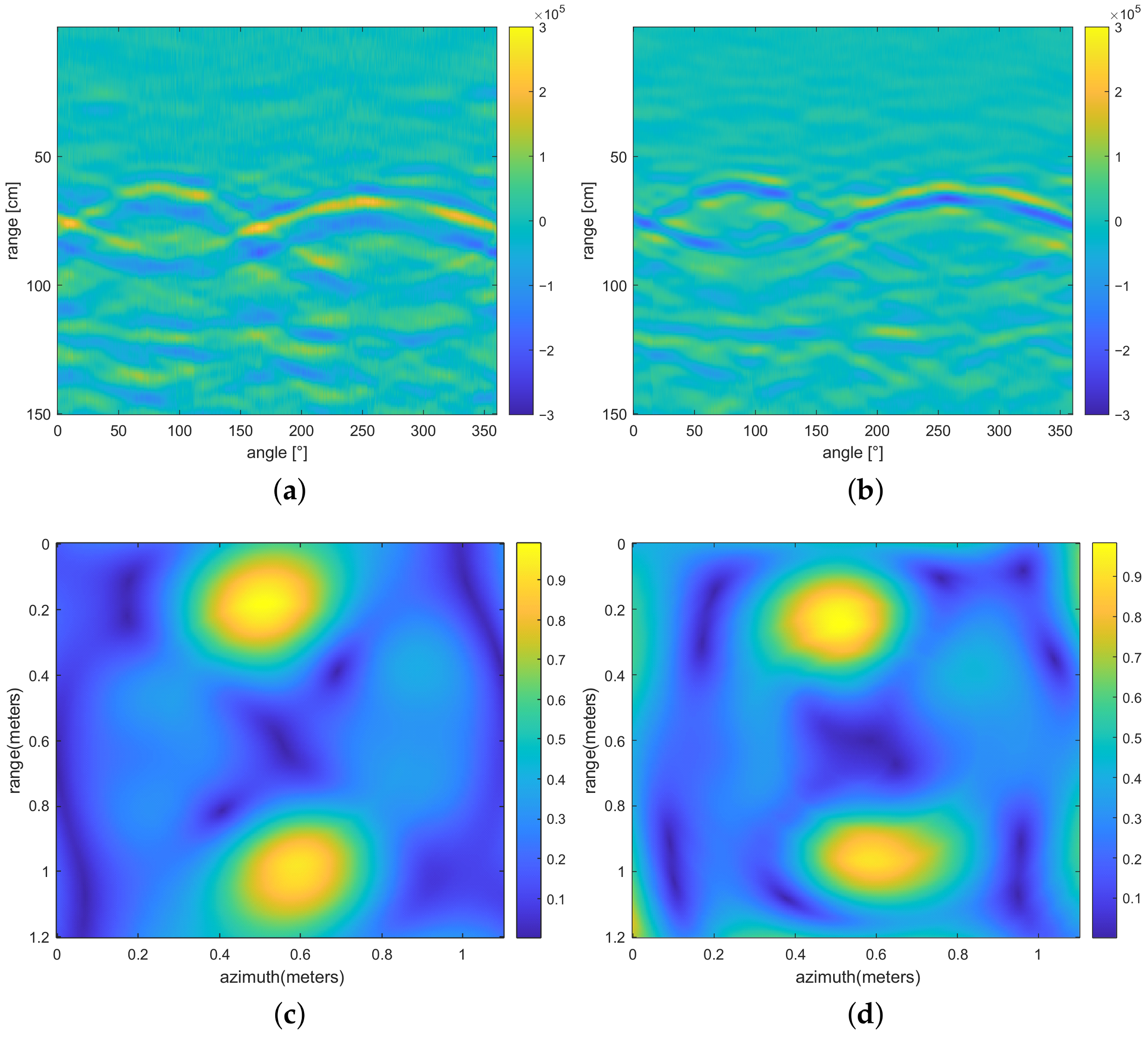
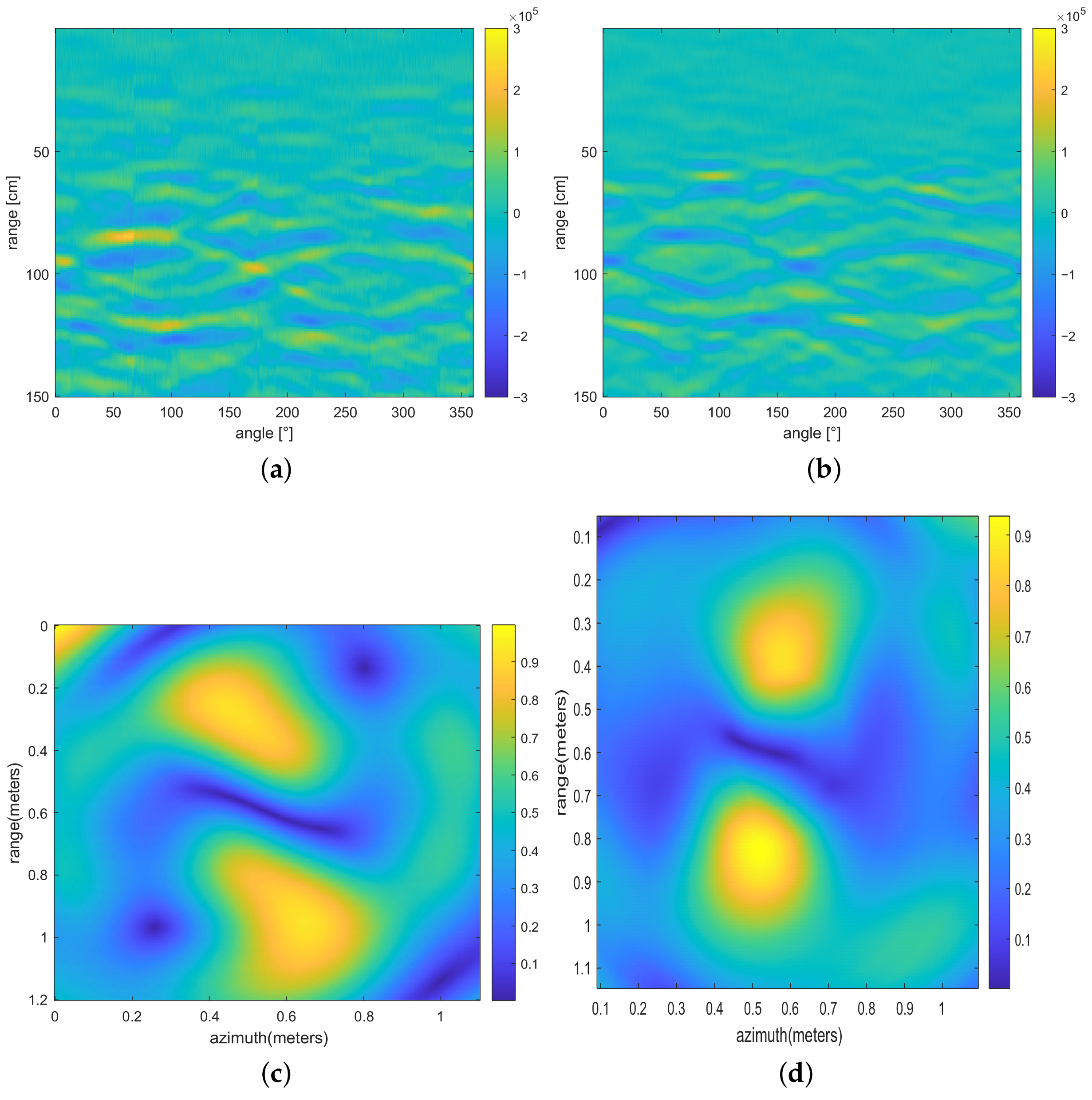
4.3. Circular GPR Configuration
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPR | Ground Penetrating Radar |
| SFCW | Stepped Frequency Continuous Wave |
| UAV | Unmanned Aerial Vehicle |
| SAR | Synthetic Aperture Radar |
| GPSAR | Ground Penetrating Synthetic Aperture Radar |
| ADC | Analog-to-Digital Converter |
| BP | Backprojection |
| IFFT | Inverse Fast Fourier Transform |
References
- Catapano, I.; Gennarelli, G.; Ludeno, G.; Noviello, C.; Esposito, G.; Soldovieri, F. Contactless Ground Penetrating Radar Imaging: State of the art, challenges, and microwave tomography-based data processing. IEEE Geosci. Remote Sens. Mag. 2022, 10, 251–273. [Google Scholar] [CrossRef]
- Dai, Q.; Lee, Y.H.; Sun, H.H.; Ow, G.; Yusof, M.L.M.; Yucel, A.C. 3DInvNet: A Deep Learning-Based 3D Ground-Penetrating Radar Data Inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Rodríguez-Santalla, I.; Gomez-Ortiz, D.; Martín-Crespo, T.; Sánchez-García, M.J.; Montoya-Montes, I.; Martín-Velázquez, S.; Barrio, F.; Serra, J.; Ramírez-Cuesta, J.M.; Gracia, F.J. Study and Evolution of the Dune Field of La Banya Spit in Ebro Delta (Spain) Using LiDAR Data and GPR. Remote Sens. 2021, 13, 802. [Google Scholar] [CrossRef]
- Qiu, Z.; Zeng, J.; Tang, W.; Yang, H.; Lu, J.; Zhao, Z. Research on Real-Time Automatic Picking of Ground-Penetrating Radar Image Features by Using Machine Learning. Horticulturae 2022, 8, 1116. [Google Scholar] [CrossRef]
- Fu, L.; Liu, S.; Liu, L.; Lei, L. Development of an Airborne Ground Penetrating Radar System: Antenna Design, Laboratory Experiment, and Numerical Simulation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 761–766. [Google Scholar] [CrossRef]
- Ŝipoŝ, D.; Planinŝiĉ, P.; Gleich, D. Simulation and Implementation of Air-Coupled SFCW Radar on VNA. In Proceedings of the 2018 25th International Conference on Systems, Signals and Image Processing (IWSSIP), Maribor, Slovenia, 20–22 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- García Fernández, M.; Álvarez Narciandi, G.; Arboleya, A.; Vázquez Antuña, C.; Andrés, F.L.H.; Álvarez López, Y. Development of an Airborne-Based GPR System for Landmine and IED Detection: Antenna Analysis and Intercomparison. IEEE Access 2021, 9, 127382–127396. [Google Scholar] [CrossRef]
- Peters, L.; Daniels, J.; Young, J. Ground penetrating radar as a subsurface environmental sensing tool. Proc. IEEE 1994, 82, 1802–1822. [Google Scholar] [CrossRef]
- Soumekh, M. Synthetic Aperture Radar Signal Processing; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Jol, H.M. Ground Penetrating Radar: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Wu, K.; Rodriguez, G.A.; Zajc, M.; Jacquemin, E.; Clément, M.; De Coster, A.; Lambot, S. A new drone-borne GPR for soil moisture mapping. Remote Sens. Environ. 2019, 235, 111456. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, C.; Xiao, Z.; Lu, B.; Zhang, J.; Li, J.; Liu, C. A novel target state detection method for accurate cardiopulmonary signal extraction based on FMCW radar signals. Front. Physiol. 2023, 14, 1206471. [Google Scholar] [CrossRef]
- Pereira, M.; Burns, D.; Orfeo, D.; Zhang, Y.; Jiao, L.; Huston, D.; Xia, T. 3-D Multistatic Ground Penetrating Radar Imaging for Augmented Reality Visualization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5666–5675. [Google Scholar] [CrossRef]
- Tosti, F.; Gennarelli, G.; Lantini, L.; Catapano, I.; Soldovieri, F.; Giannakis, I.; Alani, A.M. The Use of GPR and Microwave Tomography for the Assessment of the Internal Structure of Hollow Trees. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Lei, Y.; Jiang, B.; Su, G.; Zou, Y.; Qi, F.; Li, B.; Jia, F.; Tian, T.; Qu, Q. Application of Air-Coupled Ground Penetrating Radar Based on F-K Filtering and BP Migration in High-Speed Railway Tunnel Detection. Sensors 2023, 23, 4343. [Google Scholar] [CrossRef] [PubMed]
- Edemsky, D.; Popov, A.; Prokopovich, I.; Garbatsevich, V. Airborne Ground Penetrating Radar, Field Test. Remote Sens. 2021, 13, 667. [Google Scholar] [CrossRef]
- Liu, P.; Ding, Z.; Zhang, W.; Ren, Z.; Yang, X. Using Ground-Penetrating Radar and Deep Learning to Rapidly Detect Voids and Rebar Defects in Linings. Sustainability 2023, 15, 11855. [Google Scholar] [CrossRef]
- Vergnano, A.; Franco, D.; Godio, A. Drone-Borne Ground-Penetrating Radar for Snow Cover Mapping. Remote Sens. 2022, 14, 1763. [Google Scholar] [CrossRef]
- González-Díaz, M.; García-Fernández, M.; Álvarez López, Y.; Las-Heras, F. Improvement of GPR SAR-Based Techniques for Accurate Detection and Imaging of Buried Objects. IEEE Trans. Instrum. Meas. 2020, 69, 3126–3138. [Google Scholar] [CrossRef]
- García-Fernández, M.; Álvarez Narciandi, G.; Álvarez López, Y.; Las-Heras Andrés, F. Analysis and Validation of a Hybrid Forward-Looking Down-Looking Ground Penetrating Radar Architecture. Remote Sens. 2021, 13, 1206. [Google Scholar] [CrossRef]
- Noviello, C.; Gennarelli, G.; Esposito, G.; Ludeno, G.; Fasano, G.; Capozzoli, L.; Soldovieri, F.; Catapano, I. An Overview on Down-Looking UAV-Based GPR Systems. Remote Sens. 2022, 14, 3245. [Google Scholar] [CrossRef]
- Mohammadpoor, M.; Abdullah, R.S.A.R.; Ismail, A.; Abas, A.F. A circular synthetic aperture radar for on-the-ground object detection. Prog. Electromagn. Res. 2012, 122, 269–292. [Google Scholar] [CrossRef]
- Mohammadpoor, M.; Abdullah, R.R.; Ismail, A.; Abas, A. A ground based circular synthetic aperture radar. In Proceedings of the 2013 14th International Radar Symposium (IRS), Dresden, Germany, 19–21 June 2013; Volume 1, pp. 521–526. [Google Scholar]
- Grathwohl, A.; Arendt, B.; Grebner, T.; Waldschmidt, C. Detection of Objects Below Uneven Surfaces with a UAV-Based GPSAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- García Fernández, M.; Álvarez López, Y.; Arboleya Arboleya, A.; González Valdés, B.; Rodríguez Vaqueiro, Y.; Las-Heras Andrés, F.; Pino García, A. Synthetic Aperture Radar Imaging System for Landmine Detection Using a Ground Penetrating Radar on Board a Unmanned Aerial Vehicle. IEEE Access 2018, 6, 45100–45112. [Google Scholar] [CrossRef]
- Saleh, B.; Teich, M. Fundamentals of Photonics; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gorham, L.A.; Moore, L.J. SAR image formation toolbox for MATLAB. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XVII, Orlando, FL, USA, 5–9 April 2010; Volume 7699, p. 769906. [Google Scholar] [CrossRef]
- Rigling, B.; Moses, R. Taylor expansion of the differential range for monostatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 60–64. [Google Scholar] [CrossRef]
- Šipoš, D.; Gleich, D. A Lightweight and Low-Power UAV-Borne Ground Penetrating Radar Design for Landmine Detection. Sensors 2020, 20, 2234. [Google Scholar]
- Smogavec, P.; Pongrac, B.; Gleich, D. Evaluation of Compact and Modular SFCW GPR Systems for Detecting Buried Objects. In Proceedings of the 2023 30th International Conference on Systems, Signals and Image Processing (IWSSIP), Ohrid, North Macedonia, 27–29 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Ahmed, A.; Zhang, Y.; Burns, D.; Huston, D.; Xia, T. Design of UWB Antenna for Air-Coupled Impulse Ground-Penetrating Radar. IEEE Geosci. Remote Sens. Lett. 2016, 13, 92–96. [Google Scholar] [CrossRef]
- Wu, M.; Ferro-Famil, L.; Boutet, F.; Wang, Y. Comparison of Imaging Radar Configurations for Roadway Inspection and Characterization. Sensors 2023, 23, 8522. [Google Scholar] [CrossRef]
- GmBH, S.S. SWM 5000 Soil Moisture Meter. Available online: https://www.stepsystems.de/en/products/moisture-measurement/soil-moisture/swm-5000 (accessed on 24 September 2024).
- Weik, M.H. Full-width at half-maximum. In Computer Science and Communications Dictionary; Springer: Boston, MA, USA, 2001; p. 661. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smogavec, P.; Pongrac, B.; Sarjaš, A.; Kafedziski, V.; Dončov, N.; Gleich, D. Comparative Study of GPR Acquisition Methods for Shallow Buried Object Detection. Remote Sens. 2024, 16, 3931. https://doi.org/10.3390/rs16213931
Smogavec P, Pongrac B, Sarjaš A, Kafedziski V, Dončov N, Gleich D. Comparative Study of GPR Acquisition Methods for Shallow Buried Object Detection. Remote Sensing. 2024; 16(21):3931. https://doi.org/10.3390/rs16213931
Chicago/Turabian StyleSmogavec, Primož, Blaž Pongrac, Andrej Sarjaš, Venceslav Kafedziski, Nabojša Dončov, and Dušan Gleich. 2024. "Comparative Study of GPR Acquisition Methods for Shallow Buried Object Detection" Remote Sensing 16, no. 21: 3931. https://doi.org/10.3390/rs16213931
APA StyleSmogavec, P., Pongrac, B., Sarjaš, A., Kafedziski, V., Dončov, N., & Gleich, D. (2024). Comparative Study of GPR Acquisition Methods for Shallow Buried Object Detection. Remote Sensing, 16(21), 3931. https://doi.org/10.3390/rs16213931










