A Novel ISAR Image Feature Suppression Method Based on Arbitrary Phase Encoding
Abstract
:1. Introduction
2. The Proposed Feature Suppression Method Using Arbitrary Phase Modulation
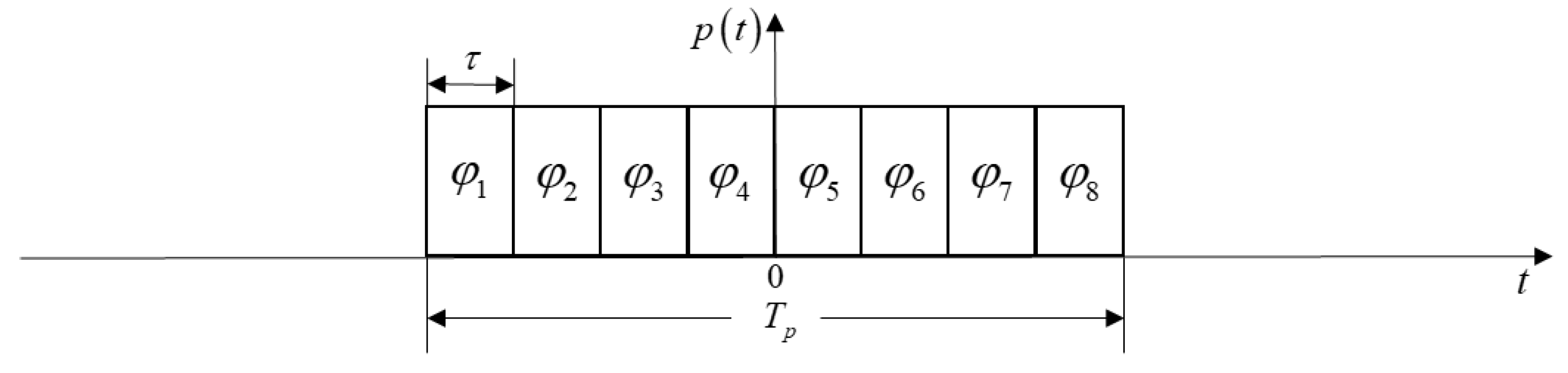
2.1. Signal Characteristic of Arbitrary Phase Modulation
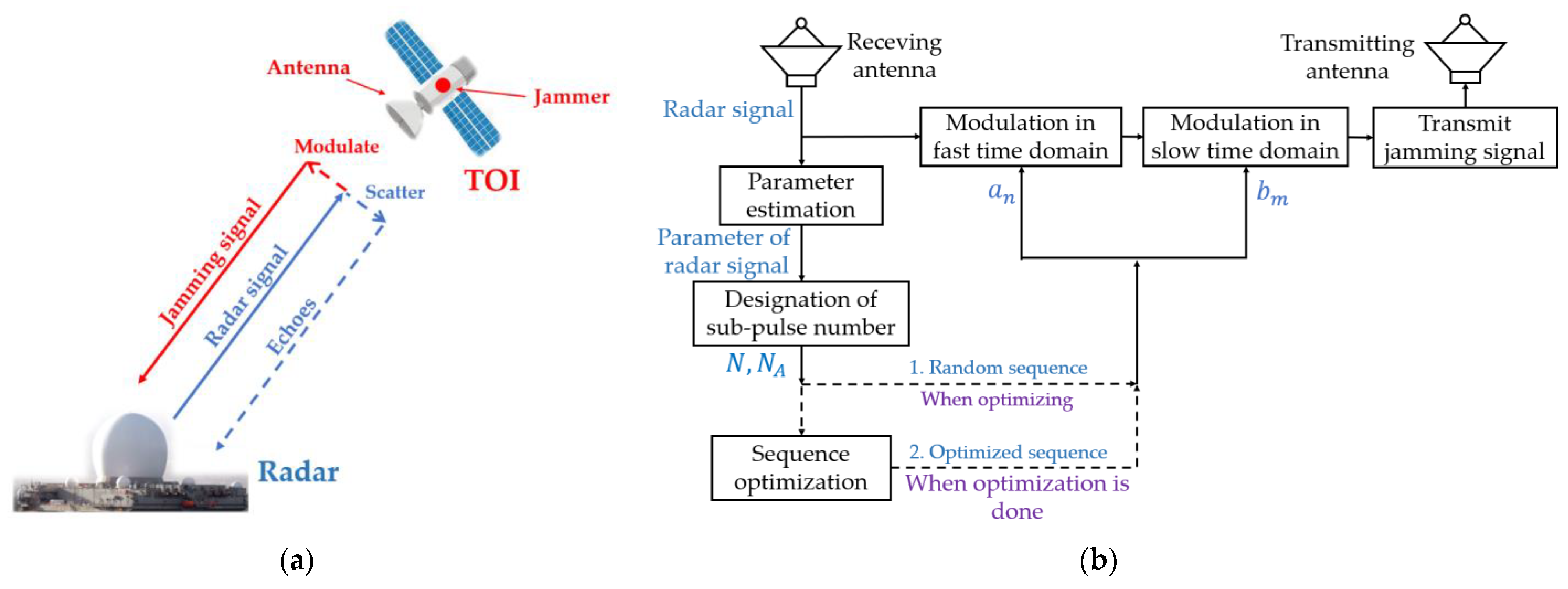
2.2. The Proposed Method
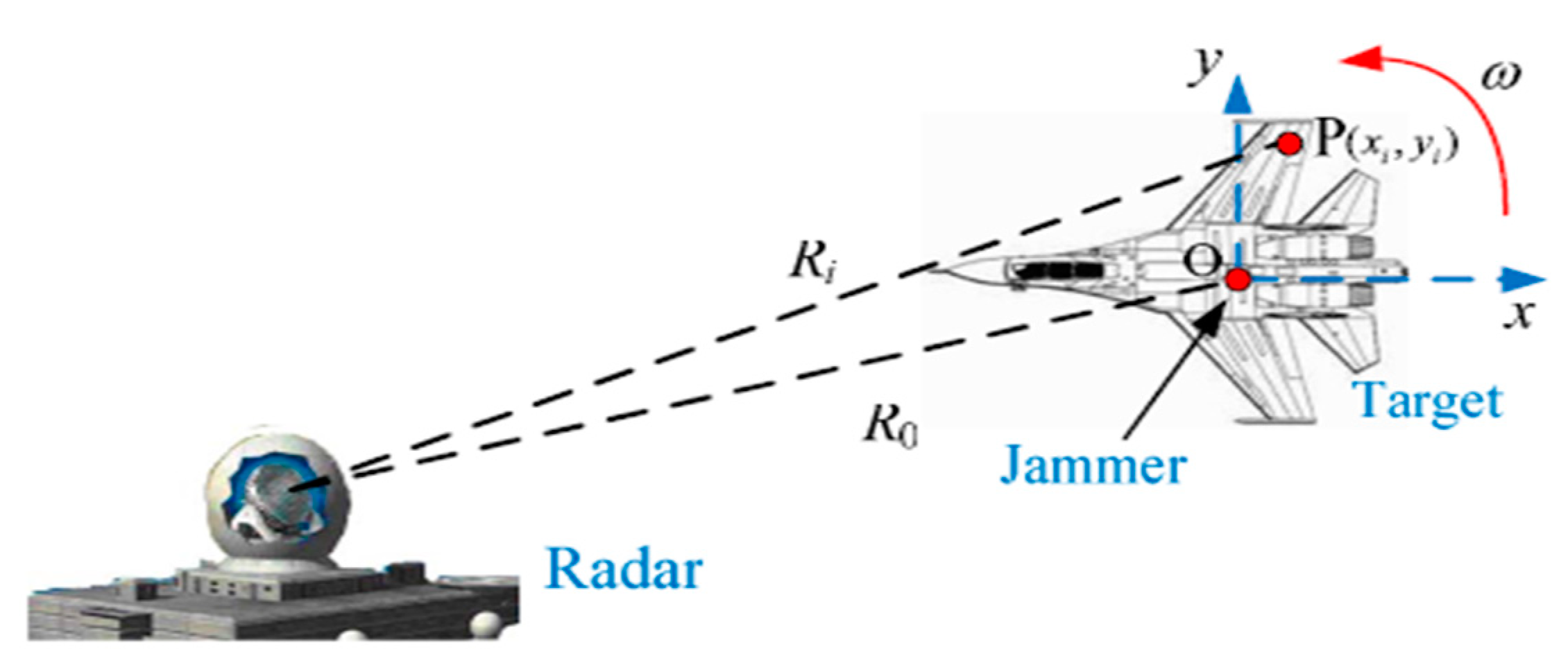
2.2.1. Feature Suppression Signal Model
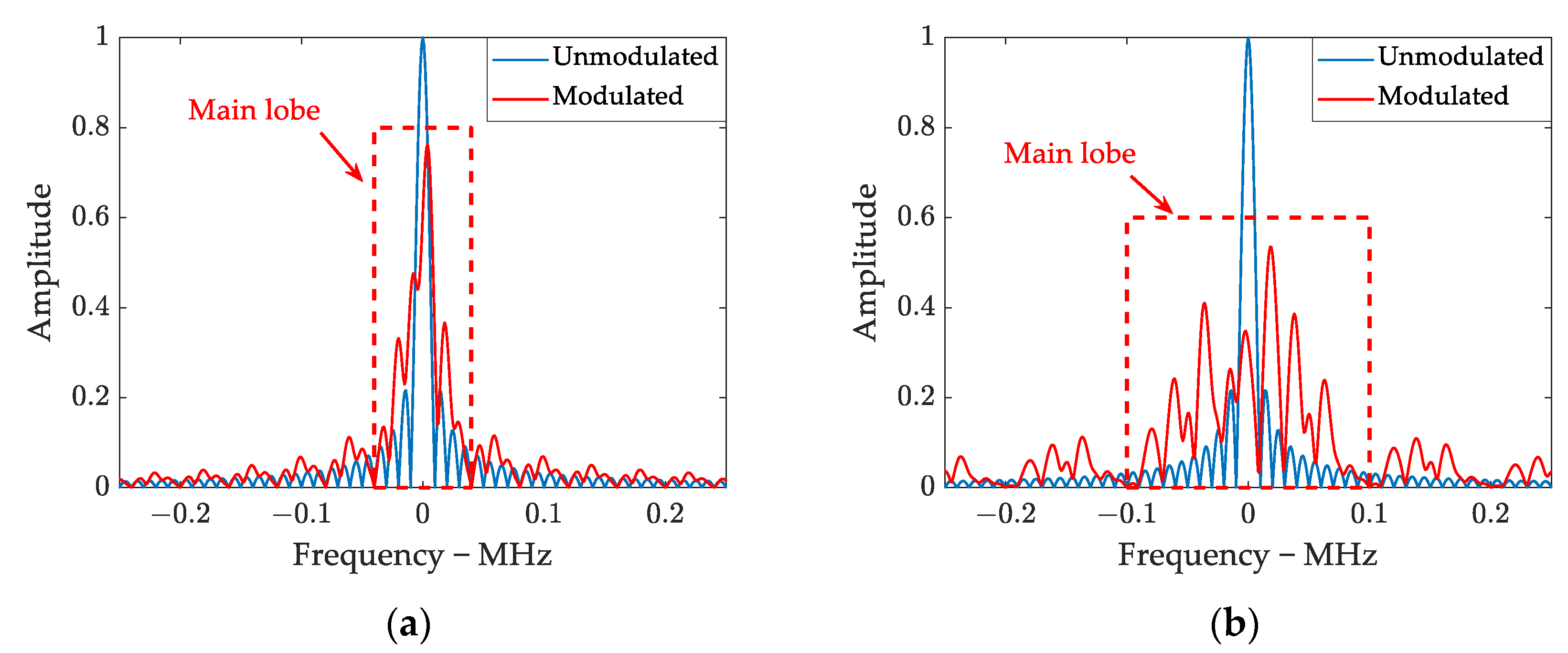
2.2.2. Property in the Range Direction
2.2.3. Property in the Azimuth Direction
2.2.4. The Flow Chart of the Proposed Method
3. Feature Suppression Performance Evaluation and Parameter Design
3.1. Performance Evaluation for Feature Suppression
3.1.1. Suppression Area
3.1.2. Image Entropy
3.1.3. Peak Jamming-to-Signal Ratio (PJSR)
3.2. Parameter Design and Optimization
3.2.1. Sub-Pulse Width Design
3.2.2. Phase Modulation Sequence Optimization
4. Simulation Result
4.1. Simulation Scene Description
4.2. Feature Suppression Performance Evaluation
4.2.1. Jamming Performance with Various Code Widths
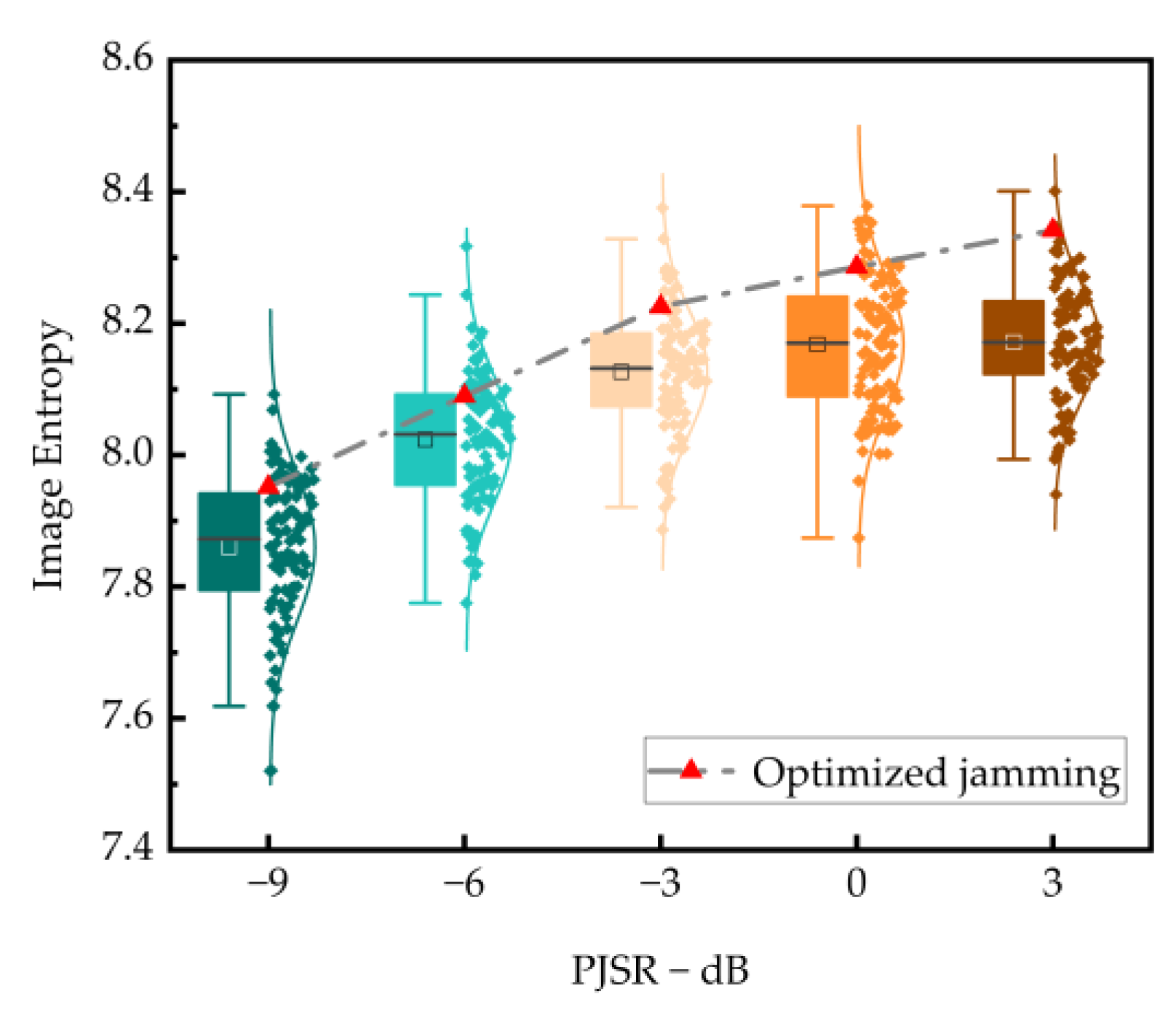
4.2.2. Jamming Performance with Various PJSR
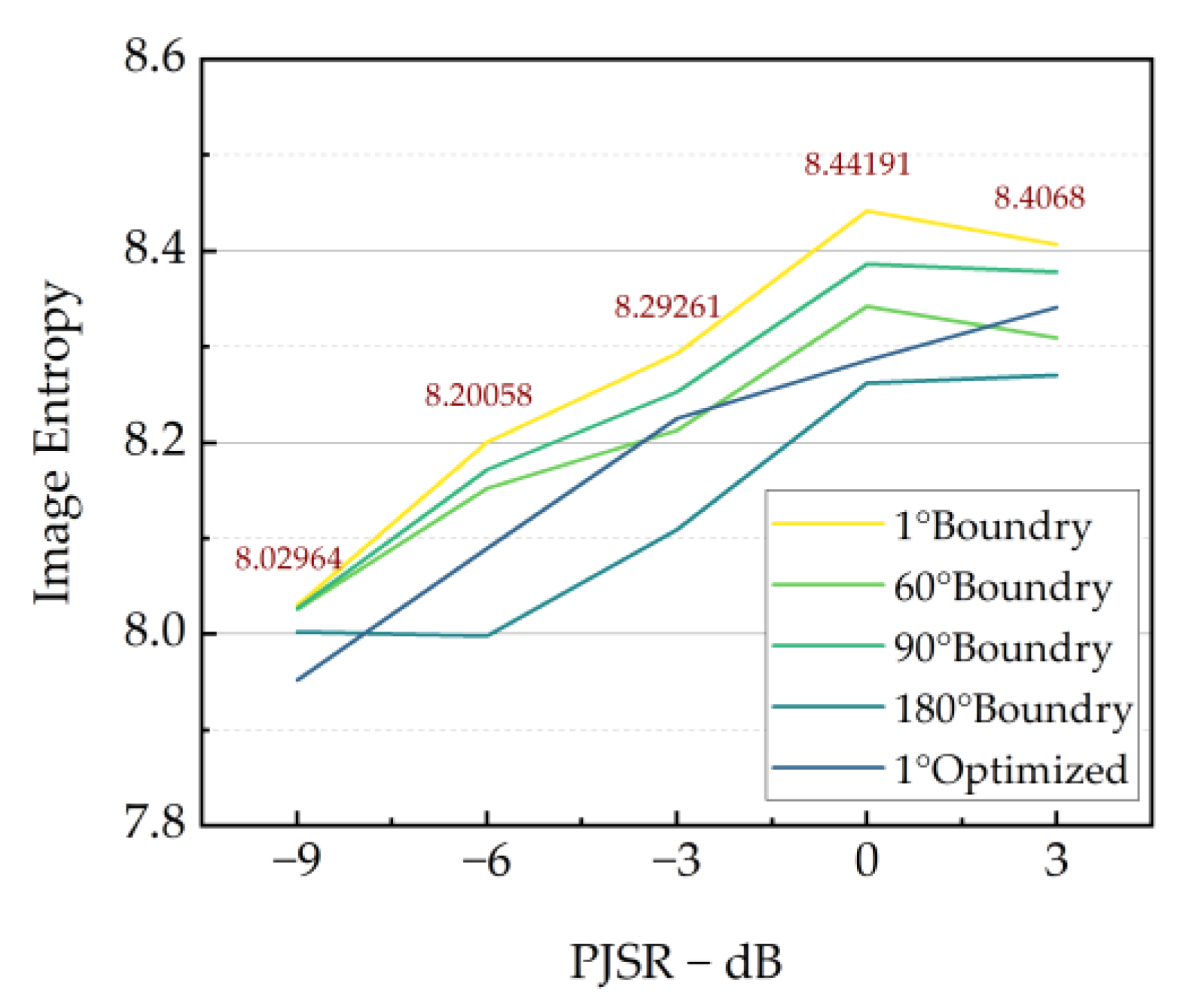
4.2.3. Analyses for Optimization of Coding Sequence
4.2.4. Comparison of the Proposed Method and Binary Phase Modulation
4.3. Comparison with Nonperiodic ISRJ
4.3.1. Experimental Settings
4.3.2. Analyses of Jamming Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, X.; Jin, G.; He, F.; Zhang, Y. A New Waveform Design Method for Multi-Target Inverse Synthetic Aperture Radar Imaging Based on Orthogonal Frequency Division Multiplexing Chirp. Remote Sens. 2024, 16, 308. [Google Scholar] [CrossRef]
- Anger, S.; Jirousek, M.; Dill, S.; Peichl, M. Inverse Synthetic Aperture Radar Imaging of Space Targets Using Wideband Pseudo-Noise Signals with Low Peak-to-Average Power Ratio. Remote Sens. 2024, 16, 1809. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Liu, B. Joint Customer Assignment, Power Allocation, and Subchannel Allocation in a UAV-Based Joint Radar and Communication Network. IEEE Internet Things J. 2024, 11, 29643–29660. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Chen, H.; Liu, W.; Zhu, Y.; Luo, J.; Ni, L. Interrupted-Sampling Repeater Jamming Countermeasure Based on Intrapulse Frequency–Coded Joint Frequency Modulation Slope Agile Waveform. Remote Sens. 2024, 16, 2810. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Fei, T. A robust joint frequency spectrum and power allocation strategy in a coexisting radar and communication system. Chin. J. Aeronaut. 2024, 37, 393–409. [Google Scholar] [CrossRef]
- Wang, J.; Feng, D.; Xu, Z.; Wu, Q.; Hu, W. Time-Domain Digital-Coding Active Frequency Selective Surface Absorber/Reflector and Its Imaging Characteristics. IEEE Trans. Antennas Propag. 2021, 69, 3322–3331. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Ming, F.; Sun, X.; Hong, J. A Controllable Suppression Jamming Method against SAR Based on Active Radar Transponder. Remote Sens. 2022, 14, 3949. [Google Scholar] [CrossRef]
- Song, C.; Wang, Y.; Jin, G.; Wang, Y.; Dong, Q.; Wang, B.; Zhou, L.; Lu, P.; Wu, Y. A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sens. 2022, 14, 5370. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Z.; Liu, X.; Zhao, T.; Wang, Y.; Zhao, F. Synthetic Aperture Radar Image Transform Using Periodic-Coded Phase Modulation. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4013505. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Chen, H. ISAR Interference Method Based on Sinusoidal Phase Modulation. Signal Process. 2007, 23, 101–105. (In Chinese) [Google Scholar]
- Jiang, J.; Wu, Y.; Wang, H.; Lv, Y.; Qiu, L.; Yu, D. Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization. Electronics 2019, 8, 160. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, J.; Pu, J.; Wu, Y.; Ran, D. Low Sidelobe Multi-phase Segmented Modulation Interference Method Based on Cosine Amplitude Weighting. J. Syst. Eng. Electron. 2021, 43, 3185–3193. (In Chinese) [Google Scholar]
- Sun, J.; Wang, C.; Shi, Q.; Ren, W.; Yao, Z.; Yuan, N. Intelligent Optimization of Phase Modulation Waveform Based on Genetic Algorithm. J. Syst. Eng. Electron. 2022, 33, 916–923. (In Chinese) [Google Scholar] [CrossRef]
- Xu, H.; Quan, Y.; Zhou, X.; Chen, H.; Cui, T.J. A Novel Approach for Radar Passive Jamming Based on Multiphase Coding Rapid Modulation. IEEE Trans. Geosci. Remote Sensing. 2023, 61, 5101614. [Google Scholar] [CrossRef]
- Wang, J.; Feng, D.; Zhang, R.; Xu, L.; Hu, W. An Inverse Synthetic Aperture Radar Image Modulation Method Based on Coding Phase-Switched Screen. IEEE Sens. J. 2019, 19, 7915–7922. [Google Scholar] [CrossRef]
- Lang, W.; Mei, S.; Liu, Y.; Zhou, F.; Yang, X. A Periodic Multiple Phases Modulation Active Deception Jamming for Multistatic Radar System. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3435–3451. [Google Scholar] [CrossRef]
- Yu, D.; Wu, Y.; Wang, H.; Jia, X. Study on Multi-phase Segmented Modulation Interference Method for Inverse Synthetic Aperture Radar. J. Electron. Inf. Technol. 2017, 39, 423–429. (In Chinese) [Google Scholar]
- Shi, Q. Research on ISAR Interference Technology Based on Phase Modulation. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2019. (In Chinese). [Google Scholar]
- Li, S.; Wang, J.; Fang, X.; Lu, G.; Li, M.; Chen, W.; Chen, C. Jamming of ISAR Imaging With Time-Modulated Metasurface Partially Covered on Targets. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 372–376. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Xu, Z.; Zhao, F.; Gu, Z.; Xiao, S. Flexible blanket synthetic aperture radar jamming using joint frequency and phase modulation. IET Radar Sonar Navig. 2023, 17, 1129–1141. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, F.; Wang, J.; Xu, Z.; Xiao, S. ISAR image feature control method based on phase coded modulation. Syst. Eng. Electron. 2023, 45, 1000–1007. (In Chinese) [Google Scholar]
- Wu, Q.; Zhao, F.; Ai, X.; Liu, X.; Xiao, S. Two-Dimensional Blanket Jamming Against ISAR Using Nonperiodic ISRJ. IEEE Sens. J. 2019, 19, 4031–4038. [Google Scholar] [CrossRef]
- Cao, P.; Xing, M.; Sun, G.; Li, Y.; Bao, Z. Minimum Entropy via Subspace for ISAR Autofocus. IEEE Geosci. Remote Sens. Lett. 2010, 7, 205–209. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]








| Parameter | Method | |
|---|---|---|
| APE | ISRJ | |
| coding number in range direction | 64 | 64 |
| coding number in azimuth direction | 80 | 80 |
| modulation sequence | random multi-valued sequence | random binary sequence |
| minimum modulation phase | 1° | - |
| duty cycle | - | 0.5 (in range direction) 0.5 (in azimuth direction) |
| object of modulation | phase | amplitude |
| number of simulations | 100 | 100 |
| Setting | PJSR (dB) | Output JSR (dB) | Image Entropy | ||
|---|---|---|---|---|---|
| APE | ISRJ | APE | ISRJ | ||
| scene1 | 3 | 12.55 | −52.23 | 8.1520 | 6.8859 |
| scene2 | −3 | 6.62 | −52.69 | 8.1241 | 6.8876 |
| scene3 | −9 | 0.99 | −53.57 | 7.8802 | 6.8886 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, Q.; Liu, X.; Xu, Z.; Zhao, F.; Xiao, S. A Novel ISAR Image Feature Suppression Method Based on Arbitrary Phase Encoding. Remote Sens. 2024, 16, 3960. https://doi.org/10.3390/rs16213960
Wang Y, Wu Q, Liu X, Xu Z, Zhao F, Xiao S. A Novel ISAR Image Feature Suppression Method Based on Arbitrary Phase Encoding. Remote Sensing. 2024; 16(21):3960. https://doi.org/10.3390/rs16213960
Chicago/Turabian StyleWang, Yanfeng, Qihua Wu, Xiaobin Liu, Zhiming Xu, Feng Zhao, and Shunping Xiao. 2024. "A Novel ISAR Image Feature Suppression Method Based on Arbitrary Phase Encoding" Remote Sensing 16, no. 21: 3960. https://doi.org/10.3390/rs16213960
APA StyleWang, Y., Wu, Q., Liu, X., Xu, Z., Zhao, F., & Xiao, S. (2024). A Novel ISAR Image Feature Suppression Method Based on Arbitrary Phase Encoding. Remote Sensing, 16(21), 3960. https://doi.org/10.3390/rs16213960







