Three-Dimensional Reconstruction of Retaining Structure Defects from Crosshole Ground Penetrating Radar Data Using a Generative Adversarial Network
Abstract
:1. Introduction
2. Methodology
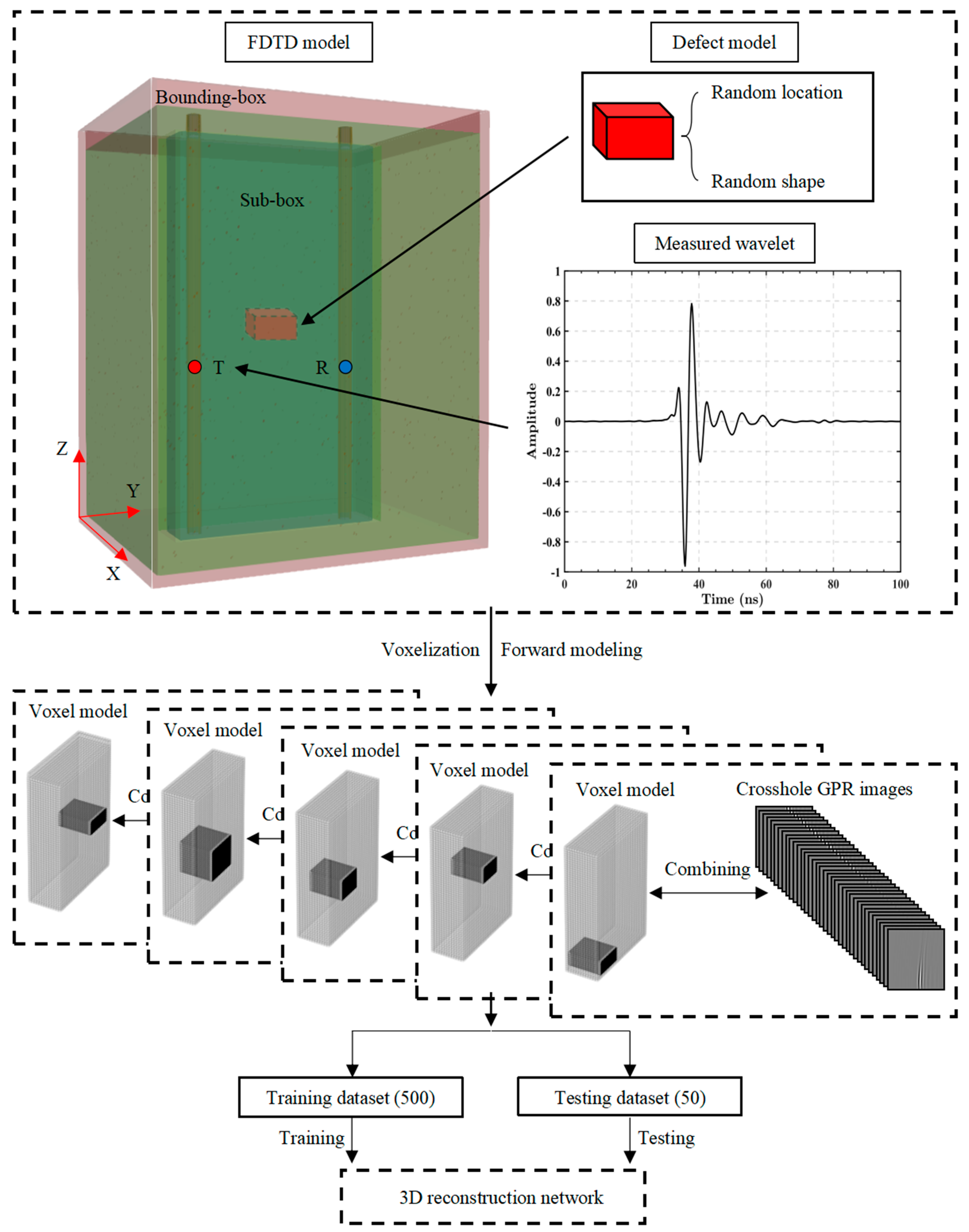
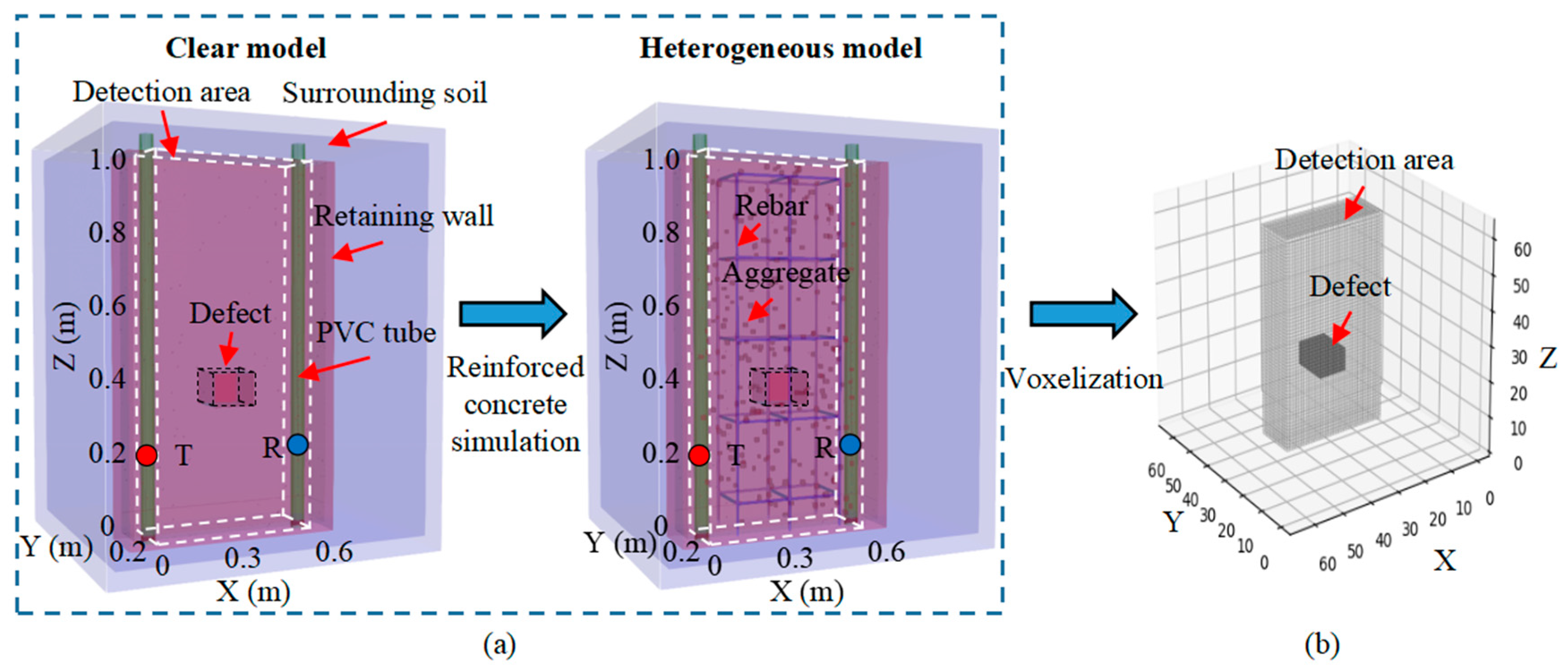
2.1. Crosshole GPR Measurement
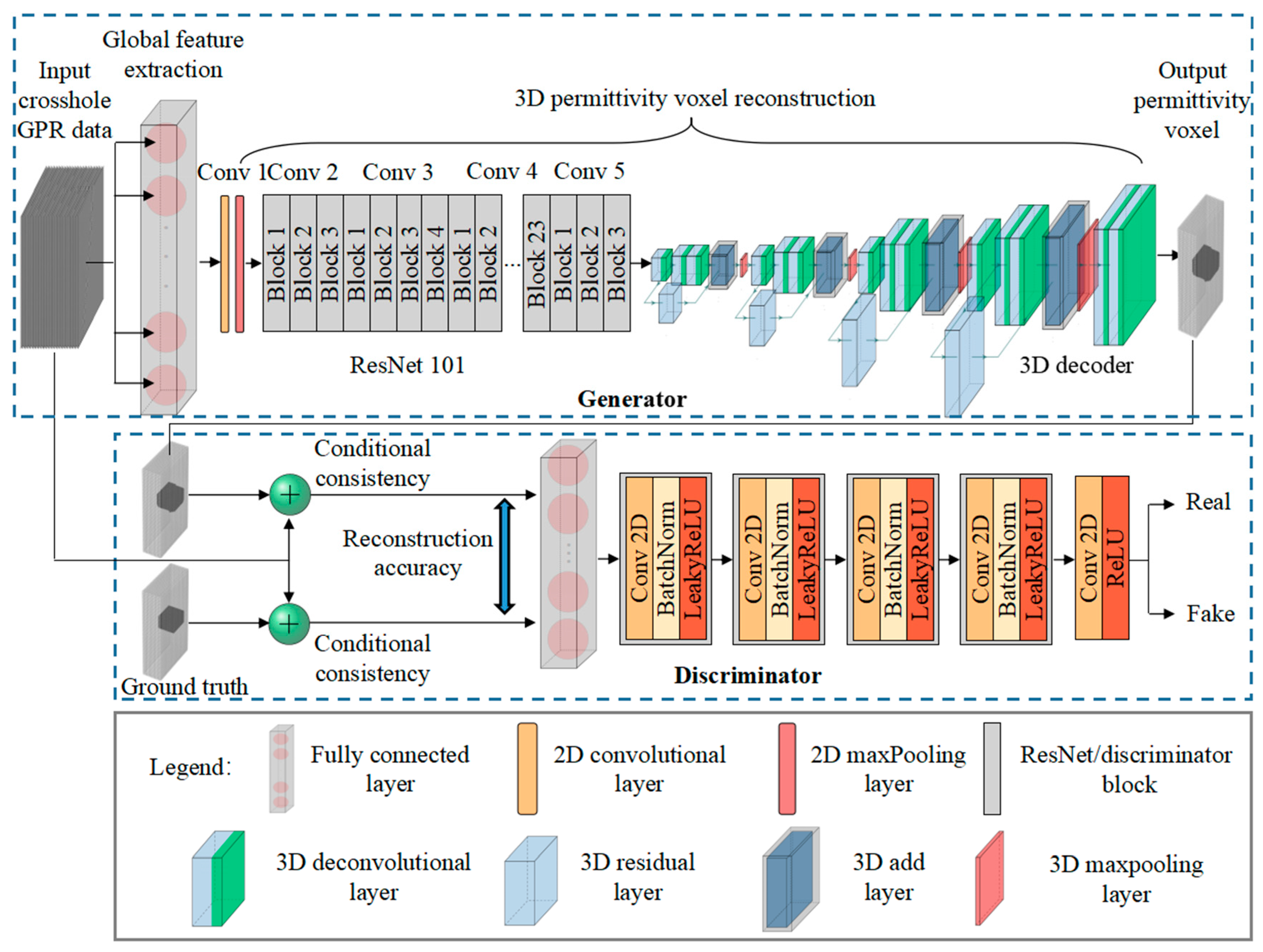
2.2. 3D Reconstruction Network
2.2.1. Global Feature Extraction
2.2.2. 3D Permittivity Voxel Reconstruction
2.2.3. Discriminator
2.2.4. Loss Function
3. Network Training and Testing
3.1. Training Dataset
3.2. Evaluation Metrics
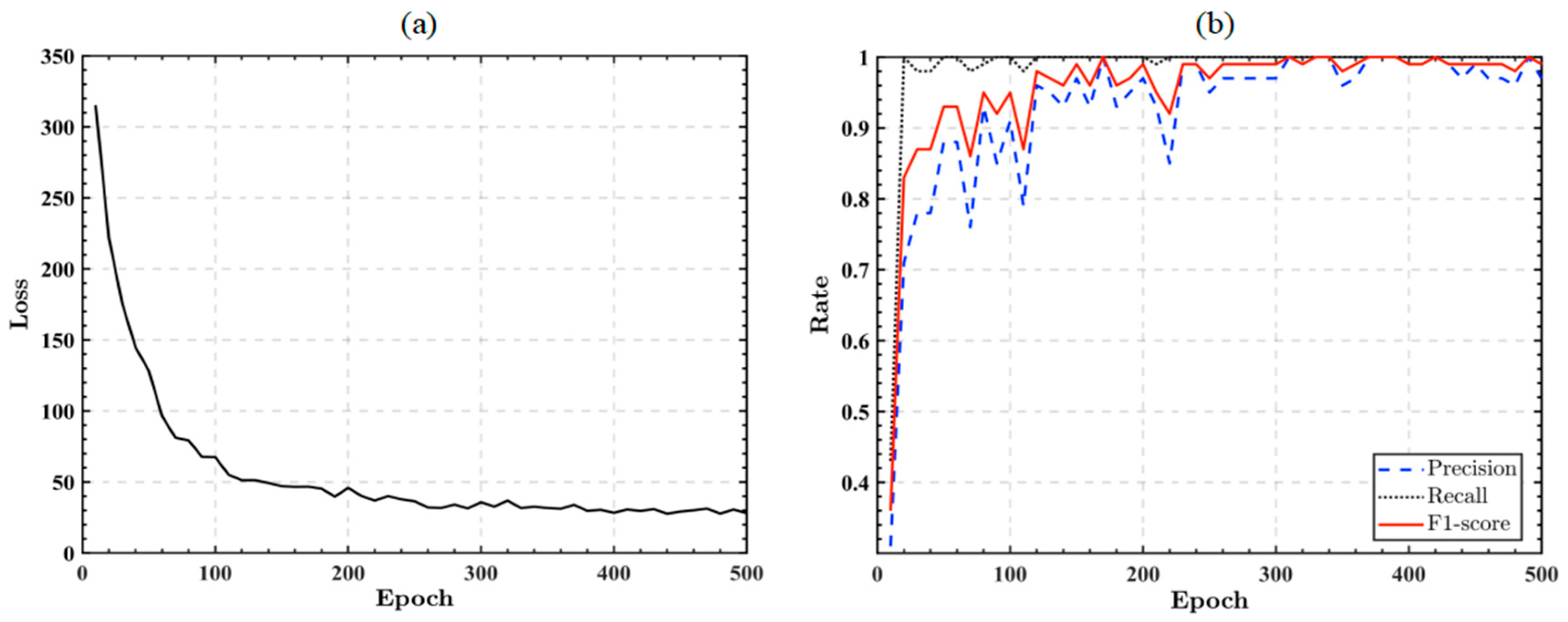
3.3. Network Training
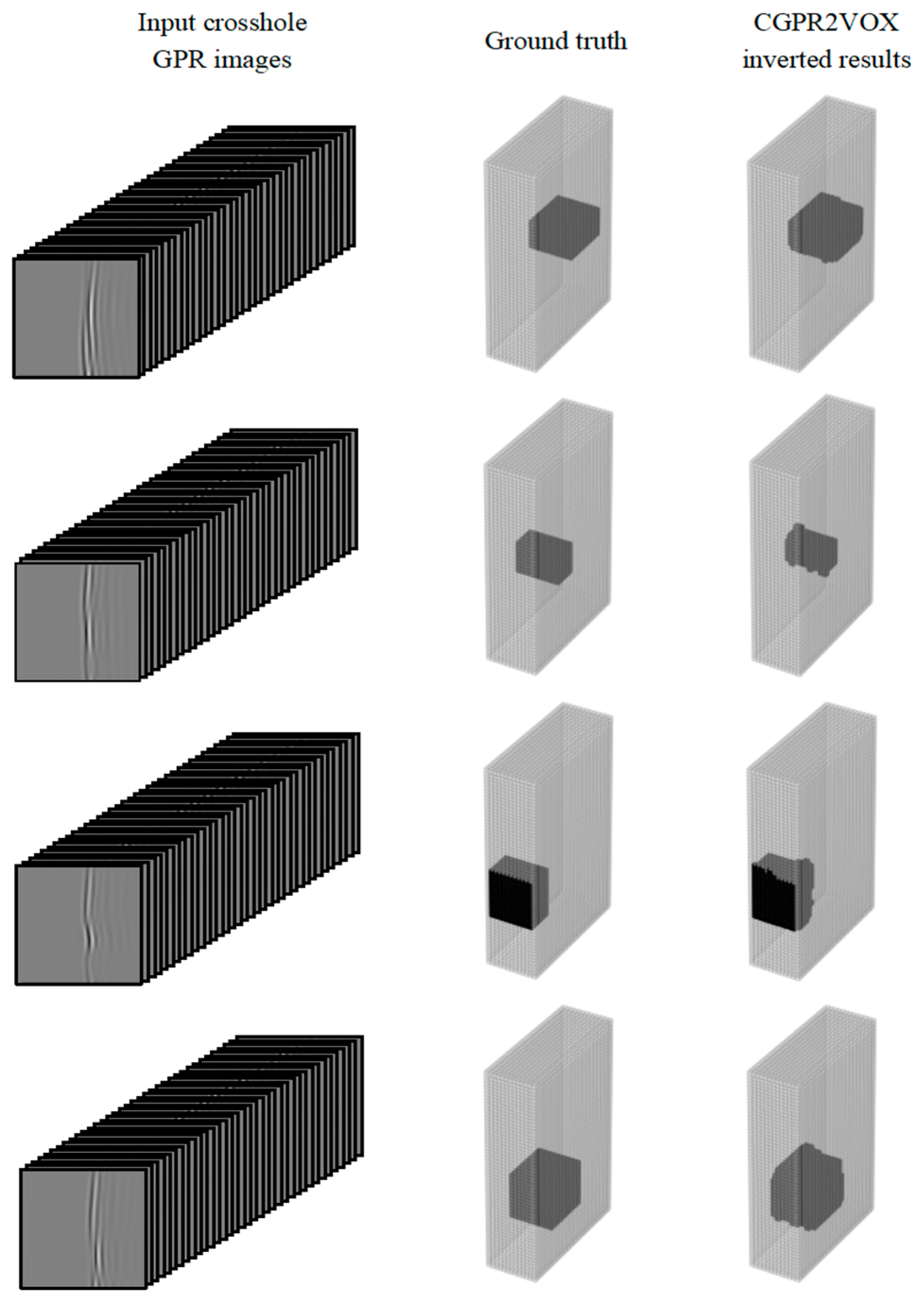
3.4. Reconstruction Accuracy
3.5. Generalization Ability
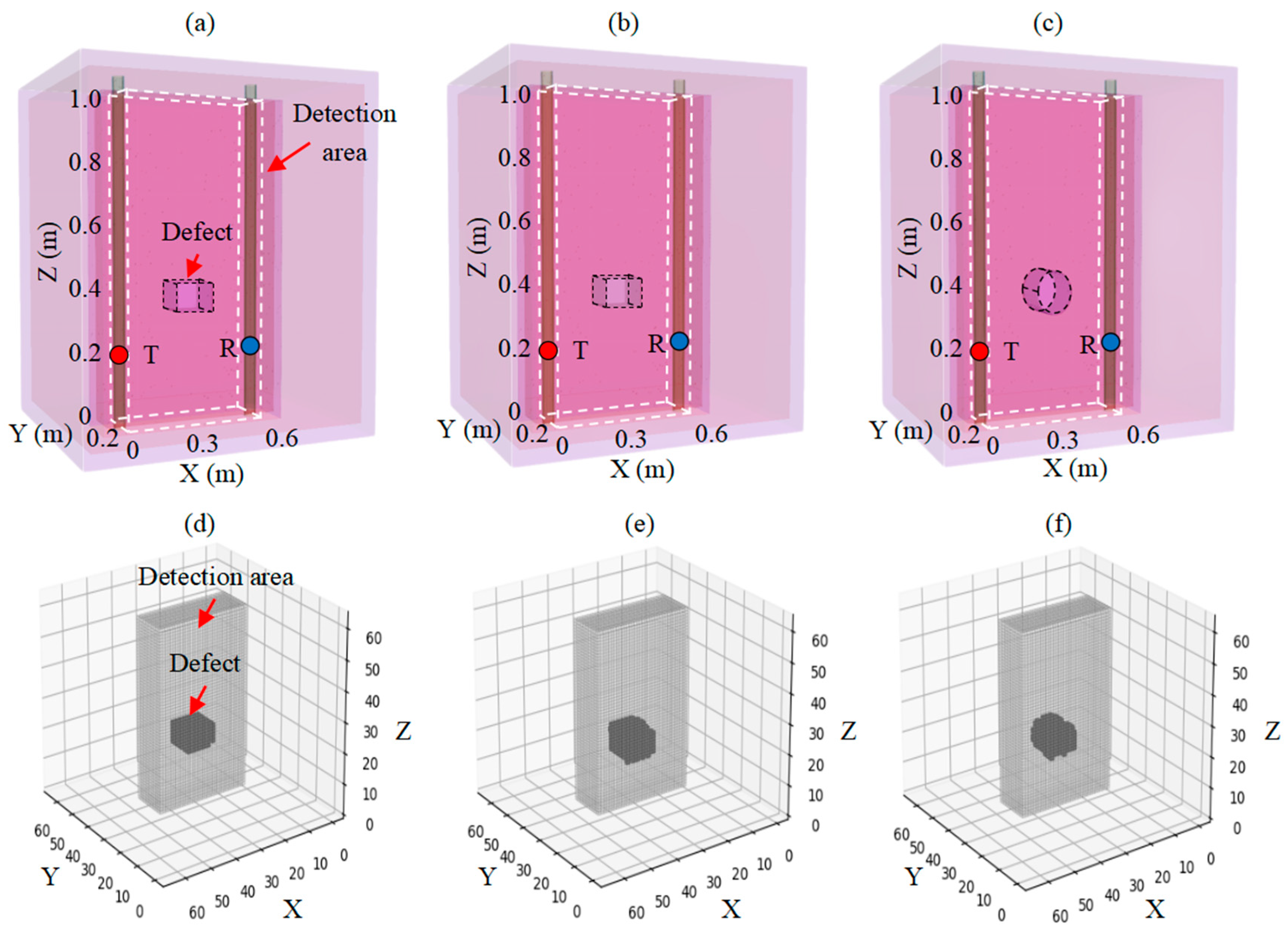
3.5.1. Defect Condition Variations
3.5.2. Heterogeneous Materials and Noise
4. Model Experiment
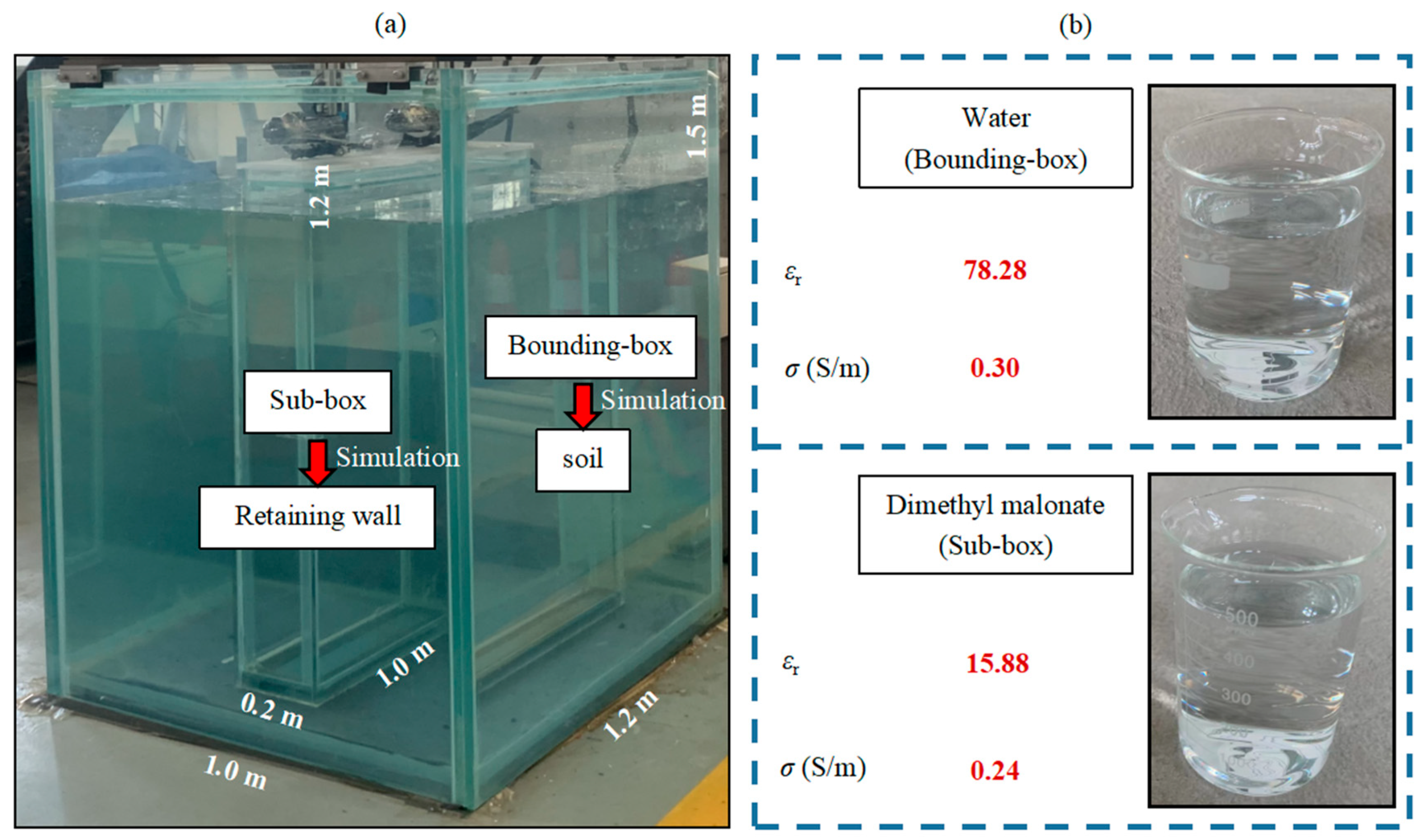
4.1. Experiment System
4.1.1. Crosshole GPR System
4.1.2. Experiment Model Box
4.2. Data Acquisition
4.3. Experiment Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhai, J.; Wang, Q.; Xie, X.; Qin, H.; Zhu, T.; Jiang, Y.; Ding, H. A New Method for 3D Detection of Defects in Diaphragm Walls during Deep Excavations Using Cross-Hole Sonic Logging and Ground-Penetrating Radar. J. Perform. Constr. Facil. 2023, 37, 4022065. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hu, J.; Pan, W.; Long, Y.; Cao, A.; Li, H.; Sun, Y. Mechanism of Detecting the Construction Quality of a Diaphragm Wall by an Infrared Thermal Field and Engineering Application. Materials 2023, 16, 1052. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Shao, Y.; Zhang, Y. Leakage Detection and Long-Term Monitoring in Diaphragm Wall Joints Using Fiber Bragg Grating Sensing Technology. Tunn. Undergr. Space Technol. 2020, 98, 103331. [Google Scholar] [CrossRef]
- Keskinen, J.; Looms, M.C.; Klotzsche, A.; Nielsen, L. Practical Data Acquisition Strategy for Time-Lapse Experiments Using Crosshole GPR and Full-Waveform Inversion. J. Appl. Geophys. 2021, 191, 104362. [Google Scholar] [CrossRef]
- Wang, S.; Han, L.; Gong, X.; Zhang, S.; Huang, X.; Zhang, P. Full-Waveform Inversion of Time-Lapse Crosshole GPR Data Using Markov Chain Monte Carlo Method. Remote Sens. 2021, 13, 4530. [Google Scholar] [CrossRef]
- Svendsen, E.B.; Nielsen, L.; Nilsson, B.; Kjær, K.H.; Looms, M.C. Crosshole Ground-Penetrating Radar in Clay-Rich Quaternary Deposits: Towards Characterization of High-Loss Media. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025909. [Google Scholar] [CrossRef]
- Wang, S.; Han, L.; Gong, X.; Zhang, S.; Huang, X.; Zhang, P. MCMC Method of Inverse Problems Using a Neural Network—Application in GPR Crosshole Full Waveform Inversion: A Numerical Simulation Study. Remote Sens. 2022, 14, 1320. [Google Scholar] [CrossRef]
- Klotzsche, A.; Vereecken, H.; van der Kruk, J. Review of Crosshole Ground-Penetrating Radar Full-Waveform Inversion of Experimental Data: Recent Developments, Challenges, and Pitfalls. Geophysics 2019, 84, H13–H28. [Google Scholar] [CrossRef]
- Pereira, M.; Burns, D.; Orfeo, D.; Zhang, Y.; Jiao, L.; Huston, D.; Xia, T. 3-D Multistatic Ground Penetrating Radar Imaging for Augmented Reality Visualization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5666–5675. [Google Scholar] [CrossRef]
- van der Kruk, J.; Liu, T.; Mozaffari, A.; Gueting, N.; Klotzsche, A.; Vereecken, H.; Warren, C.; Giannopoulos, A. GPR Full-Waveform Inversion, Recent Developments, and Future Opportunities. In Proceedings of the IEEE 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–6. [Google Scholar]
- Gueting, N.; Vienken, T.; Klotzsche, A.; van der Kruk, J.; Vanderborght, J.; Caers, J.; Vereecken, H.; Englert, A. High Resolution Aquifer Characterization Using Crosshole GPR Full-Waveform Tomography: Comparison with Direct-Push and Tracer Test Data. Water Resour. Res. 2017, 53, 49–72. [Google Scholar] [CrossRef]
- Mozaffari, A.; Klotzsche, A.; He, G.; Vereecken, H.; van der Kruk, J.; Warren, C.; Giannopoulos, A. Towards 3D Full-Waveform Inversion of Crosshole GPR Data. In Proceedings of the IEEE 2016 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; pp. 1–4. [Google Scholar]
- Ernst, J.R.; Green, A.G.; Maurer, H.; Holliger, K. Application of a New 2D Time-Domain Full-Waveform Inversion Scheme to Crosshole Radar Data. Geophysics 2007, 72, J53–J64. [Google Scholar] [CrossRef]
- Busch, S.; van der Kruk, J.; Bikowski, J.; Vereecken, H. Quantitative Conductivity and Permittivity Estimation Using Full-Waveform Inversion of on-Ground GPR Data. Geophysics 2012, 77, H79–H91. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, J.; Liu, D.; Li, Z.; Yong, P.; Yang, Z. 3D Variable-Grid Full-Waveform Inversion on GPU. Pet. Sci. 2019, 16, 1001–1014. [Google Scholar] [CrossRef]
- Deng, J.; Rogez, Y.; Zhu, P.; Herique, A.; Jiang, J.; Kofman, W. 3D Time-Domain Electromagnetic Full Waveform Inversion in Debye Dispersive Medium Accelerated by Multi-GPU Paralleling. Comput. Phys. Commun. 2021, 265, 108002. [Google Scholar] [CrossRef]
- Mozaffari, A.; Klotzsche, A.; Warren, C.; He, G.; Giannopoulos, A.; Vereecken, H.; van der Kruk, J. 2.5 D Crosshole GPR Full-Waveform Inversion with Synthetic and Measured Data. Geophysics 2020, 85, H71–H82. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, B.; Wang, J.; Li, Y.; Nie, L.; Wang, Z.; Zhang, C. Two-Dimensional Time-Domain Full Waveform Inversion of on-Ground Common-Offset GPR Data Based on Integral Preprocessing. J. Environ. Eng. Geophys. 2020, 25, 369–380. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Tjoa, E.; Guan, C. A Survey on Explainable Artificial Intelligence (XAI): Toward Medical (XAI). IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4793–4813. [Google Scholar] [CrossRef]
- Yue, G.H.; Liu, C.L.; Li, Y.S.; Du, Y.C.; Guo, S.L. GPR Data Augmentation Methods by Incorporating Domain Knowledge. Appl. Sci. 2022, 12, 10896. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine Learning and Deep Learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Laloy, E.; Linde, N.; Jacques, D. Approaching Geoscientific Inverse Problems with Vector-to-Image Domain Transfer Networks. Adv. Water Resour. 2021, 152, 103917. [Google Scholar] [CrossRef]
- Laloy, E.; Linde, N.; Ruffino, C.; Hérault, R.; Gasso, G.; Jacques, D. Gradient-Based Deterministic Inversion of Geophysical Data with Generative Adversarial Networks: Is It Feasible? Comput. Geosci. 2019, 133, 104333. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Z.; Qin, H.; Geng, T.; Pan, S. GAN-Based Inversion of Crosshole GPR Data to Characterize Subsurface Structures. Remote Sens. 2023, 15, 3650. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR2017), Honolulu, HI, USA, 22–25 July 2017; pp. 5967–5976. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015, Proceedings, Part III 18; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Saad, O.M.; Fomel, S.; Abma, R.; Chen, Y. Unsupervised Deep Learning for 3D Interpolation of Highly Incomplete. Geophysics 2023, 88, WA189–WA200. [Google Scholar] [CrossRef]
- Guo, P.; Visser, G.; Saygin, E. Bayesian Trans-Dimensional Full Waveform Inversion: Synthetic and Field Application. Geophys. J. Int. 2020, 222, 610–627. [Google Scholar] [CrossRef]
- Klotzsche, A.; Vereecken, H.; van der Kruk, J. GPR Full-Waveform Inversion of a Variably Saturated Soil-Aquifer System. J. Appl. Geophys. 2019, 170, 103823. [Google Scholar] [CrossRef]
- Feng, X.; Ren, Q.; Liu, C.; Zhang, X. Joint Acoustic Full-Waveform Inversion of Crosshole Seismic and ground-Penetrating Radar Data in the Frequency Domain. Geophysics 2017, 82, H41–H56. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Qin, H.; Xie, X.; Vrugt, J.A.; Zeng, K.; Hong, G. Underground Structure Defect Detection and Reconstruction Using Crosshole GPR and Bayesian Inversion. Autom. Constr. 2016, 68, 156–169. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. Adv. Neural Inf. Process Syst. 2014, 27, 2672–2680. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Hodson, T.O.; Over, T.M.; Foks, S.S. Mean Squared Error, Deconstructed. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002681. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. GprMax: Open Source Software to Simulate Electromagnetic Wave Propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Lin, D. An Information-Theoretic Definition of Similarity. In Proceedings of the Fifteenth International Conference on Machine Learning (ICML’98), Madison, WI, USA, 24–27 July 1998; pp. 296–304. [Google Scholar]
- Deka, B.; Deka, D. An Improved Multiscale Distribution Entropy for Analyzing Complexity Of-World Signals. Chaos Solitons Fractals 2022, 158, 112101. [Google Scholar] [CrossRef]
- Hunziker, J.; Laloy, E.; Linde, N. Bayesian Full-Waveform Tomography with Application to Crosshole Ground Radar Data. Geophys. J. Int. 2019, 218, 913–931. [Google Scholar] [CrossRef]
- Dines, K.A.; Lytle, R.J. Computerized Geophysical Tomography. Proc. IEEE 1979, 67, 1065–1073. [Google Scholar] [CrossRef]






| Evaluation Index | Value | |
|---|---|---|
| Precision | 91.43% | |
| Recall | 96.97% | |
| F1-score | 94.12% | |
| Mean position error | X-direction | 0.86 cm (0.80%) |
| Y-direction | 0.10 cm (0.09%) | |
| Z-direction | 1.37 cm (1.28%) | |
| Mean processing time | 3.70 s | |
| Mean number of artifacts | 0.08 | |
| Condition | Position Error | ||
|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | |
| Training dataset | 0.75 cm (1.25%) | 0.16 cm (0.78%) | 0.47 cm (0.47%) |
| Permittivity deviation | 0.86 cm (1.42%) | 0.55 cm (2.73%) | 1.28 cm (1.28%) |
| Defect deformation | 1.09 cm (1.81%) | 0.31 cm (1.56%) | 0.52 cm (0.52%) |
| Experimental Parameter | Value |
|---|---|
| Antenna center frequency | 0.78 GHz |
| Frequence-scanning range | 0.65–1.20 GHz |
| Time window | 100 ns |
| Sampling points for each A-scan | 1024 |
| Number of transmitting/receiving points | 36 |
| Number of measuring lines | 1296 |
| Transmitting/receiving interval | 2.86 cm |
| Method | Position Error | Number of Artifacts | Processing Time | ||
|---|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | |||
| Proposed method | 1.02 cm (1.71%) | 0.26 cm (1.32%) | 1.30 cm (1.30%) | 0 | 3.73 s |
| Ray-based tomography | 6.71 cm (11.18%) | - | 3.27 cm (3.27%) | 3 | 4.59 s |
| FWI | 13.87 cm (23.11%) | 0.84 cm (4.18%) | 4.26 cm (4.26%) | 1 | 13.05 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, Z.; Tang, Y.; Pan, S.; Pan, T. Three-Dimensional Reconstruction of Retaining Structure Defects from Crosshole Ground Penetrating Radar Data Using a Generative Adversarial Network. Remote Sens. 2024, 16, 3995. https://doi.org/10.3390/rs16213995
Zhang D, Wang Z, Tang Y, Pan S, Pan T. Three-Dimensional Reconstruction of Retaining Structure Defects from Crosshole Ground Penetrating Radar Data Using a Generative Adversarial Network. Remote Sensing. 2024; 16(21):3995. https://doi.org/10.3390/rs16213995
Chicago/Turabian StyleZhang, Donghao, Zhengzheng Wang, Yu Tang, Shengshan Pan, and Tianming Pan. 2024. "Three-Dimensional Reconstruction of Retaining Structure Defects from Crosshole Ground Penetrating Radar Data Using a Generative Adversarial Network" Remote Sensing 16, no. 21: 3995. https://doi.org/10.3390/rs16213995
APA StyleZhang, D., Wang, Z., Tang, Y., Pan, S., & Pan, T. (2024). Three-Dimensional Reconstruction of Retaining Structure Defects from Crosshole Ground Penetrating Radar Data Using a Generative Adversarial Network. Remote Sensing, 16(21), 3995. https://doi.org/10.3390/rs16213995











