Analysis of Multi-GNSS Multipath for Parameter-Unified Autocorrelation-Based Mitigation and the Impact of Constellation Shifts
Abstract
:1. Introduction
2. Multipath Modelling and Mathematic Tools for Analysis
2.1. Multipath Models
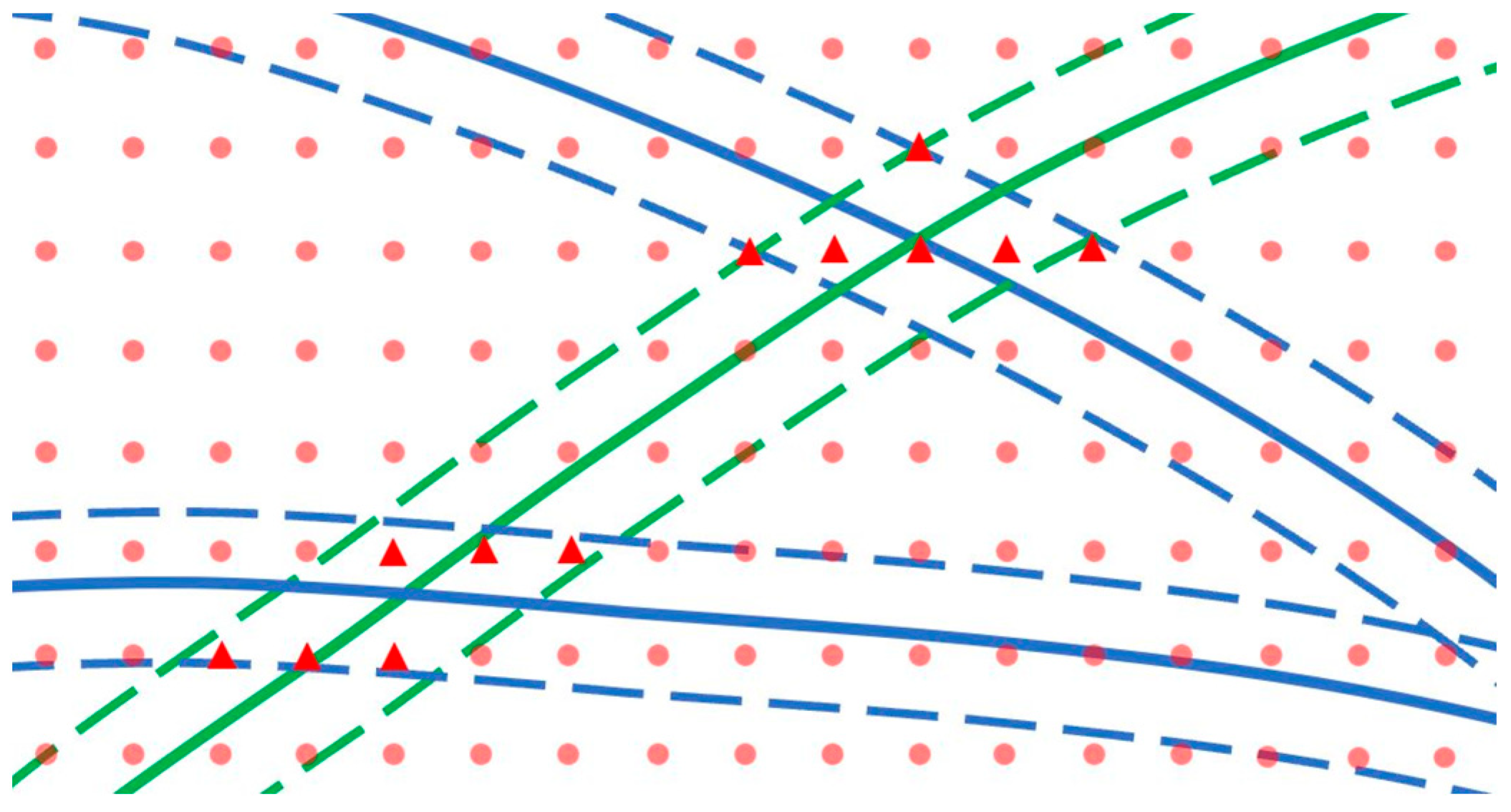
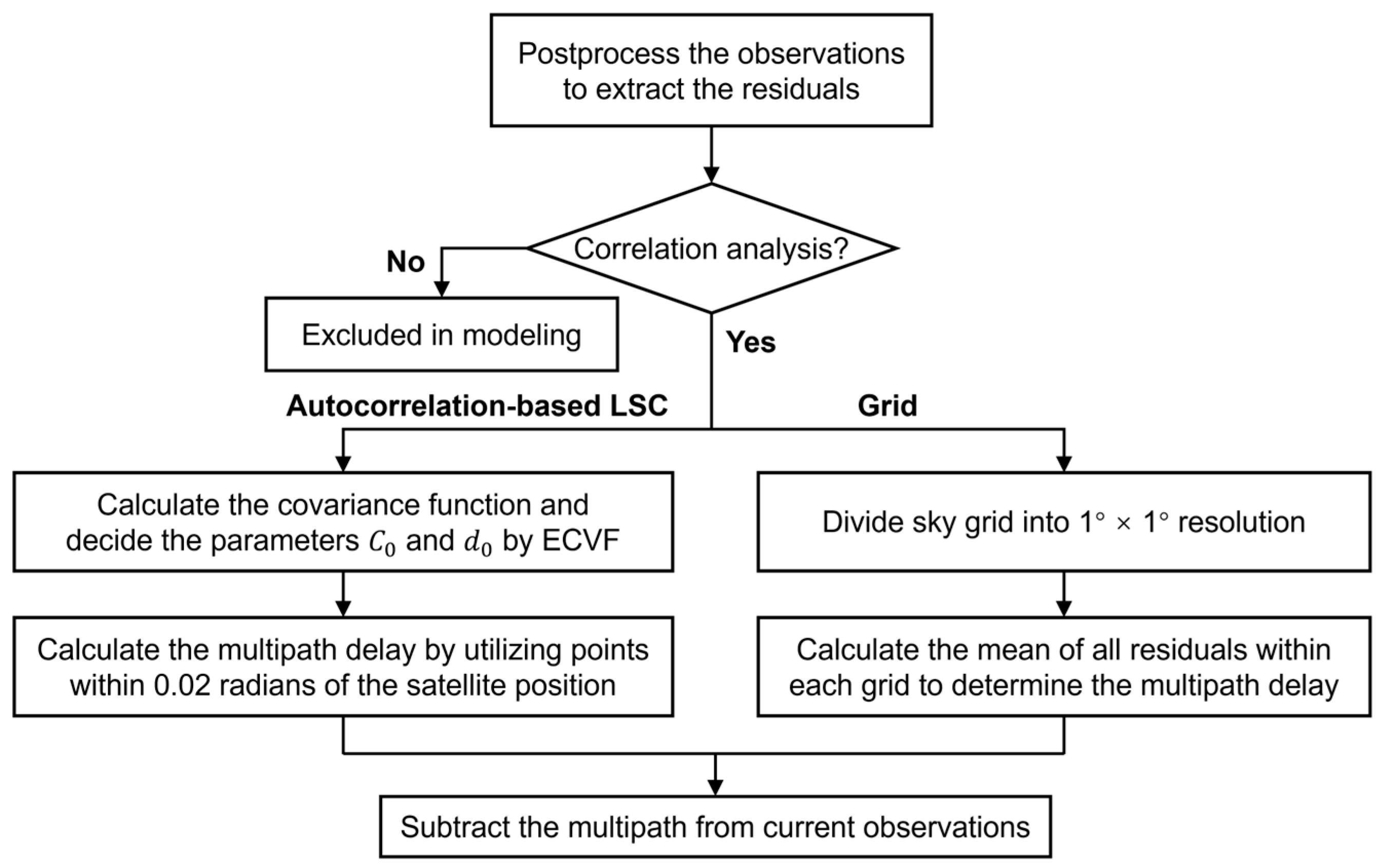
2.2. Interpolation with Grid Method
2.3. Interpolation with Moving-Neighborhood LSC
2.4. Covariance Function
2.5. Correlation
3. Computation and Analysis
3.1. Employed Data
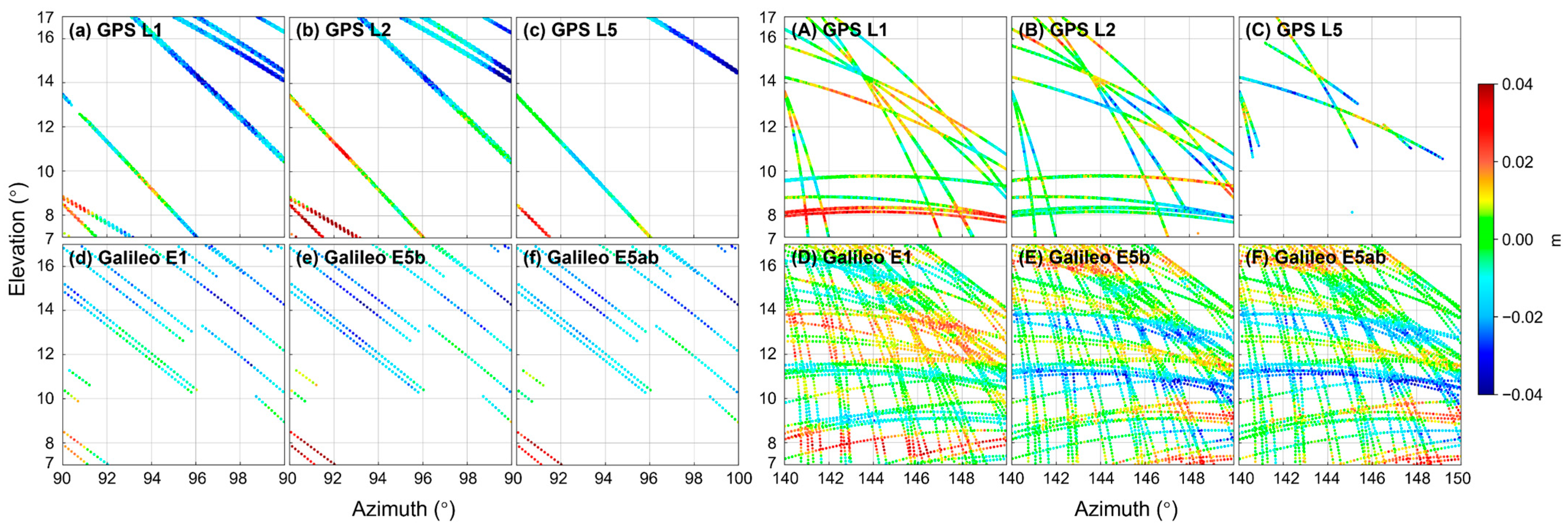
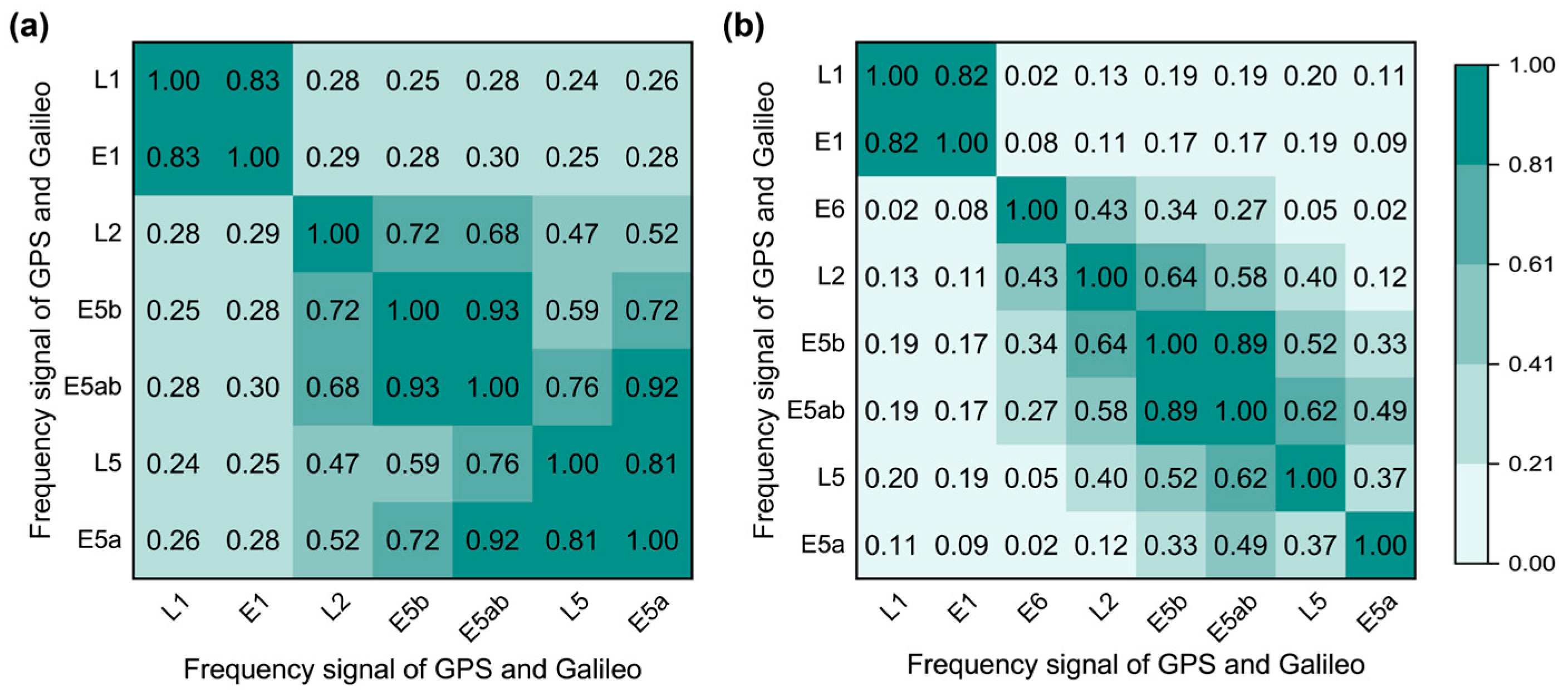
3.2. Correlation Analysis Between GPS/Galileo Frequencies
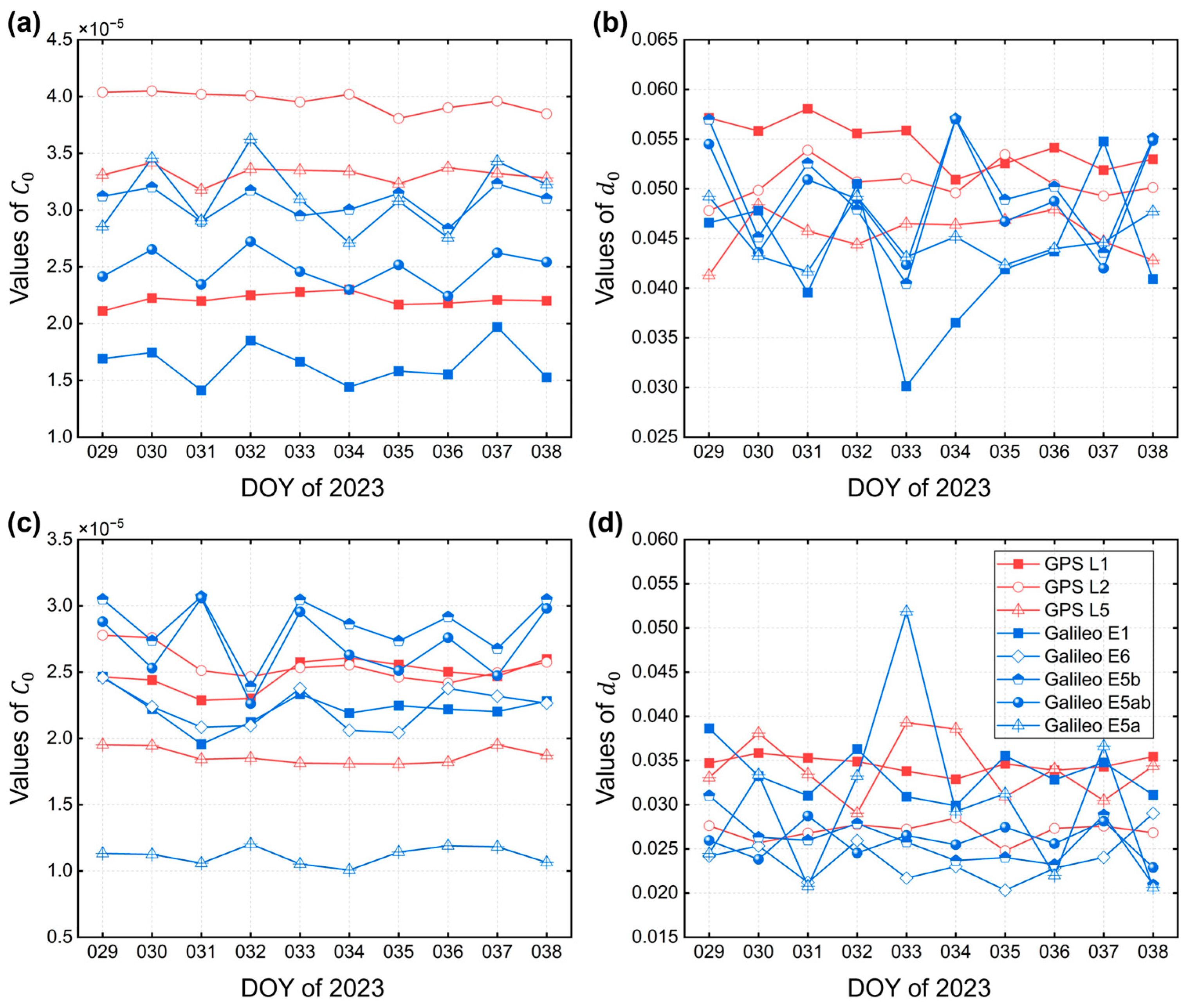
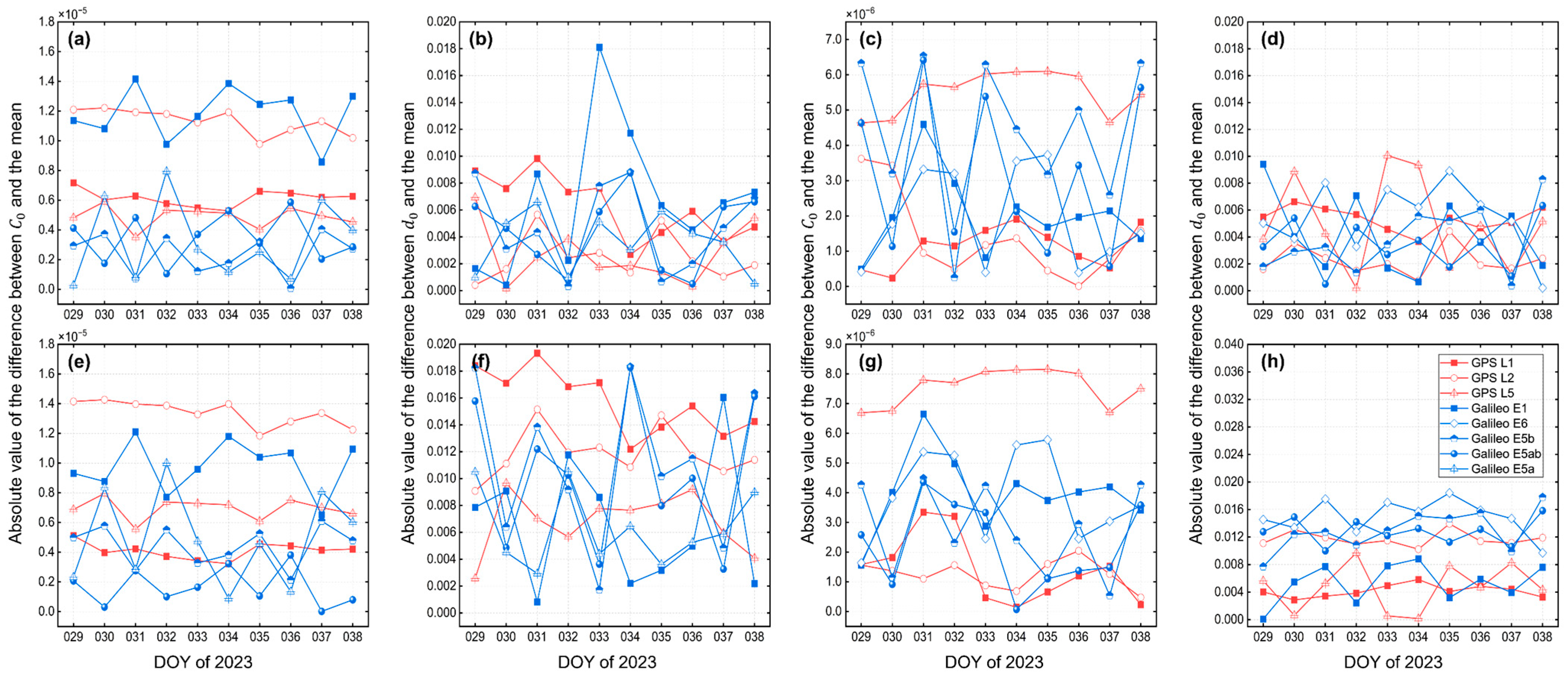
3.3. Parameters of Covariance Function
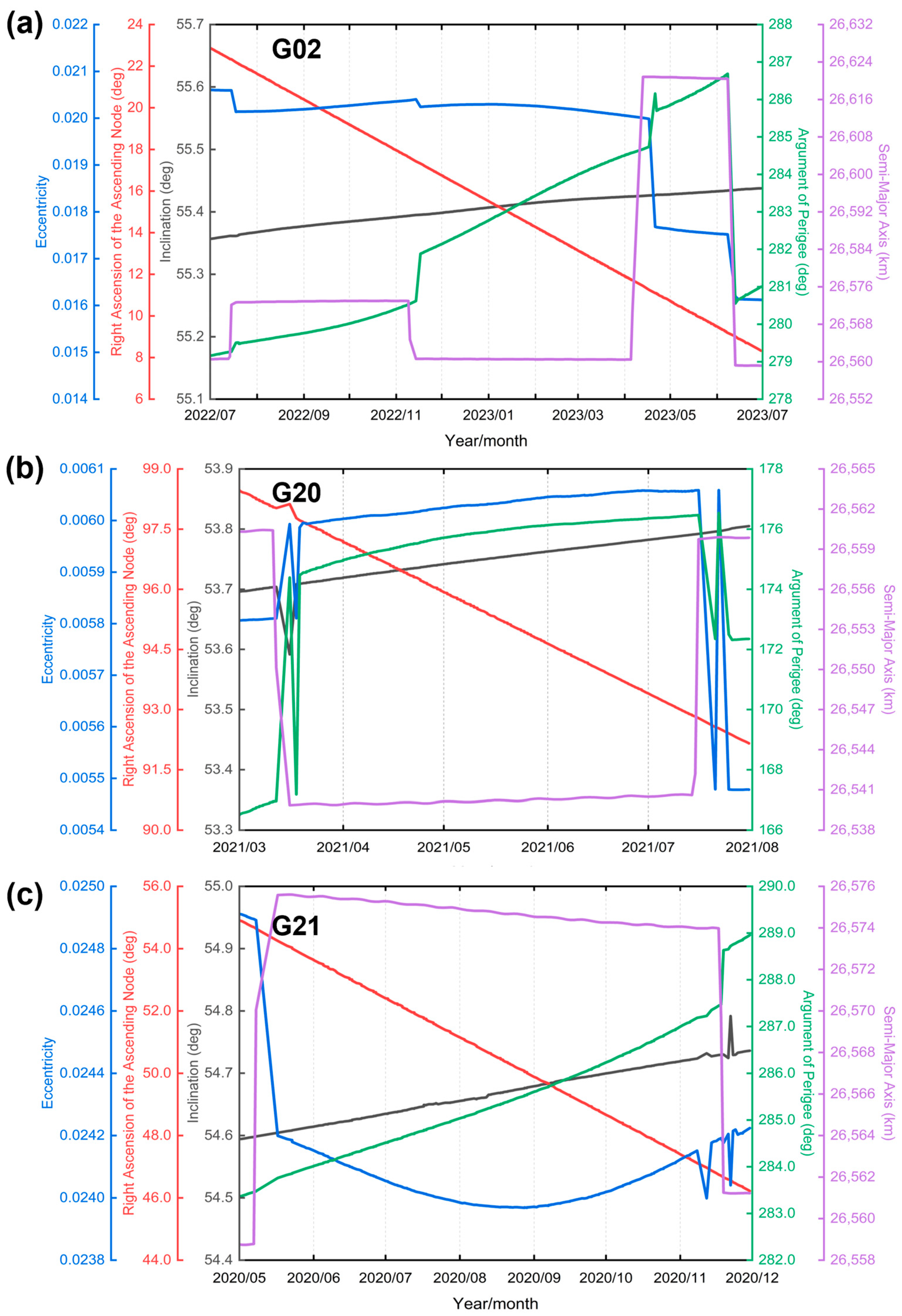
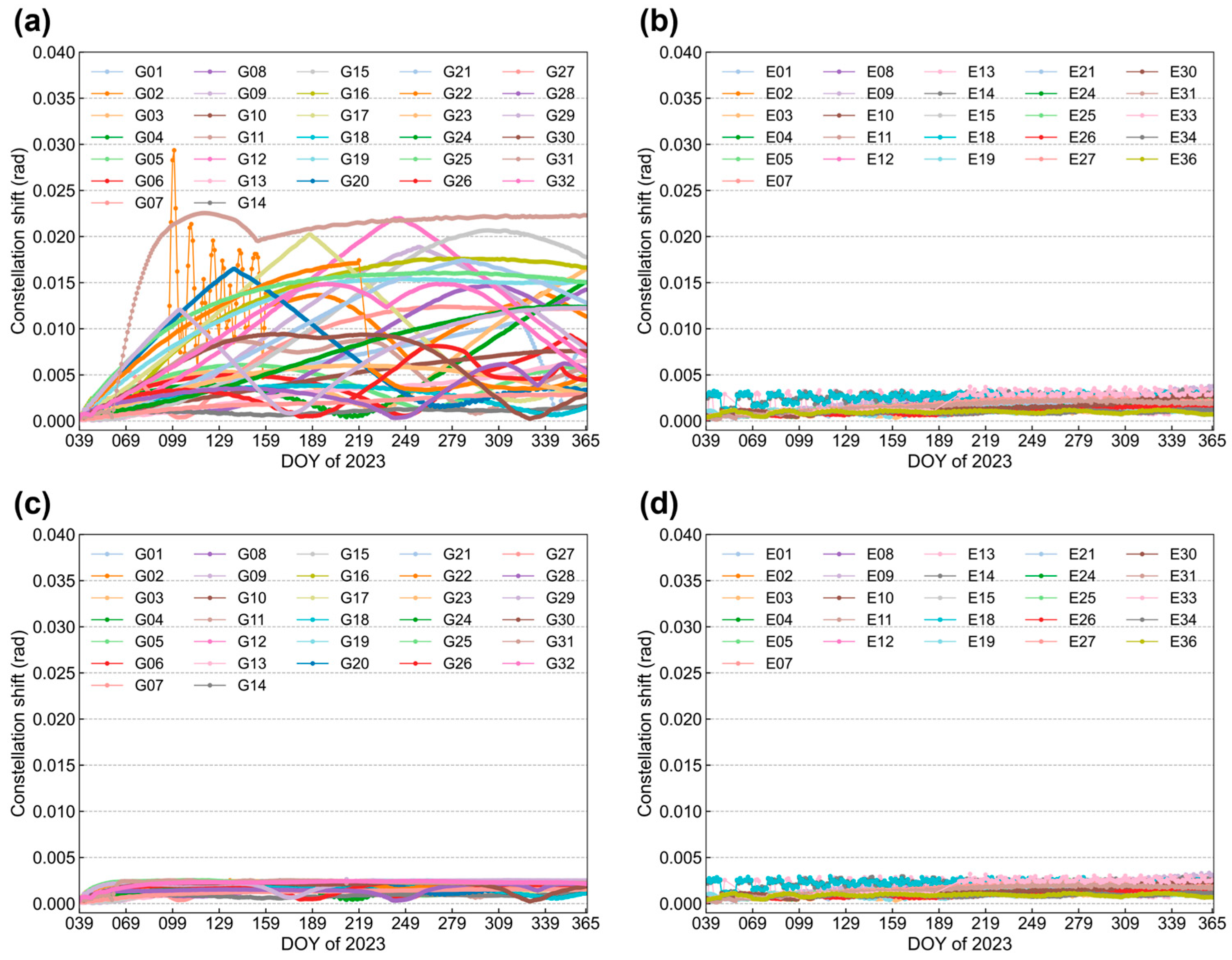
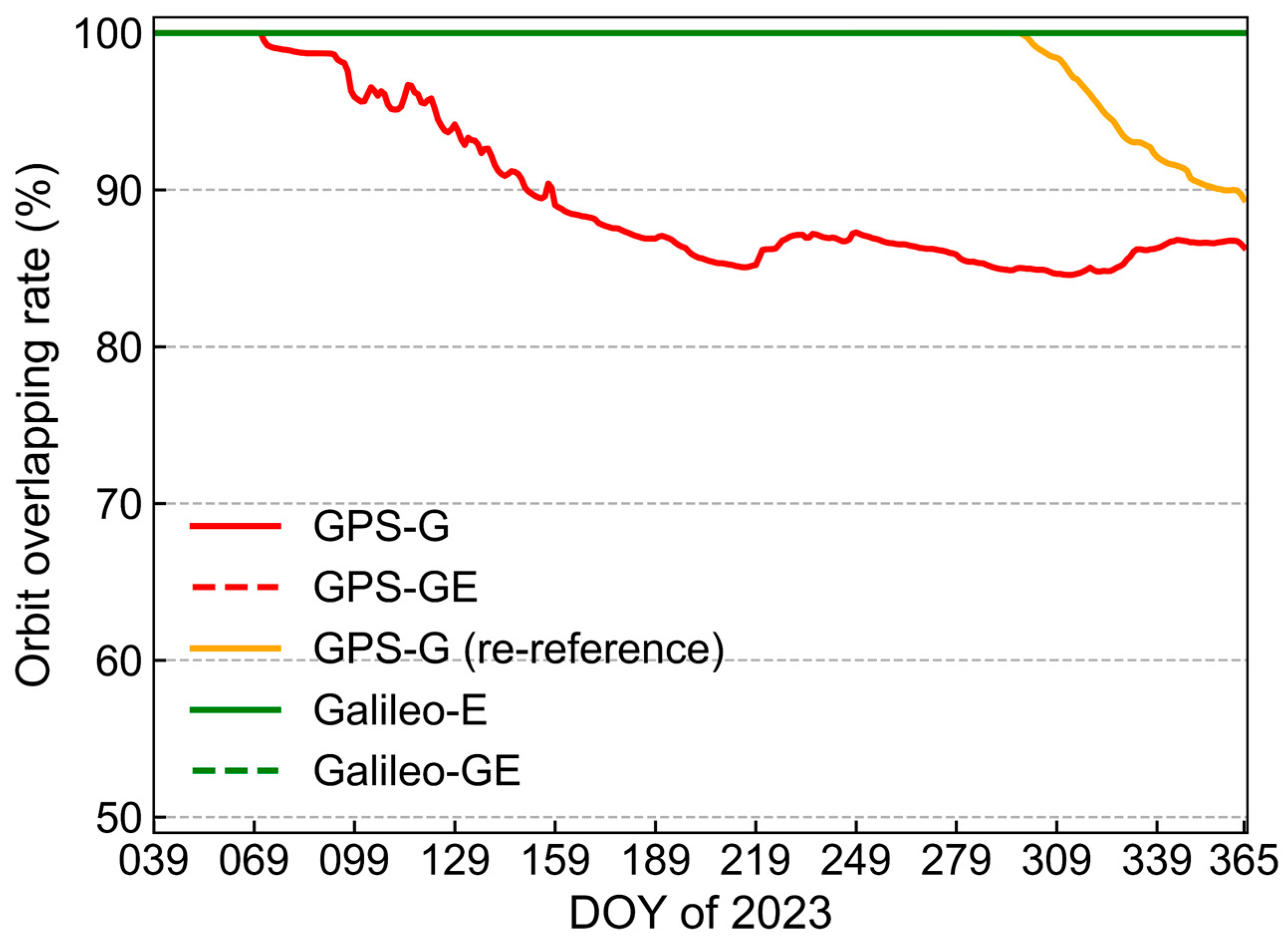
3.4. Orbit Shift over a Long Time Span
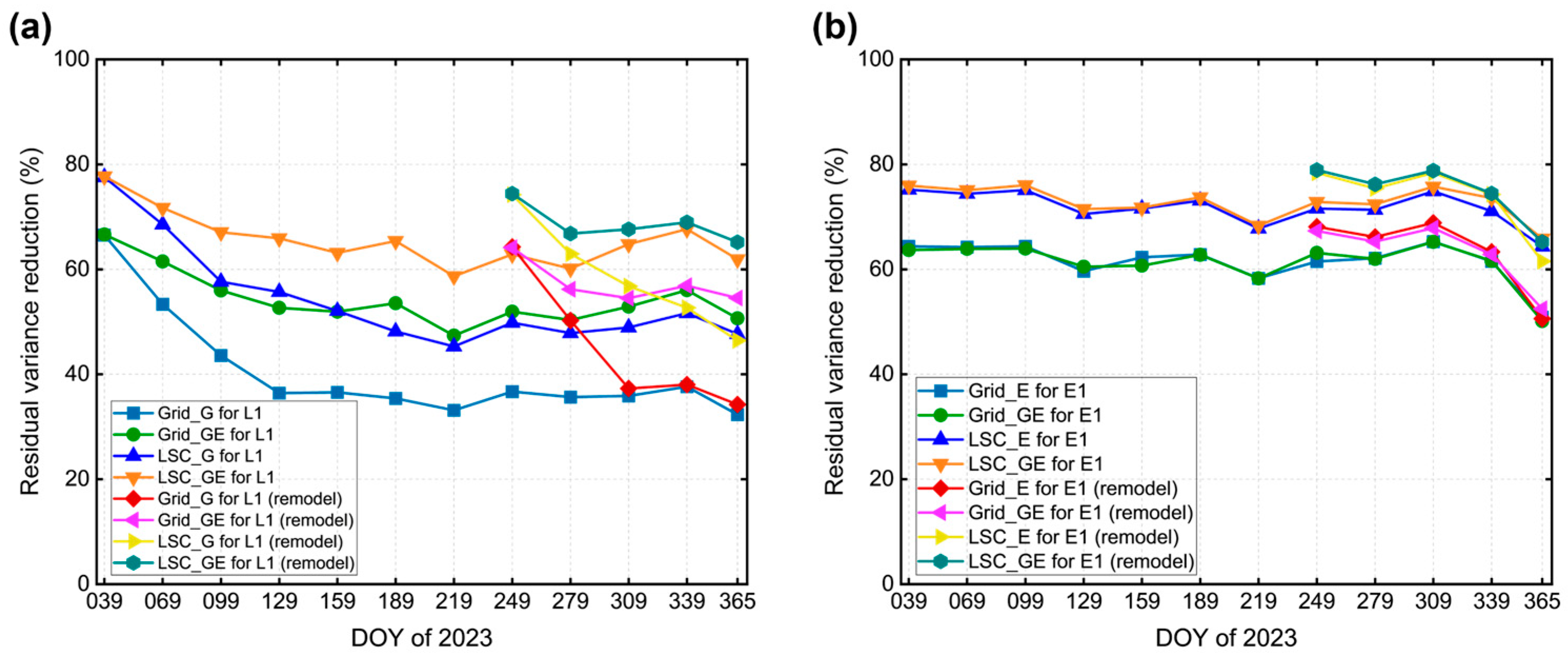
3.5. Unified Covariance Function Parameters for Short and Long-Term Multipath Correction Analysis
4. Results
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Groves, P.D.; Jiang, Z. Height Aiding, Weighting and Consistency Checking for GNSS NLOS and Multipath Mitigation in Urban Areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef]
- Manandhar, D.; Shibasaki, R.; Torimoto, H. GPS Reflected Signal Analysis using Software Receiver. J. Glob. Position. Syst. 2006, 5, 29–34. [Google Scholar] [CrossRef]
- Tranquilla, J.M.; Carr, J.P.; Alrizzo, H.M. Analysis of a choke ring groundplane for multipath control in global positioning system (gps) applications. IEEE Trans. Antennas Propag. 1994, 42, 905–911. [Google Scholar] [CrossRef]
- Tatarnikov, D.V.; Stepanenko, A.P.; Astakhov, A.V. Moderately compact helix antennas with cutoff patterns for millimeter RTK positioning. Gps Solut. 2016, 20, 587–594. [Google Scholar] [CrossRef]
- Vandierendonck, A.J.; Fenton, P.; Ford, T.; Inst, N. Theory and performance of narrow correlator spacing in a gps receiver. In Proceedings of the National Technical Meeting of the Inst of Navigation, San Diego, CA, USA, 27–29 January 1992; pp. 115–124. [Google Scholar]
- Axelrad, P.; Comp, C.J.; MacDoran, P.F. SNR-based multipath error correction for GPS differential phase. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 650–660. [Google Scholar] [CrossRef]
- Bilich, A.; Larson, K.M. Mapping the GPS multipath environment using the signal-to-noise ratio (SNR). Radio Sci. 2008, 43, RS6003. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Li, B.F.; Gao, Y.; Shen, Y.Z. Real-time carrier phase multipath detection based on dual-frequency C/N0 data. Gps Solut. 2019, 23, 7. [Google Scholar] [CrossRef]
- Zheng, D.W.; Zhong, P.; Ding, X.L.; Chen, W. Filtering GPS time-series using a Vondrak filter and cross-validation. J. Geod. 2005, 79, 363–369. [Google Scholar] [CrossRef]
- Satirapod, C.; Rizos, C. Multipath mitigation by wavelet analysis for GPS base station applications. Surv. Rev. 2005, 38, 2–10. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.L.; Zheng, D.W.; Chen, W.; Huang, D.F. Adaptive wavelet transform based on cross-validation method and its application to GPS multipath mitigation. Gps Solut. 2008, 12, 109–117. [Google Scholar] [CrossRef]
- Bernelli-Zazzera, F.; Campana, R.; Gottifredi, F.; Marradi, L. GPS attitude determination by Kalman filtering: Simulation of multipath rejection. In Proceedings of the 8th Annual Space Flight Mechanics Meeting, Monterey, CA, USA, 9–11 February 1998; pp. 1391–1405. [Google Scholar]
- Agnew, D.C.; Larson, K.M. Finding the repeat times of the GPS constellation. Gps Solut. 2007, 11, 71–76. [Google Scholar] [CrossRef]
- Genrich, J.F.; Bock, Y. Rapid resolution of crustal motion at short ranges with the global positioning system. J. Geophys. Res. Solid. Earth 1992, 97, 3261–3269. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.L.; Yuan, L.G.; Xu, Y.L.; Kwok, K.; Chen, Y.Q. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Cohen, C.E.; Parkinson, B.W. Mitigating multipath error in gps based attitude determination. In Proceedings of the 14th Annual Rocky Mountain Conf on Guidance and Control, Keystone, CO, USA, 2–6 February 1991; pp. 53–68. [Google Scholar]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Luo, X.G.; Knöpfler, A.; Mayer, M. Generating statistically robust multipath stacking maps using congruent cells. Gps Solut. 2015, 19, 83–92. [Google Scholar] [CrossRef]
- Wang, Z.R.; Chen, W.; Dong, D.N.; Wang, M.H.; Cai, M.M.; Yu, C.; Zheng, Z.Q.; Liu, M. Multipath mitigation based on trend surface analysis applied to dual-antenna receiver with common clock. Gps Solut. 2019, 23, 104. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.H.; Li, P.; Li, X.X.; Ge, M.R.; Guo, F.; Sang, J.Z.; Schuh, H. Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning. J. Geod. 2019, 93, 2037–2051. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: Vienna, Austria, 2005. [Google Scholar]
- Lin, M. Regional Gravity Field Recovery Using The Point Mass Method. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2016. [Google Scholar]
- Moritz, H. Advanced Physical Geodesy; Wichmann: Berlin, Germany, 1980. [Google Scholar]
- Tian, Y.; Liu, Z.; Lin, M.; Li, K. Modelling and mitigation of GNSS multipath effects by least-squares collocation considering spatial autocorrelation. J. Geod. 2023, 97, 37. [Google Scholar] [CrossRef]
- Lu, R.; Chen, W.; Li, Z.; Dong, D.A.; Jiang, W.P.; Wang, Z.R.; Huang, L.Y.; Duan, X.L. An improved joint modeling method for multipath mitigation of GPS, BDS-3, and Galileo overlapping frequency signals in typical environments. J. Geod. 2023, 97, 95. [Google Scholar] [CrossRef]
- Geng, J.H.; Li, P.B.; Li, G.C. Combining the GPS/Galileo/BDS-3 signals on overlap frequencies for interoperable multipath hemispherical maps. J. Geod. 2024, 98, 32. [Google Scholar] [CrossRef]
- Krag, H.; Leonard, A.; Ranaudo, P.; Blomenhofer, E. Global Implications of GPS and Galileo RAAN Drifts on GNSS Performance. In Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2003. [Google Scholar]
- Pellegrino, M.M.; Scheeres, D.J.; Streetman, B.J. The Feasibility of Targeting Chaotic Regions in the GNSS Regime. J. Astronaut. Sci. 2021, 68, 553–584. [Google Scholar] [CrossRef]
- Sosnica, K.; Bury, G.; Zajdel, R.; Ventura-Traveset, J.; Mendes, L. GPS, GLONASS, and Galileo orbit geometry variations caused by general relativity focusing on Galileo in eccentric orbits. Gps Solut. 2022, 26, 5. [Google Scholar] [CrossRef]
- Moritz, H. Covariance Functions in Least-Squares Collocation; Ohio State University Research Foundation: Columbus, OH, USA, 1976; Volume 240. [Google Scholar]
- Moritz, H. Advanced Least-Squares Methods; Ohio State University Research Foundation: Columbus, OH, USA, 1972; Volume 175. [Google Scholar]
- Pearson, W.H. Estimation of a correlation coefficient from an uncertainty measure. Psychometrika 1966, 31, 421–433. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.F.; Tian, Y.M.; Xiong, W.H.; Liang, Y.B.; Li, K.G.; Tan, S.H.; Yang, X.W.; Li, N. A local filtering approach to mitigating the GNSS multipath effects in relative precise positioning considering the multipath spatial correlation. Adv. Space Res. 2024, 74, 2709–2727. [Google Scholar] [CrossRef]
- Ragheb, A.E.; Clarke, P.J.; Edwards, S.J. GPS sidereal filtering: Coordinate- and carrier-phase-level strategies. J. Geod. 2007, 81, 325–335. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Li, H.; Han, L.; Chen, W. Comparison of Three Methods for Estimating GPS Multipath Repeat Time. Remote Sens. 2018, 10, 6. [Google Scholar] [CrossRef]
- Larson, K.M.; Bilich, A.; Axelrad, P. Improving the precision of high-rate GPS. J. Geophys. Res.-Solid. Earth 2007, 112, B05422. [Google Scholar] [CrossRef]










| Frequency (MHz) | Signal | Baselines | ||
|---|---|---|---|---|
| GPS | Galileo | MATE_MAT1 | KERG_KRGG | |
| 1575.420 | L1 | E1 | √ | √ |
| 1278.750 | E6 | × | √ | |
| 1227.600 | L2 | √ | √ | |
| 1207.140 | E5b | √ | √ | |
| 1191.795 | E5ab * | √ | √ | |
| 1176.450 | L5 | E5a | √ | √ |
| Frequencies to be Corrected | Method | Modeling Date | Frequencies Used for Correction | Abbreviations |
|---|---|---|---|---|
| GPS L1 | Grid | 2023 DOY 029–038 | GPS L1 | Grid_G for L1 |
| GPS L1/Galileo E1 | Grid_GE for L1 | |||
| 2023 DOY 239–248 | GPS L1 | Grid_G for L1 (remodel) | ||
| GPS L1/Galileo E1 | Grid_GE for L1 (remodel) | |||
| Autocorrelation-based LSC | 2023 DOY 029–038 | GPS L1 | LSC_G for L1 | |
| GPS L1/Galileo E1 | LSC_GE for L1 | |||
| 2023 DOY 239–248 | GPS L1 | LSC_G for L1 (remodel) | ||
| GPS L1/Galileo E1 | LSC_GE for L1 (remodel) | |||
| Galileo E1 | Grid | 2023 DOY 029–038 | Galileo E1 | Grid_E for E1 |
| GPS L1/Galileo E1 | Grid_GE for E1 | |||
| 2023 DOY 239–248 | Galileo E1 | Grid_E for E1 (remodel) | ||
| GPS L1/Galileo E1 | Grid_GE for E1 (remodel) | |||
| Autocorrelation-based LSC | 2023 DOY 029–038 | Galileo E1 | LSC_E for E1 | |
| GPS L1/Galileo E1 | LSC_GE for E1 | |||
| 2023 DOY 239–248 | Galileo E1 | LSC_E for E1 (remodel) | ||
| GPS L1/Galileo E1 | LSC_GE for E1 (remodel) |
| DOY of 2023 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 039 | 069 | 099 | 129 | 159 | 189 | 219 | 249 | 279 | 309 | 339 | 365 | |
| Uncalibrated | 5.14 | 5.38 | 5.31 | 5.12 | 5.12 | 5.17 | 5.76 | 5.63 | 5.75 | 5.59 | 5.85 | 5.66 |
| Grid_G | 2.97 | 3.67 | 3.99 | 4.08 | 4.08 | 4.15 | 4.71 | 4.48 | 4.61 | 4.47 | 4.62 | 4.66 |
| Grid_GE | 2.96 | 3.34 | 3.53 | 3.52 | 3.55 | 3.52 | 4.18 | 3.91 | 4.05 | 3.83 | 3.88 | 3.97 |
| LSC_G | 2.43 | 3.02 | 3.46 | 3.41 | 3.54 | 3.72 | 4.26 | 3.99 | 4.15 | 3.99 | 4.07 | 4.09 |
| LSC_GE | 2.43 | 2.86 | 3.05 | 2.99 | 3.11 | 3.04 | 3.70 | 3.43 | 3.63 | 3.31 | 3.33 | 3.49 |
| Grid_G (remodel) | 3.37 | 4.05 | 4.42 | 4.61 | 4.59 | |||||||
| Grid_GE (remodel) | 3.37 | 3.81 | 3.77 | 3.84 | 3.82 | |||||||
| LSC_G (remodel) | 2.86 | 3.50 | 3.67 | 4.03 | 4.14 | |||||||
| LSC_GE (remodel) | 2.85 | 3.31 | 3.18 | 3.26 | 3.34 | |||||||
| DOY of 2023 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 039 | 069 | 099 | 129 | 159 | 189 | 219 | 249 | 279 | 309 | 339 | 365 | |
| Uncalibrated | 4.12 | 4.10 | 4.46 | 4.20 | 4.09 | 4.44 | 4.56 | 4.45 | 4.65 | 4.65 | 4.89 | 5.09 |
| Grid_E | 2.46 | 2.45 | 2.66 | 2.66 | 2.51 | 2.71 | 2.95 | 2.76 | 2.86 | 2.74 | 3.04 | 3.56 |
| Grid_GE | 2.49 | 2.46 | 2.68 | 2.64 | 2.56 | 2.71 | 2.95 | 2.70 | 2.87 | 2.75 | 3.03 | 3.59 |
| LSC_E | 2.05 | 2.07 | 2.23 | 2.28 | 2.18 | 2.30 | 2.59 | 2.37 | 2.49 | 2.33 | 2.63 | 3.04 |
| LSC_GE | 2.02 | 2.05 | 2.18 | 2.24 | 2.17 | 2.27 | 2.57 | 2.32 | 2.45 | 2.29 | 2.52 | 2.97 |
| Grid_E (remodel) | 2.51 | 2.71 | 2.60 | 2.96 | 3.58 | |||||||
| Grid_GE (remodel) | 2.54 | 2.74 | 2.64 | 2.98 | 3.51 | |||||||
| LSC_E (remodel) | 2.07 | 2.31 | 2.16 | 2.48 | 3.16 | |||||||
| LSC_GE (remodel) | 2.04 | 2.27 | 2.14 | 2.47 | 3.00 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, W.; Tian, Y.; Dai, X.; Zhang, Q.; Liang, Y.; Ruan, X. Analysis of Multi-GNSS Multipath for Parameter-Unified Autocorrelation-Based Mitigation and the Impact of Constellation Shifts. Remote Sens. 2024, 16, 4009. https://doi.org/10.3390/rs16214009
Xiong W, Tian Y, Dai X, Zhang Q, Liang Y, Ruan X. Analysis of Multi-GNSS Multipath for Parameter-Unified Autocorrelation-Based Mitigation and the Impact of Constellation Shifts. Remote Sensing. 2024; 16(21):4009. https://doi.org/10.3390/rs16214009
Chicago/Turabian StyleXiong, Wenhao, Yumiao Tian, Xiaolei Dai, Qichao Zhang, Yibing Liang, and Xiongwei Ruan. 2024. "Analysis of Multi-GNSS Multipath for Parameter-Unified Autocorrelation-Based Mitigation and the Impact of Constellation Shifts" Remote Sensing 16, no. 21: 4009. https://doi.org/10.3390/rs16214009
APA StyleXiong, W., Tian, Y., Dai, X., Zhang, Q., Liang, Y., & Ruan, X. (2024). Analysis of Multi-GNSS Multipath for Parameter-Unified Autocorrelation-Based Mitigation and the Impact of Constellation Shifts. Remote Sensing, 16(21), 4009. https://doi.org/10.3390/rs16214009





