Adaptive Multi-Function Radar Temporal Behavior Analysis
Abstract
1. Introduction
- Building upon existing research in behavior analysis, we conducted behavior modeling from the radar perspective while observing from the reconnaissance perspective. We performed MFRBA through interactive engagement in the environmental aspect, providing a frame of reference for analyzing AMFR behavior while preserving its inherent interpretability (the term ‘inherent interpretability’ pertains to the extent to which human analysts can comprehend and rationalize the internal mechanisms and decision-making processes of a model without relying on supplementary explanatory tools. In this article, the radar system’s generation of waveforms and task sequences is based on its model’s structure and parameters, thereby facilitating transparency and comprehensibility).
- We have developed a digital radar simulation system that incorporates three entities (radar, reconnaissance, and environment), operates at three levels (function, pulse, and signal), and provides two types of feedback (positive and negative) to accurately simulate the temporal dynamics observed in real radar operations and generate signal flows with temporal characteristics (the term ‘temporal features’ refers to the fundamental attributes of signal data in terms of time, including temporal dependency, sequence, and order. In this article, a signal stream with temporal features pertains to the radar’s execution of task sequences and emission signals based on precise control of time slot information according to specific rules. As a result, the acquired signal stream not only encompasses task status and signal parameter characteristics but also exhibits inherent temporal properties). Furthermore, we have explored the hierarchical structure at the signal level to enable effective interaction.
- We propose an adaptive resource management and task scheduling method for AMFR. This method leverages a closed-loop feedback framework encompassing five working modes, allowing dynamic adjustments to waveform parameters and task prioritization based on real-time environmental and reconnaissance data. By integrating mathematical models for optimal resource allocation and implementing priority-based scheduling, we can enhance radar efficiency and adaptability in complex operational scenarios.
2. Related Work
3. Materials and Methods
3.1. Digital Radar Simulation System Model
3.1.1. Adaptive Resource Management and Task Scheduling Framework
3.1.2. LRS Working Mode
S State
C State
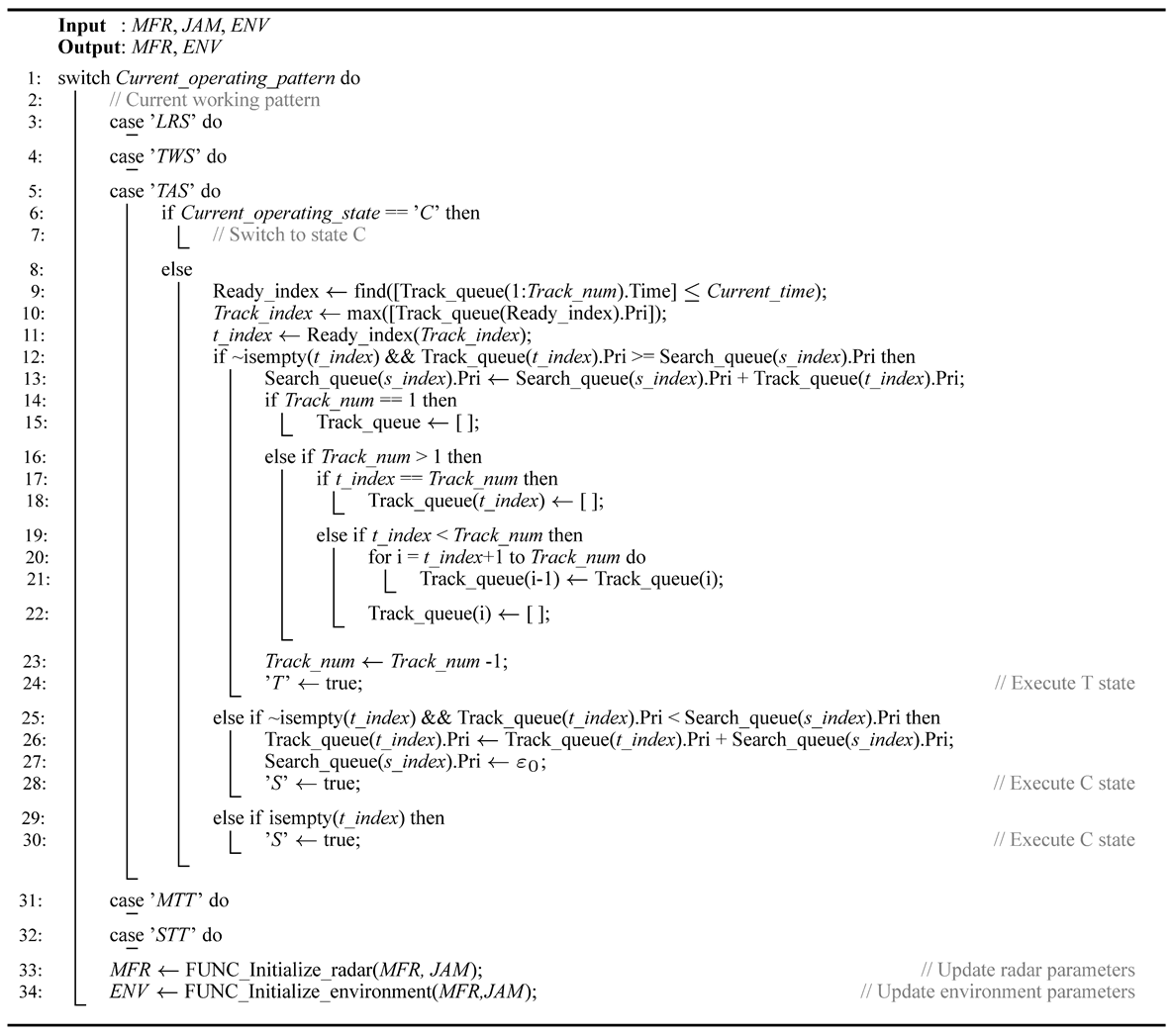
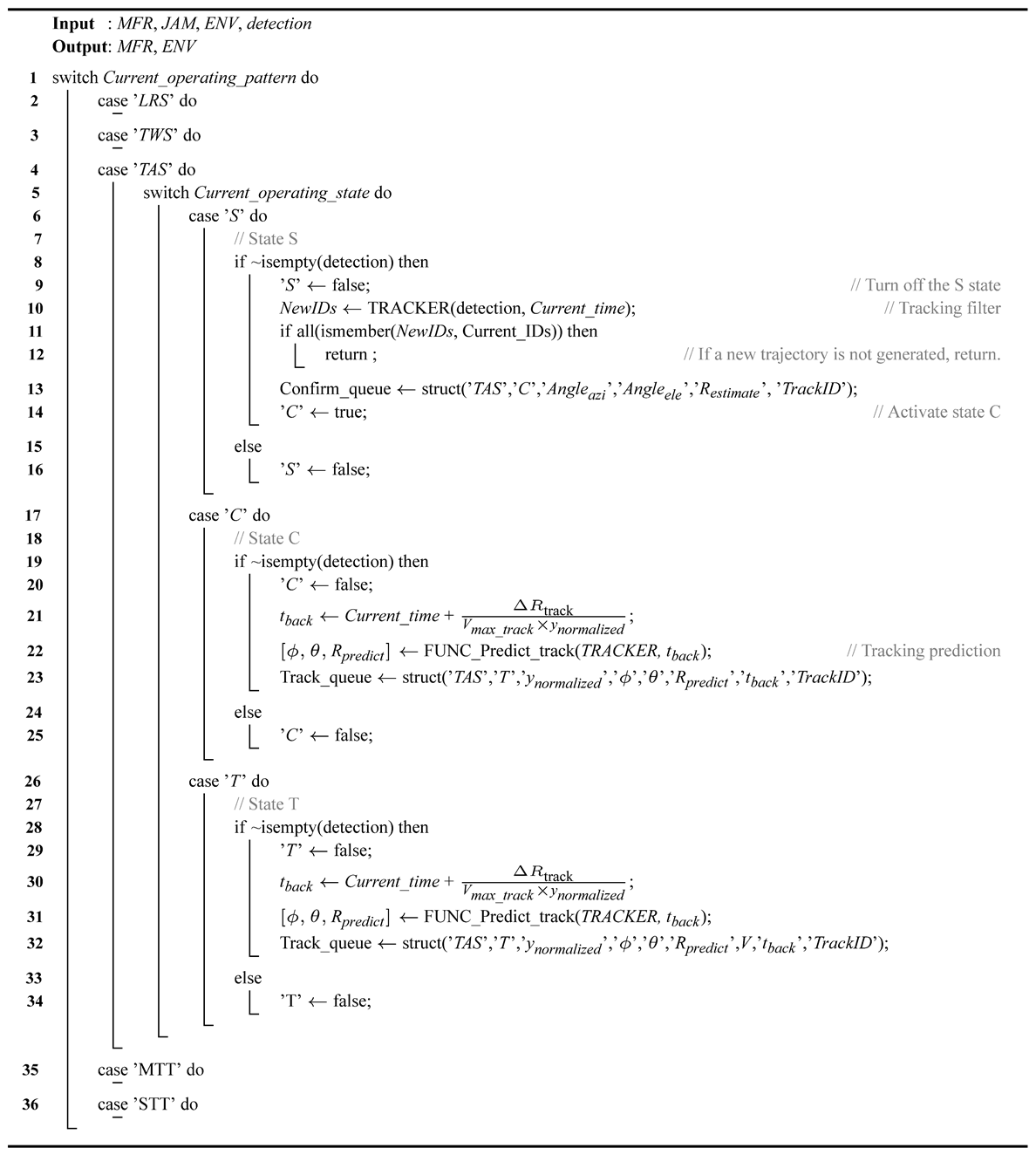
3.1.3. TAS Working Mode
S State
C State
T State
3.1.4. JAM Signal Processing
TOA Estimation Based on Autocorrelation Method
TOA Estimation Based on Binary Division STFT
Time–Frequency Analysis Based on the WVD
Time–Frequency Analysis Based on FrFT
3.2. Behavioral Interaction Model
3.2.1. Management Behavior in MFR
3.2.2. Assessment Behavior in MFR
3.2.3. MFR External Behavior
4. Experiments and Results
- Constructing simulation scenarios for MFR, JAM, and ENV. An adaptive resource management and task scheduling framework is introduced to simulate AMFR in MFR. For JAM, reconfigure the composition and parameters of the deployed reconnaissance team. The physical spatial positions of MFR and JAM as well as their respective environmental parameters are defined in ENV.
- The simulation system autonomously generates signal flow data with temporal characteristics and stores the processed data in a pulse stream format. The temporal dynamics within the pulse flow data are revealed by conducting an analysis following the interaction between both parties.
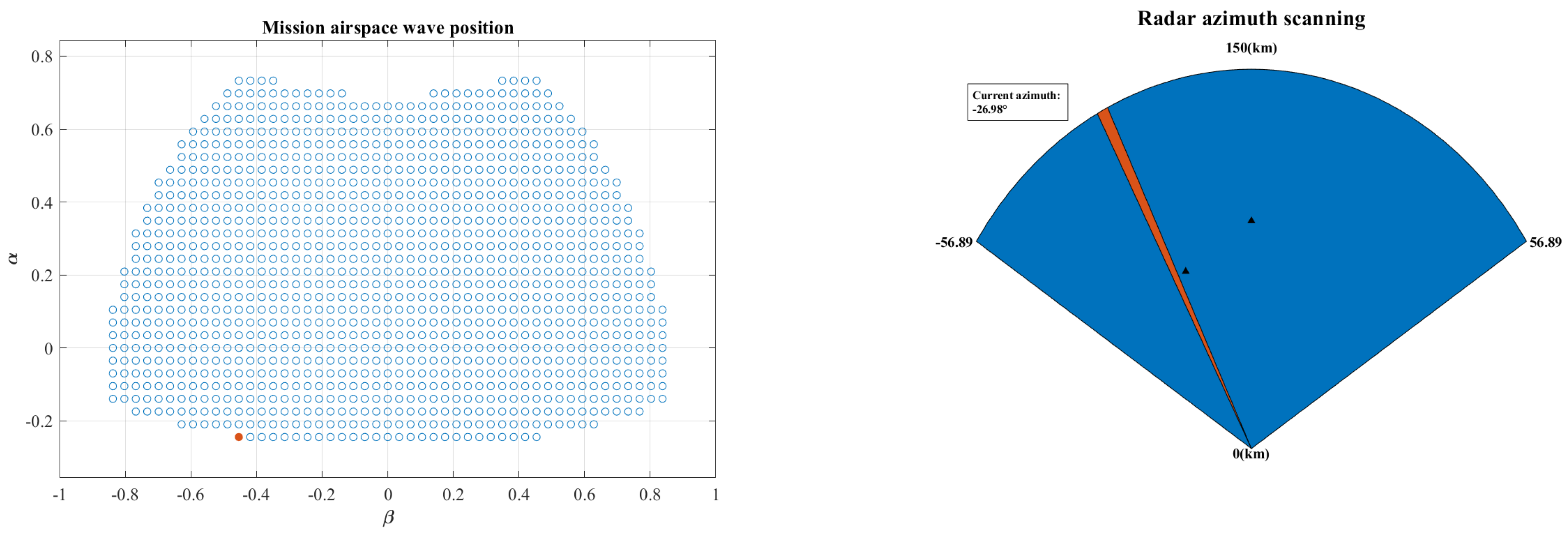
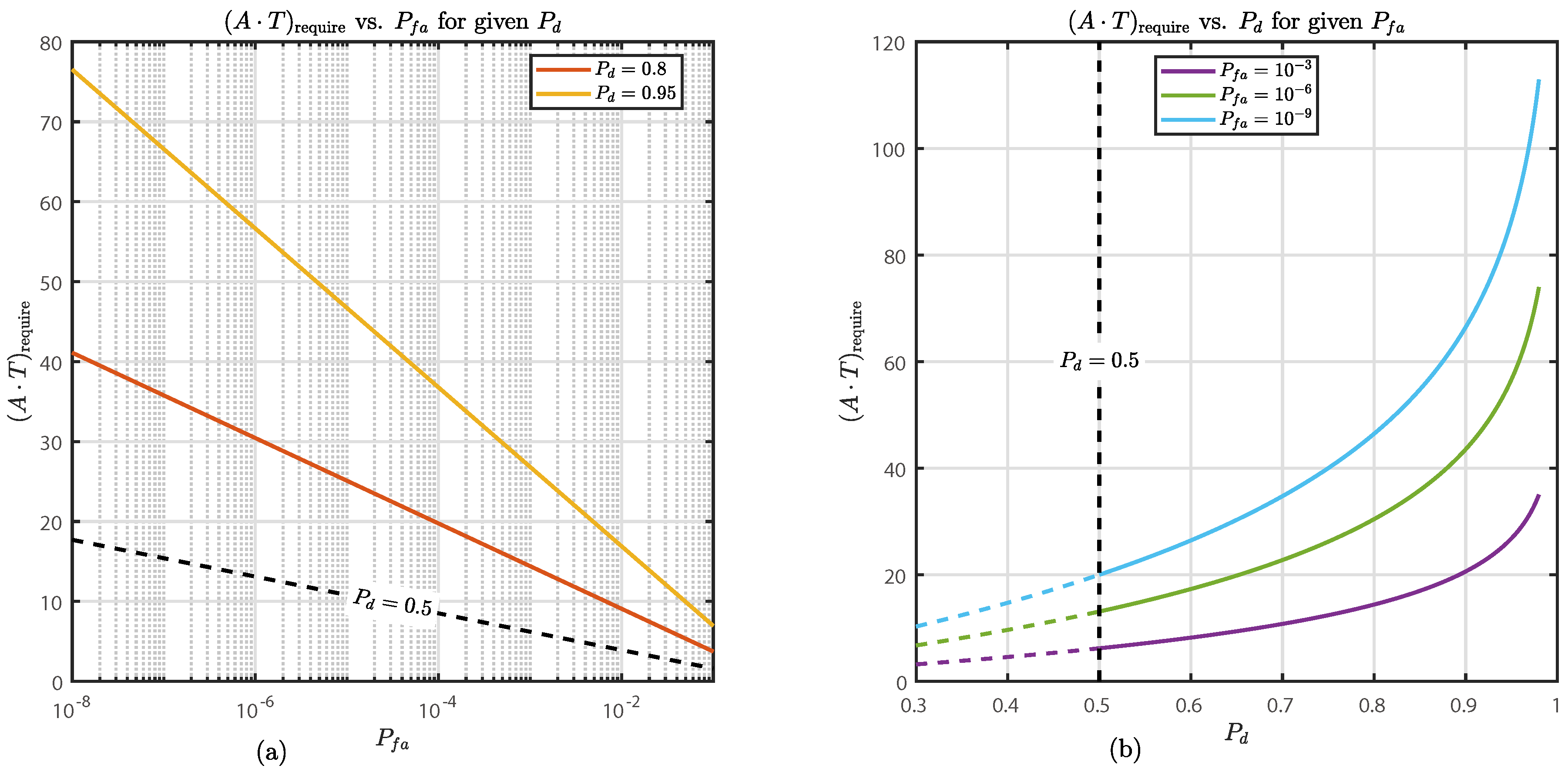
4.1. Simulation Parameter Settings
4.2. Temporal Behavior Analysis
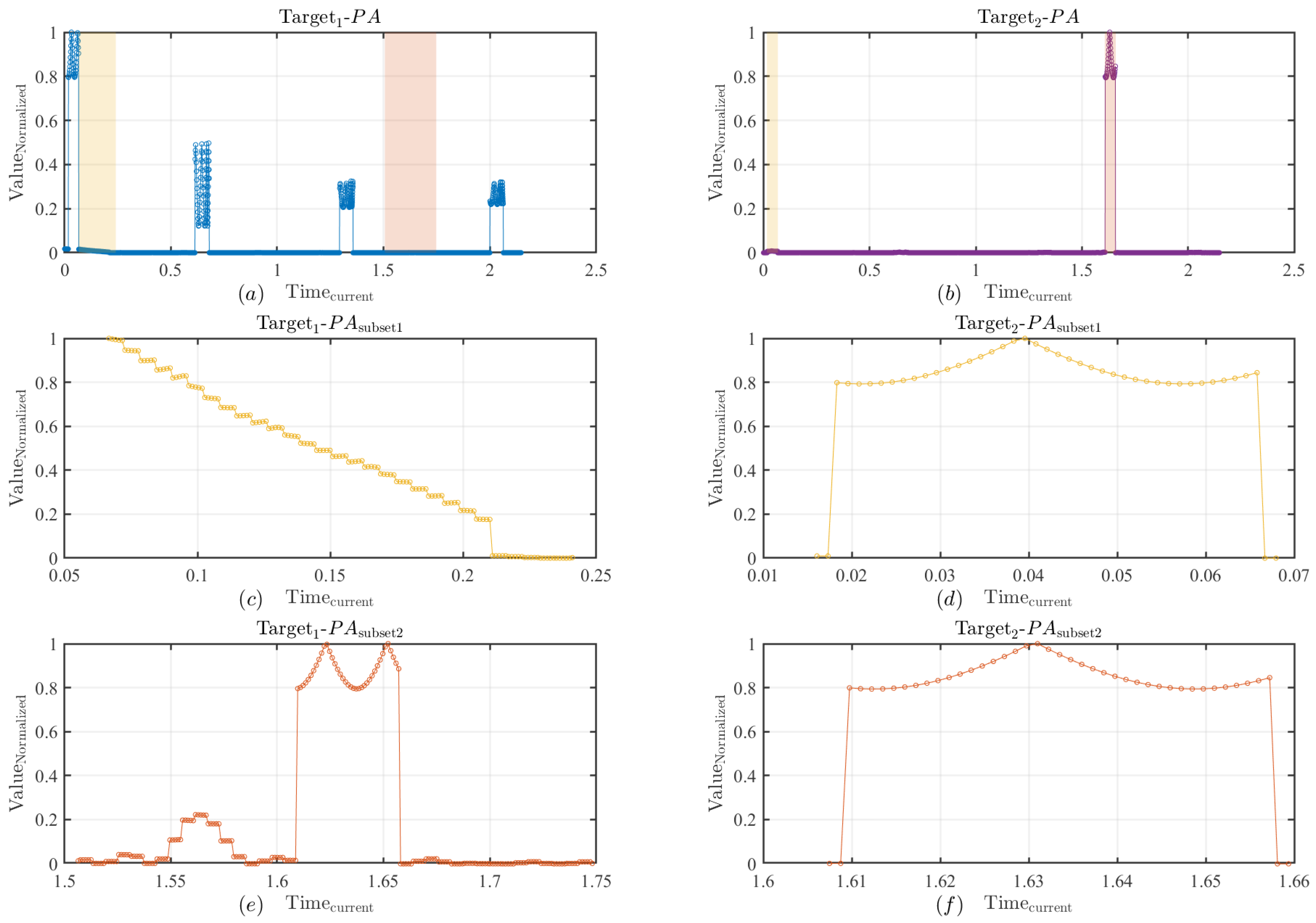
4.2.1. Evaluation Behavior Analysis of MFR
4.2.2. Outward Behavior Assessment of MFR
4.2.3. Analysis on the Applicability of MFR
5. Discussion
- Different perspectives on differences: The areas of interest between MFR and JAM exhibit disparities from different perspectives. MFR primarily focuses on comprehensive control and optimization of internal resource management, as well as task scheduling mechanisms, with the objective of enhancing radar efficiency in resource utilization and task execution capability. Conversely, JAM places emphasis on real-time evaluation of behavioral threats posed by MFR, specifically highlighting the detection and identification of potential impacts on environmental targets resulting from radar behavior.
- The importance of key temporal information: In the MFRBA process, the amplitude information of signals with time stamps plays a crucial role that cannot be overlooked. Different targets may exhibit distinct temporal characteristics even when receiving identical waveform parameters. By integrating detection results from multiple devices, signal leakage caused by sidelobe attenuation in individual devices can be compensated for, thereby enhancing the integrity and precision of temporal pulse flow analysis.
- Multi-machine collaborative fusion: The accuracy and robustness of the overall analysis are enhanced through real-time collaborative fusion of data from multiple machines, enabling comprehensive behavioral analysis of single or even multiple radars.
- Pulse flow temporal correlation modeling: Incorporating time correlation modeling of pulse streams into deep learning network structures can effectively mitigate uncertainty in behavior analysis, thereby enhancing the accuracy and reliability of analysis given the sparse and localized nature of effective radar signals in signal flow.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
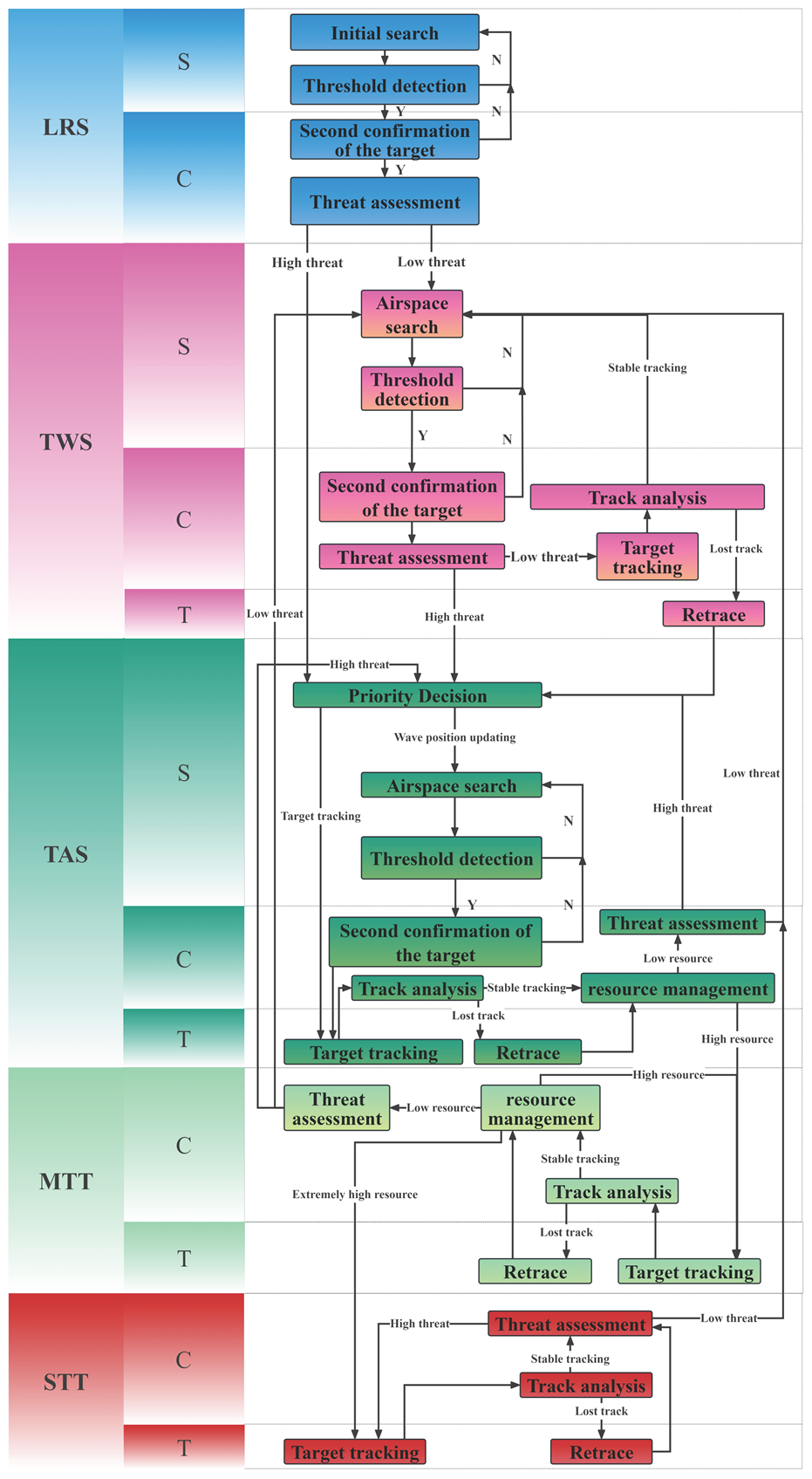
Appendix A. Working Pattern Closed-Loop Switching Diagram
Appendix B. Simulation Parameter Information Table
| Variable Symbol | Definition | Variable Values | Variable Symbol | Definition | Variable Values | |
| MFR | c | Speed of light | 3 (m/s) | k | Boltzmann constant | 1.38 × 10−23 |
| Noise temperature | 290 (k) | Maximum frame count | / | |||
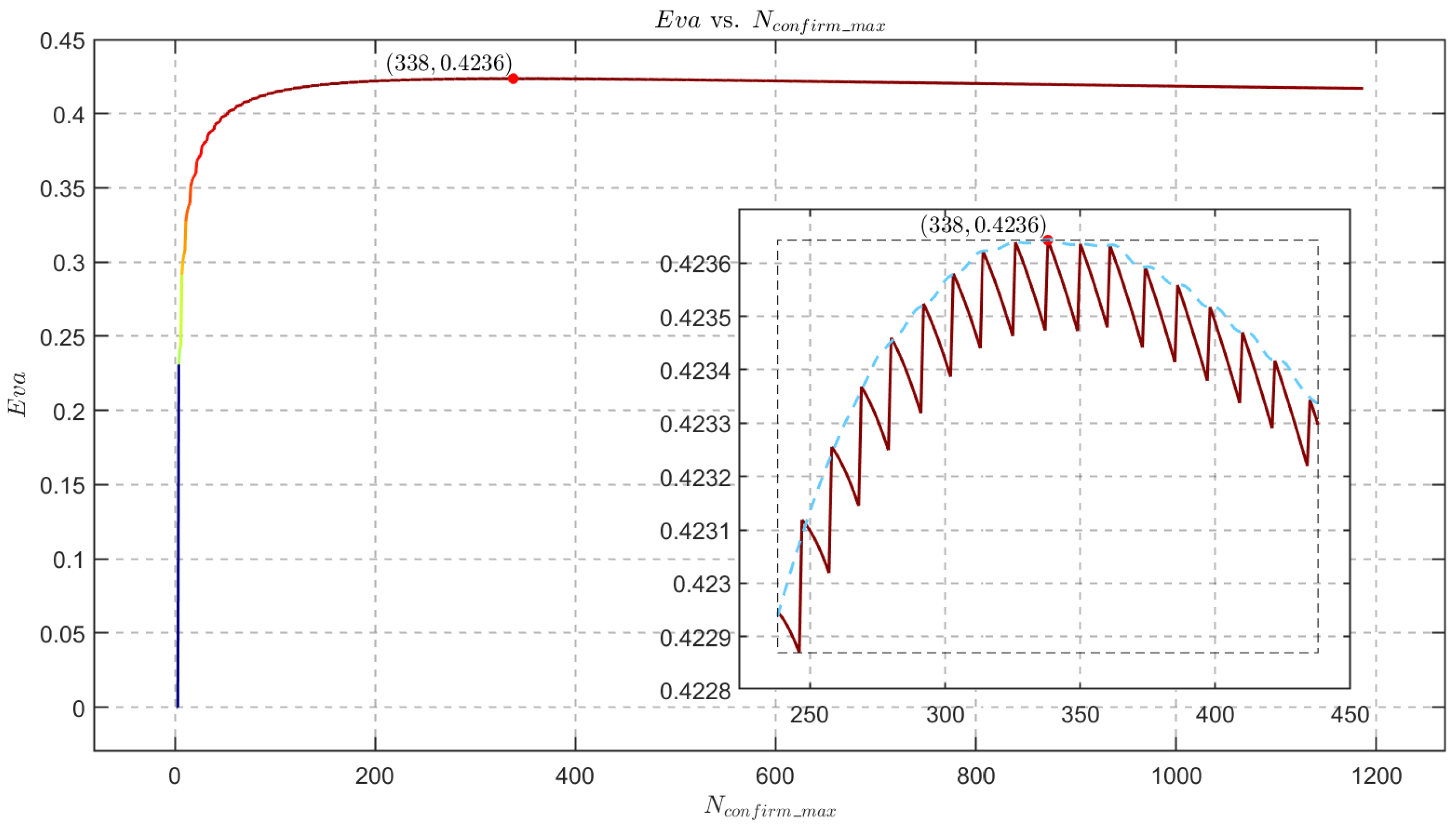
| Current time | / | Detection probability | ||||
| Frame period | / | Number of effective wave positions | / | |||
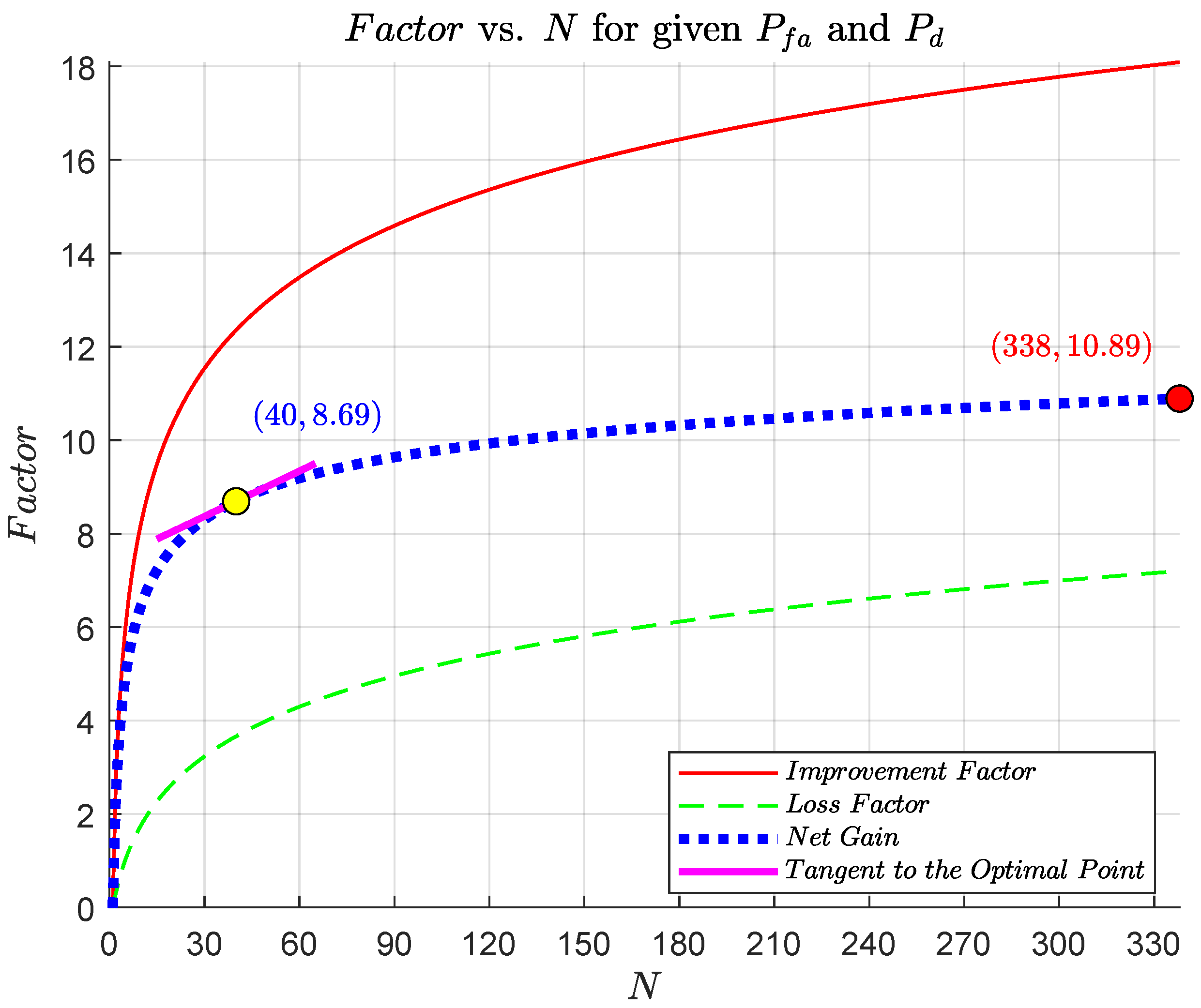
| Maximum tracking number | / | False alarm probability | 1 × 10−6 | |||
| S state range resolution | 100 (m) | S state unambiguous range | 150 (km) | |||
| C state rr | 100 (m) | C state ur | 150 (km) | |||
| T state rr | 100 (m) | T state ur | / | |||
| S state unambiguous velocity | / | Target azimuth angle | / | |||
| C state uv | 343 (m/s) | Target elevation angle | / | |||
| T state uv | 343 (m/s) | Central azimuth angle | 0 (°) | |||
| Max azimuth angle | (rad) | Max elevation angle | (rad) | |||
| Min elevation angle | 0 (°) | Level 3 dB beamwidth | / | |||
| Distance estimation | / | Vertical 3 dB beamwidth | / | |||
| Velocity estimation | / | X-axis quantity | 70 | |||
| Threat value | / | Y-axis quantity | 70 | |||
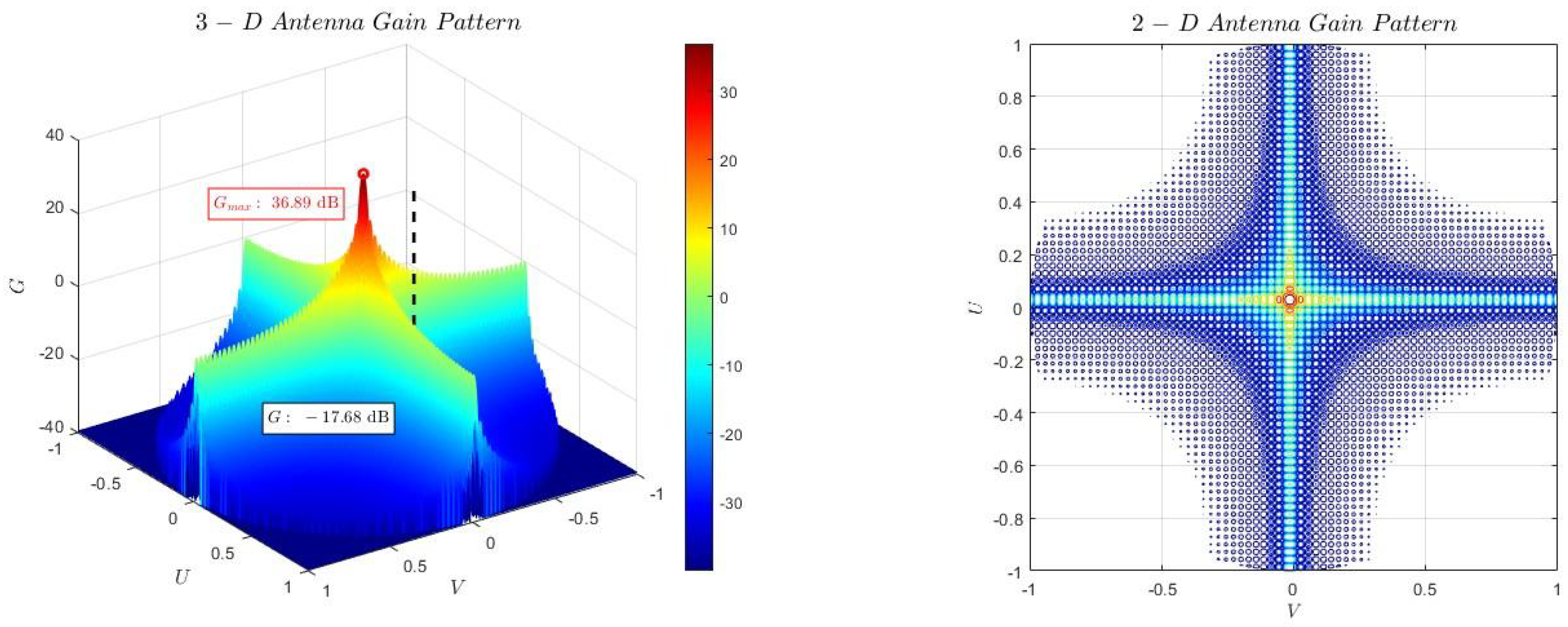
| G | Gain of antenna array | / | Number of channels | 4900 | ||
| F | Noise factor | 7 (dB) | Radar loss | 7 (dB) | ||
| Reference RCS | 10 (m2) | Reference RF | 1.3 GHz | |||
| Peak power | 100 kw | Pulse repetition frequency | / | |||
| Radio frequency | / | Pulse repetition interval | / | |||
| Pulse width | / | Duty cycle | / | |||
| Band width | / | Pulse compression ratio | / | |||
| Pattern one | LRS | Pattern two | TWS | |||
| Pattern three | TAS | Pattern four | MTT | |||
| Pattern five | STT | State one | S | |||
| State two | C | State three | T | |||
| Transmitter preamplifier | / | Receiver preamplifier | / | |||
| Radiator | / | Collector | / | |||
| Signal waveform | / | Radar transceiver | / | |||
| Monopulse measuring apparatus | / | Matched filter | / | |||
| Time varying gain | / | Tracker | / | |||
| JAM | Target quantity | / | Target number | |||
| Radar cross section | / | Target location | / | |||
| Target velocity | / | X-axis quantity | / | |||
| Working frequency | / | Y-axis quantity | / | |||
| Sample frequency | / | |||||
| ENV | Scene | / | Channel | / | ||
| Radar platform | / | Target platform | / |
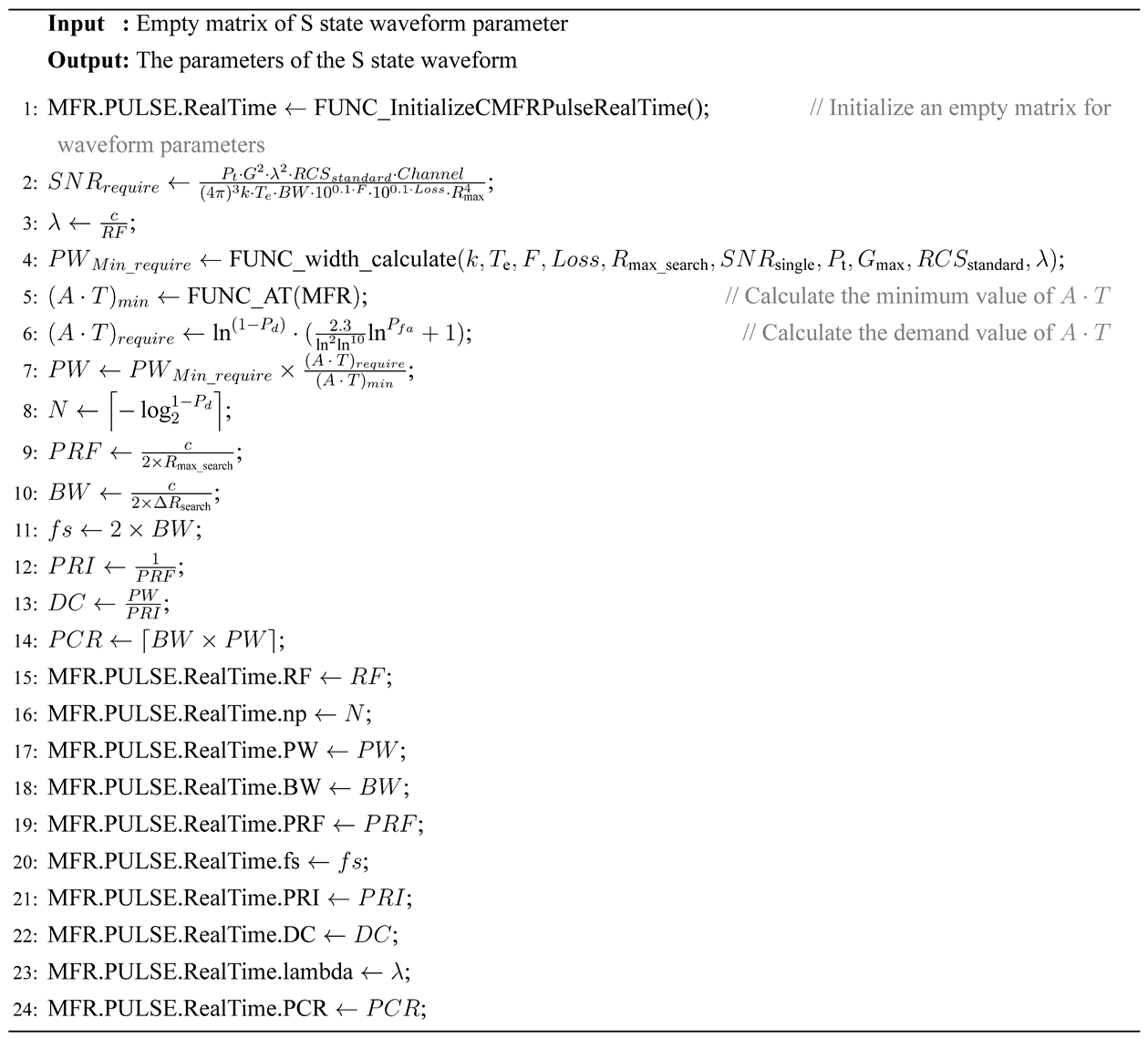
Appendix C. The Design of Waveform Parameters for LRS Mode S State
Appendix D. The Design of Waveform Parameters for LRS Mode C State

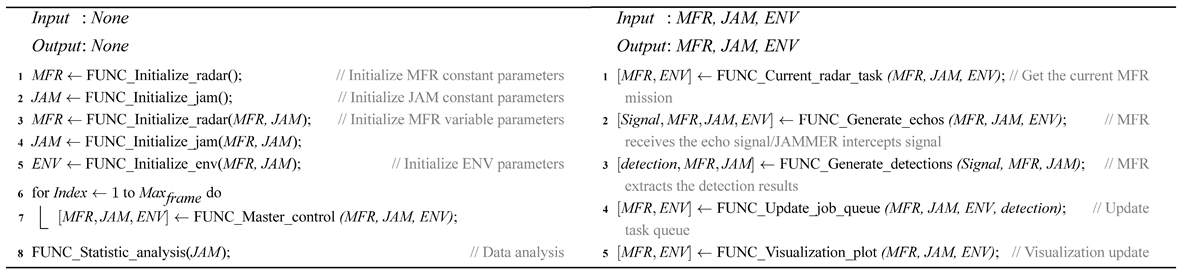
Appendix E. (Left) Digital Radar Simulation System Framework. (Right) Function FUNC_Master_control
Appendix F. Function FUNC_Current_radar_task
Appendix G. Function FUNC_Update_job_queue
Appendix H. Function FUNC_Generate_echos

Appendix I. Function FUNC_Generate_detection

References
- Wang, S.; Zhu, M.; Li, Y.; He, J.; Liang, K.; Zhang, L.; Su, K.; Ma, H.; Chen, L.; Dong, X.; et al. Recognition, reasoning, and prediction of advanced multifunction radar system behavior: Overview and prospects. Signal Process. 2024, 40, 17–55. [Google Scholar]
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Charlish, A.; Hoffmann, F.; Degen, C.; Soloviev, A.; Dale, C.; Griffiths, H. The development from adaptive to cognitive radar resource management. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 8–19. [Google Scholar] [CrossRef]
- Bi, Z.; Xu, C.; Zhang, X.; Lu, L. Phased Array Radar Resource Management Technology; National Defense Industry Press: Beijing, China, 2016. [Google Scholar]
- Martone, A.F.; Charlish, A. Cognitive radar for waveform diversity utilization. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 10–14 May 2021; pp. 1–6. [Google Scholar]
- Wang, B.; Wang, J.; Song, X.; Han, Y. Research on adaptive waveform selection algorithm in cognitive radar. J. Commun. 2010, 5, 467–474. [Google Scholar] [CrossRef]
- Liu, H.; Yan, J.; Zhang, P.; Wei, H.; Li, S.; Jiang, T. A phased array radar resource management method for multi-task scheduling. Mod. Radar 2023, 45, 8–16. [Google Scholar]
- Ghadian, M.; Fatemi Mofrad, R.; Abbasi Arand, B. Robust time resource management in cognitive radar using adaptive waveform design. IETE J. Res. 2023, 69, 1070–1080. [Google Scholar] [CrossRef]
- Klemm, R.; Griffiths, H.; Koch, W. Novel Radar Techniques and Applications: Volume 1: Real Aperture Array Radar, Imaging Radar, and Passive and Multistatic Radar; IET Publishing: London, UK, 2017; pp. 1–500. [Google Scholar]
- Li, Y.; Huang, P. Radar Engineering; National Defense Industry Press: Beijing, China, 1999. [Google Scholar]
- Mahafza, R.B.; Elsherbeni, A.Z. MATLAB Simulations for Radar Systems Design; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Xiong, J.; Pan, J.; Zhuo, Y.; Guo, L. A review of radar working mode recognition methods. Mod. Radar 2023, 45, 1–10. [Google Scholar]
- Dong, X.; Cheng, S. Radar Working Modes Recognition Based on Discrete Process Neural Network. IOP Conf. Ser. Mater. Sci. Eng. 2018, 394, 042088. [Google Scholar] [CrossRef]
- Liu, H. Research on Radar Operating Pattern Recognition Based on Automatic Encoder and Gradient Lift Model. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2018. (In Chinese). [Google Scholar]
- Liu, H.; Jin, W.; Chen, C. Working Pattern Recognition of Phased Array Radar Based on Noise Reduction Autoencoder. J. Syst. Simul. 2017, 29, 1960–1967. [Google Scholar]
- Li, X.; Liu, Z.-M.; Huang, Z. Denoising of Radar Pulse Streams With Autoencoders. IEEE Commun. Lett. 2020, 24, 797–801. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Li, X.; Liu, Z.; Huang, Z. Attention-Based Radar PRI Modulation Recognition With Recurrent Neural Networks. IEEE Access 2020, 8, 57426–57436. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, M.; Ma, Y.; Yan, J. Work Modes Recognition and Boundary Identification of MFR Pulse Sequences with a Hierarchical Seq2Seq LSTM. IET Radar Sonar Navig. 2020, 14, 1343–1353. [Google Scholar] [CrossRef]
- Fang, Y.; Zhai, Q.; Zhang, Z.; Yang, J. Change Point Detection for Fine-Grained MFR Work Modes with Multi-Head Attention-Based Bi-LSTM Network. Sensors 2023, 23, 3326. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, J.; Dong, J.; Wen, Z.; Zhang, Z. Deep Learning-Aided Modulation Recognition for Non-Orthogonal Signals. Sensors 2023, 23, 5234. [Google Scholar] [CrossRef]
- Tang, W.; Long, G.; Liu, L.; Zhou, T.; Blumenstein, M.; Jiang, J. Omni-scale CNNs: A Simple and Effective Kernel Size Configuration for Time Series Classification. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Pan, J.; Zhang, S.; Xia, L.; Tan, L.; Guo, L. Embedding Soft Thresholding Function into Deep Learning Models for Noisy Radar Emitter Signal Recognition. Electronics 2022, 11, 2142. [Google Scholar] [CrossRef]
- Qiao, J.; Yue, X. Multi-label Recognition of Radar Radiation Source Based on Improved Residual Network. Mod. Radar 2022, 44, 39–44. (In Chinese) [Google Scholar]
- Han, Z. Radar Data Fusion Tracking and Working Pattern Recognition. Master’s Thesis, Xidian University, Xi’an, China, 2019. (In Chinese). [Google Scholar]
- Chen, X.; Qiu, P.; Zhu, W.; Li, H.; Wang, H.; Sotiras, A.; Wang, Y.; Razi, A. TimeMIL: Advancing Multivariate Time Series Classification via a Time-aware Multiple Instance Learning. arXiv 2024, arXiv:2405.03140. [Google Scholar]
- Yu, X.; Ji, K.; Li, H.; He, Y.; Qi, H.; Cui, G. Multi-function radar work mode recognition based on clustering data annotation. Inf. Countermeas. Technol. 2023, 2, 29–46. [Google Scholar]
- Fu, Y.; Huang, J.; Wang, J.; Dang, T.; Li, Y.; Sun, Z. Overview of multifunction phased array radar behavior recognition. Telecommun. Eng. 2024, 64, 643–654. [Google Scholar]
- Ma, S. Research on Key Technologies of Multifunction Radar Electronic Intelligence Signal Processing. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Ou, J. Research on Behavior Recognition and Prediction Technology of Multifunction Radar. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2017. [Google Scholar]
- Liu, Z.; Yuan, S.; Kang, S. Semantic coding and model reconstruction of multifunctional radar pulse train. J. Radars 2021, 10, 559–570. [Google Scholar]
- Pan, J.; Xiong, J.; Zhuo, Y. Working mode recognition of non-specific radar based on ResNet-SVM learning framework. Sensors 2023, 23, 3123. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Sun, M.; Tang, X.; Tian, X.; Yu, C. Multifunction radar working mode recognition based on entropy map. J. Detect. Control 2024, 46, 129–138. [Google Scholar]
- Liu, S.; Zhao, S.; Wang, H. New advances in radar emitter recognition technology. J. China Acad. Electron. Inf. Technol. 2022, 17, 523–533. [Google Scholar]
- Xu, J. Research on Radar Emitter Recognition Technology Based on Deep Learning. Ph.D. Thesis, Xidian University, Xi’an, China, 2019. [Google Scholar]
- Zhang, Z.; Li, Y.; Zhai, Q.; Li, Y.; Gao, M. Mode recognition of multi-function radars for few-shot learning based on compound alignments. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5328–5342. [Google Scholar] [CrossRef]
- Zhai, Q.; Li, Y.; Zhang, Z.; Li, Y.; Wang, S. Few-shot recognition of multi-function radar modes via refined prototypical random walk network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5567–5578. [Google Scholar]
- Ye, F.; Zhang, W.; Gao, J.; Jiang, S. Radar small-sample working pattern recognition based on domain adaptation. In Proceedings of the 2023 IEEE 6th International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 9–11 September 2023; pp. 1–4. [Google Scholar]
- Zhao, K.; Jin, X.; Wang, Y. A survey of few-shot learning research. J. Softw. 2021, 32, 349–369. [Google Scholar]
- Li, Q.; Zhang, W.; Jin, Q.; Liu, K.; Sun, W.; Jiang, T.; Peng, J. Recognition of multifunctional radar working modes with small samples based on knowledge prototypical network. Acta Electron. Sin. 2022, 50, 1344–1350. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Lin, J. TapNet: Multivariate time series classification with attentional prototypical network. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; Volume 34, pp. 6845–6852. [Google Scholar]
- Fawaz, H.I.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. InceptionTime: Finding AlexNet for time series classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Li, G.; Choi, B.; Xu, J.; Bhowmick, S.S.; Chun, K.P.; Wong, G.L.H. ShapeNet: A shapelet-neural network approach for multivariate time series classification. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; AAAI Press: New York, NY, USA, 2021; Volume 35, pp. 8365–8373. [Google Scholar]

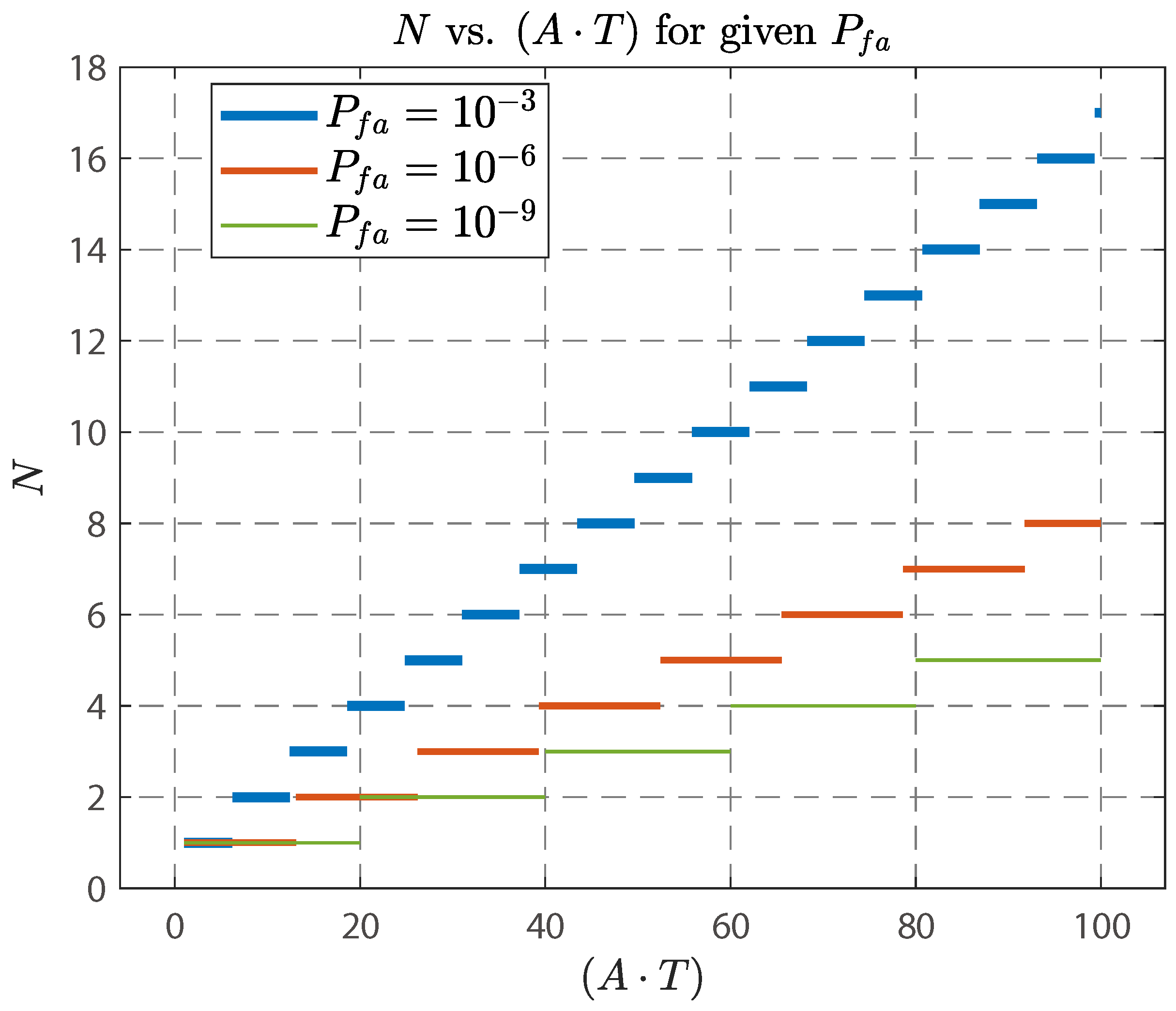


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Zhou, Q.; Li, Z.; Qian, J.; Ding, Y.; Chen, Q.; Xu, Q. Adaptive Multi-Function Radar Temporal Behavior Analysis. Remote Sens. 2024, 16, 4131. https://doi.org/10.3390/rs16224131
Xu Z, Zhou Q, Li Z, Qian J, Ding Y, Chen Q, Xu Q. Adaptive Multi-Function Radar Temporal Behavior Analysis. Remote Sensing. 2024; 16(22):4131. https://doi.org/10.3390/rs16224131
Chicago/Turabian StyleXu, Zhenjia, Qingsong Zhou, Zhihui Li, Jialong Qian, Yi Ding, Qinxian Chen, and Qiyun Xu. 2024. "Adaptive Multi-Function Radar Temporal Behavior Analysis" Remote Sensing 16, no. 22: 4131. https://doi.org/10.3390/rs16224131
APA StyleXu, Z., Zhou, Q., Li, Z., Qian, J., Ding, Y., Chen, Q., & Xu, Q. (2024). Adaptive Multi-Function Radar Temporal Behavior Analysis. Remote Sensing, 16(22), 4131. https://doi.org/10.3390/rs16224131





