Review of Research Progress on Passive Direction-of-Arrival Tracking Technology for Underwater Targets
Abstract
1. Introduction
2. Underwater Target Direction Estimation Using Passive Sonar Systems
2.1. Traditional Bearing Estimation Techniques
2.2. Discussion
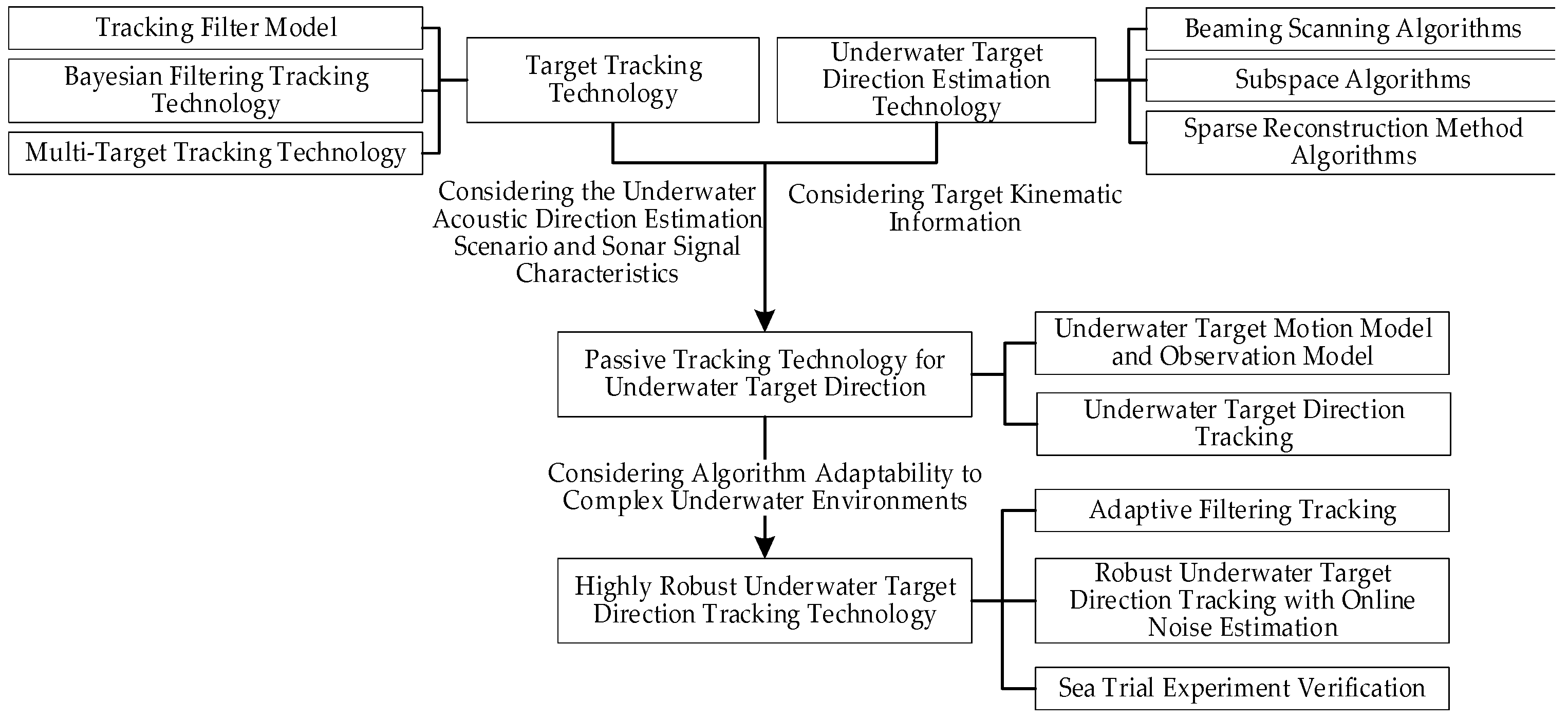
3. Target Tracking Techniques
3.1. Tracking Filter Model
3.2. Bayesian Filtering for Tracking
3.3. Multi-Target Tracking
3.4. Discussion
4. Underwater Target Bearing Passive Tracking Technology
4.1. Underwater Target Bearing Motion Model and Observation Model
4.1.1. Target Motion Model
4.1.2. Measurement Model
4.2. Underwater Target Bearing Tracking
4.2.1. Single Target Bearing Tracking
- Algorithm 1: EKF Target Bearing Tracking Algorithm
4.2.2. Multi-Target Bearing Tracking
- Algorithm 2: GM-CPHD Filtering Bearing Tracking Algorithm
4.3. Discussion
5. High-Robustness Adaptive Underwater Target Tracking
5.1. Adaptive Filtering and Tracking
5.2. Robust Underwater Target Bearing Tracking Based on Adaptive Filtering for Online Noise Estimation
- (1)
- Robust Underwater Target Bearing Tracking Based on the Improved Sage–Husa Algorithm
- (2)
- Robust Underwater Target Bearing Tracking Based on Variational Bayesian Method
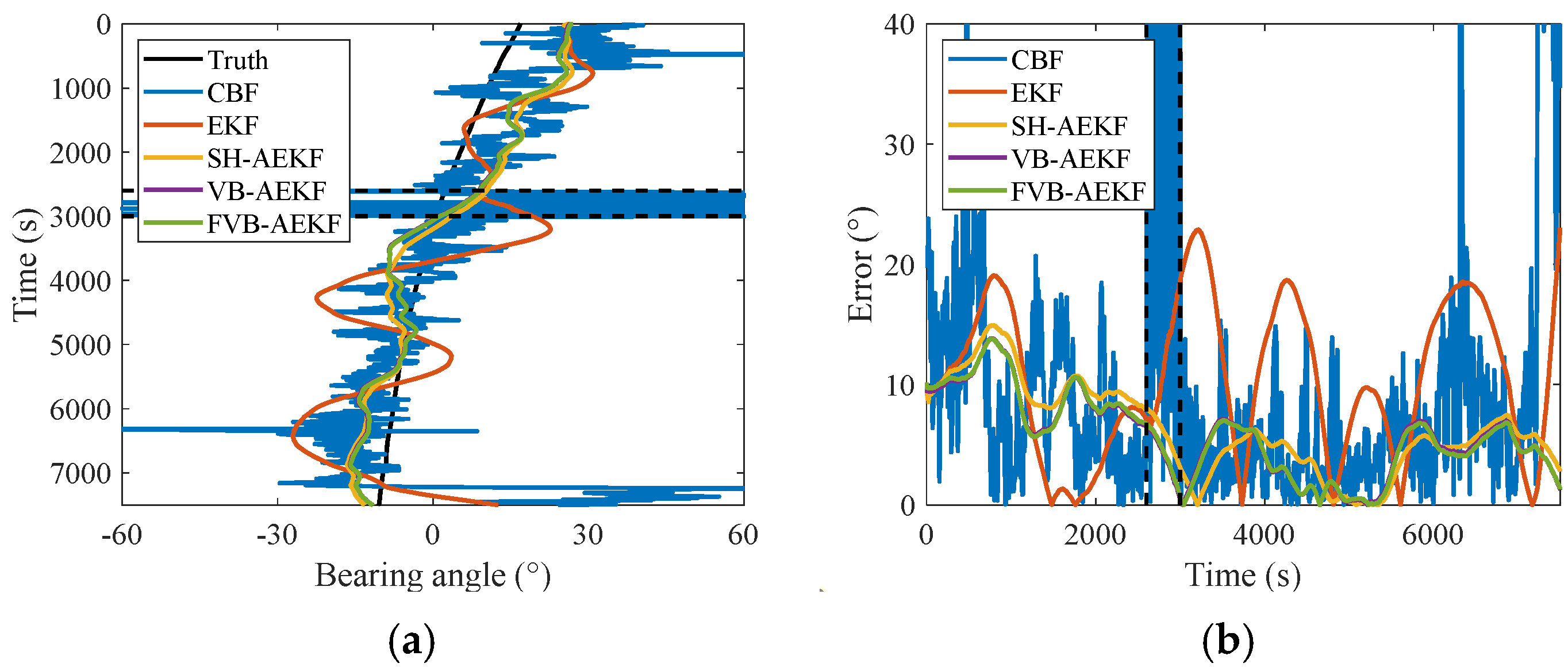
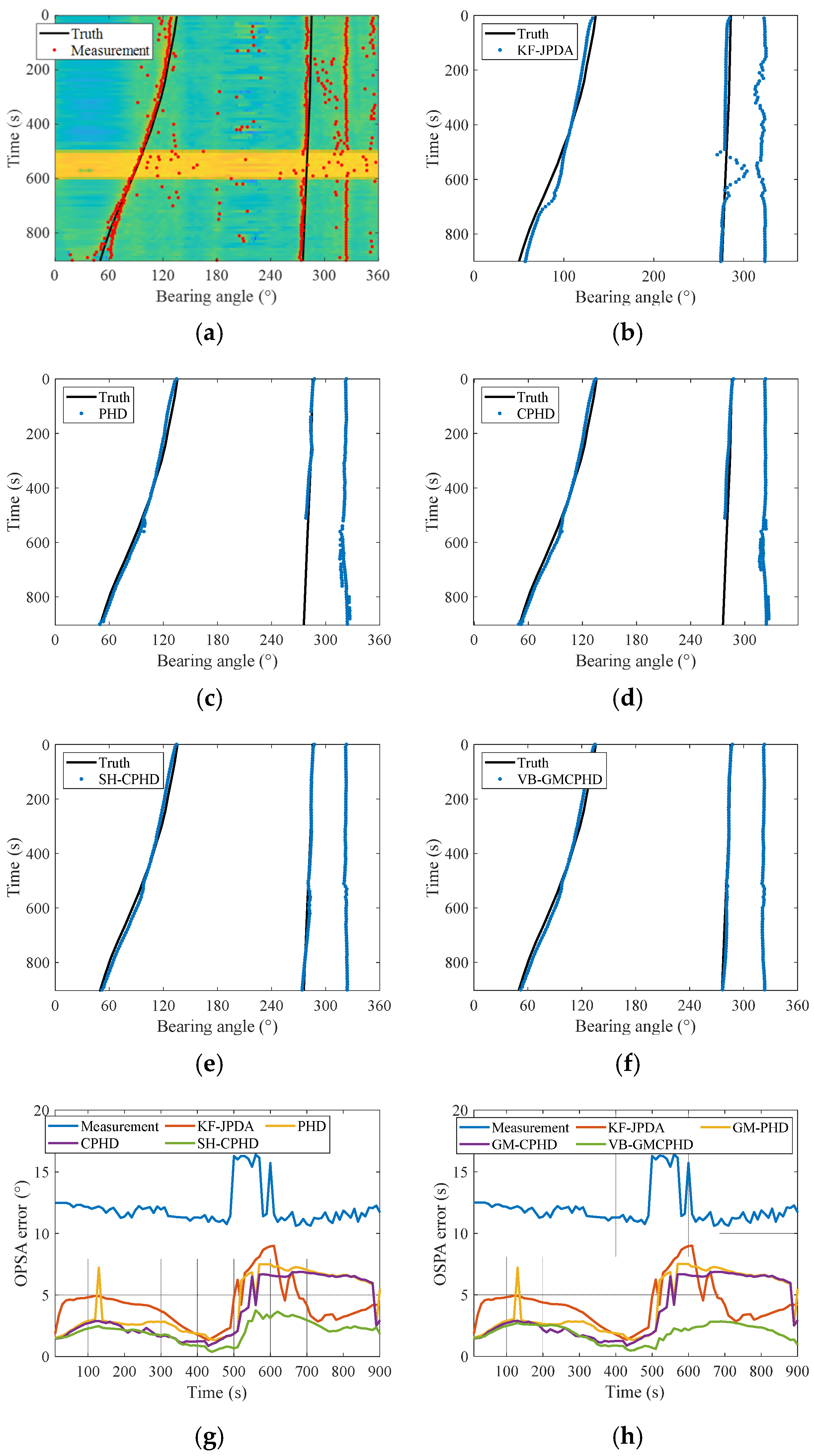
5.3. Overview of Sea Trial Experimental Data for Robust Underwater DOA Tracking Algorithms
5.3.1. Sea Trial Data Processing for Single Underwater Target Bearing Tracking
5.3.2. Processing of Experimental Data from Underwater Multi-Target Bearing Tracking Sea Trial
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hou, X.; Qiao, G.; Zhou, J.; Yang, Y. Adaptive tracking algorithm for underwater maneuvering target based on vector dual quaternions. J. Harbin Eng. Univ. 2020, 41, 1444–1449, 1463. [Google Scholar]
- Hou, X.; Yang, L.; Yang, Y.; Zhou, J.; Qiao, G. Bearing-only underwater uncooperative target tracking for non-Gaussian environment using fast particle filter. IET Radar Sonar Nav. 2022, 16, 501–514. [Google Scholar] [CrossRef]
- Hou, X.; Zhou, J.; Yang, Y.; Yang, L.; Qiao, G. 3D underwater uncooperative target tracking for a time-varying non-Gaussian environment by distributed passive underwater buoys. Entropy 2021, 23, 902. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Yang, Y.; Wang, Y.; Zhuo, J. Direction-of-arrival estimation of a modified sparse asymptotic minimum variance approach. Acta Acust. 2016, 41, 465–476. [Google Scholar]
- Yao, L.; Liu, X.; Cao, J.; Wang, S.; Zhang, D.; Wang, Y. Weighted beamspace direction-of-arrival estimation based on subarrays. Acta Acust. 2020, 45, 497–505. [Google Scholar]
- Yang, Y.; Zhang, Y.; Yang, L. Wideband sparse spatial spectrum estimation using matrix filter with nulling in a strong interference environment. J. Acoust. Soc. Am. 2018, 143, 3891–3898. [Google Scholar] [CrossRef]
- Yan, F.; Jin, M.; Qiao, X. Low-complexity DOA estimation based on compressed MUSIC and its performance analysis. IEEE Trans. Signal Process. 2013, 61, 1915–1930. [Google Scholar] [CrossRef]
- Cao, R.; Liu, B.; Gao, F.; Zhang, X. A low-complex one-snapshot DOA estimation algorithm with massive ULA. IEEE Commun. Lett. 2017, 21, 1071–1074. [Google Scholar] [CrossRef]
- Yan, H.; Fan, H.H. Signal-selective DOA tracking for wideband cyclostationary sources. IEEE Trans. Signal Process. 2007, 55, 2007–2015. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, W.; Wu, Y.; Chen, T.; Hu, Z. Joint algorithm based on interference suppression and Kalman filter for bearing-only weak target robust tracking. IEEE Access 2019, 7, 131653–131662. [Google Scholar] [CrossRef]
- El-Hawary, F.; Jing, Y. Robust regression-based EKF for tracking underwater targets. IEEE J. Ocean. Eng. 1995, 20, 31–41. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, X.; Yang, Y. Robust underwater direction-of-arrival tracking with uncertain environmental disturbances using a uniform circular hydrophone array. J. Acoust. Soc. Am. 2022, 151, 4101–4113. [Google Scholar] [CrossRef] [PubMed]
- Saucan, A.A.; Chonavel, T.; Sintes, C.; Le Caillec, J.M. Marked Poisson point process PHD filter for DOA tracking. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 2621–2625. [Google Scholar]
- Saucan, A.A.; Chonavel, T.; Sintes, C.; Le Caillec, J.-M. Track before detect DOA tracking of extended targets with marked Poisson point processes. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 754–760. [Google Scholar]
- Saucan, A.A.; Chonavel, T.; Sintes, C.; Le Caillec, J.M. CPHD-DOA tracking of multiple extended sonar targets in impulsive environments. IEEE Trans. Signal Process. 2016, 64, 1147–1160. [Google Scholar] [CrossRef]
- Masnadi-Shirazi, A.; Rao, B.D. A covariance-based superpositional CPHD filter for multisource DOA tracking. IEEE Trans. Signal Process. 2017, 66, 309–323. [Google Scholar] [CrossRef]
- Li, G.; Wei, P.; Li, Y.; Chen, Y. A labeled multi-Bernoulli filter for multisource DOA tracking. In Proceedings of the 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 23–26 October 2019; pp. 1–6. [Google Scholar]
- Zhao, J.; Gui, R.; Dong, X. A new measurement association mapping strategy for DOA tracking. Digit. Signal Process. 2021, 118, 103228. [Google Scholar] [CrossRef]
- Yardim, C.; Michalopoulou, Z.H.; Gerstoft, P. An overview of sequential Bayesian filtering in ocean acoustics. IEEE J. Ocean. Eng. 2011, 36, 71–89. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, H.; Wang, S. Principles of Kalman Filtering and Integrated Navigation, 3rd ed.; Northwestern Polytechnical University Press: Xi’an, China, 2015; pp. 33–35. [Google Scholar]
- Guo, X.; Ge, F.; Guo, L. Improved adaptive Kalman filtering and its application in acoustic maneuvering target tracking. Acta Acust. 2011, 36, 611–618. [Google Scholar]
- Sun, X.; Li, R.; Hu, P. A tracking filter method of active sonar subject to unknown target maneuvering. Acta Acust. 2016, 41, 371–378. [Google Scholar]
- Hu, Y.; Sun, J. Study of underwater passive motion target analysis (TMA) in revised extended Kalman filter. Acta Acust. 2002, 27, 449–454. [Google Scholar]
- Koteswara Rao, S.; Raja Rajeswari, K.; Lingamurty, K.S. Unscented Kalman filter with application to bearings-only target tracking. IETE J. Res. 2009, 55, 63–67. [Google Scholar]
- Wang, P.; Liu, Y. Underwater target tracking algorithm based on improved adaptive IMM-UKF. J. Electron. Inf. Technol. 2022, 44, 1999–2005. [Google Scholar]
- Leong, P.H.; Arulampalam, S.; Lamahewa, T.A.; Abhayapala, T.D. A Gaussian-sum based cubature Kalman filter for bearings-only tracking. IEEE T. Aero. Elec. Sys. 2013, 49, 1161–1176. [Google Scholar] [CrossRef]
- Shi, G.; Yan, S.; Hao, C.; Hou, C.; Liu, Y. Target tracking algorithm for underwater ranges-only long baseline system with incomplete measurements. Acta Acust. 2019, 44, 480–490. [Google Scholar]
- Orton, M.; Fitzgerald, W. A Bayesian approach to tracking multiple targets using sensor arrays and particle filters. IEEE Trans. Signal Process. 2002, 50, 216–223. [Google Scholar] [CrossRef]
- Jin, S.; Li, Y.; Huang, H. A unified method for underwater multi-target bearing detection and tracking. Acta Acust. 2019, 44, 503–512. [Google Scholar]
- Qiu, W.; Li, L.; Lei, P.; Wang, Z. Multiple targets tracking by using probability data association and cubature Kalman filter. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–5. [Google Scholar]
- Li, X.; Willett, P.; Baum, M.; Baum, M.; Li, Y. PMHT approach for underwater bearing-only multisensory-multitarget tracking in clutter. IEEE J. Ocean. Eng. 2016, 41, 831–839. [Google Scholar] [CrossRef]
- Xie, Z.; Jiang, C.; Wu, J.; Fang, Z.; Li, J. Method of multi-platform cooperative localization and tracking for underwater targets. Acta Acust. 2021, 46, 1028–1038. [Google Scholar]
- Li, X.; Li, Y.; Lu, X.; Zhao, C.; Yu, J. Underwater bearing-only multitarget tracking in dense clutter environment based on PMHT. J. Northwestern Polytech. Univ. 2020, 38, 359–365. [Google Scholar] [CrossRef]
- Yang, F.; Wang, Y.-Q.; Liang, Y.; Pan, Q. A survey of PHD filter based multi-target tracking. Acta Autom. Sin. 2013, 39, 1944–1956. [Google Scholar] [CrossRef]
- Wang, X.; Han, C.; Lian, F. Research and latest developments on target tracking methods based on random finite sets. J. Eng. Math. 2012, 29, 567–578. [Google Scholar]
- Mahler, R.P.S. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multitarget filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Clark, D.E.; Panta, K.; Vo, B.N. The GM-PHD filter multiple target tracker. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Mahler, R. A theory of PHD filters of higher order in target number. Proc. SPIE 2006, 6235, 193–204. [Google Scholar]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Yang, Y. Research on Sonar Beamforming and High-Resolution Direction Estimation Technology in Beam Domain. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2002. [Google Scholar]
- Lee, J.H.; Park, Y.; Gerstoft, P. Compressive frequency-difference direction-of-arrival estimation. J. Acoust. Soc. Am. 2023, 154, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Cong, J.; Wang, X.; Huang, M.; Wan, L. Robust DOA estimation method for MIMO radar via deep neural networks. IEEE Sens. J. 2020, 21, 7498–7507. [Google Scholar] [CrossRef]
- Cheng, Z.; Liao, B. QoS-aware hybrid beamforming and DOA estimation in multi-carrier dual-function radar-communication systems. IEEE J. Sel. Areas Commun. 2022, 40, 1890–1905. [Google Scholar] [CrossRef]
- Yu, Y.; Mei, J.; Zhai, C.; Hui, J.; Hui, J. Sea trial researches on the measurements of passive source space distribution imaging and positioning. Acta Acust. 2009, 34, 103–109. [Google Scholar]
- Yang, Y.; Yang, L.; Tang, J.; Feng, J. Sonar System Beamforming and Accurate Target Direction Estimation; Harbin Engineering University Press: Harbin, China, 2018. [Google Scholar]
- Douglass, A.S.; Song, H.C.; Dowling, D.R. Performance comparisons of frequency-difference and conventional beamforming. J. Acoust. Soc. Am. 2017, 142, 1663–1673. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Paulraj, A.; Kailath, T. ESPRIT--A subspace rotation approach to estimation of parameters of cisoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1340–1342. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Dogan, M.C.; Mendel, J.M. Applications of cumulants to array processing. I. aperture extension and array calibration. IEEE Trans. Signal Process. 1995, 43, 1200–1216. [Google Scholar] [CrossRef]
- Chevalier, P.; Ferréol, A.; Albera, L. High-resolution direction finding from higher order statistics: The 2rmq-MUSIC algorithm. IEEE Trans. Signal Process. 2006, 54, 2986–2997. [Google Scholar] [CrossRef]
- Gonen, E.; Mendel, J.M.; Dogan, M.C. Applications of cumulants to array processing. IV. Direction finding in coherent signals case. IEEE Trans. Signal Process. 1997, 45, 2265–2276. [Google Scholar] [CrossRef]
- Zeng, W.J.; Li, X.L. High-resolution multiple wideband and nonstationary source localization with unknown number of sources. IEEE Trans. Signal Process. 2010, 58, 3125–3136. [Google Scholar] [CrossRef]
- Bush, D.; Xiang, N. A model-based Bayesian framework for sound source enumeration and direction of arrival estimation using a coprime microphone array. J. Acoust. Soc. Am. 2018, 143, 3934–3945. [Google Scholar] [CrossRef]
- Madadi, Z.; Anand, G.V.; Premkumar, A.B. Three-dimensional localization of multiple acoustic sources in shallow ocean with non-Gaussian noise. Digit. Signal Process. 2014, 32, 85–99. [Google Scholar] [CrossRef]
- Padois, T.; Berry, A. Orthogonal matching pursuit applied to the deconvolution approach for the mapping of acoustic sources inverse problem. J. Acoust. Soc. Am. 2015, 138, 3678–3685. [Google Scholar] [CrossRef]
- Chen, T.; Wu, H.; Liu, L. A joint Doppler frequency shift and DOA estimation algorithm based on sparse representations for collocated TDM-MIMO radar. J. Appl. Math. 2014, 2014, 1–9. [Google Scholar]
- Markopoulos, P.P.; Tsagkarakis, N.; Pados, D.A.; Karystinos, G.N. Direction-of-arrival estimation by L1-norm principal components. In Proceedings of the 2016 IEEE International Symposium on Phased Array Systems and Technology (PAST), Waltham, MA, USA, 18–21 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Zheng, J.; Kaveh, M. Sparse spatial spectral estimation: A covariance fitting algorithm, performance and regularization. IEEE Trans. Signal Process. 2013, 61, 2767–2777. [Google Scholar] [CrossRef]
- Xenaki, A.; Gerstoft, P.; Mosegaard, K. Compressive beamforming. J. Acoust. Soc. Am. 2014, 136, 260–271. [Google Scholar] [CrossRef] [PubMed]
- Stoica, P.; Babu, P.; Li, J. SPICE: A sparse covariance-based estimation method for array processing. IEEE Trans. Signal Process. 2010, 59, 629–638. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. New method of sparse parameter estimation in separable models and its use for spectral analysis of irregularly sampled data. IEEE Trans. Signal Process. 2010, 59, 35–47. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. A discretization-free sparse and parametric approach for linear array signal processing. IEEE Trans. Signal Process. 2014, 62, 4959–4973. [Google Scholar] [CrossRef]
- Abeida, H.; Zhang, Q.; Li, J.; Merabtine, N. Iterative sparse asymptotic minimum variance based approaches for array processing. IEEE Trans. Signal Process. 2012, 61, 933–944. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–46. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2015; Volume 51, p. 591. [Google Scholar]
- Senne, K. Review of Stochastic Processes and Filtering Theory-Andrew H. Jazwinski. IEEE Trans. Autom. Control 1972, 17, 752–753. [Google Scholar] [CrossRef]
- Schmidt, S.F. The Kalman filter-Its recognition and development for aerospace applications. J. Guid. Control Dyn. 2012, 4, 4–7. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, Z.; Fu, X. Attitude determination for MAVs using a Kalman filter. Tsinghua Sci. Technol. 2008, 13, 593–597. [Google Scholar] [CrossRef]
- Murrell, J.W. Precision attitude determination for multimission spacecraft. In Proceedings of the AIAA, Palo Alto, CA, USA, 7 August–9 August 1978. [Google Scholar]
- Lefferts, E.; Markley, F.; Shuster, M.D. Kalman filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrantwhyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the Advances in Computing and Communications, Seattle, WA, USA, 21–23 June 1995; pp. 1628–1632. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Signal Processing, Sensor Fusion, and Target Recognition VI; International Society for Optics and Photonics: Bellingham, WA, USA, 1997. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K.; Durrantwhyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Romanenko, A.; Castro, J.A.A.M. The unscented filter as an alternative to the EKF for nonlinear state estimation: A simulation case study. Comput. Chem. Eng. 2004, 28, 347–355. [Google Scholar] [CrossRef]
- Doucet, A. An introduction to sequential Monte Carlo methods. Seq. Monte Carlo Methods Pract. 2001, 18, 3–14. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hammersley, J.M.; Morton, K.W. Poor man’s Monte Carlo. J. R. Stat. Soc. Ser. B Methodol. 1954, 16, 23–38. [Google Scholar] [CrossRef]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F-Radar Signal Process. IET 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Pitt, M.K.; Shephard, N. Filtering via simulation: Auxiliary particle filters. J. Am. Stat. Assoc. 1999, 94, 590–599. [Google Scholar] [CrossRef]
- Wang, H. Improved extend Kalman particle filter based on Markov chain Monte Carlo for nonlinear state estimation. In Proceedings of the 2012 2nd International Conference on Uncertainty Reasoning and Knowledge Engineering (URKE), Jakarta, Indonesia, 14–15 August 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 281–285. [Google Scholar]
- Bar-Shalom, Y.; Fortmann, T.E.; Cable, P.G. Tracking and Data Association. J. Acoust. Soc. Am. 1990, 87, 918–919. [Google Scholar] [CrossRef]
- Blackman, S. Design and Analysis of Modern Tracking Systems; Artech House: New York, NY, USA, 1999. [Google Scholar]
- Bar-Shalom, Y. Multi-Target Multi-Sensor Tracking: Principles and Techniques; YBS Publishing: Storrs, CT, USA, 1995. [Google Scholar]
- Bar-Shalom, Y.; Tse, E. Tracking in a cluttered environment with probabilistic data association. Automatica 1975, 11, 451–460. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, M.; Zhang, S.; Zheng, R.; Fan, Z. Feature-Aided Passive Tracking of Noncooperative Multiple Targets Based on the Underwater Sensor Networks. IEEE Internet Things J. 2023, 10, 4579–4591. [Google Scholar] [CrossRef]
- Baser, E.; Bilik, I. Modified unscented particle filter using variance reduction factor. In Proceedings of the Radar Conference, Arlington, VI, USA, 10–14 May 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 893–898. [Google Scholar]
- Chen, J.; Leung, H.; Lo, T.; Litva, J.; Blanchette, M. A modified probabilistic data association filter in a real clutter environment. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 300–313. [Google Scholar] [CrossRef]
- Roecker, J.A. A class of near-optimal JPDA algorithms. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 504–510. [Google Scholar] [CrossRef]
- Musicki, D.; Evans, R. Joint integrated probabilistic data association: JIPDA. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1093–1099. [Google Scholar] [CrossRef]
- Zhu, Z. Iterated joint probabilistic data association. In Proceedings of the CIE International Conference of Radar, Beijing, China, 8–10 October 1996; pp. 434–438. [Google Scholar]
- Deb, S.; Yeddanapudi, M.; Pattipati, K.; Bar-Shalom, Y. A generalized S-D assignment algorithm for multisensor-multitarget state estimation. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 523–538. [Google Scholar]
- Lin, L.; Bar-Shalom, Y.; Kirubarajan, T. New assignment-based data association for tracking move-stop-move targets. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 714–725. [Google Scholar] [CrossRef]
- Reid, D.B. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. Analytic implementations of the cardinalized probability hypothesis density filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, M.; Zhang, S.; Zheng, R.; Dong, S.; Liu, Z. Underwater Target Tracking Based on the Feature-Aided GM-PHD Method. IEEE Trans. Instrum. Meas. 2024, 73, 5500412. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, Y.; Zhang, L.; Chen, B.; Yu, X. Underwater Multitarget Tracking Method Based on Threshold Segmentation. IEEE J. Ocean. Eng. 2023, 48, 1255–1269. [Google Scholar] [CrossRef]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Feng, L.; Chen, L.; Han, C.; Chen, H. Convergence analysis for the SMC-MeMBer and SMC-CBMeMBer filters. J. Appl. Math. 2012, 3, 701–708. [Google Scholar]
- Bar-Shalom, Y.; Willett, P.K.; Tian, X. Tracking and Data Fusion; YBS Publishing: Storrs, CT, USA, 2011. [Google Scholar]
- Erdinc, O.; Willett, P.; Bar-Shalom, Y. Probability hypothesis density filter for multitarget multisensor tracking. In Proceedings of the 8th International Conference on Information Fusion, Philadelphia, PA, USA, 27 June–1 July 2005; pp. 1–8. [Google Scholar]
- Mählisch, M.; Schweiger, R.; Ritter, W.; Dietmayer, K. Multisensor vehicle tracking with the probability hypothesis density filter. In Proceedings of the 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Fränken, D.; Schmidt, M.; Ulmke, M. “Spooky action at a distanc” in the cardinalized probability hypothesis density filter. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1657–1664. [Google Scholar] [CrossRef]
- Reuter, S. Multi-object tracking using random finite sets. Diss. Universität Ulm 2014. [Google Scholar]
- Vo, B.-T.; Vo, B.-N.; Hoseinnezhad, R.; Mahler, R. Robust multiBernoulli filtering. IEEE J. Sel. Top. Signal Process. 2013, 7, 399–409. [Google Scholar] [CrossRef]
- Reuter, S.; Meissner, D.; Wilking, B.; Dietmayer, K. Cardinality balanced multi-target multi-Bernoulli filtering using adaptive birth distributions. In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey 9–12 July 2013; pp. 1608–1615. [Google Scholar]
- Dunne, D.; Kirubarajan, T. Multiple model multi-Bernoulli filters for manoeuvering targets. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2679–2692. [Google Scholar] [CrossRef]
- Shen, X.; Song, Z.; Fan, H.; Hu, Q. A general cardinalized probability hypothesis density filter. EURASIP J. Adv. Signal Process. 2022, 2022, 94. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Svensson, L. Trajectory PHD and CPHD filters. IEEE Trans. Signal Process. 2019, 67, 5702–5714. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Papi, F.; Vo, B.N.; Vo, B.T.; Fantacci, C.; Beard, M. Generalized labeled multi-Bernoulli approximation of multi-object densities. IEEE Trans. Signal Process. 2015, 63, 5487–5497. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, J.; Sun, M.; Zhang, X.; Wang, Y. A Modified δ-Generalized Labeled Multi-Bernoulli Filtering for Multi-Source DOA Tracking with Coprime Array. IEEE Trans. Wireless Commun. 2023, 22, 9424–9437. [Google Scholar] [CrossRef]
- Cai, H.; Houssineau, J.; Jones, B.A.; Jah, M.; Zhang, J. Possibility Generalized Labeled Multi-Bernoulli Filter for Multitarget Tracking Under Epistemic Uncertainty. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1312–1326. [Google Scholar]
- Lee, J.Y.; Shim, C.; Van Nguyen, H.; Nguyen, T.T.D.; Choi, H.; Kim, Y. Label Space Partition Selection for Multi-Object Tracking Using Two-Layer Partitioning. In Proceedings of the 2023 12th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 27–29 November 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Do, C.-T.; Nguyen, T.T.D.; Moratuwage, D.; Shim, C.; Chung, Y.D. Multi-object tracking with an adaptive generalized labeled multi-Bernoulli filter. Signal Process. 2022, 196, 108532. [Google Scholar] [CrossRef]
- Shim, C.; Vo, B.-T.; Vo, B.-N.; Ong, J.; Moratuwage, D. Linear complexity Gibbs sampling for generalized labeled multi-Bernoulli filtering. IEEE Trans. Signal Process. 2023, 71, 1981–1994. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The Labeled multi Bernoulli filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Nguyen, T.T.D.; Shim, C.; Anuar, M. The Smooth Trajectory Estimator for LMB Filters. In Proceedings of the 2023 12th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 27–29 November 2023; pp. 115–120. [Google Scholar]
- Li, G.; Battistelli, G.; Chisci, L.; Gao, L.; Wei, P. Distributed Joint Detection, Tracking, and Classification via Labeled Multi-Bernoulli Filtering. IEEE Trans. Cybernet. 2024, 54, 1429–1441. [Google Scholar]
- Li, G.; Li, G.; He, Y. Distributed Multiple Resolvable Group Targets Tracking Based on Hypergraph Matching. IEEE Sens. J. 2023, 23, 9669–9676. [Google Scholar]
- Uney, M.; Stinco, P.; Dreo, R.; Micheli, M.; De Magistris, G.; Tesei, A. Passive Sensor Fusion and Tracking in Underwater Surveillance with the GLMB model. In Proceedings of the 2022 25th International Conference on Information Fusion (FUSION), Linköping, Sweden, 4–7 July 2022; pp. 1–8. [Google Scholar]
- Mohinder, S.G. Kalman Filtering: Theory and Practice Using MATLAB; Angus, P.A., Ed.; Wiley: Hoboken, NJ, USA, 2001; pp. 133–144. [Google Scholar]
- Zhou, H.; Jing, Z.; Wang, P. Maneuvering Target Tracking; National Defense Industry Press: Beijing, China, 1991; pp. 12–13. [Google Scholar]
- Singer, R.A. Estimating optimal tracking performance for manned maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1970, AES-6, 473–483. [Google Scholar] [CrossRef]
- Moose, R.L. An adaptive state estimation solution to the maneuvering target problem. IEEE Trans. Autom. Control 1975, 20, 359–362. [Google Scholar] [CrossRef]
- Zhou, H. Statistical Model of “Current” Maneuvering Target and Adaptive Tracking Algorithm. Aeronaut. Astronaut. Sin. 1983, 4, 72–86. [Google Scholar]
- Mehrotra, K.; Mahapatra, P.R. A jerk model for tracking highly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 1094–1105. [Google Scholar] [CrossRef]
- Blom, H.A.P.; Bar-Shalom, Y. The interacting multiple model algorithm for systems with Markovian switching coefficients. IEEE Trans. Autom. Control 1988, 33, 780–783. [Google Scholar] [CrossRef]
- Dang, J. Underwater Multi-Target Tracking Theory; Northwestern Polytechnical University Press: Xi’an, China, 2009; p. 38. [Google Scholar]
- Xu, J.; Xu, M.; Zhou, X. The bearing only target tracking of UUV based on cubature Kalman filter with noise estimator. In Proceedings of the 2017 36th Chinese Control Conference, Dalian, China, 26–28 July 2017; pp. 5288–5293. [Google Scholar]
- Wang, X.; Xu, M.X.; Wang, H.B.; Wu, Y. Combination of interacting multiple models with the particle filter for three-dimensional target tracking in underwater wireless sensor networks. Math. Probl. Eng. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Zhang, J.X.; Liu, M.Q.; Fan, Z. Classify motion model via SVM to track underwater maneuvering target. In Proceedings of the 2019 IEEE International Conference on Signal Processing Communications and Computing, Dalian, China, 20–22 September 2019; pp. 1–6. [Google Scholar]
- He, C.F.; Wang, Y.Y.; Chen, C.L.; Guan, X.P. Target localization for a distributed SIMO sonar with an isogradient sound speed profile. IEEE Access 2018, 6, 29770–29783. [Google Scholar] [CrossRef]
- Ramezani, H.; Jamali-Rad, H.; Leus, G. Target localization and tracking for an isogradient sound speed profile. IEEE Trans. Signal Process. 2013, 61, 1434–1446. [Google Scholar] [CrossRef]
- Zhang, D. Research on Self-Organizing Target Tracking Algorithm Based on Underwater Wireless Sensor Networks. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2019. [Google Scholar]
- Liao, B.; Zhang, Z.G.; Chan, S.C. DOA estimation and tracking of ULAs with mutual coupling. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 891–905. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Jason, F.; Dai, W. A sequential Bayesian algorithm for DOA tracking in time-varying environments. Chin. J. Electron. 2015, 24, 140–145. [Google Scholar] [CrossRef]
- Kong, D.; Chun, J. A fast DOA tracking algorithm based on the extended Kalman filter. In Proceedings of the IEEE 2000 National Aerospace and Electronics Conference, Dayton, OH, USA, 10–12 October 2000; pp. 235–238. [Google Scholar]
- Cevher, V.; McClellan, J.H. General direction-of-arrival tracking with acoustic nodes. IEEE Trans. Signal Process. 2004, 53, 1–12. [Google Scholar] [CrossRef]
- Cevher, V.; Velmurugan, R.; McClellan, J.H. Acoustic multitarget tracking using direction-of-arrival batches. IEEE Trans. Signal Process. 2007, 55, 2810–2825. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M.; Mahler, R. Computationally-tractable approximate PHD and CPHD filters for superpositional sensors. IEEE J. Sel. Top. Signal Process. 2013, 7, 410–420. [Google Scholar] [CrossRef]
- Gao, X.; You, D.; Katayama, S. Seam tracking monitoring based on adaptive Kalman filter embedded elman neural network during high-power fiber laser welding. IEEE Trans. Ind. Electron. 2012, 59, 4315–4325. [Google Scholar] [CrossRef]
- Mehra, R. Approaches to adaptive filtering. IEEE Trans. Automat. Control 1972, 17, 693–698. [Google Scholar] [CrossRef]
- Mohamed, H.; Schwarz, K.P. Adaptive Kalman filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Karasalo, M.; Hu, X.M. An optimization approach to adaptive Kalman filtering. Automatica 2011, 47, 1785–1793. [Google Scholar] [CrossRef]
- Li, X.R.; Bar-Shalom, Y. A recursive multiple model approach to noise identification. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 671–684. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Automat. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Hartikainen, S.S.J. Variational Bayesian adaptation of noise covariance in nonlinear Kalman filtering. arXiv 2013, arXiv:1302.0681. [Google Scholar]
- Huang, D.; Leung, H.; Naser, E.S. Expectation maximization-based GPS/INS integration for land-vehicle navigation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1168–1177. [Google Scholar] [CrossRef]
- Bavdekar, V.A.; Deshpande, A.P.; Patwardhan, S.C. Identification of process and measurement noise covariance for state and parameter estimation using extended Kalman filter. J. Process Control 2011, 21, 585–601. [Google Scholar] [CrossRef]
- Ardeshiri, T.; Ozkan, E.; Orguner, U.; Gustafsson, F. Approximate Bayesian smoothing with unknown process and measurement noise covariances. IEEE Signal Process. Lett. 2015, 22, 2450–2454. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xu, B.; Wu, Z.; Chambers, J.A. A new adaptive extended Kalman filter for cooperative localization. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 353–368. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Control 2017, 63, 594–601. [Google Scholar] [CrossRef]
- Xu, G.; Huang, Y.; Gao, Z.; Zhang, Y. A computationally efficient variational adaptive Kalman filter for transfer alignment. IEEE Sens. J. 2020, 20, 13682–13693. [Google Scholar] [CrossRef]
- Hou, X.; Qiao, Y.; Zhang, B.; Yang, Y. Robust underwater direction-of-arrival tracking based on variational Bayesian extended Kalman filter. JASA Express Lett. 2023, 3, 014801. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Xiang, L.; Xu, X. DOA estimation with circular array via spatial averaging algorithm. IEEE Antenn. Wirel. Propag. Lett. 2007, 6, 74–76. [Google Scholar] [CrossRef]
- Hao, Y.; Zou, N.; Qiu, L.; Li, C.; Wang, Y.; Liang, G. Spatial rotation-based direction-of-arrival estimation for uniform circular hydrophone array. Appl. Acoust. 2021, 178, 107945. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, X.; Yang, Y. A fast variational Bayesian adaptive extended Kalman filter for robust underwater direction-of-arrival tracking. IEEE Sens. J. 2023, 23, 14709–14720. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, Y.; Hou, X. Robust underwater multi-target direction-of-arrival tracking with uncertain measurement noise. Acta Acust. 2023, 48, 605–617. [Google Scholar]
- Zhang, B.; Hou, X.; Yang, Y. Variational Bayesian cardinalized probability hypothesis density filter for robust underwater multi-target DOA tracking with uncertain measurement noise. Front. Phys. 2023, 11, 1142400. [Google Scholar]
| Type | Type of Multi-Target Filter | Reference | Accuracy | Computational Complexity |
|---|---|---|---|---|
| Data Association | NN | [84,85] | Medium Low High | |
| PDA | [86,87] | Low | ||
| JPDA | [88,89,90,91] | Medium | ||
| MHT | [96] | High | ||
| RFS | PHD | [36,37,38] | Low | |
| CPHD | [40,97,98,99] | Medium | ||
| CBMeMBer | [100,101] | Medium |
| Method | CBF | EKF | SH-AEKF | VB-AEKF | FVB-AEKF |
|---|---|---|---|---|---|
| ABEE/(°) | 19.9 | 12.2 | 7.3 | 6.5 | 6.5 |
| Date | Runing Time/(ms) | ||||
|---|---|---|---|---|---|
| CBF | EKF | SH-AEKF | VB-AEKF | FVB-AEKF | |
| Raw data | 1.12 | 0.11 | 0.13 | 0.70 | 0.34 |
| Data with noise | 1.08 | 0.11 | 0.14 | 0.75 | 0.35 |
| KF-JPDA | PHD | CPHD | SH-CPHD | VB-CPHD | |
|---|---|---|---|---|---|
| Average OSPA Error (°) | 4.26 | 4.22 | 3.71 | 2.06 | 1.97 |
| Average Running Time (ms) | 4.25 | 0.72 | 0.86 | 0.90 | 1.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Chen, Y.; Zhang, B.; Yang, Y. Review of Research Progress on Passive Direction-of-Arrival Tracking Technology for Underwater Targets. Remote Sens. 2024, 16, 4511. https://doi.org/10.3390/rs16234511
Hou X, Chen Y, Zhang B, Yang Y. Review of Research Progress on Passive Direction-of-Arrival Tracking Technology for Underwater Targets. Remote Sensing. 2024; 16(23):4511. https://doi.org/10.3390/rs16234511
Chicago/Turabian StyleHou, Xianghao, Yuxuan Chen, Boxuan Zhang, and Yixin Yang. 2024. "Review of Research Progress on Passive Direction-of-Arrival Tracking Technology for Underwater Targets" Remote Sensing 16, no. 23: 4511. https://doi.org/10.3390/rs16234511
APA StyleHou, X., Chen, Y., Zhang, B., & Yang, Y. (2024). Review of Research Progress on Passive Direction-of-Arrival Tracking Technology for Underwater Targets. Remote Sensing, 16(23), 4511. https://doi.org/10.3390/rs16234511





