Shallow Water Bathymetry Inversion Based on Machine Learning Using ICESat-2 and Sentinel-2 Data
Abstract
:1. Introduction
2. Materials and Methods
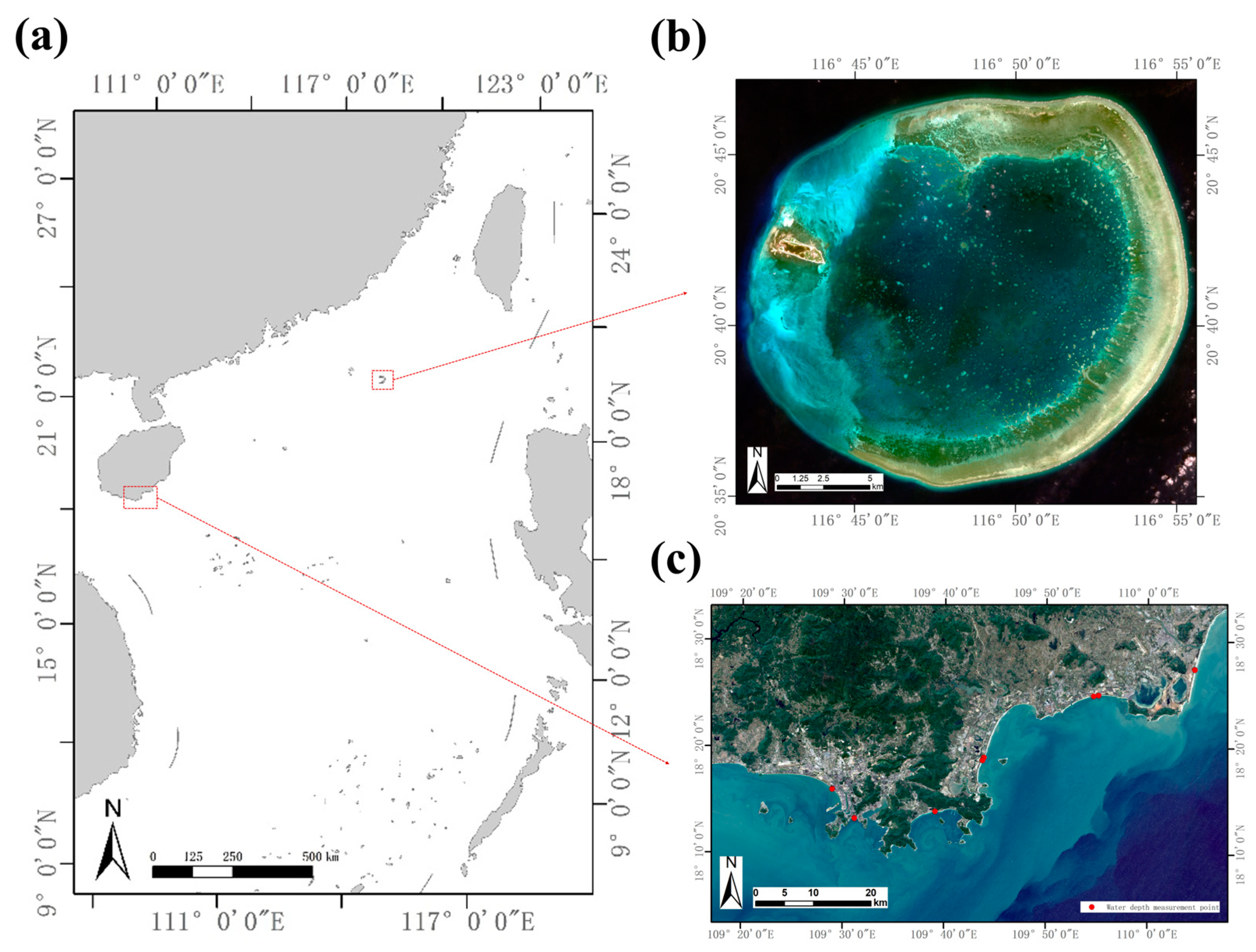
2.1. Study Area and Data
2.1.1. Study Area and In Situ Bathymetric Data
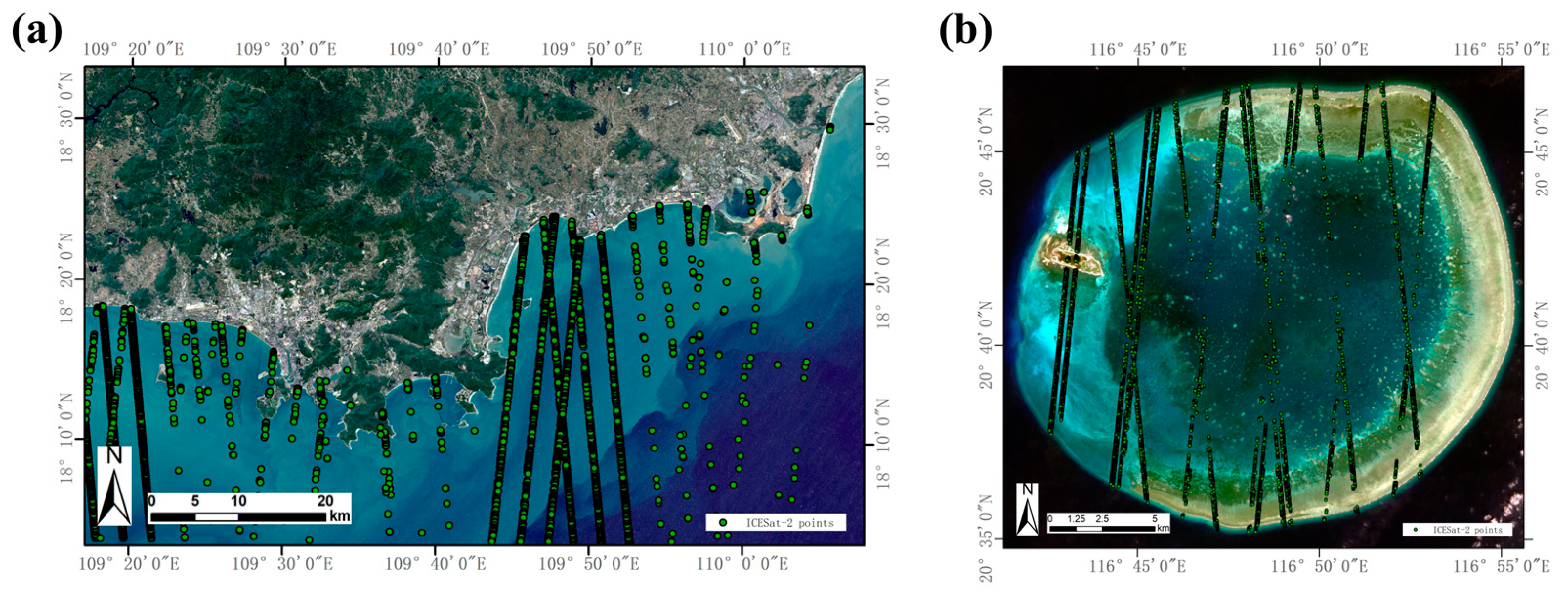
2.1.2. ICESat-2 Data
2.1.3. Sentinel-2 Data
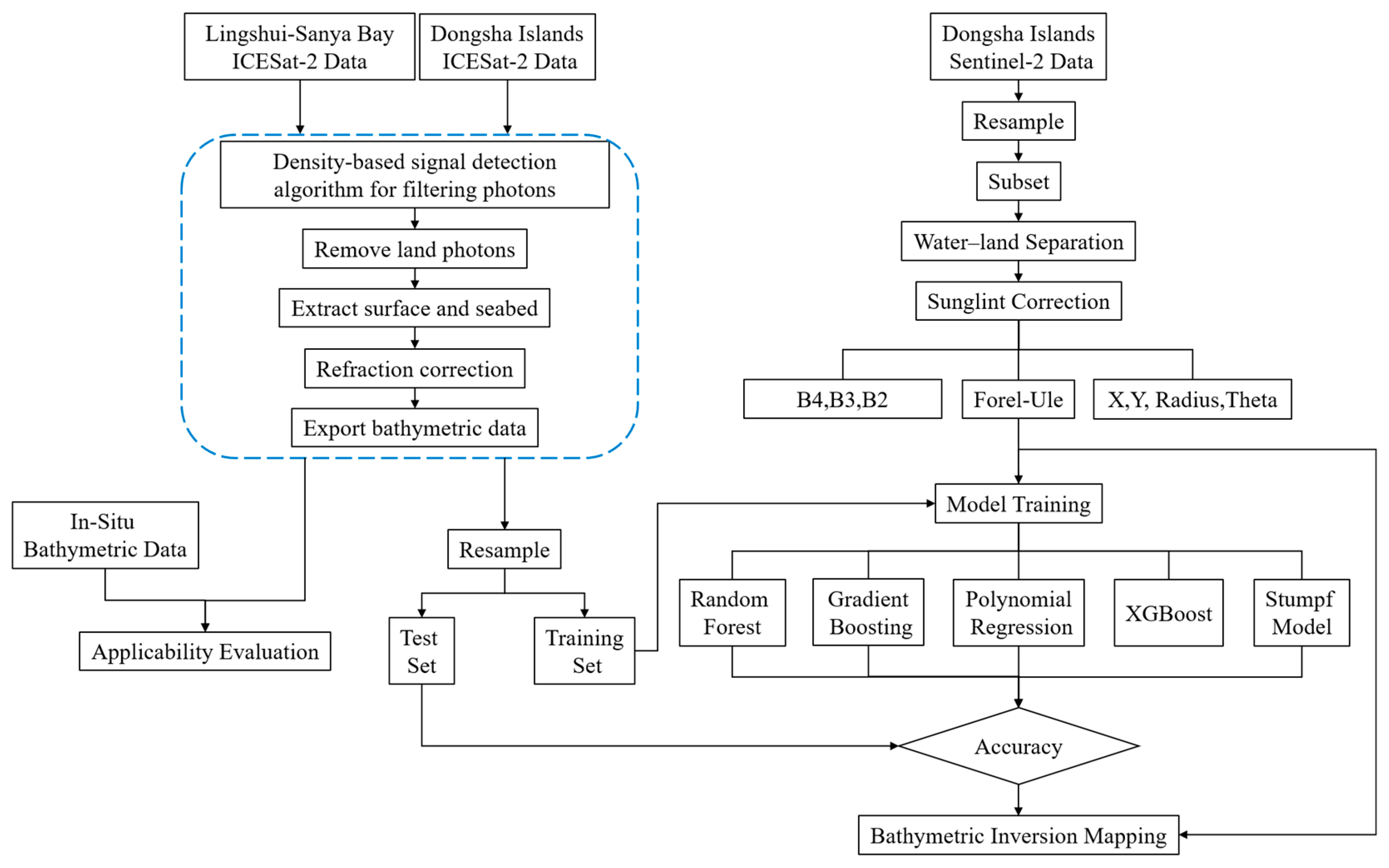
2.2. Methodology
2.2.1. Lingshui-Sanya Bay Measured Data Acquisition
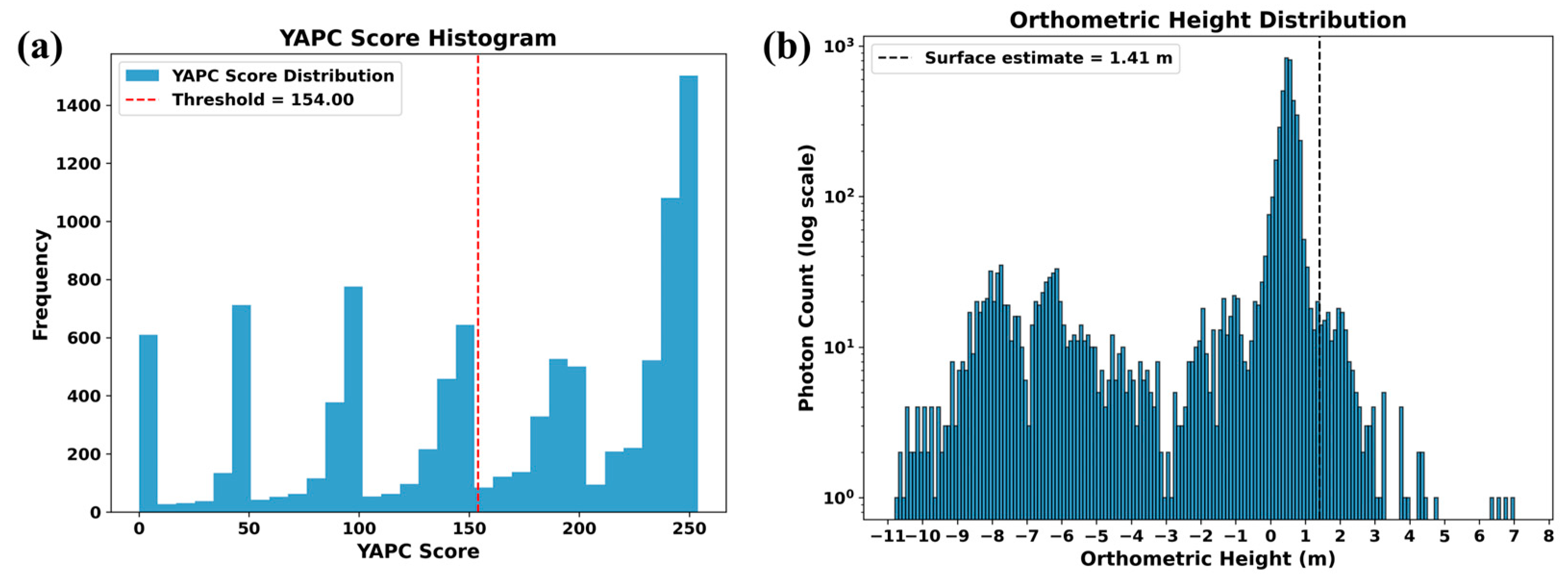
2.2.2. ICESat-2 Data Preprocessing
2.2.3. Sentinel-2 Image Preprocessing
2.2.4. Bathymetric Inversion Model for the Dongsha Islands
Creation of a Comprehensive Information Dataset
Model Training
3. Results
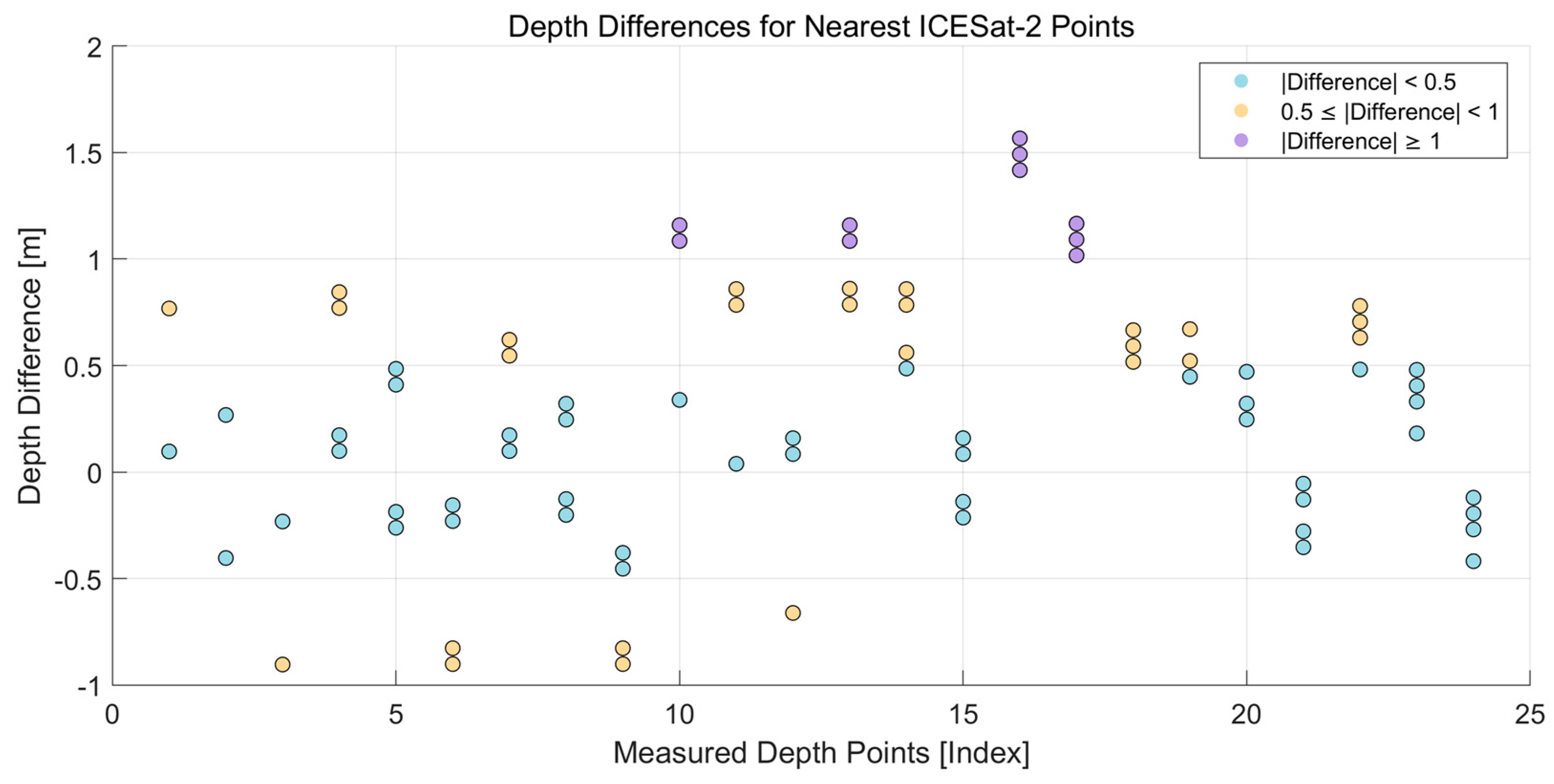
3.1. ICESat-2 Bathymetric Photon Extraction Results and Bathymetric Performance Evaluation
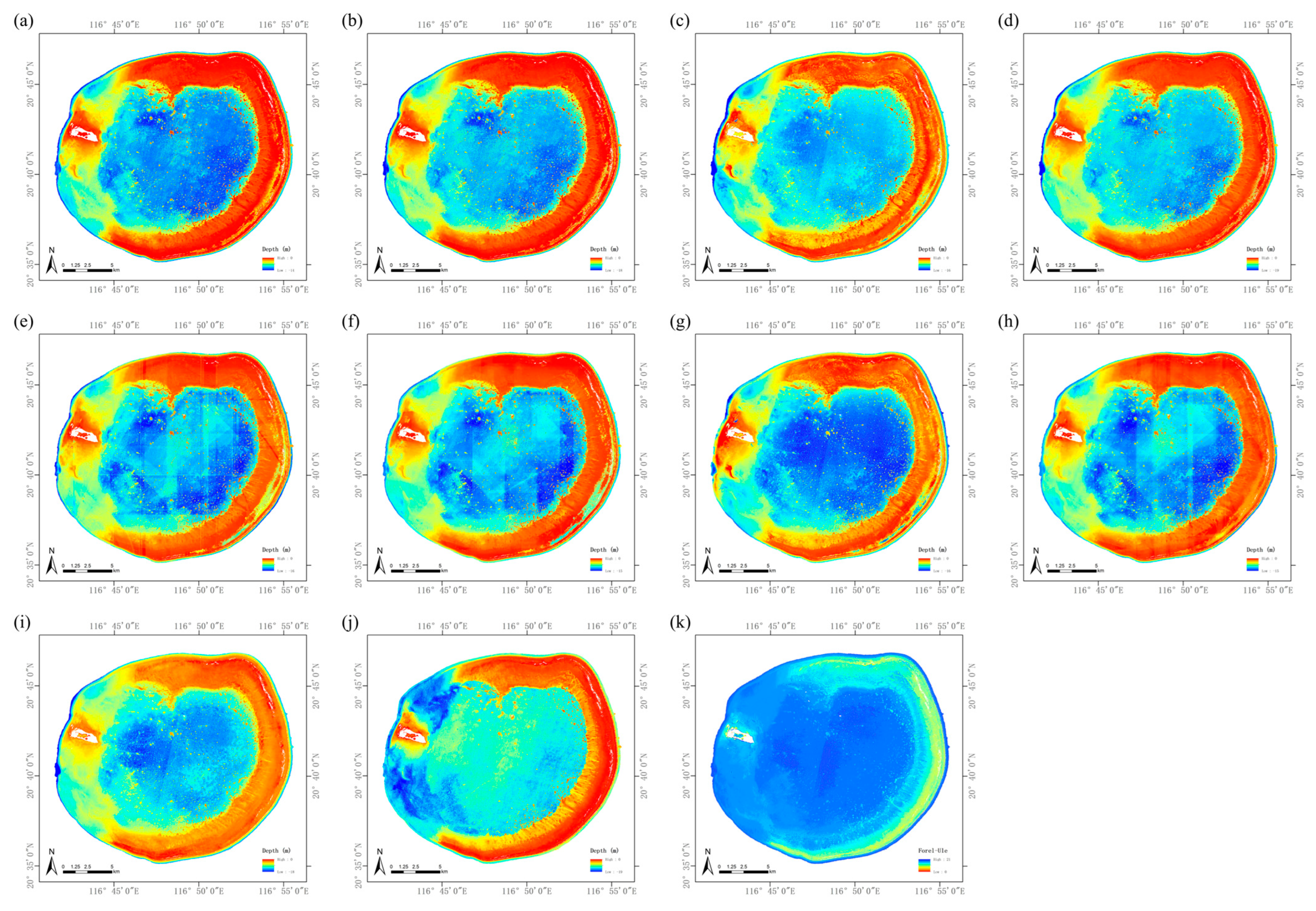
3.2. Bathymetric Inversion Based on Sentinel-2 Data
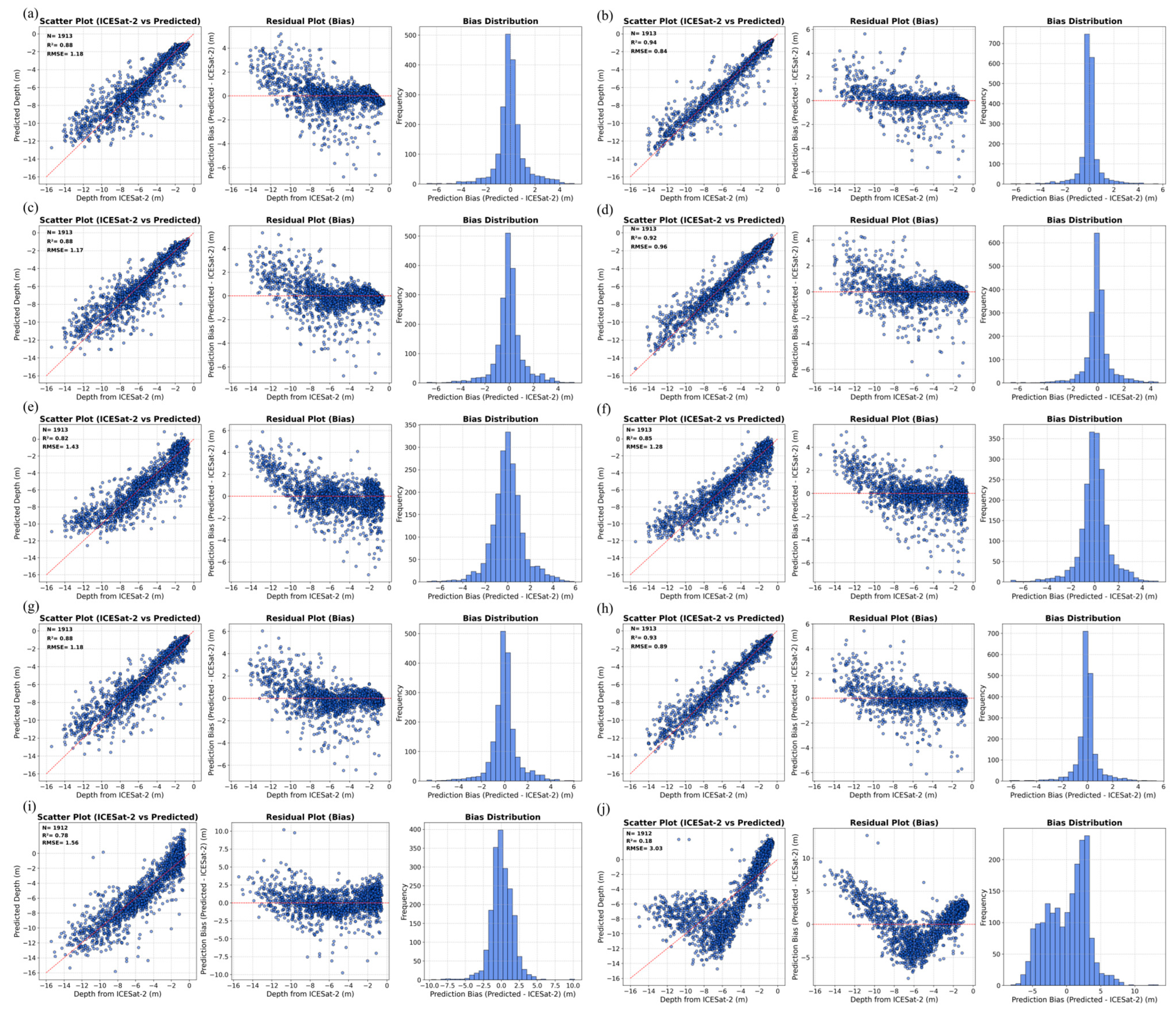
3.3. Evaluation of Model Accuracy
4. Discussion
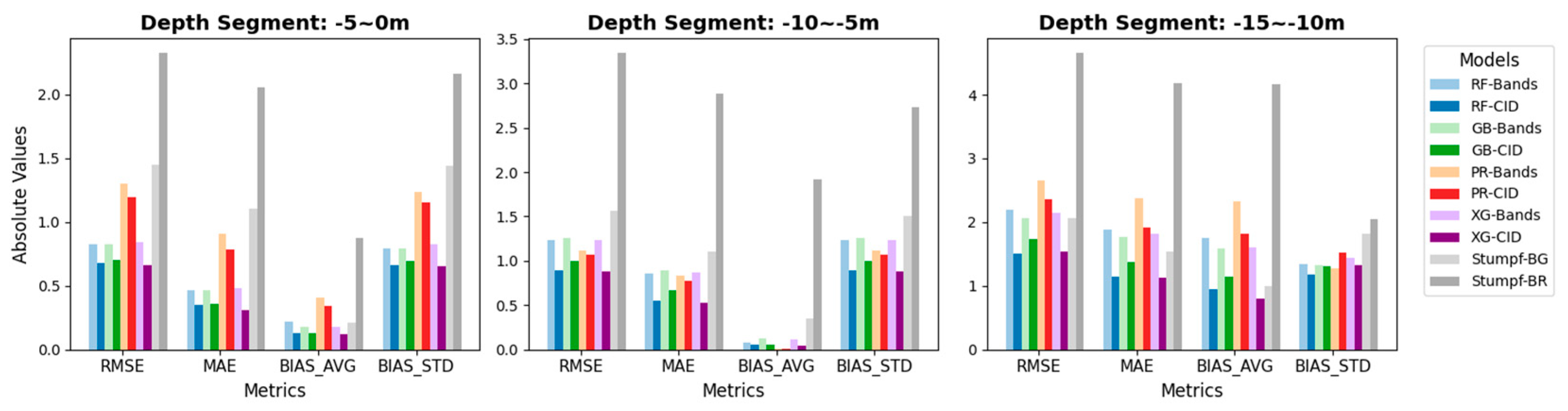
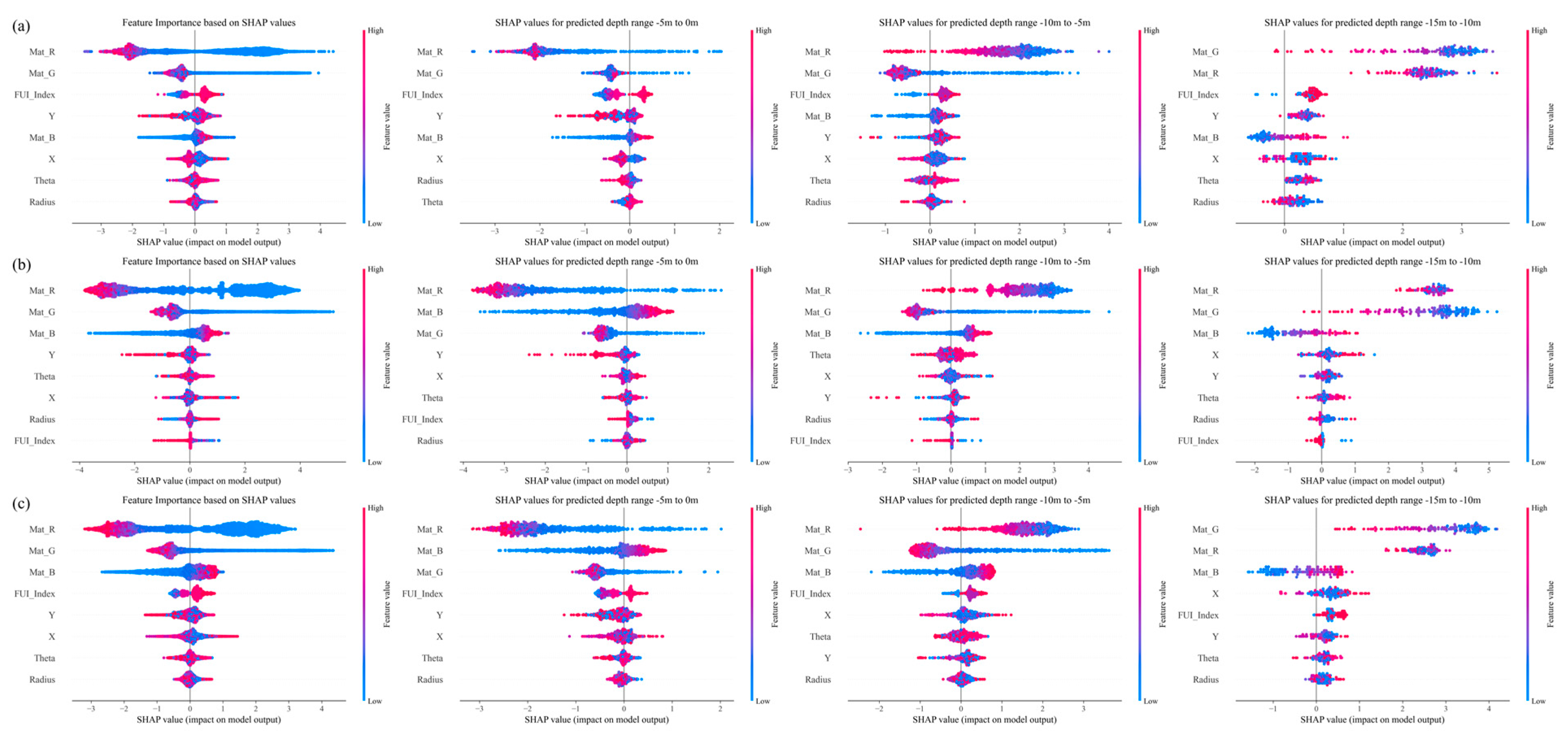
4.1. The Rationality of Feature Selection
4.2. Model Evaluation
4.3. Limitations and Directions for Improvement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; He, X.; Bai, Y.; Wang, D.; Zhu, Q.; Gong, F.; Yang, D.; Li, T. Satellite retrieval of benthic reflectance by combining lidar and passive high-resolution imagery: Case-I water. Remote Sens. Environ. 2022, 272, 112955. [Google Scholar] [CrossRef]
- da Silveira, C.B.L.; Strenzel, G.M.R.; Maida, M.; Araujo, T.C.M.; Ferreira, B.P. Multiresolution Satellite-Derived Bathymetry in Shallow Coral Reefs: Improving Linear Algorithms with Geographical Analysis. J. Coast. Res. 2020, 36, 1247–1265. [Google Scholar] [CrossRef]
- Kutser, T.; Hedley, J.; Giardino, C.; Roelfsema, C.; Brando, V.E. Remote sensing of shallow waters—A 50 year retrospective and future directions. Remote Sens. Environ. 2020, 240, 111619. [Google Scholar] [CrossRef]
- Ma, S.; Tao, Z.; Yang, X.; Yu, Y.; Zhou, X.; Li, Z. Bathymetry Retrieval from Hyperspectral Remote Sensing Data in Optical-Shallow Water. Ieee Trans. Geosci. Remote Sens. 2014, 52, 1205–1212. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Li, C.; Chen, Y.; Yang, L. Bathymetry Model Based on Spectral and Spatial Multifeatures of Remote Sensing Image. Ieee Geosci. Remote Sens. Lett. 2020, 17, 37–41. [Google Scholar] [CrossRef]
- Kulbacki, A.; Lubczonek, J.; Zaniewicz, G. Acquisition of Bathymetry for Inland Shallow and Ultra-Shallow Water Bodies Using PlanetScope Satellite Imagery. Remote Sens. 2024, 16, 3165. [Google Scholar] [CrossRef]
- Bannari, A.; Kadhem, G. MBES-CARIS Data Validation for Bathymetric Mapping of ShallowWater in the Kingdom of Bahrain on the Arabian Gulf. Remote Sens. 2017, 9, 385. [Google Scholar] [CrossRef]
- Costa, B.M.; Battista, T.A.; Pittman, S.J. Comparative evaluation of airborne LiDAR and ship-based multibeam SoNAR bathymetry and intensity for mapping coral reef ecosystems. Remote Sens. Environ. 2009, 113, 1082–1100. [Google Scholar] [CrossRef]
- Ji, X.; Ma, Y.; Zhang, J.; Xu, W.; Wang, Y. A Sub-Bottom Type Adaption-Based Empirical Approach for Coastal Bathymetry Mapping Using Multispectral Satellite Imagery. Remote Sens. 2023, 15, 3570. [Google Scholar] [CrossRef]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Review of near-shore satellite derived bathymetry: Classification and account of five decades of coastal bathymetry research. J. Ocean Eng. Sci. 2021, 6, 340–359. [Google Scholar] [CrossRef]
- Xie, C.; Chen, P.; Zhang, S.; Huang, H. Nearshore Bathymetry from ICESat-2 LiDAR and Sentinel-2 Imagery Datasets Using Physics-Informed CNN. Remote Sens. 2024, 16, 511. [Google Scholar] [CrossRef]
- Knudby, A.; Richardson, G. Incorporation of neighborhood information improves performance of SDB models. Remote Sens. Appl. -Soc. Environ. 2023, 32, 101033. [Google Scholar] [CrossRef]
- He, C.L.; Jiang, Q.G.; Wang, P. An Improved Physics-Based Dual-Band Model for Satellite-Derived Bathymetry Using SuperDove Imagery. Remote Sens. 2024, 16, 3801. [Google Scholar] [CrossRef]
- Klotz, A.N.; Almar, R.; Quenet, Y.; Bergsma, E.W.J.; Youssefi, D.; Artigues, S.; Rascle, N.; Sy, B.A.; Ndour, A. Nearshore satellite-derived bathymetry from a single-pass satellite video: Improvements from adaptive correlation window size and modulation transfer function. Remote Sens. Environ. 2024, 315, 114411. [Google Scholar] [CrossRef]
- Richardson, G.; Foreman, N.; Knudby, A.; Wu, Y.L.; Lin, Y.W. Global deep learning model for delineation of optically shallow and optically deep water in Sentinel-2 imagery. Remote Sens. Environ. 2024, 311, 114302. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Zhao, Y.C.; Wu, S.L.; Chen, H.D.; Song, C.H.; Mao, Z.H.; Shen, W. Satellite-Derived Bathymetry Using a Fast Feature Cascade Learning Model in Turbid Coastal Waters. J. Remote Sens. 2024, 4. [Google Scholar] [CrossRef]
- Dietrich, J.T. Bathymetric Structure-from-Motion: Extracting shallow stream bathymetry from multi-view stereo photogrammetry. Earth Surf. Process. Landf. 2017, 42, 355–364. [Google Scholar] [CrossRef]
- Lubczonek, J.; Kazimierski, W.; Zaniewicz, G.; Lacka, M. Methodology for Combining Data Acquired by Unmanned Surface and Aerial Vehicles to Create Digital Bathymetric Models in Shallow and Ultra-Shallow Waters. Remote Sens. 2022, 14, 105. [Google Scholar] [CrossRef]
- Hodúl, M.; Chénier, R.; Faucher, M.A.; Ahola, R.; Knudby, A.; Bird, S. Photogrammetric Bathymetry for the Canadian Arctic. Mar. Geod. 2020, 43, 23–43. [Google Scholar] [CrossRef]
- Del Savio, A.A.; Torres, A.L.; Olivera, M.A.V.; Rojas, S.R.L.; Ibarra, G.T.U.; Neckel, A. Using UAVs and Photogrammetry in Bathymetric Surveys in Shallow Waters. Appl. Sci. 2023, 13, 3420. [Google Scholar] [CrossRef]
- Bandini, F.; Sunding, T.P.; Linde, J.; Smith, O.; Jensen, I.K.; Köppl, C.J.; Butts, M.; Bauer-Gottwein, P. Unmanned Aerial System (UAS) observations of water surface elevation in a small stream: Comparison of radar altimetry, LIDAR and photogrammetry techniques. Remote Sens. Environ. 2020, 237, 111487. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Polcyn, F.C.; Rollin, R.A. Remote sensing techniques for the location and measurement of shallow-water features. Available online: https://deepblue.lib.umich.edu/handle/2027.42/7114 (accessed on 6 June 2024).
- Polcyn, F.C.; Brown, W.L.; Sattinger, I.J. The Measurement of Water Depth by Remote Sensing Techniques. Available online: https://agris.fao.org/search/en/providers/122415/records/647368ca53aa8c89630d65ca (accessed on 6 June 2024).
- Polcyn, F.C. Calculations of water depth from ERTS-MSS data. Available online: https://ntrs.nasa.gov/citations/19730019626 (accessed on 6 June 2024).
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.J.; Barrilero, O.; Laporte, J.; Koetz, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Sandidge, J.; Holyer, R.J. Coastal bathymetry from hyperspectral observations of water radiance. Remote Sens. Environ. 1998, 65, 341–352. [Google Scholar] [CrossRef]
- Manessa, M.D.M.; Kanno, A.; Sekine, M.; Haidar, M.; Yamamoto, K.; Imai, T.; Higuchi, T. Satellite-Derived Bathymetry Using Random Forest Algorithm and Worldview-2 Imagery. Geoplanning J. Geomat. Plan. 2016, 3, 117–126. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.; Su, H.; Wang, J. Bathymetry retrieval from optical images with spatially distributed support vector machines. Giscience Remote Sens. 2019, 56, 323–337. [Google Scholar] [CrossRef]
- Leng, Z.; Zhang, J.; Ma, Y.; Zhang, J. Underwater Topography Inversion in Liaodong Shoal Based on GRU Deep Learning Model. Remote. Sens. 2020, 12, 4068. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite-2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T.; et al. The ICESat-2 Laser Altimetry Mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar] [CrossRef]
- Smith, B.; Fricker, H.A.; Holschuh, N.; Gardner, A.S.; Adusumilli, S.; Brunt, K.M.; Csatho, B.; Harbeck, K.; Huth, A.; Neumann, T.; et al. Land ice height-retrieval algorithm for NASA’s ICESat-2 photon-counting laser altimeter. Remote Sens. Environ. 2019, 233, 111352. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, X.; Nie, S.; Xi, X.; Li, D.; Zheng, W.; Chen, S. Ground elevation accuracy verification of ICESat-2 data: A case study in Alaska, USA. Opt. Express 2019, 27, 38168–38179. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Hsu, H.-J.; Huang, C.-Y.; Jasinski, M.; Li, Y.; Gao, H.; Yamanokuchi, T.; Wang, C.-G.; Chang, T.-M.; Ren, H.; Kuo, C.-Y.; et al. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: A case study in the South China Sea. Isprs J. Photogramm. Remote Sens. 2021, 178, 1–19. [Google Scholar] [CrossRef]
- Chen, Y.; Le, Y.; Zhang, D.; Wang, Y.; Qiu, Z.; Wang, L. A photon-counting LiDAR bathymetric method based on adaptive variable ellipse filtering. Remote Sens. Environ. 2021, 256, 112326. [Google Scholar] [CrossRef]
- Xie, C.; Chen, P.; Pan, D.; Zhong, C.; Zhang, Z. Improved Filtering of ICESat-2 Lidar Data for Nearshore Bathymetry Estimation Using Sentinel-2 Imagery. Remote Sens. 2021, 13, 4303. [Google Scholar] [CrossRef]
- Peng, K.; Xie, H.; Xu, Q.; Huang, P.; Liu, Z. A Physics-Assisted Convolutional Neural Network for Bathymetric Mapping Using ICESat-2 and Sentinel-2 Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3213248. [Google Scholar] [CrossRef]
- Guo, X.; Jin, X.; Jin, S. Shallow Water Bathymetry Mapping from ICESat-2 and Sentinel-2 Based on BP Neural Network Model. Water 2022, 14, 3862. [Google Scholar] [CrossRef]
- van der Woerd, H.J.; Wernand, M.R. Hue-Angle Product for Low to Medium Spatial Resolution Optical Satellite Sensors. Remote Sens. 2018, 10, 180. [Google Scholar] [CrossRef]
- Fronkova, L.; Greenwood, N.; Martinez, R.; Graham, J.A.; Harrod, R.; Graves, C.A.; Devlin, M.J.; Petus, C. Can Forel-Ule Index Act as a Proxy of Water Quality in Temperate Waters? Application of Plume Mapping in Liverpool Bay, UK. Remote Sens. 2022, 14, 2375. [Google Scholar] [CrossRef]
- Nie, Y.F.; Guo, J.T.; Sun, B.N.; Lv, X.Q. An evaluation of apparent color of seawater based on the in-situ and satellite-derived Forel-Ule color scale. Estuar. Coast. Shelf Sci. 2020, 246, 107032. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, J.; Li, X.; Wang, L.; Chen, B.; Gong, H.; Ni, R.; Zhou, B.; Yang, C. Leaf area index retrieval with ICESat-2 photon counting LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102488. [Google Scholar] [CrossRef]
- Xing, Y.; Huang, J.; Gruen, A.; Qin, L. Assessing the Performance of ICESat-2/ATLAS Multi-Channel Photon Data for Estimating Ground Topography in Forested Terrain. Remote Sens. 2020, 12, 2084. [Google Scholar] [CrossRef]
- Xiang, J.; Li, H.; Zhao, J.; Cai, X.; Li, P. Inland water level measurement from spaceborne laser altimetry: Validation and comparison of three missions over the Great Lakes and lower Mississippi River. J. Hydrol. 2021, 597, 126312. [Google Scholar] [CrossRef]
- Magruder, L.; Neumann, T.; Kurtz, N. ICESat-2 Early Mission Synopsis and Observatory Performance. Earth Space Sci. 2021, 8, e2020EA001555. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Zhao, G.; Tseng, K.-H. A high-resolution bathymetry dataset for global reservoirs using multi-source satellite imagery and altimetry. Remote Sens. Environ. 2020, 244, 111831. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Jasinski, M.F.; Zhang, S.; Stoll, J.D. Deriving High-Resolution Reservoir Bathymetry From ICESat-2 Prototype Photon-Counting Lidar and Landsat Imagery. Ieee Trans. Geosci. Remote Sens. 2019, 57, 7883–7893. [Google Scholar] [CrossRef]
- Gwenzi, D.; Lefsky, M.A.; Suchdeo, V.P.; Harding, D.J. Prospects of the ICESat-2 laser altimetry mission for savanna ecosystem structural studies based on airborne simulation data. Isprs J. Photogramm. Remote Sens. 2016, 118, 68–82. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Markel, J. Shallow Water Bathymetry with ICESat-2 (Tutorial Led by Jonathan Markel at the 2023 ICESat-2 Hackweek). Available online: https://icesat-2-2023.hackweek.io/tutorials/bathymetry/bathymetry_tutorial.html (accessed on 24 February 2024).
- Sutterley, T. Python Interpretation of the NASA Goddard Space Flight Center YAPC (“Yet Another Photon Classifier”) Algorithm. Available online: https://yapc.readthedocs.io/en/latest/ (accessed on 24 February 2024).
- Xu, X.; Xu, S.; Jin, L.; Song, E. Characteristic analysis of Otsu threshold and its applications. Pattern Recognit. Lett. 2011, 32, 956–961. [Google Scholar] [CrossRef]
- Bernardis, M.; Nardini, R.; Apicella, L.; Demarte, M.; Guideri, M.; Federici, B.; Quarati, A.; De Martino, M. Use of ICEsat-2 and Sentinel-2 Open Data for the Derivation of Bathymetry in Shallow Waters: Case Studies in Sardinia and in the Venice Lagoon. Remote Sens. 2023, 15, 2944. [Google Scholar] [CrossRef]
- Harmel, T.; Chami, M.; Tormos, T.; Reynaud, N.; Danis, P.-A. Sunglint correction of the Multi-Spectral Instrument (MSI)-SENTINEL-2 imagery over inland and sea waters from SWIR bands. Remote Sens. Environ. 2018, 204, 308–321. [Google Scholar] [CrossRef]
- He, C.L.; Jiang, Q.G.; Tao, G.F.; Zhang, Z.C. A Convolutional Neural Network with Spatial Location Integration for Nearshore Water Depth Inversion. Sensors 2023, 23, 8493. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C.; Assoc Comp, M. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Xu, N.; Wang, L.; Zhang, H.-S.; Tang, S.; Mo, F.; Ma, X. Machine Learning Based Estimation of Coastal Bathymetry From ICESat-2 and Sentinel-2 Data. Ieee J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1748–1755. [Google Scholar] [CrossRef]


| Site | Lingshui-Sanya Bay | Dongsha Islands |
|---|---|---|
| Latitude | 18°3.84′N–18°33.3′N | 20°34.75′N–20°47.20′N |
| Longitude | 109°17.1′E–110°7.8′E | 116°41.34′E–116°55.61′E |
| ICESat-2 Data | ATL03_20200130213819_05370607_006_01 ATL03_20200427052044_04840701_006_02 ATL03_20200430171804_05370707_006_02 ATL03_20200530034826_09870701_006_01 ATL03_20200727010031_04840801_006_01 ATL03_20200828232813_09870801_006_01 ATL03_20200901112535_10400807_006_02 ATL03_20200930100134_00950907_006_02 ATL03_20210502234906_05981107_006_01 ATL03_20210524103607_09261101_006_01 ATL03_20210524103607_09261101_006_01 ATL03_20220624154329_00421601_006_01 ATL03_20220628034053_00951607_006_01 ATL03_20220829004446_10401607_006_01 | ATL03_20190129144159_04910207_006_02 ATL03_20190730060118_04910407_006_02 ATL03_20191021135212_03770501_006_02 ATL03_20191029014115_04910507_006_01 ATL03_20200420051144_03770701_006_02 ATL03_20200427170047_04910707_006_02 |
| Sentinel-2 Data | S2A_MSIL2A_20201203T031109_N0500_R075_T49QCA_20230303T030821 | S2A_MSIL2A_20240222T023721_N0510_R089_T50QMH_20240222T061746 |
| Longitude | Latitude | Distance from Shore (m) | Measured Water Depth (m) | Tide-Corrected Water Depth (m) | Time |
|---|---|---|---|---|---|
| 110.07672 | 18.45667 | 23.7 | 0.1 | 0.5 | 11:49 |
| 110.07676 | 18.45665 | 27.4 | 0.6 | 1 | 11:49 |
| 110.07686 | 18.45660 | 39.1 | 1.1 | 1.5 | 11:52 |
| 109.91875 | 18.41580 | 57.8 | 0.1 | 1.02 | 16:50 |
| 109.91877 | 18.41569 | 70.5 | 0.46 | 1.38 | 16:50 |
| 109.91878 | 18.41562 | 78.1 | 1.1 | 2.02 | 16:53 |
| 109.91078 | 18.41475 | 85.8 | 0.1 | 1.02 | 17:12 |
| 109.91079 | 18.41464 | 97.5 | 0.4 | 1.32 | 17:13 |
| 109.91082 | 18.41454 | 109.4 | 1.1 | 2.02 | 17:15 |
| 109.73072 | 18.31802 | 11.8 | 0.1 | 0.78 | 18:24 |
| 109.73077 | 18.31799 | 18.9 | 0.4 | 1.08 | 18:25 |
| 109.73118 | 18.31777 | 67.4 | 1.1 | 1.78 | 18:30 |
| 109.72836 | 18.31361 | 32.1 | 0.1 | 0.78 | 18:41 |
| 109.72848 | 18.31354 | 46.1 | 0.4 | 1.08 | 18:42 |
| 109.72884 | 18.31329 | 93.2 | 1.1 | 1.78 | 18:47 |
| 109.65143 | 18.23303 | 15.2 | 0.1 | 0 | 10:17 |
| 109.65143 | 18.23300 | 18.5 | 0.5 | 0.4 | 10:18 |
| 109.65144 | 18.23284 | 36.4 | 1 | 0.9 | 10:22 |
| 109.51883 | 18.22201 | 15.8 | 0.1 | 0.97 | 14:24 |
| 109.51884 | 18.22172 | 48.2 | 0.3 | 1.17 | 14:25 |
| 109.51886 | 18.22095 | 133.9 | 0.9 | 1.77 | 14:32 |
| 109.48227 | 18.26732 | 40.2 | 0.1 | 1.01 | 15:07 |
| 109.48217 | 18.26719 | 57.2 | 0.4 | 1.31 | 15:08 |
| 109.48197 | 18.26691 | 95.5 | 1 | 1.91 | 15:13 |
| MeasuredPointIndex | MeanDepthDiff (m) | VarDepthDiff (m) | MSE (m) | RMSE (m) |
|---|---|---|---|---|
| 1 | 0.50 | 0.14 | 0.36 | 0.60 |
| 2 | 0.00 | 0.14 | 0.11 | 0.33 |
| 3 | −0.50 | 0.14 | 0.36 | 0.60 |
| 4 | 0.55 | 0.14 | 0.41 | 0.64 |
| 5 | 0.19 | 0.14 | 0.15 | 0.39 |
| 6 | −0.45 | 0.14 | 0.32 | 0.57 |
| 7 | 0.40 | 0.06 | 0.20 | 0.45 |
| 8 | 0.10 | 0.06 | 0.06 | 0.24 |
| 9 | −0.60 | 0.06 | 0.41 | 0.64 |
| 10 | 0.98 | 0.13 | 1.06 | 1.03 |
| 11 | 0.68 | 0.13 | 0.57 | 0.75 |
| 12 | −0.02 | 0.13 | 0.10 | 0.32 |
| 13 | 0.94 | 0.03 | 0.90 | 0.95 |
| 14 | 0.64 | 0.03 | 0.43 | 0.65 |
| 15 | −0.06 | 0.03 | 0.03 | 0.17 |
| 16 | 1.49 | 0.00 | 2.23 | 1.49 |
| 17 | 1.09 | 0.00 | 1.19 | 1.09 |
| 18 | 0.59 | 0.00 | 0.35 | 0.59 |
| 19 | 0.52 | 0.01 | 0.28 | 0.53 |
| 20 | 0.32 | 0.01 | 0.11 | 0.33 |
| 21 | −0.22 | 0.02 | 0.06 | 0.24 |
| 22 | 0.62 | 0.02 | 0.39 | 0.63 |
| 23 | 0.32 | 0.02 | 0.11 | 0.34 |
| 24 | −0.28 | 0.02 | 0.09 | 0.31 |
| ALL | 0.32 | 0.33 | 0.43 | 0.65 |
| Model | Segment | N | RMSE | MAE | BIAS_AVG | BIAS_STD |
|---|---|---|---|---|---|---|
| RF-Bands | −5~0 m | 1006 | 0.82 | 0.46 | −0.22 | 0.79 |
| −10~−5 m | 727 | 1.23 | 0.86 | −0.08 | 1.23 | |
| −15~−10 m | 179 | 2.20 | 1.88 | 1.75 | 1.34 | |
| GB-Bands | −5~0 m | 1006 | 0.82 | 0.46 | −0.18 | 0.79 |
| −10~−5 m | 727 | 1.26 | 0.89 | −0.12 | 1.26 | |
| −15~−10 m | 179 | 2.07 | 1.77 | 1.58 | 1.33 | |
| PR-Bands | −5~0 m | 1006 | 1.30 | 0.91 | −0.41 | 1.23 |
| −10~−5 m | 727 | 1.12 | 0.83 | −0.01 | 1.12 | |
| −15~−10 m | 179 | 2.65 | 2.37 | 2.32 | 1.28 | |
| XG-Bands | −5~0 m | 1006 | 0.84 | 0.48 | −0.18 | 0.82 |
| −10~−5 m | 727 | 1.23 | 0.87 | −0.11 | 1.23 | |
| −15~−10 m | 179 | 2.15 | 1.81 | 1.60 | 1.43 | |
| RF-CID | −5~0 m | 1006 | 0.68 | 0.35 | −0.13 | 0.66 |
| −10~−5 m | 727 | 0.89 | 0.55 | −0.05 | 0.89 | |
| −15~−10 m | 179 | 1.51 | 1.15 | 0.94 | 1.18 | |
| GB-CID | −5~0 m | 1006 | 0.70 | 0.36 | −0.13 | 0.69 |
| −10~−5 m | 727 | 1.00 | 0.67 | −0.05 | 1.00 | |
| −15~−10 m | 179 | 1.74 | 1.37 | 1.15 | 1.31 | |
| PR-CID | −5~0 m | 1006 | 1.19 | 0.78 | −0.34 | 1.15 |
| −10~−5 m | 727 | 1.07 | 0.77 | −0.01 | 1.07 | |
| −15~−10 m | 179 | 2.36 | 1.91 | 1.81 | 1.52 | |
| XG-CID | −5~0 m | 1006 | 0.66 | 0.31 | −0.12 | 0.65 |
| −10~−5 m | 727 | 0.88 | 0.53 | −0.04 | 0.88 | |
| −15~−10 m | 179 | 1.54 | 1.12 | 0.79 | 1.32 | |
| Stumpf-BG | −5~0 m | 998 | 1.45 | 1.10 | 0.21 | 1.44 |
| −10~−5 m | 737 | 1.56 | 1.10 | −0.35 | 1.51 | |
| −15~−10 m | 175 | 2.06 | 1.54 | 0.99 | 1.81 | |
| Stumpf-BR | −5~0 m | 998 | 2.32 | 2.05 | 0.87 | 2.16 |
| −10~−5 m | 737 | 3.34 | 2.89 | −1.92 | 2.73 | |
| −15~−10 m | 175 | 4.65 | 4.18 | 4.17 | 2.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Yang, C.; Zhang, X.; Li, S.; Peng, X.; Li, Y.; Chen, T. Shallow Water Bathymetry Inversion Based on Machine Learning Using ICESat-2 and Sentinel-2 Data. Remote Sens. 2024, 16, 4603. https://doi.org/10.3390/rs16234603
Ye M, Yang C, Zhang X, Li S, Peng X, Li Y, Chen T. Shallow Water Bathymetry Inversion Based on Machine Learning Using ICESat-2 and Sentinel-2 Data. Remote Sensing. 2024; 16(23):4603. https://doi.org/10.3390/rs16234603
Chicago/Turabian StyleYe, Mengying, Changbao Yang, Xuqing Zhang, Sixu Li, Xiaoran Peng, Yuyang Li, and Tianyi Chen. 2024. "Shallow Water Bathymetry Inversion Based on Machine Learning Using ICESat-2 and Sentinel-2 Data" Remote Sensing 16, no. 23: 4603. https://doi.org/10.3390/rs16234603
APA StyleYe, M., Yang, C., Zhang, X., Li, S., Peng, X., Li, Y., & Chen, T. (2024). Shallow Water Bathymetry Inversion Based on Machine Learning Using ICESat-2 and Sentinel-2 Data. Remote Sensing, 16(23), 4603. https://doi.org/10.3390/rs16234603








