Radar Signal Sorting Method with Mimetic Image Mapping Based on Antenna Scan Pattern via SOLOv2 Network
Abstract
1. Introduction
- 1.
- To globally visualize the changes in PA over the long term, mimetic image mapping, which simulates human vision, is utilized to map PDW to a mimetic point graph (i.e., 2D image). Moreover, the index is reversible.
- 2.
- Starting from a new perspective of antenna scan pattern, pulse deinterleaving can be achieved through instance segmentation of point images, which can automatically divide pulses with almost identical parameters (such as CF) from different emitters into different groups, thereby alleviating the problem of “parameter overlap”.
2. Methodology
2.1. Problem Formulation
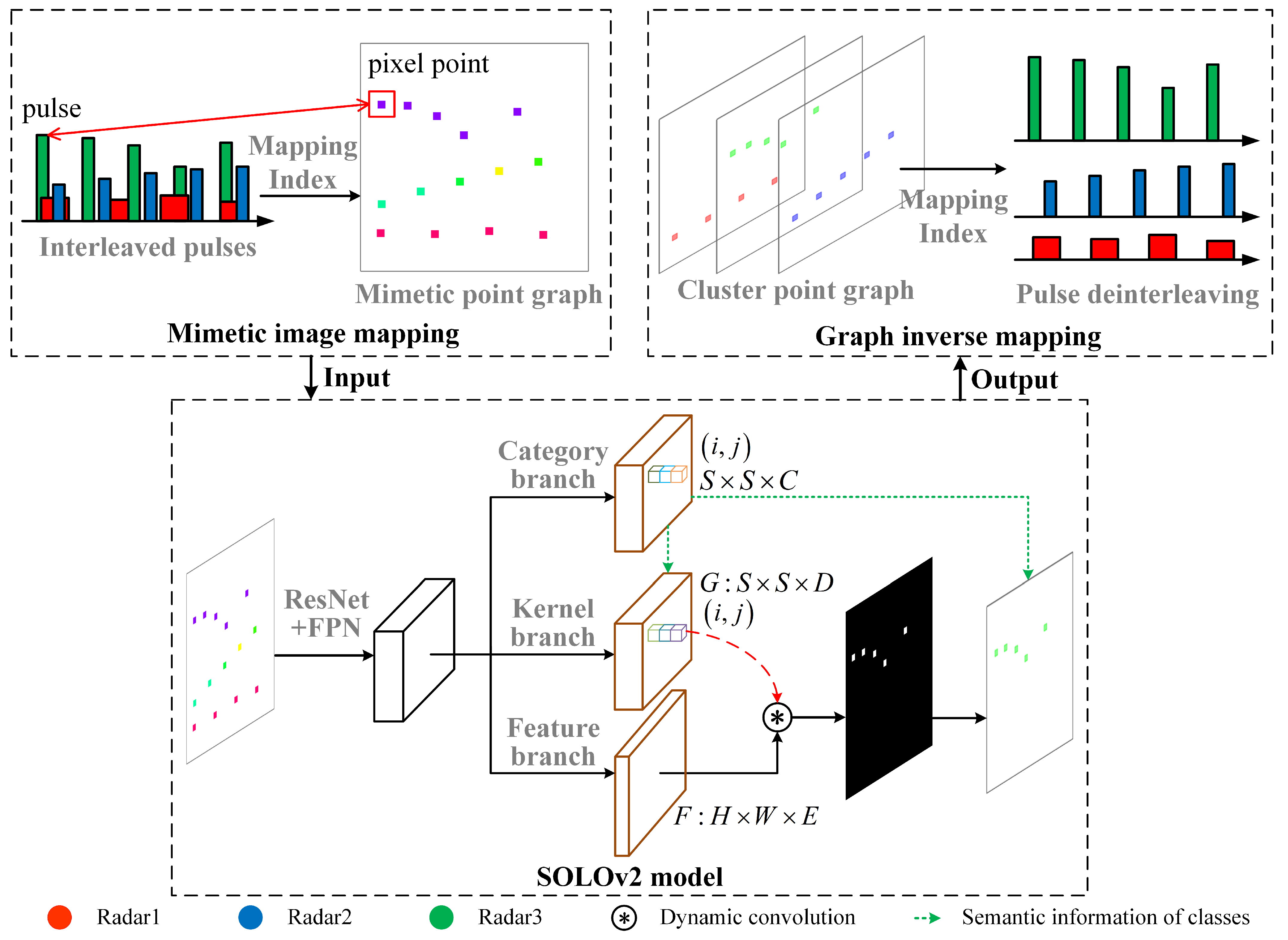
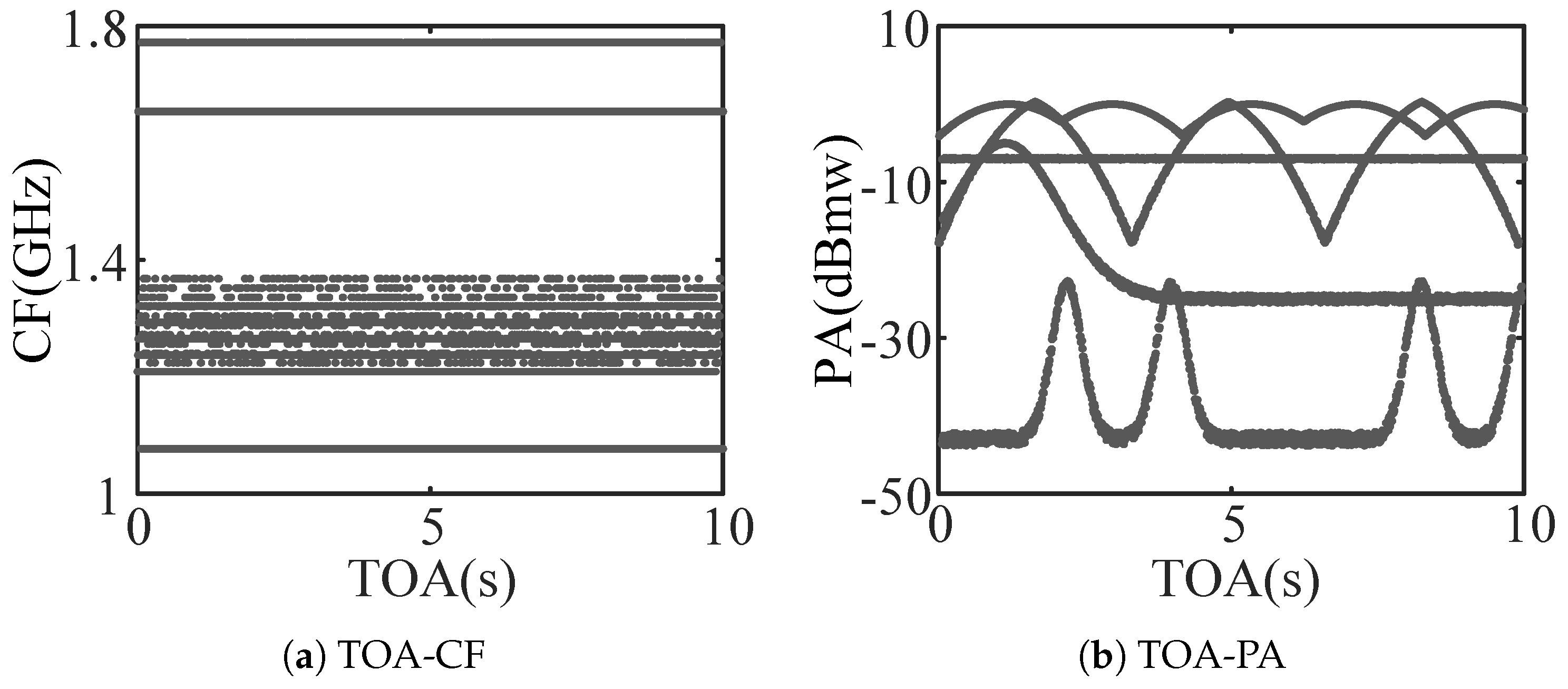
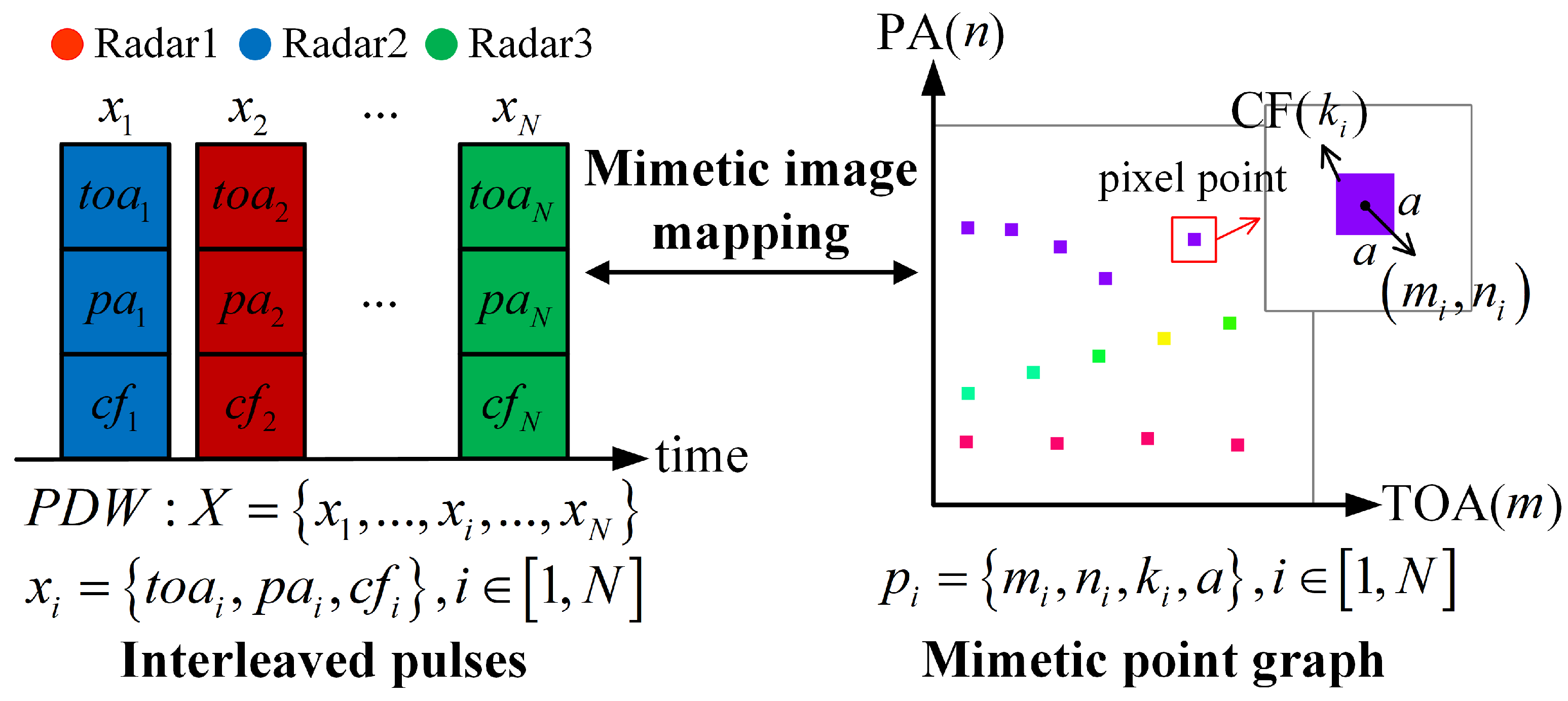
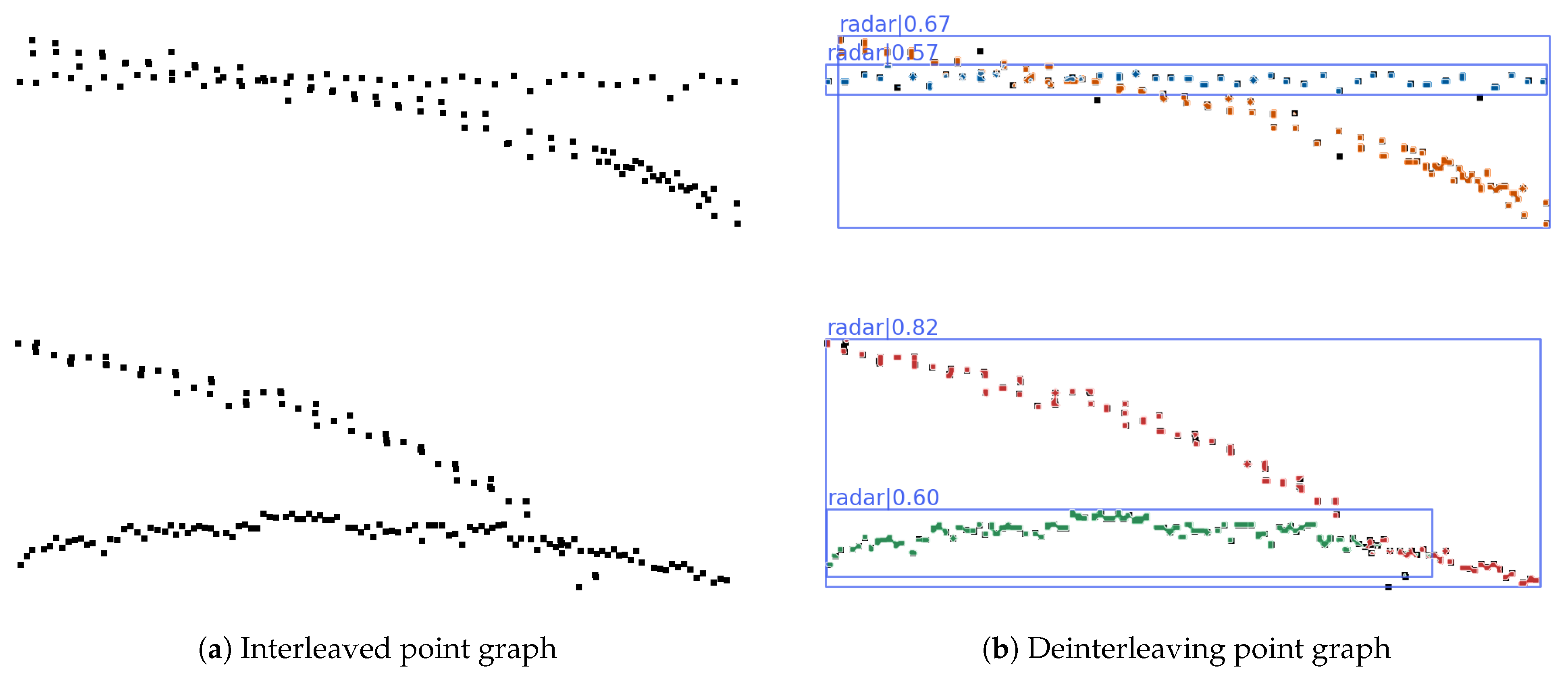
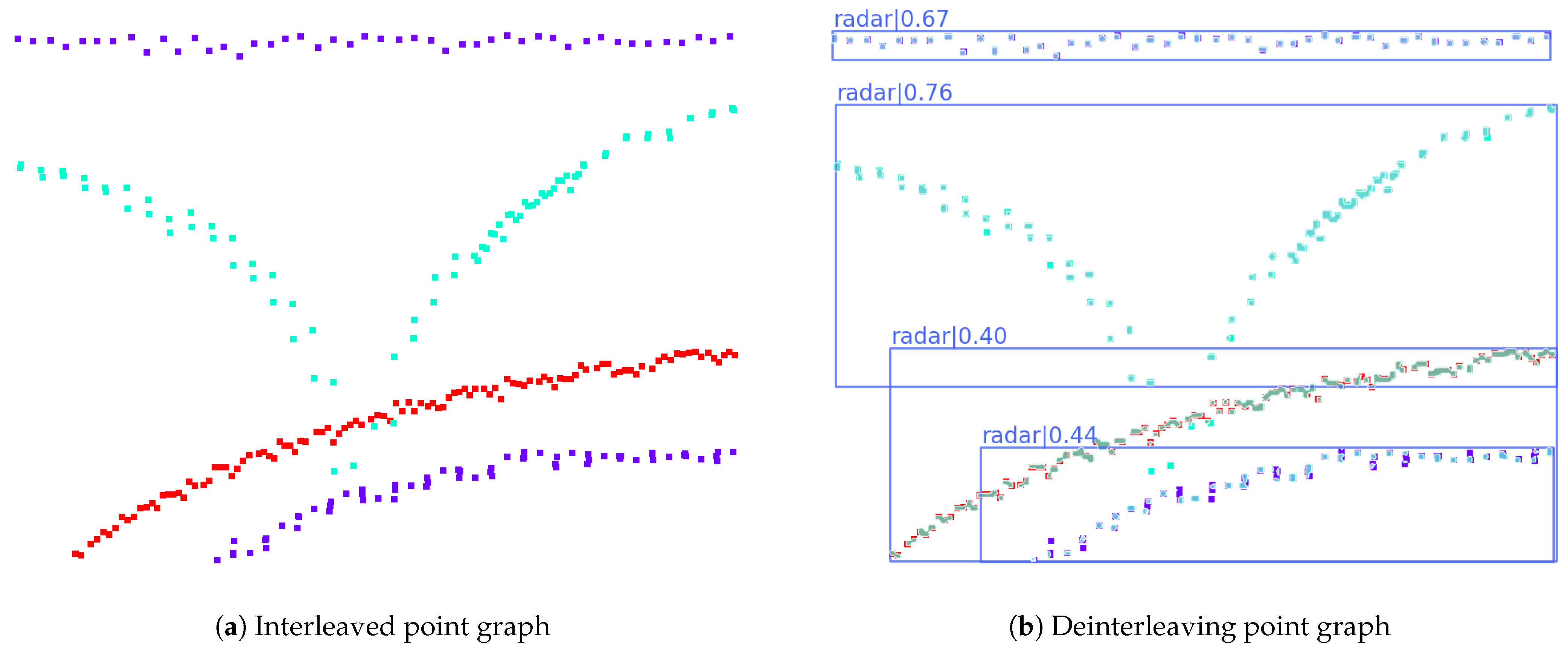
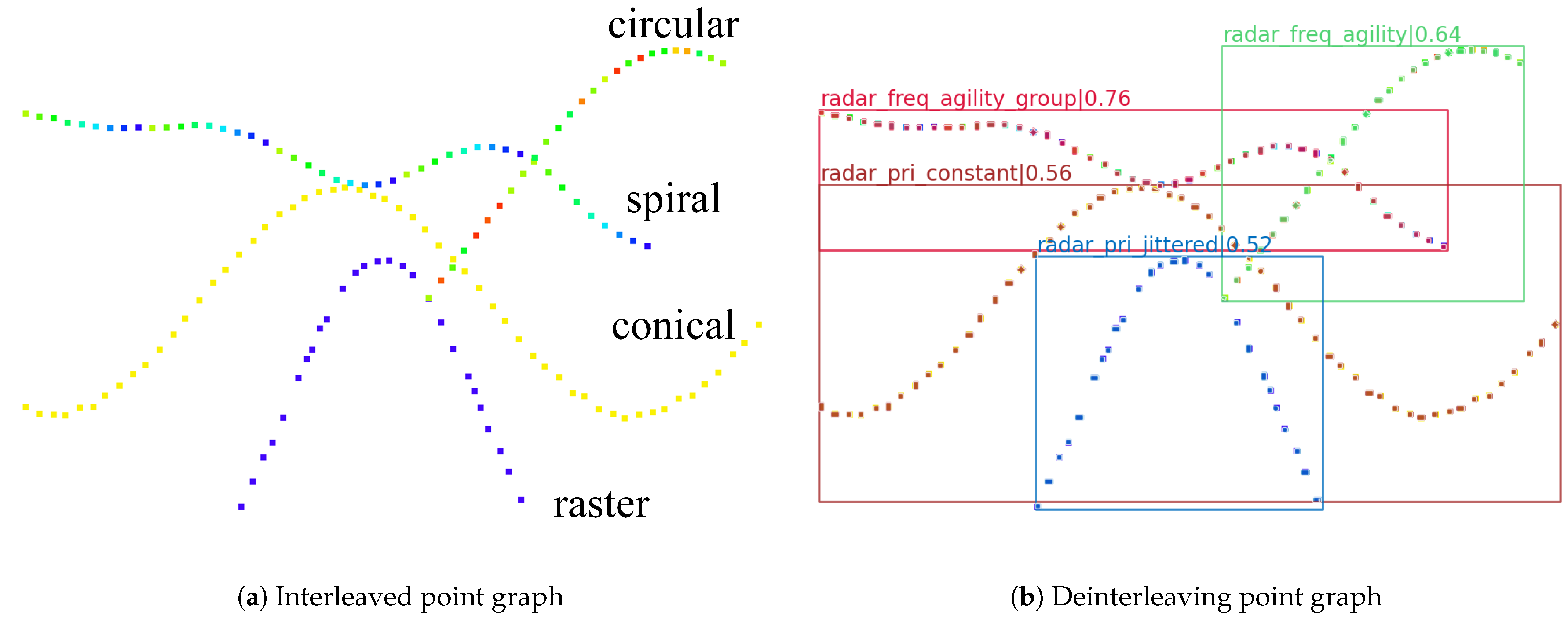
2.2. Mimetic Image Mapping Construction Based on ASP
2.3. Single-Stage-Based Instance Segmentation Network
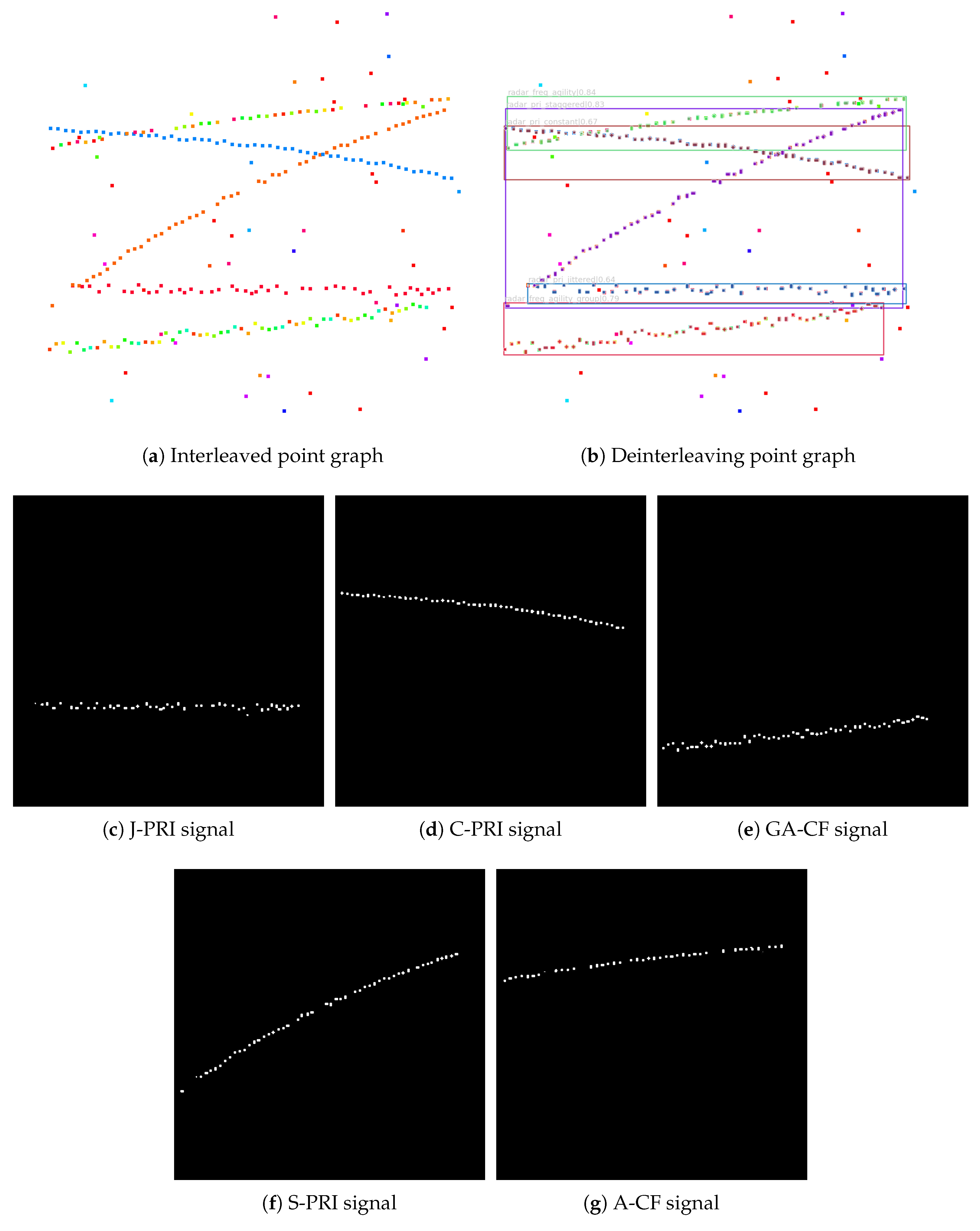
2.4. Pulse Clustering via Graph Inverse Mapping
- 1.
- Based on the pulse-pixel point mapping index relationship recorded during the construction of the mimetic image mapping (as shown in Table 1), determine whether each pixel point corresponds to multiple pulses or one pulse.
- 2.
- Return the segmentation results of the points mapped by one pulse to the pulse clustering based on the mapping index. And count the parameters of each pulse in the clustering group to obtain the parameter range of each group, i.e., and . Since most pulses and points are one-on-one, pulse clustering is basically completed at this point. However, there are remaining pulses that are not clustered.
- 3.
- Solve the situation where multiple pulses correspond to one point and unclassified pulses correspond to one point. Compare the multiple pulses corresponding to the same point and the remaining pulses corresponding to one point with the parameter range of the successfully sorted group one by one. If the CF and PW of a pulse are both within the parameter range of the group, then the pulse is assigned to the group. Until all remaining pulses undergo parameter matching once.
3. Experiments and Results
3.1. Experimental Setup
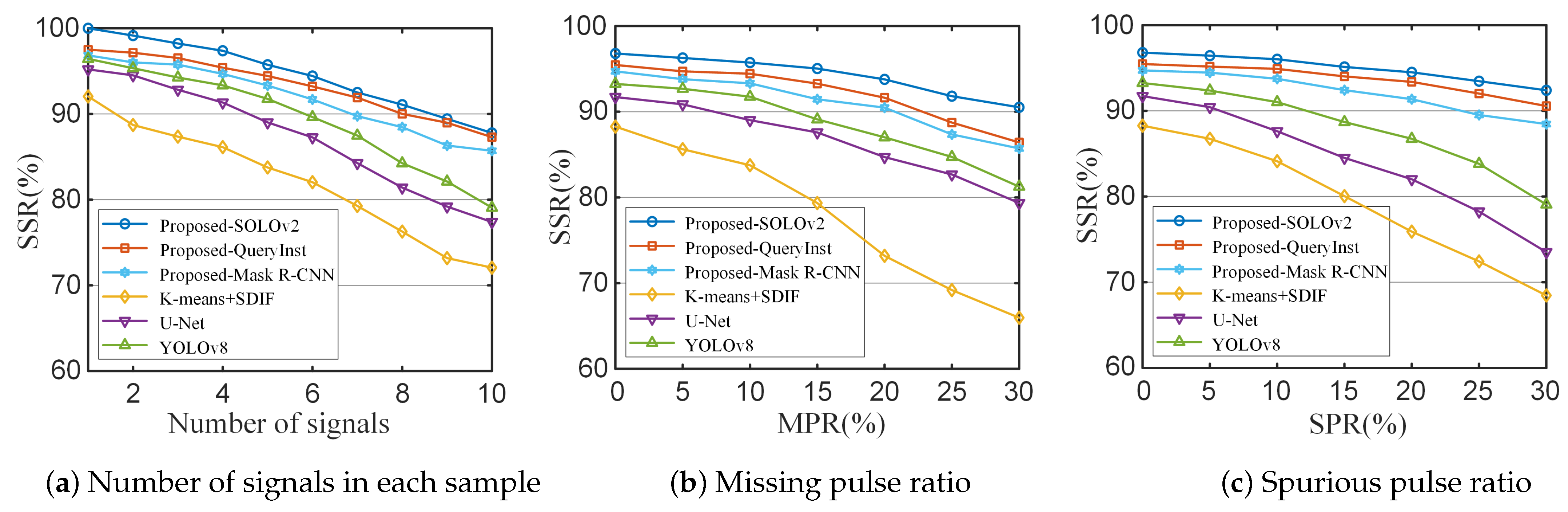
3.2. Performance Analysis of the Proposed Algorithm in Non-Ideal Conditions
3.3. Generalization Analysis of the Proposed Method
3.4. Applicability of the Proposed Method in Multiple Scan Patterns
3.5. Comparison with Other Method
4. Conclusions
- 1.
- In order to effectively extract the envelope of received power changes, the research method performs signal sorting on PDW under long-term observation. Long-term observation helps to analyze the patterns of antenna scanning. However, the excessively long sampling time can lead to increased computational complexity and prolonged processing time. In order to take advantage of different signal sorting methods, it is worth considering combining the sorting method for short sampling time with this method. At the small processing time scale, the characteristics of inter-pulse modulation of signals are more easily captured. However, at the large processing time scale, the characteristics of scan types and work modes are more pronounced.
- 2.
- The proposed method has achieved relatively good results, but there are still some limitations in real-world electronic reconnaissance scenarios. Especially in real-time systems, the processing of complex scan patterns by the method may require higher computing resources, and the real-time requirements of the system are difficult to meet. In order to overcome the problems of large memory consumption and long processing time, the method can be optimized through hardware implementation of the field programmable gate array (FPGA) in the future.
- 3.
- With the development of multi-functional phased array radar technology, corresponding electronic reconnaissance processing technology is crucial. By introducing antenna scanning into the field of radar signal sorting, radar signal sorting, antenna scan type recognition, and work mode recognition can be further linked together. Under different work modes, a radar adopts different antenna scan patterns and modulation parameter ranges. Thus, the combination of signal sorting and recognition steps can provide support for the acquisition of multifunctional radar information.
- 4.
- In cognitive electronic reconnaissance scenarios, non-cooperative emitters may be completely unknown. The complete absence of signal samples poses a serious challenge to deep learning-based signal sorting methods. The establishment of radar databases and real-time learning and updating of models may be the processing methods. Radar signal sorting based on continuous massive data models may be one of the research directions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whittall, N. Signal sorting in ESM systems. IEE Proc. Part F Commun. Radar Signal Process. 1985, 132, 226–228. [Google Scholar] [CrossRef]
- Haigh, K.; Andrusenko, J. Cognitive Electronic Warfare: An Artificial Intelligence Approach; Artech House: London, UK, 2021. [Google Scholar]
- Weber, M.E.; Cho, J.Y.; Thomas, H.G. Command and control for multifunction phased array radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5899–5912. [Google Scholar] [CrossRef]
- Mardia, H. New techniques for the deinterleaving of repetitive sequences. IEE Proc. Part F Commun. Radar Signal Process. 1989, 136, 149–154. [Google Scholar] [CrossRef]
- Milojević, D.; Popović, B.M. Improved algorithm for the deinterleaving of radar pulses. IEE Proc. Part F Commun. Radar Signal Process. 1992, 139, 98–104. [Google Scholar] [CrossRef]
- Young, J.; Høst-Madsen, A.; Nosal, E.M. Deinterleaving of mixtures of renewal processes. IEEE Trans. Signal Process. 2018, 67, 885–898. [Google Scholar] [CrossRef]
- Liu, Z.M.; Philip, S.Y. Classification, denoising, and deinterleaving of pulse streams with recurrent neural networks. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1624–1639. [Google Scholar] [CrossRef]
- Xiang, H.; Shen, F.; Zhao, J. Deep ToA mask-based recursive radar pulse deinterleaving. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 989–1006. [Google Scholar] [CrossRef]
- Xie, M.; Zhao, C.; Han, X.; Wang, Z.; Hu, D. Separation of Interleaved Pulse Stream Based on Directed Acyclic Graphs. IEEE Signal Process. Lett. 2023, 30, 613–617. [Google Scholar] [CrossRef]
- Guo, Q.; Huang, S.; Qi, L.; Wang, Y.; Kaliuzhnyi, M. A radar pulse train deinterleaving method for missing and short observations. Digit. Signal Process. 2023, 141, 104162. [Google Scholar] [CrossRef]
- Su, S.; Fu, X.; Zhao, C.; Yang, J.; Xie, M.; Gao, Z. Unsupervised k-means combined with SOFM structure adaptive radar signal sorting algorithm. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Chi, K.; Shen, J.; Li, Y.; Li, Y.; Wang, S. Multi-function radar signal sorting based on complex network. IEEE Signal Process. Lett. 2020, 28, 91–95. [Google Scholar] [CrossRef]
- Lang, P.; Fu, X.; Cui, Z.; Feng, C.; Chang, J. Subspace decomposition based adaptive density peak clustering for radar signals sorting. IEEE Signal Process. Lett. 2021, 29, 424–428. [Google Scholar] [CrossRef]
- Scholl, S.; Brüggenwirth, S. Incremental deinterleaving of radar emitters. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 26–36. [Google Scholar] [CrossRef]
- Dai, D.; Qiao, G.; Zhang, C.; Tian, R.; Zhang, S. A Sorting Method of SAR Emitter Signal Sorting Based on Self-Supervised Clustering. Remote Sens. 2023, 15, 1867. [Google Scholar] [CrossRef]
- Qu, M.; Liu, R.; Zhang, Y.; Si, W. DOA estimation and signal sorting methods of multi-baseline polarized interferometer. Digit. Signal Process. 2024, 148, 104434. [Google Scholar] [CrossRef]
- Sabeti, M.; Norouzi, Y.; Bahabadi, M.A. Simultaneous direct position determination and pulse deinterleaving by a moving receiver. Digit. Signal Process. 2019, 93, 13–21. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Huang, Z. Deinterleaving of pulse streams with denoising autoencoders. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4767–4778. [Google Scholar] [CrossRef]
- Gasperini, S.; Paschali, M.; Hopke, C.; Wittmann, D.; Navab, N. Signal clustering with class-independent segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3982–3986. [Google Scholar]
- Chao, W.; Liting, S.; Zhangmeng, L.; Zhitao, H. A radar signal deinterleaving method based on semantic segmentation with neural network. IEEE Trans. Signal Process. 2022, 70, 5806–5821. [Google Scholar] [CrossRef]
- Wan, L.; Liu, R.; Sun, L.; Nie, H.; Wang, X. UAV swarm based radar signal sorting via multi-source data fusion: A deep transfer learning framework. Inf. Fusion 2022, 78, 90–101. [Google Scholar] [CrossRef]
- Fuyue, L.; Jinxin, L. End-to-end radar signal sorting based on deep segmentation. Syst. Eng. Electron. 2023, 45, 1351–1358. [Google Scholar]
- Wang, Y.; Liao, H.; Yuan, S.; Liu, N. A learning-based signal parameter extraction approach for multi-source frequency-hopping signal sorting. IEEE Signal Process. Lett. 2023, 30, 1162–1166. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Huang, Z.; Liu, W. Radar emitter classification with attention-based multi-RNNs. IEEE Commun. Lett. 2020, 24, 2000–2004. [Google Scholar] [CrossRef]
- Lang, P.; Fu, X.; Dong, J.; Yang, H.; Yang, J. A Novel Radar Signals Sorting Method via Residual Graph Convolutional Network. IEEE Signal Process. Lett. 2023, 30, 753–757. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Wang, G. Emitter Signal Deinterleaving Based on Single PDW with Modulation-Hypothesis-Augmented Transformer. Remote Sens. 2024, 16, 3830. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, C.; Zhang, S.; Zheng, L. Characterization and identification of active electronically scanned array radar. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2318–2321. [Google Scholar]
- Dutt, R.; Baloria, A.; Prasad V, R.C.; ESMP, R.; Acharyya, A. Discrete wavelet transform based unsupervised underdetermined blind source separation methodology for radar pulse deinterleaving using antenna scan pattern. IET Radar Sonar Navig. 2019, 13, 1350–1358. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Li, X.; Ke, D. A deinterleaving method for mechanical-scanning radar signals based on deep learning. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 138–143. [Google Scholar]
- Kocamış, M.B.; Orduyılmaz, A.; Taşcıoğlu, S. Object detection based deinterleaving of radar signals using deep learning for cognitive EW. Signal Image Video Process. 2024, 18, 7789–7800. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Wang, X.; Zhang, R.; Kong, T.; Li, L.; Shen, C. Solov2: Dynamic and fast instance segmentation. Adv. Neural Inf. Process. Syst 2020, 33, 17721–17732. [Google Scholar]
- Wang, X.; Kong, T.; Shen, C.; Jiang, Y.; Li, L. Solo: Segmenting objects by locations. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVIII 16; Springer: Cham, Switzerland, 2020; pp. 649–665. [Google Scholar]
- Fang, Y.; Yang, S.; Wang, X.; Li, Y.; Fang, C.; Shan, Y.; Feng, B.; Liu, W. Instances as queries. In Proceedings of the IEEE/CVF international Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6910–6919. [Google Scholar]
- Xu, X.; Zhang, L.; Cheong, L.F.; Li, Z.; Zhu, C. Learning clustering for motion segmentation. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 908–919. [Google Scholar] [CrossRef]
- Karim, M.R.; Beyan, O.; Zappa, A.; Costa, I.G.; Rebholz-Schuhmann, D.; Cochez, M.; Decker, S. Deep learning-based clustering approaches for bioinformatics. Brief. Bioinform. 2021, 22, 393–415. [Google Scholar] [CrossRef]
- Chen, T.; Yang, B.; Guo, L. Radar Pulse Stream Clustering Based on MaskRCNN Instance Segmentation Network. IEEE Signal Process. Lett. 2023, 30, 1022–1026. [Google Scholar] [CrossRef]
- Ayazgok, S.; Erdem, C.; Ozturk, M.T.; Orduyilmaz, A.; Serin, M. Automatic antenna scan type classification for next-generation electronic warfare receivers. IET Radar Sonar Navig. 2018, 12, 466–474. [Google Scholar] [CrossRef]
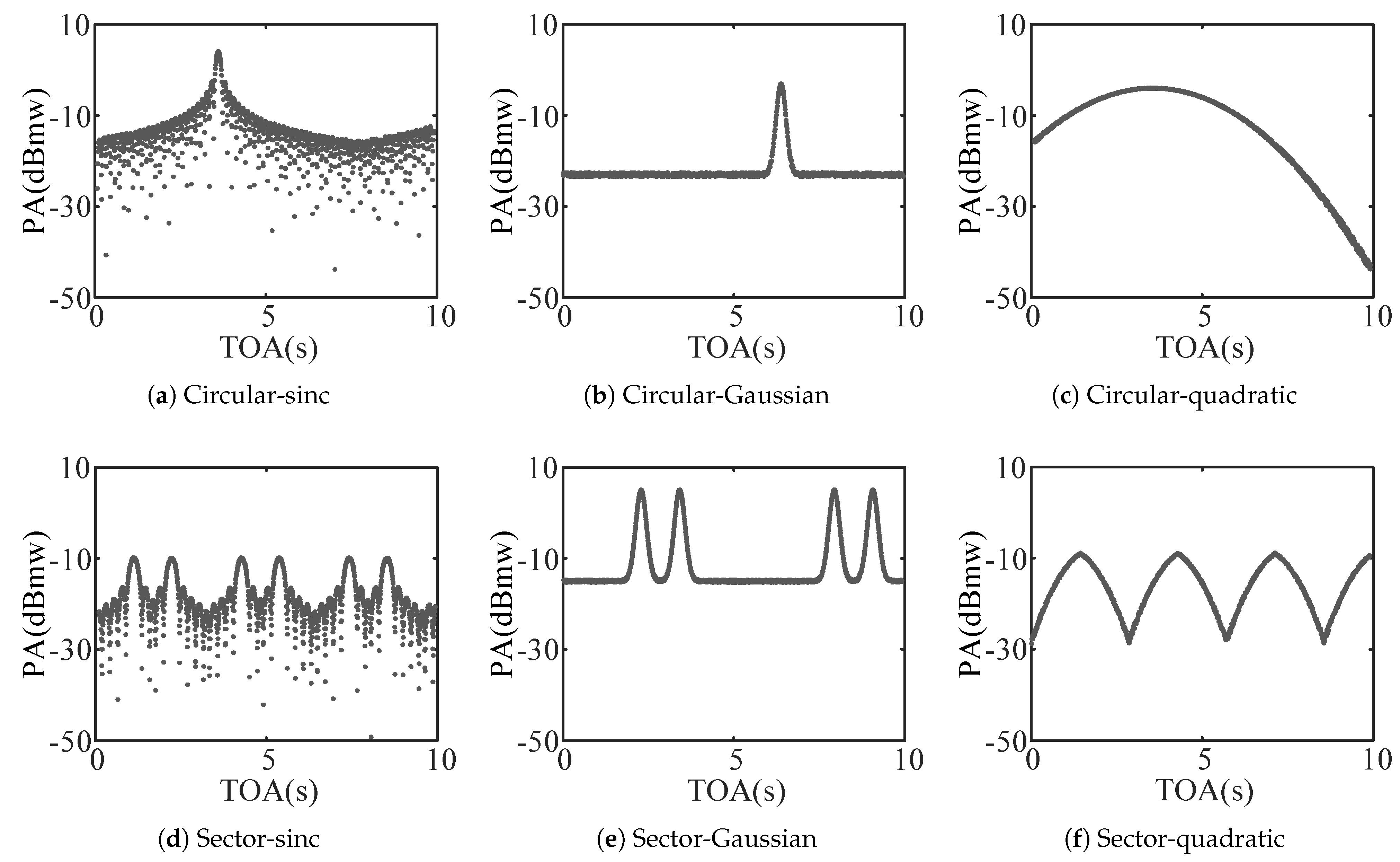
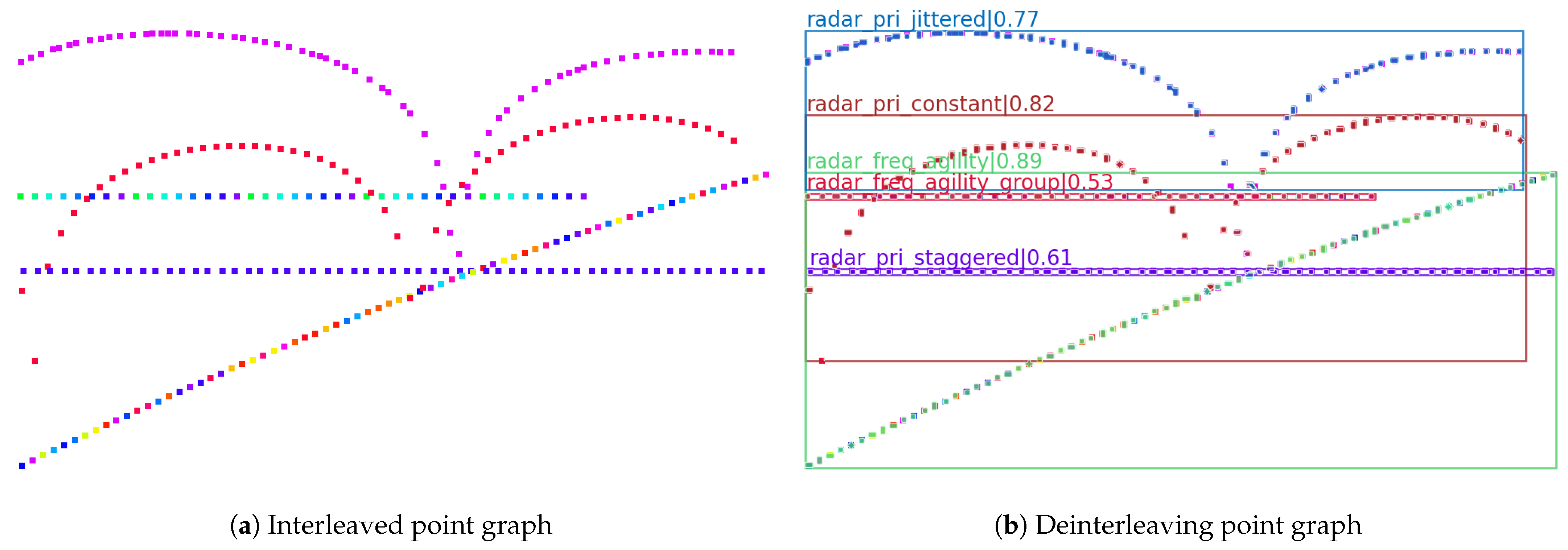
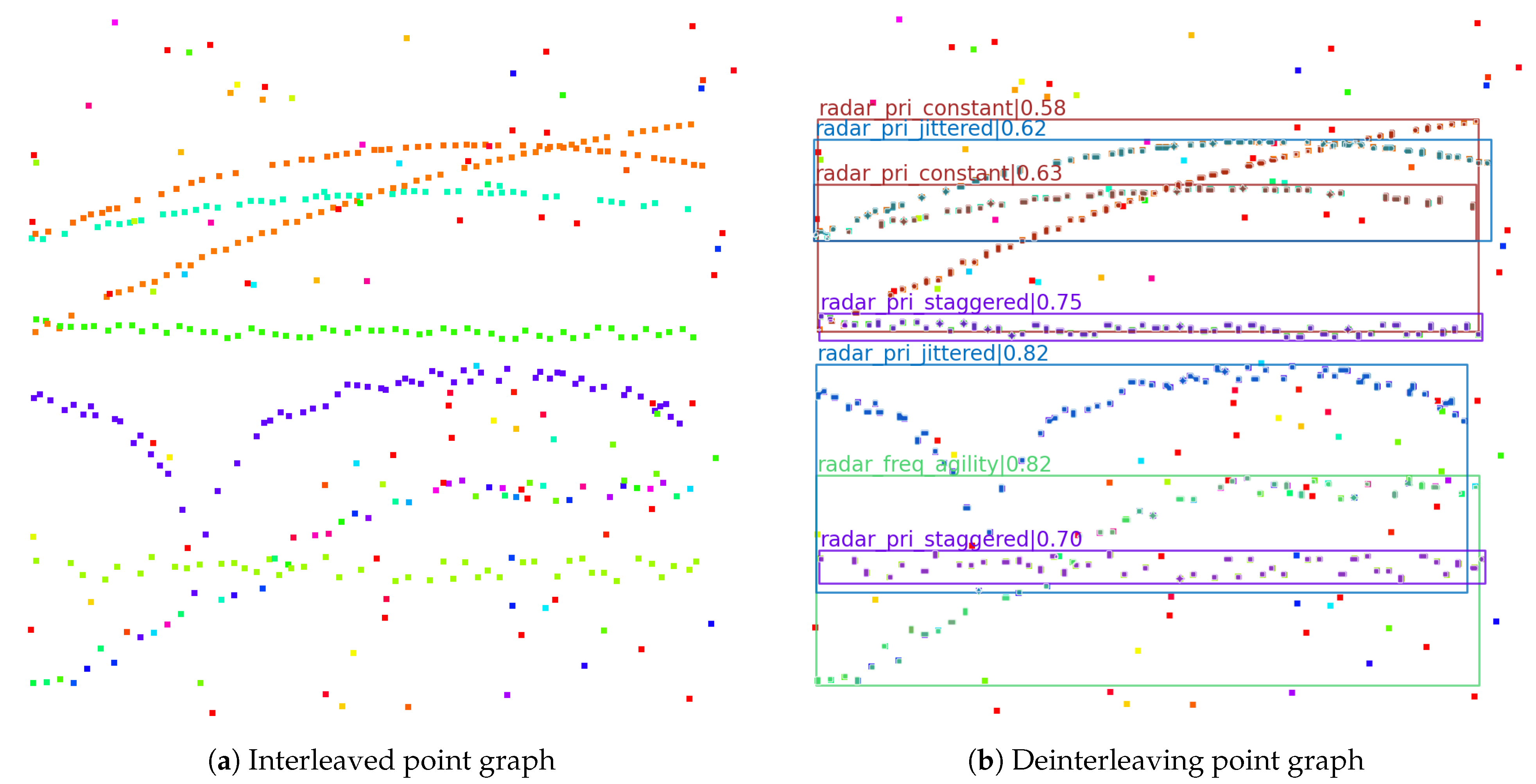



| Point Center Coordinates | 2 | ⋯ | |||
|---|---|---|---|---|---|
| 1 | - | - | ⋯ | - | |
| - | ⋯ | - | |||
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | |
| - | - | - | ⋯ |
| Modulation Type | PRI/ms | PA/dBmw | CF/MHz | PRI Number | Jitter Rate/% | CF Interval/ MHz | CF Range/ MHz | Scan Pattern | Gain Pattern | Scan Cycle/s | Mainlobe Width/ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C-PRI 1 | 6.5∼10 | −50∼10 | 1000∼2000 | - | - | - | - | 0∼1 2 | 0∼3 2 | 2∼7 | 2∼30 |
| J-PRI 1 | 6.5∼10 | −50∼10 | 1000∼2000 | - | 20∼40 | - | - | 0∼1 2 | 0∼3 2 | 2∼7 | 2∼30 |
| S-PRI 1 | 7∼10 | −50∼10 | 1000∼2000 | 3∼5 | - | - | - | 0∼1 2 | 0∼3 2 | 2∼7 | 2∼30 |
| A-CF 1 | 6.5∼10 | −50∼10 | 1000∼2000 | - | - | 20∼30 | 300∼600 | 0∼1 2 | 0∼3 2 | 2∼7 | 2∼30 |
| GA-CF 1 | 6.5∼10 | −50∼10 | 1000∼2000 | - | - | 40∼60 | 300∼500 | 0∼1 2 | 0∼3 2 | 2∼7 | 2∼30 |
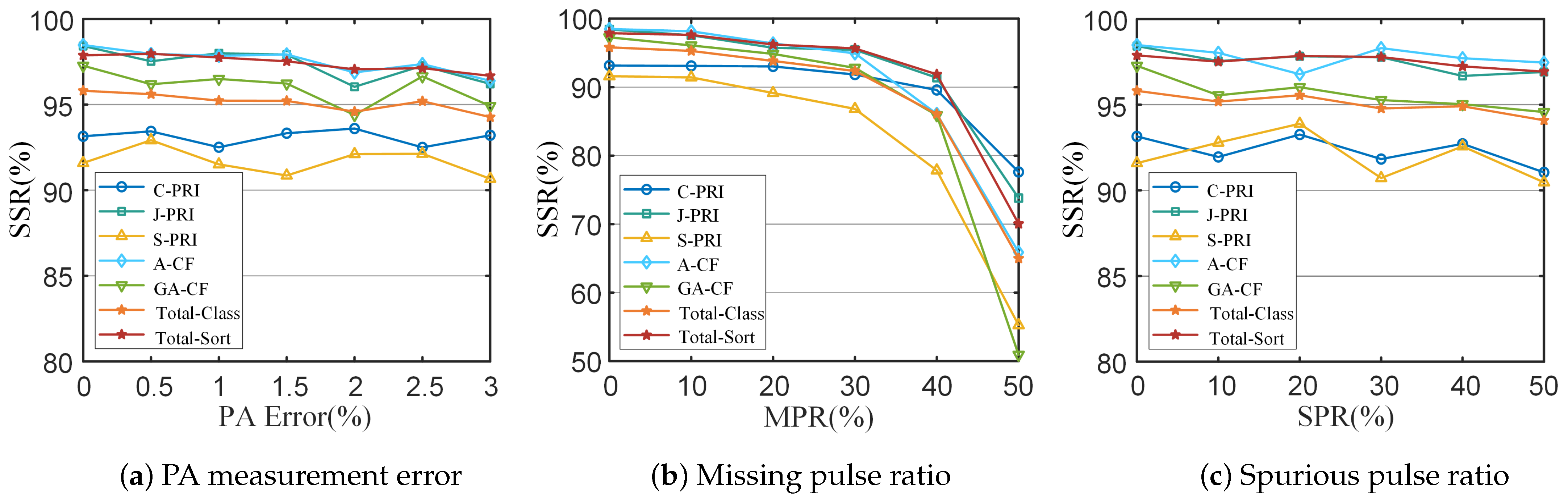
| Pulse Ratio | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
|---|---|---|---|---|---|---|
| Missing-SSR (%) 1 | 92.25 | 91.46 | 89.86 | 88.66 | 85.20 | 68.35 |
| Spurious-SSR (%) 2 | 92.25 | 91.69 | 90.88 | 89.75 | 89.42 | 88.99 |
| Algorithm Step | Parameter | Clustering Tolerance | SDIF Tolerance (PRI) |
|---|---|---|---|
| Routine Processing | CF | 3 MHz | 5 s |
| PW | 0.5 s | ||
| Jitter Analysis | CF | 3 MHz | 0.4 times 1 |
| PW | 0.5 s | ||
| Frequency Agile Analysis | CF | 0.6 times 1 | 5 s |
| PW | 0.5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Guo, X.; Li, J. Radar Signal Sorting Method with Mimetic Image Mapping Based on Antenna Scan Pattern via SOLOv2 Network. Remote Sens. 2024, 16, 4639. https://doi.org/10.3390/rs16244639
Chen T, Guo X, Li J. Radar Signal Sorting Method with Mimetic Image Mapping Based on Antenna Scan Pattern via SOLOv2 Network. Remote Sensing. 2024; 16(24):4639. https://doi.org/10.3390/rs16244639
Chicago/Turabian StyleChen, Tao, Xiaoqi Guo, and Jinxin Li. 2024. "Radar Signal Sorting Method with Mimetic Image Mapping Based on Antenna Scan Pattern via SOLOv2 Network" Remote Sensing 16, no. 24: 4639. https://doi.org/10.3390/rs16244639
APA StyleChen, T., Guo, X., & Li, J. (2024). Radar Signal Sorting Method with Mimetic Image Mapping Based on Antenna Scan Pattern via SOLOv2 Network. Remote Sensing, 16(24), 4639. https://doi.org/10.3390/rs16244639






