Evaluation and Projection of Global Burned Area Based on Global Climate Models and Satellite Fire Product
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. GCM Datasets on BA
2.2.2. Satellite-Based BA Monitor Dataset
2.3. Methods
2.3.1. Statistical Indicators
2.3.2. Bayesian Model Averaging (BMA)
2.3.3. Mann–Kendall (MK) Trend Test
2.3.4. Uncertainty Analysis
3. Results
3.1. Evaluation of Historical Fire BA Simulation
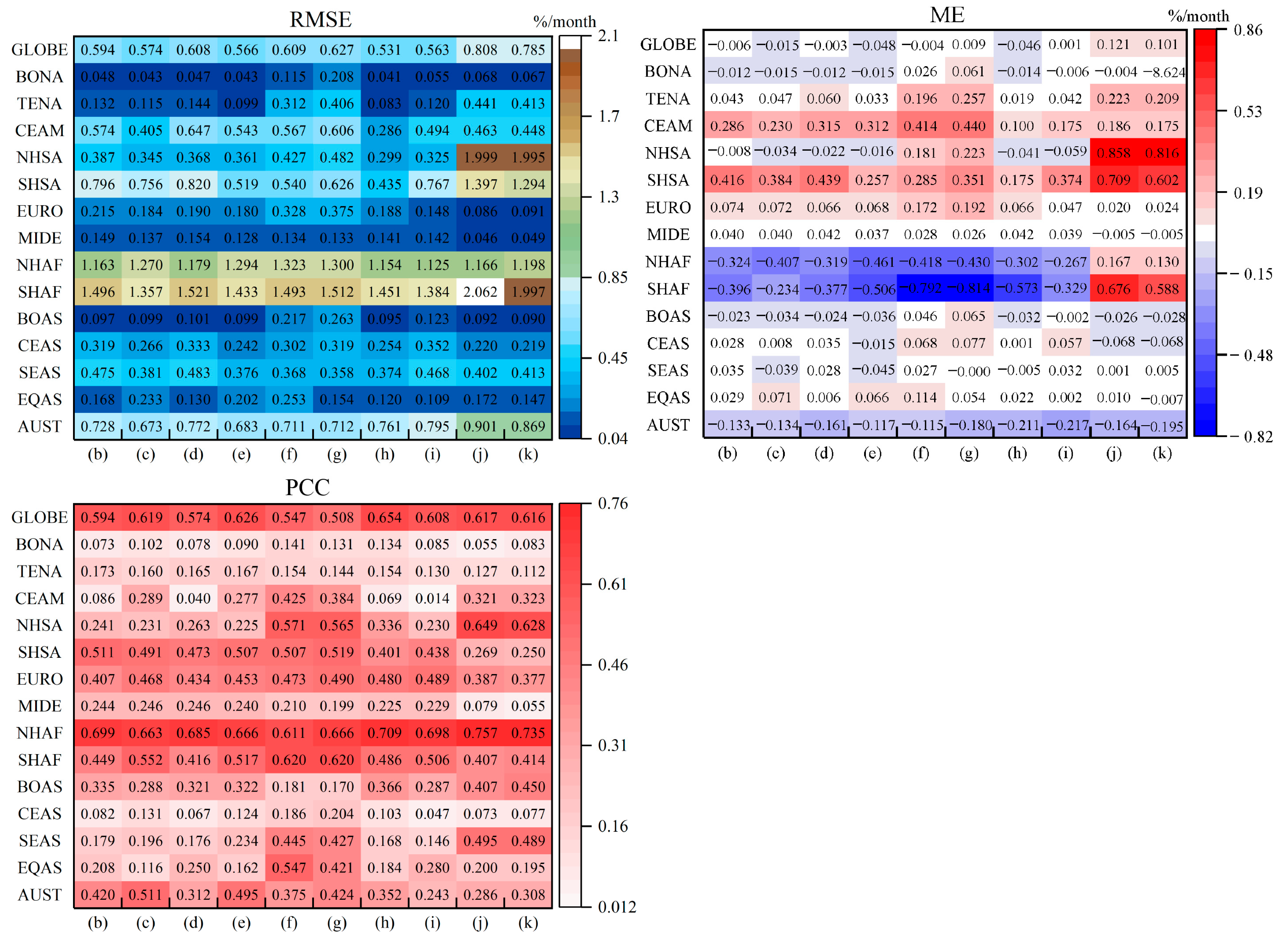
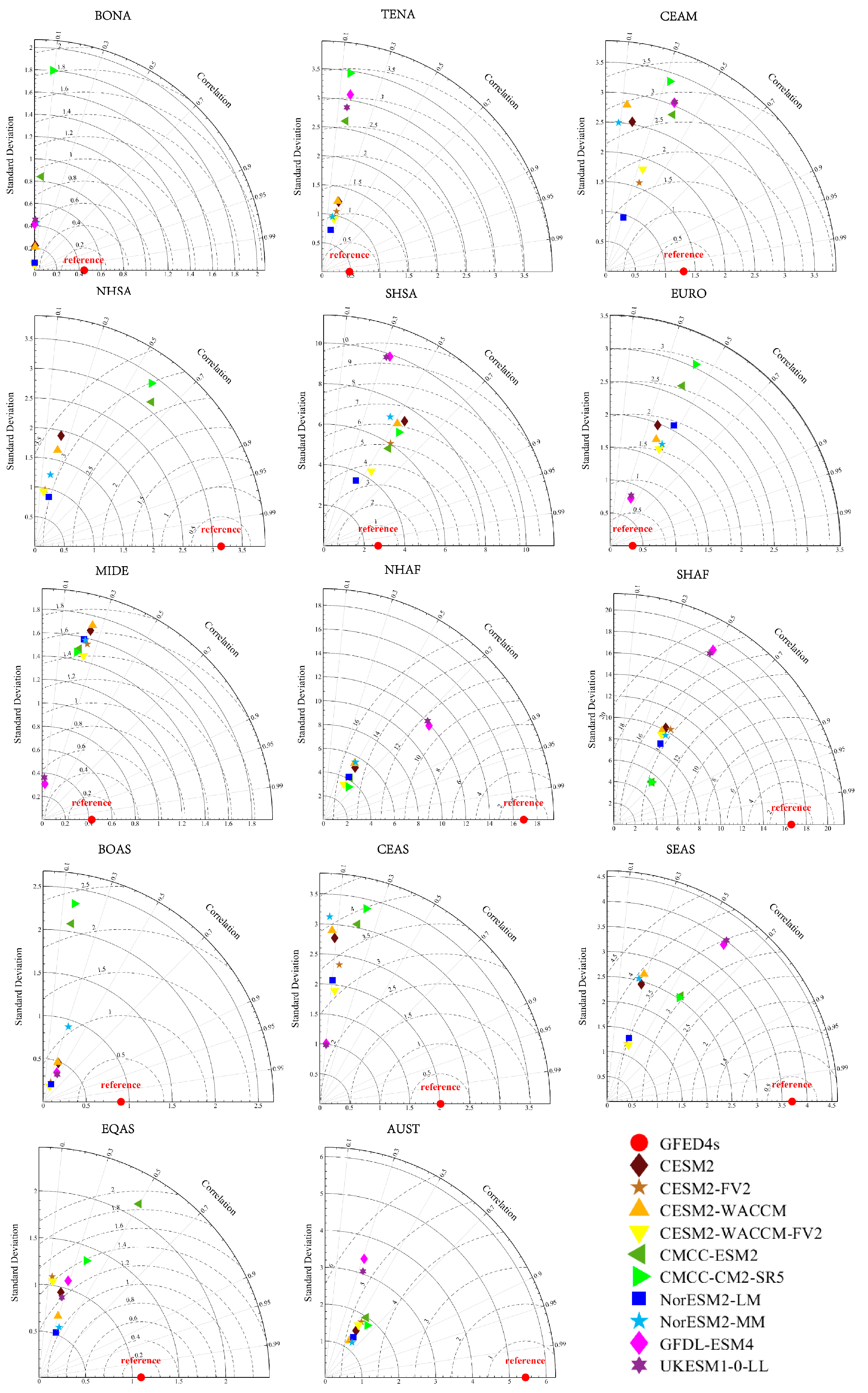
3.1.1. Annual Assessment
3.1.2. Monthly Assessment
3.1.3. Seasonal Assessment
3.1.4. Comparisons of Global BAF Classes
3.2. Multi-Model Ensemble for Historical Fire BA Simulations
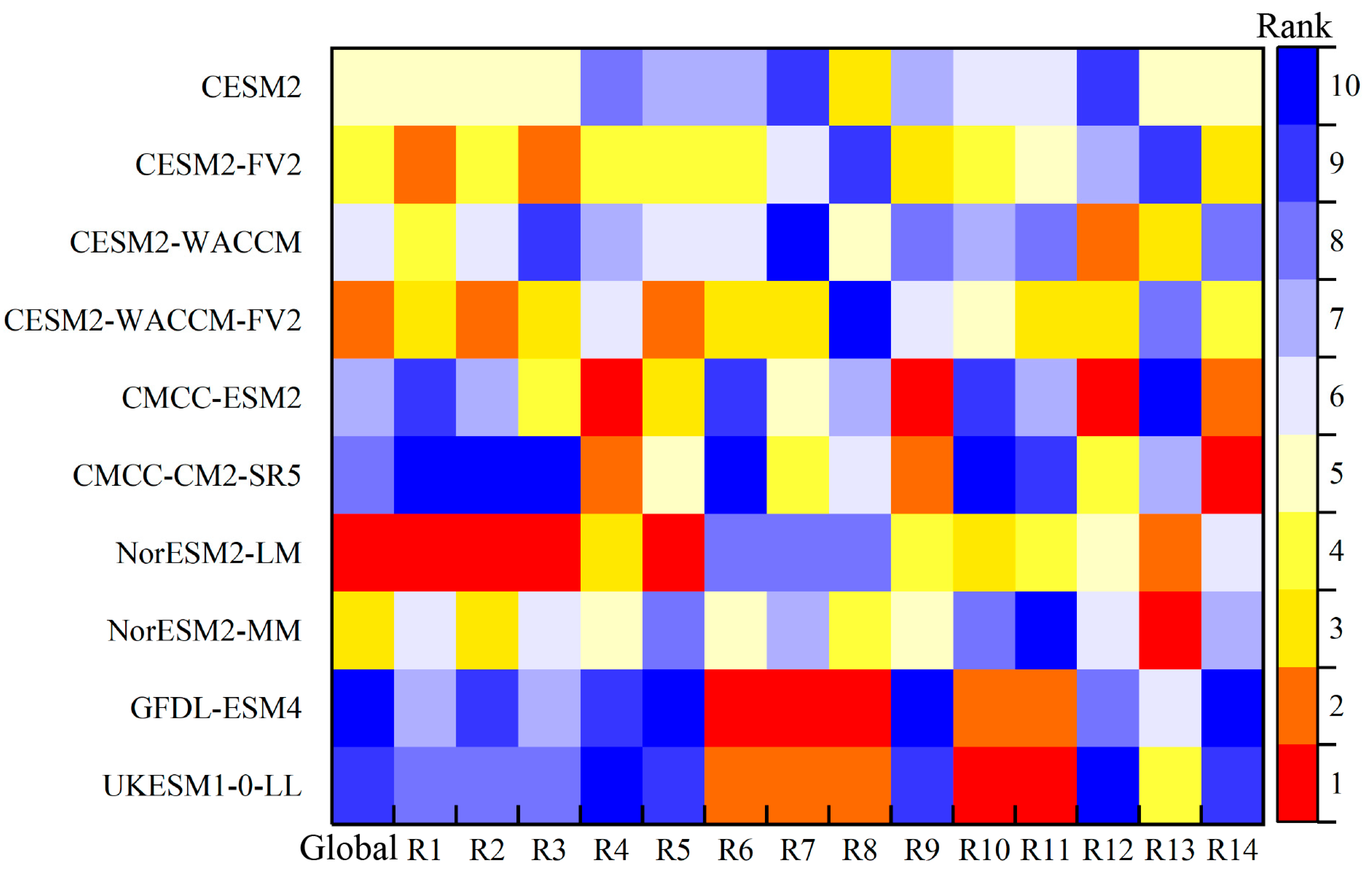
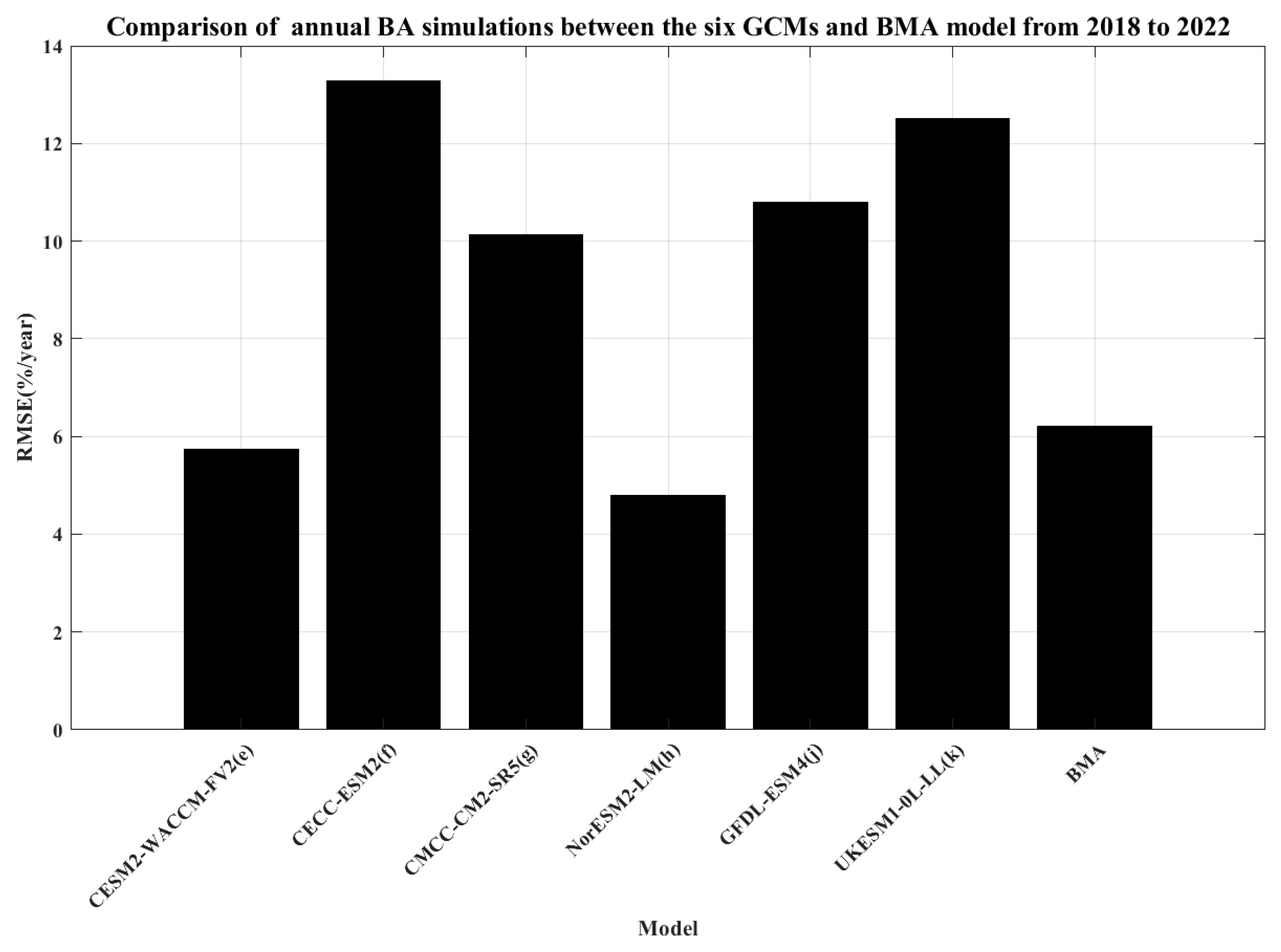
3.2.1. Model Ranking and Screening
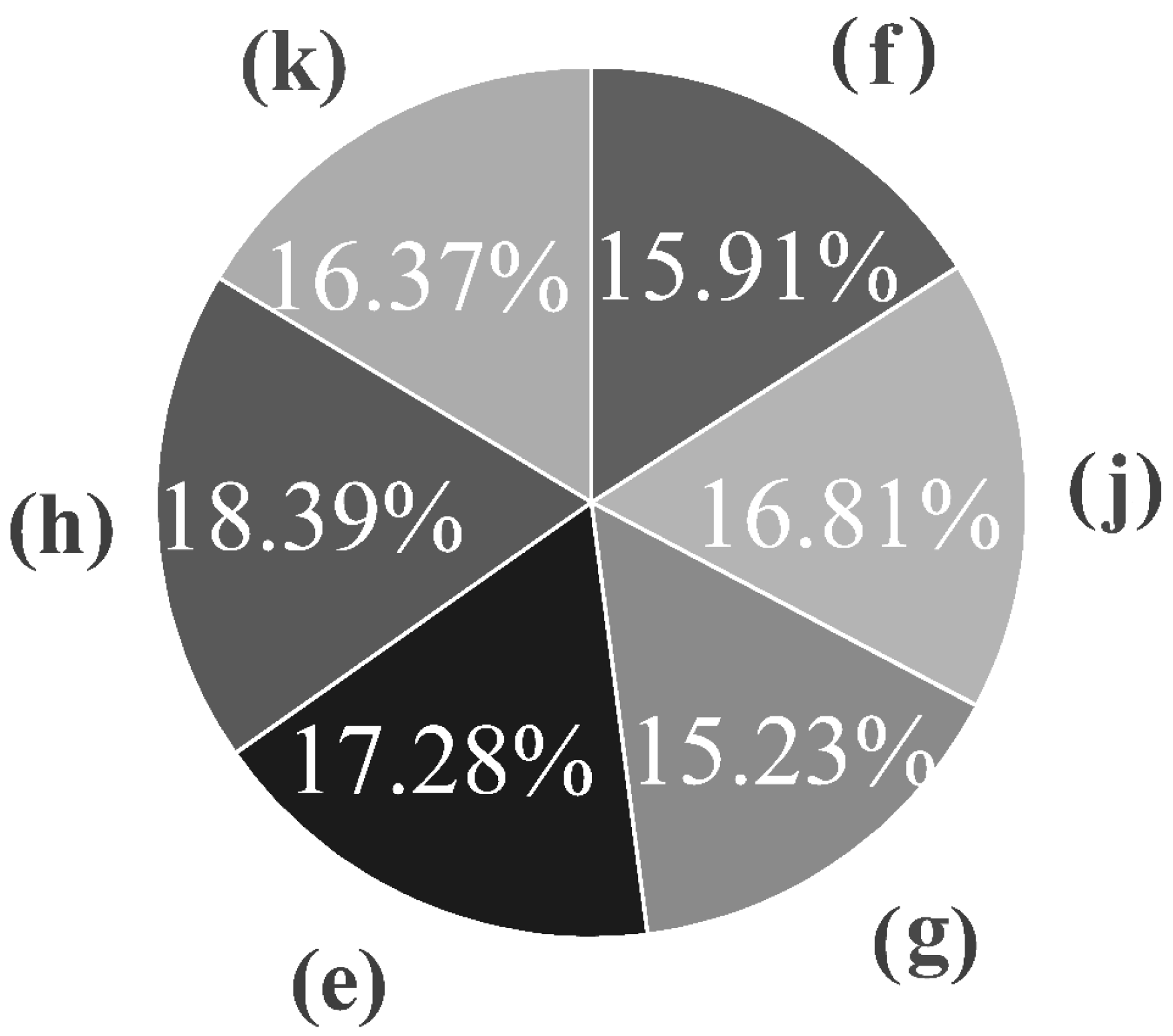
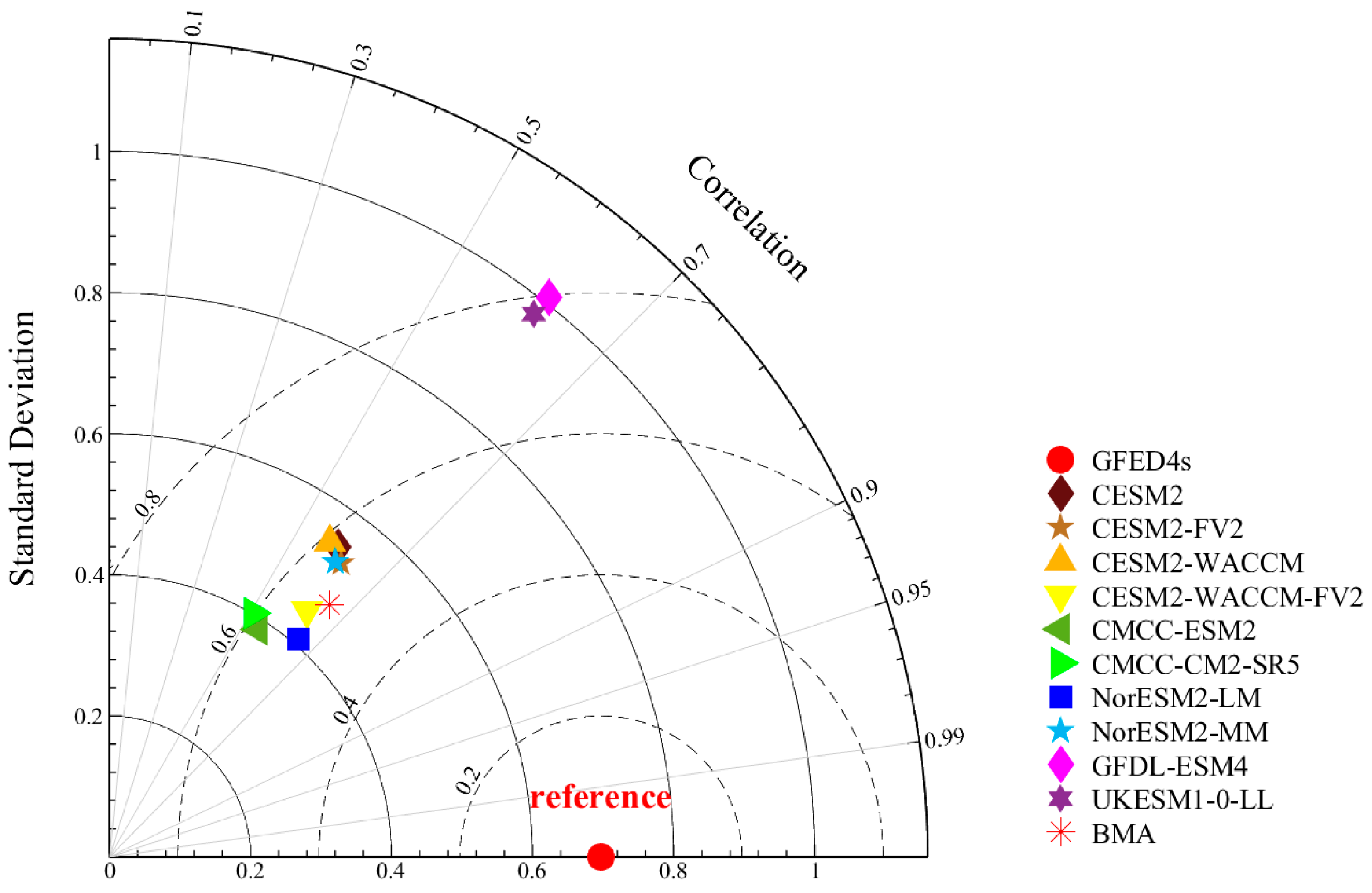
3.2.2. The Weights of Optimal Models and BMA Simulation
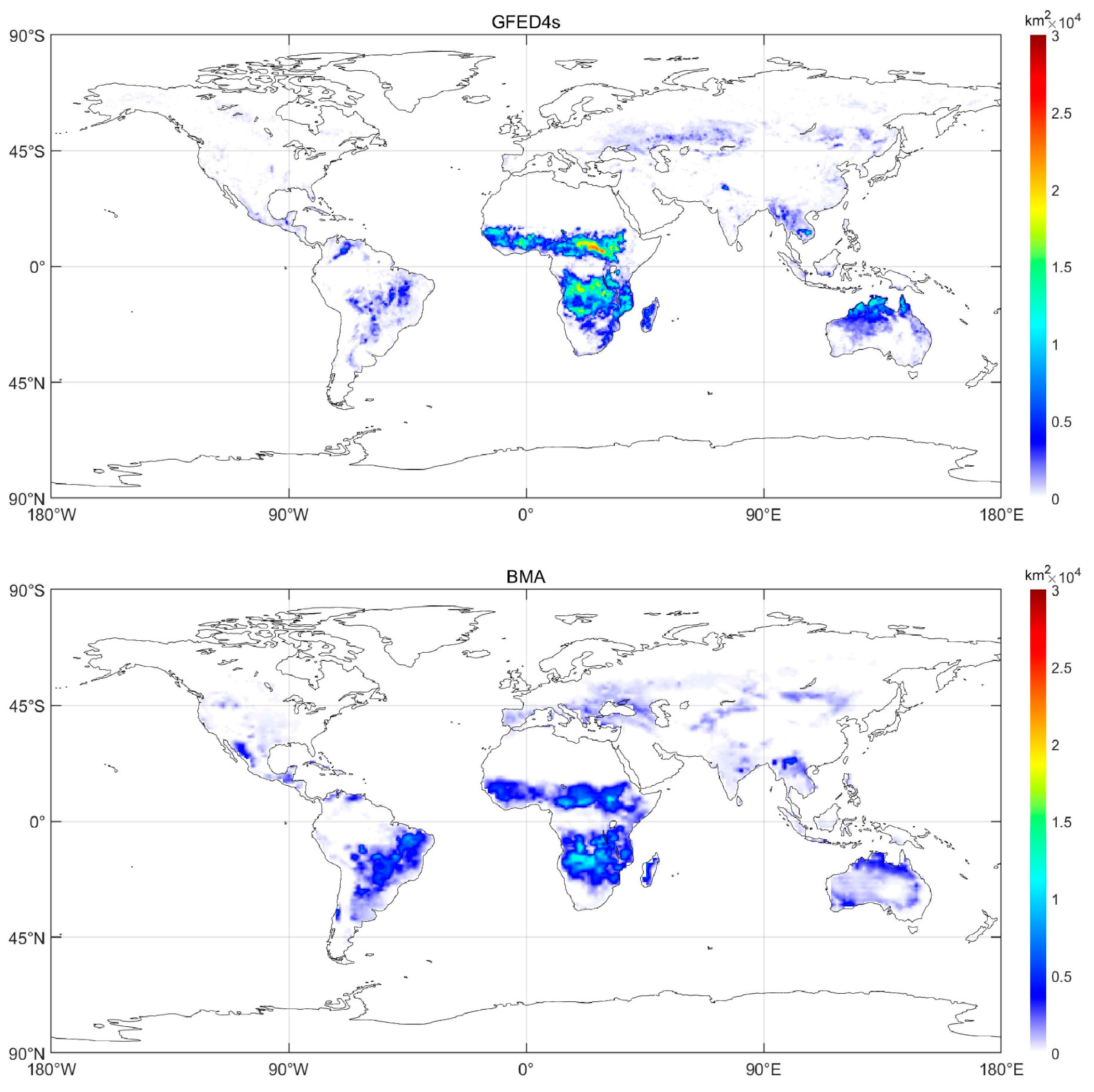
3.2.3. Spatial Comparison of Monthly BA Between BMA Model and GFED4s
3.3. Future Fire BA Prediction Based on the BMA Model
3.3.1. Validation of the Projections for the 2015–2040 Period
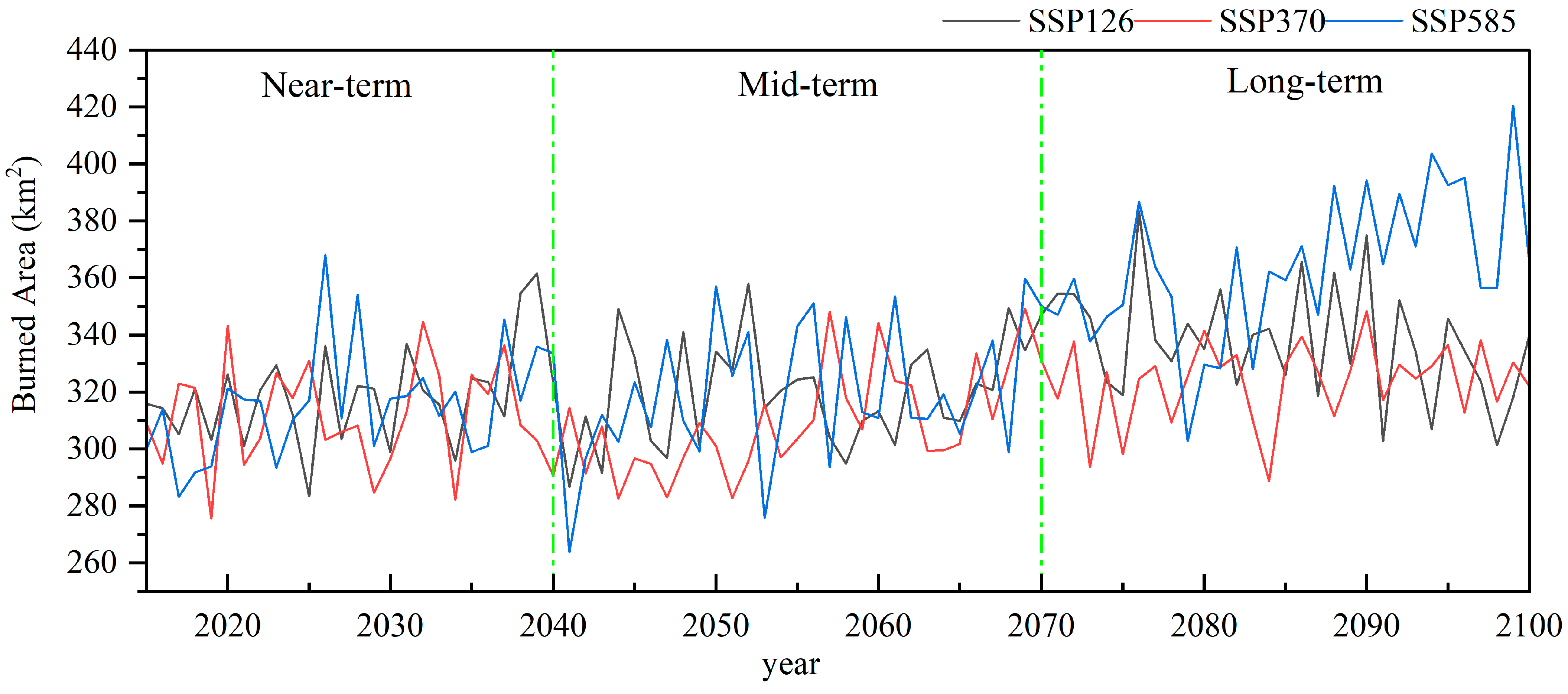
3.3.2. Future Temporal Changes in the Annual BA Under Different Scenarios
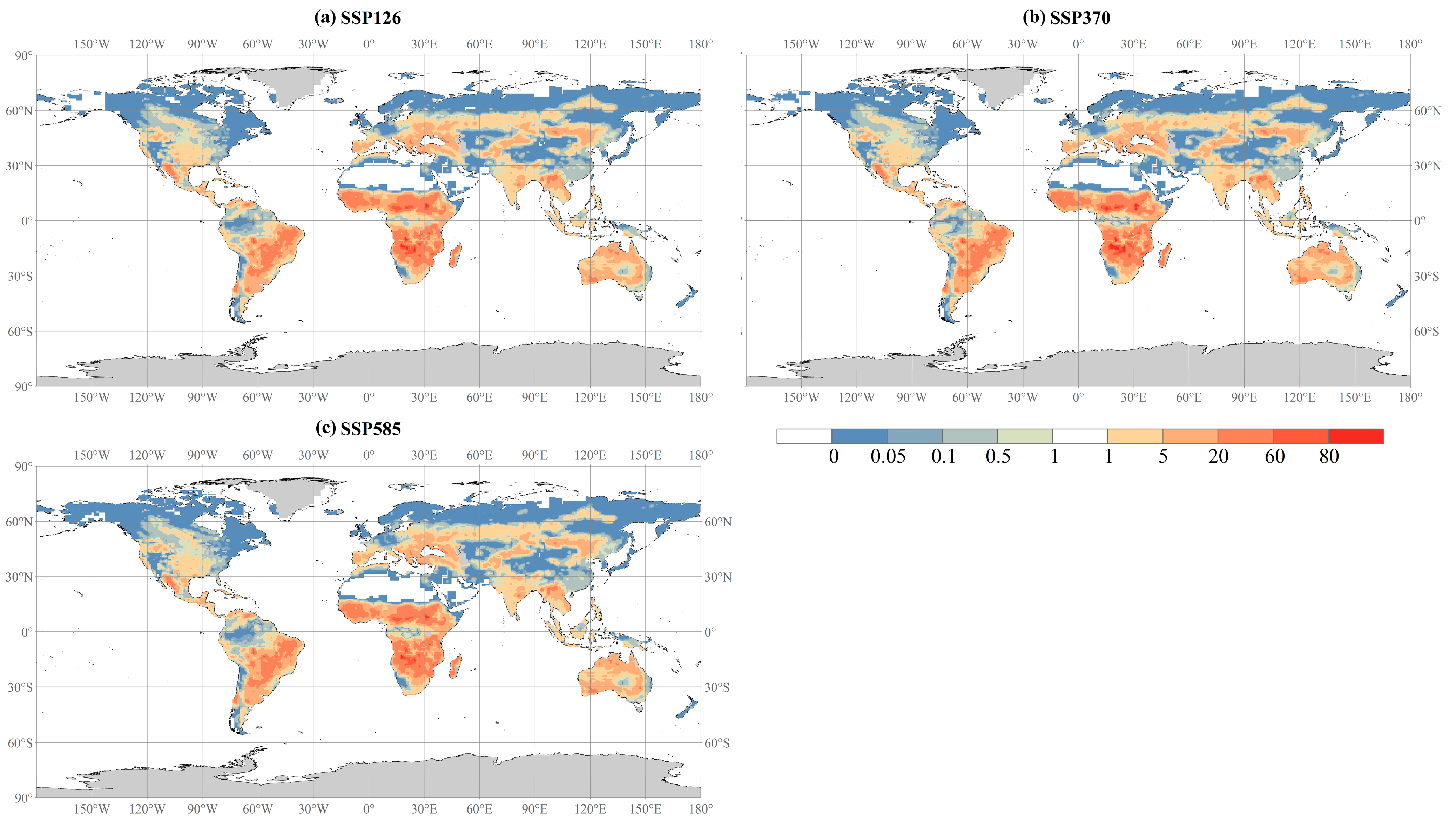
3.3.3. Future Spatial Changes in BA Under Different Scenarios
4. Discussion
4.1. Uncertainty Analysis of BA Under Different Scenarios
4.2. Uncertainty in Historical Simulation Results
4.3. Effects of Different Land Cover Types
4.4. Selection of Different Assessment Methods
4.5. Future Implications of BA Increases
4.6. Potential Limitations of GCMs and Satellite Data for BA Projections
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richardson, D.; Black, A.S.; Irving, D.; Matear, R.J.; Monselesan, D.P.; Risbey, J.S.; Squire, D.T.; Tozer, C.R. Global increase in wildfire potential from compound fire weather and drought. npj Clim. Atmos. Sci. 2022, 5, 23. [Google Scholar] [CrossRef]
- Cunningham, C.X.; Williamson, G.J.; Bowman, D.M.J.S. Increasing frequency and intensity of the most extreme wildfires on Earth. Nat. Ecol. Evol. 2024, 8, 1420–1425. [Google Scholar] [CrossRef] [PubMed]
- Bedia, J.; Herrera, S.; Gutiérrez, J.M.; Benali, A.; Brands, S.; Mota, B.; Moreno, J.M. Global patterns in the sensitivity of burned area to fire-weather: Implications for climate change. Agric. For. Meteorol. 2015, 214, 369–379. [Google Scholar] [CrossRef]
- Zheng, B.; Ciais, P.; Chevallier, F.; Chuvieco, E.; Chen, Y.; Yang, H. Increasing forest fire emissions despite the decline in global burned area. Sci. Adv. 2021, 7, eabh2646. [Google Scholar] [CrossRef]
- Chen, Y.; Morton, D.C.; Randerson, J.T. Remote sensing for wildfire monitoring: Insights into burned area, emissions, and fire dynamics. One Earth 2024, 7, 1022–1028. [Google Scholar] [CrossRef]
- Coop, J.D.; Parks, S.A.; Stevens-Rumann, C.S.; Ritter, S.M.; Hoffman, C.M. Extreme fire spread events and area burned under recent and future climate in the western USA. Glob. Ecol. Biogeogr. 2020, 31, 1949–1959. [Google Scholar] [CrossRef]
- David, E.C.; Krista, M.G.; Greg, J.; Ronald, P.N. Forest Service Large Fire Area Burned and Suppression Expenditure Trends, 1970–2002. J. For. 2005, 103, 179–183. [Google Scholar] [CrossRef]
- Lydersen, J.M.; Collins, B.M.; Brooks, M.L.; Matchett, J.R.; Shive, K.L.; Povak, N.A.; Kane, V.R.; Smith, D.F. Evidence of fuels management and fire weather influencing fire severity in an extreme fire event. Ecol. Appl. 2017, 27, 2013–2030. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, F.; Li, M. Probabilistic path planning for UAVs in forest fire monitoring: Enhancing patrol efficiency through risk assessment. Fire 2024, 7, 254. [Google Scholar] [CrossRef]
- Giglio, L.; Boschetti, L.; Roy, D.P.; Humber, M.L.; Justice, C.O. The Collection 6 MODIS burned area mapping algorithm and product. Remote Sens. Environ. 2018, 217, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Copernicus Climate Change Service, Climate Data Store, 2019. Fire Burned Area from 2001 to Present Derived from Satellite Observation. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/datasets/satellite-fire-burned-area?tab=overview (accessed on 11 March 2023).
- Van Der Werf, G.R.; Randerson, J.T.; Giglio, L.; Van Leeuwen, T.T.; Chen, Y.; Rogers, B.M.; Mu, M.; van Marle, M.J.E.; Morton, D.C.; Collatz, G.J.; et al. Global fire emissions estimates during 1997–2016. Earth Syst. Sci. Data 2017, 9, 697–720. [Google Scholar] [CrossRef]
- Mangeon, S.; Field, R.; Fromm, M.; Mchugh, C.; Voulgarakis, A. Satellite versus ground-based estimates of burned area: A comparison between MODIS based burned area and fire agency reports over North America in 2007. Am. Polit. Sci. Rev. 2015, 72, 76–92. [Google Scholar] [CrossRef]
- Joshi, J.; Sukumar, R. Improving prediction and assessment of global fires using multilayer neural networks. Sci. Rep. 2021, 11, 3295. [Google Scholar] [CrossRef]
- Wang, X.; Di, Z.; Liu, J. Evaluating the Abilities of Satellite-Derived Burned Area Products to Detect Forest Burning in China. Remote Sens. 2023, 15, 3260. [Google Scholar] [CrossRef]
- Grishin, A.M.; Filkov, A.I. A deterministic-probabilistic system for predicting forest fire danger. Fire Saf. J. 2011, 46, 56–62. [Google Scholar] [CrossRef]
- Guyette, R.P.; Stambaugh, M.C.; Dey, D.C. Predicting Fire Frequency with Chemistry and Climate. Ecosystems 2012, 15, 322–335. [Google Scholar] [CrossRef]
- Baranovskii, N.V.; Kirienko, V.A. Ignition of Forest Combustible Materials in a High-Temperature Medium. J. Eng. Phys. Thermophy 2020, 93, 1266–1271. [Google Scholar] [CrossRef]
- Anderson, K. A model to predict lightning-caused fire occurrences. Int. J. Wildland Fire 2002, 11, 163–172. [Google Scholar] [CrossRef]
- Baranovskiy, N.V.; Kirienko, V.A. Forest Fuel Drying, Pyrolysis and Ignition Processes during Forest Fire: A Review. Processes 2022, 10, 89. [Google Scholar] [CrossRef]
- Wen, J.X. Fire modelling: The success, the challenges, and the dilemma from a modeller’s perspective. Fire Saf. J. 2024, 144, 104087. [Google Scholar] [CrossRef]
- Singh, H.; Ang, L.M.; Lewis, T.; Paudyal, D.; Acuna, M.; Srivastava, P.K.; Srivastava, S.K. Trending and emerging prospects of physics-based and ML-based wildfire spread models: A comprehensive review. J. For. Res. 2024, 35, 135. [Google Scholar] [CrossRef]
- Marcozzi, A.; Wells, L.; Parsons, R.; Mueller, E.; Linn, R.; Hiers, J.K. FastFuels: Advancing wildland fire modeling with high-resolution 3D fuel data and data assimilation. Environ. Modell. Softw. 2025, 183, 106214. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Hetzer, J.; Forrest, M.; Ribalaygua, J.; Prado-López, C.; Hickler, T. The fire weather in Europe: Large-scale trends towards higher danger. Environ. Res. Lett. 2024, 19, 084017. [Google Scholar] [CrossRef]
- Quilcaille, Y.; Batibeniz, F.; Ribeiro, A.F.S.; Padrón, R.S. Fire weather index data under historical and SSP projections in CMIP6 from 1850 to 2100. Earth Syst. Sci. Data 2023, 15, 2153–2177. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Burton, C.; Lampe, S.; Kelley, D.I.; Thiery, W.; Hantson, S.; Christidis, N.; Gudmundsson, L.; Forrest, M.; Burke, E.; Chang, J.; et al. Global burned area increasingly explained by climate change. Nat. Clim. Chang. 2024, 14, 1186–1192. [Google Scholar] [CrossRef]
- Hantson, S.; Hamilton, D.S.; Burton, C. Changing fire regimes: Ecosystem impacts in a shifting climate. One Earth 2024, 7, 942–945. [Google Scholar] [CrossRef]
- Wang, T.; Tu, X.; Singh, V.P.; Chen, X.; Lin, K. Global data assessment and analysis of drought characteristics based on CMIP6. J. Hydrol. 2021, 596, 126091. [Google Scholar] [CrossRef]
- Kim, Y.; Min, S.; Zhang, X.; Sillmann, J.; Sandstad, M. Evaluation of the CMIP6 multi-model ensemble for climate extreme indices. Weather Clim. Extremes 2020, 29, 100269. [Google Scholar] [CrossRef]
- Gallo, C.; Eden, J.M.; Dieppois, B.; Drobyshev, I.; Fulé, P.Z.; San-Miguel-Ayanz, J.; Blackett, M. Evaluation of CMIP6 model performances in simulating fire weather spatiotemporal variability on global and regional scales. Geosci. Model Dev. 2023, 16, 3103–3122. [Google Scholar] [CrossRef]
- Wang, S.S.-C.; Leung, L.R.; Qian, Y. Projection of future fire emissions over the contiguous US using explainable artificial intelligence and CMIP6 models. J. Geophys. Res.-Atmos. 2023, 128, 14. [Google Scholar] [CrossRef]
- Tian, C.; Yue, X.; Zhu, J.; Liao, H.; Yang, Y.; Chen, L.; Zhou, X.; Lei, Y.; Zhou, H.; Cao, Y. Projections of fire emissions and the consequent impacts on air quality under 1.5 °C and 2 °C global warming. Environ. Pollut. 2023, 323, 121311. [Google Scholar] [CrossRef] [PubMed]
- Randerson, J.T.; van der Werf, G.R.; Giglio, L.; Collatz, G.J.; Kasibhatla, P.S. Global Fire Emissions Database, Version 4, (GFEDv4); ORNL DAAC: Oak Ridge, TN, USA, 2018. [Google Scholar]
- Raftery, A.E.; Madigan, D.; Hoeting, J.A. Bayesian model averaging for linear regression models. J. Am. Stat. Assoc. 1997, 92, 179–191. [Google Scholar] [CrossRef]
- Kim, J.; Mohanty, B.P.; Shin, Y. Effective soil moisture estimate and its uncertainty using multimodel simulation based on Bayesian Model Averaging. J. Geophys. Res. Atmos. 2015, 120, 8023–8042. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric test against the trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Forthofer, R.N.; Lehnen, R.G. Rank Correlation Methods. In Public Program Analysis; Springer: Boston, MA, USA, 1981. [Google Scholar] [CrossRef]
- Carrara, A.; Guzzetti, F.; Cardinali, M.; Reichenbach, P. Use of GIS Technology in the Prediction and Monitoring of Landslide Hazard. Nat. Hazards 1999, 20, 117–135. [Google Scholar] [CrossRef]
- Cai, L.; He, H.S.; Liang, Y.; Wu, Z. Analysis of the uncertainty of fuel model parameters in wildland fire modelling of a boreal forest in north-east China. Int. J. Wildland Fire 2019, 28, 205–215. [Google Scholar] [CrossRef]
- Roe, K.; Stevens, D.; McCord, C. High Resolution Weather Modeling for Improved Fire Management. In Proceedings of the 2001 ACM/IEEE Conference on Supercomputing (SC ‘01), Association for Computing Machinery, New York, NY, USA, 10–16 November 2001; p. 48. [Google Scholar] [CrossRef]
- Wei, L.; Xin, X.; Xiao, C.; Li, Y.; Wu, Y. Performance of BCC-CSM Models with Different Horizontal Resolutions in Simulating Extreme Climate Events in China. J. Meteorol. Res. 2019, 33, 720–733. [Google Scholar] [CrossRef]
- Palmer, T. Climate forecasting: Build high-resolution global climate models. Nature 2014, 515, 338–339. [Google Scholar] [CrossRef] [PubMed]
- Rummukainen, M. Added value in regional climate modeling. WIREs Clim. Chang. 2016, 7, 145–159. [Google Scholar] [CrossRef]
- Badhan, M.; Shamsaei, K.; Ebrahimian, H.; Bebis, G.; Lareau, N.P.; Rowell, E. Deep Learning Approach to Improve Spatial Resolution of GOES-17 Wildfire Boundaries Using VIIRS Satellite Data. Remote Sens. 2024, 16, 715. [Google Scholar] [CrossRef]
- Bounoua, L.; Defries, R.; Collatz, G.J. Effects of Land Cover Conversion on Surface Climate. Clim. Chang. 2002, 52, 29–64. [Google Scholar] [CrossRef]
- Elena, K.; Amber, S.; Alexander, P.; Evgeni, P. Fire emissions estimates in Siberia: Evaluation of uncertainties in area burned, land cover, and fuel consumption. Can. J. For. Res. 2013, 43, 493–506. [Google Scholar] [CrossRef]
- Barros, A.M.; Pereira, J.M. Wildfire selectivity for land cover type: Does size matter? PLoS ONE 2014, 9, e84760. [Google Scholar] [CrossRef]
- ISFR. 2021. State of Forest Report, 2021. Forest Survey of India, Dehradun, India. Available online: https://fsi.nic.in/forest-report-2021-details (accessed on 9 March 2023).
- Bajocco, S.; Ricotta, C. Evidence of selective burning in Sardinia (Italy): Which land-cover classes do wildfires prefer? Landsc. Ecol. 2008, 23, 241–248. [Google Scholar] [CrossRef]
- Afitah, I.; Mariaty; Isra, E.P. Analysis of Forest and Land Fire with Hotspot Modis on Various Types of Land Cover in Central Kalimantan Province. AgBioForum 2021, 23, 13–21. [Google Scholar]
- Jaime, C.; Mauricio, A.; Alejandro, M. Exploring the multidimensional effects of human activity and land cover on fire occurrence for territorial planning. J. Environ. Manag. 2021, 297, 113428. [Google Scholar] [CrossRef]
- Desmet, Q.; Ngo-Duc, T. A novel method for ranking CMIP6 global climate models over the southeast Asian region. Int. J. Climatol. 2022, 42, 97–117. [Google Scholar] [CrossRef]
- Khadka, D.; Babel, M.S.; Abatan, A.A. An evaluation of CMIP5 and CMIP6 climate models in simulating summer rainfall in the Southeast Asian monsoon domain. Int. J. Climatol. 2022, 42, 1181–1202. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Donoghue, D.N.; Deshayes, M. Preface: 2007 ForestSAT. Int. J. Remote Sens. 2009, 30, 4911–4914. [Google Scholar] [CrossRef]
- Emre, Ç.; Filiz, S. Evaluation of forest fire risk in the Mediterranean Turkish forests: A case study of Menderes region, Izmir. Int. J. Disaster Risk Reduct. 2020, 45, 101479. [Google Scholar] [CrossRef]
- Nolè, A.; Rita, A.; Spatola, M.F.; Borghetti, M. Biogeographic variability in wildfire severity and post-fire vegetation recovery across the European forests via remote sensing-derived spectral metrics. Sci. Total Environ. 2022, 823, 153807. [Google Scholar] [CrossRef]
- Gajendiran, K.; Kandasamy, S.; Narayanan, M. Influences of wildfire on the forest ecosystem and climate change: A comprehensive study. Environ. Res. 2024, 240, 117537. [Google Scholar] [CrossRef]
- Roces-Díaz, J.V.; Santín, C.; Martínez-Vilalta, J.; Doerr, S.H. A global synthesis of fire effects on ecosystem services of forests and woodlands. Front. Ecol. Environ. 2022, 20, 170–178. [Google Scholar] [CrossRef]


| Name | Source | Country | Organization | Horizontal Grid (Lat × lon) |
|---|---|---|---|---|
| GFED4s (a) | MODIS and TRMM | USA | NASA | - |
| CESM2 (b) | CMIP6 | USA | NCAR | 288 × 192 |
| CESM2-FV2 (c) | CMIP6 | USA | NCAR | 288 × 192 |
| CESM2-WACCM (d) | CMIP6 | USA | NCAR | 288 × 192 |
| CESM2-WACCM-FV2 (e) | CMIP6 | USA | NCAR | 288 × 192 |
| CMCC-ESM2 (f) | CMIP6 | Italy | CMCC | 288 × 192 |
| CMCC-CM2-SR5 (g) | CMIP6 | Italy | CMCC | 288 × 192 |
| NorESM2-LM (h) | CMIP6 | Norway | NCC | 144 × 96 |
| NorESM2-MM (i) | CMIP6 | Norway | NCC | 288 × 192 |
| GFDL-ESM4 (j) | ISIMIP | USA | NOAA-GFDL | 288 × 180 |
| UKESM1-0-LL (k) | ISIMIP | UK | MOHC | 192 × 144 |
| Scenario | Radiative Forcing | Radiative Forcing in 2100/(W·m−2) | SSP |
|---|---|---|---|
| SSP1-2.6 (SSP126) | low | 2.6 | Sustainability |
| SSP3-7.0 (SSP370) | high | 7.0 | Regional rivalry |
| SSP5-8.5 (SSP585) | high | 8.5 | Fossil-fueled development |
| Model | (b–a) | (c–a) | (d–a) | (e–a) | (f–a) | (g–a) | (h–a) | (i–a) | (j–a) | (k–a) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | |||||||||||
| BONA | −0.120 | −0.156 | −0.123 | −0.155 | 0.293 | 0.675 | −0.150 | −0.063 | −0.031 | 0.004 | |
| TENA | 0.490 | 0.539 | 0.679 | 0.376 | 2.261 | 2.968 | 0.230 | 0.517 | 2.674 | 2.512 | |
| CEAM | 2.230 | 1.543 | 2.493 | 2.260 | 3.356 | 3.585 | 1.049 | 1.946 | 2.018 | 1.885 | |
| NHSA | −0.125 | −0.432 | −0.275 | −0.238 | 1.927 | 2.385 | −0.516 | −0.729 | 10.176 | 9.676 | |
| SHSA | 4.663 | 4.220 | 4.921 | 2.805 | 3.170 | 3.923 | 2.057 | 4.441 | 8.402 | 7.130 | |
| EURO | 0.156 | 0.514 | 0.459 | 0.485 | 1.178 | 1.324 | 0.783 | 0.546 | 0.142 | 0.167 | |
| MIDE | 0.443 | 0.458 | 0.471 | 0.427 | 0.306 | 0.286 | 0.502 | 0.466 | −0.062 | −0.057 | |
| NHAF | −4.377 | −5.378 | −4.315 | −6.011 | −5.466 | −5.602 | −4.119 | −3.694 | 1.481 | 1.045 | |
| SHAF | −4.604 | −2.815 | −4.384 | −5.819 | −8.980 | −9.232 | −6.773 | −3.850 | 8.077 | 7.032 | |
| BOAS | −0.257 | −0.388 | −0.271 | −0.410 | 0.536 | 0.750 | −0.380 | −0.012 | −0.302 | −0.321 | |
| CEAS | −0.120 | −0.156 | −0.123 | −0.155 | 0.293 | 0.675 | −0.150 | −0.063 | −0.031 | 0.004 | |
| SEAS | 0.296 | −0.510 | 0.216 | −0.578 | 0.234 | −0.066 | −0.046 | 0.400 | 0.026 | 0.074 | |
| EQAS | −0.136 | 0.075 | −0.295 | 0.042 | 0.520 | 0.075 | 0.111 | −0.130 | −0.049 | −0.236 | |
| AUST | −2.044 | −2.331 | −2.351 | −2.148 | −2.206 | −2.903 | −2.858 | −2.858 | −2.231 | −2.597 | |
| Model | GFED4s | (b) | (c) | (d) | (e) | (f) | (g) | (h) | (i) | (j) | (k) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | ||||||||||||
| BONA | 6–8 | 7–9 | 7–10 | 7–9 | 7–10 | 7–9 | 7–9 | 6–10 | 6–9 | 6–10 | 6–9 | |
| TENA | 3–4, 7–9 | 7–9 | 7–10 | 7–10 | 7–10 | 7–9 | 7–9 | 7–9 | 6–10 | 6–10 | 6–10 | |
| CEAM | 3–5 | 4–7 | 4–8 | 3–7 | 4–8 | 4–8 | 4–8 | 4–8 | 3–7 | 2–6 | 2–6 | |
| NHSA | 12–3 | 1–5 | 2–5 | 2–5 | 2–5 | 1–5 | 1–5 | 2–5 | 2–5 | 1–4 | 1–4 | |
| SHSA | 7–10 | 8–11 | 8–11 | 8–11 | 8–11 | 8–10 | 8–10 | 8–11 | 8–11 | 7–11 | 7–11 | |
| EURO | 7–10 | 7–9 | 7–9 | 7–9 | 7–9 | 7–9 | 7–9 | 7–9 | 7–9 | 6–9 | 6–9 | |
| MIDE | 6–10 | 7–10 | 7–10 | 7–10 | 7–10 | 6–9 | 6–9 | 6–10 | 6–10 | 7–10 | 6–10 | |
| NHAF | 11–2 | 12–4 | 12–4 | 12–4 | 1–4 | 12–3, 5 | 1–5 | 1–4 | 12–4 | 12–4 | 12–4 | |
| SHAF | 6–10 | 9–11 | 9–12 | 9–11 | 9–11 | 8–11 | 8–11 | 8–11 | 8–11 | 6–10 | 6–19 | |
| BOAS | 4–5, 7–8 | 4, 7–9 | 4–5, 8–9 | 4–5, 7–9 | 4–5, 8 | 7–8 | 7–9 | 4–5, 7–9 | 7–9 | 6–9 | 6–8 | |
| CEAS | 4–9 | 6–9 | 6–9 | 6–9 | 6–9 | 6–9 | 7–9 | 7–10 | 4–9 | 5–9 | 5–9 | |
| SEAS | 1–4 | 2–6 | 1–5 | 2–5 | 1–5 | 2–5 | 2–5 | 1–6 | 2–6 | 1–5 | 1–5 | |
| EQAS | 8–10 | 9–10, 12 | 8–11 | 8–10 | 8–11 | 8–11 | 8–10 | 3–4, 8–11 | 8–11 | 8–11 | 8–11 | |
| AUST | 8–11 | 10–2 | 10–2 | 10–2 | 10–1 | 10–2 | 10–2 | 10–2 | 10–2 | 8–1 | 9–1 | |
| Region | Better Models |
|---|---|
| BONA | (b)(c)(d)(e)(h)(i)(j)(k) |
| TENA | (b)(c)(e)(h)(i) |
| CEAM | (h)(c)(e) |
| NHSA | (h)(c)(e) |
| SHSA | (h)(c)(e)(f) |
| EURO | (j)(k) |
| MIDE | (j)(k) |
| NHAF | (h)(j)(k) |
| SHAF | (f)(g) |
| BOAS | (b)(c)(d)(e)(h)(j)(k) |
| CEAS | (j)(k) |
| SEAS | (c)(e)(f)(g)(h) |
| EQAS | (h)(i) |
| AUST | (b)(c)(d)(e)(f)(h)(i)(g) |
| Model | <1% | <2% | 2~5% | 5~10% | 10–50% | >50% |
|---|---|---|---|---|---|---|
| GFED4s (a) | 93.828% | 95.559% | 1.840% | 0.931% | 1.455% | 0.215% |
| CESM2 (b) | 92.810% | 94.507% | 2.085% | 1.407% | 1.971% | 0.029% |
| CESM2-FV2 (c) | 92.948% | 94.558% | 2.195% | 1.352% | 1.873% | 0.021% |
| CESM2-WACCM (d) | 92.803% | 94.494% | 2.010% | 1.458% | 2.020% | 0.018% |
| CESM2-WACCM-FV2 (e) | 93.181% | 94.799% | 2.218% | 1.395% | 1.586% | 0.003% |
| CMCC-ESM2 (f) | 90.540% | 92.435% | 3.007% | 2.469% | 2.086% | 0.004% |
| CMCC-CM2-SR5 (g) | 90.394% | 92.262% | 2.917% | 2.480% | 2.338% | 0.003% |
| NorESM2-LM (h) | 91.371% | 93.772% | 2.801% | 1.858% | 1.567% | 0.002% |
| NorESM2-MM (i) | 91.647% | 93.728% | 2.537% | 1.727% | 1.979% | 0.029% |
| GFDL-ESM4 (j) | 93.437% | 94.608% | 1.637% | 1.164% | 2.025% | 0.566% |
| UKESM1-0-LL (k) | 93.580% | 94.824% | 1.645% | 1.133% | 1.877% | 0.522% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Di, Z.; Zhang, W.; Zhang, S.; Sun, H.; Tian, X.; Meng, H.; Wang, X. Evaluation and Projection of Global Burned Area Based on Global Climate Models and Satellite Fire Product. Remote Sens. 2024, 16, 4751. https://doi.org/10.3390/rs16244751
Wang X, Di Z, Zhang W, Zhang S, Sun H, Tian X, Meng H, Wang X. Evaluation and Projection of Global Burned Area Based on Global Climate Models and Satellite Fire Product. Remote Sensing. 2024; 16(24):4751. https://doi.org/10.3390/rs16244751
Chicago/Turabian StyleWang, Xueyan, Zhenhua Di, Wenjuan Zhang, Shenglei Zhang, Huiying Sun, Xinling Tian, Hao Meng, and Xurui Wang. 2024. "Evaluation and Projection of Global Burned Area Based on Global Climate Models and Satellite Fire Product" Remote Sensing 16, no. 24: 4751. https://doi.org/10.3390/rs16244751
APA StyleWang, X., Di, Z., Zhang, W., Zhang, S., Sun, H., Tian, X., Meng, H., & Wang, X. (2024). Evaluation and Projection of Global Burned Area Based on Global Climate Models and Satellite Fire Product. Remote Sensing, 16(24), 4751. https://doi.org/10.3390/rs16244751







