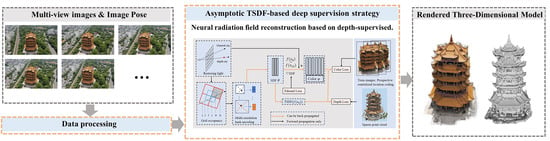
3D Reconstruction of Ancient Buildings Using UAV Images and Neural Radiation Field with Depth Supervision
Abstract
:1. Introduction
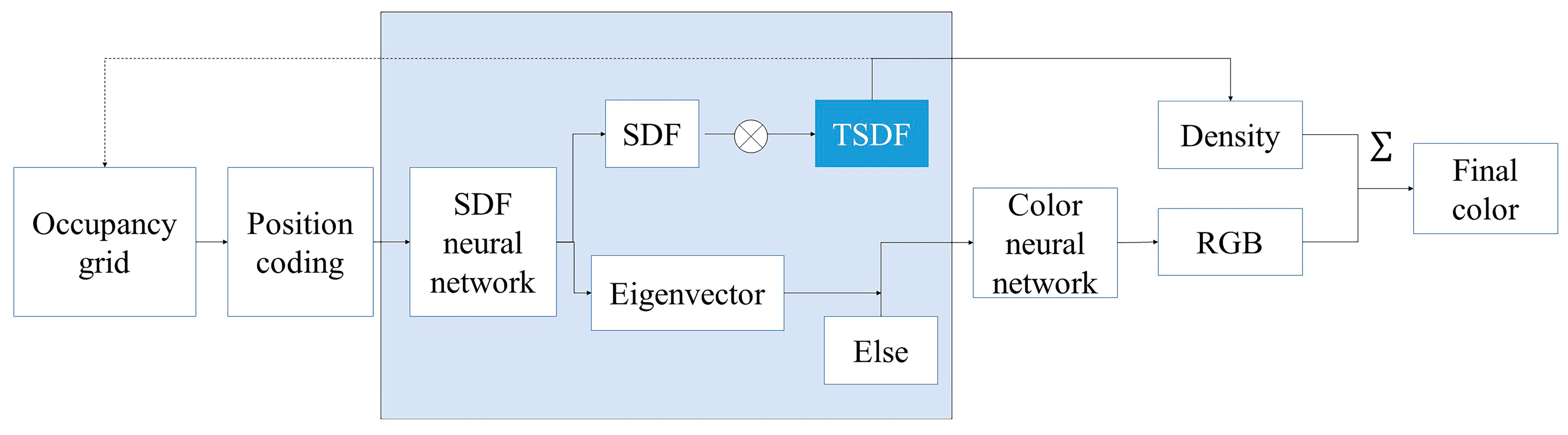
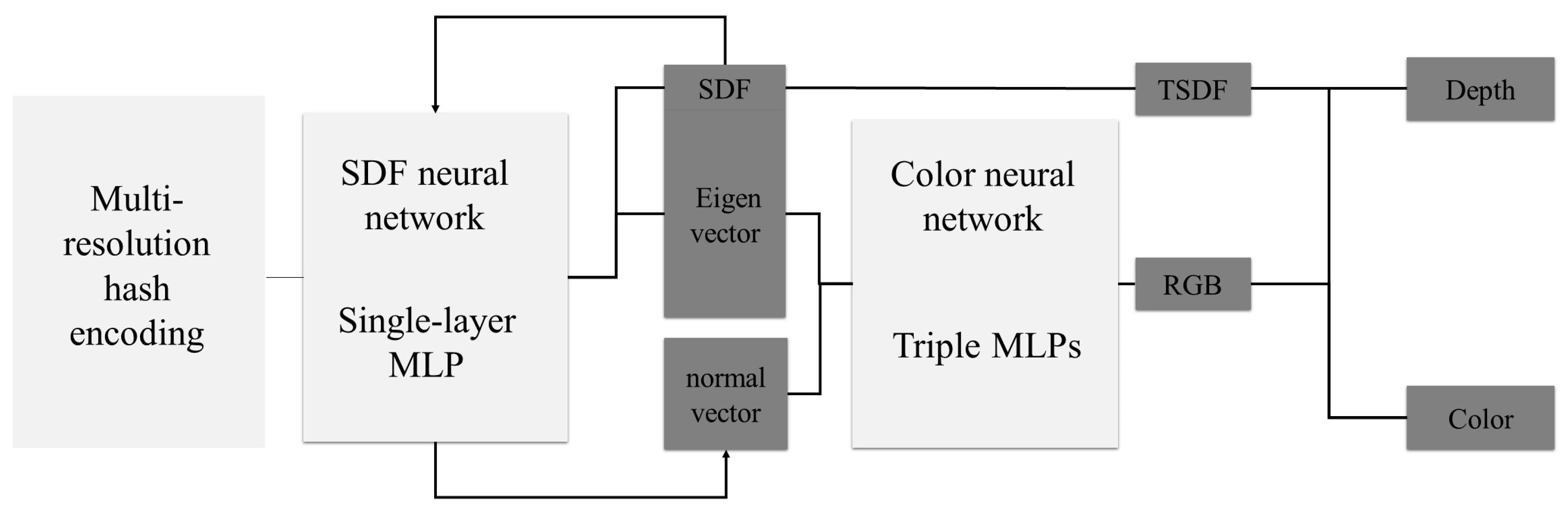
- Combined network training with the TSDF and depth supervision: Our approach combines the TSDF and depth supervision in network training. Integrating the TSDF into the signed distance function (SDF) neural network to improve geometric representation within the neural network. Simultaneously, this study utilizes sparse point cloud depth information to supervise the training of the SDF neural network, further enhancing the geometric accuracy of three-dimensional mesh models.
- A progressive training method that gradually enhances the resolution of hash coding during the training process has been designed. This approach focuses on improving the characteristics of the scene and hash coding, effectively utilizing the feature hash table’s capacity. By doing so, it mitigates hash conflicts within the mesh feature hash table under multi-resolution conditions. The ultimate goal is to produce rendered images with clear, detailed textures, enriching the visual quality.
2. Related Work
3. Methods
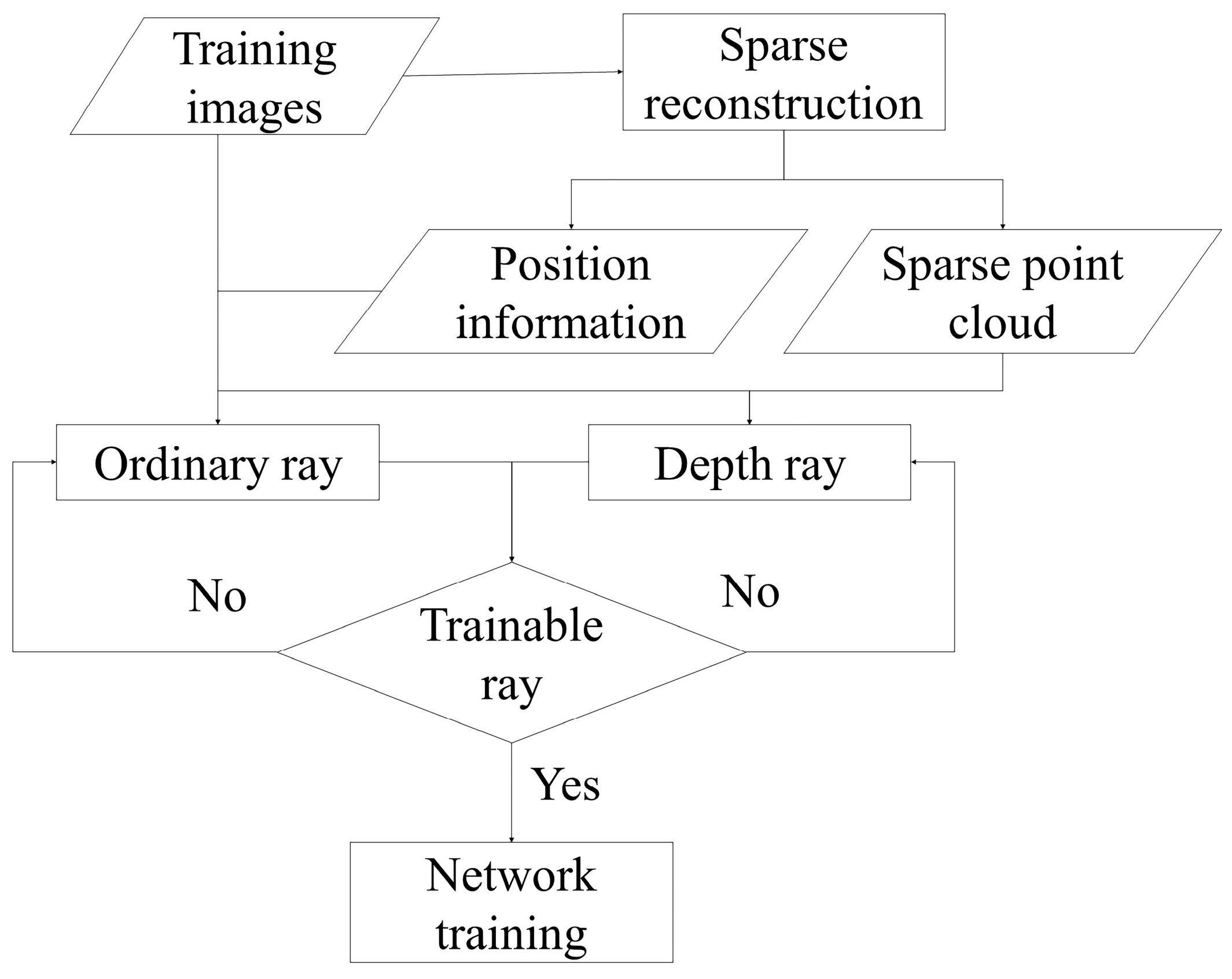
3.1. Data Processing
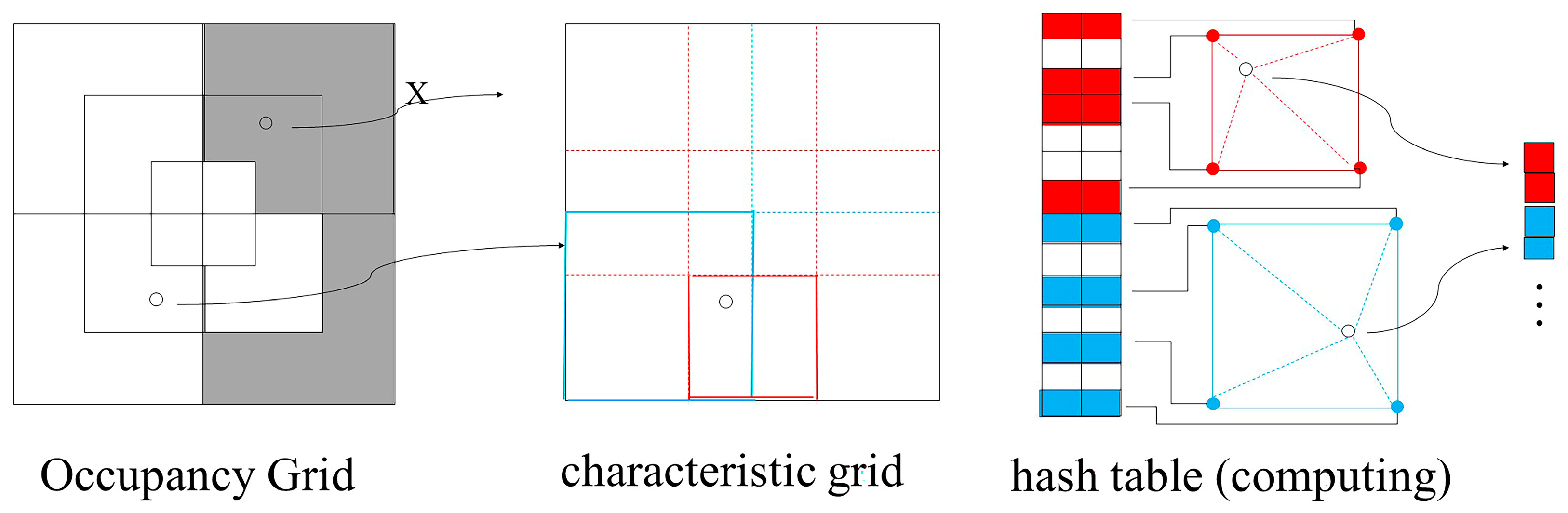
3.2. Progressive Multi-Resolution Hash Coding
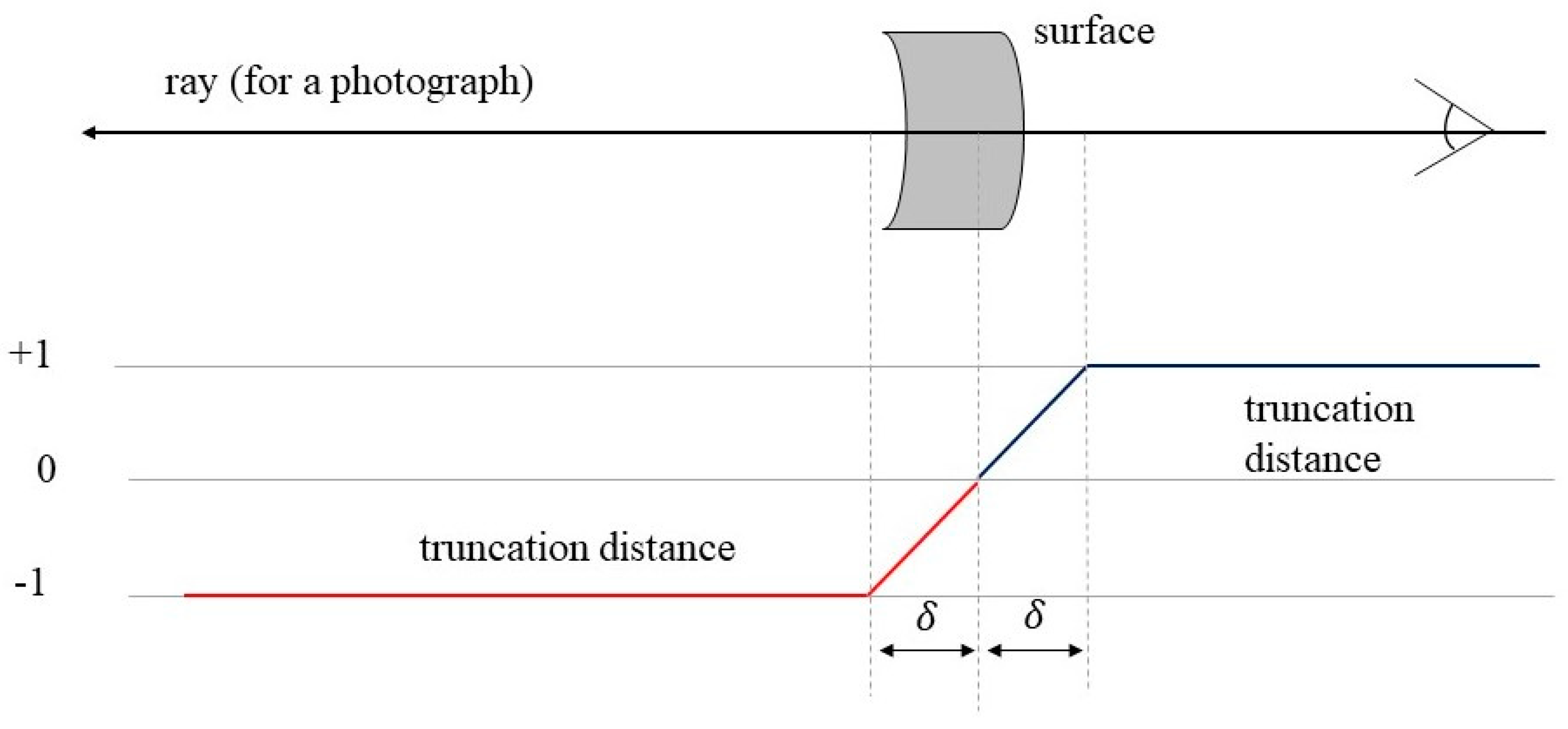
3.3. Asymptotic TSDF-Based Deep Supervision Strategy
4. Experiments
4.1. Experimental Data
4.2. Evaluation Indicators
4.3. Hash Coding Experiment
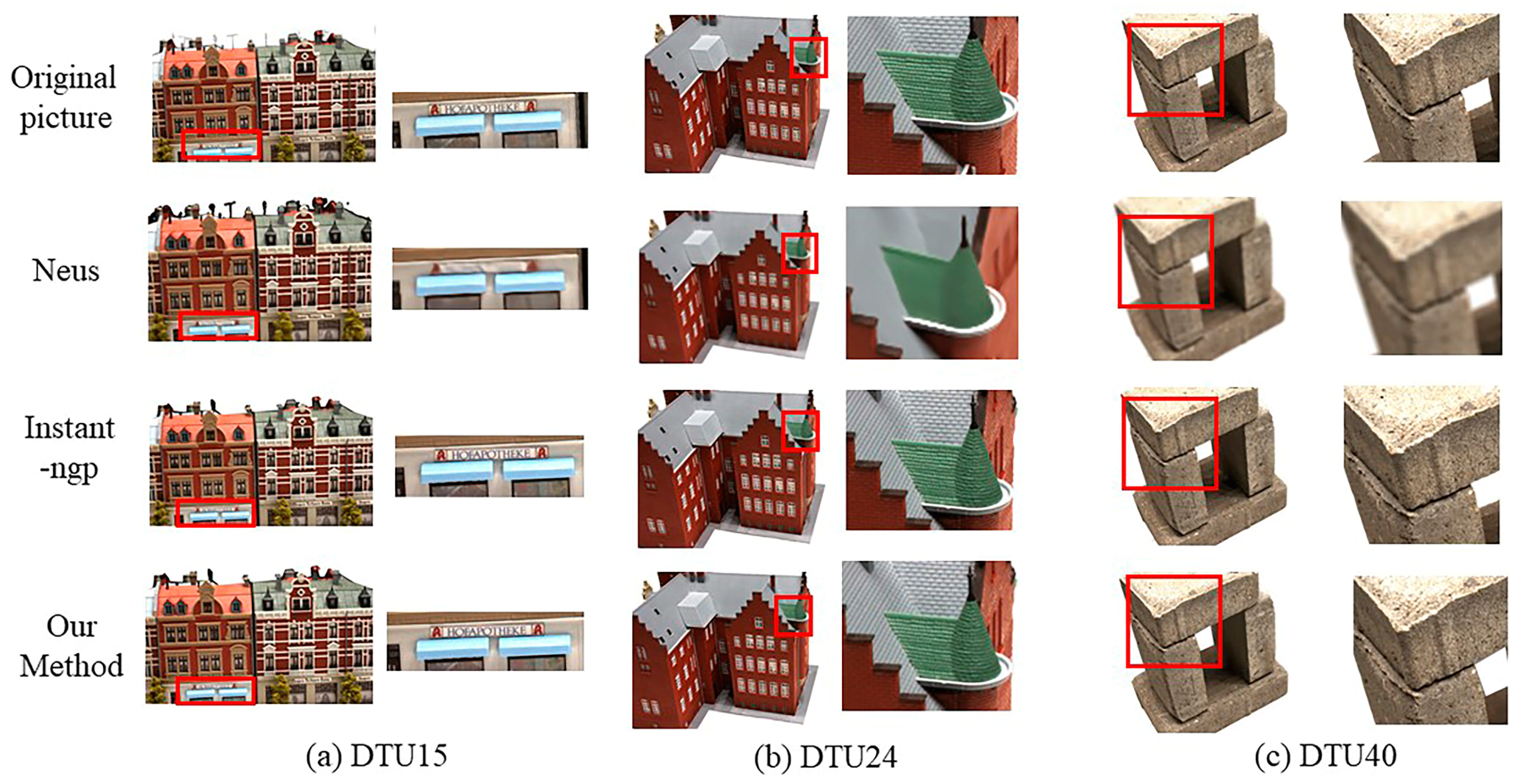
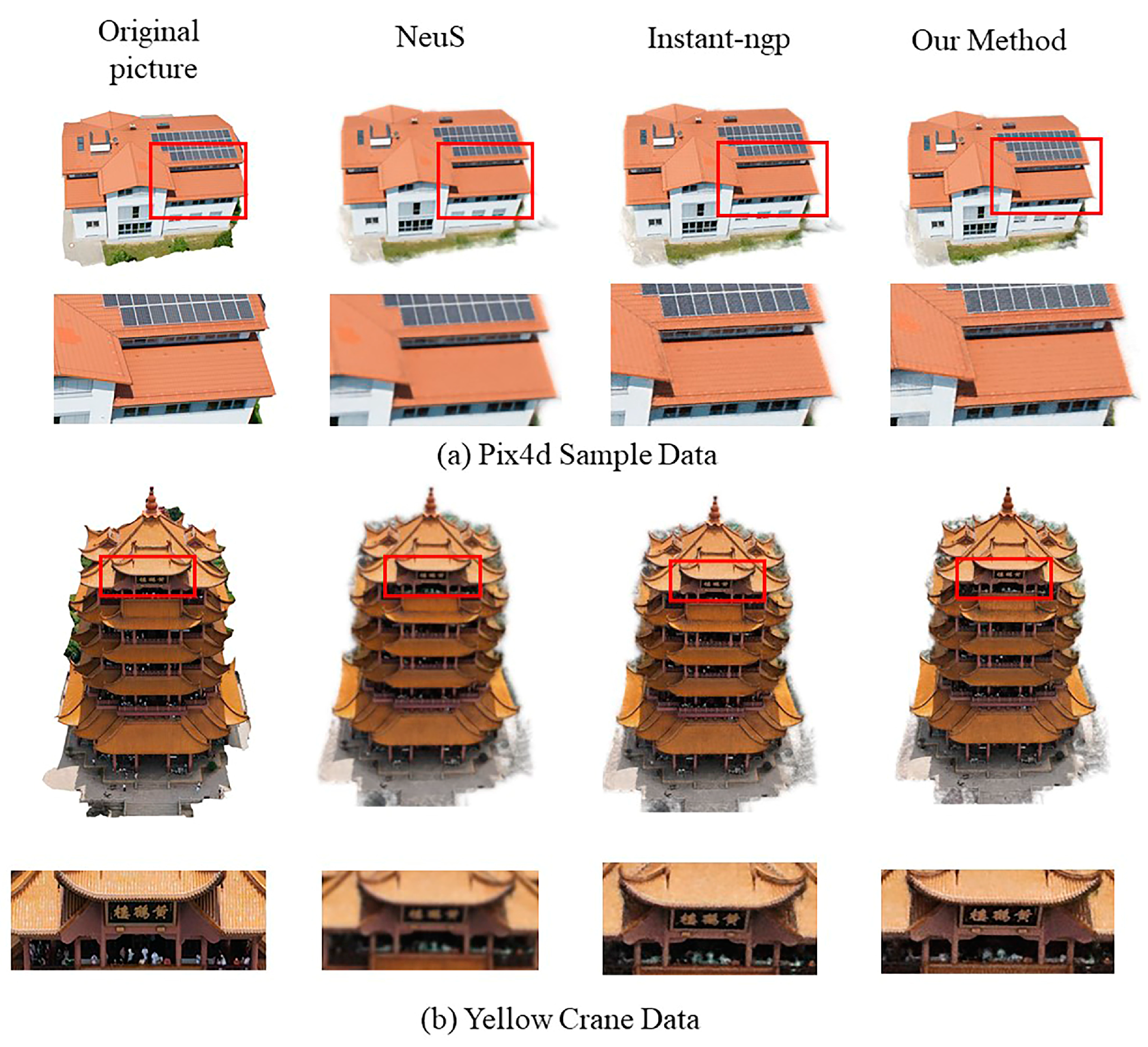
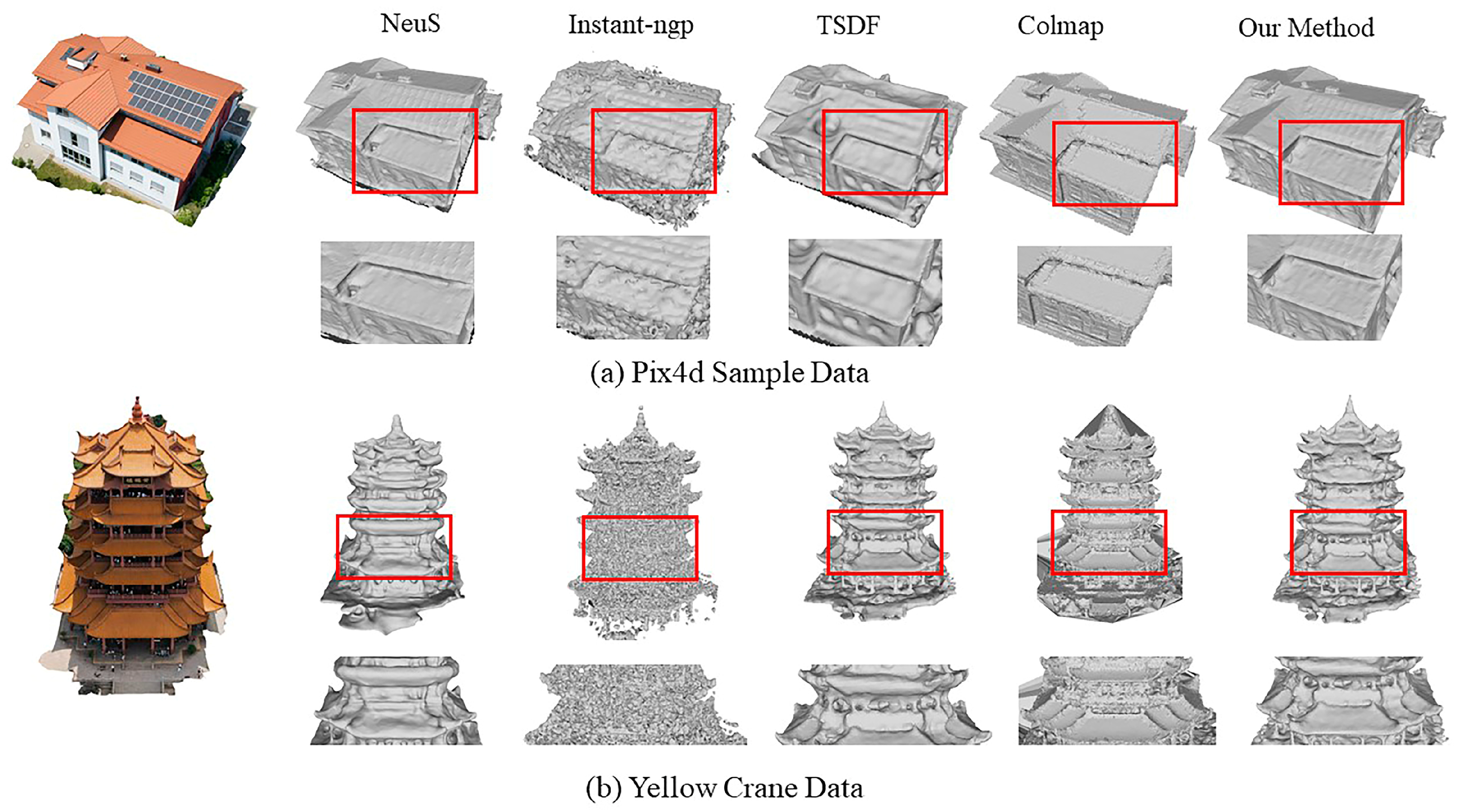
4.3.1. Qualitative Experimental Analysis
4.3.2. Quantitative Experimental Analysis
4.4. Depth-Supervised Ablation Experiments on Ancient Buildings
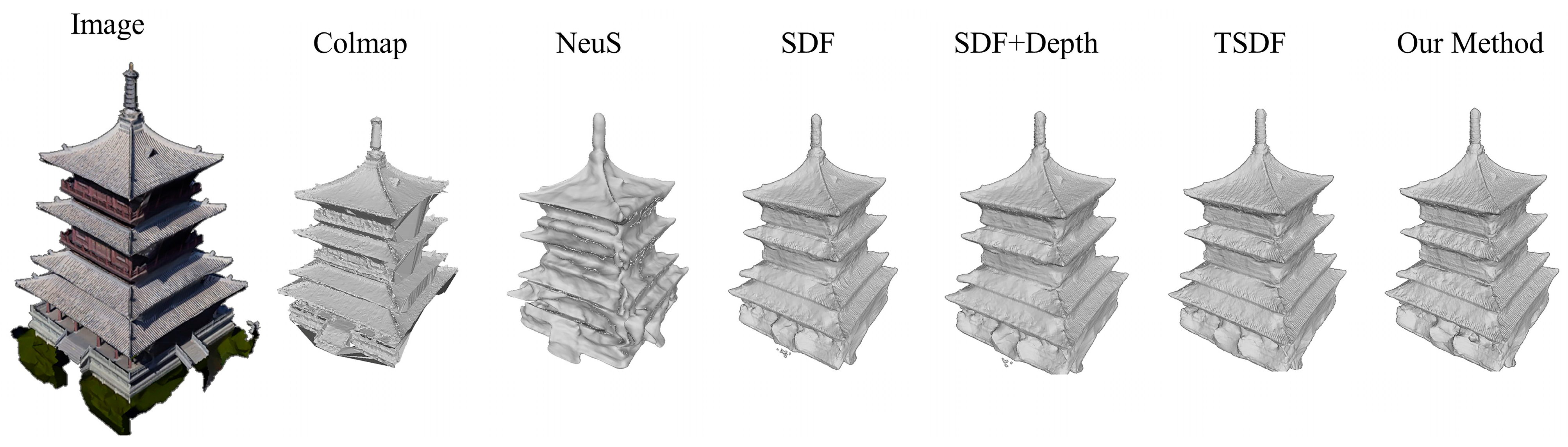
4.4.1. Qualitative Experimental Analysis
4.4.2. Quantitative Experimental Analysis
5. Discussion
- (1)
- Reasons for improvement in rendered image quality: In this study, the images were preprocessed during the model training phase, employing a strategy of masking the background area to reduce the interference from background noise. Additionally, the adoption of progressive multi-resolution hash coding combined with occupying a three-dimensional grid fully exploits the high-resolution feature space in the hash table. Such a strategy allows the high-resolution grid to more accurately and intensively represent the detailed structure of the scene. This not only effectively resolves hash conflicts but also substantially improves the quality of the rendered images, leading to a more precise and detailed visual output.
- (2)
- Reasons for improvement in model geometric structure: The integration of the TSDF values in this method ensures that the voxels in the occupied grid more closely adhere to the object’s surface. This mechanism effectively filters out key points that significantly impact the reconstructed surface while eliminating points with little or no effect. Furthermore, the incorporation of depth supervision information enhances the model’s depth representation capability, significantly improving the geometric structure of the generated model.
- (3)
- Reasons for improvement in network training efficiency: At the initial stage of training, this study employed progressive multi-resolution hash coding, accelerating the ray sampling process by eliminating ineffective grids in the occupied grid. As the training progresses, the strategic application of the TSDF values for the threshold truncation continuously updates the occupancy of the grid, further speeding up the ray sampling efficiency. Moreover, integrating depth supervision information into the training regimen significantly hastens the model’s convergence towards high-quality outcomes, ensuring the rapid attainment of superior results.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klimkowska, A.; Cavazzi, S.; Leach, R.; Grebby, S. Detailed three-dimensional building façade reconstruction: A review on applications, data and technologies. Remote Sens. 2022, 14, 2579. [Google Scholar] [CrossRef]
- Geiger, A.; Ziegler, J.; Stiller, C. Stereoscan: Dense 3d reconstruction in real-time. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden, Germany, 5–9 June 2011; pp. 963–968. [Google Scholar]
- Wang, T.; Zhao, L. Virtual reality-based digital restoration methods and applications for ancient buildings. J. Math. 2022, 2022, 2305463. [Google Scholar] [CrossRef]
- Qu, Y.; Huang, J.; Zhang, X. Rapid 3D reconstruction for image sequence acquired from UAV camera. Sensors 2018, 18, 225. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Shang, L.; Wang, C. Three-Dimensional Reconstruction and Protection of Mining Heritage Based on Lidar Remote Sensing and Deep Learning. Mob. Inf. Syst. 2022, 2022, 2412394. [Google Scholar] [CrossRef]
- Pepe, M.; Alfio, V.S.; Costantino, D.; Scaringi, D. Data for 3D reconstruction and point cloud classification using machine learning in cultural heritage environment. Data Brief 2022, 42, 108250. [Google Scholar] [CrossRef] [PubMed]
- Schonberger, J.L.; Frahm, J.-M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Pepe, M.; Alfio, V.S.; Costantino, D. UAV platforms and the SfM-MVS approach in the 3D surveys and modelling: A review in the cultural heritage field. Appl. Sci. 2022, 12, 12886. [Google Scholar] [CrossRef]
- Pei, S.; Yang, R.; Liu, Y.; Xu, W.; Zhang, G. Research on 3D reconstruction technology of large-scale substation equipment based on NeRF. IET Sci. Meas. Technol. 2023, 17, 71–83. [Google Scholar] [CrossRef]
- Lee, J.Y.; DeGol, J.; Zou, C.; Hoiem, D. Patchmatch-rl: Deep mvs with pixelwise depth, normal, and visibility. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11 October 2021; pp. 6158–6167. [Google Scholar]
- Schönberger, J.L.; Price, T.; Sattler, T.; Frahm, J.-M.; Pollefeys, M. A vote-and-verify strategy for fast spatial verification in image retrieval. In Proceedings of the Computer Vision–ACCV 2016: 13th Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; Revised Selected Papers, Part I 13, 2017. pp. 321–337. [Google Scholar]
- Dang, W.; Xiang, L.; Liu, S.; Yang, B.; Liu, M.; Yin, Z.; Yin, L.; Zheng, W. A Feature Matching Method based on the Convolutional Neural Network. J. Imaging Sci. Technol. 2023, 67, 030402. [Google Scholar] [CrossRef]
- Cubes, M. A high resolution 3d surface construction algorithm/william e. Lorensen Harvey E. Cline–SIG 1987, 87, 76. [Google Scholar]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J. Mlp-mixer: An all-mlp architecture for vision. Adv. Neural Inf. Process. Syst. 2021, 34, 24261–24272. [Google Scholar]
- Yu, A.; Li, R.; Tancik, M.; Li, H.; Ng, R.; Kanazawa, A. Plenoctrees for real-time rendering of neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11 October 2021; pp. 5752–5761. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. (ToG) 2022, 41, 102. [Google Scholar] [CrossRef]
- Zhao, F.; Jiang, Y.; Yao, K.; Zhang, J.; Wang, L.; Dai, H.; Zhong, Y.; Zhang, Y.; Wu, M.; Xu, L. Human performance modeling and rendering via neural animated mesh. ACM Trans. Graph. (TOG) 2022, 41, 1–17. [Google Scholar] [CrossRef]
- Wang, P.; Liu, L.; Liu, Y.; Theobalt, C.; Komura, T.; Wang, W. Neus: Learning neural implicit surfaces by volume rendering for multi-view reconstruction. arXiv 2021, arXiv:2106.10689. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-nerf: A multiscale representation for anti-aliasing neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11 October 2021; pp. 5855–5864. [Google Scholar]
- Li, Z.; Müller, T.; Evans, A.; Taylor, R.H.; Unberath, M.; Liu, M.-Y.; Lin, C.-H. Neuralangelo: High-Fidelity Neural Surface Reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 8456–8465. [Google Scholar]
- Kerbl, B.; Kopanas, G.; Leimkühler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Trans. Graph. 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Condorelli, F.; Rinaudo, F.; Salvadore, F.; Tagliaventi, S. A comparison between 3D reconstruction using nerf neural networks and mvs algorithms on cultural heritage images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 565–570. [Google Scholar] [CrossRef]
- Lehtola, V.V.; Koeva, M.; Elberink, S.O.; Raposo, P.; Virtanen, J.-P.; Vahdatikhaki, F.; Borsci, S. Digital twin of a city: Review of technology serving city needs. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 102915. [Google Scholar] [CrossRef]
- Gao, K.; Gao, Y.; He, H.; Lu, D.; Xu, L.; Li, J. Nerf: Neural radiance field in 3d vision, a comprehensive review. arXiv 2022, arXiv:2210.00379. [Google Scholar]
- Villanueva, A.J.; Marton, F.; Gobbetti, E. SSVDAGs: Symmetry-aware sparse voxel DAGs. In Proceedings of the 20th ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, Redmond, WA, USA, 27–28 February 2016; pp. 7–14. [Google Scholar]
- Verbin, D.; Hedman, P.; Mildenhall, B.; Zickler, T.; Barron, J.T.; Srinivasan, P.P. Ref-nerf: Structured view-dependent appearance for neural radiance fields. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 5481–5490. [Google Scholar]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohi, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. Kinectfusion: Real-time dense surface mapping and tracking. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 127–136. [Google Scholar]
- Ma, L.; Li, X.; Liao, J.; Zhang, Q.; Wang, X.; Wang, J.; Sander, P.V. Deblur-nerf: Neural radiance fields from blurry images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12861–12870. [Google Scholar]
- Zhang, K.; Riegler, G.; Snavely, N.; Koltun, V. Nerf++: Analyzing and improving neural radiance fields. arXiv 2020, arXiv:2010.07492. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Mip-nerf 360: Unbounded anti-aliased neural radiance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5470–5479. [Google Scholar]
- Oechsle, M.; Peng, S.; Geiger, A. Unisurf: Unifying neural implicit surfaces and radiance fields for multi-view reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11 October 2021; pp. 5589–5599. [Google Scholar]
- Fridovich-Keil, S.; Yu, A.; Tancik, M.; Chen, Q.; Recht, B.; Kanazawa, A. Plenoxels: Radiance fields without neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5501–5510. [Google Scholar]
- Liu, L.; Gu, J.; Zaw Lin, K.; Chua, T.-S.; Theobalt, C. Neural sparse voxel fields. Adv. Neural Inf. Process. Syst. 2020, 33, 15651–15663. [Google Scholar]
- Huang, X.; Alkhalifah, T. Efficient physics-informed neural networks using hash encoding. arXiv 2023, arXiv:2302.13397. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, Z.; Philip, J.; Bi, S.; Shu, Z.; Sunkavalli, K.; Neumann, U. Point-nerf: Point-based neural radiance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5438–5448. [Google Scholar]
- Zhang, J.; Yao, Y.; Quan, L. Learning signed distance field for multi-view surface reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11 October 2021; pp. 6525–6534. [Google Scholar]
- Wei, Y.; Liu, S.; Rao, Y.; Zhao, W.; Lu, J.; Zhou, J. Nerfingmvs: Guided optimization of neural radiance fields for indoor multi-view stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11 October 2021; pp. 5610–5619. [Google Scholar]
- Rother, C.; Kolmogorov, V.; Blake, A. “GrabCut” interactive foreground extraction using iterated graph cuts. ACM Trans. Graph. (TOG) 2004, 23, 309–314. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]



| Dataset | Numbers of Image | Data Content |
|---|---|---|
| DTU15 | 49 | Resolution (of a photo) 1600 × 1200 Camera parameters Mask data Point cloud data |
| DTU24 | 49 | Resolution (of a photo) 1600 × 1200 Camera parameters Mask data Point cloud data |
| DTU40 | 49 | Resolution (of a photo) 1600 × 1200 Camera parameters Mask data Point cloud data |
| Dataset | Number of Images | Image Size |
|---|---|---|
| Pix4d sample Data | 36 | 4592 × 3056 |
| Yellow Crane Data | 60 | 3965 × 2230 |
| Huayan Temple Data | 40 | 6000 × 4000 |
| Instant-ngp | NeuS | Ours | ||
|---|---|---|---|---|
| DTU15 | 1 | 21.5906 | 17.8316 | 24.5007 |
| 2 | 22.8636 | 16.7975 | 21.3661 | |
| 3 | 20.4145 | 16.8967 | 23.5825 | |
| 4 | 20.2797 | 18.2014 | 21.3009 | |
| 5 | 19.2271 | 16.1140 | 20.8408 | |
| 6 | 21.0331 | 18.9674 | 21.7025 | |
| Average | 20.9014 | 17.4681 | 22.2156 | |
| DTU24 | 1 | 23.8592 | 19.6505 | 24.0335 |
| 2 | 19.9375 | 19.8496 | 21.9429 | |
| 3 | 23.5673 | 21.7333 | 24.5284 | |
| 4 | 25.3783 | 17.9581 | 29.2147 | |
| 5 | 21.3128 | 18.5247 | 22.9470 | |
| 6 | 18.0817 | 18.3397 | 23.3875 | |
| Average | 22.0228 | 19.3427 | 24.3423 | |
| DTU40 | 1 | 26.8330 | 21.1750 | 29.2166 |
| 2 | 26.9306 | 20.4683 | 29.2910 | |
| 3 | 27.3707 | 21.6330 | 28.7746 | |
| 4 | 27.7076 | 19.8074 | 28.3549 | |
| 5 | 28.7993 | 19.5547 | 28.1579 | |
| 6 | 29.4745 | 21.3349 | 28.5163 | |
| Average | 27.8526 | 20.6622 | 28.7186 |
| Instant-ngp | NeuS | Ours | ||
|---|---|---|---|---|
| DTU15 | 1 | 0.8540 | 0.7951 | 0.8883 |
| 2 | 0.8975 | 0.5711 | 0.9267 | |
| 3 | 0.9107 | 0.6188 | 0.9142 | |
| 4 | 0.8301 | 0.7983 | 0.8395 | |
| 5 | 0.9002 | 0.9002 | 0.9076 | |
| 6 | 0.8497 | 0.8497 | 0.8666 | |
| Average | 0.8450 | 0.6953 | 0.8809 | |
| DTU24 | 1 | 0.9313 | 0.7350 | 0.8795 |
| 2 | 0.6199 | 0.7510 | 0.9290 | |
| 3 | 0.9090 | 0.7978 | 0.9299 | |
| 4 | 0.9164 | 0.6847 | 0.9471 | |
| 5 | 0.8806 | 0.7028 | 0.9176 | |
| 6 | 0.8055 | 0.8079 | 0.7687 | |
| Average | 0.8438 | 0.7465 | 0.8953 | |
| DTU40 | 1 | 0.9193 | 0.7186 | 0.9246 |
| 2 | 0.9210 | 0.6985 | 0.9228 | |
| 3 | 0.9179 | 0.6346 | 0.9020 | |
| 4 | 0.9119 | 0.7381 | 0.9193 | |
| 5 | 0.9041 | 0.7309 | 0.9324 | |
| 6 | 0.9025 | 0.7215 | 0.9437 | |
| Average | 0.9128 | 0.7070 | 0.9275 |
| Ours Method/min | Instant-ngp/min | NeuS/min | |
|---|---|---|---|
| DTU15 | 10.1 | 10 | 497 |
| DTU24 | 10.3 | 10 | 501 |
| DTU40 | 10.2 | 10 | 494 |
| Instant-ngp | NeuS | Our Method | ||
|---|---|---|---|---|
| Pix4d | 1 | 25.4210 | 21.5347 | 25.8437 |
| 2 | 24.4684 | 22.8885 | 25.4387 | |
| 3 | 24.8765 | 21.9155 | 25.8641 | |
| 4 | 24.7463 | 22.7518 | 26.5812 | |
| 5 | 24.7451 | 21.5997 | 24.8237 | |
| 6 | 24.1549 | 21.7302 | 24.4624 | |
| Average | 24.7353 | 22.0701 | 25.5023 | |
| Yellow Crane | 1 | 22.0467 | 20.5486 | 23.9559 |
| 2 | 22.3473 | 19.5063 | 24.2902 | |
| 3 | 21.7972 | 22.2307 | 23.7182 | |
| 4 | 21.6883 | 22.6365 | 23.7127 | |
| 5 | 22.3321 | 20.8539 | 24.3762 | |
| 6 | 22.0755 | 21.5008 | 24.0845 | |
| Average | 22.0479 | 21.2128 | 24.0229 |
| Instant-ngp | NeuS | Our Method | ||
|---|---|---|---|---|
| Pix4d | 1 | 0.9469 | 0.9024 | 0.9470 |
| 2 | 0.9517 | 0.9100 | 0.9518 | |
| 3 | 0.9437 | 0.9052 | 0.9535 | |
| 4 | 0.9465 | 0.9127 | 0.9559 | |
| 5 | 0.9404 | 0.9082 | 0.9493 | |
| 6 | 0.9395 | 0.9070 | 0.9563 | |
| Average | 0.9448 | 0.9076 | 0.9523 | |
| Yellow Crane | 1 | 0.9276 | 0.8943 | 0.9406 |
| 2 | 0.9278 | 0.8982 | 0.9397 | |
| 3 | 0.9255 | 0.8867 | 0.9394 | |
| 4 | 0.9264 | 0.8999 | 0.9389 | |
| 5 | 0.9288 | 0.8922 | 0.9427 | |
| 6 | 0.9274 | 0.8972 | 0.9416 | |
| Average | 0.9273 | 0.8948 | 0.9405 |
| Dataset | Instant-ngp/min | NeuS/min | Colmap/min | Our Method/min |
|---|---|---|---|---|
| Pix4d | 9 | 504 | 41 | 16 |
| Yellow Crane | 10 | 517 | 44 | 16 |
| NeuS | SDF | SDF + Depth | TSDF | Our Method | ||
|---|---|---|---|---|---|---|
| Huayan temple | 1 | 20.0790 | 19.7807 | 18.6804 | 22.0038 | 21.4941 |
| 2 | 21.4474 | 21.8201 | 19.8980 | 20.3897 | 23.0139 | |
| 3 | 20.1258 | 20.5362 | 21.3039 | 20.1366 | 21.4459 | |
| 4 | 19.4199 | 19.5288 | 20.8696 | 21.6823 | 22.2220 | |
| 5 | 19.3783 | 19.7992 | 18.2688 | 19.7121 | 20.1800 | |
| 6 | 18.2056 | 21.7851 | 20.9672 | 22.3610 | 21.0538 | |
| Average | 19.7760 | 20.5417 | 19.9980 | 21.0476 | 21.5683 |
| NeuS | SDF | SDF + Depth | TSDF | Our Method | ||
|---|---|---|---|---|---|---|
| Huayan Temple | 1 | 0.8131 | 0.8327 | 0.8915 | 0.9105 | 0.9012 |
| 2 | 0.8512 | 0.7858 | 0.8854 | 0.8654 | 0.8733 | |
| 3 | 0.8859 | 0.8069 | 0.7965 | 0.8421 | 0.9102 | |
| 4 | 0.7964 | 0.7934 | 0.8701 | 0.8369 | 0.9171 | |
| 5 | 0.7842 | 0.8610 | 0.8531 | 0.8554 | 0.8760 | |
| 6 | 0.8701 | 0.8714 | 0.8068 | 0.9024 | 0.8821 | |
| Average | 0.8335 | 0.8252 | 0.8506 | 0.8514 | 0.8933 |
| Dataset | Colmap/min | NeuS/min | SDF/min | SDF + Depth/min | TSDF/min | Our Method/min |
|---|---|---|---|---|---|---|
| Huayan Temple | 35 | 311 | 23 | 24 | 22 | 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Guo, B.; Zha, P.; Jiang, S.; Jiang, Z.; Li, D. 3D Reconstruction of Ancient Buildings Using UAV Images and Neural Radiation Field with Depth Supervision. Remote Sens. 2024, 16, 473. https://doi.org/10.3390/rs16030473
Ge Y, Guo B, Zha P, Jiang S, Jiang Z, Li D. 3D Reconstruction of Ancient Buildings Using UAV Images and Neural Radiation Field with Depth Supervision. Remote Sensing. 2024; 16(3):473. https://doi.org/10.3390/rs16030473
Chicago/Turabian StyleGe, Yingwei, Bingxuan Guo, Peishuai Zha, San Jiang, Ziyu Jiang, and Demin Li. 2024. "3D Reconstruction of Ancient Buildings Using UAV Images and Neural Radiation Field with Depth Supervision" Remote Sensing 16, no. 3: 473. https://doi.org/10.3390/rs16030473
APA StyleGe, Y., Guo, B., Zha, P., Jiang, S., Jiang, Z., & Li, D. (2024). 3D Reconstruction of Ancient Buildings Using UAV Images and Neural Radiation Field with Depth Supervision. Remote Sensing, 16(3), 473. https://doi.org/10.3390/rs16030473