A Method for Low Sidelobe Substrate-Integrated Waveguide Slot Antenna Design Applied for Millimeter-Wave Radars
Abstract
:1. Introduction
2. Materials and Methods
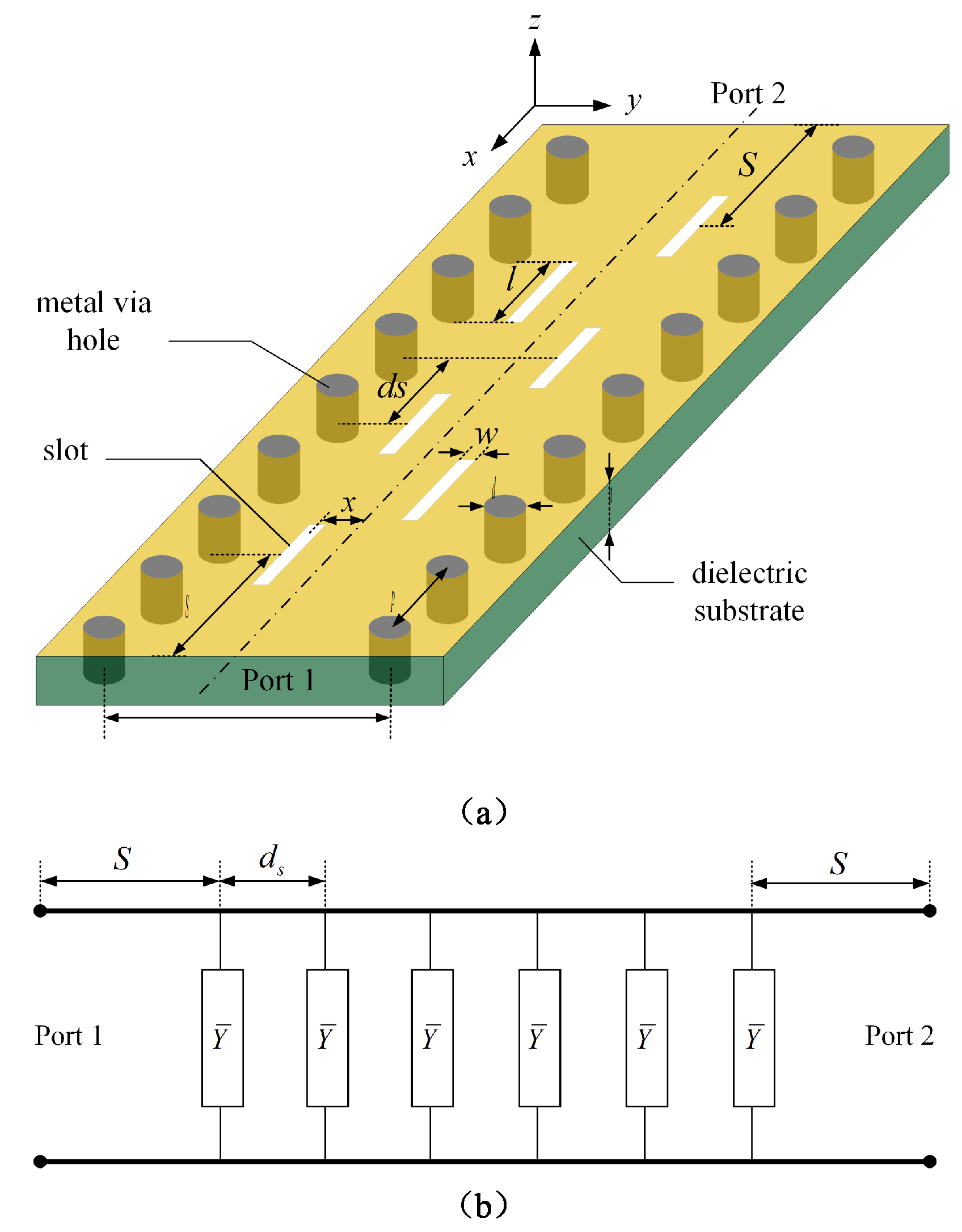
2.1. The Method of Admittance Calculation
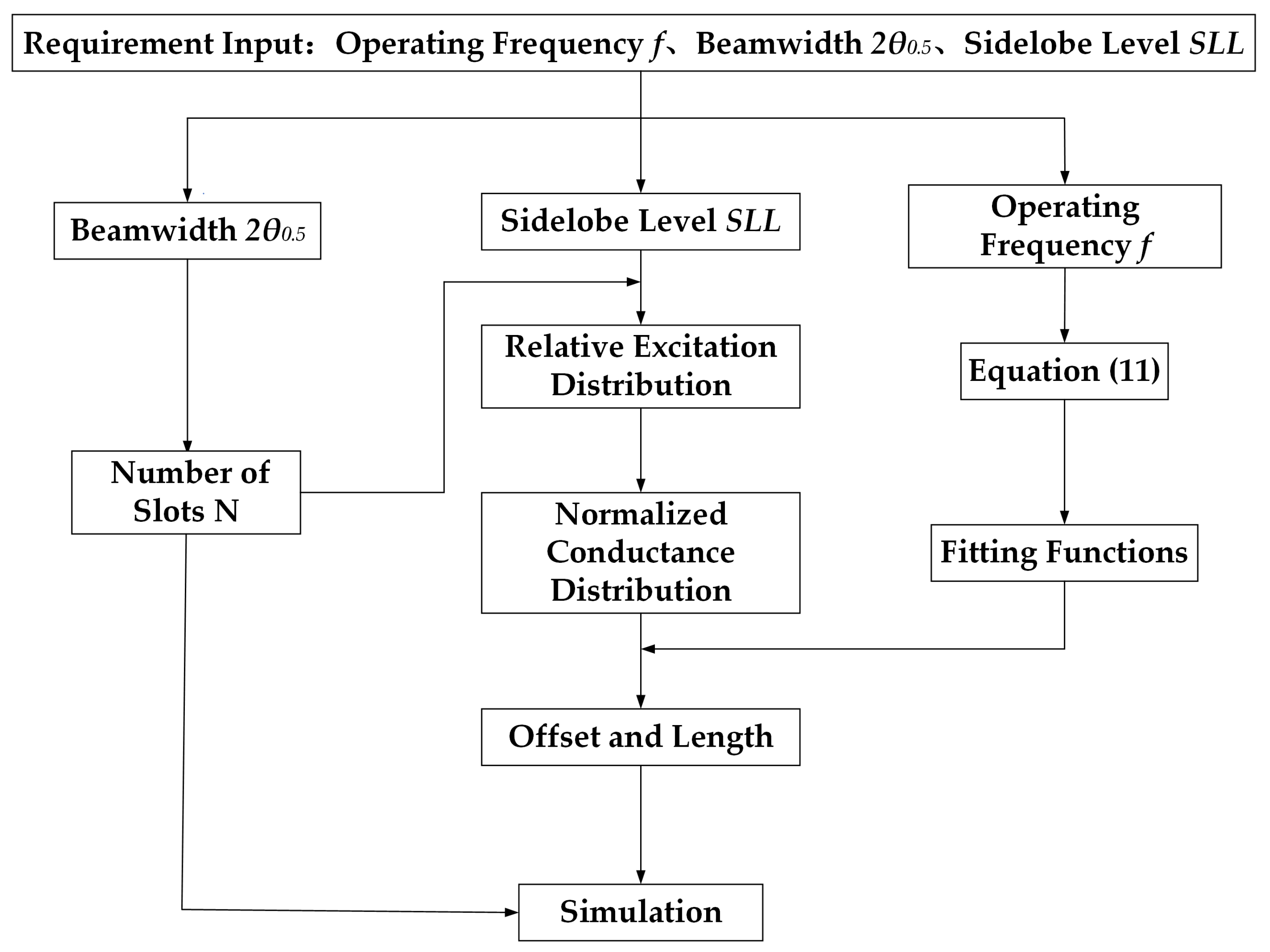
2.2. The Antenna Design Process
- Give design requirements, including the operating frequency f, the beamwidth , and the sidelobe lever ;
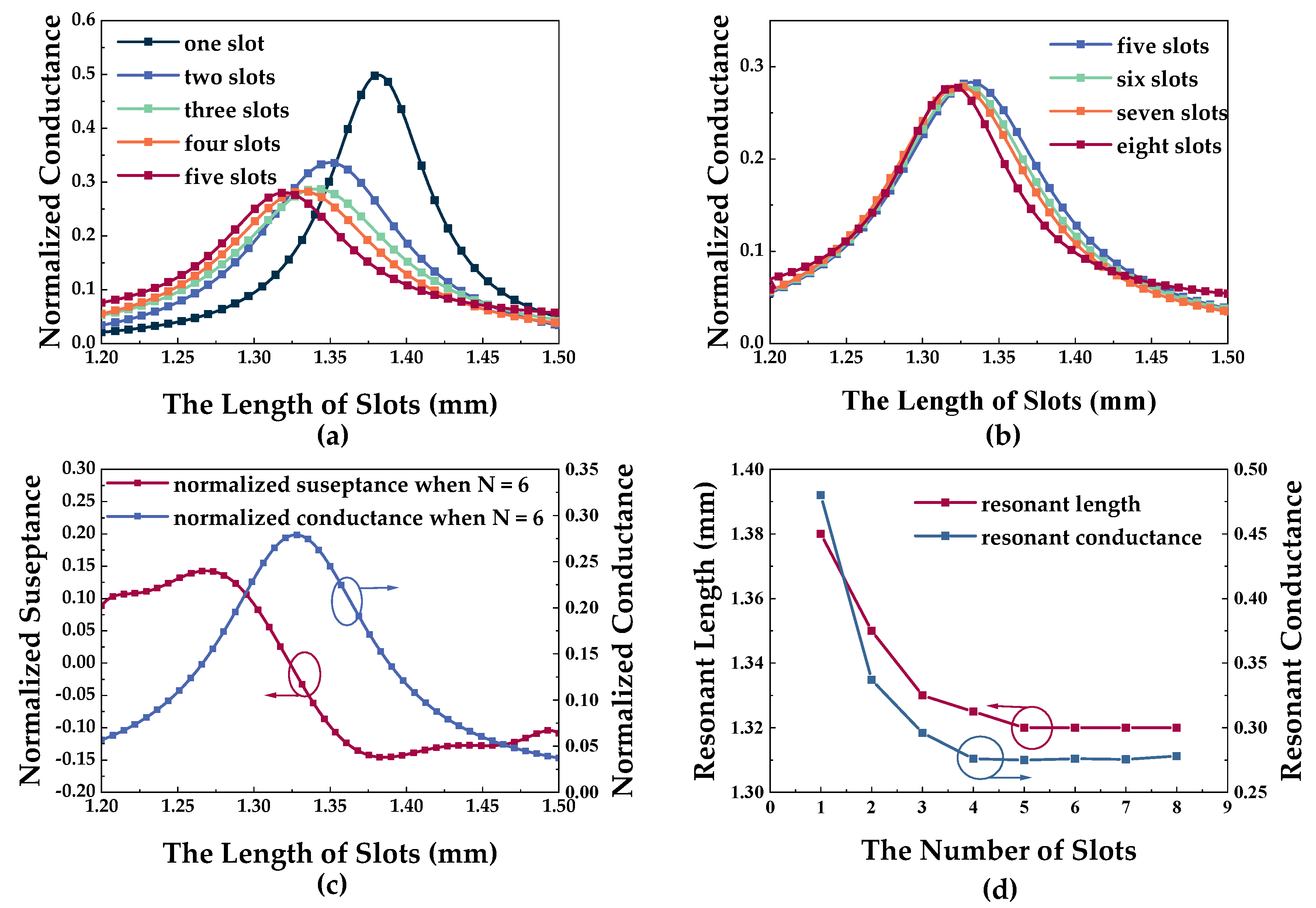
- Calculate the number of slots N according to the beamwidth ;
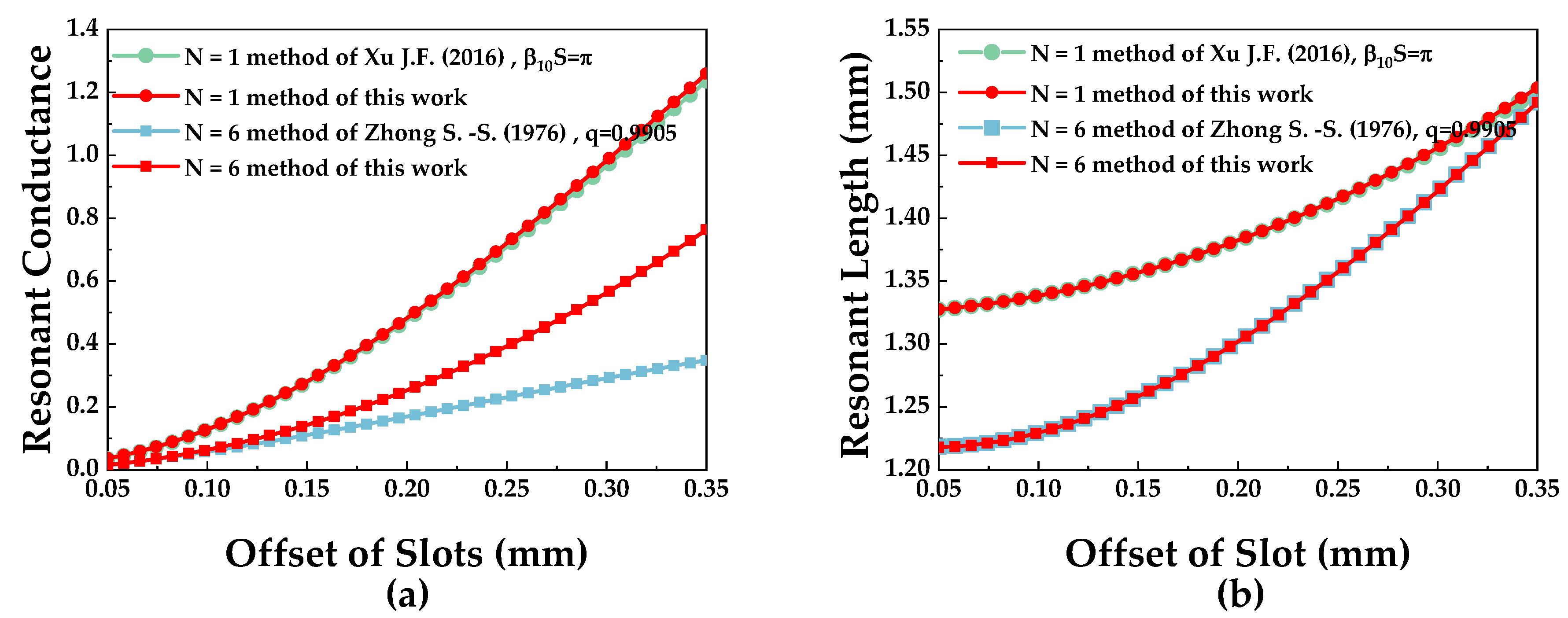
- Establish the multislot simulated and analytical model and calculate the fitting functions and ;
- Calculate the normalized conductance of each slot using the Chebyshev or Taylor line source synthesis methods according to the sidelobe lever ;
- Calculate the offset and length of each slot according to normalized conductance and length fitting functions;
- Establish the antenna model, simulating model, and optimizing model.
3. Experiments and Results
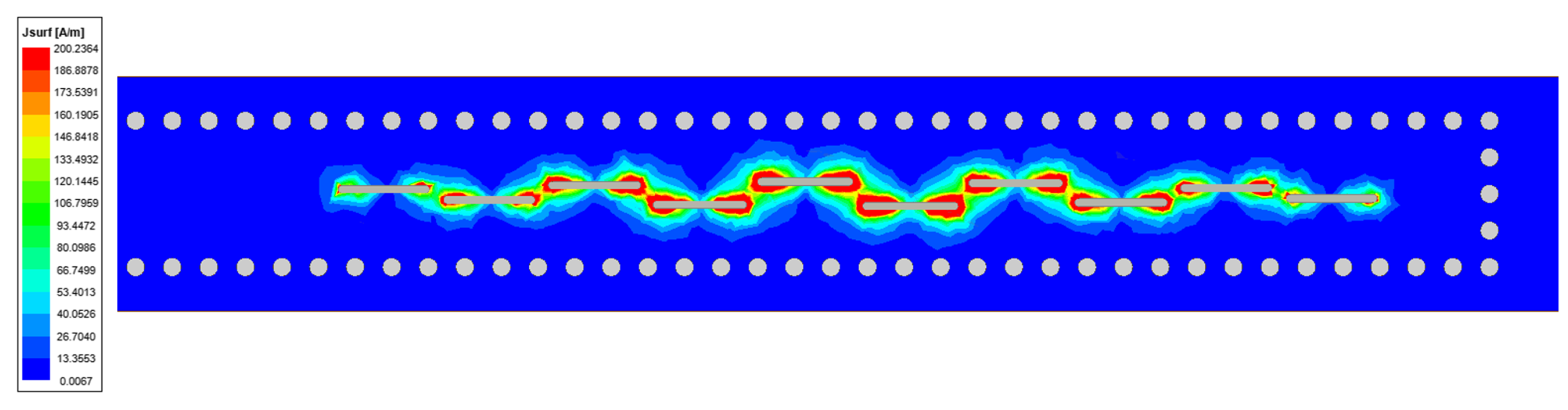
3.1. Antenna Design and Simulation
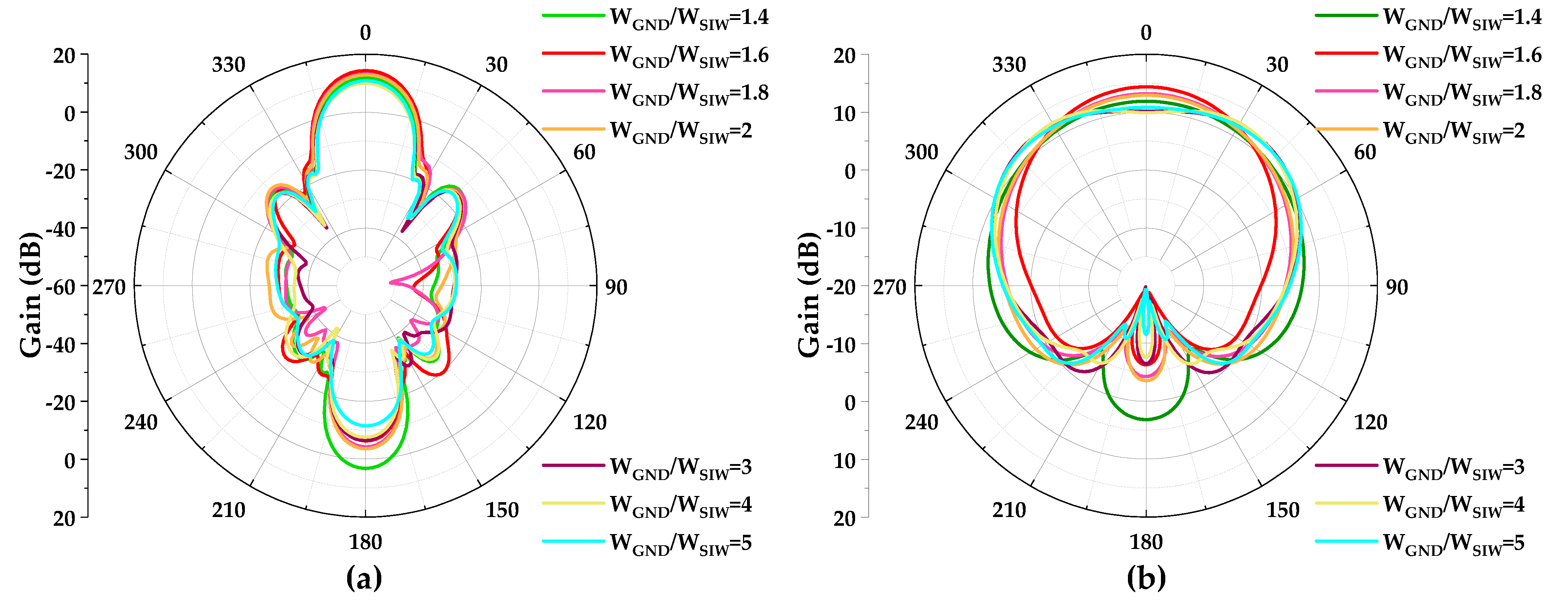
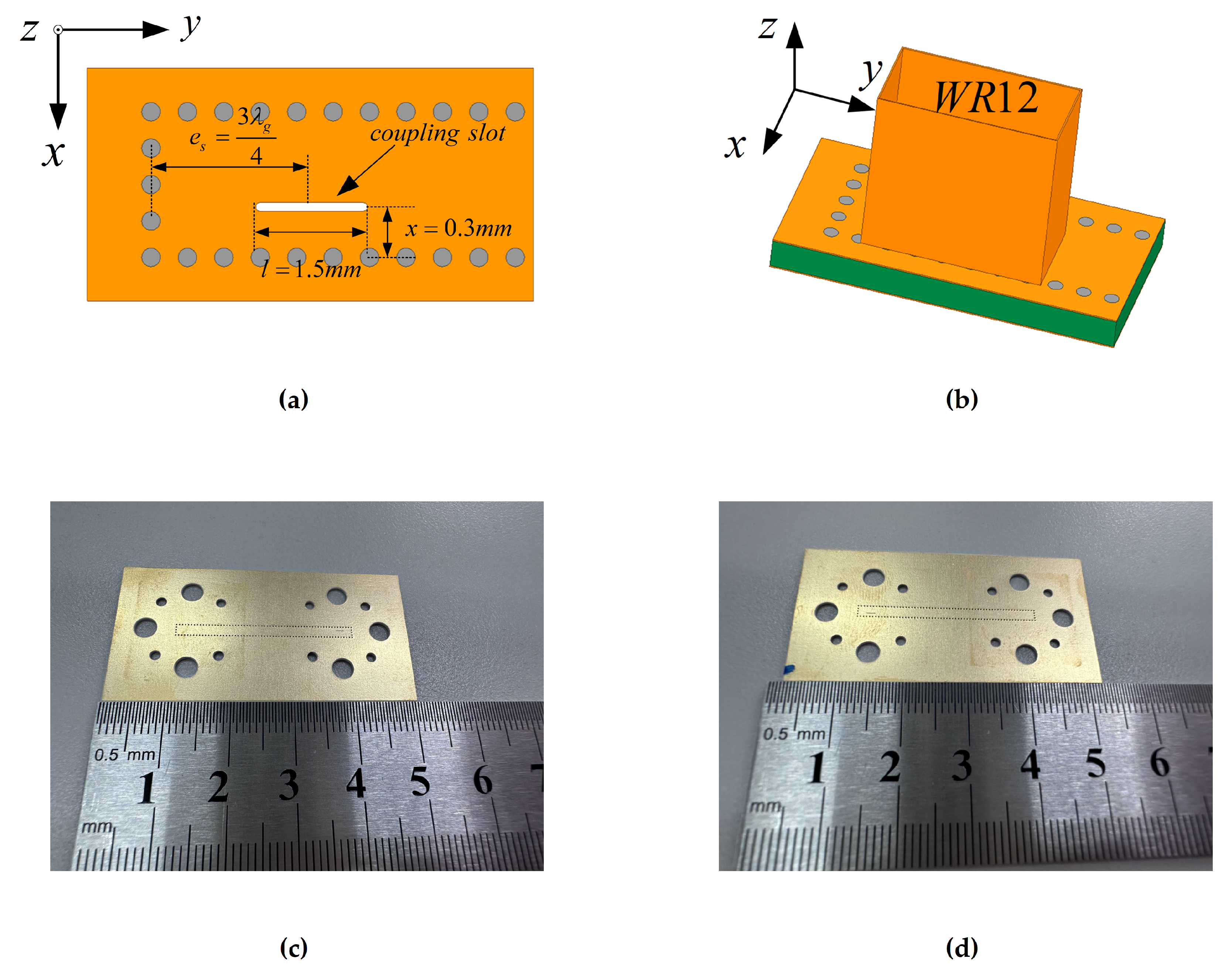
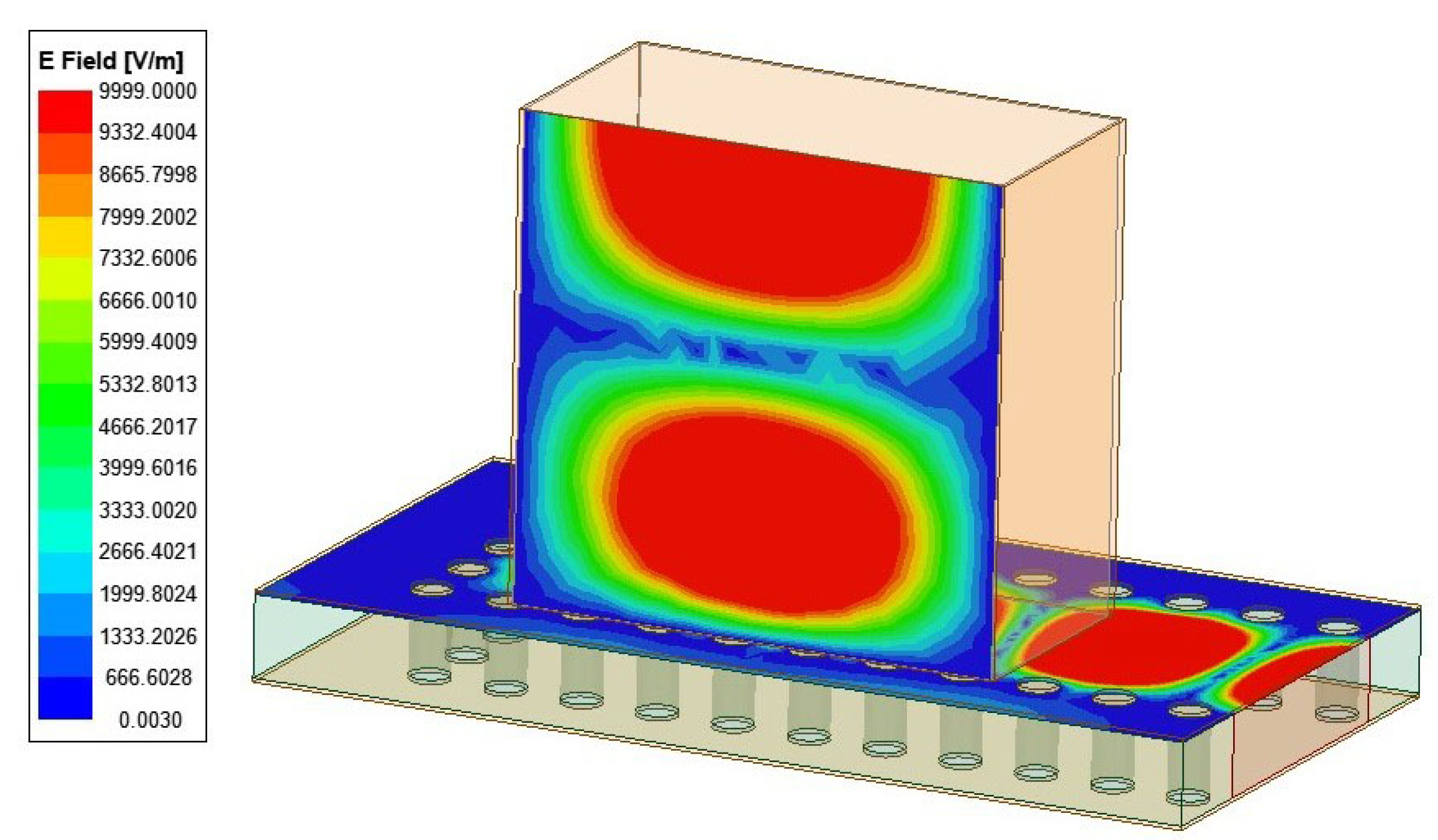
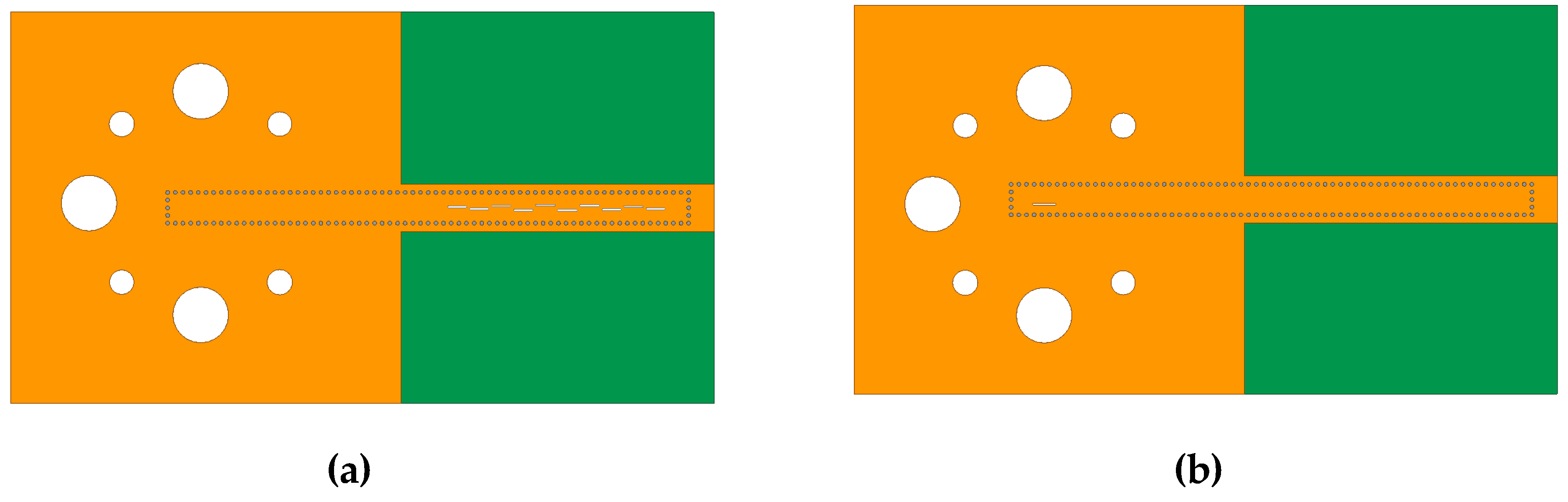
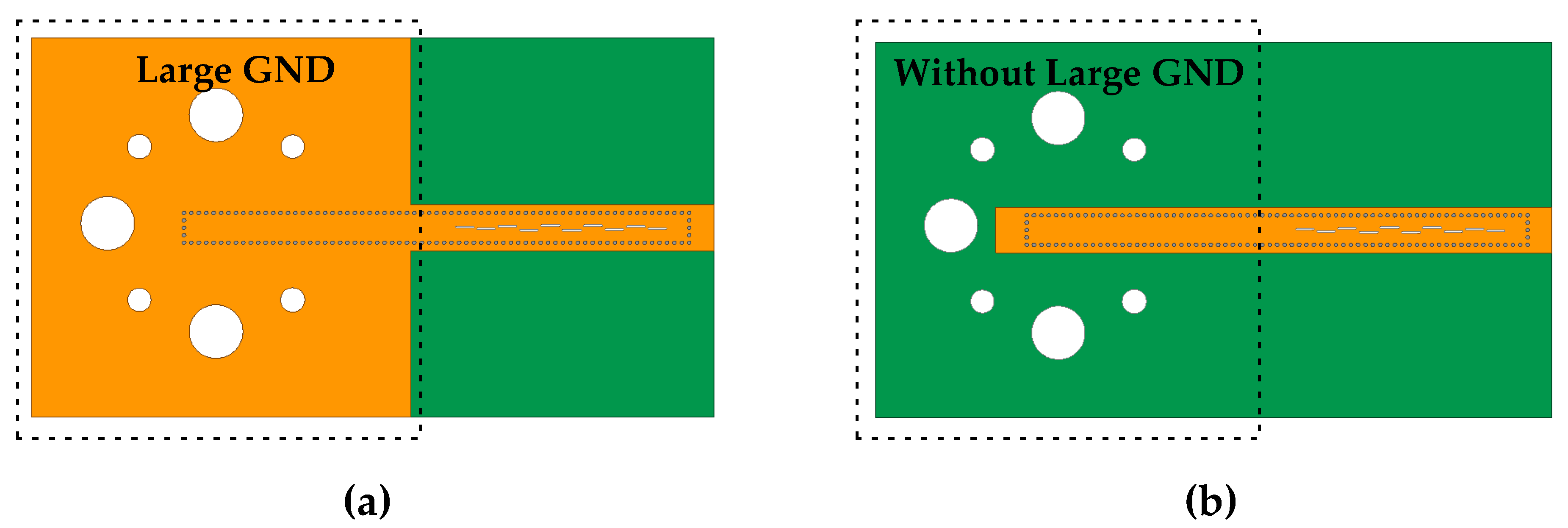
3.2. The Design of the Transition from RWG to SIW
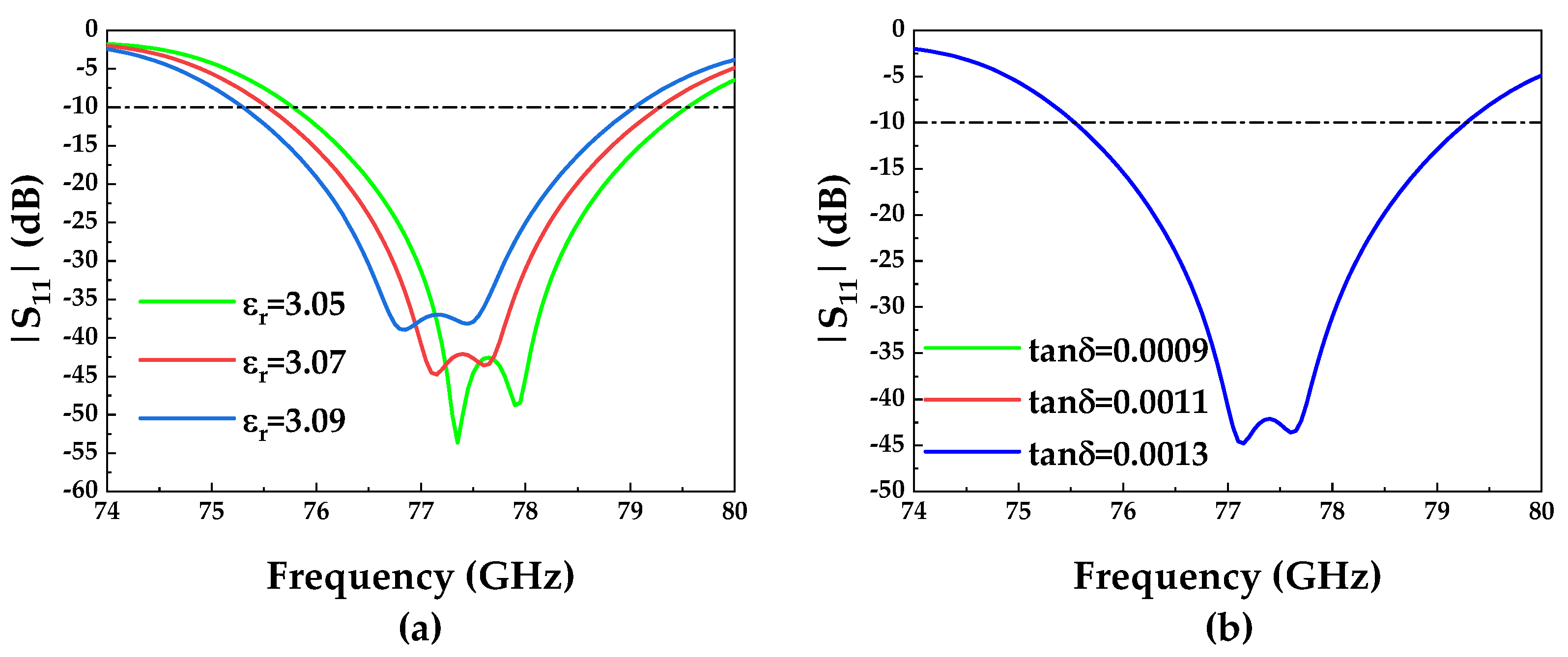
- The variation in the permittivity results in a shift in the operating frequency. The dielectric substrate employed in this work is Rogers RO3003, which exhibits a permittivity of 3.0 at 10 GHz. Drawing on engineering experience, the permittivity of this material fluctuates within a range of 3.0 to 3.12 at 77 GHz. In simulations, the permittivity is set as 3.07 in this work. Figure 17a illustrates the impact of permittivity variation on . The simulation results indicate a decrease in operating frequency as the permittivity increases. Therefore, the actual measured permittivity values should be less than the simulated permittivity values, which leads to a shift in measured operating frequency.
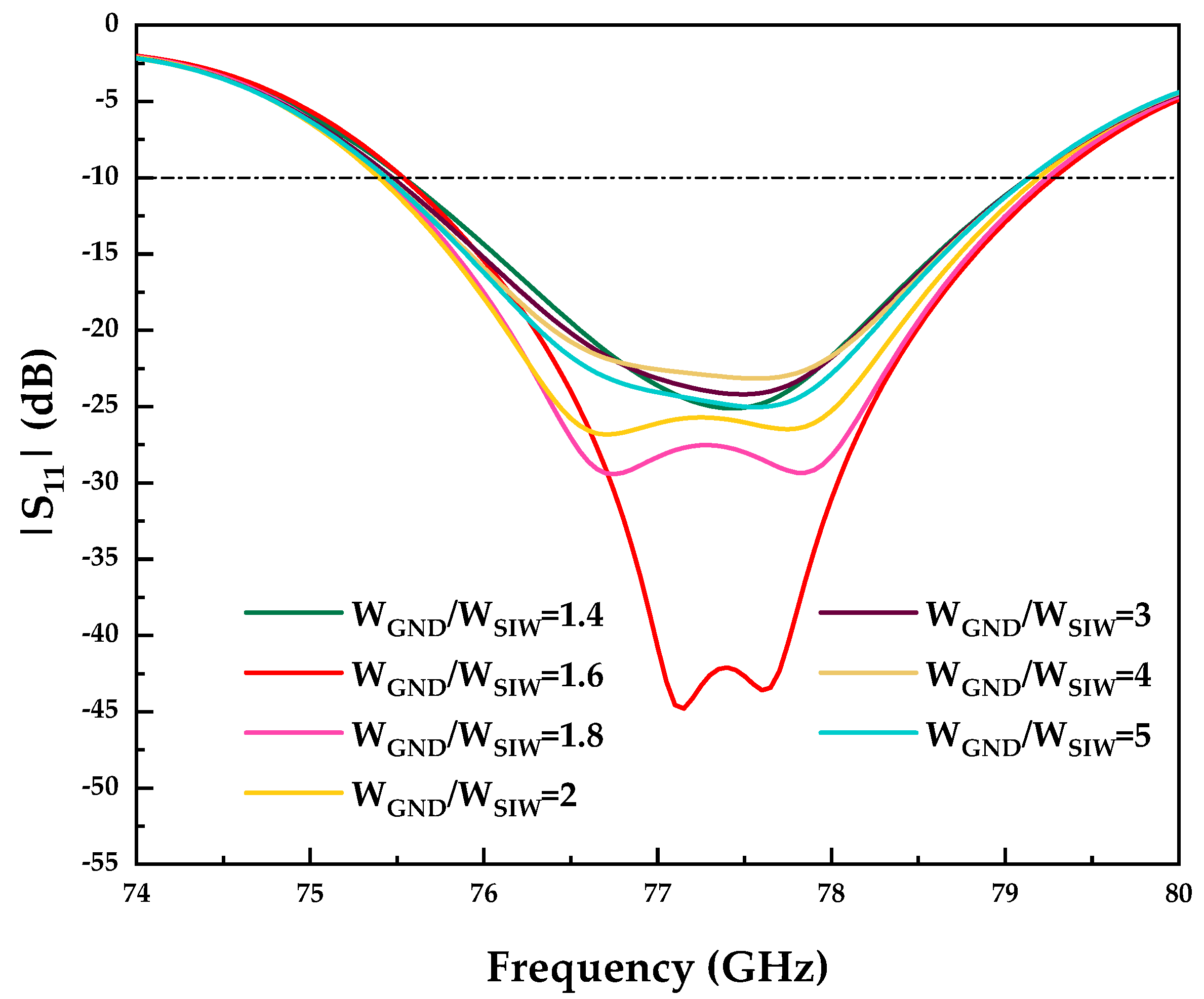
- Manufacturing errors have a certain impact on impedance matching. Figure 17b illustrates the impact of the length l variation of slots on . While this variation influences the impedance matching, it does not affect the operating frequency.
- The variation in the copper layer thickness influences the performance. The metallization via holes results in an approximate 10 m increase in the thickness of the copper layer. Figure 17c shows the impact of this variation on , leading to a slight shift in the operating frequency.
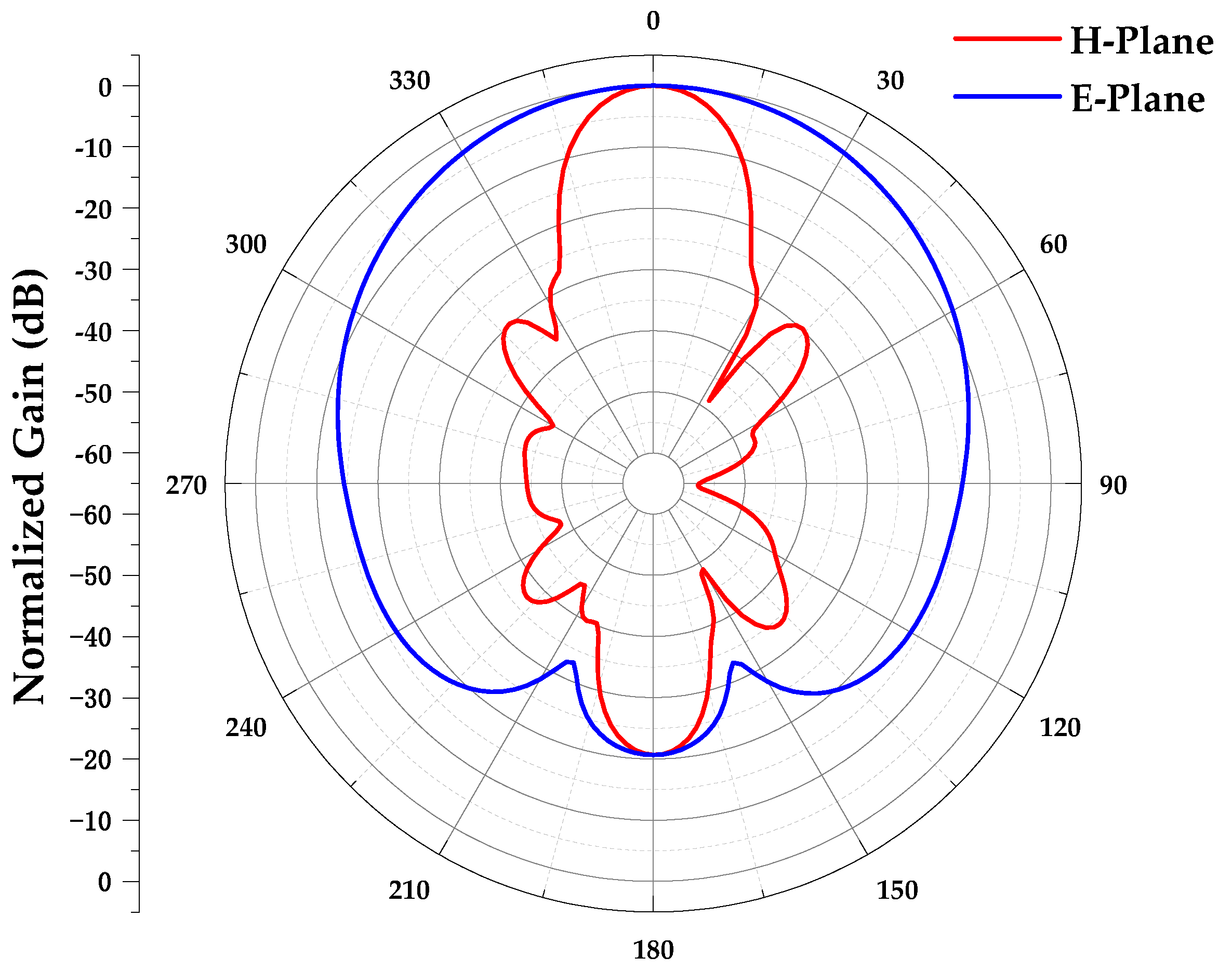
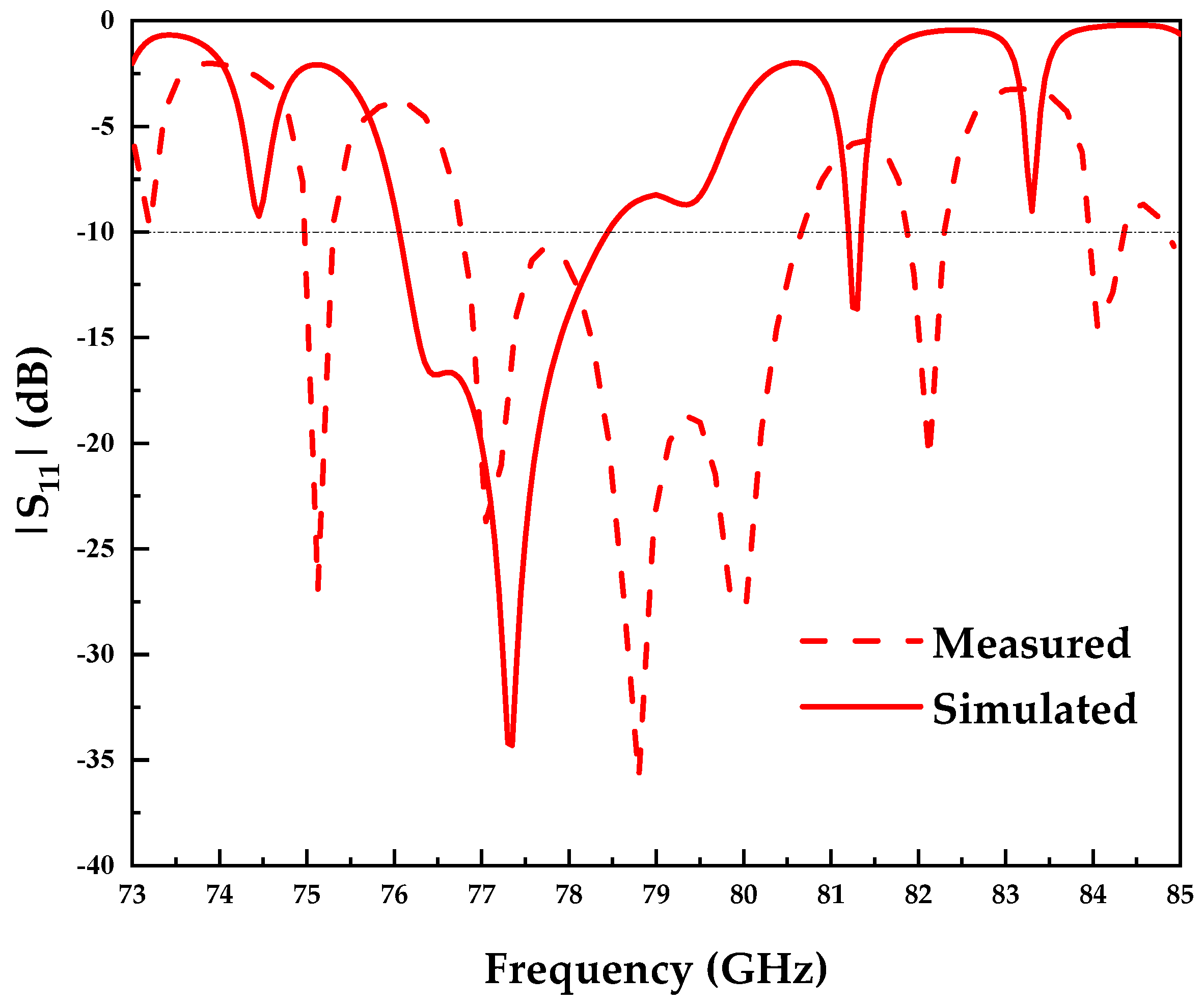
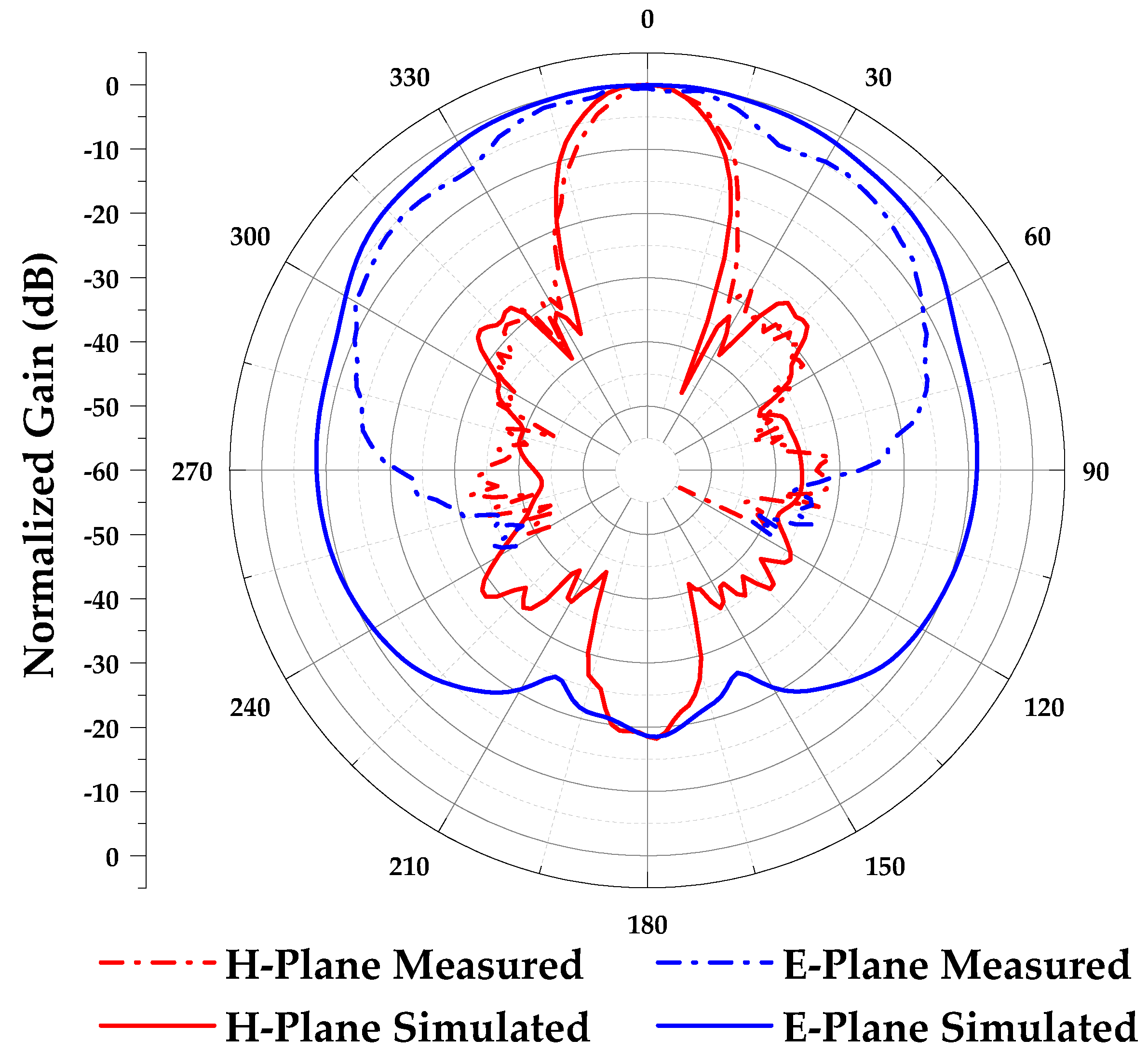
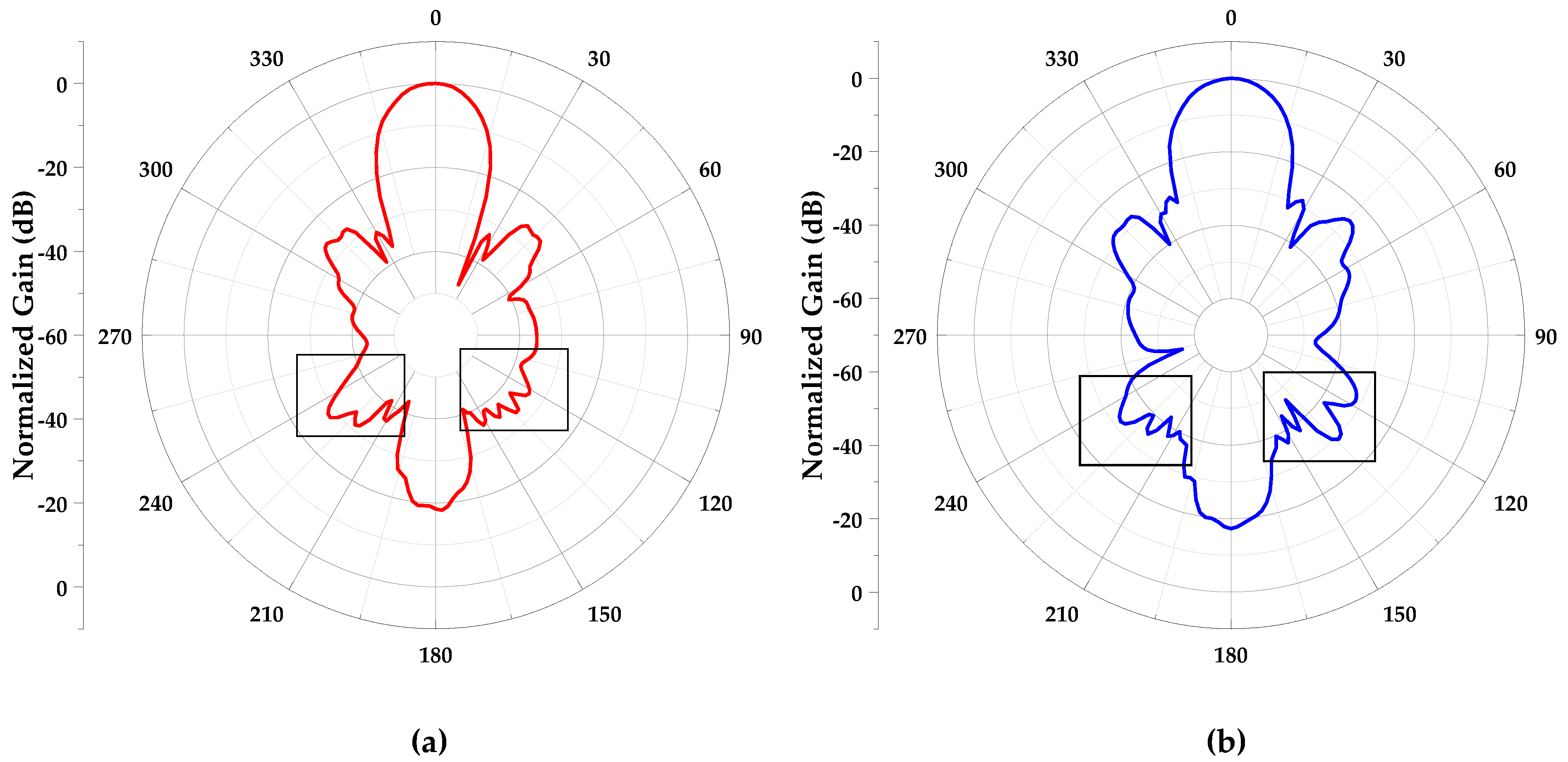
3.3. Simulation and Measurement Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hirokawa, J.; Ando, M. Single-layer feed waveguide consisting of posts for plane TEM wave excitation in parallel plates. IEEE Trans. Antennas Propag. 1998, 46, 625–630. [Google Scholar] [CrossRef]
- Hiroshi, U.; Takenoshita, T.; Fujii, M. Development of a laminated waveguide. IEEE Trans. Microw. Theory Tech. 1998, 12, 2438–2443. [Google Scholar]
- Deslandes, D.; Wu, K. Integrated Microstrip, and Rectangular Waveguide in Planar Firm. IEEE Microw. Guid. Wave Lett. 2001, 11, 68–70. [Google Scholar] [CrossRef]
- Xu, F.; Wu, K. Guided-wave and leakage characteristics of substrate integrated waveguide. IEEE Trans. Microw. Theory Tech. 2005, 53, 66–73. [Google Scholar]
- Li, L.; Zhang, C.; Qiao, X.; Shao, Y. A Broadband SIW-Fed Rhombic Loop Antenna with Endfire Radiation for Millimeter-Wave Applications. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1293–1297. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; He, Y.; Mao, C.; Wong, S.; Li, W.; Chu, P.; Gao, S. Broadband High-Gain SIW Horn Antenna Loaded with Tapered Multistrip Transition and Dielectric Slab for mm-Wave Application. IEEE Antennas Wirel. Propag. Lett. 2022, 70, 5947–5952. [Google Scholar] [CrossRef]
- Alistarh, C.; Anitori, L.; van Rossum, W.L.; Podilchak, S.K.; Thompson, J.; Sellathurai, M. Compressed Sensing for MIMO Radar using SIW Antennas for High Resolution Detection. In Proceedings of the 2021 18th European Radar Conference (EuRAD), London, UK, 5–7 April 2022; pp. 485–488. [Google Scholar]
- Gao, D.; Li, S.; Chen, A.Y.-K.; Wu, C.-T.M. A W-band Self-Injection-Locked Vital Sign Radar Sensor with On-Chip SIW Monopole Antenna in 0.1-µm GaAs pHEMT. In Proceedings of the 2023 IEEE/MTT-S International Microwave Symposium, San Diego, CA, USA, 11–16 June 2023; pp. 871–874. [Google Scholar]
- Yamamoto, S.I.; Hikono, N.; Hirokawa, J.; Ando, M. A 120-degree beamwidth post-wall waveguide slot array with a three-way power divider on a single-layer dielectric substrate. In Proceedings of the IEEE Wireless Communication Technology Conference, Honolulu, HI, USA, 15–17 October 2003; pp. 354–355. [Google Scholar]
- Zhang, J.-P.; Li, B.; Zhou, Z.-P. A substrate integrated waveguide slot antenna for 79-GHz applications. In Proceedings of the 2018 International Workshop on Antenna Technology (iWAT), Nanjing, China, 5–7 March 2018; pp. 142–149. [Google Scholar]
- Zhang, Y.; Cheng, Y.J.; Yang, H.N.; Zhao, M.H.; Fan, Y. SIW Slot Array Antenna with Non-Alternating Slot Placement for Impedance Bandwidth Enhancement. In Proceedings of the 2020 IEEE 3rd International Conference on Electronic Information and Communication Technology (ICEICT), Shenzhen, China, 13–15 November 2020. [Google Scholar]
- Cheng, T.; Jiang, W.; Gong, S.; Yu, Y. Broadband SIW cavity-backed modified dumbbell-shaped slot antenna. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 936–940. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, Y.; Ding, C.; Qian, Z. A wideband multilayer substrate integrated waveguide cavity-backed slot antenna array. IEEE Trans. Antennas Propag. 2017, 65, 936–940. [Google Scholar] [CrossRef]
- Hong, W.; Liu, B.; Luo, G.Q.; Lai, Q.H.; Xu, J.F.; Hao, Z.C.; He, F.F.; Yin, X.X. Integrated microwave and millimeter wave antennas based on SIW and HMSIW technology. In Proceedings of the 2007 International Workshop on Antenna Technology: Small and Smart Antennas Metamaterials and Applications, Cambridge, UK, 21–23 March 2007. [Google Scholar]
- Miralles, E.; Esteban, H.; Bachiller, C.; Belenguer, A.; Boria, V.E. Improvement for the design equations for tapered mi-crostrip-to-substrate integrated waveguide transitions. In Proceedings of the 2011 International Conference on Electromagnetics in Advanced Applications, Turin, Italy, 12–16 September 2011; pp. 652–655. [Google Scholar]
- Kordiboroujeni, Z.; Bornemann, J. New Wideband Transition From Microstrip Line to Substrate Integrated Waveguide. IEEE Trans. Microw. Theory Tech. 2014, 62, 2983–2989. [Google Scholar] [CrossRef]
- Ding, Y.; Wu, K. Substrate integrated waveguide-to-microstrip transition in multilayer substrate. IEEE Trans. Microw. Theory Tech. 2007, 55, 2839–2844. [Google Scholar] [CrossRef]
- Caballero, E.D.; Martinez, A.B.; Gonzalez, H.E.; Belda, O.M.; Esbert, V.B. A novel transition from microstrip to a substrate integrated waveguide with higher characteristic impedance. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–4. [Google Scholar]
- Zerfaine, A.; Djerafi, T. Ultra-Wideband Microstrip to Substrate Integrated Waveguide (SIW) Vertical Transition. In Proceedings of the 2022 IEEE/MTT-S International Microwave Symposium, Denver, CO, USA, 19–24 June 2022; pp. 765–767. [Google Scholar]
- Zerfaine, A.; Djerafi, T. Ultrabroadband Circularly Polarized Antenna Array Based on Microstrip to SIW Junction. IEEE Trans. Antennas Propag. 2022, 70, 2346–2351. [Google Scholar] [CrossRef]
- Zhu, K.; Tan, Y.X.W.; Luo, H.; Sun, H. A Broadband E-Band Single-Layer-SIW-to-Waveguide Transition for Automotive Radar. IEEE Microw. Wirel. Components Lett. 2022, 32, 523–526. [Google Scholar] [CrossRef]
- Yang, C.-Y.; Zeng, G.-T.; Chu, H.N.; Ma, T.-G. A Compact D-band Transition from Rectangular Waveguide to Substrate Integrated Waveguide. In Proceedings of the 2021 International Symposium on Antennas and Propagation (ISAP), Taipei, Taiwan, 19–22 October 2021; pp. 1–2. [Google Scholar]
- Jankovic, U.; Chauhan, S.S.; Basu, A.; Budimir, D. Multilayer Universal Transitions between Substrate Integrated Waveguides and Rectangular Waveguides. In Proceedings of the 2022 52nd European Microwave Conference (EuMC), Milan, Italy, 27–29 September 2022; pp. 480–483. [Google Scholar]
- Wang, J.; Hao, Z.-C.; Fan, K.-K. A 110–150 GHz SIW-rectangular waveguide transition for terahertz applications. In Proceedings of the 2016 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Chengdu, China, 20–22 July 2016; pp. 692–695. [Google Scholar]
- Cano, J.L.; Mediavilla, A.; Perez, R. Full-band air-filled waveguide-to-substrate integrated waveguide (SIW) direction transition. IEEE Microw. Wirel. Components Lett. 2015, 25, 79–81. [Google Scholar] [CrossRef]
- Ghiotto, A.; Marah, I.; Marque, A.; Lotz, F. Rectangular Waveguide Test Fixture for SIW Component and Circuit Measurements. In Proceedings of the 2021 IEEE MTT-S International Microwave and RF Conference (IMARC), Kanpur, India, 17–19 December 2021. [Google Scholar]
- Park, S.-J.; Shin, D.-H.; Park, S.-O. Low Side-Lobe Substrate-Integrated-Waveguide Antenna Array Using Broadband Unequal Feeding Network for Millimeter-Wave Handset Device. IEEE Trans. Antennas Propag. 2016, 64, 923–932. [Google Scholar] [CrossRef]
- Cheng, Y.J.; Wang, J.; Liu, X.L. 94 GHz Substrate Integrated Waveguide Dual-Circular-Polarization Shared-Aperture Parallel-Plate Long-Slot Array Antenna With Low Sidelobe Level. IEEE Trans. Antennas Propag. 2017, 65, 5855–5861. [Google Scholar] [CrossRef]
- Yang, T.; Zhao, Z.; Yang, D.; Nie, Z. Low Cross-Polarization SIW Slots Array Antenna with a Compact Feeding Network. IEEE Trans. Antennas Propag. 2021, 20, 189–193. [Google Scholar] [CrossRef]
- Wang, D.; Fan, Y.; Cheng, Y.J. A W-Band, Low-Cost and High-Efficiency Antenna Array Using Multilayer SIW-to-SIW Transition with Leakage-Suppressing Scheme. IEEE Trans. Antennas Propag. 2023, 71, 10014–10019. [Google Scholar] [CrossRef]
- Chandan, R.K.; Cheng, S.P. Development and Analysis of a HMSIW-Fed Broadband Superstrate Patch Array Using Dual-Resonance Mechanism for Ka-Band Applications. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 849–853. [Google Scholar] [CrossRef]
- Li, H.; Li, Y. Low-Sidelobe Antenna Array Based on Evanescent Mode of Cutoff Waveguide. IEEE Antennas Wirel. Propag. Lett. 2022, 70, 11608–11616. [Google Scholar] [CrossRef]
- Talbi, L.; Sellal, K.; LeBel, J.; Denidni, T.A. Study of a round-ended banana-shaped slot integrated antenna at X-band. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11 July 2008; pp. 1–4. [Google Scholar]
- Sellal, K.; Talbi, L. Experimental study of new-shaped slot integrated antennas at X-band. In Proceedings of the 2009 IEEE Antennas and Propagation Society International Symposium, North Charleston, SC, USA, 1–5 June 2009; Volume 10, pp. 1–4. [Google Scholar]
- Mbaye, M.; Hautcoeur, J.; Talbi, L.; Hettak, K. Bandwidth Broadening of Dual-Slot Antenna Using Substrate Integrated Waveguide (SIW). IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1169–1171. [Google Scholar] [CrossRef]
- Stevenson, A.F. Theory of slots in rectangular waveguides. J. Appl. Phys. 1948, 19, 24–38. [Google Scholar] [CrossRef]
- Xu, J.F.; Hong, W.; Chen, P.; Wu, K. Design and implementation of low sidelobe substrate integrated waveguide longitudinal slot array antennas. IET Microw. Antennas Propag. 2016, 3, 288–292. [Google Scholar] [CrossRef]
- Mikulasek, T.; Lacik, J.; Puskely, J.; Raida, Z. Design of aperture-coupled microstrip patch antenna array fed by SIW for 60 GHz band. IET Microw. Antennas Propag. 2015, 10, 882–888. [Google Scholar] [CrossRef]
- Teng, L.; Dou, W.B. Millimetre-wave slotted array antenna based on double-layer substrate integrated waveguide. IET Microw. Antennas Propag. 2015, 9, 882–888. [Google Scholar]
- Zhong, S.-S.; Fei, Q.-T.; Sun, Y.-L. Design of an edge slotted waveguide array. J. Xidian Univ. 1976, 165–184. [Google Scholar]
- Ghasemi, A.; Laurin, J.-J. A Continuous Beam Steering Slotted Waveguide Antenna Using Rotating Dielectric Slabs. IEEE Trans. Antennas Propag. 2019, 67, 6362–6370. [Google Scholar] [CrossRef]
- Dewantari, A.; Kim, J.; Scherbatko, I.; Ka, M. A sidelobe level reduction method for mm-wave substrate integrated waveguide slot array antenna. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1557–1561. [Google Scholar] [CrossRef]
- Wu, Y.F.; You, Q.; Zhang, Y.; Guo, Y.; Cheng, Y.J. Sidelobe Level Reduction for a W-Band SIW Slot Array Antenna by Only Reversing Offset Direction of Partial Slots. IEEE Antennas Wirel. Propag. Lett. 2023, 71, 8360–8365. [Google Scholar] [CrossRef]

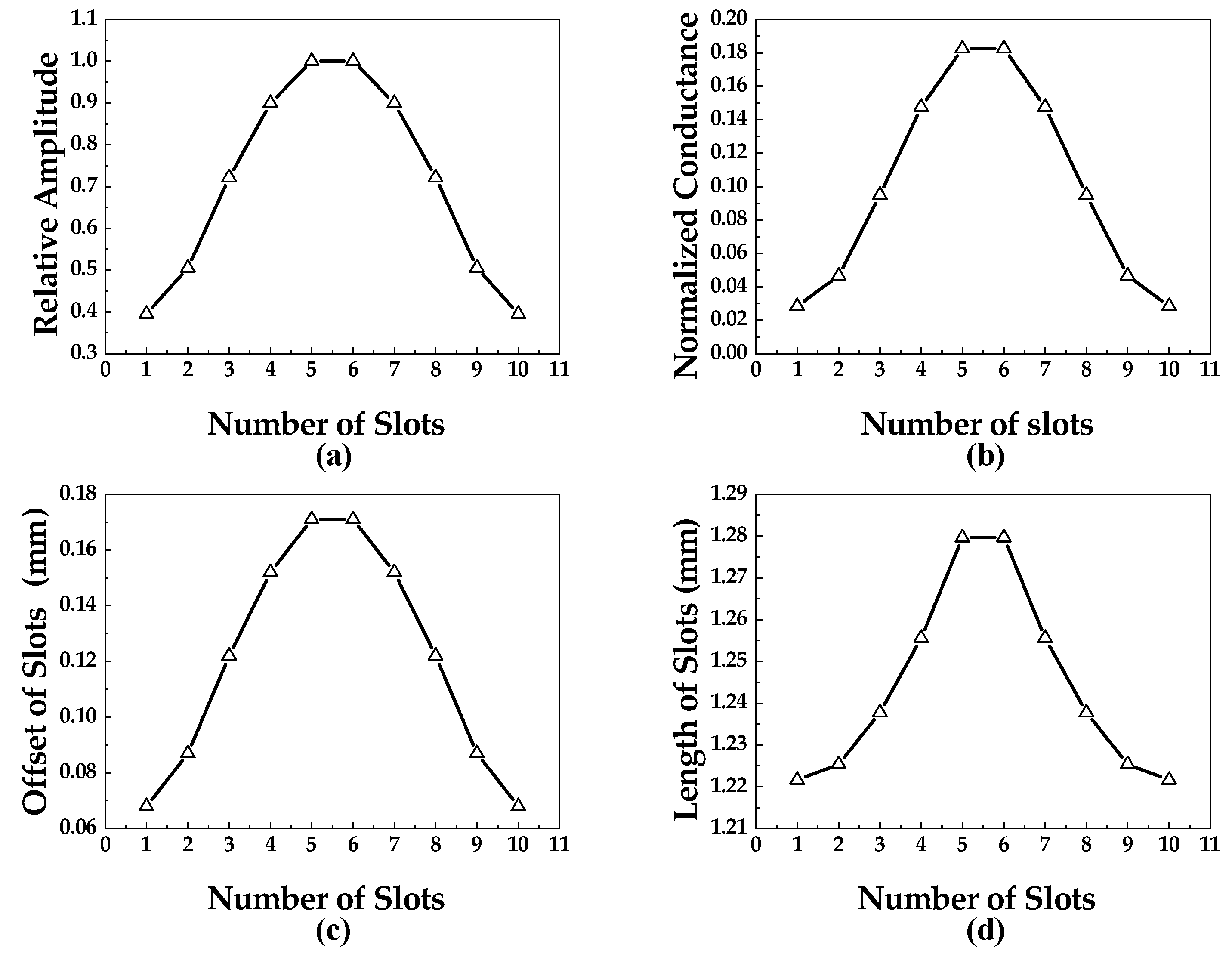

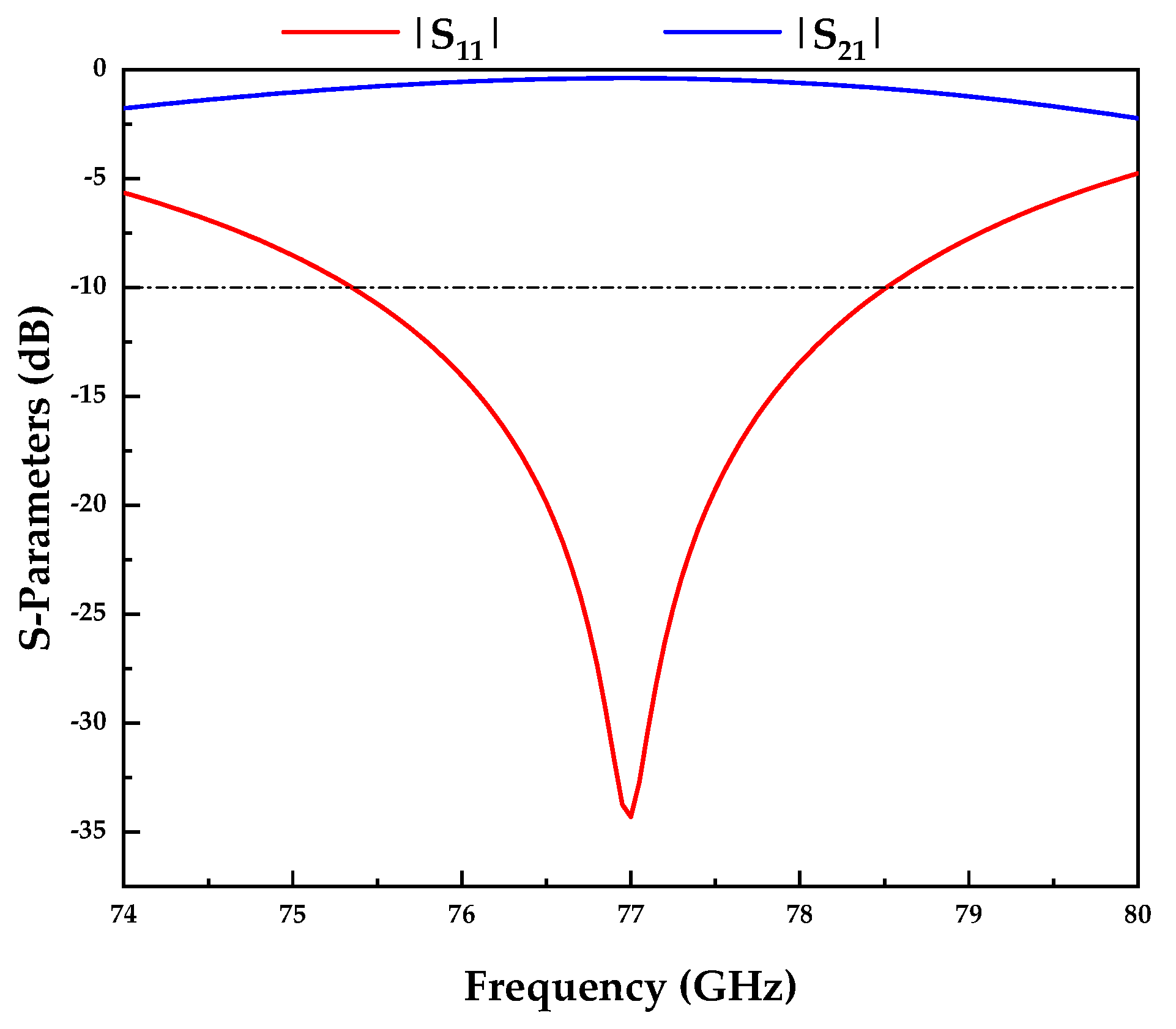
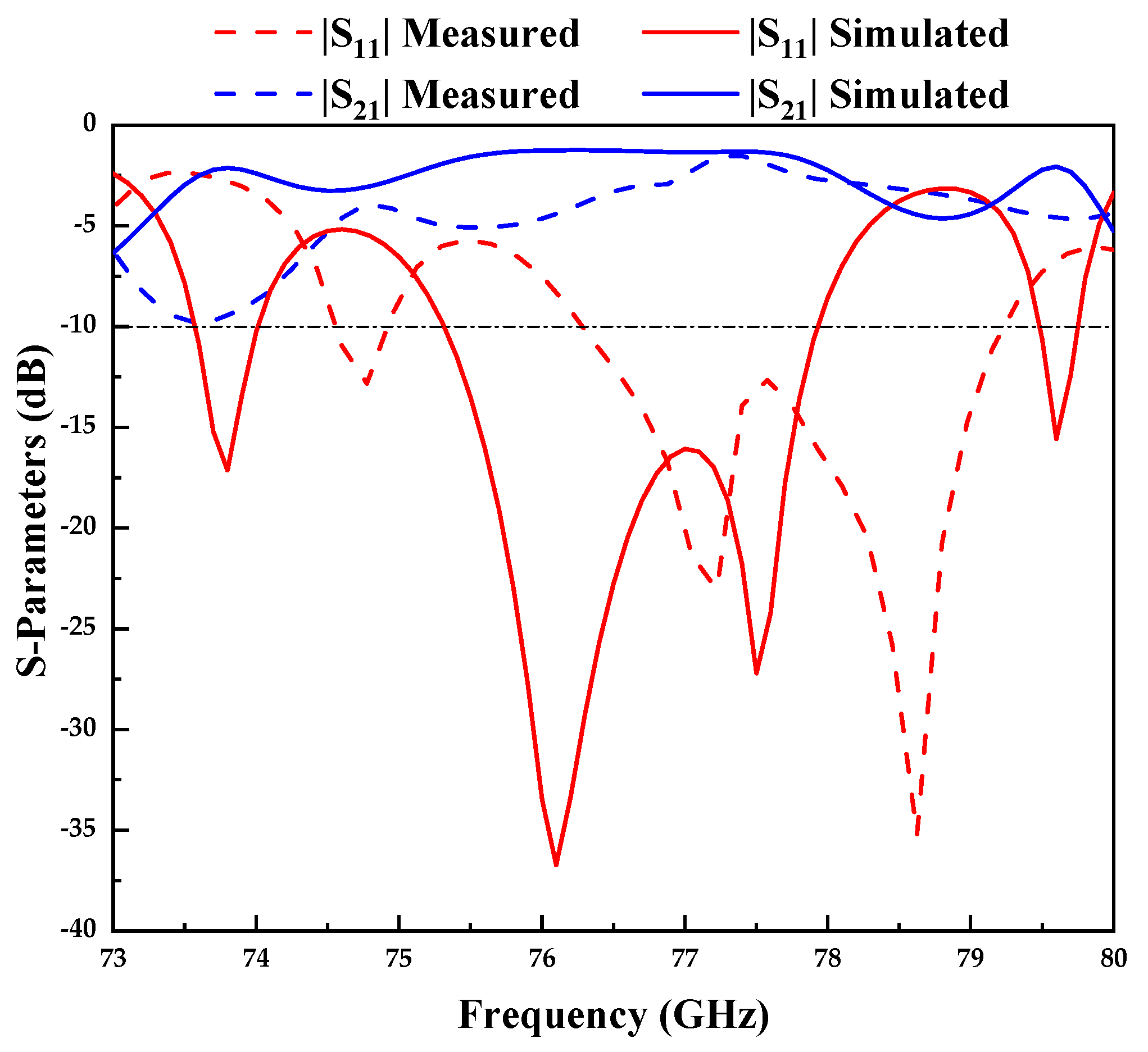
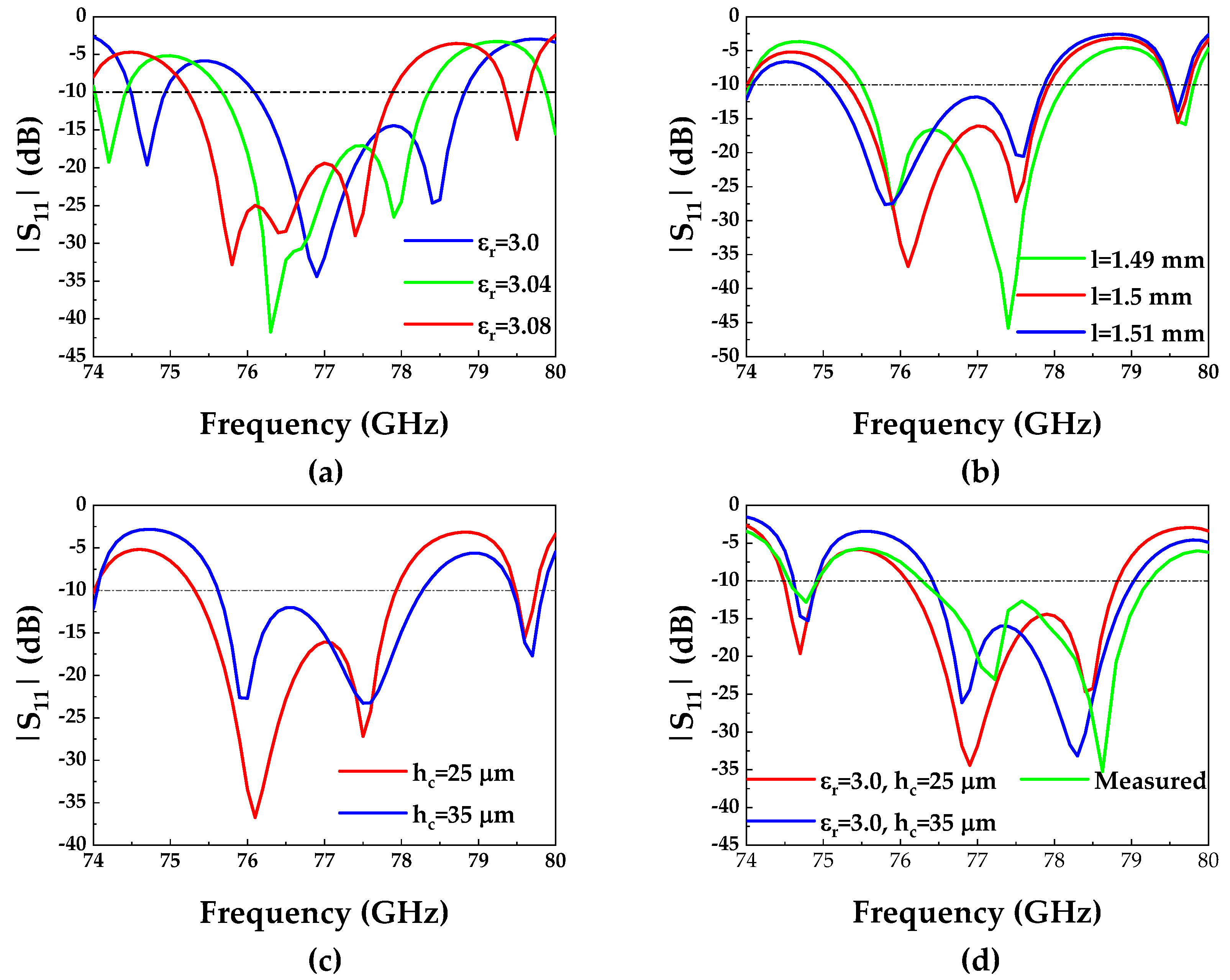
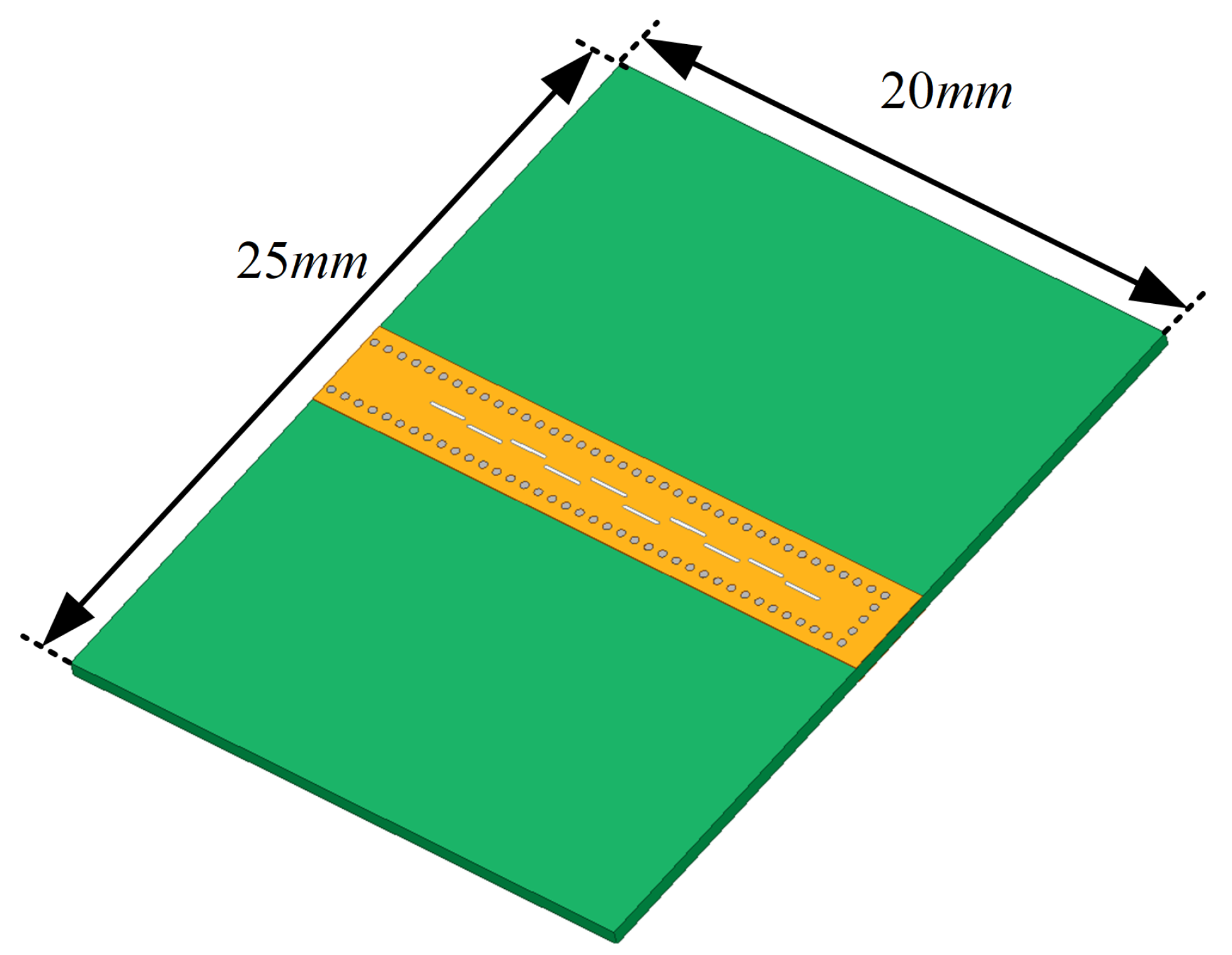



| Slot Number | Length (mm) | Offset (mm) | Normalized Conductance |
|---|---|---|---|
| 1 and 10 | 1.225 | 0.05 | 0.0285 |
| 2 and 9 | 1.226 | 0.058 | 0.0466 |
| 3 and 8 | 1.236 | 0.085 | 0.0949 |
| 4 and 7 | 1.25 | 0.105 | 0.1475 |
| 5 and 6 | 1.263 | 0.117 | 0.1824 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhou, B.; Fang, G. A Method for Low Sidelobe Substrate-Integrated Waveguide Slot Antenna Design Applied for Millimeter-Wave Radars. Remote Sens. 2024, 16, 474. https://doi.org/10.3390/rs16030474
Wang S, Zhou B, Fang G. A Method for Low Sidelobe Substrate-Integrated Waveguide Slot Antenna Design Applied for Millimeter-Wave Radars. Remote Sensing. 2024; 16(3):474. https://doi.org/10.3390/rs16030474
Chicago/Turabian StyleWang, Shuqi, Bin Zhou, and Guangyou Fang. 2024. "A Method for Low Sidelobe Substrate-Integrated Waveguide Slot Antenna Design Applied for Millimeter-Wave Radars" Remote Sensing 16, no. 3: 474. https://doi.org/10.3390/rs16030474
APA StyleWang, S., Zhou, B., & Fang, G. (2024). A Method for Low Sidelobe Substrate-Integrated Waveguide Slot Antenna Design Applied for Millimeter-Wave Radars. Remote Sensing, 16(3), 474. https://doi.org/10.3390/rs16030474






