Evaluation of an Adaptive Soil Moisture Bias Correction Approach in the ECMWF Land Data Assimilation System
Abstract
:1. Introduction
2. Materials and Methods
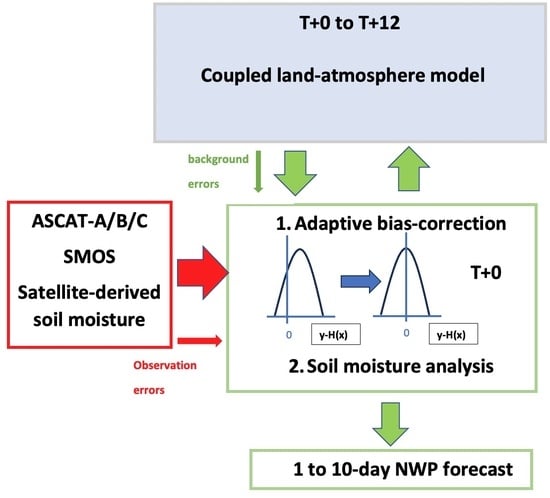
2.1. The Bias-Free SEKF Soil Moisture Analysis
2.2. The Two-Stage Bias Filter
2.3. Satellite-Derived Soil Moisture Observations and Preprocessing
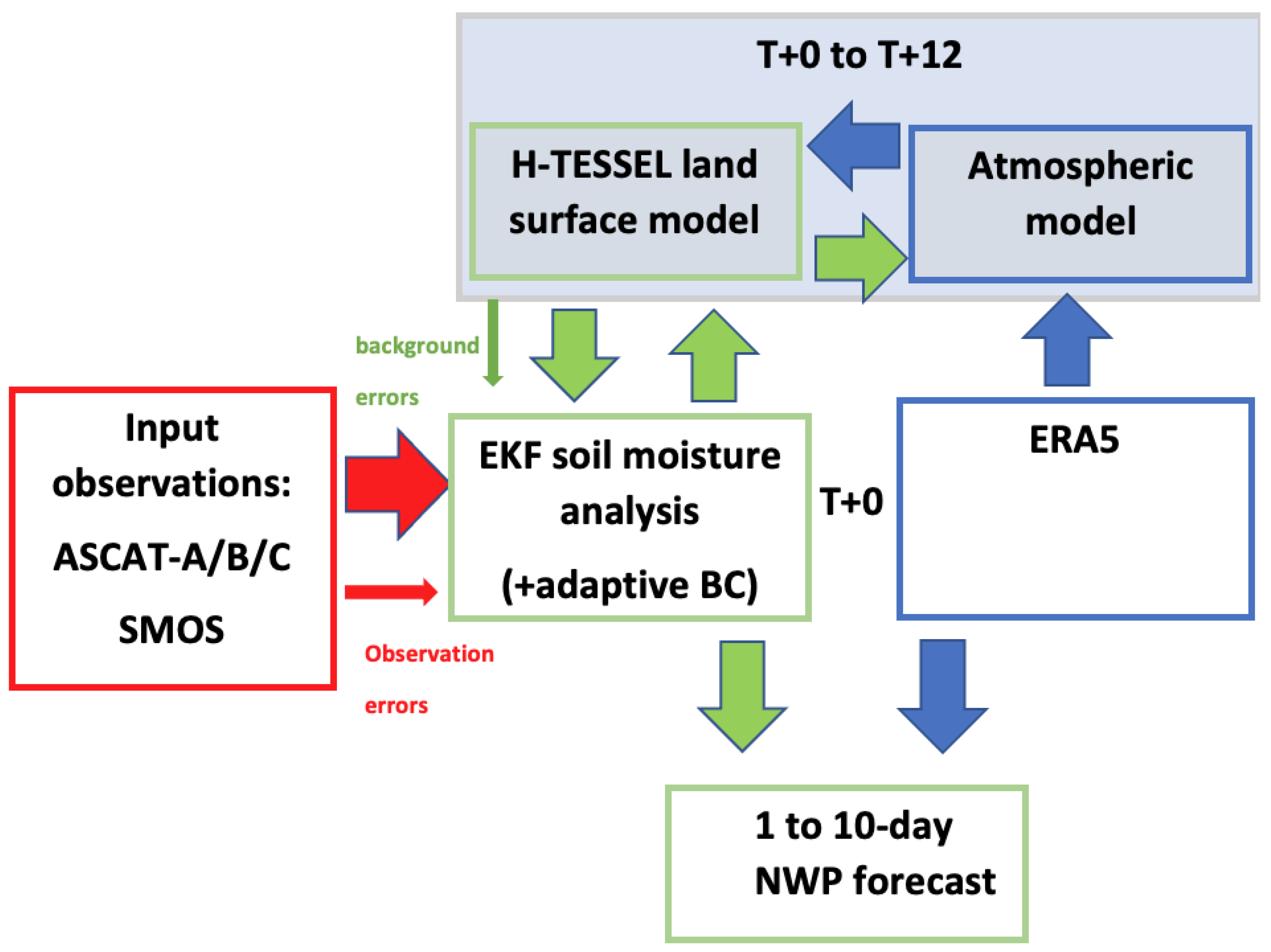
2.4. ECland Surface Model
2.5. The Stand-Alone Surface Analysis
2.6. Experiments
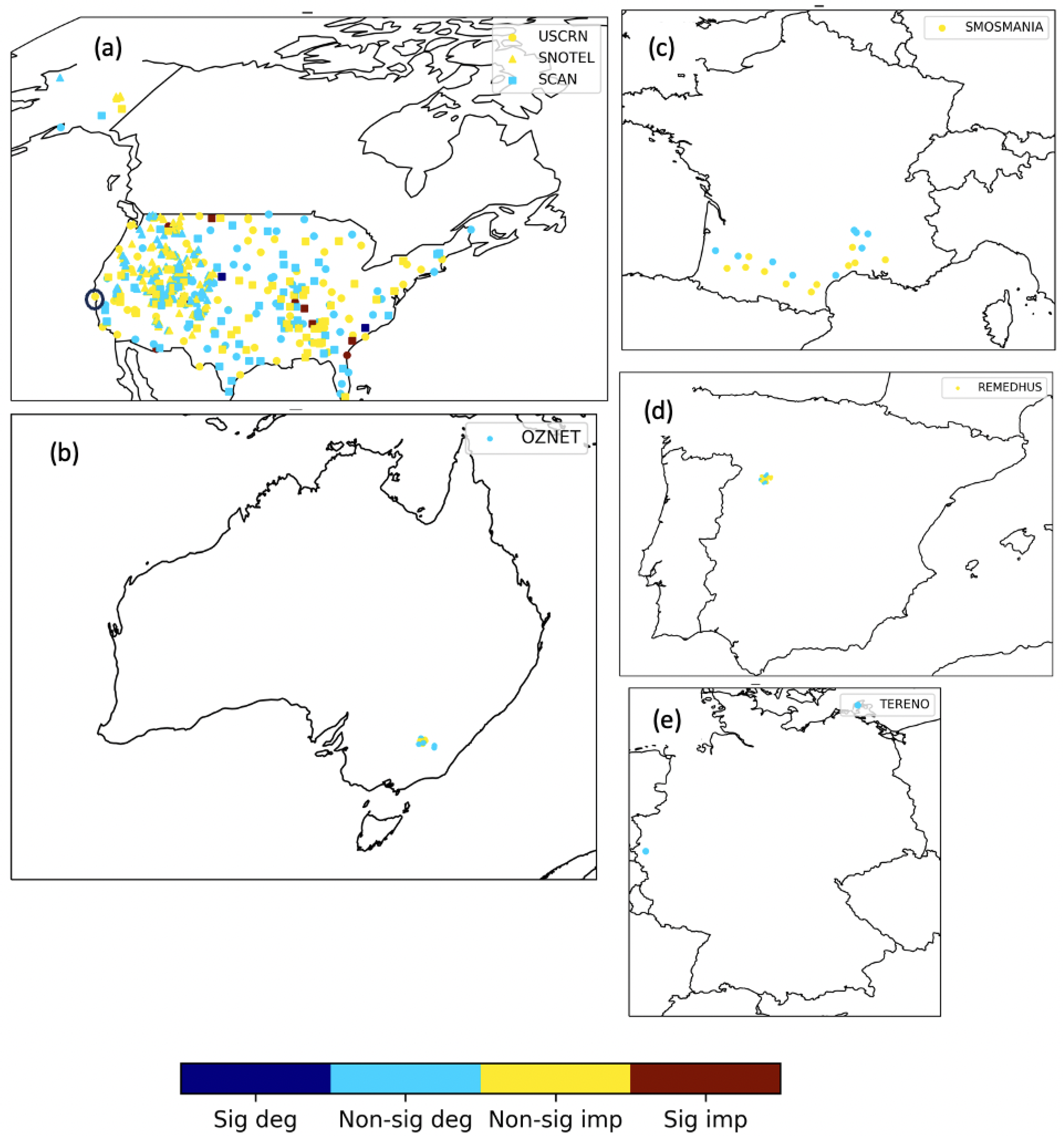
2.7. SM and ST Validation Approach
2.8. Atmospheric Validation Approach
3. Results
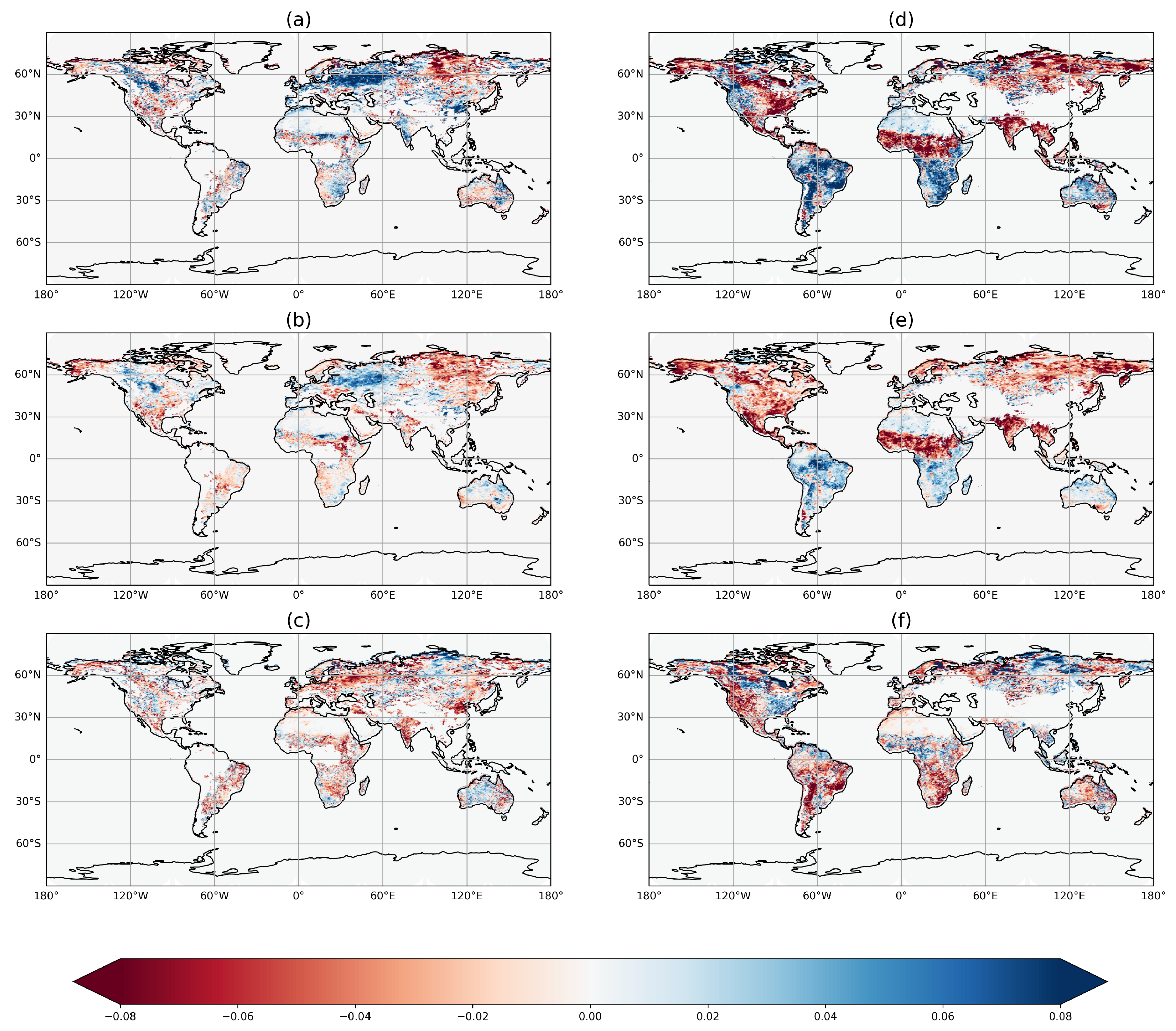
3.1. Internal DA Diagnostics
3.2. SM and ST Validation
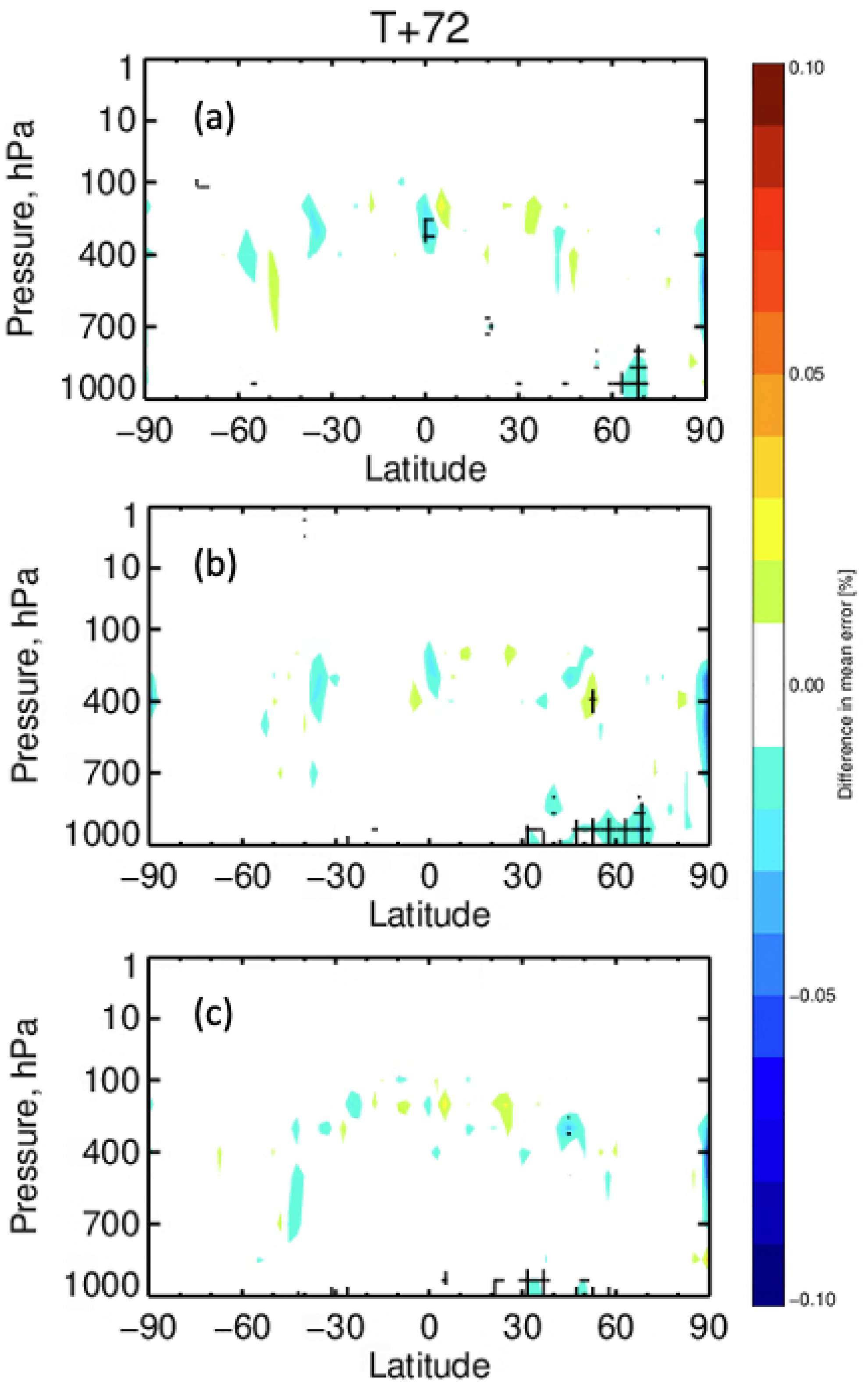
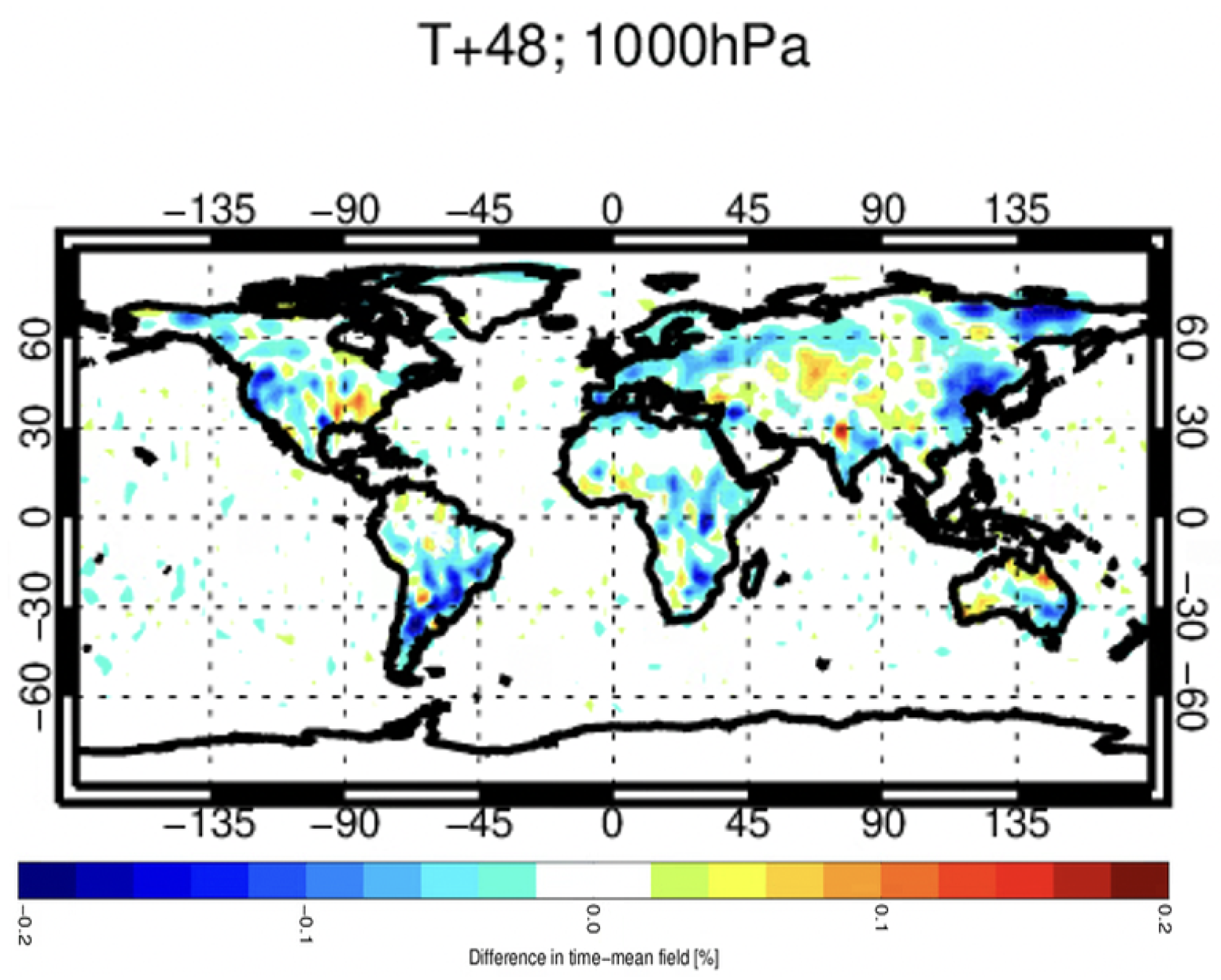
3.3. Atmospheric Validation
4. Discussion
4.1. Adaptive Bias Correction vs. Seasonal Rescaling
4.2. Geographical and Temporal Variations in the Bias Correction
4.3. Performance Validation
4.4. Assumptions in the Bias Correction Approach
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dee, D.; Todling, R. Data assimilation in the presence of forecast bias: The GEOS moisture analysis. Mon. Weather Rev. 2000, 128, 3268–3282. [Google Scholar] [CrossRef]
- Hahn, S.; Wagner, W.; Steele-Dunn, S.; Vreugdenhil, M.; Melzer, T. Improving ASCAT soil moisture retrievals with an enhanced spatially variable vegetation parameterization. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8241–8256. [Google Scholar] [CrossRef]
- Harris, B.; Kelly, G. A satellite radiance-bias correction scheme for data assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1453–1468. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S. Variational bias correction of satellite radiance data in the ERA-Interim reanalysis. Q. J. R. Meteorol. Soc. 2009, 135, 1830–1841. [Google Scholar] [CrossRef]
- Francis, D.; Fowler, A.; Lawless, A.; Eyre, J.; Migliorini, S. The effective use of anchor observations in variational bias correction in the presence of model bias. Q. J. R. Meteorol. Soc. 2023, 149, 1789–1809. [Google Scholar] [CrossRef]
- Crow, W.; Berg, A.; Cosh, M.; Loew, A.; Mohanty, B.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50, RG2002. [Google Scholar] [CrossRef]
- Drusch, M.; Wood, E.; Gao, H. Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, L15403. [Google Scholar] [CrossRef]
- Reichle, R.; Koster, R. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Albergel, C.; Munier, S.; Leroux, D.; Dewaele, H.; Fairbairn, D.; Barbu, A.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C.; et al. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8.0: LDAS-Monde assessment over the Euro-Mediterranean area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef]
- de Rosnay, P.; Muñoz-Sabater, J.; Albergel, C.; Isaksen, L.; English, S.; Drusch, M.; Wigneron, J. SMOS brightness temperature forward modelling and long term monitoring at ECMWF. Remote Sens. Environ. 2020, 237, 111424. [Google Scholar] [CrossRef]
- Dharssi, I.; Bovis, K.; Macpherson, B.; Jones, D. Operational assimilation of ASCAT surface soil wetness at the Met Office. Hydrol. Earth Syst. Sci. 2011, 15, 2729–2746. [Google Scholar] [CrossRef]
- Kumar, S.; Reichle, R.; Harrison, K.; Peters-Lidard, C.; Yatheendradas, S.; Santanello, J. A comparison of methods for a priori bias correction in soil moisture data assimilation. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.; De Rosnay, P.; Albergel, C.; Richaume, P.; Aires, F.; Prigent, C.; Kerr, Y. SMOS Neural Network Soil Moisture Data Assimilation in a Land Surface Model and Atmospheric Impact. Remote Sens. 2019, 11, 1334. [Google Scholar] [CrossRef]
- Aires, F.; Weston, P.; de Rosnay, P.; Fairbairn, D. Statistical approaches to assimilate ASCAT soil moisture information—I. Methodologies and first assessment. Q. J. R. Meteorol. Soc. 2021, 147, 1823–1852. [Google Scholar] [CrossRef]
- de Rosnay, P.; Drusch, M.; Vasiljevic, D.; Balsamo, G.; Albergel, C.; Isaksen, L. A simplified Extended Kalman Filter for the global operational soil moisture analysis at ECMWF. Q. J. R. Meteorol. Soc. 2013, 139, 1199–1213. [Google Scholar] [CrossRef]
- de Rosnay, P.; Browne, P.; de Boisséson, E.; Fairbairn, D.; Hirahara, Y.; Ochi, K.; Schepers, D.; Weston, P.; Zuo, H.; Alonso-Balmaseda, M.; et al. Coupled data assimilation at ECMWF: Current status, challenges and future developments. Q. J. R. Meteorol. Soc. 2022, 148, 2672–2702. [Google Scholar] [CrossRef]
- Dee, D.; Silva, A.D. Data assimilation in the presence of forecast bias. Q. J. R. Meteorol. Soc. 1998, 124, 269–295. [Google Scholar] [CrossRef]
- Chepurin, G.; Carton, J.; Dee, D. Forecast model bias correction in ocean data assimilation. Mon. Weather Rev. 2005, 133, 1328–1342. [Google Scholar] [CrossRef]
- Keppenne, C.; Rienecker, M.; Kurkowski, N.; Adamec, D. Ensemble Kalman filter assimilation of temperature and altimeter data with bias correction and application to seasonal prediction. Nonlinear Process. Geophys. 2005, 12, 491–503. [Google Scholar] [CrossRef]
- Bosilovich, M.; da Silva, A.; Todling, R.; Verter, F. Skin temperature analysis and bias correction in a coupled land–atmosphere data assimilation system. J. Meteorol. Soc. Jpn. 2007, 85A, 205–228. [Google Scholar] [CrossRef]
- De Lannoy, G.; Reichle, R.; Houser, P.; Pauwels, V.; Verhoest, N. Correcting for forecast bias in soil moisture assimilation with the ensemble Kalman filter. Water Resour. Res. 2007, 43, W09410. [Google Scholar] [CrossRef]
- Reichle, R.; Kumar, S.; Mahanama, S.; Koster, R.; Liu, Q. Assimilation of satellite-derived skin temperature observations into land surface models. J. Hydrometeor. 2010, 11, 1103–1122. [Google Scholar] [CrossRef]
- Pauwels, V.; De Lannoy, G.; Hendricks Franssen, H.J.; Vereecken, H. Simultaneous estimation of model state variables and observation and forecast biases using a two-stage hybrid Kalman filter. Hydrol. Earth Syst. Sci. 2013, 17, 3499–3521. [Google Scholar] [CrossRef]
- Draper, C.; Reichle, R.; Lannoy, G.D.; Scarino, B. A dynamic approach to addressing observation-minus-forecast bias in a land surface skin temperature data assimilation system. J. Hydrometeor. 2015, 16, 449–464. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Arduini, G.; Dutra, E.; McNorton, J.; Choulga, M.; Agustí-Panareda, A.; Beljaars, A.; Wedi, N.; Munõz-Sabater, J.; et al. ECLand: The ECMWF land surface modelling system. Atmosphere 2021, 12, 723. [Google Scholar] [CrossRef]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified Notation for Data Assimilation Operational Sequential and Variational. J. Meteorol. Soc. Jpn. 1997, 75, 181–189. [Google Scholar] [CrossRef]
- ECMWF. IFS Documentation CY47R3. Technical Report. 2021. Available online: https://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-model/ifs-documentation (accessed on 24 January 2024).
- Bonavita, M.; Isaksen, L.; Hólm, E. On the use of EDA background error variances in the ECMWF 4D–Var. Q. J. R. Meteorol. Soc. 2015, 138, 1540–1559. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- HSAF. Algorithm Theoretical Baseline Document (ATBD) Soil Moisture NRT, METOP ASCAT Soil Moisture Orbit. Tech. Rep. Doc. No: SAF/HSAF/CDOP2/ATBD-SM_ASCAT_NRT. Technical Report. 2016. Available online: https://hsaf.meteoam.it/Products/ProductsList?type=soil_moisture (accessed on 24 January 2024).
- Draper, C.; Mahfouf, J.F.; Walker, J. An EKF assimilation of AMSR-E soil moisture into the ISBA land surface scheme. J. Geophys. Res. 2009, 114, D20104. [Google Scholar] [CrossRef]
- Barbu, A.; Calvet, J.; Mahfouf, J.; Lafont, S. Integrating ASCAT surface soil moisture and GEOV1 leaf area index into the SURFEX modelling platform: A land data assimilation application over France. Hydrol. Earth Syst. Sci. 2014, 18, 173–192. [Google Scholar] [CrossRef]
- Fairbairn, D.; de Rosnay, P.; Browne, P. The new stand-alone surface analysis at ECMWF: Implications for land–atmosphere DA coupling. J. Hydrometeor. 2019, 20, 2023–2042. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.; Sabater, J.M.; Richaume, P.; De Rosnay, P.; Kerr, Y.; Albergel, C.; Drusch, M.; Mecklenburg, S. SMOS near-real-time soil moisture product: Processor overview and first validation results. Hydrol. Earth Syst. Sci. 2017, 21, 5201–5216. [Google Scholar] [CrossRef]
- Moré, J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2006; pp. 105–116. [Google Scholar]
- Balsamo, G.; Beljaars, A.; Scipal, K.; Viterbo, P.; van den Hurk, B.; Hirschi, M.; Betts, A. A Revised Hydrology for the ECMWF Model: Verification from Field Site to Terrestrial Water Storage and Impact in the Integrated Forecast System. J. Hydrometeor. 2009, 10, 623–643. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.; Brown, J.; Ohlen, D.; Zhu, Z.; Youing, L.; Merchant, J. Development of a Global Land Cover Characteristics Database and IGB6 DISCover from the 1km AVHRR Data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Beljaars, A.; Kral, T.; Jarlan, L. Impact of a satellite–derived leaf area index monthly climatology in a global numerical weather prediction model. Int. J. Remote Sens. 2013, 34, 3520–3542. [Google Scholar] [CrossRef]
- Richards, L. Capillary conduction of liquids in porous medium. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Viterbo, P.; Beljaars, A. An improved land surface parameterization scheme in the ECMWF model and its validation. J. Climate 1995, 8, 2716–2748. [Google Scholar] [CrossRef]
- Arduini, A.; Balsamo, G.; Dutra, E.; Day, J.; Sandy, I.; Boussetta, S.; Haiden, T. Impact of a multi-layer snow scheme on near-surface weather forecasts. J. Adv. Model. Earth Syst. 2019, 11, 4687–4710. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Haseler, J. Early–Delivery Suite. Technical Report, ECMWF. 2004. Available online: http://www.ecmwf.int/publications/ (accessed on 24 January 2024).
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Bell, J.E.; Palecki, M.A.; Baker, C.; Collins, W.; Lawrimore, J.; Leeper, R.; Hall, M.; Kochendorfer, J.; Meyers, T.; Wilson, T.; et al. U.S. Climate Reference Network soil moisture and temperature observations. J. Hydrometeor. 2013, 14, 977–988. [Google Scholar] [CrossRef]
- Schaefer, G.; Cosh, M.; Jackson, T. The USDA natural resources conservation service soil climate analysis network (SCAN). J. Atmos. Ocean. Technol. 2007, 24, 2073–2077. [Google Scholar] [CrossRef]
- Calvet, J.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B. In situ soil moisture observations for the CAL/VAL of SMOS: The SMOSMANIA network. In Proceedings of the Geoscience and Remote Sensing Symposium, IGARSS, Barcelona, Spain, 23–28 July 2007; IEEE International: Piscataway, NJ, USA, 2007; Volume 16, pp. 1293–1314. [Google Scholar]
- Martinez-Fernández, J.; Caballos, A. Mean soil moisture estimation using temporal stability analysis. J. Hydrol. 2005, 312, 28–38. [Google Scholar] [CrossRef]
- Zacharias, S.; Bogena, H.; Samaniego, L.; Mauder, M.; Fuß, R.; Pütz, T.; Frenzel, M.; Schwank, M.; Baessler, C.; Butterbach-Bahl, K.; et al. A Network of Terrestrial Environmental Observatories in Germany. Vadose Zone J. 2011, 10, 955–973. [Google Scholar] [CrossRef]
- Smith, A.; Walker, J.; Young, R.; Ellett, K.; Pipunic, R.; Grayson, R.; Siriwardena, L.; Chiew, F.; Richter, H. The Murrumbidgee soil moisture monitoring network data set. Water Resour. Res. 2012, 48, W07701. [Google Scholar] [CrossRef]
- Albergel, C.; Dorigo, W.; Reichle, R.; Balsamo, G.; De Rosnay, P.; Muñoz Sabater, J.; Isaksen, L.; De Jeu, R.; Wagner, W. Skill and global trend analysis of soil moisture from reanalyses and microwave remote sensing. J. Hydrometeor. 2013, 14, 1259–1277. [Google Scholar] [CrossRef]
- Draper, C.; Reichle, R.; De Lannoy, G.; Liu, Q. Assimilation of passive and active microwave soil moisture retrievals. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Reichle, R.; De Lannoy, G.; Liu, Q.; Ardizzone, J.; Colliander, A.; Conaty, A.; Crow, W.; Jackson, T.; Jones, L.; Kimball, J.; et al. Assessment of the SMAP Level-4 surface and root-zone soil moisture product using in situ measurements. J. Hydrometeor. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
- Dorigo, W.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiova, A.; Sanchis-Dufau, A.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global automated quality control of in situ soil moisture data from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 1–21. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.; Koster, R.; Crow, W. Performance metrics for soil moisture retrievals and application requirements. J. Hydrometeor. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Geer, A. Significance of changes in medium–range forecast scores. Tellus A 2016, 68, 30229. [Google Scholar] [CrossRef]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of observation, background and analysis-error statistics in observation space. Q. J. R. Meteorol. Soc. 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Hahn, S.; Wagner, W.; Alves, O.; Sanjeevamurthy, P.M.; Vreugdenhil, M.; Melzer, T. Metop ASCAT soil moisture trends: Mitigating the effects of long-term land cover changes. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 23–28 April 2023. EGU23-16205. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Montzka, C.; Moradkhani, H.; Weihermuller, L.; Canty, M.; Frassen, H.H.; Vereecken, H. Hydraulic parameter estimation by remotely-sensed top soil moisture observations with the particle filter. J. Hydrol. 2011, 399, 410–421. [Google Scholar] [CrossRef]
- Abramowitz, G.; Ukkola, A.; Hobeichi, S.; Cranko Page, J.; Lipson, M.; De Kauwe, M.; Green, S.; Brenner, C.; Frame, J.; Nearing, G.; et al. On the predictability of turbulent fluxes from land: PLUMBER2 MIP experimental description and preliminary results. EGUsphere 2024. preprint. [Google Scholar] [CrossRef]





| Study | Observation Type | Model Type | Region | BC Variable |
|---|---|---|---|---|
| Bosilovich et al. [21] | Skin temp | Land-atmos | Global | Model surface temp |
| De Lannoy et al. [22] | In situ SM | Land only | Regional | Model SM |
| Reichle et al. [23] | Skin temp | Land only | Global | Model surface temp |
| Pauwels et al. [24] | Streamflow | Hydrological | Regional | Streamflow model and obs |
| Draper et al. [25] | Skin temp | Land only | Regional | Skin temp model and obs |
| Present | SM | Land-atmos | Global | SM obs |
| Experiment | C | ||||
|---|---|---|---|---|---|
| ASCAT adaptive BC | False | True | False | True | True |
| SMOS adaptive BC | False | False | True | True | True |
| ASCAT seasonal rescaling | True | True | True | True | False |
| Name | Reference Type | Vertical Depths or Levels | Spatial Res. | Num. of Stations |
|---|---|---|---|---|
| SMOSMANIA | In situ SM or ST | 5, 10, 20 and 30 cm depth | Point-wise | 20 stations, France |
| SCAN | In situ SM or ST | 5, 10, 20, 50 and 100 cm depth | Point-wise | 133 stations, US |
| USCRN | In situ SM or ST | 5, 10, 20, 50 and 100 cm depth | Point-wise | 106 stations, US |
| SNOTEL | In situ SM or ST | 5, 10, 20 and 50 cm depth | Point-wise | 292 stations, US |
| REMEDHUS | In situ SM or ST | 5 cm depth | Point-wise | 15 stations, Spain |
| OZNET | In situ SM or ST | 4, 15, 45 and 75 cm depth | Point-wise | 13 stations, Australia |
| TERENO | In situ SM or ST | 5, 20 and 50 cm depth | Point-wise | 1 station, Germany |
| ECMWF* | Air temp analysis | 137 levels (1–1000 hPa) | 31 km | Global analysis |
| ECMWF* | Air RH analysis | 137 levels (1–1000 hPa) | 31 km | Global analysis |
| Variable | C | ||||
|---|---|---|---|---|---|
| ASCAT SM depar. () | |||||
| Absolute ASCAT SM depar. () | |||||
| SMOS SM depar. () | −2 ± 0.1 | −2 ± 0.1 | 3 ± 0.1 | 3 ± 0.1 | 3 ± 0.1 |
| Absolute SMOS SM depar. () | 37 ± 0.03 | 37 ± 0.04 | 32 ± 0.03 | 32 ± 0.04 | 32 ± 0.03 |
| SSM inc. () | 16 ± 0.4 | 13 ± 0.4 | 14 ± 0.4 | 10 ± 0.3 | 12 ± 0.3 |
| Absolute SSM inc. () | 204 ± 0.3 | 202 ± 0.3 | 201 ± 0.3 | 200 ± 0.3 | 202 ± 0.3 |
| RZSM inc. () | 4 ± 0.2 | 4 ± 0.2 | 3 ± 0.2 | 3 ± 0.2 | 3 ± 0.2 |
| Absolute RZSM inc. () | 98 ± 0.3 | 98 ± 0.3 | 97 ± 0.3 | 97 ± 0.3 | 97 ± 0.3 |
| Global Mean Score | C | ||||
|---|---|---|---|---|---|
| SSM R anomaly (-) | 0.439 | 0.439 | 0.441 | 0.441 | 0.441 |
| SSM UbRMSE () | 0.063 | 0.063 | 0.063 | 0.063 | 0.063 |
| SSM bias () | 0.065 | 0.065 | 0.065 | 0.065 | 0.065 |
| RZSM R anomaly (-) | 0.440 | 0.441 | 0.442 | 0.444 | 0.438 |
| RZSM UbRMSE () | 0.045 | 0.045 | 0.045 | 0.045 | 0.045 |
| RZSM bias () | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 |
| SST R anomaly (-) | 0.675 | 0.675 | 0.675 | 0.675 | 0.675 |
| SST UbRMSE (°K) | 4.13 | 4.12 | 4.13 | 4.12 | 4.13 |
| SST bias (°K) | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 |
| RZST R anomaly (-) | 0.630 | 0.630 | 0.630 | 0.630 | 0.630 |
| RZST UbRMSE (°K) | 2.25 | 2.26 | 2.26 | 2.26 | 2.25 |
| RZST bias (°K) | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fairbairn, D.; de Rosnay, P.; Weston, P. Evaluation of an Adaptive Soil Moisture Bias Correction Approach in the ECMWF Land Data Assimilation System. Remote Sens. 2024, 16, 493. https://doi.org/10.3390/rs16030493
Fairbairn D, de Rosnay P, Weston P. Evaluation of an Adaptive Soil Moisture Bias Correction Approach in the ECMWF Land Data Assimilation System. Remote Sensing. 2024; 16(3):493. https://doi.org/10.3390/rs16030493
Chicago/Turabian StyleFairbairn, David, Patricia de Rosnay, and Peter Weston. 2024. "Evaluation of an Adaptive Soil Moisture Bias Correction Approach in the ECMWF Land Data Assimilation System" Remote Sensing 16, no. 3: 493. https://doi.org/10.3390/rs16030493
APA StyleFairbairn, D., de Rosnay, P., & Weston, P. (2024). Evaluation of an Adaptive Soil Moisture Bias Correction Approach in the ECMWF Land Data Assimilation System. Remote Sensing, 16(3), 493. https://doi.org/10.3390/rs16030493