Coseismic Deformation Obtained by Various Technical Methods and Its Constraint Ability to Slip Models of Maduo Earthquake
Abstract
:1. Introduction
2. Data and Methods
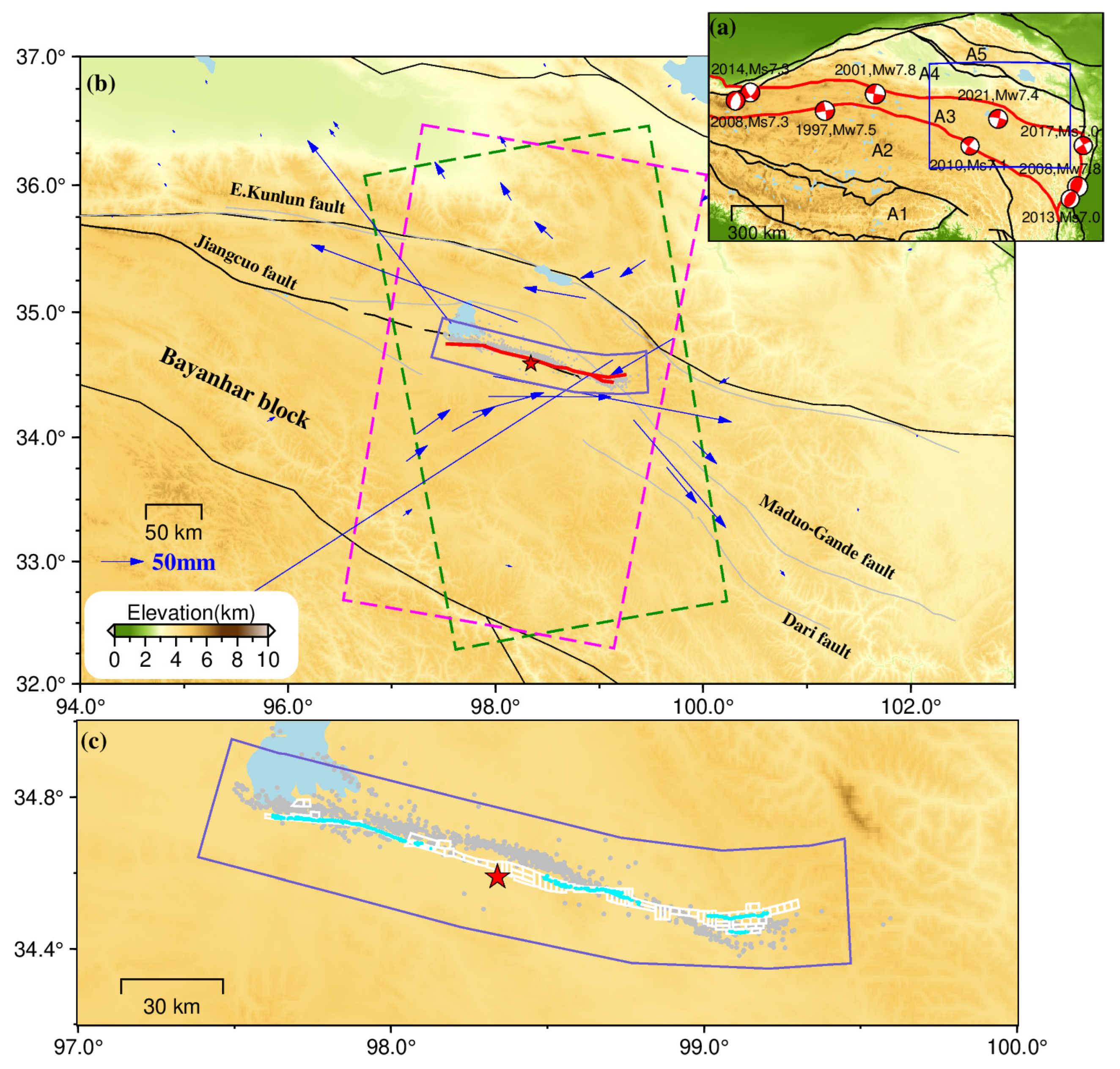
2.1. Different Types of Coseismic Deformation Data
2.2. Normalisation and Comparison of Different Types of Coseismic Displacement Data
2.3. Inversion and Comparison of Coseismic Slip Models with Different Data and Different Fault Geometric Constraints
2.3.1. Determination of the Geometric Model of the Maduo Earthquake Seismogenic Fault
2.3.2. Inversion of Slip Distribution Models with Different Datasets and Different Fault Geometry Constraints
3. Results
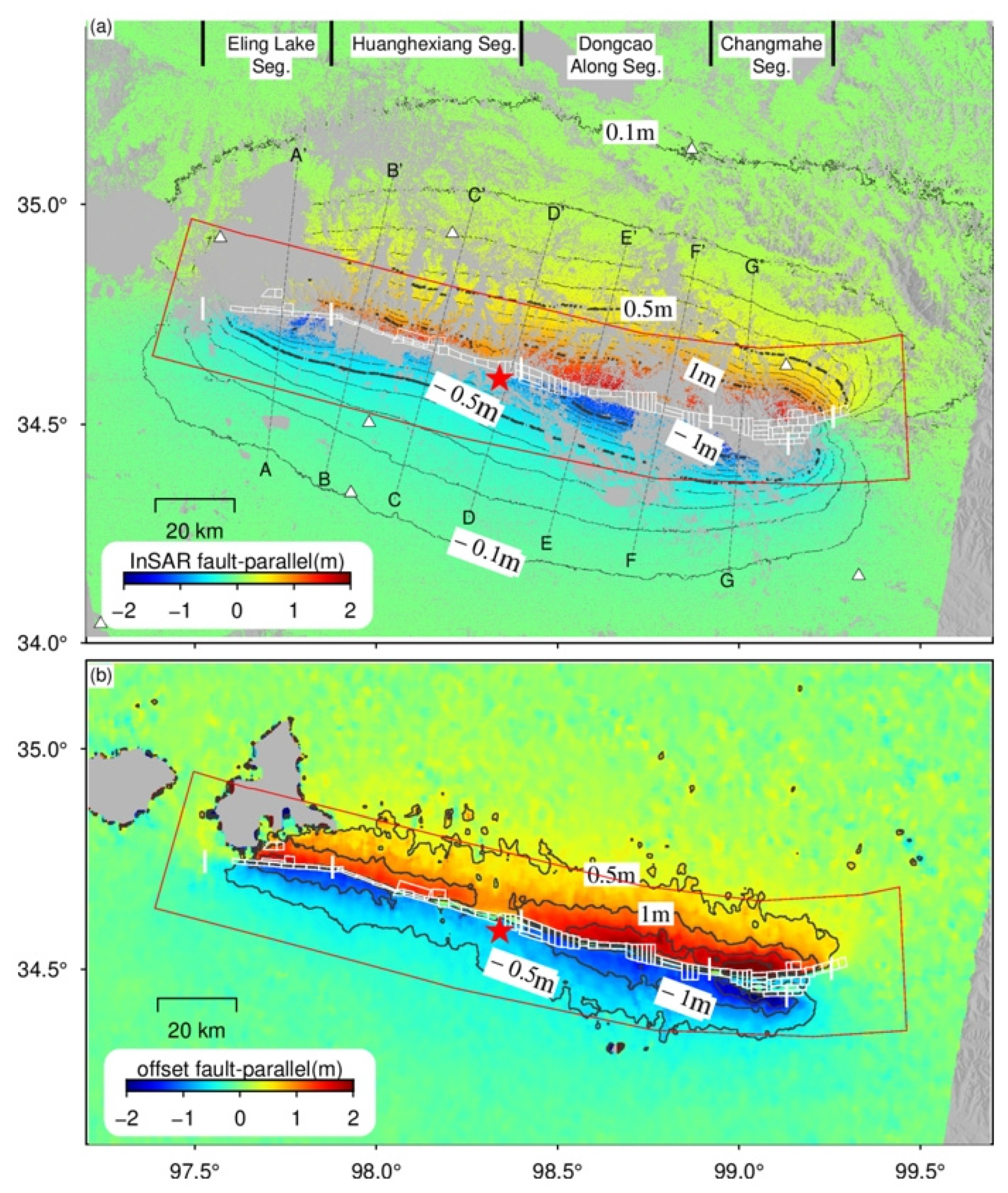
3.1. InSAR Coseismic Deformation Field
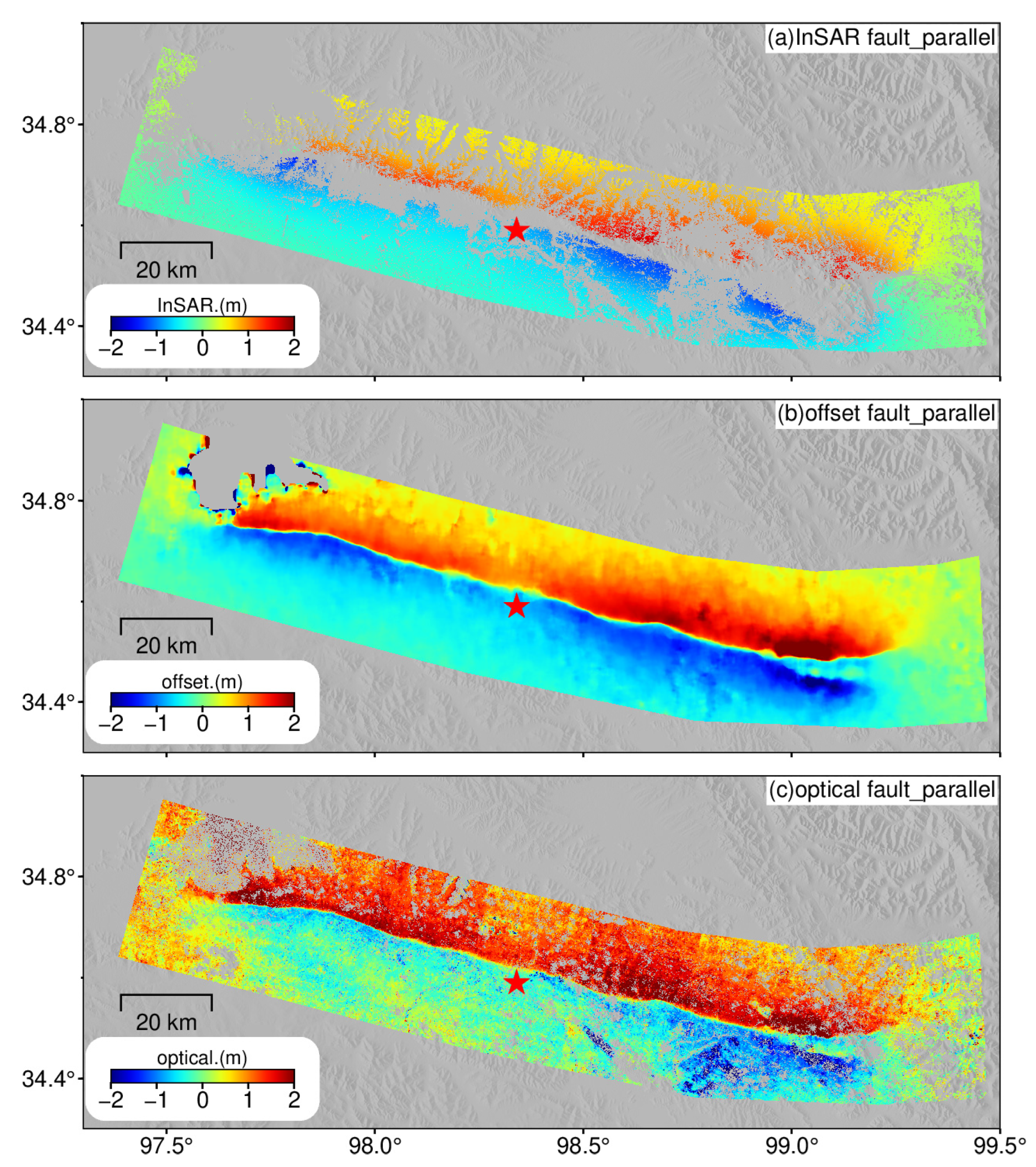
3.2. Comparative Analysis of Coseismic Displacement Field Obtained from InSAR, Offset and Optical Images
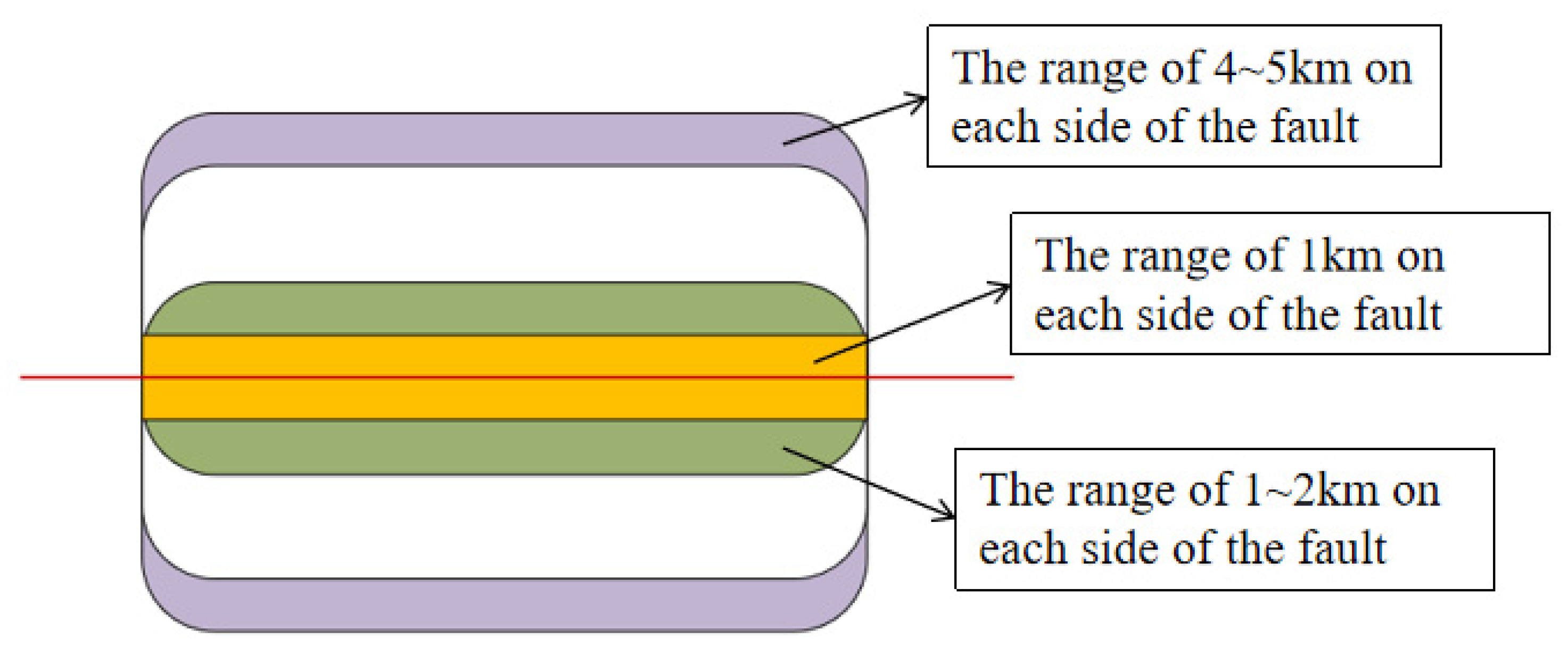
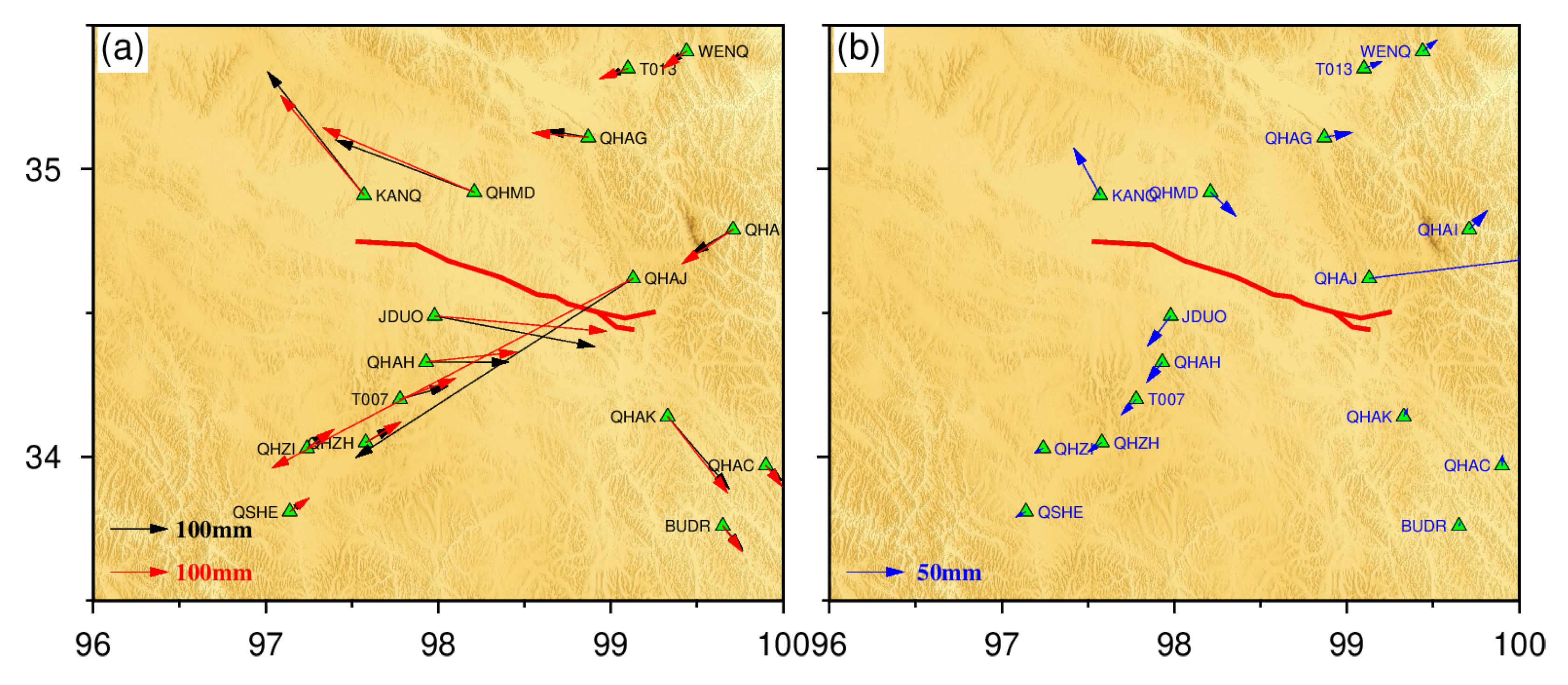
3.3. Comparison of Near-Field Cross-Fault Strike-Slip Deformations Obtained from Different Data Sources
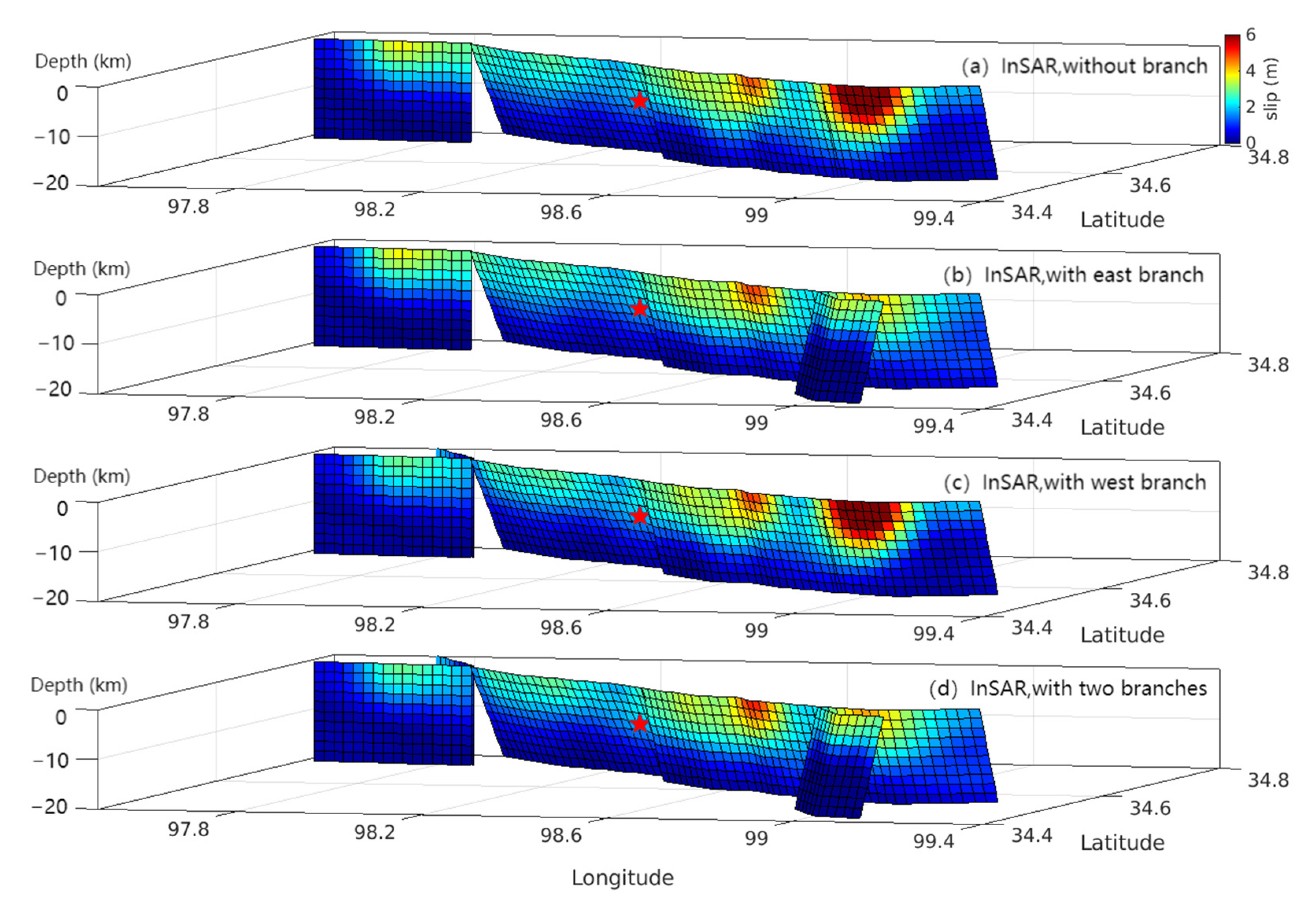
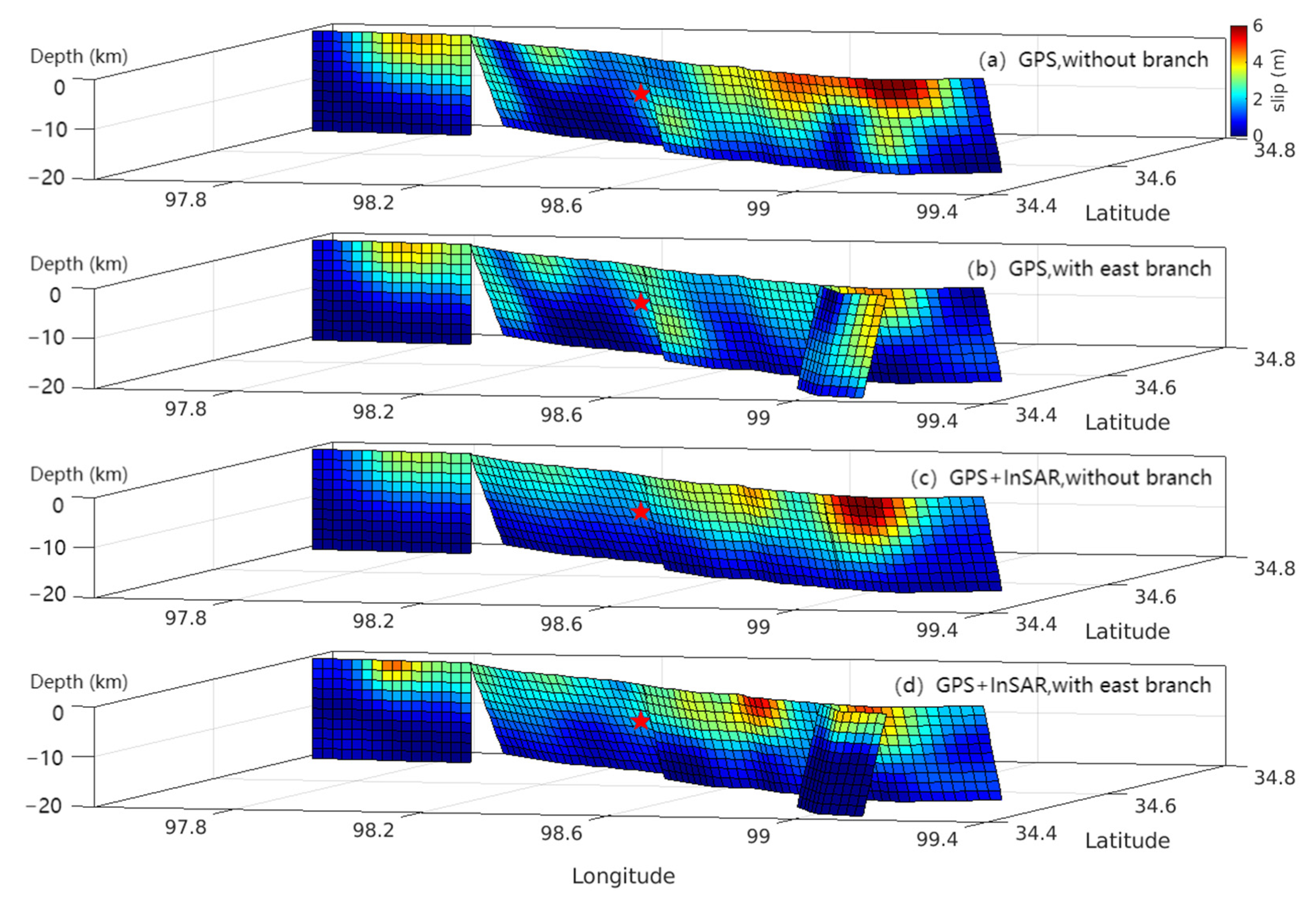
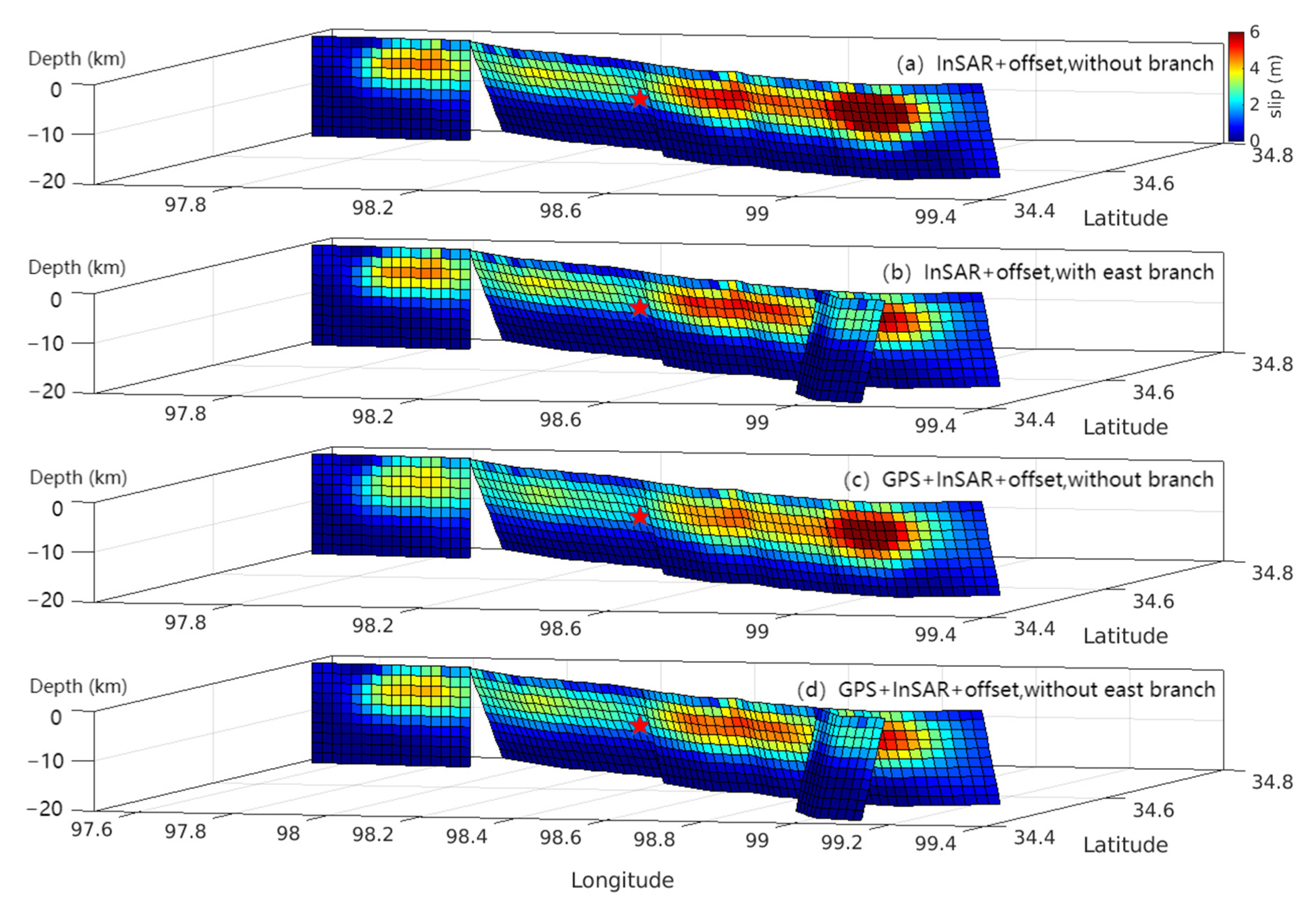
3.4. Coseismic Slip Model Inversion Results Constrained by Different Datasets and Different Fault Models
4. Discussion
4.1. The Ability of Different Observation Methods to Identify Near-Fault Deformation
4.2. Differences in Slip Models Constrained by Different Datasets
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, Q.; Cheng, S.; Ma, J.; Du, P. Seismic activities and earthquake potential in the Tibetan Plateau. Chin. J. Geophys. 2014, 57, 2025–2042. (In Chinese) [Google Scholar]
- Deng, Q.; Gao, X.; Chen, G.; Yang, H. The latest activity of the Kunlun-Wenchuan earthquake series on the Tibetan Plateau and the Bayankala fault. Earth Sci. Front. 2010, 17, 163–178. (In Chinese) [Google Scholar]
- Yuan, Z.; Li, T.; Su, P.; Sun, H.; Ha, G.; Guo, P.; Chen, G.; Jobe, J.T. Large surface-rupture gaps and low surface fault slip of the 2021 Mw 7.4 Maduo earthquake along a low-activity strike-slip fault, Tibetan Plateau. Geophys. Res. Lett. 2022, 49, e2021GL096874. [Google Scholar] [CrossRef]
- Jin, Z.; Fialko, Y. Coseismic and early postseismic deformation due to the 2021 M 7.4 Maduo (China) earthquake. Geophys. Res. Lett. 2021, 48, e2021GL095213. [Google Scholar] [CrossRef]
- Li, C.; Li, T.; Shan, X.; Zhang, G. Extremely Large Off-Fault Deformation during the 2021 Mw 7.4 Maduo, Tibetan Plateau, Earthquake. Seismol. Res. Lett. 2022, 94, 39–51. [Google Scholar] [CrossRef]
- Yue, H.; Shen, Z.; Zhao, Z.; Wang, T.; Cao, B.; Li, Z. Rupture process of the 2021 M 7. 4 Maduo earthquake and implication for deformation mode of the Songpan-Ganzi terrane in Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2022, 119, e2116445119. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Xu, X.; Chen, S. Coseismic Slip Model of the 2021 Maduo Earthquake, China from Sentinel-1 InSAR Observation. Remote Sens. 2022, 14, 436. [Google Scholar] [CrossRef]
- Wang, M.; Wang, F.; Jiang, X.; Tian, J.; Li, Y.; Sun, J.; Shen, Z. GPS determined coseismic slip of the 2021 Mw 7.4 Maduo, China, earthquake and its tectonic implication. Geophys. J. Int. 2022, 228, 2048–2055. [Google Scholar] [CrossRef]
- Fang, J.; Ou, Q.; Wright, T.J.; Okuwaki, R.; Amey, R.M.; Craig, T.J.; Elliott, J.R.; Hooper, A.; Lazecký, M.; Maghsoudi, Y. Earthquake cycle deformation associated with the 2021 Mw 7.4 Maduo (eastern Tibet) earthquake: An intrablock rupture event on a slow-slipping fault from Sentinel-1 InSAR and teleseismic data. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024268. [Google Scholar] [CrossRef]
- Wang, W.; Fang, L.; Wu, J.; Tu, H.; Chen, L.; Lai, G.; Zhang, L. Aftershock sequence relocation of the 2021 Ms7.4 Maduo Earthquake, Qinghai, China. Sci. China Earth Sci. 2021, 51, 1193–1202. [Google Scholar] [CrossRef]
- Li, Q.; Wan, Y.; Li, C.; Tang, H.; Tan, K.; Wang, D. Source Process Featuring Asymmetric Rupture Velocities of the 2021 Mw 7.4 Maduo, China, Earthquake from Teleseismic and Geodetic Data. Seismol. Res. Lett. 2022, 93, 1429–1439. [Google Scholar] [CrossRef]
- Pan, J.; Bai, M.; Li, C.; Liu, F.; Li, H.; Liu, D.; Chevalier, M.-L.; Wu, K.; Wang, P.; Lu, H.; et al. Coseismic surface rupture and seismogenic structure of the 2021-05-22 Maduo (Qinghai) Ms 7.4 earthquake. Acta Geol. Sin. 2021, 95, 1655–1670. [Google Scholar]
- Li, Z.; Li, W.; Li, T.; Xu, Y.; Su, P.; Guo, P.; Sun, Y.; Ha, G.; Chen, G.; Yao, Z.; et al. Seismogenic fault and coseismic surface deformation of the Maduo Ms7.4 earthquake in Qinghai, China: A quick report. Seismol. Geol. 2021, 43, 722–737. (In Chinese) [Google Scholar]
- Zhao, D.; Qu, C.; Chen, H.; Shan, X.; Song, X.; Gong, W. Tectonic and geometric control on fault kinematics of the 2021 Mw7.3 Maduo (China) earthquake inferred from interseismic, coseismic, and postseismic InSAR observations. Geophys. Res. Lett. 2021, 48, e2021GL095417. [Google Scholar] [CrossRef]
- He, K.; Wen, Y.; Xu, C.; Zhao, Y. Fault Geometry and Slip Distribution of the 2021 Mw 7.4 Maduo, China, Earthquake Inferred from InSAR Measurements and Relocated Aftershocks. Seismol. Res. Lett. 2021, 93, 8–20. [Google Scholar] [CrossRef]
- He, L.; Feng, G.; Wu, X.; Lu, H.; Xu, W.; Wang, Y.; Liu, J.; Hu, J.; Li, Z. Coseismic and early postseismic slip models of the 2021 Mw 7.4 Maduo earthquake (western China) estimated by space-based geodetic data. Geophys. Res. Lett. 2021, 48, e2021GL095860. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Cai, Y.; Jiang, L.; Shi, H.; Jiang, Z.; Gan, W. Coseismic displacement and slip distribution of the 2021 Mw 7.4 Madoi earthquake derived from GNSS observations. Chin. J. Geophys. 2022, 65, 523–536. (In Chinese) [Google Scholar]
- Chen, H.; Qu, C.; Zhao, D.; Ma, C.; Shan, X. Rupture Kinematics and Coseismic Slip Model of the 2021 Mw 7.3 Maduo (China) Earthquake: Implications for the Seismic Hazard of the Kunlun Fault. Remote Sens. 2021, 13, 3327. [Google Scholar] [CrossRef]
- Wang, D.; Wang, D.; Zhao, B.; Li, Y.; Zhao, L.; Wang, Y.; Nie, Z.; Qiao, X.; Wang, Q. 2021 Qinghao Madoi Mw 7.4 earthquake coseismic deformation field and fault-slip distribution using GNSS observations. Chin. J. Geophys. 2022, 65, 537–551. (In Chinese) [Google Scholar]
- Li, Z.; Ding, K.; Zhang, P.; Wen, Y.; Zhao, L.; Chen, J. Coseismic Deformation and Slip Distribution of 2021 Mw 7.4 Madoi Earthquake from GNSS Observation. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1489–1497. [Google Scholar]
- Yu, P.; Xiong, W.; Chen, W.; Qiao, X.; Wang, D.; Liu, G.; Zhao, B.; Nie, Z.; Li, Y.; Zhao, L.; et al. Slip model of the 2021 Ms 7.4 Madoi earthquake constrained by GNSS and InSAR coseismic deformation. Chin. J. Geophys. 2022, 65, 509–522. (In Chinese) [Google Scholar]
- Xiong, W.; Chen, W.; Wang, D.; Wen, Y.; Nie, Z.; Liu, G.; Wang, D.; Yu, P.; Qiao, X.; Zhao, B. Coseismic slip and early afterslip of the 2021 Mw 7.4 Maduo, China earthquake constrained by GPS and InSAR data. Tectonophysics 2022, 840, 229558. [Google Scholar] [CrossRef]
- Hong, S.; Liu, M.; Liu, T.; Dong, Y.; Chen, L.; Meng, G.; Xu, Y. Fault Source Model and Stress Changes of the 2021 Mw 7.4 Maduo Earthquake, China, Constrained by InSAR and GPS Measurements. Bull. Seismol. Soc. Am. 2022, 112, 1284–1296. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Q.; Yang, Y.; Xu, Q.; Zhao, J.; Xu, L.; Liu, R. The 2021 Mw7.4 Maduo earthquake: Coseismic slip model, triggering effect of historical earthquakes and implications for adjacent fault rupture potential. J. Geodyn 2022, 151, 101920. [Google Scholar] [CrossRef]
- Guo, R.; Yang, H.; Li, Y.; Zheng, Y.; Zhang, L. Complex Slip Distribution of the 2021 Mw 7.4 Maduo, China, Earthquake: An Event Occurring on the Slowly Slipping Fault. Seismol. Res. Lett. 2021, 93, 653–665. [Google Scholar] [CrossRef]
- Wang, S.; Ji, L.; Zhu, L.; Liu, C. Co-seismic Deformation Field and Fault Slip Distribution of the 2021 Maduo Mw 7.4 Earthquake in Qinghai, China Based on InSAR Technology. J. Earth Sci. Environ. 2022, 44, 1016–1026. [Google Scholar]
- Tang, X.; Guo, R.; Xu, J.; Zheng, Y. Role of Poroelasticity and Viscoelasticity during the Postseismic Deformation of the 2021 Mw 7.4 Maduo, China, Earthquake. Seismol. Res. Lett. 2023, 94, 2192–2201. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Ji, C.; Meng, L.; Fielding, E.J.; Zinke, R.; Bao, H. Understanding the rupture kinematics and slip model of the 2021 Mw 7.4 Maduo earthquake: A bilateral event on bifurcating faults. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025936. [Google Scholar] [CrossRef]
- Liu, C.; Bai, L.; Hong, S.; Dong, Y.; Jiang, Y.; Li, H.; Zhan, H.; Chen, Z. Coseismic deformation of the 2021 Mw 7.4 Maduo earthquake from joint inversion of InSAR, GPS, and teleseismic data. Earthq. Sci. 2021, 34, 436–446. [Google Scholar] [CrossRef]
- Feng, W.; Li, Z.; Elliott, J.R.; Fukushima, Y.; Hoey, T.; Singleton, A.; Cook, R.; Xu, Z. The 2011 MW 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophys. J. Int. 2013, 195, 650–660. [Google Scholar] [CrossRef]
- Wang, R.; Diao, F.; Hoechner, A. SDM-A geodetic inversion code incorporating with layered crust structure and curved fault geometry. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Ren, J.; Xu, X.; Zhang, G.; Wang, Q.; Zhang, Z.; Gai, H.; Kang, W. Coseismic surface ruptures, slip distribution, and 3D seismogenic fault for the 2021 Mw 7.3 Maduo earthquake, central Tibetan Plateau, and its tectonic implications. Tectonophysics 2022, 827, 229275. [Google Scholar] [CrossRef]
- Li, C.; Li, T.; Hollingsworth, J.; Zhang, Y.; Qian, L.; Shan, X. Strain threshold for the formation of coseismic surface rupture. Geophys. Res. Lett. 2023, 50, e2023GL103666. [Google Scholar] [CrossRef]
- Shao, Y.; Liu, J.; Gao, Y.; Wang, W.; Yao, W.; Han, L.; Liu, Z.; Zou, X.; Wang, Y.; Li, Y.; et al. Coseismic displacement measurement and distributed deformation characterization: A case of 2021 Mw 7.4 Madoi earthquake. Seismol. Geol. 2022, 44, 506–523. (In Chinese) [Google Scholar]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved Version Released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Qu, C.; Ma, C.; Shan, X.; Zhang, G.; Chen, H.; Wu, D. Coseismic Deformation Obtained by Various Technical Methods and Its Constraint Ability to Slip Models of Maduo Earthquake. Remote Sens. 2024, 16, 615. https://doi.org/10.3390/rs16040615
Song Y, Qu C, Ma C, Shan X, Zhang G, Chen H, Wu D. Coseismic Deformation Obtained by Various Technical Methods and Its Constraint Ability to Slip Models of Maduo Earthquake. Remote Sensing. 2024; 16(4):615. https://doi.org/10.3390/rs16040615
Chicago/Turabian StyleSong, Yujing, Chunyan Qu, Chao Ma, Xinjian Shan, Guohong Zhang, Han Chen, and Donglin Wu. 2024. "Coseismic Deformation Obtained by Various Technical Methods and Its Constraint Ability to Slip Models of Maduo Earthquake" Remote Sensing 16, no. 4: 615. https://doi.org/10.3390/rs16040615
APA StyleSong, Y., Qu, C., Ma, C., Shan, X., Zhang, G., Chen, H., & Wu, D. (2024). Coseismic Deformation Obtained by Various Technical Methods and Its Constraint Ability to Slip Models of Maduo Earthquake. Remote Sensing, 16(4), 615. https://doi.org/10.3390/rs16040615





