Inversion of Sub-Bottom Profile Based on the Sediment Acoustic Empirical Relationship in the Northern South China Sea
Abstract
1. Introduction
2. Materials and Methods
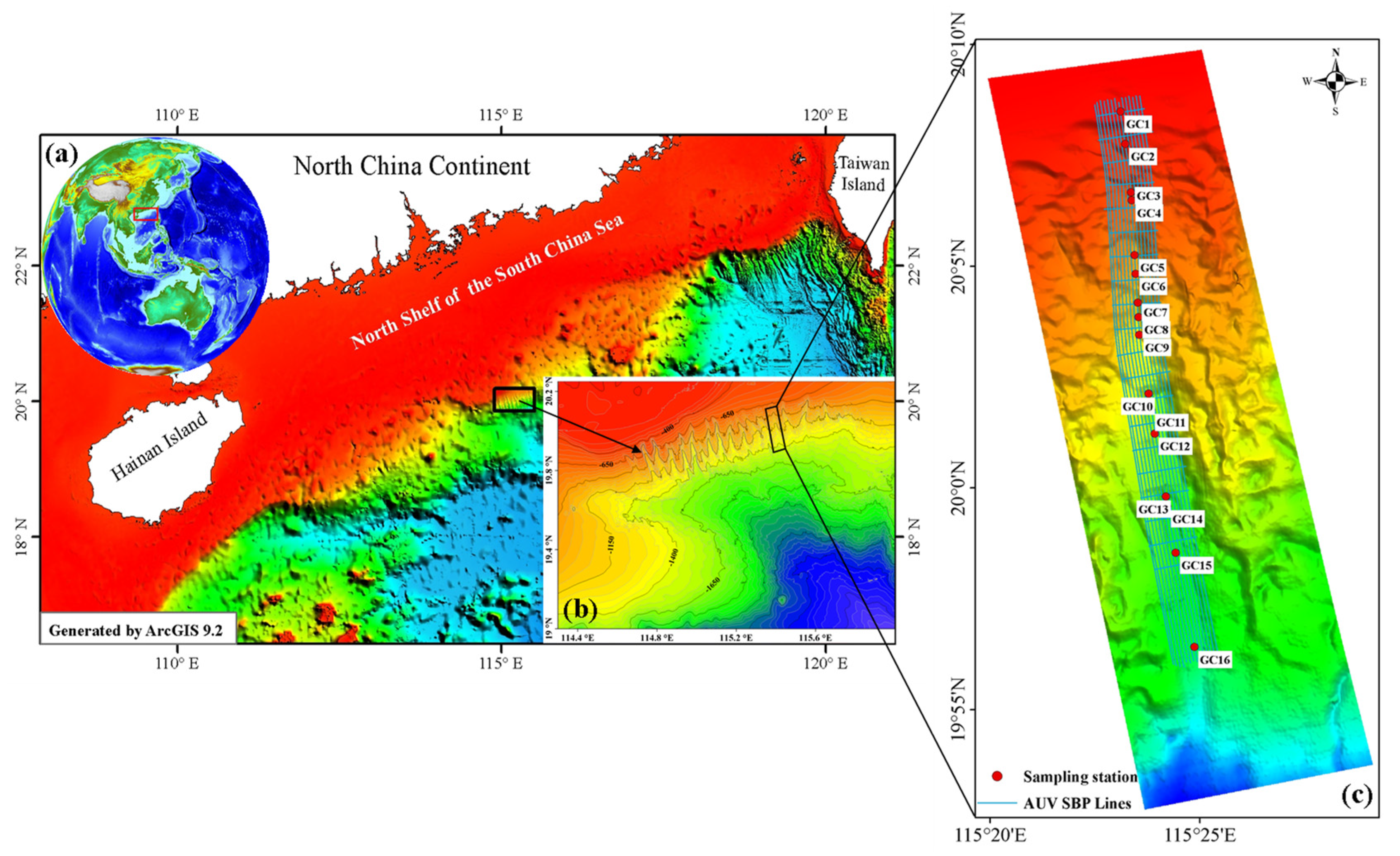
2.1. Study Area and Geological Background
2.2. Method
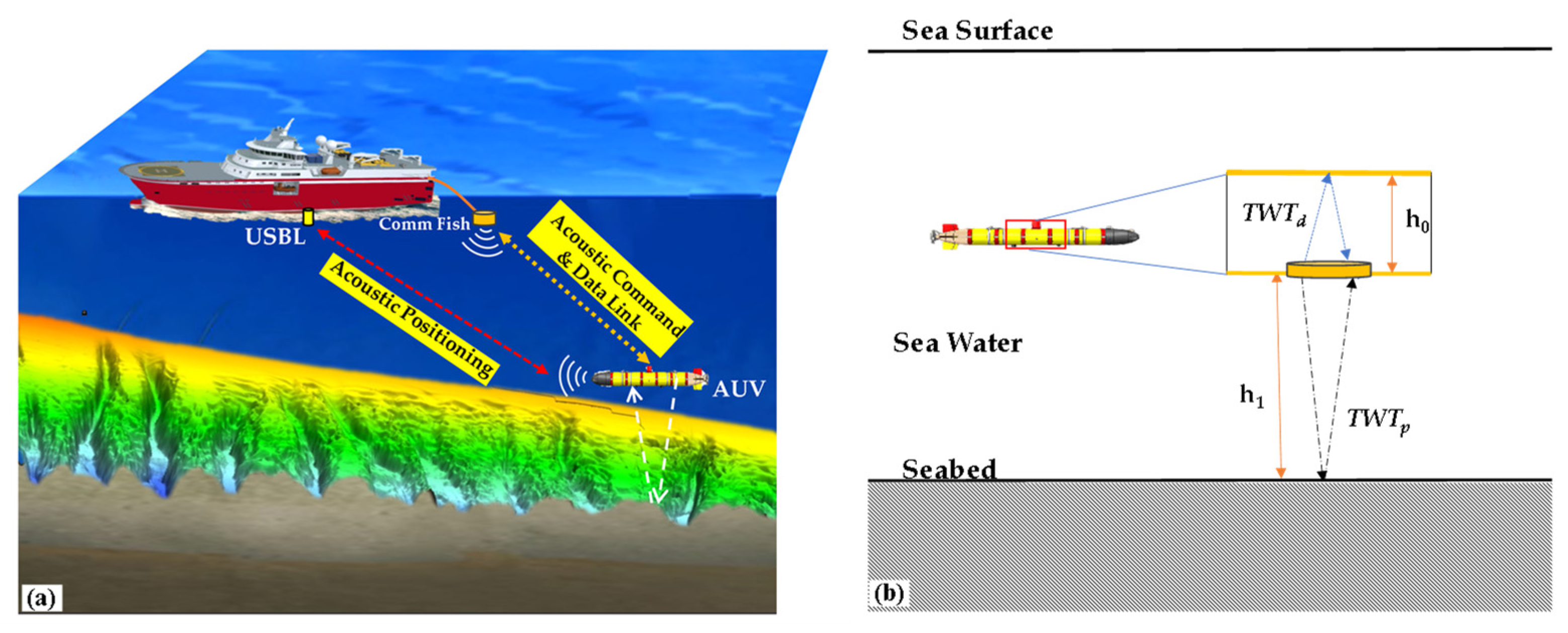
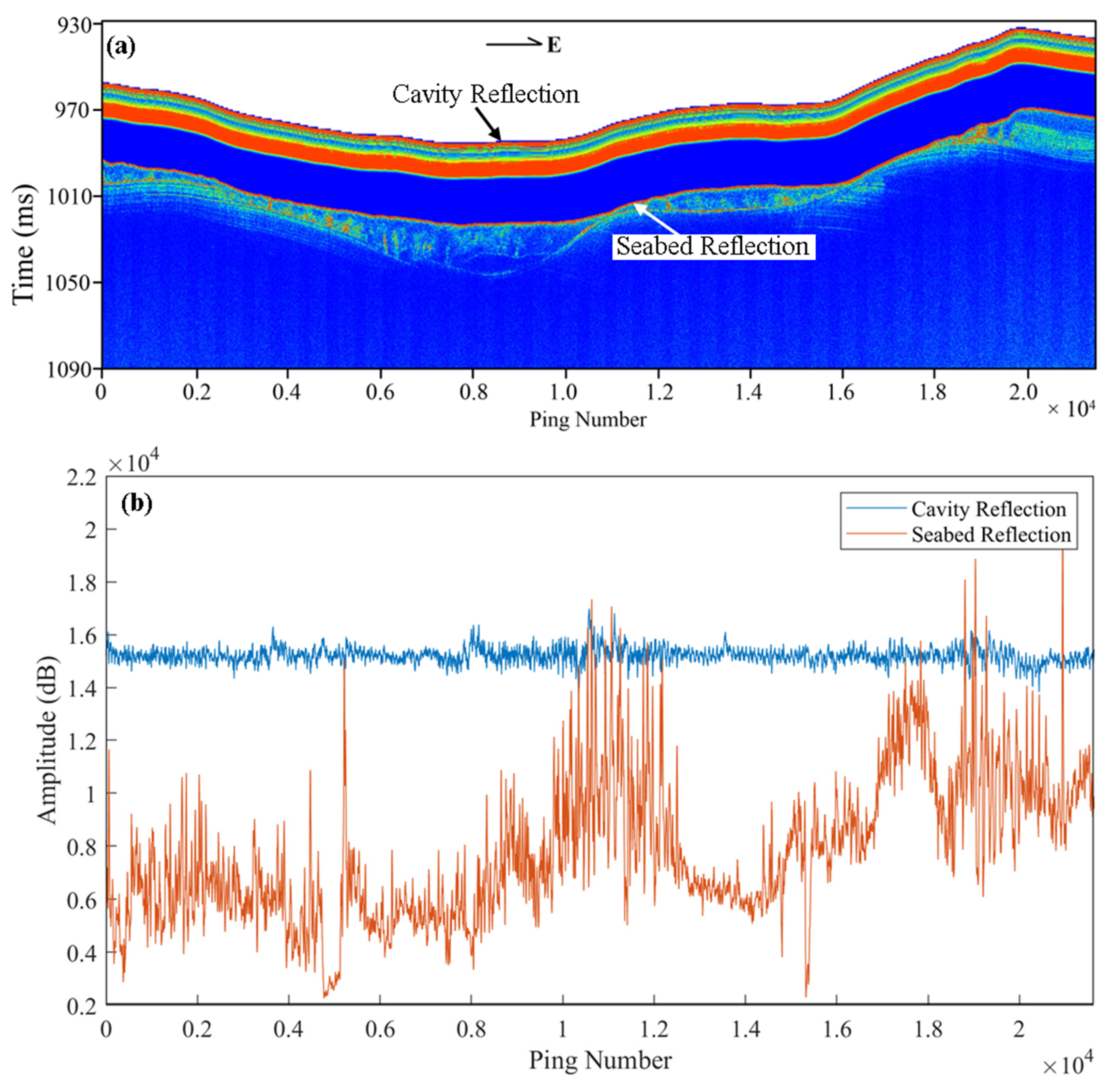
2.2.1. Calculation of Seabed Reflection Coefficient
2.2.2. Establish the Relationship between Seabed Reflection Coefficient and Physical Parameters
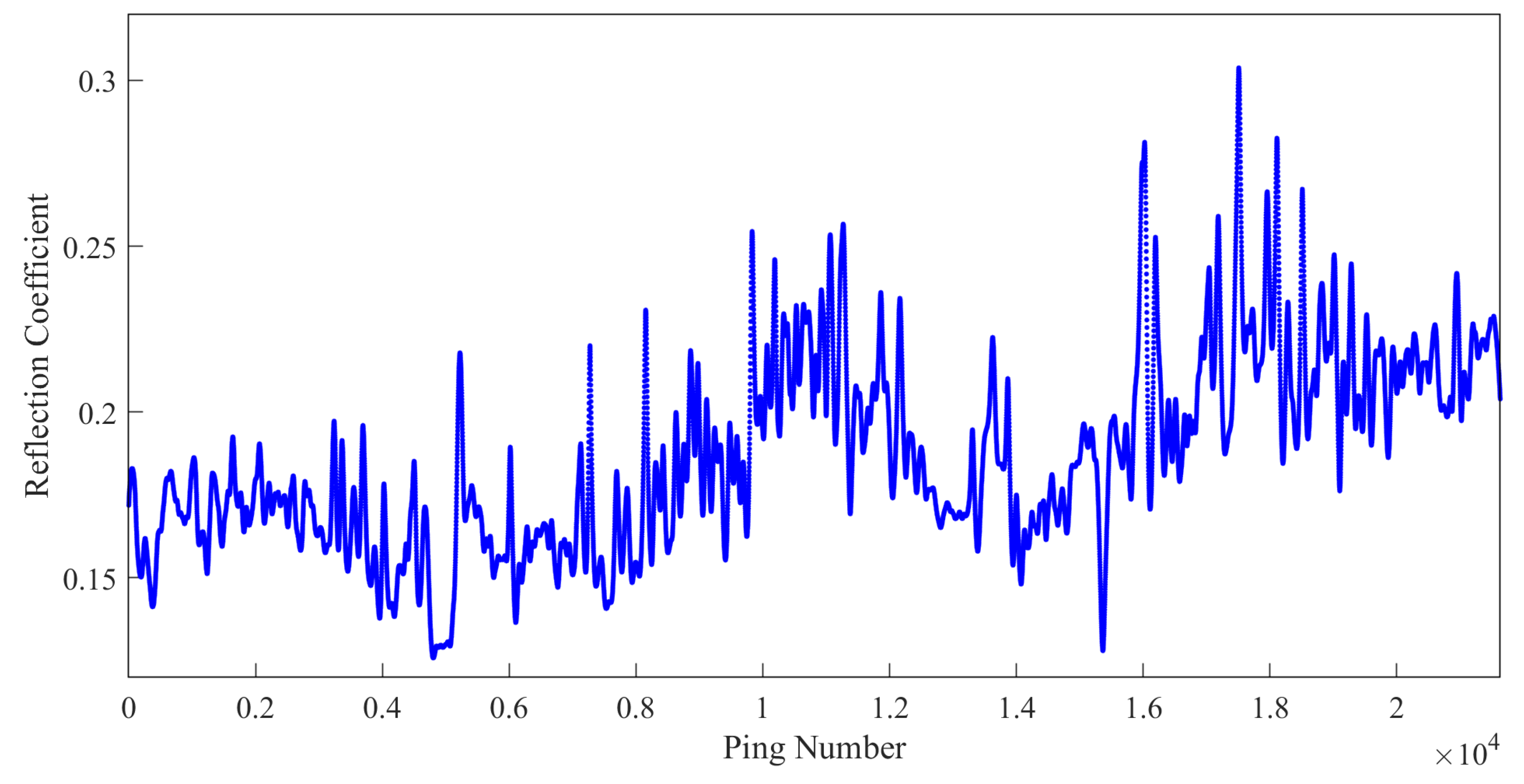
3. Results
4. Discussion
4.1. Result Discussion
- (1)
- (2)
- (3)
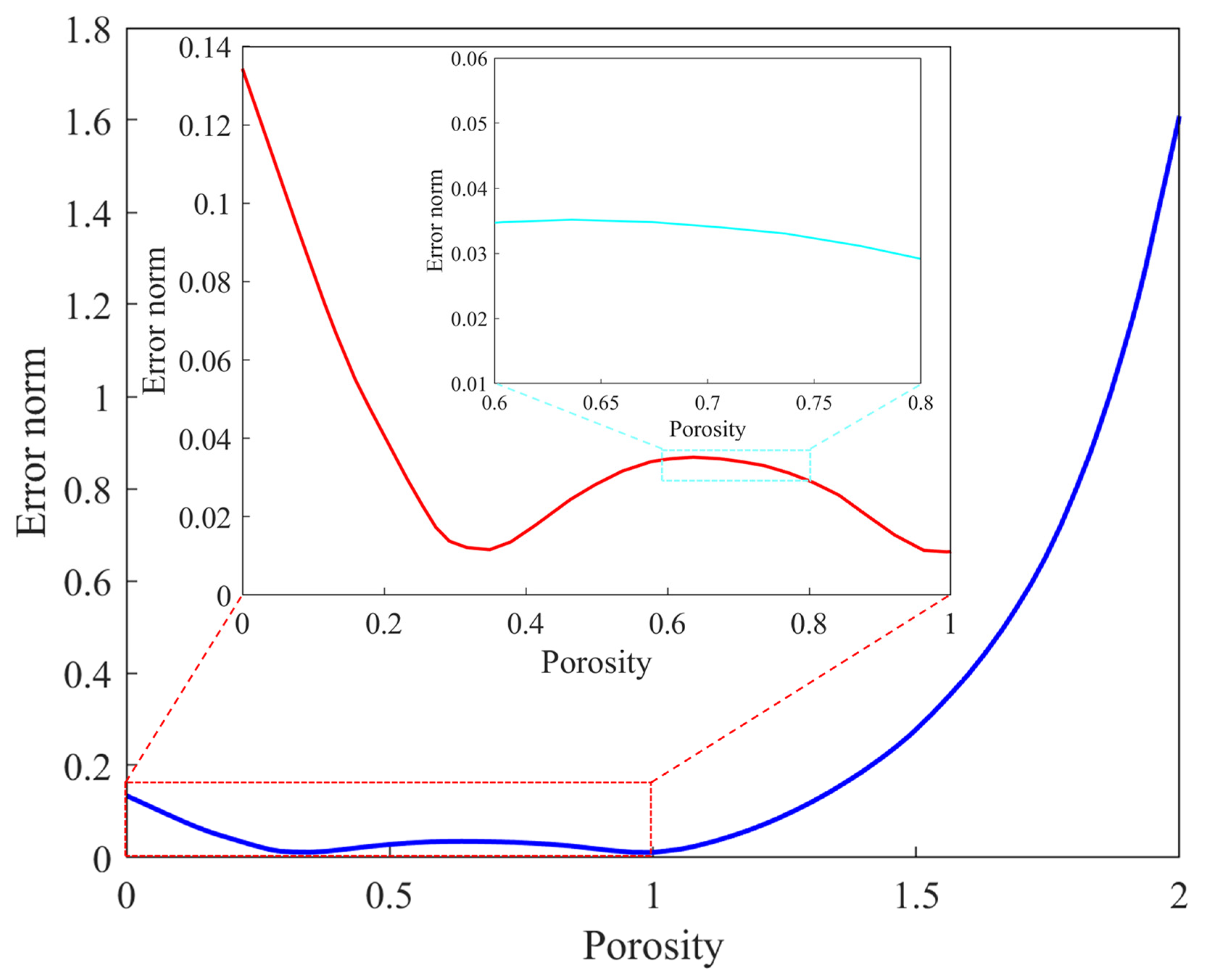
4.2. Sensitivity Analysis
5. Conclusions
- (1)
- We derived an equation that relates the seabed reflection coefficient to sediment particle porosity, sediment density, and average grain size at 4 kHz (the main frequency). The equation showed a high degree of fit with a coefficient of determination R2 greater than 0.99. This equation provides a reliable basis for inverting sediment physical properties using the seabed reflection coefficient.
- (2)
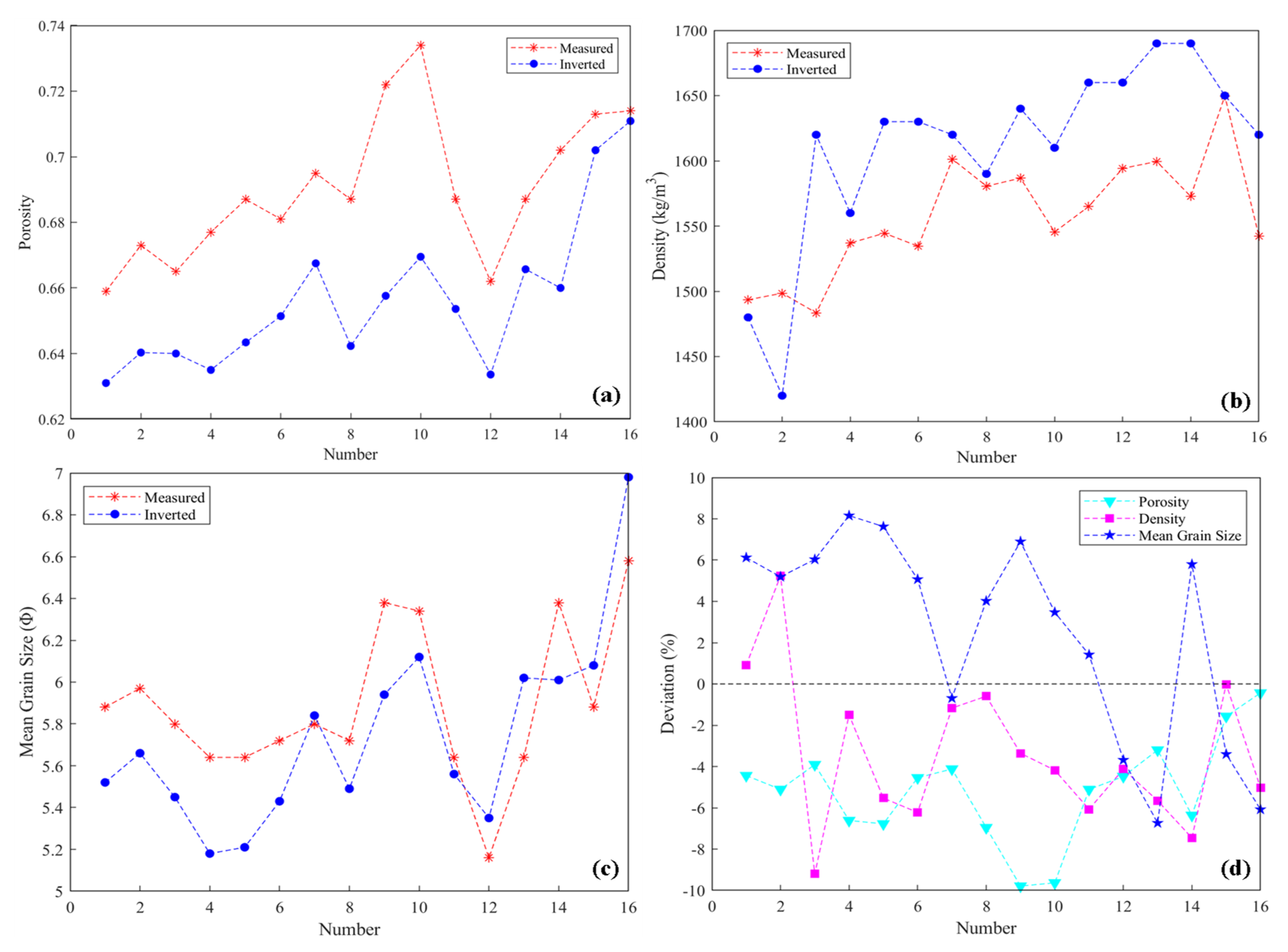
- We compared the reflection coefficient calculated by the sub-bottom profile with sampled test data and retrieved physical parameters such as particle porosity, sediment density, and average grain size of the seabed surface sediments. The comparative analysis showed that the inversion results had an error range of -8.92% to 9.2%, which is less than 10.0%. In comparison, Zhou et al. achieved an error range within 15% using the Biot–Stoll model [55]. This demonstrates the feasibility and higher accuracy of inverting sediment physical property parameters based on the relation equation of sediment acoustics in our study area compared to general acoustic theoretical models.
- (3)
- Based on the inversed values, we observed that the seabed reflection coefficient decreased with increasing water depth, corresponding to an increase in sediment particle porosity, a gradual decrease in sediment density, and an increasing trend in average grain size (decreasing sediment particle size). These changes were consistent with variations in sediment type, water depth topography, and hydrodynamic conditions in the area. This finding further confirms the accuracy of the inversion outcomes and introduces a novel approach for indirectly and swiftly obtaining the physical characteristics of seabed sediments.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bao, C. Buride ancient channels and deltas in the Zhujiang River mouth shelf area. Mar. Geol. Quat. Geol. 1995, 15, 25–36. [Google Scholar]
- Luan, X.W.; Ran, W.M.; Wang, K.; Wei, X.Y.; Shi, Y.F.; Zhang, H. New interpretation for the main sediment source of the rapidly deposited sediment drifts on the northern slope of the South China Sea. J. Asi. Ear. Sci. 2019, 171, 118–133. [Google Scholar] [CrossRef]
- Li, Z.X.; Zeng, Q.B.; Xu, M.; Wang, D.D.; Song, G.Z.; Wang, P.L.; Li, X.J.; Zheng, X. Peat formation and accumulation mechanism in northern marginal basin of South China Sea. Acta Oceanol. Sin. 2021, 40, 95–106. [Google Scholar] [CrossRef]
- Zhu, C.Q.; Jia, Y.G.; Zhang, M.S.; Wang, Z.; Shen, Z.; Zhang, B.; Shan, H. Intensity characteristics of surface sediments on continental slope of northern South China Sea. J. Eng. Geo. 2016, 24, 863–870. [Google Scholar] [CrossRef]
- Li, Z.Y.; Li, Q. Comprehensive detection device and physical testing for mechanical properties of seabed sediments and shallow gas. J. Phys. Conf. Ser. 2021, 2083, 022105. [Google Scholar] [CrossRef]
- Liu, J.; Liu, L.J.; Li, P. Physical-mechanical properties of sediments and their correlation with near seafloor seismic amplitude in the Liwan canyon area, northern South China Sea. Acta Oceanol. Sin. 2023, 42, 130–138. [Google Scholar] [CrossRef]
- Zhu, C.Q.; Zhou, L.; Zhang, H.; Cheng, S.; Jiao, X.; Jiang, J.; Shen, Z.; Jia, Y. Preliminary study of physical and mechanical properties of surface sediments in northern South China Sea. J. Eng. Geo. 2017, 25, 1566–1573. [Google Scholar] [CrossRef]
- Liu, X.L.; Sun, J.K.; Lu, Y.; Guo, X.S. Control of ambient fluid on turbidity current evolution: Mechanisms, feedbacks and influencing factors. Geosyst. Geoenviron. 2023, 2, 100214. [Google Scholar] [CrossRef]
- Dong, Y.K.; Liao, Z.X.; Liu, Q.B.; Cui, L. Potential failure patterns of a large landslide complex in the Three Gorges Reservoir area. Bull. Eng. Geol. Environ. 2023, 82, 41. [Google Scholar] [CrossRef]
- Lu, B. Study on sediments and their physical properties in the waters of Dongsha Islands. Acta Oceanol. Sin. 1996, 18, 82–89. [Google Scholar]
- Li, G.B.; Wang, J.Q.; Meng, X.M.; Liu, B.H.; Kan, G.M.; Han, G.; Hua, Q.; Pei, Y.; Sun, L. Relationships between the sound speed ratio and physical properties of surface sediments in the South Yellow Sea. Acta Oceanol. Sin. 2021, 40, 65–73. [Google Scholar] [CrossRef]
- Zhang, R.H.; Li, F.H. Normal wave theory of beam-shifted sound line for sound propagation in shallow sea. Sci. China Ser. A 1999, 29, 241–251. [Google Scholar]
- Chapman, N.R.; Chin-Bing, S.; King, D.; Evans, R.B. Benchmarking geoacoustic inversion methods for range-dependent waveguides. IEEE J. Ocean. Eng. 2003, 28, 320–330. [Google Scholar] [CrossRef]
- Peng, Z.H.; Li, Z.L. The effects of sound field by sediment in shallow water. Acoust. Tech. 2004, z1, 7–9. [Google Scholar]
- Zhou, J.X.; Zhang, X.Z.; Knobles, D.P. Low-frequency geoacoustic model for the effective properties of sandy seabottoms. J. Acoust. Soc. Am. 2009, 125, 2847–2866. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.Y.; Wang, J.Q.; Li, G.B. A Sound Velocity Prediction Model for Seafloor Sediments Based on Deep Neural Networks. Remote Sens. 2023, 15, 4483. [Google Scholar] [CrossRef]
- Hamilton, E.L. Elastic Properties of Marine Sediments. J. Geophy. Res. 1971, 76, 579–603. [Google Scholar] [CrossRef]
- Bachman, R.T. Acoustic and physical property relationships in marine sediment. J. Acoust. Soc. Am. 1985, 78, 616–621. [Google Scholar] [CrossRef]
- Jackson, D.R.; Richardson, M.D.; Isakson, M.J.; Wilson, P.S. High-Frequency Seafloor Acoustics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 2497. [Google Scholar]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Stoll, R.D. Acoustic waves in saturated sediments: In Physics of Sound in Marine Sediments; Hampton, L., Ed.; Plenum: New York, NY, USA, 1974; pp. 19–39. [Google Scholar]
- Buckingham, M.J. Theory of compressional and shear waves in fluidlike marine sediments. J. Acoust. Soc. Am. 1998, 103, 288–299. [Google Scholar] [CrossRef]
- Williams, K.L. An effective density fluid model for acoustic propagation in sediments derived from Biot theory. J. Acoust. Soc. Am. 2001, 110, 2276–2281. [Google Scholar] [CrossRef] [PubMed]
- Chotiros, N.P.; Isakson, M.J. A broadband model of sandy ocean sediments: Biot-Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am. 2004, 116, 2011–2022. [Google Scholar] [CrossRef]
- Kan, G.M.; Su, Y.F.; Li, G.B.; Liu, B.H.; Meng, X.M. The relationship between in-situ acoustic velocity and physical properties of seafloor sediments in the middle of the South Yellow Sea. Acta Oceanol. Sin. 2013, 35, 166–171. [Google Scholar]
- Zou, D.P.; Wu, Z.L.; Sun, H.; Liu, W.; Ji, X.R.; Xiao, T.B. Basic geoacoustic structure and geoacoustic model for seafloor sediments. Haiyang Xuebao 2022, 44, 145–155. [Google Scholar] [CrossRef]
- Wang, J.Q.; Hou, Z.Y.; Li, G.B.; Kan, G.M.; Liu, B.H.; Meng, X.; Hua, Q.; Sun, L. High-Frequency Dependence of Acoustic Properties of Three Typical Sediments in the South China Sea. J. Mar. Sci. Eng. 2022, 10, 1295. [Google Scholar] [CrossRef]
- Ding, W.W.; Li, M.B.; He, M.; Tang, Y.; Fang, Y.X. Cenozoic tectonic sedimentary evolution in the continental shelf-slope area of the north-central south China sea. Geol. J. China Univ. 2009, 15, 339–350. [Google Scholar]
- Zhu, L.; Fu, M.Z.; Liu, L.J.; Li, J.; Gao, S. Canyon morphology and sediments on northern slope of the Baiyun Sag. Mar. Geol. Quat. Geol. 2014, 34, 1–9. [Google Scholar] [CrossRef]
- Li, X.S.; Zhou, Q.J.; Su, T.Y.; Liu, L.J.; Gao, S.; Zhou, S.W. Slope-confined submarine canyons in the Baiyun deep-water area, northern South China Sea: Variation in their modern morphology. Mar. Geophy. Res. 2016, 37, 95–112. [Google Scholar] [CrossRef]
- Liu, L.J.; Fu, M.Z.; Li, J.G.; Li, X.S.; Chen, Y.L.; Gao, S. Geologic Hazards in the Deep Pipeline Routing Area of the Liwan 3-1 Gas Field in the South China Sea. Advan. Mar. Sci. 2014, 3202, 162–174. [Google Scholar]
- Zhang, Y.F.; Sun, Z.; Zhang, J.Y.; Wang, L.J. The structure, depositional style and accumulation characteristics of continental margin with diachronous breakup in the northern South China Sea. Int. Geol. Rev. 2019, 62, 1006–1018. [Google Scholar] [CrossRef]
- Li, A.X.; Li, Y.H.; Le, G.L. Origin of tellurium anomalies in deep-sea sediments. Acta Geosci. Sin. 2005, 26, 186–189. [Google Scholar]
- Liu, J.G.; Xiang, R.; Chen, Z.; Chen, M.H.; Yan, W.; Zhang, L.; Chen, H. Sources, transport and deposition of surface sediments from the South China Sea. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2013, 71, 92–102. [Google Scholar] [CrossRef]
- Shi, X.; Liu, S.; Qiao, S.; Liu, Y.; Wang, K. Sediment Type Map of the South China Sea; Science Press: Beijing, China, 2022. [Google Scholar]
- Lu, B.; Li, C.X.; Huang, S.J.; Zhang, F. Comparison of acoustic physical properties of shallow seafloor sediments in Yellow Sea, East China Sea and northern South China Sea. Mar. Tech. 2005, 28–33. [Google Scholar]
- Zou, D.P.; Wu, B.H.; Lu, B.; Zhang, W.F.; Chen, F.Y. Cluster analysis of acoustic physico-mechanical properties of seafloor sediments. J. Tro. Ocean. 2008, 5, 12–17. [Google Scholar]
- Petillot, Y.R.; Reed, S.R.; Bell, J.M. Real Time AUV Pipeline Detection and Tracking Using Side Scan Sonar and Multi-Beam Echosounder. In Proceedings of the Oceans-Conference, Biloxi, MI, USA, 29–31 October 2002; Volume 1, pp. 217–223. [Google Scholar]
- Holland, C.W.; Nielsen, P.L.; Dettmer, J.; Dosso, S. Resolving meso-scale seabed variability using reflection measurements from an autonomous underwater vehicle. J. Acoust. Soc. Am. 2012, 131, 1066–1078. [Google Scholar] [CrossRef]
- Chotiros, N.P.; Pallayil, V. Seabed characterization using acoustic communication signals on an autonomous underwater vehicle with a thin-line towed array. IEEE J. Ocean. Eng. 2013, 38, 410–418. [Google Scholar] [CrossRef]
- Ding, W.; Li, J.; Li, J.; Fang, Y.; Tang, Y. Morphotectonics and evolutionary controls on the Pearl River Canyon system, South China Sea. Mar. Geophys. Res. 2013, 34, 221–238. [Google Scholar] [CrossRef]
- Zhu, M.; Graham, S.; Pang, X.; McHargue, T. Characteristics of migrating sub-marine canyons from the middle Miocene to present: Implications for paleoceanographic circulation, northern South China Sea. Mar. Pet. Geol. 2010, 27, 307–319. [Google Scholar] [CrossRef]
- Pang, X.; Chen, C.M.; Shao, L.; Wang, C.; Zhu, M.; He, M. Baiyun movement, a great tectonic event on the oligocene-miocene boundary in the northern South China Sea and its implications. Geol. Rev. 2007, 53, 145–151. [Google Scholar]
- Su, M.; Lin, Z.X.; Wang, C.; Kuang, Z.; Liang, J.; Chen, H.; Liu, S.; Zhang, B.; Luo, K.; Huang, S.; et al. Geomorphologic and infilling characteristics of the slope-confined submarine canyons in the Pearl River Mouth Basin, northern South China Sea. Mar. Geol. 2020, 424, 106–166. [Google Scholar] [CrossRef]
- Wu, S.G.; Qin, Y.S. Study on deep water depositional system of northern continental slope of South China Sea. Acta Sedimentol. 2009, 27, 922–930. [Google Scholar]
- Borella, D.R.; de Souza, A.P.; de Almeida, F.T.; de Abreu, D.C.; Hoshide, A.K.; Carvalho, G.A.; Pereira, R.R.; da Silva, A.F. Dynamics of Sediment Transport in the Teles Pires River Basin in the Cerrado-Amazon, Brazil. Sustainability 2022, 14, 16050. [Google Scholar] [CrossRef]
- Chao, S.Y.; Shaw, P.T.; Wu, S.Y. Deep water ventilation in the South China Sea. Deep-Sea Res Part I. Oceanogr. Res. Pap. 1996, 43, 445–466. [Google Scholar] [CrossRef]
- Tang, D.L.; Sun, Z.; Sui, G.J. Geological environment in the South China Sea. J. Oceanol. Limnol. 2023, 41, 403–408. [Google Scholar] [CrossRef]
- Wang, X.; Kneller, B.; Sun, Q. Sediment waves control origins of submarine canyons. Geology 2023, 51, 310–314. [Google Scholar] [CrossRef]
- Bull, J.M.; Quinn, R.; Dix, J.K. Reflection Coefficient Calculation from Marine High Resolution Seismic Reflection (Chirp) Data and Application to an Archaeological Case Study. Mar. Geophys. Res. 1998, 20, 1–11. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, L.; Zhang, R.W. Method of identifying MTD and BSR through AVO theory. Prog. Geophys. 2018, 33, 1289–1296. [Google Scholar] [CrossRef]
- Zheng, J.L.; Xu, J.; Tong, S.Y.; Huang, Y.; Zhou, H. Estimation of seafloor reflectivity in shallow water based on seismic data of sparker sources. Mar. Geophys. Res. 2021, 42, 33. [Google Scholar] [CrossRef]
- Zhou, Q.J.; Li, X.S.; Huang, B.G.; Liu, L.J.; Liu, B.; Zhang, C. Inversion of the physical properties of seafloor surface sediments based on AUV sub-bottom profile data in the northern slope of the South China Sea. Sci. Rep. 2021, 11, 6539. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.Y. Acoustic Characteristics and Correlation Analysis of Physical Parameters of Seabed Sediments in the Southern South China Sea. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2016. [Google Scholar]


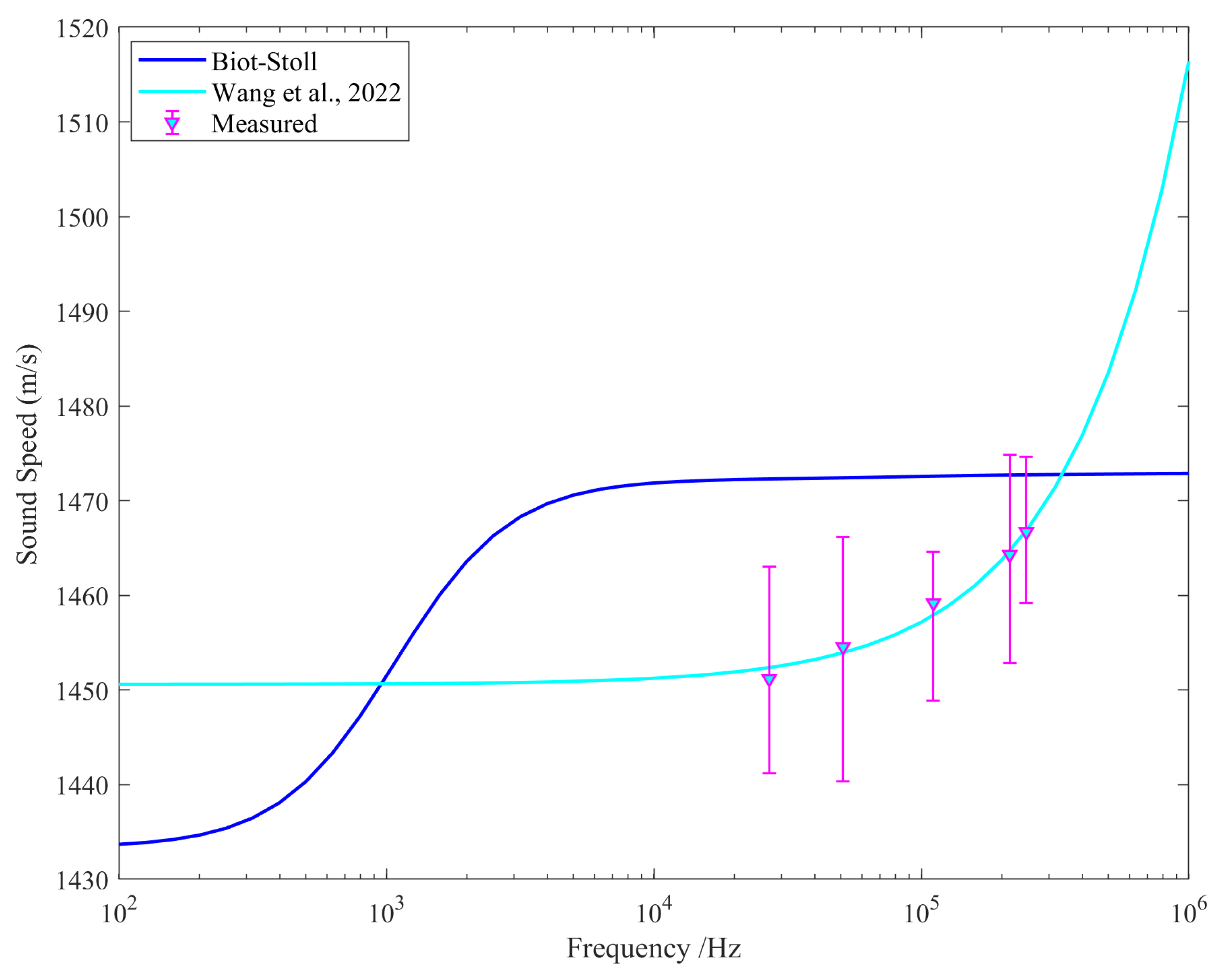

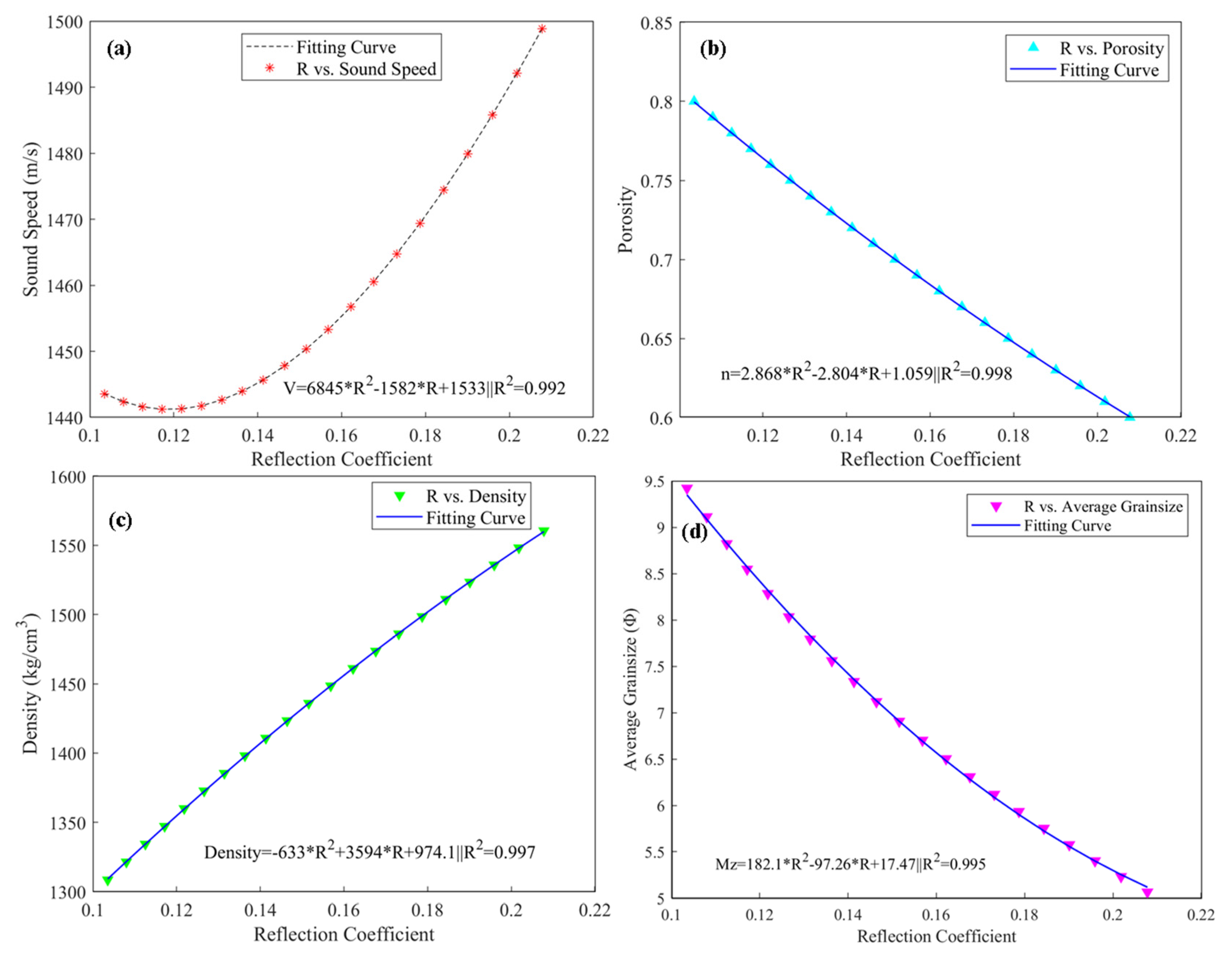
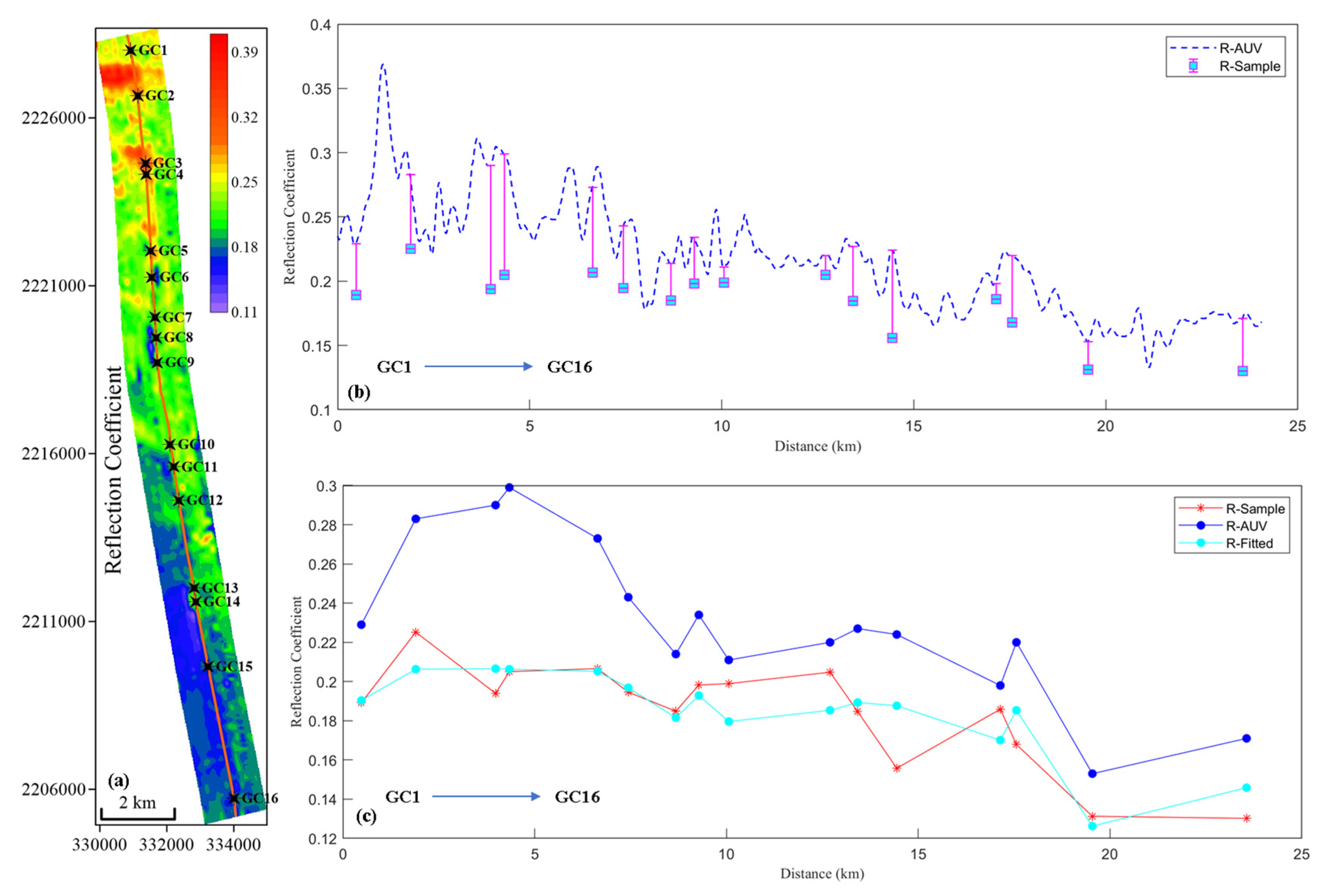
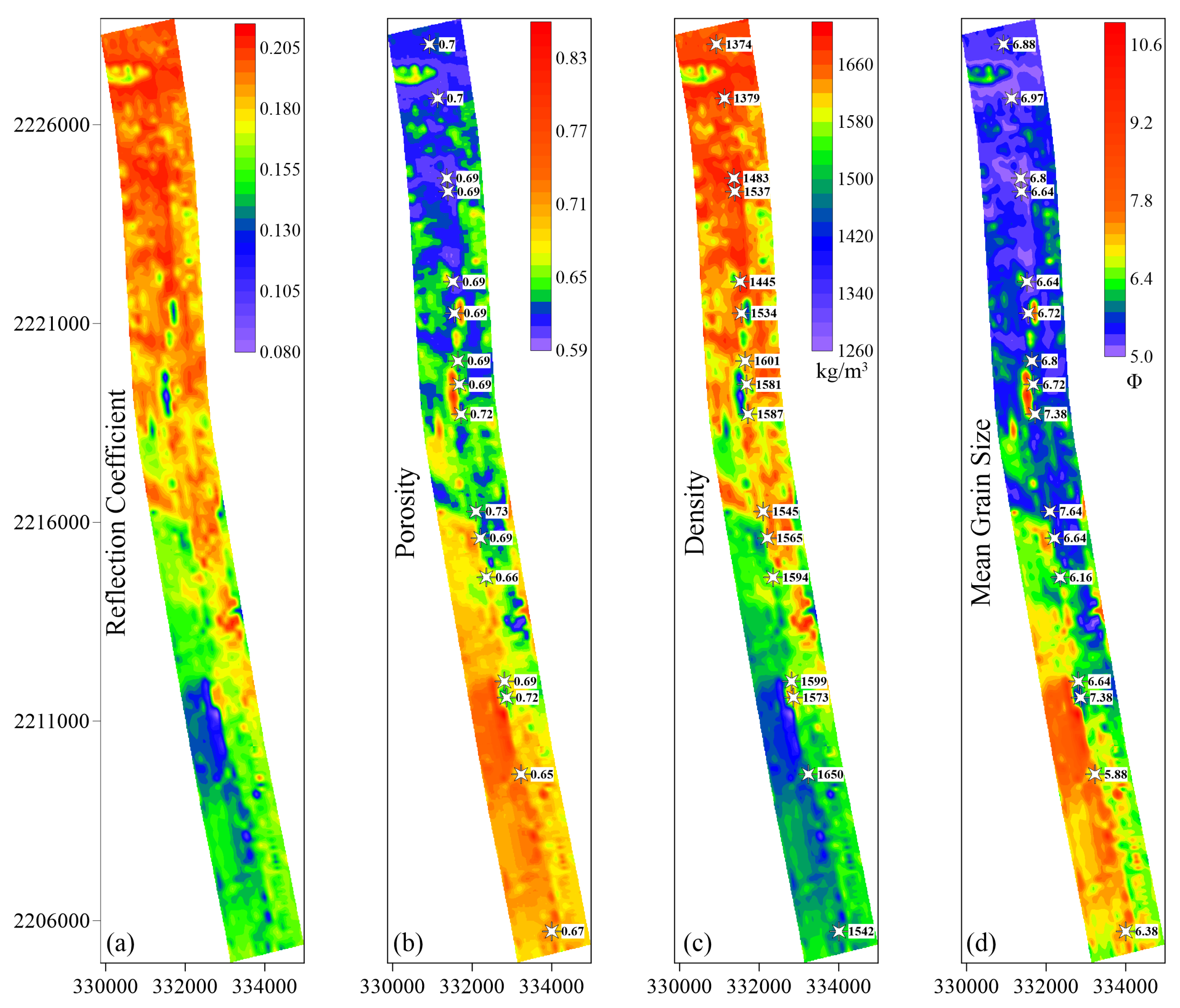
| Sediment Type | Range | Sound Speed (m/s) | ||||
|---|---|---|---|---|---|---|
| 27 kHz | 51 kHz | 111 kHz | 214 kHz | 247 kHz | ||
| Silty sand | Maximum | 1641.13 | 1637.64 | 1643.92 | 1657.43 | 1671.05 |
| Minimum | 1576.70 | 1586.23 | 1591.61 | 1586.86 | 1598.36 | |
| Mean | 1609.17 | 1616.43 | 1622.47 | 1627.38 | 1634.16 | |
| Silt | Maximum | 1568.66 | 1568.77 | 1574.62 | 1580.10 | 1583.05 |
| Minimum | 1529.86 | 1527.96 | 1537.80 | 1539.12 | 1547.14 | |
| Mean | 1546.16 | 1550.56 | 1555.20 | 1560.32 | 1565.04 | |
| Silty clay | Maximum | 1461.18 | 1468.78 | 1469.51 | 1475.72 | 1474.19 |
| Minimum | 1439.92 | 1442.96 | 1453.8 | 1453.74 | 1458.77 | |
| Mean | 1451.19 | 1454.56 | 1459.20 | 1464.30 | 1466.70 | |
| Porosity (n) | Relationship (V vs. f) |
|---|---|
| 0.48 | V = 0.0956 f + 1609.5 |
| 0.50 | V = 0.0846 f + 1586.5 |
| 0.52 | V = 0.0832 f + 1568.7 |
| 0.55 | V = 0.0759 f + 1545.6 |
| 0.57 | V = 0.0719 f + 1519.4 |
| 0.60 | V = 0.0699 f + 1493.3 |
| 0.63 | V = 0.0682 f + 1479.7 |
| 0.65 | V = 0.0675 f + 1468.5 |
| 0.67 | V = 0.0663 f + 1459.4 |
| 0.69 | V = 0.0658 f + 1450.6 |
| 0.73 | V = 0.0658 f + 1445.7 |
| 0.75 | V = 0.0642 f + 1442.1 |
| 0.78 | V = 0.0637 f + 1439.8 |
| 0.80 | V = 0.0625 f + 1439.6 |
| Station Number | Porosity | Density (kg/m3) | Average Gran Size (Φ) | Sediments’ Sound Speed (m/s) | |
|---|---|---|---|---|---|
| GC1 | 0.70 | 1374 | 6.88 | 1450.64 | 0.189 |
| GC2 | 0.70 | 1379 | 6.97 | 1449.55 | 0.225 |
| GC3 | 0.69 | 1483 | 6.80 | 1451.79 | 0.194 |
| GC4 | 0.69 | 1537 | 6.64 | 1454.31 | 0.205 |
| GC5 | 0.69 | 1445 | 6.64 | 1454.31 | 0.207 |
| GC6 | 0.69 | 1534 | 6.72 | 1453.02 | 0.195 |
| GC7 | 0.69 | 1601 | 6.80 | 1451.79 | 0.185 |
| GC8 | 0.69 | 1581 | 6.72 | 1453.02 | 0.198 |
| GC9 | 0.72 | 1587 | 7.38 | 1445.29 | 0.199 |
| GC10 | 0.73 | 1545 | 7.64 | 1443.37 | 0.205 |
| GC11 | 0.69 | 1565 | 6.64 | 1454.31 | 0.185 |
| GC12 | 0.66 | 1594 | 6.16 | 1463.87 | 0.156 |
| GC13 | 0.69 | 1599 | 6.64 | 1454.31 | 0.186 |
| GC14 | 0.72 | 1573 | 7.38 | 1445.29 | 0.168 |
| GC15 | 0.65 | 1650 | 5.88 | 1470.86 | 0.131 |
| GC16 | 0.67 | 1542 | 6.38 | 1458.96 | 0.130 |
| Empirical Relationship | R-Square |
|---|---|
| R vs. Sound Speed: | 0.992 |
| R vs. Porosity: | 0.998 |
| R vs. Density: | 0.997 |
| R vs. Average Grainsize: | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Li, X.; Zheng, J.; Li, X.; Kan, G.; Liu, B. Inversion of Sub-Bottom Profile Based on the Sediment Acoustic Empirical Relationship in the Northern South China Sea. Remote Sens. 2024, 16, 631. https://doi.org/10.3390/rs16040631
Zhou Q, Li X, Zheng J, Li X, Kan G, Liu B. Inversion of Sub-Bottom Profile Based on the Sediment Acoustic Empirical Relationship in the Northern South China Sea. Remote Sensing. 2024; 16(4):631. https://doi.org/10.3390/rs16040631
Chicago/Turabian StyleZhou, Qingjie, Xianfeng Li, Jianglong Zheng, Xishuang Li, Guangming Kan, and Baohua Liu. 2024. "Inversion of Sub-Bottom Profile Based on the Sediment Acoustic Empirical Relationship in the Northern South China Sea" Remote Sensing 16, no. 4: 631. https://doi.org/10.3390/rs16040631
APA StyleZhou, Q., Li, X., Zheng, J., Li, X., Kan, G., & Liu, B. (2024). Inversion of Sub-Bottom Profile Based on the Sediment Acoustic Empirical Relationship in the Northern South China Sea. Remote Sensing, 16(4), 631. https://doi.org/10.3390/rs16040631






