Scattering Field Intensity and Orbital Angular Momentum Spectral Distribution of Vortex Electromagnetic Beams Scattered by Electrically Large Targets Comprising Different Materials
Abstract
:1. Introduction
- A calculation method for analyzing the scattering of a polarized transmitting and receiving vortex beam by electrically large targets of varying materials is presented, utilizing the angular spectrum expansion technique. The impact of diverse polarization transmission and reception methods, as well as sampling directions, on the scattering field intensity and OAM spectrum, is thoroughly examined. It is suggested that target scattering data can be multi-dimensionally sampled to supplement the information required for target recognition. Based on this, the scattering field intensity and OAM spectra of different material targets under different incidence conditions are calculated and analyzed.
- The correlation between the beam parameters, target parameters, the scattering field intensity, and the OAM spectra of the scattering field was constructed, confirming that the spiral spectrum of the scattering field carries the target information. It is proposed that the beam and target parameters can be inferred and inverted based on the differences in the scattering field intensity and OAM spectrum. A complete classification and recognition database based on the different scattering results can be established to lay the foundation for identifying different target geometries and dielectric properties.
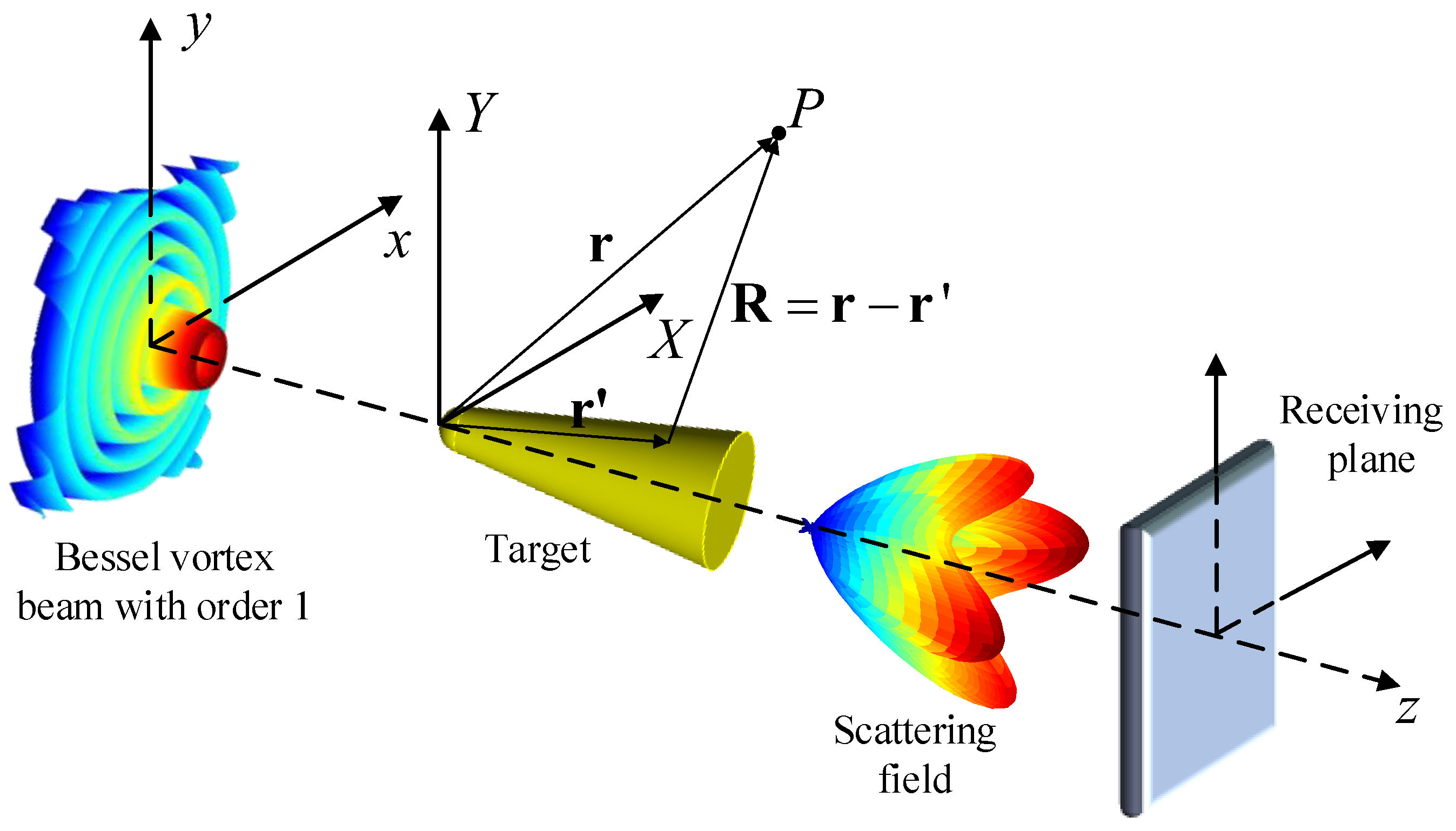
2. Theoretical Background
2.1. Angular Spectral Decomposition Method for Bessel Vortex Beam
2.2. Physical Optics Algorithm of an Electrically-Large Target Illuminated by Vortex Beam
2.3. Spiral Spectral Expansion Method
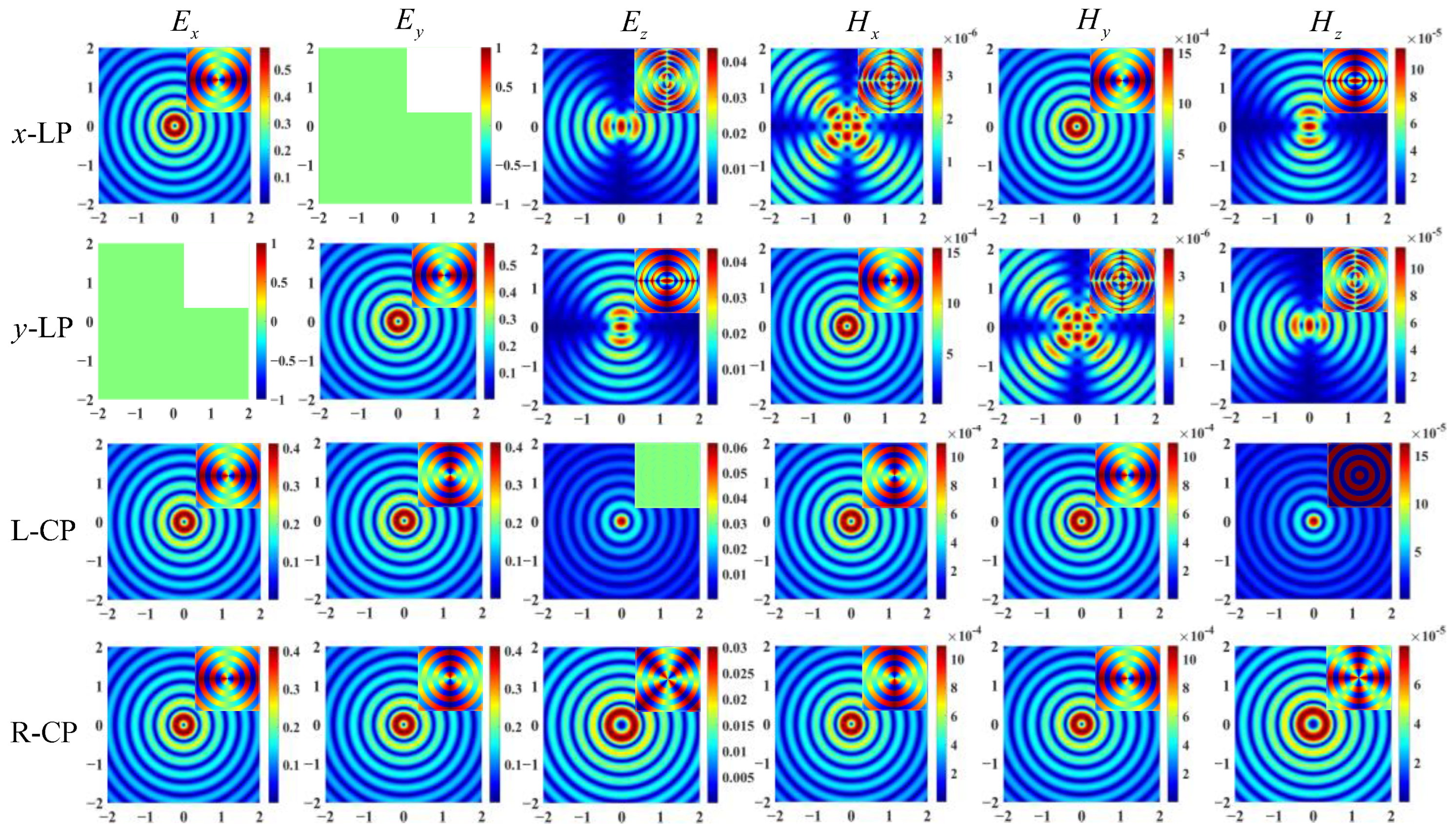
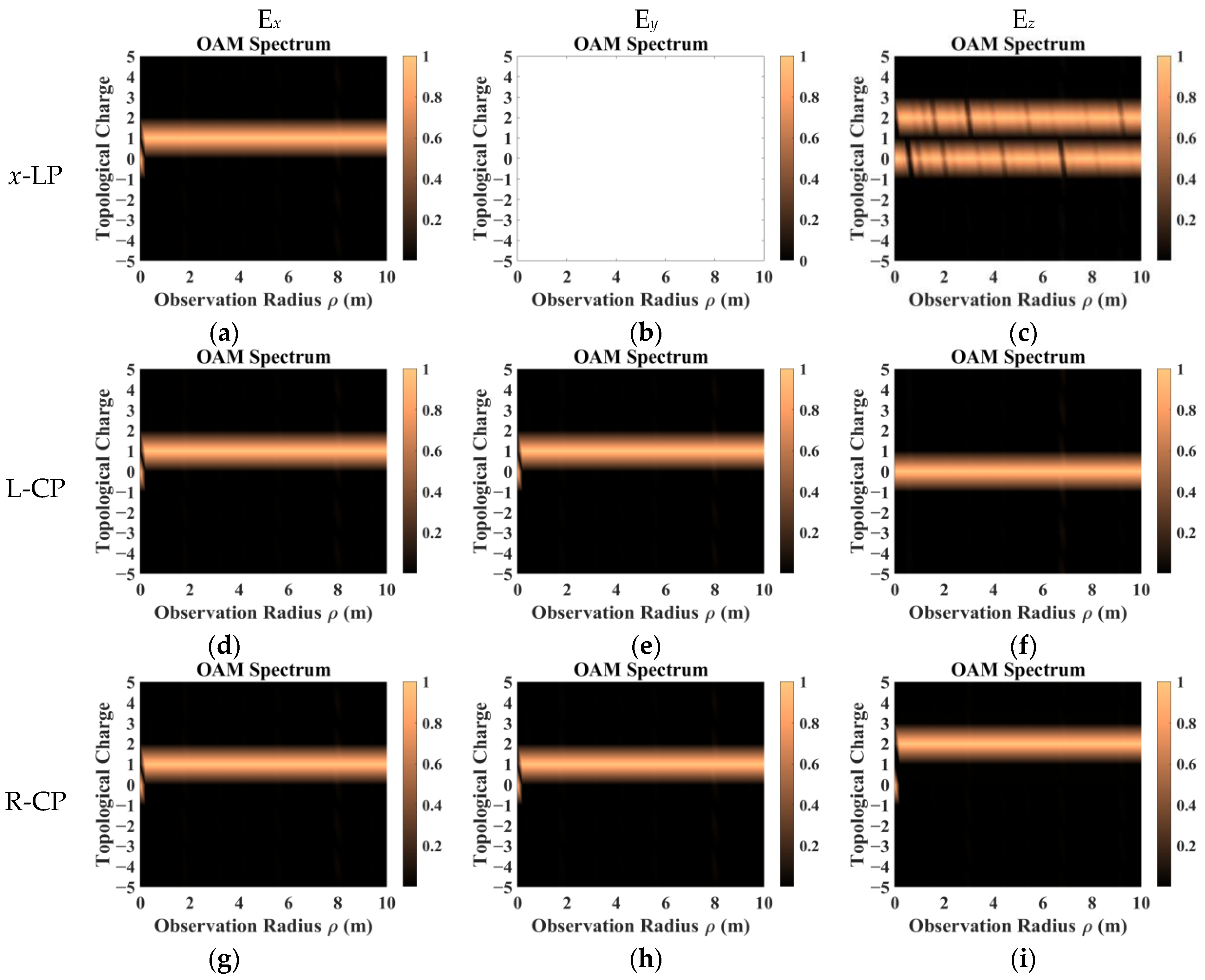
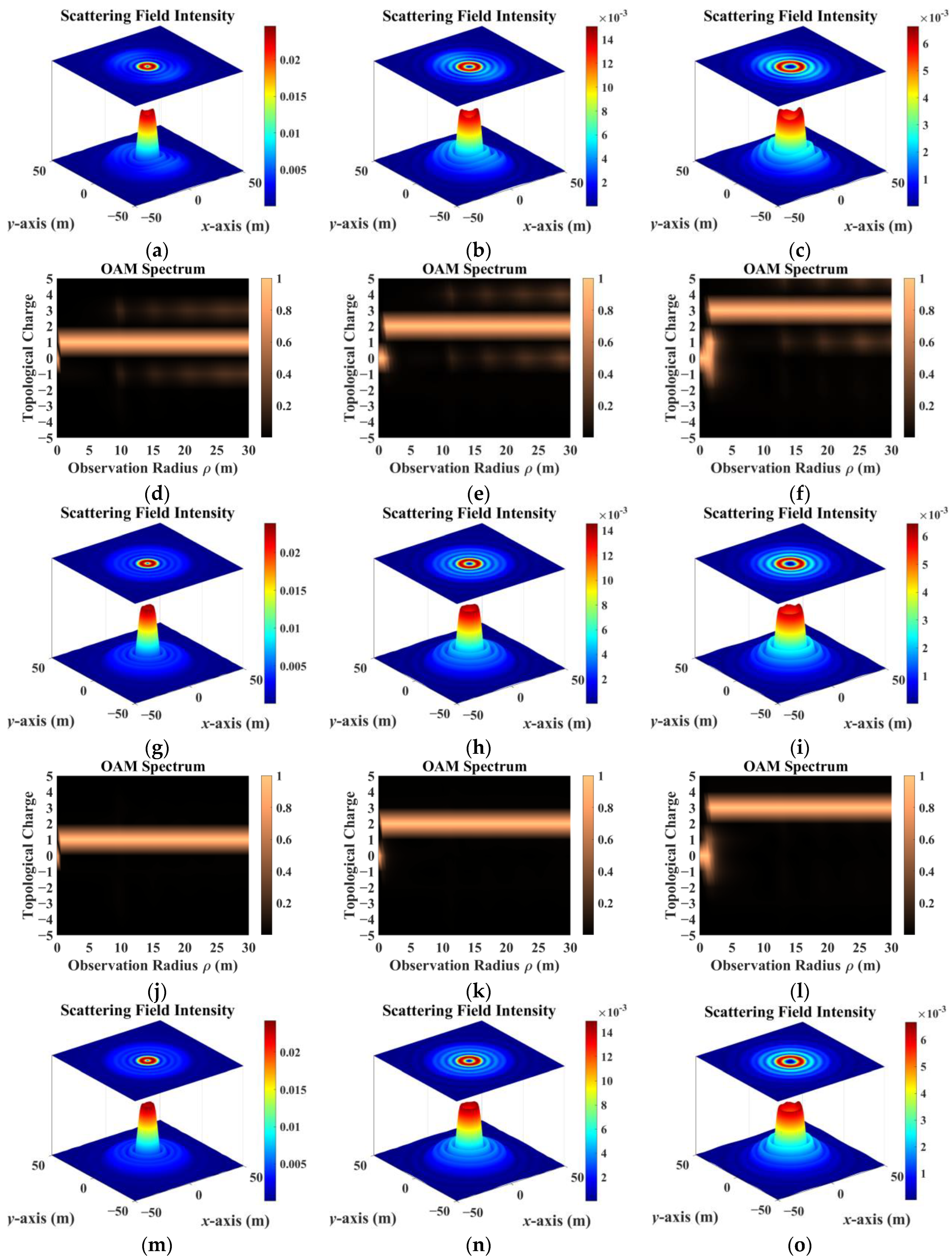
3. Simulation and Discussion
4. Conclusions
- (1)
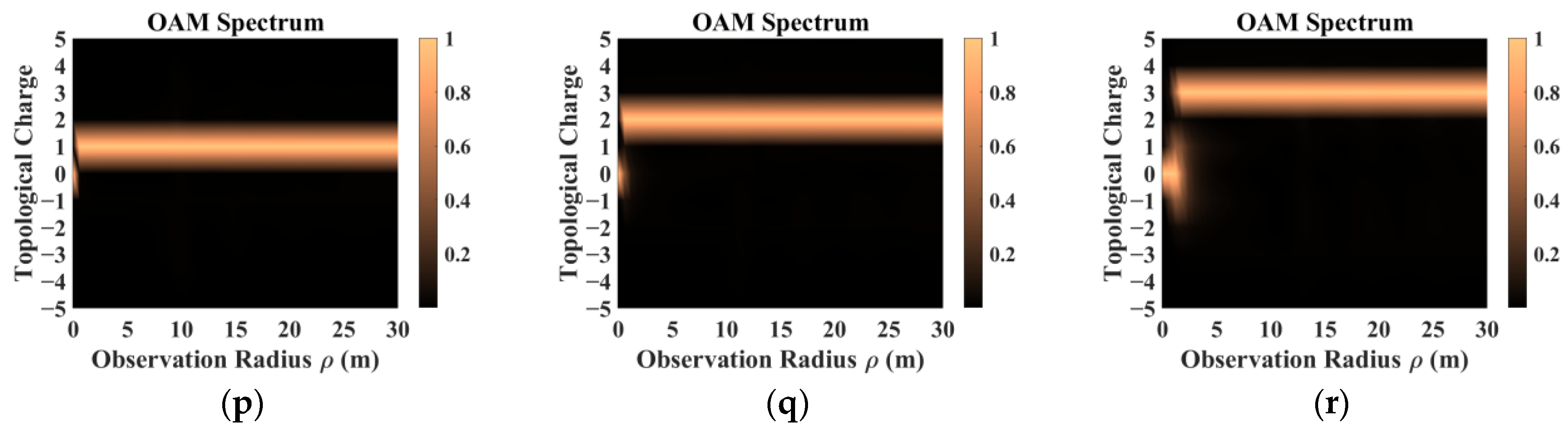
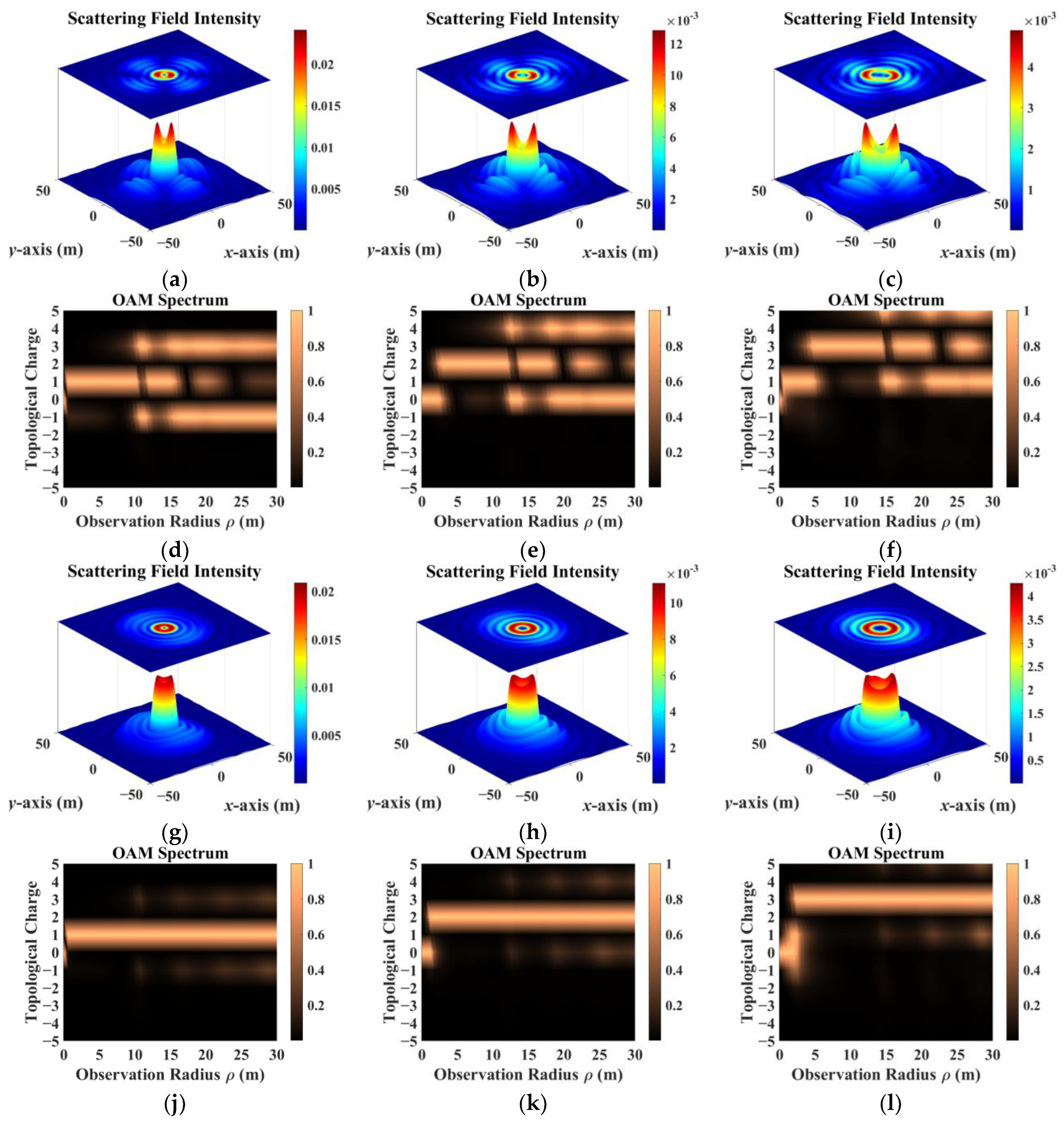
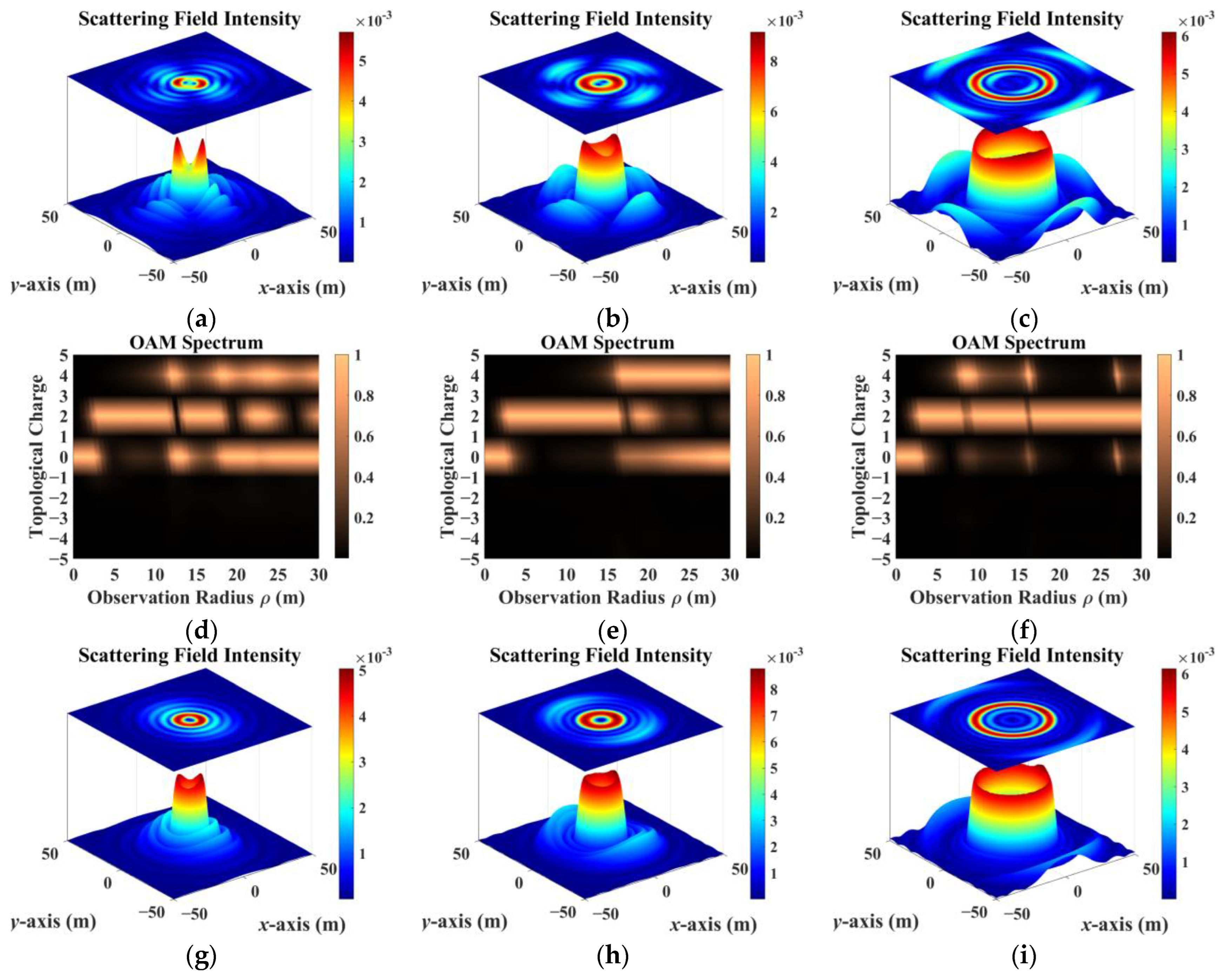
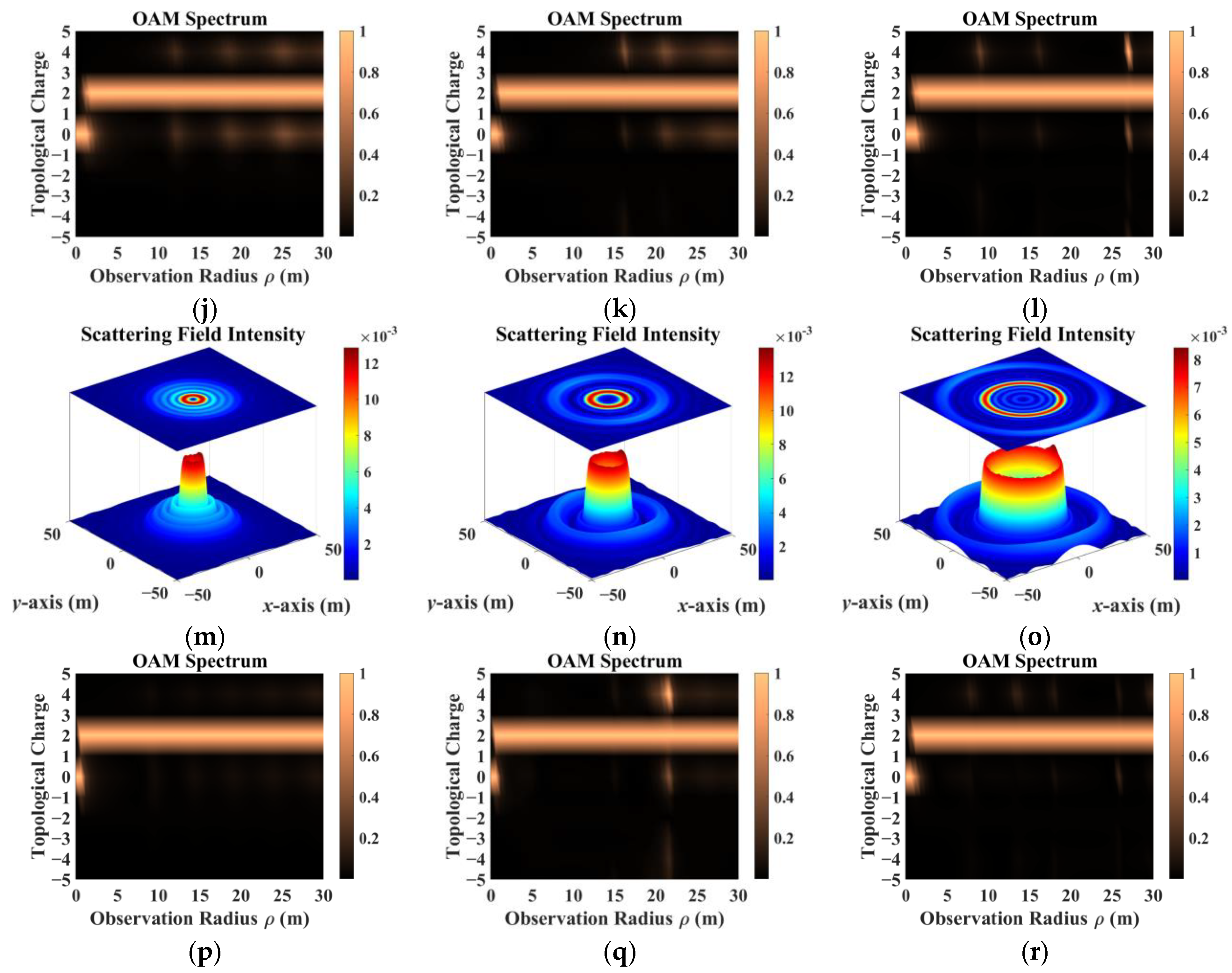
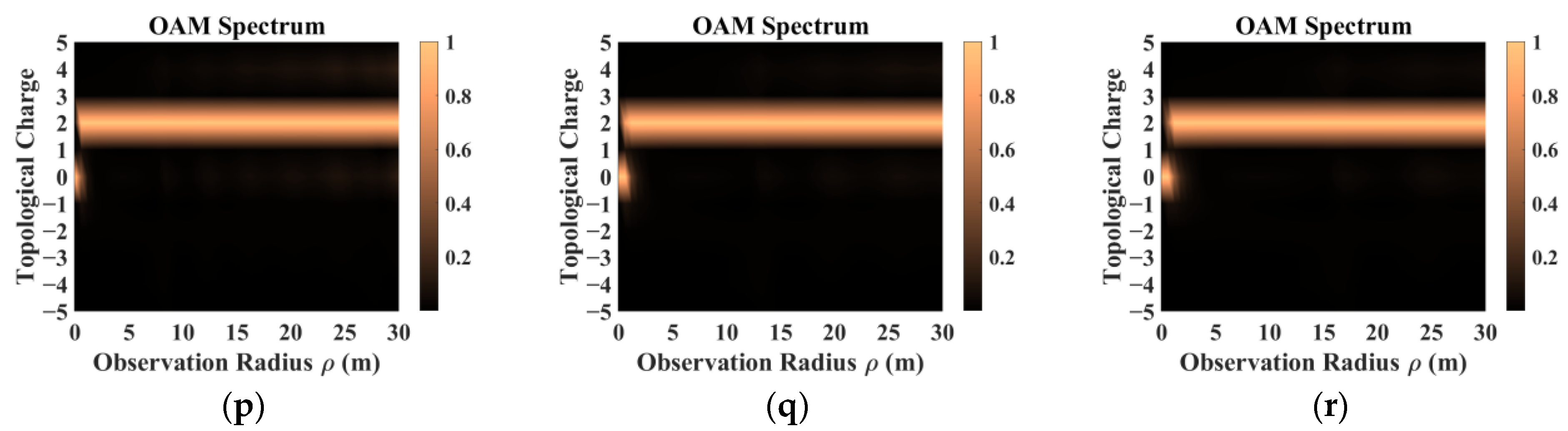
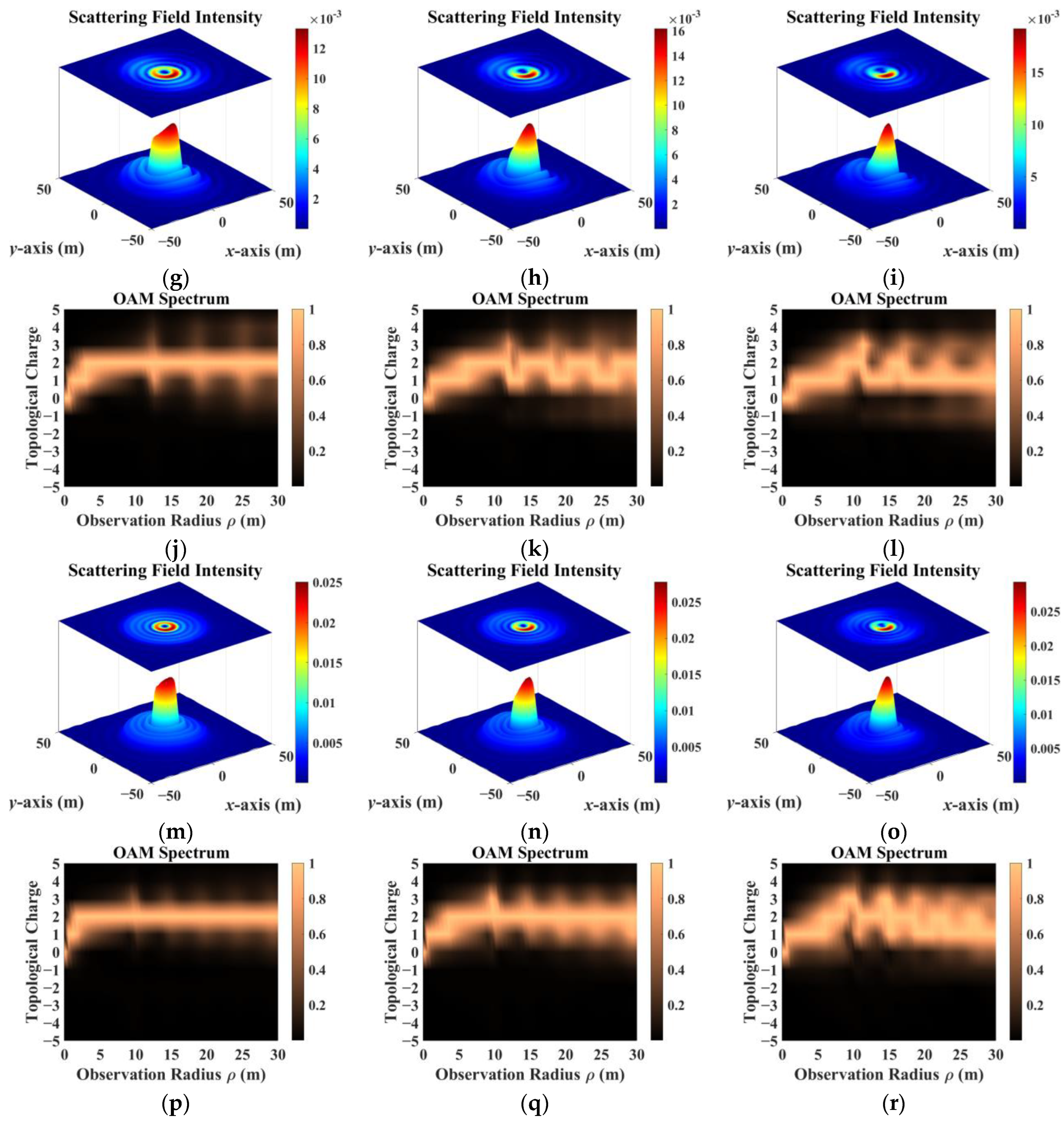
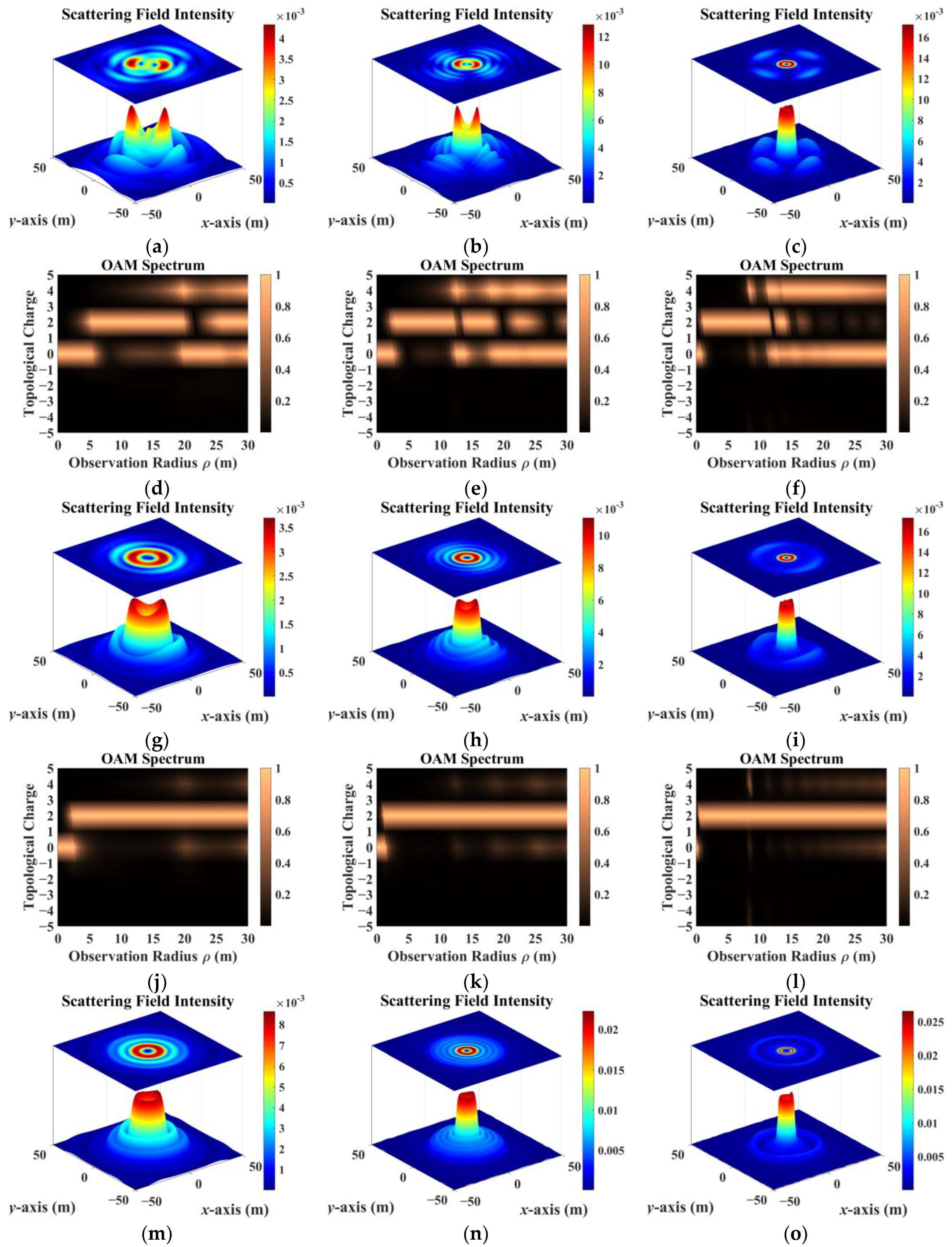
- The sampling results obtained by co-polarization transmission and receiving methods were relatively similar, but the results for different directions of the scattering field were inconsistent. Therefore, the sampling direction can be used as the calculation dimension to construct a target-scattering database.
- (2)
- The scattering field of the target was extremely sensitive to different incidence parameters. As topological charge increased, the scattering field intensity distribution showed a clear outward diffusion trend, and the proportion of modes consistent with the incident field decreased. The scattering field of the non-diffracting vortex beam underwent diffraction, and the intensity gradually decreased with increasing receiving distance. The position of the receiving plane directly affected the scattering-field sampling results. Choosing the appropriate sampling distance and receiving-plane size facilitated receiving more information. The scattering field intensity distribution maintained a profile similar to that of an on-axis incident beam, but when incidence was off-axis, the scattering field was significantly distorted and the topological charge could not be preserved.
- (3)
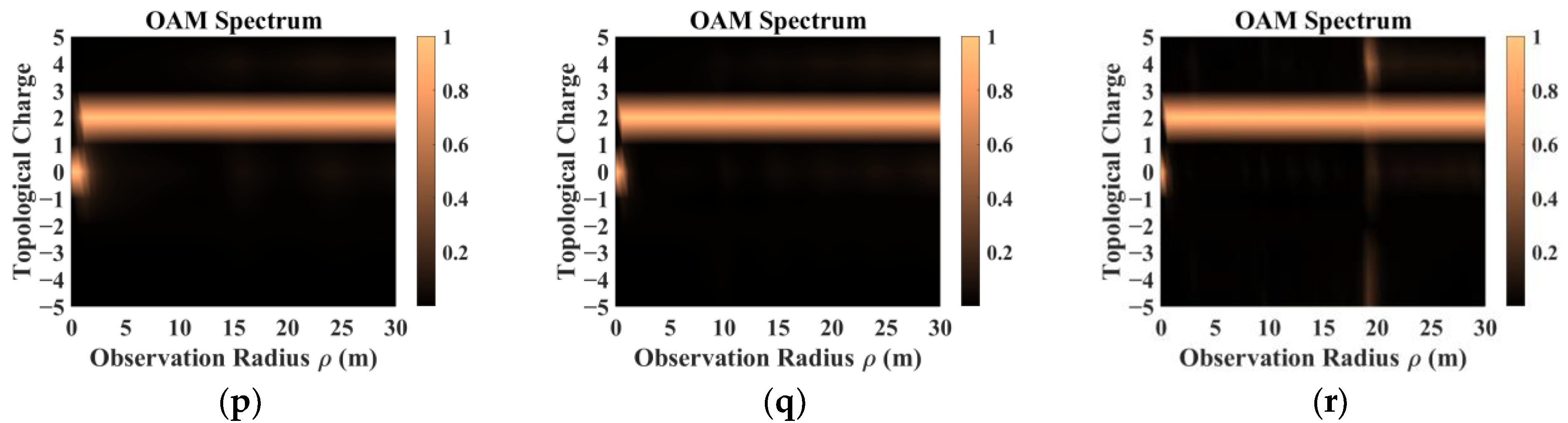
- In addition, beams with the same parameters incident on targets with different dielectric parameters produced significantly different scattering results. The intensity distribution and patterns most similar to those of the incident beam came from scattering by a dielectric coating.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Fazal, I.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.J.; Erkmen, B.I.; Birnbaum, K.M.; et al. 100 Tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Lett. 2014, 39, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.; Liu, G.N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C.; et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Ahmed, N.; Zhao, Z.; Li, L.; Huang, H.; Lavery, M.P.J.; Liao, P.; Yan, Y.; Wang, Z.; Xie, G.; Ren, Y.; et al. Mode-division-multiplexing of multiple Bessel-Gaussian beams carrying orbital-angular-momentum for obstruction-tolerant free-space optical and millimetre-wave communication links. Sci. Rep. 2017, 7, 15412. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef]
- Lavery, M.P.J.; Barnett, S.M.; Speirits, F.C.; Padgett, M.J. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body. Optica 2014, 1, 1–4. [Google Scholar] [CrossRef]
- Fu, S.; Wang, T.; Zhang, Z.; Zhai, Y.; Gao, C. Non-diffractive Bessel-Gauss beams for the detection of rotating object free of obstructions. Opt. Express 2017, 25, 20098–20108. [Google Scholar] [CrossRef]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Garcés-Chávez, V.; McGloin, D.; Melville, H.; Sibbett, W.; Dholakia, K. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Nature 2002, 419, 145–147. [Google Scholar] [CrossRef]
- Meier, M.; Romano, V.; Feurer, T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl. Phys. A 2007, 86, 329–334. [Google Scholar] [CrossRef]
- Thidé, B.; Then, H.; Sjöholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.D.; Istomin, Y.N.; Ibragimov, N.H.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef] [PubMed]
- Shen, F.; Mu, J.; Guo, K.; Guo, Z. Generating circularly polarized vortex electromagnetic waves by the conical conformal patch antenna. IEEE Trans. Antennas Propag. 2019, 67, 5763–5771. [Google Scholar] [CrossRef]
- Dang, W.; Zhu, Y.; Yu, Y.; Zuo, K. A miniaturized dual-orbital-angular-momentum (OAM)–mode helix antenna. IEEE Access 2018, 6, 57056–57060. [Google Scholar]
- Wang, L.; Chen, H.; Guo, K.; Shen, F.; Guo, Z. An inner- and outer-fed dual-arm archimedean spiral antenna for generating multiple orbital angular momentum modes. Electronics 2019, 8, 251. [Google Scholar] [CrossRef]
- Mohammadi, S.M.; Daldorff, L.K.S.; Bergman, J.E.S.; Karlsson, R.L.; Thidé, B.; Forozesh, K.; Carozzi, T.D.; Isham, B. Orbital angular momentum in radio—A system study. IEEE Trans. Antennas Propag. 2010, 58, 565–572. [Google Scholar] [CrossRef]
- Yang, L.; Sun, S.; Sha, W.E.I. Ultrawideband reflection-type metasurface for generating integer and fractional orbital angular momentum. IEEE Trans. Antennas Propag. 2020, 68, 2166–2175. [Google Scholar] [CrossRef]
- Tamburini, F.; Mari, E.; Sponselli, A.; Thidé, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Boaga, V.; Carraro, F.; del Pup, M.; Bianchini, A.; Someda, C.G.; Romanato, F. Experimental demonstration of free-space information transfer using phase modulated orbital angular momentum radio. arXiv 2013, arXiv:1302.2990. [Google Scholar]
- Edfors, O.; Johansson, A.J. Is Orbital Angular Momentum (OAM) Based Radio Communication an Unexploited Area? IEEE Trans. Antennas Propag. 2011, 60, 1126–1131. [Google Scholar] [CrossRef]
- Gaffoglio, R.; Cagliero, A.; Vecchi, G.; Andriulli, F.P. Vortex waves and channel capacity: Hopes and reality. IEEE Access 2017, 6, 19814–19822. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Yang, Z.; Wang, H.; Qin, Y.; Li, X. Orbital-angular-momentum-based electromagnetic vortex imaging. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 711–714. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Li, X.; Wang, H.; Qin, Y.; Jiang, Y. Study on the theory and method of vortex-electromagnetic-wave-based radar imaging. IET Microw. Antennas Propag. 2016, 10, 961–968. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Liu, H.; Cao, K.; Cheng, Y.; Wang, H. 3-D object imaging method with electromagnetic vortex. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2000512. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, K.; Wang, H.; Deng, B.; Zhuang, Z. Orbital-angular-momentum-based ISAR imaging at terahertz frequencies. IEEE Sensors J. 2018, 18, 9230–9235. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Guo, K.; Guo, Z. Detecting targets’ longitudinal and angular accelerations based on vortex electromagnetic waves. Measurement 2022, 187, 110278. [Google Scholar] [CrossRef]
- Mitri, F.G. Electromagnetic wave scattering of a high-order Bessel vortex beam by a dielectric sphere. IEEE Trans. Antennas Propag. 2011, 59, 4375–4379. [Google Scholar] [CrossRef]
- Liu, K.; Gao, Y.; Li, X.; Cheng, Y. Target scattering characteristics for OAM-based radar. AIP Adv. 2018, 8, 0250022. [Google Scholar] [CrossRef]
- Wu, Z.; Qu, T.; Wu, J.; Wu, Z.; Yang, L.; Li, X. Scattering of electromagnetic waves with orbital angular momentum on metallic sphere. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 136–1369. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, J.; Li, H.; Qu, T.; Meng, X.; Xu, Q.; Wu, Z.; Bai, J.; Yang, L.; Gong, L.; et al. Integrated physical optics for calculating electric-large metallic sphere scattering irradiated by vortex wave in microwave frequency band. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1288–1292. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, J.; Qu, T.; Wu, Z.; Xu, Q.; Li, H.; Yang, L.; Meng, X.; Bai, J. Scattering characteristics of an electrically-large aircraft objects illuminated by Bessel vortex beams. IEEE Access 2022, 10, 126023–126029. [Google Scholar] [CrossRef]
- Zhang, X.; Su, X.; Wu, Z.; Ma, L.; Li, X.; Bai, J. Analysis of electromagnetic scattering from typical targets for orbital-angular-momentum waves: Theoretical model. IET Microw. Antennas Propag. 2022, 16, 699–708. [Google Scholar] [CrossRef]
- Chen, X.; Li, H.; Wu, T.; Meng, X.; Li, F. Near-field electromagnetic scattering of Bessel vortex beam by metal target. Acta Phys. Sin. 2023, 72, 100302. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, M.; Zhang, Y. Propagation of the OAM mode carried by partially coherent modified Bessel-Gaussian beams in an anisotropic non-Kolmogorov marine atmosphere. J. Opt. Soc. Am. A 2016, 33, 2277–2283. [Google Scholar] [CrossRef]
- Cui, X.; Yin, X.; Chang, H.; Zhang, Z.; Wang, Y.; Wu, G. A new method of calculating the orbital angular momentum spectra of Laguerre–Gaussian beams in channels with atmospheric turbulence. Chin. Phys. B 2017, 26, 232–238. [Google Scholar] [CrossRef]
- Watkins, R.J.; Dai, K.; White, G.; Li, W.; Miller, J.K.; Morgan, K.S.; Johnson, E.G. Experimental probing of turbulence using a continuous spectrum of asymmetric OAM beams. Opt. Express 2020, 28, 924–935. [Google Scholar] [CrossRef]
- Petrov, D.; Rahuel, N.; Molina-Terriza, G.; Torner, L. Characterization of dielectric spheres by spiral imaging. Opt. Lett. 2012, 37, 869–871. [Google Scholar] [CrossRef] [PubMed]
- Qu, T.; Wu, Z.; Shang, Q.; Wu, J.; Bai, L. Interactions of high-order Bessel vortex beam with a multilayered chiral sphere: Scattering and orbital angular momentum spectrum analysis. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 363–372. [Google Scholar] [CrossRef]
- Liu, K.; Liu, H.; Sha, W.; Cheng, Y.; Wang, H. Backward scattering of electrically large standard objects illuminated by OAM Beams. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1167–1171. [Google Scholar] [CrossRef]
- Shi, C.; Cheng, M.; Guo, L.; Lavery, M.P.J.; Wang, P.; Liu, S.; Li, R.; Li, J. Particle Scattering Induced Orbital Angular Momentum Spectrum Change of Vector Bessel–Gaussian Vortex Beam. Remote Sens. 2022, 14, 4550. [Google Scholar] [CrossRef]
- Sun, M.; Liu, S.; Guo, L.; Huang, K.; Cheng, M. Scattering characteristics of electrically large arbitrarily shaped targets illuminated by an off-axis vortex electromagnetic beam. J. Appl. Phys. 2023, 133, 124905. [Google Scholar] [CrossRef]
- Song, P.; Cui, Z.; Hui, Y.; Zhao, W.; Wang, J.; Han, Y. Explicit analytical expressions for the electromagnetic field components of typical structured light beams. J. Quant. Spectrosc. Radiat. Transf. 2020, 241, 106715. [Google Scholar] [CrossRef]
- Knott, E.F.; Shaeffer, J.F.; Tuley, M.T. Radar Cross Section, 2nd ed.; SciTech Publishing: Boston, MA, USA, 2004; pp. 189–193. [Google Scholar]
- Zhao, W. Study on Prediction Techniques of Radar Cross Section of Complex Targets. Ph.D. thesis, Xidian University, Xi’an, China, 1999. [Google Scholar]
- Swift, C.T.; Beck, F.B.; Thomson, J.; Castellow, S.L., Jr. RAM C-III S-band diagnostic experiment. In Proceedings of the Entry Plasma Sheath and its Effects on Space Vehicle Electromagnetic Systems, Hampton, VA, USA, 1 January 1971. [Google Scholar]
- Liu, S.; Guo, L. Analyzing the Electromagnetic Scattering Characteristics for 3-D Inhomogeneous Plasma Sheath Based on PO Method. IEEE Trans. Plasma Sci. 2016, 44, 2838–2843. [Google Scholar] [CrossRef]
- Michielssen, E.; Sajer, J.; Ranjithan, S.; Mittra, R. Design of lightweight, broad-band microwave absorbers using genetic algorithms. IEEE Trans. Microw. Theory 1993, 41, 1024–1031. [Google Scholar] [CrossRef]





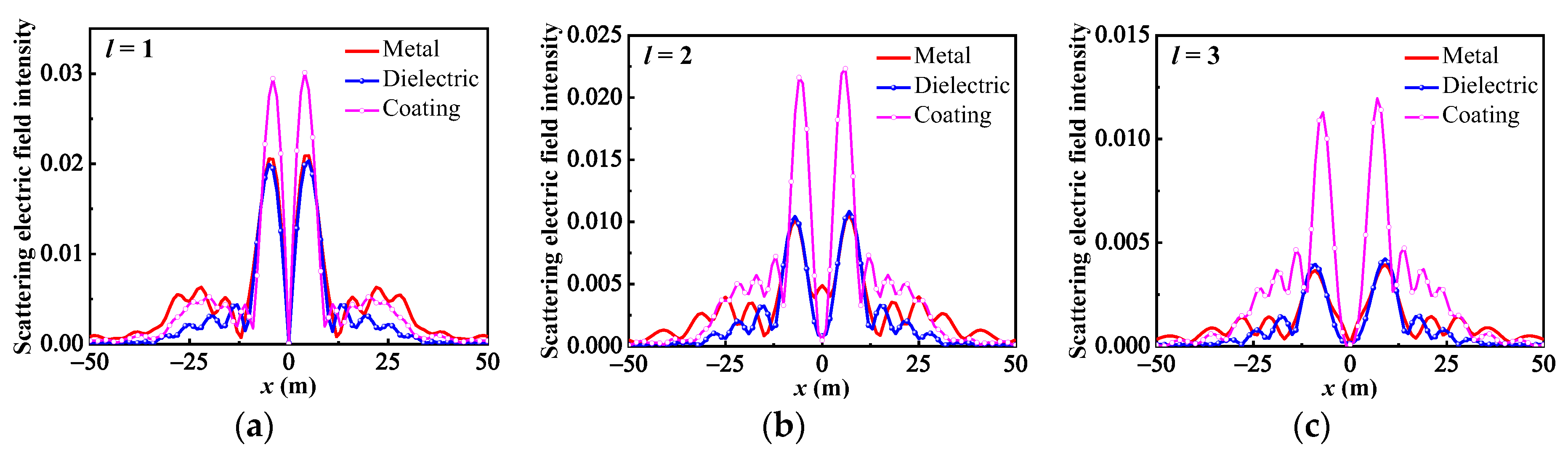

| Total Mode Proportions of the Scattering Field of Targets Made from Different Materials | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| OAM Modes | l = 1 | l = 2 | l = 3 | ||||||
| Metal | Dielectric | Coating | Metal | Dielectric | Coating | Metal | Dielectric | Coating | |
| −5 | 0.0007 | 0.0009 | 0.0012 | 0.0012 | 0.0014 | 0.0016 | 0.0028 | 0.0016 | 0.0016 |
| −4 | 0.0017 | 0.0014 | 0.0019 | 0.0029 | 0.0019 | 0.0022 | 0.0039 | 0.0022 | 0.0025 |
| −3 | 0.0031 | 0.0024 | 0.0042 | 0.0027 | 0.0024 | 0.0035 | 0.0093 | 0.0095 | 0.0097 |
| −2 | 0.0022 | 0.0033 | 0.0055 | 0.0059 | 0.0092 | 0.0099 | 0.0110 | 0.0152 | 0.0116 |
| −1 | 0.2223 | 0.0588 | 0.0260 | 0.0063 | 0.0099 | 0.0072 | 0.0190 | 0.0263 | 0.0150 |
| 0 | 0.0055 | 0.0049 | 0.0044 | 0.2795 | 0.0813 | 0.0307 | 0.0221 | 0.0290 | 0.0101 |
| 1 | 0.5539 | 0.8611 | 0.9168 | 0.0052 | 0.0092 | 0.0082 | 0.2676 | 0.0885 | 0.0300 |
| 2 | 0.0074 | 0.0087 | 0.0106 | 0.4922 | 0.8102 | 0.8916 | 0.0101 | 0.0133 | 0.0122 |
| 3 | 0.1966 | 0.0557 | 0.0254 | 0.0088 | 0.0121 | 0.0131 | 0.4656 | 0.7396 | 0.8581 |
| 4 | 0.0044 | 0.0017 | 0.0027 | 0.1895 | 0.0600 | 0.0291 | 0.0108 | 0.0150 | 0.0168 |
| 5 | 0.0023 | 0.0011 | 0.0012 | 0.0056 | 0.0024 | 0.0029 | 0.1778 | 0.0598 | 0.0324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Liu, S.; Guo, L. Scattering Field Intensity and Orbital Angular Momentum Spectral Distribution of Vortex Electromagnetic Beams Scattered by Electrically Large Targets Comprising Different Materials. Remote Sens. 2024, 16, 754. https://doi.org/10.3390/rs16050754
Sun M, Liu S, Guo L. Scattering Field Intensity and Orbital Angular Momentum Spectral Distribution of Vortex Electromagnetic Beams Scattered by Electrically Large Targets Comprising Different Materials. Remote Sensing. 2024; 16(5):754. https://doi.org/10.3390/rs16050754
Chicago/Turabian StyleSun, Minghao, Songhua Liu, and Lixin Guo. 2024. "Scattering Field Intensity and Orbital Angular Momentum Spectral Distribution of Vortex Electromagnetic Beams Scattered by Electrically Large Targets Comprising Different Materials" Remote Sensing 16, no. 5: 754. https://doi.org/10.3390/rs16050754
APA StyleSun, M., Liu, S., & Guo, L. (2024). Scattering Field Intensity and Orbital Angular Momentum Spectral Distribution of Vortex Electromagnetic Beams Scattered by Electrically Large Targets Comprising Different Materials. Remote Sensing, 16(5), 754. https://doi.org/10.3390/rs16050754






