Biomass Change Estimated by TanDEM-X Interferometry and GEDI in a Tanzanian Forest
Abstract
1. Introduction
2. Materials and Methods
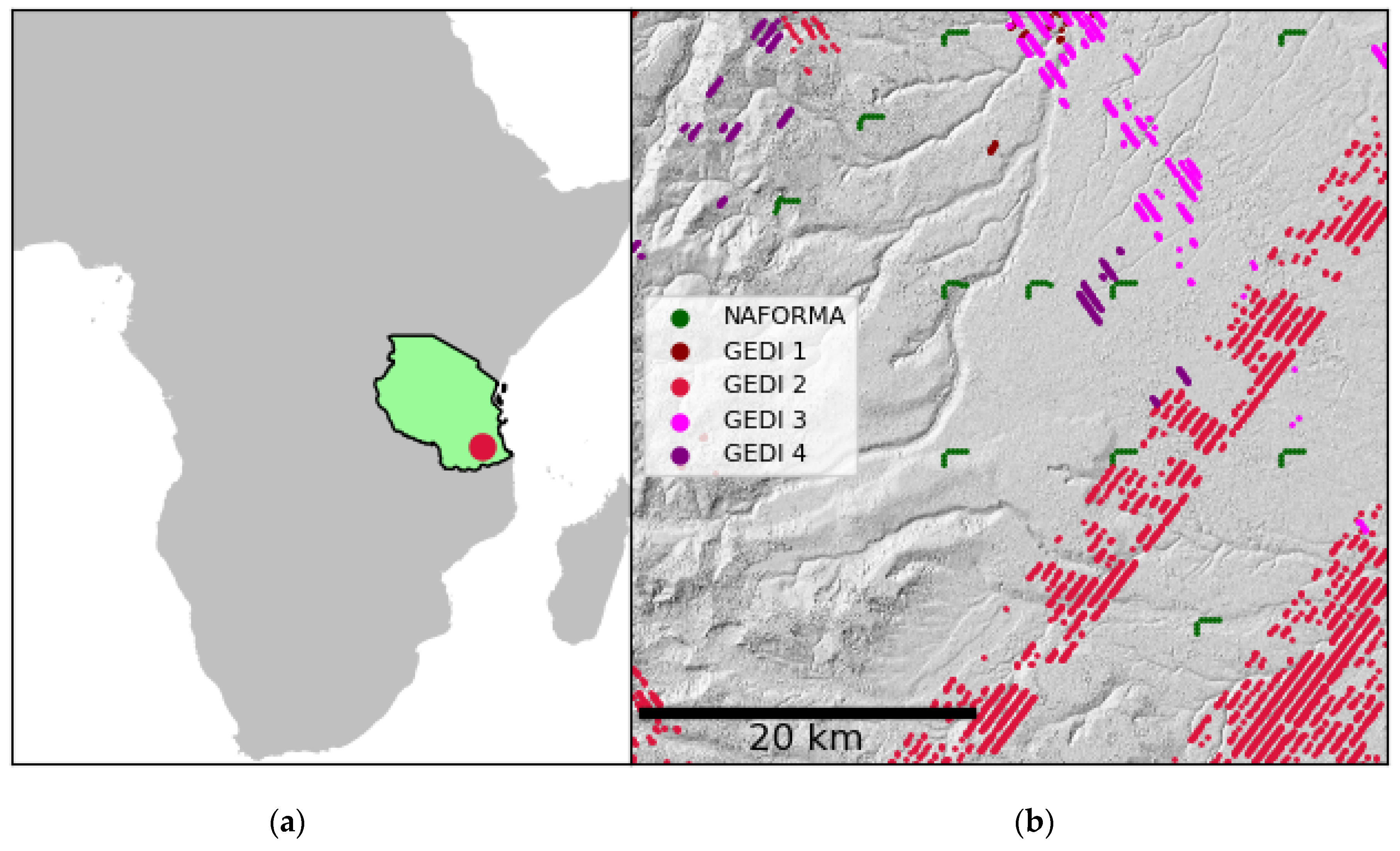
2.1. NAFORMA National Forest Inventory Data
2.2. GEDI
2.3. TanDEM-X
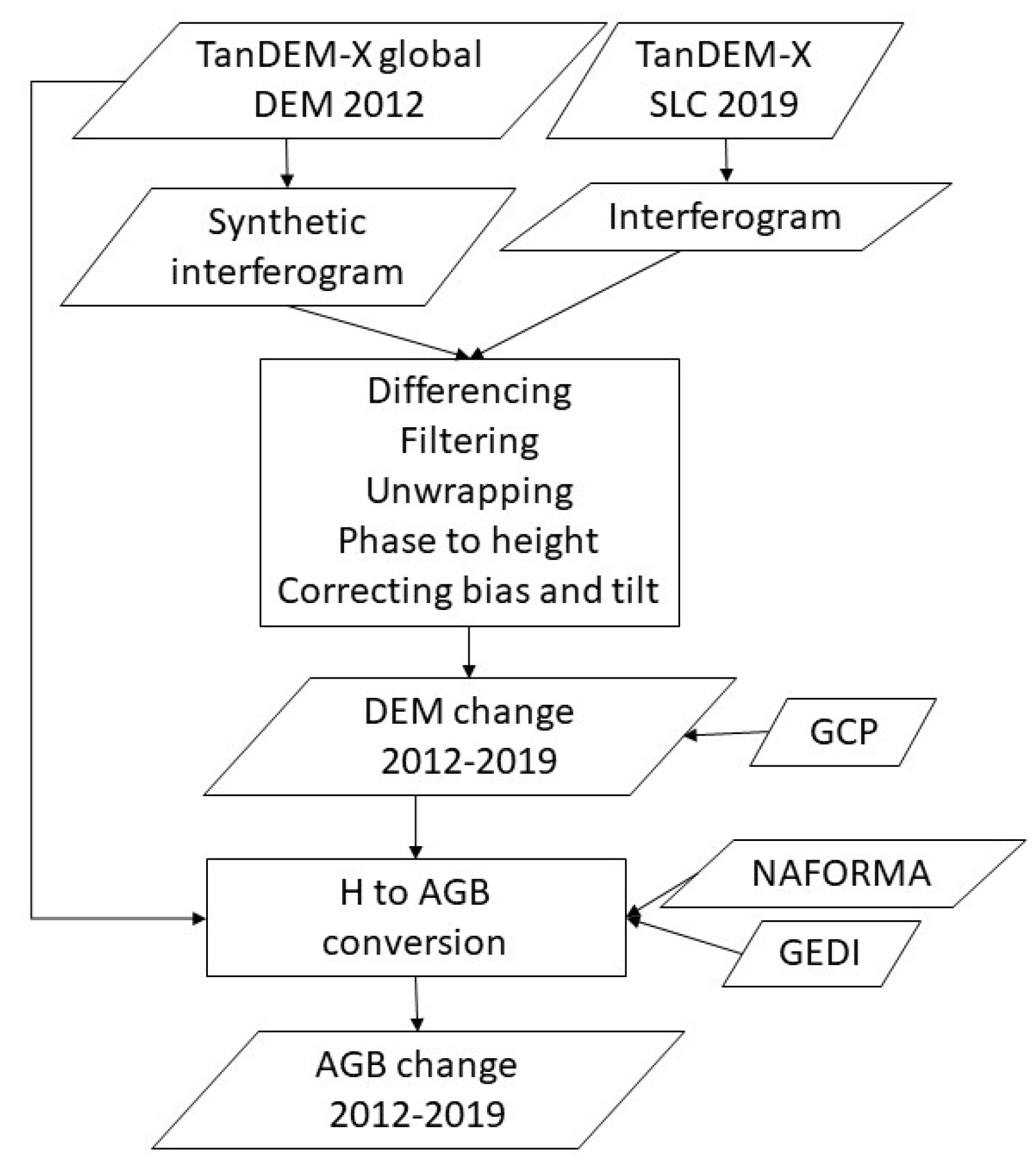
2.4. TanDEM-X Processing
2.5. Height-to-Biomass Conversion
2.6. Geography of Change
2.7. Estimating Above-Ground Biomass Change
3. Results
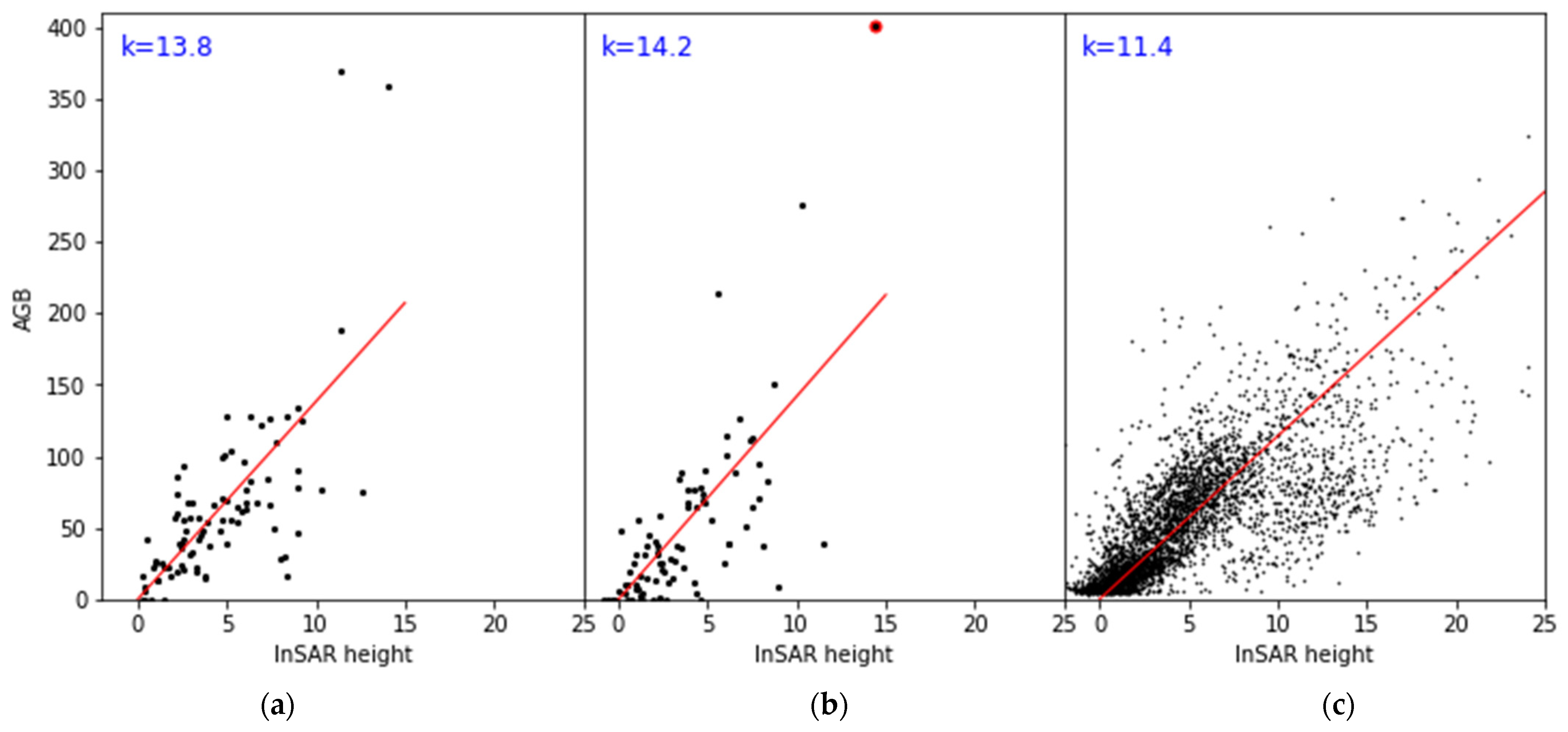
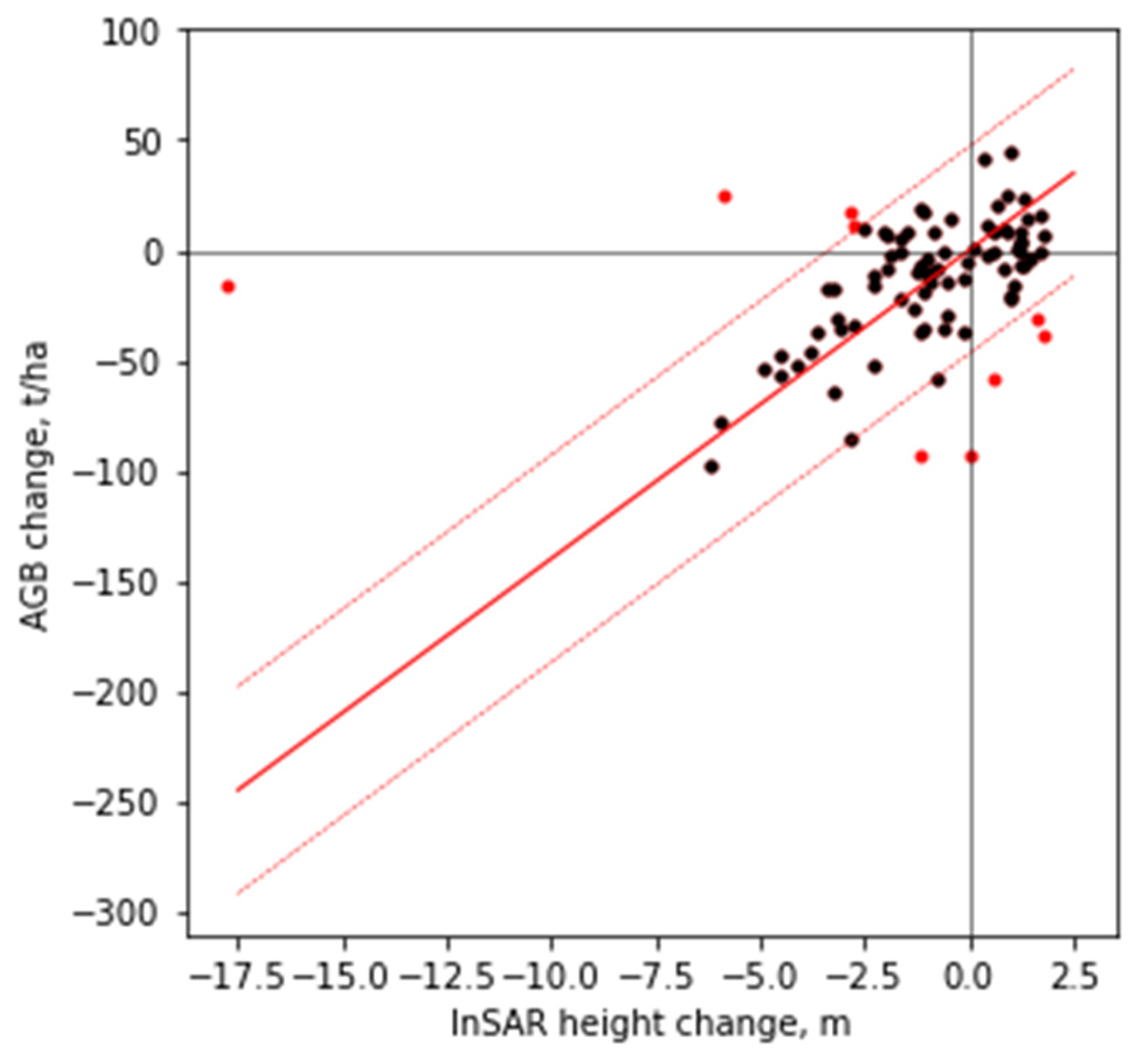
3.1. Height-to-Biomass Conversion
3.2. Geography of Change
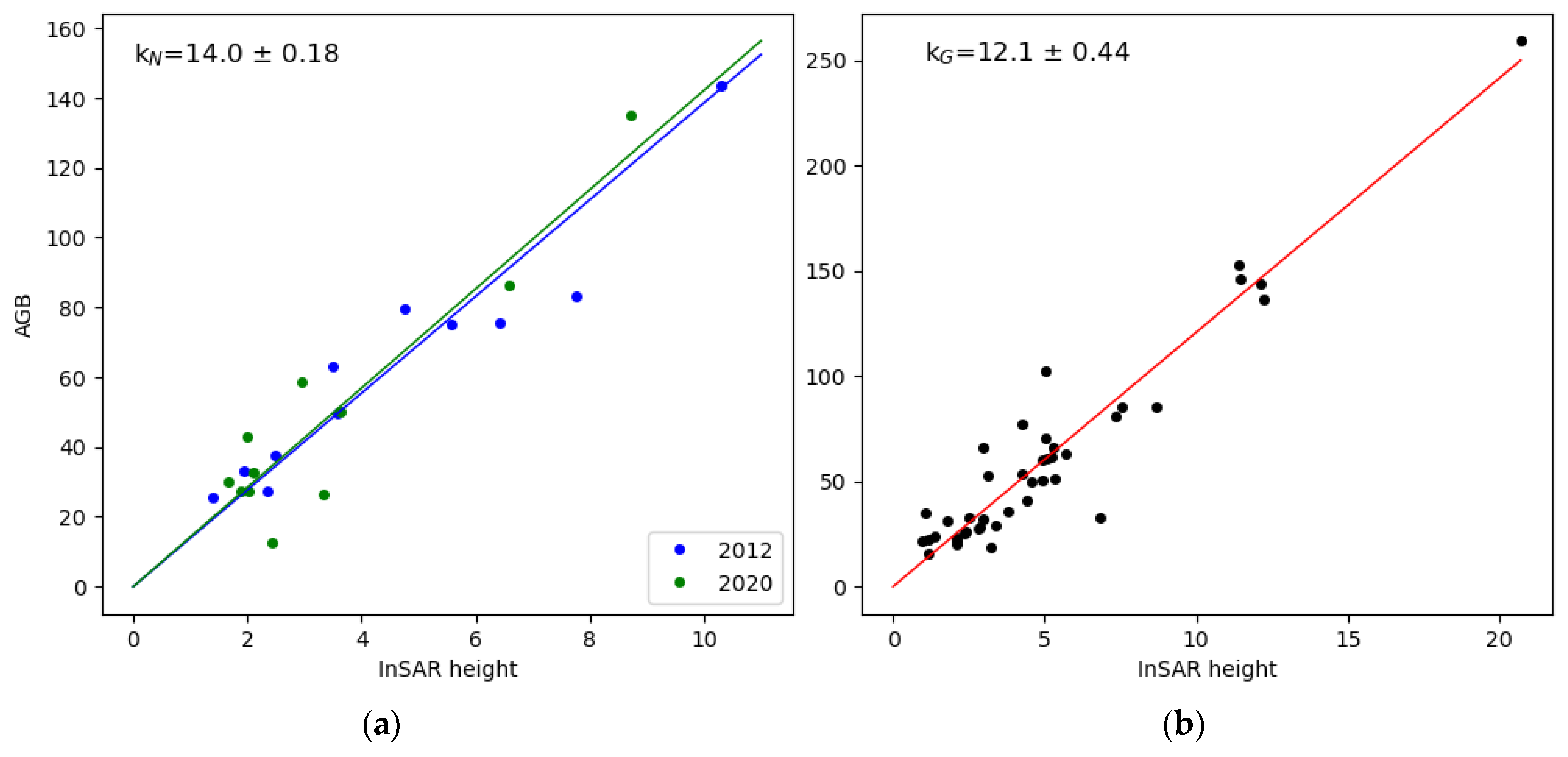
3.3. Estimated Above-Ground Biomass Change
4. Discussion
4.1. Geography
4.2. Conversion from InSAR Height to Above-Ground Biomass
4.3. Comparability of the Two Points in Time
4.4. Vertical Adjustment
4.5. GEDI and TanDEM-X Combination
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Le Toan, T.; Quegan, S.; Davidson, M.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014.
- UNFCCC. Decision 2/CP. 13: Reducing Emissions from Deforestation in Developing Countries: Approaches to Stimulate Action; United Nations Framework Convention on Climate Chgange: Bonn, Germany, 2007. Available online: http://unfccc.int/resource/docs/2007/cop13/eng/06a01.pdf (accessed on 19 September 2014).
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated Carbon Dioxide Emissions from Tropical Deforestation Improved by Carbon-Density Maps. Nat. Clim. Change 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Saatchi, S.; Harris, N.; Brown, S.; Lefsky, M.; Mitchard, E.; Salas, W.; Zutta, B.; Buermann, W.; Lewis, S.; Hagen, S.; et al. Benchmark Map of Forest Carbon Stocks in Tropical Regions across Three Continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Feldpausch, T.R.; Brienen, R.J.W.; Lopez-Gonzalez, G.; Monteagudo, A.; Baker, T.R.; Lewis, S.L.; Lloyd, J.; Quesada, C.A.; Gloor, M.; et al. Markedly Divergent Estimates of Amazon Forest Carbon Density from Ground Plots and Satellites. Glob. Ecol. Biogeogr. 2014, 23, 935–946. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Henry, M.; Schmullius, C. Mapping Biomass with Remote Sensing: A Comparison of Methods for the Case Study of Uganda. Carbon Balance Manag. 2011, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Dubayah, R.; Armston, J.; Healey, S.P.; Bruening, J.M.; Patterson, P.L.; Kellner, J.R.; Duncanson, L.; Saarela, S.; Ståhl, G.; Yang, Z. GEDI Launches a New Era of Biomass Inference from Space. Environ. Res. Lett. 2022, 17, 095001. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Gobakken, T.; Næsset, E.; Weydahl, D.J. Estimating Spruce and Pine Biomass with Interferometric X-band SAR. Remote Sens. Environ. 2010, 114, 2353–2360. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Breidenbach, J.; Nilsen, B.; Weydahl, D. Monitoring Spruce Volume and Biomass with InSAR Data from TanDEM-X. Remote Sens. Environ. 2013, 139, 60–67. [Google Scholar] [CrossRef]
- Solberg, S.; Gizachew, B.; Næsset, E.; Gobakken, T.; Bollandsås, O.M.; Mauya, E.W.; Olsson, H.; Malimbwi, R.; Zahabu, E. Monitoring Forest Carbon in a Tanzanian Woodland Using Interferometric SAR: A Novel Methodology for REDD+. Carbon Balance Manag. 2015, 10, 14. [Google Scholar] [CrossRef]
- Solberg, S.; Hansen, E.H.; Gobakken, T.; Naesset, E.; Zahabu, E. Biomass and InSAR Height Relationship in a Dense Tropical Forest. Remote Sens. Environ. 2017, 192, 166–175. [Google Scholar] [CrossRef]
- Puliti, S.; Solberg, S.; Næsset, E.; Gobakken, T.; Zahabu, E.; Mauya, E.; Malimbwi, R.E. Modelling above Ground Biomass in Tanzanian Miombo Woodlands Using TanDEM-X WorldDEM and Field Data. Remote Sens. 2017, 9, 984. [Google Scholar] [CrossRef]
- Karila, K.; Yu, X.; Vastaranta, M.; Karjalainen, M.; Puttonen, E.; Hyyppä, J. TanDEM-X Digital Surface Models in Boreal Forest above-Ground Biomass Change Detection. ISPRS-J. Photogramm. Remote Sens. 2019, 148, 174–183. [Google Scholar] [CrossRef]
- Næsset, E.; Ørka, H.O.; Solberg, S.; Bollandsås, O.M.; Hansen, E.H.; Mauya, E.; Zahabu, E.; Malimbwi, R.; Chamuya, N.; Olsson, H.; et al. Mapping and Estimating Forest Area and Aboveground Biomass in Miombo Woodlands in Tanzania Using Data from Airborne Laser Scanning, TanDEM-X, RapidEye, and Global Forest Maps: A Comparison of Estimated Precision. Remote Sens. Environ. 2016, 175, 282–300. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Weydahl, D.J. Detection of Forest Clear-Cuts with Shuttle Radar Topography Mission (SRTM) and Tandem-X InSAR Data. Remote Sens. 2013, 5, 5449–5462. [Google Scholar] [CrossRef]
- Solberg, S.; May, J.; Bogren, W.; Breidenbach, J.; Torp, T.; Gizachew, B. Interferometric SAR DEMs for Forest Change in Uganda 2000–2012. Remote Sens. 2018, 10, 228. [Google Scholar] [CrossRef]
- Gizachew, B.; Solberg, S.; Puliti, S. Forest Carbon Gain and Loss in Protected Areas of Uganda: Implications to Carbon Benefits of Conservation. Land 2018, 7, 138. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Gobakken, T.; Bollandsås, O.-M. Forest Biomass Change Estimated from Height Change in Interferometric SAR Height Models. Carbon Balance Manag. 2014, 9, 5. [Google Scholar] [CrossRef]
- Solberg, S.; Lohne, T.-P.; Karyanto, O. Temporal Stability of InSAR Height in a Tropical Rainforest. Remote Sens. Lett. 2015, 6, 209–217. [Google Scholar] [CrossRef]
- Solberg, S.; Weydahl, D.J.; Astrup, R. Temporal Stability of X-Band Single-Pass InSAR Heights in a Spruce Forest: Effects of Acquisition Properties and Season. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1607–1614. [Google Scholar] [CrossRef]
- Carcarra-Bes, V.; Pardini, M.; Choi, C.; Guliaev, R.; Papathanassiou, K.P. Tandem-X and Gedi Data Fusion for a Continuous Forest Height Mapping at Large Scales. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 796–799. [Google Scholar]
- Qi, W.; Saarela, S.; Armston, J.; Ståhl, G.; Dubayah, R. Forest Biomass Estimation over Three Distinct Forest Types Using TanDEM-X InSAR Data and Simulated GEDI Lidar Data. Remote Sens. Environ. 2019, 232, 111283. [Google Scholar] [CrossRef]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Gregoire, T.G.; Stahl, G.; Holm, S. A Simulation Approach for Accuracy Assessment of Two-Phase Post-Stratified Estimation in Large-Area LiDAR Biomass Surveys. Remote Sens. Environ. 2013, 133, 210–224. [Google Scholar] [CrossRef]
- Vesa, L.; Malimbwi, R.E.; Tomppo, E.; Zahabu, E.; Maliondo, S.; Chamuya, N.; Nssoko, E.; Otieno, J.; Miceli, G.; Kaaya, A.K.; et al. National Forestry Resources Monitoring and Assessment of Tanzania (NAFORMA). Field Manual—Biophysical Survey; Ministry of Natural Re sources & Tourism: Dar es Salaam, The United Republic of Tanzania, 2011.
- Mugasha, W.A.; Eid, T.; Bollandsas, O.M.; Malimbwi, R.E.; Chamshama, S.A.O.; Zahabu, E.; Katani, J.Z. Allometric Models for Prediction of Above- and Belowground Biomass of Trees in the Miombo Woodlands of Tanzania. For. Ecol. Manag. 2013, 310, 87–101. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Armston, J.; Kellner, J.R.; Duncanson, L.; Healey, S.P.; Patterson, P.L.; Hancock, S.; Tang, H.; Bruening, J.; Hofton, M.A.; et al. GEDI L4A Footprint Level Aboveground Biomass Density, Version 2.1; ORNL DAAC: Oak Ridge, TN, USA, 2022.
- Kellner, J.R.; Armston, J.; Duncanson, L. Algorithm Theoretical Basis Document for GEDI Footprint Aboveground Biomass Density. Earth Space Sci. 2023, 10, e2022EA002516. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground Biomass Density Models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) Lidar Mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Mauya, E.W.; Bollandsås, O.M.; Gregoire, T.G.; Ståhl, G.; Zahabu, E. Large-Scale Estimation of Aboveground Biomass in Miombo Woodlands Using Airborne Laser Scanning and National Forest Inventory Data. Remote Sens. Environ. 2016, 186, 626–636. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Solberg, S.; McRoberts, R.E. The Effects of Field Plot Size on Model-Assisted Estimation of Aboveground Biomass Change Using Multitemporal Interferometric SAR and Airborne Laser Scanning Data. Remote Sens. Environ. 2015, 168, 252–264. [Google Scholar] [CrossRef]
- Tang, H.; Stoker, J.M.; Luthcke, S.; Armston, J.; Lee, K.; Blair, B.; Hofton, M. Evaluating and Mitigating the Impact of Systematic Geolocation Error on Canopy Height Measurement Performance of GEDI. Remote Sens. Environ. 2023, 291, 113571. [Google Scholar] [CrossRef]
- Soja, M.J.; Persson, H.J.; Ulander, L.M.H. Estimation of Forest Biomass from Two-Level Model Inversion of Single-Pass InSAR Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5083–5099. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.V.; dos Santos, J.R.; Freitas, C.D.; Araujo, L.S. Tropical Forest Measurement by Interferometric Height Modeling and P-Band Radar Backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar]
- Praks, J.; Demirpolat, C.; Antropov, O.; Hallikainen, M. On Forest Height Retrival from Spaceborne X-Band Inferometic SAR Images under Variable Seasonal Conditions. In Proceedings of the XXXII Finnish URSI Convention on Radio Science and SMARAD Seminar, Otaniemi, Finland, 24–25 April 2013; pp. 115–118. [Google Scholar]
- Way, J.; Paris, J.; Kasischke, E.; Slaughter, C.; Viereck, L.; Christensen, N.; Dobson, M.C.; Ulaby, F.; Richards, J.; Milne, A.; et al. The Effect of Changing Environmental-Conditions on Microwave Signatures of Forest Ecosystems—Preliminary-Results of the March 1988 Alaskan Aircraft SAR Experiment. Int. J. Remote Sens. 1990, 11, 1119–1144. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. Investigating the Impact of Freezing on the ALOS PALSAR InSAR Phase over Siberian Forests. Remote Sens. Lett. 2013, 4, 900–909. [Google Scholar] [CrossRef]
- Persson, H.J.; Olsson, H.; Soja, M.J.; Ulander, L.M.H.; Fransson, J.E.S. Experiences from Large-Scale Forest Mapping of Sweden Using TanDEM-X Data. Remote Sens. 2017, 9, 1253. [Google Scholar] [CrossRef]

| Data Set | Date | HoA |
|---|---|---|
| A | 20 December 2019 | 55.7 |
| B | 31 December 2019 | 55.2 |
| C | 31 December 2019 | 55.3 |
| Alt. | N | % GEDI Area | k |
|---|---|---|---|
| 2 × 2 | 4 | 100 | 11.5 |
| 4 × 4 | 16 | 88 | 11.9 |
| 8 × 8 | 64 | 66 | 12.1 |
| 16 × 16 | 256 | 39 | 11.6 |
| 32 × 32 | 1024 | 26 | 11.7 |
| NAFORMA Plots | Study Area | |
|---|---|---|
| ΔDSMTDX | −1.14 | −1.10 |
| ΔAGB, ground truth | −14.5 | |
| ΔAGB = kN ΔDSMTDX | −16.0 ± 0.21 | −15.4 ± 0.20 |
| ΔAGB = kG ΔDSMTDX | −13.8 ± 0.50 | −13.3 ± 0.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solberg, S.; Bollandsås, O.M.; Gobakken, T.; Næsset, E.; Basak, P.; Duncanson, L.I. Biomass Change Estimated by TanDEM-X Interferometry and GEDI in a Tanzanian Forest. Remote Sens. 2024, 16, 861. https://doi.org/10.3390/rs16050861
Solberg S, Bollandsås OM, Gobakken T, Næsset E, Basak P, Duncanson LI. Biomass Change Estimated by TanDEM-X Interferometry and GEDI in a Tanzanian Forest. Remote Sensing. 2024; 16(5):861. https://doi.org/10.3390/rs16050861
Chicago/Turabian StyleSolberg, Svein, Ole Martin Bollandsås, Terje Gobakken, Erik Næsset, Paromita Basak, and Laura Innice Duncanson. 2024. "Biomass Change Estimated by TanDEM-X Interferometry and GEDI in a Tanzanian Forest" Remote Sensing 16, no. 5: 861. https://doi.org/10.3390/rs16050861
APA StyleSolberg, S., Bollandsås, O. M., Gobakken, T., Næsset, E., Basak, P., & Duncanson, L. I. (2024). Biomass Change Estimated by TanDEM-X Interferometry and GEDI in a Tanzanian Forest. Remote Sensing, 16(5), 861. https://doi.org/10.3390/rs16050861







