Wind Profile Reconstruction Based on Convolutional Neural Network for Incoherent Doppler Wind LiDAR

Abstract

The rapid development of artificial intelligence (AI) and deep learning has revolutionized the field of data analysis in recent years, including signal data acquired by remote sensors. Light Detection and Ranging (LiDAR) technology is widely used in atmospheric research for measuring various atmospheric parameters. Wind measurement using LiDAR data has traditionally relied on the spectral centroid (SC) algorithm. However, this approach has limitations in handling LiDAR data, particularly in low signal-to-noise ratio (SNR) regions. To overcome these limitations, this study leverages the capabilities of customized deep-learning techniques to achieve accurate wind profile reconstruction. The study uses datasets obtained from the European Centre for Medium Weather Forecasting (ECMWF) Reanalysis v5 (ERA5) and the mobile Incoherent Doppler LiDAR (ICDL) system constructed by the University of Science and Technology of China. We present a simulation-based approach for generating wind profiles from the statistical data and the associated theoretical calculations. Whereafter, our team constructed a convolutional neural network (CNN) model based on the U-Net architecture to replace the SC algorithm for LiDAR data post-processing. The CNN-generated results are evaluated and compared with the SC results and the ERA5 data. This study highlights the potential of deep learning-based techniques in atmospheric research and their ability to provide more accurate and reliable results.

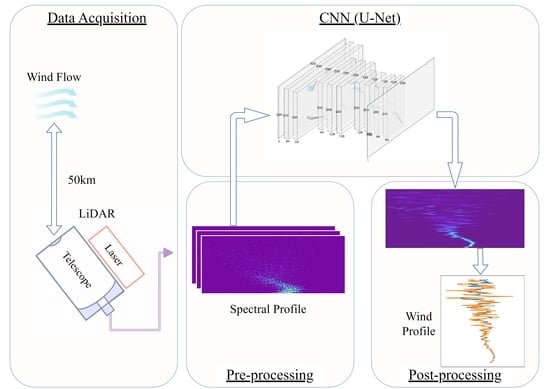
1. Introduction

Undoubtedly, artificial intelligence (AI) has the potential to change almost every aspect of our lives. Among all of the AI techniques, deep learning has gained the most significant attention due to its ability to construct intricate structures that mimic the human neuron system [1,2]. Unlike traditional algorithms, deep neural networks have the capability to learn, memorize, and generate new content. This has greatly enhanced the compatibility of data analysis in all aspects, especially in image recognition [3,4,5,6,7] and natural language processing [8,9,10,11]. Recently, deep learning has become an essential tool in numerous applications, scoping from big-data analytics in daily APPs to AI-generated content products like ChatGPT. In the field of remote sensing, in particular, it has also contributed a significant improvement from the CNN techniques, with promising potential for further innovations [12,13,14].

The acquisition of atmospheric measurement data plays a crucial role in understanding atmospheric weather patterns, climate changes, and other related phenomena. LiDAR technology has been widely deployed as an effective method for collecting various atmospheric parameters, including temperature, air densities, wind fields, humidity, and more. For wind measurement, two categories of LiDAR can be classified: coherent (or heterodyne) Doppler LiDAR [15,16] and incoherent (or direct detection) Doppler LiDAR (ICDL) [17,18,19]. Regardless of its category, its theoretical principle is to utilize the Doppler shift information from the backscattered signal to determine the wind speed. Conventionally, the spectral centroid (SC) algorithm [12,20,21] usually works as the data post-processing method for wind profile reconstruction.

The utilization of machine learning algorithms in the area of wind detection is not a novelty [12,13,14]. Some traditional algorithms such as polynomial fitting, linear regression, and spline transformation have already been implemented in analyzing and determining wind fields in several applications, such as background wind field deduction and wind profile trend fitting [22,23,24,25,26,27]. These algorithms have provided insights into wind behaviors, but their limitations in processing local delicate wind perturbations have led to expectations for new techniques. With the rise of the deep learning and CNN technique, based on its remarkable prediction and classification capability, advanced manipulations can be performed. Consequently, a more accurate wind profile reconstruction based on this new CNN approach can be utilized with the assistance of deep learning algorithms.

Previous studies have explored wind speed prediction and wind field reconstruction, yet the insight into atmospheric wind field trends remains uninvestigated [13,28]. These efforts have been limited to relatively low altitudes and bounded ranges in the hundreds or thousands of meters. Additionally, their convolutional neural network (CNN) structures were not designed specifically for this task, thus obscuring the full potential of the CNN algorithm. Here, we exploit the power of deep learning architecture to achieve precise wind profile reconstruction.

To enhance the reliability of our work, we collected data from both the mobile ICDL system shown in Figure 1 and the ERA5 dataset produced by ECMWF. Addressing the lack of a substantial quantity of dependable ground truth data for wind profiles between altitudes of 30 km and 60 km, we present a simulation-based approach for constructing wind profiles using theoretical calculations and mathematical statistics; consisting of components in wind perturbation, signal-to-noise (SNR) error, and background wind field trends. The data preprocessing involves integrating the simulated and LiDAR-derived data for format unification. To displace the spectral centroid algorithm, we construct a U-net-based [29] CNN model, due to its efficiency and detail-capturing capability, for more accurate post-processing of the LiDAR data. The network integrates both simulated wind profile lines and wind profile backscattered data into the training procedures. We subsequently evaluate the CNN-generated results and compare them with the ground truth labels from our simulations, as well as with the spectral centroid results. Moreover, we conduct an evaluation of real wind profile data obtained from our LiDAR with no ground truth and compare it to the spectral centroid results and the ERA5 dataset in the last step.

2. Methods

2.1. Data Acquisition

2.1.1. Measurement from ICDL

The raw LiDAR data, available at Science Data Bank [30], were obtained from the mobile Rayleigh Doppler LiDAR developed by the University of Science and Technology of China [31,32], during the night period at Kolar, Xinjiang (41.1°N, 87.1°E), China in 2019. The LiDAR system has been installed in the vehicles shown in Figure 1. Our ICDL employs the double-edge technique [18,28,33,34] as the primary frequency discriminator to determine the Doppler shift. The system description along with a detailed explanation of the theoretical principle can be found in our previous studies [18,32,35]. The telescope of the LiDAR is pointed at a zenith angle (ϕ) of 30 degrees with the correlated azimuth angles (ϴ) in the east–west direction.

The data collected were stored in the form of a text document, recording photon counts from each of the two photodetectors corresponding to the double-edge technique. The photon counts ratio R(∆v_d) after the two edge filters is under the following relationship:

$$\mathrm{R}\left({∆\mathrm{v}}_{\mathrm{d}}\right)=\frac{{\mathrm{I}}_1-{\mathrm{I}}_2}{{\mathrm{I}}_1+{\mathrm{I}}_2}$$

(1)

The response curve for discriminating frequency shift from the photon counts ratio will be scanned and calculated on a daily basis at the beginning of the operation. The line-of-sight (LOS) wind velocity V_LOS related to the frequency shift then can be calculated under the Doppler shift formula:

$${\mathrm{V}}_{\mathrm{L}\mathrm{O}\mathrm{S}}=\frac{{\mathsf{\lambda }}_{\mathrm{L}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}}{2}{∆\mathrm{v}}_{\mathrm{d}}$$

(2)

The horizontal wind velocity, characterized by an east–west orientation corresponding to the direction targeted by our LiDAR, adheres to the relationship delineated in Equation (3), assuming the vertical wind flow in the stratosphere remains below 2 m/s [18] and is considered negligible.

$${\mathrm{V}}_{\mathrm{E}\mathrm{W}}=\frac{{\mathrm{V}}_{\mathrm{L}\mathrm{O}\mathrm{S}}}{\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathsf{\varphi }\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{ϴ}\right)}$$

(3)

Across approximately 40,000 files, each text file is generated from the repetitional detection of 40 s, recording the backscattered signal from 4000 laser shots that have been transmitted to the targeted direction of the atmosphere. A single text file contains a total of 16,000 bins, where each bin logs the photon counts on a 50 ns interval, corresponding to a line-of-sight (LOS) distance of 7.5 m. To ensure sufficient photon counts for a feasible signal-to-noise ratio (SNR), a range gate of 30 bins and 60 bins’ combination is selected at an altitude threshold of around 40 km, where each resolution grid corresponds to 225 m and 450 m for the LOS distance, equivalent to approximately 195 m and 390 m in height, respectively. To compensate for the low SNR at high altitudes, each of our wind profiles represents an average horizontal wind speed of 30 min. An example wind data image of the real LiDAR signal after pre-processing is shown in Section 2.2.3, and the wind profile example is shown in Figure 2. More details of the signal pre-processing are described in Section 2.3.2.

2.1.2. ECMWF: ERA5 Dataset

The ERA5 dataset [36] is a comprehensive atmospheric study that employs observation data gathered from an extensive list of satellites, aircraft, and onsite stations [37]. Produced by the Copernicus Climate Change Service (C3S) at ECMWF, this global reanalysis model incorporates a variety of atmospheric indices, including pressure, temperature, density, vorticity levels, and wind field decompositions, in both zonal and meridional directions. The dataset offers a spatial resolution of 0.25° × 0.25° for longitude and latitude and covers altitudes ranging from 10 m to 80 km with an hourly time resolution, including historical data up to five days prior to the present time. Additionally, the ERA5 dataset offers forecasting capabilities, extending its calculations into future weeks. This highly accurate atmosphere re-analysis model contains wind profile data at precisely the same location and time as our LiDAR’s detection introduced in Section 2.1.1, with a neglectable direct linear distance error of approximately 14 km. Given the ERA5’s lower altitude resolution, we extract only its background wind trend to assist in simulating the background wind of our wind profile. Detailed wind extraction is specified in the next section.

2.2. Simulation of Wind Profile Reconstruction

The LiDAR-measured wind profile can be divided into two components: the true wind velocity and the uncertainty caused by errors. Traditionally, the LiDAR’s data are calculated based on the spectral centroid algorithm, which estimates the average radial wind speed of a given time and space interval. In our case, the objective is to find the averaged horizontal wind speed for the east–west direction of a 30 min interval, and the space interval depends on the range gate of 195 m and 390 m. More details of the space interval are associated with LiDAR design and introduced in Section 2.1.1. Wind profiles calculated by this method consist of a large portion of uncertainty, especially in regions with low SNR, where the resulting wind profile cannot reflect an accurate true wind field of the measured air flow.

In this paper, we introduce a newly designed CNN network to improve the accuracy of the LiDAR. When training a neural network model, the ground truth answer, known as the label of the input image, has to be fed to the network to give the machine an example of the ideal outcome of the given input data. However, using wind data based on the SC result as the label for the CNN model may not yield the desired outcome, as the label itself is not accurate. To overcome this problem, we decided to first simulate the “ground truth” of the wind profile that does not contain any errors, while the errors can be generated separately and combined into the ground truth to imitate the raw data collected from the LiDAR.

On account of various factors of atmospheric parameters, including air density, temperature, geostrophic force, atmospheric circulation, etc., the wind field can be further split into two components: wind perturbation from the local oscillation, and the background wind field. The wind perturbation and the background wind profile change in both time periods and altitude levels. To extract the background wind from the wind perturbation, several methods from former research [22,23,24,25,26,27] are all capable of this task. We used the Butterworth filter from Python’s built-in library to split the two for convenience: the background wind profile, exemplified by the orange curve shown in Figure 2, separated from the original wind profile, represented by the blue curve. After extracting the background wind, the wind profile is simply an oscillation consisting of the actual perturbation and the error. To emulate the true wind profile, the perturbation and the error need to be further discriminated.

2.2.1. Error Calculation

Previous works evaluating LiDAR errors [28,38,39] have identified several types of errors: systematic errors and random errors. The systematic errors can be divided into two categories: the sensitivity of the Fabry–Pérot Interferometer (FPI) and the signal-noise-ratio of the received photon counts. The sensitivity of the FPI is calculated based on Equation (4):

$$\Theta (\mathrm{v})=\frac{\mathrm{d}\mathrm{R}\left(\mathrm{v}\right)}{\mathrm{d}\mathrm{v}}\frac{1}{\mathrm{R}\left(\mathrm{v}\right)}$$

(4)

where Θ denotes the sensitivity of the system, R(v) is the I1/I2 ratio of the photon counts detected by the two photodetectors, and the dR(v)/dv term represents the FPI resolution for the rate of change of the detected frequency from the Doppler effect. This parameter is measured and curve-fitted based on the spectral scan from our LiDAR system mentioned in Section 2.1.1.

The error associated with the SNR is dependent on the photon counts from the photodetector; three major sources contribute to this noise: photodetector’s shot noise, background noise from other light sources, and detection errors. The SNR is calculated based on Equation (5):

$$\begin{gathered} {\mathrm{S}\mathrm{N}\mathrm{R}}_1=\frac{{\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}_1}{\sqrt{{\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}_1+{\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}_1}}, and {\mathrm{S}\mathrm{N}\mathrm{R}}_2=\frac{{\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}_2}{\sqrt{{\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}_2+{\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}_2}} \\ {\mathrm{S}\mathrm{N}\mathrm{R}}_{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\frac{1}{\sqrt{\frac{1}{{\mathrm{S}\mathrm{N}\mathrm{R}}_1^2}+\frac{1}{{\mathrm{S}\mathrm{N}\mathrm{R}}_2^2}}} \end{gathered}$$

(5)

where Signal represents the photon counts from the backscattered laser signal, Noise represents the photon counts when no laser source is activated, and SNR_total is the total SNR of edge-channel 1 and 2.

A relation of the standard deviation of the error proportional to the inverse of the SNR (error ∝ 1/SNR) is considered [28], and the total error is written as

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left(\mathrm{v}\right)=\frac{1}{\Theta \left(\mathrm{v}\right)}\frac{1}{{\mathrm{S}\mathrm{N}\mathrm{R}}_{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}$$

(6)

The relationship between the average standard deviation (SD) of the wind speed error and altitude, as calculated from the actual LiDAR signal, is illustrated in Figure 3b.

2.2.2. Wind Perturbation

The intricate interplay of various factors, including gravity waves, planetary waves, and jet streams, among others, contributes to the apparently random patterns of wind in the middle atmosphere [40,41,42]. Leveraging the unique capabilities of our LiDAR location, which is strategically positioned to observe mountain gravity waves, we have gained remarkable insights into the nature of wind perturbations.

The altitude-dependent variation in air density plays a pivotal role in shaping the amplitude of wind perturbations, as it induces the changes in the oscillatory behavior of upward-propagating waves [43,44]. As the air density decreases with increasing altitude, upward waves tend to oscillate with greater amplitudes. At each altitude level, wind perturbation variations adhere to a Gaussian distribution [26,45], represented by the standard deviation (SD), denoted as “σ sigma”, which exhibits a distinct trend with altitude. To quantify this phenomenon, we systematically analyze a vast dataset comprising 40,000 raw wind measurements collected over 3 months, from October to December 2019. Our analysis focuses primarily on zonal wind profiles across various altitudes.

As the upward-propagating waves reach a certain altitude, the wave may be resonating with and absorbed by the background wind field. Such incidence of gravity wave-breaking appears to dominantly take place around 35~50 km in altitude [23,46,47,48]. Figure 3a shows the plot of the SD of the amplitude of the wind perturbation against the altitude. This aligns with our perturbation theory, where the perturbation increases along with the altitude and eventually decreases around the 35~50 km mark. At the same time, this perturbation trend follows a similar trend from ERA5’s modeling, which will later be used to generate the ground-truth wind profiles as the labels for the CNN network.

2.2.3. Wind Profile Reconstruction

In this step, an exhaustive analysis of each component of the wind profile is conducted, and wind profiles are simulated based on the information obtained above. Initially, 10,000 samples of background wind trends are generated using the wind trends extracted from both the LiDAR system and ERA5 dataset by applying a low pass Butterworth filter to their original wind profiles. Subsequently, the wind perturbations calculated in the preceding section are incorporated into the background wind profile, resulting in the generation of 40,000 distinct combinations of the “ground truth” of wind profiles. These ground-truth wind profiles serve as the labels or references for the CNN model. Leveraging the ground truth data, the raw LiDAR wind profile is simulated by incorporating the errors identified in Section 2.2.1 into the ground truth samples. The magnitude of the assigned error is determined by the randomly generated exponential signal-to-noise ratio (SNR) profiles during the simulation process, which emulates the signal attenuation from the increasing distance and the visibility of weather conditions. This is crucial because the range of the LiDAR signals can vary significantly, with certain days exhibiting signal ranges of only up to 30 km, while on others, detectable signals may extend up to 50–60 km.

The reconstructed LiDAR signal of the wind profile through our simulation is shown in Figure 4 (top). To boost accuracy, we also generated two additional channels: the SC wind profile and the Spline Transformer wind profile of the LiDAR data. We propose that the SC can detect the local details of the minor wind transitions, while the Spline Transformer profile can assist in ascertaining the overall wind trend.

2.3. Machine Learning

2.3.1. CNN Structure

The present work describes a customized U-net architecture implemented for wind speed analysis. Several attempts with other architectures such as SqueezeNet [5], ResNet [3], and purely customized CNN structure have also been investigated, but with less promising result. Comparing these architectures’ performances is beyond this paper’s scope but may be explored in future work.

The U-net was originally designed for image segmentation and noise cancellation by dropping redundant spatial information during its middle bottleneck layers. The encoder of the U-net is composed of convolutional layers, followed by ReLU activation layers [49], and a maxpooling layer [50] that contracts the spatial dimensions of the image while boosting the feature/channel space. In the middle layers, the same principle is followed as in the encoder, where the feature space is further extended. In the decoder, convolutional and ReLU layer combinations are employed to reduce both the spatial and feature space, followed by two convolutional transpose layers to enlarge the spatial dimension to the size of the original image. The full structure of the U-net is shown in Figure 5.

The input of the network is a 3-channel image of 220 × 500 pixels, and the output is a single-channel image of the same size. During the spatial contraction, the vertical space is only contracted by a small portion, while the horizontal space is contracted to one-quarter of the original dimension. This design concept aims to let the network focus on analyzing the noised raw data obtained at each altitude level of the wind, assuming a strong randomicity of the wind profile, and considering that the vertical relation of the wind profile has less effect. Each horizontal line of the network’s output image shows the probability distribution of the wind speed at a particular altitude. For computation along each line, it forms a classification problem at each pixel, each representing a class of the 1 m/s range of wind speed. Thus, the whole architecture can be seen as a multi-classification process.

To train the network, a total of 40,000 simulated samples with ground truth labels and 10,000 true LiDAR data with spectral centroid calculated labels are used. The data are split into a 60:20:20 train, test, and validation set ratio, respectively. The ADAM optimizer [51] and mean square error criterion is adopted with a selection of 3 × 10⁻⁴ learning rate and 50 batch-size for 25 epochs, and the overfitting occurs at approximately epoch 23.

2.3.2. Pre-Processing

The raw data collected by the LiDAR instrument are stored in the text file format. Each file contains photon counts from two Fabry–Perot Interferometer (FPI) channels, resulting in a total of 16,000 bin measurements arranged along the text rows. To ensure adequate signal strength, the range of 1600 to 8200 bins was selected for analysis, providing a maximum detection range of 53 km in altitude. The LiDAR data were commonly acquired over a daily period spanning from 11:00 p.m. to 8:00 a.m. at the Xinjiang location, with a detection rate of 40 s between each file.

To enhance signal quality at the far end, 48 files, representing the averaged wind profile of 30 min, were combined for each wind profile. The resulting wind profile was represented as a 220 × 500-pixel image, where the vertical axis corresponds to range gates from 10 km up to 53 km, and the horizontal axis is defined by the wind speed domain of −250 m/s to +250 m/s. Each pixel in this configuration represents the wind speed at a specific range gate level. In the near field between 10 km and 15 km, where the signal intensity is relatively strong, each of the 48 files generated one pixel for a total of 48 pixels in each row. As the measured height increases, the quantity of files utilized to form one pixel adjusts in response to the descending SNR. Conversely, at the far field beyond 45 km, the signal from all 48 files was combined into a single pixel point to compensate for the low signal strength. An example of the pre-processed simulated LiDAR signal is shown in Figure 4 (top), and the real LiDAR signal is shown in Figure 6.

2.3.3. Post-Processing

Figure 7 (top) illustrates the output of the CNN in the form of a single-channel image that is equal in size to the input. The computation of the wind profile, based on this CNN output, can be conducted using two distinct methods. The first approach involves utilizing the “argmax” function, as this represents the standard method in classification problems. As previously mentioned, the output forms a classification problem, where each pixel on the output image corresponds to a specific wind speed value within the 1 m/s domain, ranging from −250 m/s to 250 m/s, resulting in a total of 500 pixel sections in each horizontal line of the image that represents a single altitude level. The argmax function identifies the position of the top class of the wind speed section indicating the highest probability category for each horizontal line. By connecting all wind speed section positions from each altitude level, the resulting wind profile is depicted in Figure 8a.

For the second method, we implement the spectral centroid algorithm on the output image of the CNN, and the result is shown in Figure 8b. The methodology proffers several merits: (1) It is advantageous compared to conventional object classification, where classes are not invariably linearly connected. In contrast, the classifications within our wind speed section present a linear relation within the wind speed range of −250 m/s to +250 m/s. Such arrangement enables the spectral centroid algorithm to calculate the mean wind speed class on a per-line basis. (2) The spectral centroid technique takes a greater multitude of classes into consideration, which is especially beneficial for the low signal-to-noise ratio (SNR) domain. In such regions, the most probable wind speed class may not provide sufficient accuracy for precise classification, emphasizing the value of our method’s extensive class evaluation.

3. Results

3.1. CNN Outputs

In this section, we present a comparison between the outputs of the U-Net model and the traditional raw spectral centroid algorithm for both simulated and real LiDAR signals. Figure 7(top) illustrates the output of the simulated LiDAR signal, and the output of the real LiDAR signal shows a comparable pattern. The output images clearly depict the wind profile in the high SNR and intensity region at lower altitudes, where the certainty of top classes is relatively high. Conversely, in regions with lower SNR, the probabilities of top classes are widely distributed along each altitude level. As expected, the CNN produces lower intensity and probability at higher altitudes, in accordance with our theoretical understanding. Overall, the results demonstrate the effectiveness of the proposed approach in wind speed analysis, showing promise for future applications.

3.2. Wind Profile Evaluation for Simulated Signal

By employing the two techniques presented in Section 2.3.3, we derived the wind profile depicted in Figure 8 and juxtaposed it against the ground truth. Additionally, we included the SC and Gaussian-smoothed SC (GSSC) [21] outcomes, which were obtained using the raw input image data, for comparative purposes. We utilized the R-squared (R²) coefficient of determination (Formula (7)) as our assessment metric.

$$R^2=1-\frac{\sum {(V_{actual}-V_{predict})}^2}{\sum {(V_{actual}-V_{actual\_mean})}^2}$$

(7)

Our evaluation was conducted on the validation set to eliminate any bias arising from the training and testing sets. The results of the four methods are presented in

Table 1. Score List of Coefficient of Determination for all Four Methods.

Method	Mean	Max.	Min.
AMCNN	0.0126	0.5564	−0.5051
SCCNN	0.6141	0.8232	0.3119
SCR	−0.1680	0.5530	−0.9087
GSSC	0.4702	0.7779	0.0241

, where Mean, Max., and Min. represent the average, the minimum, and the maximum performance of a single wind profile after comparing the method’s result with the ground truth label, correspondingly. Notably, the spectral centroid of the CNN (SCCNN) outperforms the argmax method (AMCNN) in nearly all scenarios. A comparison of the two results can be found in Figure 8a,b. Among the traditional algorithms, shown in Figure 8c,d, the Gaussian-smoothed SC method (GSSC) outperforms the raw SC method (SCR). In terms of the R² performance, the SCCNN achieved a superior mean score of 0.607, which was 0.137 points higher than the GSSC method’s score of 0.470, while the other two methods underperformed at the mean of 0.0126 and −0.1680. Thus, we selected the SCCNN profile from the CNN output as our primary result and the GSSC profile from the raw data as the traditional processing method for all of the subsequent comparative analyses.

In Figure 9, we observe a high correlation of the regression analysis results for the SCCNN and GSSC, indicated by a majority of data points congregating near the ground truth line. However, a portion of these points diverges substantially from this line. These points with the high deviation are dominated primarily by the detection errors in the high-altitude domain due to the weak SNR signal, subsequently affected by the increasing fluctuation of the R ratio in Formula 1. Precise wind speed restoration of the high-uncertainty domain is notably challenging via conventional techniques, such as the GSSC. In contrast, the SCCNN is able to provide conditional predictions informed by its pre-training, addressing these high-uncertainty scenarios more adeptly. It can estimate each wind speed point through the adjacent points, the overall wind profile deflection, as well as the prevailing seasonal background wind trend, consequently leading to considerable error reduction.

3.2.1. Low SNR Scenario

During the validation process, we also assessed the performance of the cases under low signal-to-noise ratio (SNR) conditions. We simulated the LiDAR signal for low visibility days, such as those with cloudy, sandstorm, or strong moonlight backgrounds, by manually increasing the noise and decreasing the SNR at 30~40 km from 35~15 to 17~9. We randomly selected 100 low SNR wind profiles from the validation set and compared the results of all four methods. In the worst case, the SCR and AMCNN methods produced negative R² values that were close to −1, as shown in Table 1. Meanwhile, the SCCNN achieved an R² value of 0.3119, whereas the GSSC from the raw data obtained an R² value of 0.0241 in their minimal performance. On average, GSSC and SCCNN achieved an overall performance of R² values of 0.423 and 0.543, respectively.

3.2.2. High SNR (Near Field) and Low SNR (Far Field) Region Reanalysis

To perform a comprehensive analysis of the benefits of the CNN result, we segregated the low and high SNR regions (near field and far field) from each wind profile, allowing us to compare the two regions independently. The boundary line was set at the 37 km altitude level, that is, where the vertical resolution changes from 30 to 60 bins for a single range gate. We reanalyzed the data solely in the high SNR region of the same wind profiles from the validation set. Both GSSC and SCCNN methods performed admirably when the signal strength was relatively strong, achieving a remarkably high R² score of 0.826 and 0.912. The regression analysis score testified to the CNN result’s reliability by accurately restoring the wind profile in high SNR scenarios.

Next, we examined the low SNR profile region. After surpassing the 37 km boundary line, the accuracy of the traditional method GSSC dropped significantly, to 0.279, whereas the SCCNN outputs still exhibited an acceptable R² of 0.457. Therefore, we can conclude that the CNN outperforms the traditional SC method, notably in the low SNR region, where the CNN’s capability to restore the wind profile pattern is particularly evident. Instead of treating each LiDAR signal’s wind profile data individually, the CNN adopts the wind pattern at a specific level from the dataset at the given time interval. This confers a significant advantage to the CNN, enabling it to partially predict the wind speed even under low signal strength conditions, thereby achieving a substantial boost in wind profile reconstruction performance.

3.3. Wind Profile Evaluation for Real LiDAR Data

After a full assessment of the CNN outputs for simulated LiDAR signals, we evaluated its performance on real LiDAR data, as depicted in Figure 10 and Figure 11. A comparative analysis is performed between GSSC, SCCNN, and the ERA5 data at the same time period and location. The constructed real LiDAR image, shown in Figure 6, is identically manipulated with the simulated data by inputting it into our U-Net and applying the SC method on the output end. The LiDAR signal measurement was collected during the nocturnal hours of 31 October 2019, from Kolar, Xinjiang. The wind profiles for the duration were derived using both GSSC and SCCNN methodologies. The overview horizontal wind profile of the east–west orientation with a 30° zenith angle on a 6.5-h timeline is shown in Figure 10, providing a basis for comparative analysis.

The result of the GSSC, depicted in the top section of Figure 10 (top), reveals a conspicuous absence of the wind speed data in the higher-altitude regions, attributed to the application of an SNR threshold of 10, as determined by Equation (6). Contrarily, at lower altitudes, specifically below 40 km, the wind profiles generated by both GSSC and the SCCNN exhibit a significant overlap, with an R² score of 0.9343. This substantial concordance not only underscores the precision of our SCCNN model but also affirms the efficacy of the traditional GSSC approach, especially in cases where LiDAR signals are abundant and the GSSC result is reliable.

Referring to the performance of the simulated signal in Section 3.2, we posit that the SCCNN outputs yield a suitable precision under low SNR circumstances, thus surpassing GSSC in the detection range. As depicted in Figure 11a, there is considerable overlap between the results obtained from the GSSC and SCCNN methodologies; however, the SCCNN exhibits lower oscillation amplitudes as the altitude rises. Upon juxtaposing these results with ERA5 data, it is evident that the ERA5 dataset aligns with the background wind trends of our wind profiles. This alignment is attributed to the lower resolution of the ERA5 dataset, especially at altitudes beyond 37 km where its vertical resolution extends to 1 km. Given that the ERA5 wind profiles lack details on local wind perturbations, we compared them against our results’ background wind, which was derived using the previously mentioned Butterworth filter. Figure 11b reveals a strong alignment between the background wind trends and the ERA5 wind profile, with the SCCNN method achieving an R² score of 0.7653. This score is significantly higher, by 0.0738, compared to the GSSC method’s score of 0.6915. This outcome represents the most favorable performance in the comparative analyses of seven ERA5 wind profiles recorded from 9:00 PM to 3:00 AM, consistent with the timeline presented in Figure 10 and within the constraints of ERA5’s hourly temporal resolution. The SCCNN method’s average performance yielded a score of 0.3157, notably higher than the GSSC method’s score of 0.1693, thus establishing a performance advantage of 0.1464 for SCCNN. Further details on the R² scores are provided in

Table 2. Score List of Coefficient of Determination for ERA5 Data’s Comparative Analysis.

Time	SCCNN	GSSC
31 October, 9:00 p.m.	0.4536	0.3068
10:00 p.m.	0.4669	0.3676
11:00 p.m.	0.3312	0.2336
1 November, 00:00 a.m.	0.0985	0.1552
1:00 a.m.	−0.0429	−0.5710
2:00 a.m.	0.7653	0.6915
3:00 a.m.	0.1371	0.0010
Mean	0.3157	0.1693

.

We conducted error estimations for both the SCCNN result and the traditional GSSC method from a randomly selected set of 100 wind profiles. In the case of the SCCNN, we estimated the error based on its performance during simulation, while the error of the GSSC was derived from real signals utilizing Formula 6 outlined in Section 2.2.1. Our evaluation reveals that the error bar reaches 10.4 m/s for SCCNN and 11.5 m/s for GSSC at the 30 km mark on average. Notably, the error increments start escalating sharply beyond 40 km, and the SCCNN changes at a slower rate than that of the GSSC. Specifically, at 40 km, the SD of the error for SCCNN is around 16.2 m/s, increasing to 27.5 m/s at 43 km. In contrast, the SD of GSSC’s error is estimated at about 24.3 m/s at 40 km, rising to 35.3 m/s at 43 km. This comparative analysis underscores a significant enhancement in accuracy attributable to our methodology.

4. Discussion

In this study, we investigated the performance of convolutional neural network (SCCNN, AMCNN) and traditional spectral centroid (SCR, GSSC) methods for wind profile signal processing of an ICDL. Our results show that the SCCNN method outperforms the GSSC method with a mean score of 0.6071 compared to 0.4702 in simulation; and a score of 0.3157 compared to 0.1693 in field measurement compared to ERA5 data. This is particularly evident at higher altitudes, where the LiDAR signal with the traditional algorithm is insufficient to provide reliable wind field information.

Moreover, the SCCNN method demonstrates superior overall performance in accomplishing this task. Despite these findings, it is important to acknowledge the limitations of our work. Firstly, the wind profile generated or detected in this study does not represent the true wind field flowing in the atmosphere. Instead, we adopted the average wind speed within each altitude level based on the range gate’s resolution, resulting in reduced accuracy in the spatial domain.

Additionally, during the wind profile reconstruction, we made several assumptions: (1) we assumed the random error to be 2 m/s [18] to include the vertical wind perturbation and other unconsidered aspects that may affect our measurement; (2) we assumed that the wind profile mainly consisted of perturbations from gravity waves, allowing us to separate and consider the perturbation and background individually during the wind profile reconstruction; and (3) we assumed that the amplitude of the wind perturbation at a single altitude level followed an idealized Gaussian distribution. These assumptions should be taken into account when interpreting the results of this study, and further improvements can be made to address these limitations.

Lastly, in Section 3.3, our LiDAR observations could potentially be verified through additional measurements from balloons or rockets. Currently, our analysis is confined to comparing the outcomes of SCCNN and GSSC against the ERA5 dataset. It is important to note that the ERA5 dataset may not accurately capture the original wind field and could include errors that surpass those in our observations. Moreover, the ERA5 dataset differs from our LiDAR in both temporal and spatial resolutions. Specifically, our LiDAR data are collected over 30 min, whereas ERA5 operates on a one-hour temporal resolution. The spatial resolution of the ERA5 dataset is 0.25° × 0.25° for both longitude and latitude, which does not align exactly with our observation site. Therefore, it should be recognized that the measurements from our LiDAR and the ERA5 dataset do not originate from an identical wind field. Despite these differences, such discrepancies are not deemed crucial for the purposes of our analysis.

5. Conclusions

In conclusion, this study highlights the transformative potential of deep learning in enhancing ICDL data processing research methodologies. We commenced with a rigorous analysis of LiDAR data alongside the ERA5 dataset, utilizing these as foundational elements for our wind profile simulations. These simulations were instrumental in training a customized U-Net architecture, specifically tailored for the task of wind profile reconstruction. The efficacy of our approach was validated by comparing the performance of our U-Net model against the traditional SC algorithm, with evaluations conducted on both the simulated dataset and the actual LiDAR signal data. Our findings indicate that the U-Net model outperforms the SC algorithm significantly, particularly in low signal-to-noise ratio environments.

In our forthcoming research, we anticipate proposing several improvements based on the work presented herein. Specifically, this study focused solely on analyzing the zonal wind, given that the zonal wind at Xinjiang exhibits a highly characteristic profile; the wind field in this region mainly produces robust eastward wind [18,32,52] at the observation time and height. Subsequent analysis of the meridional wind will enable us to combine the two wind profiles, thereby obtaining full wind speed and direction. In our verification process, incorporating measurements from additional instruments could enhance the comparative analysis, thereby increasing the reliability and validity of the LiDAR measurement. Moreover, while the U-net architecture presented in this paper is relatively simple, more extensive comparisons and fine-tuning of different convolutional neural network architectures could prove to be a fruitful avenue for further investigation. Another approach is to expand our findings by considering the effects in the time domain; with a fixed data acquisition rate of the LiDAR, the CNN can be adopted to generate contemporary wind profiles between two consecutive LiDAR detections, thus increasing the LiDAR’s detection rate in time resolution. Finally, we plan to integrate a field-programmable gate array (FPGA) into our LiDAR’s hardware to enhance the speed of both our CNN’s training and operation. We believe that integrating such advanced technologies will revolutionize ICDL data processing research, setting a new benchmark for future studies.