Focusing Algorithm of Range Profile for Plasma-Sheath-Enveloped Target
Abstract
:1. Introduction
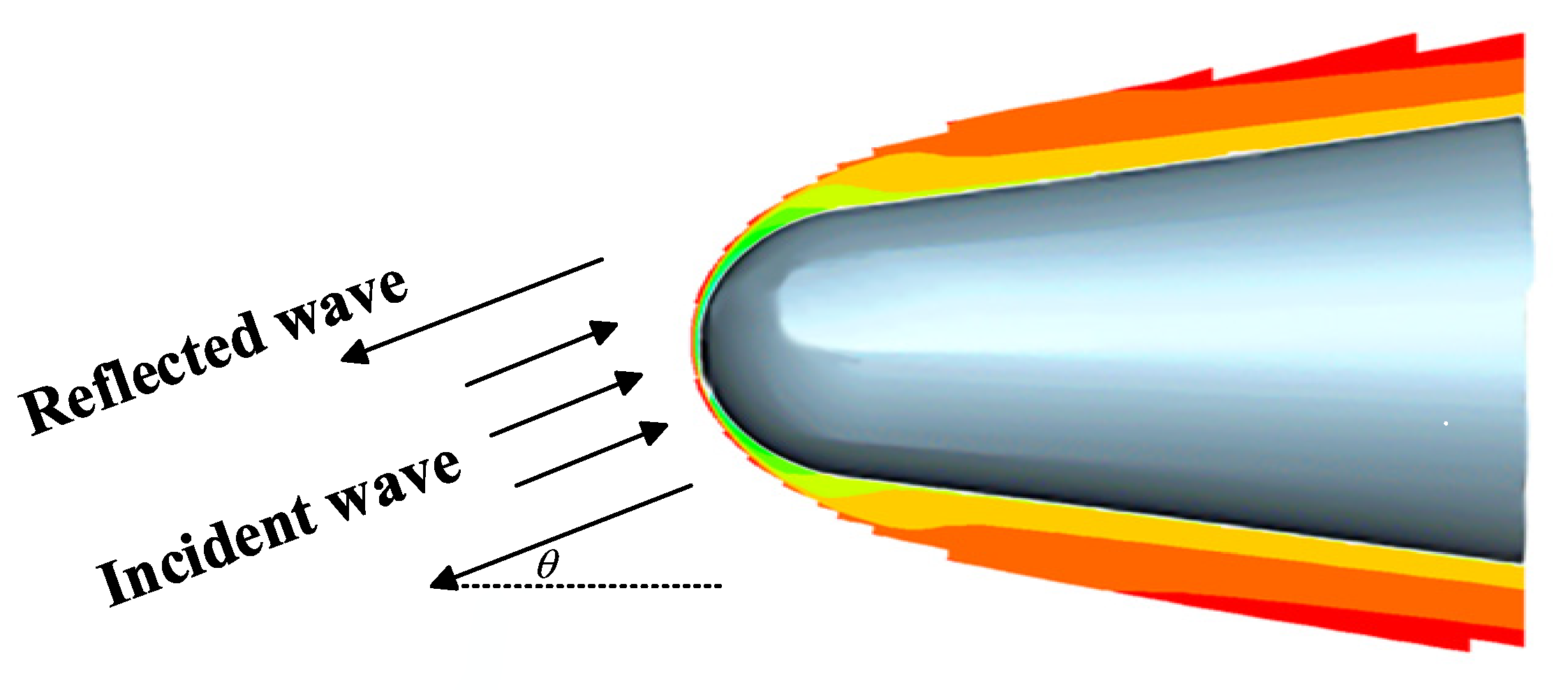
2. Analysis of EM Wave Reflection Property the Plasma Sheath
2.1. Calculation of the Plasma Reflection Coefficients
2.2. EM Reflection Property in the Plasma Sheath
3. Wideband Radar Echo Model of the Plasma-Sheath-Enveloped Target
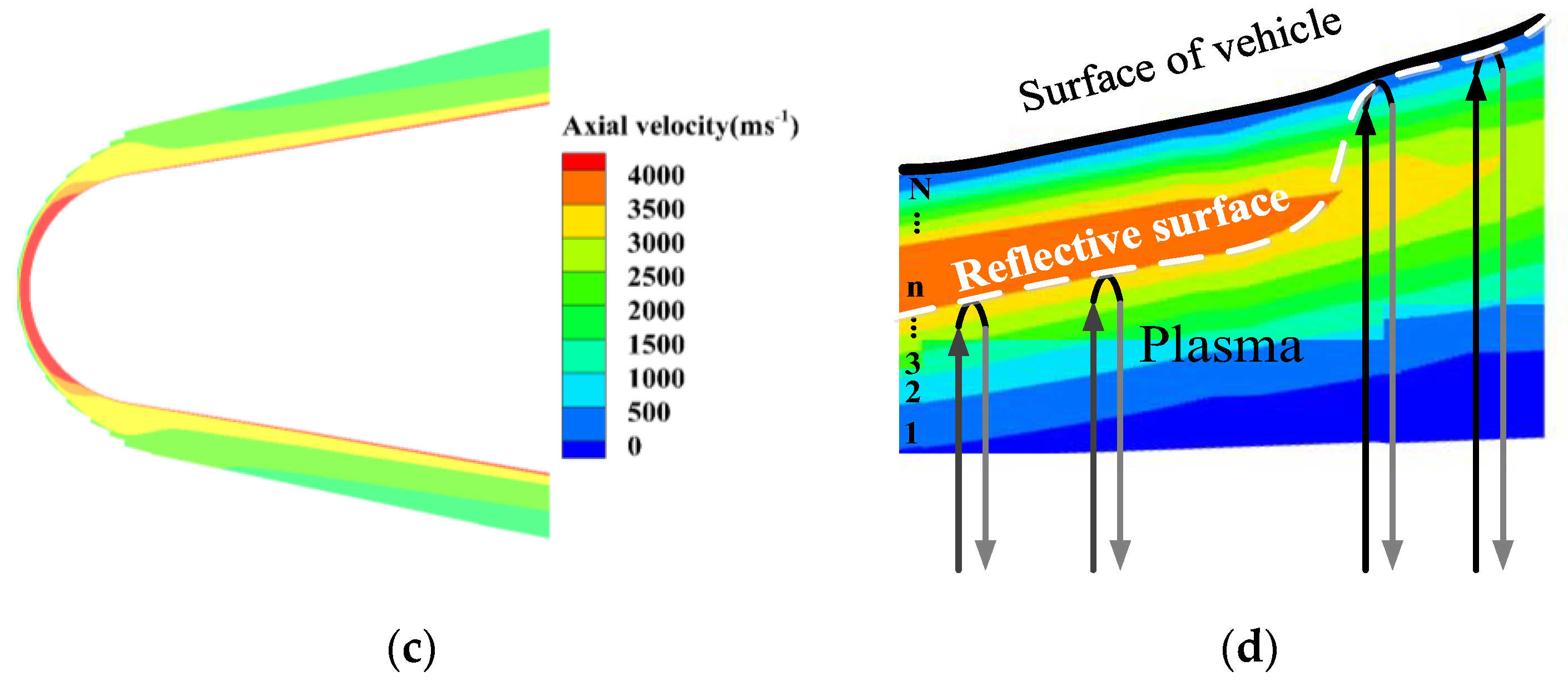
- Due to the non-uniform property of the plasma, radar signals penetrate through different propagation courses at different sub-regions for the plasma-sheath-enveloped target, resulting in varying incident depths in the sheath. As a result, the signal amplitude and its phase are weakened and distorted significantly.
- When the speed of the vehicle is greater than 10 Ma, the “stop-and-go” assumption used for low-speed targets is no longer valid and the target motion in the intra-pulse must be considered. The high speed and high maneuvering of the target will result in intra-pulse mismatch and inter-pulse range migration. Therefore, the offset and defocus phenomenon caused by an intra-pulse mismatch should be addressed to achieve a precise 1-D range profile.
- (a)
- The hypersonic target flies at a steady state with a constant velocity, which means the acceleration of the target can be ignored.
- (b)
- Time-varying characteristics of the plasma sheath are not considered. Specifically, the plasma sheath causes a fixed amplitude attenuation and a fixed phase shift for each scatter point.
- (c)
- The angle between the motion trajectory and the radar line of sight stays constant during the observation period. In this paper we assume .
4. Focusing Algorithm for 1-D Range Profile in the Presence of Plasma Sheath
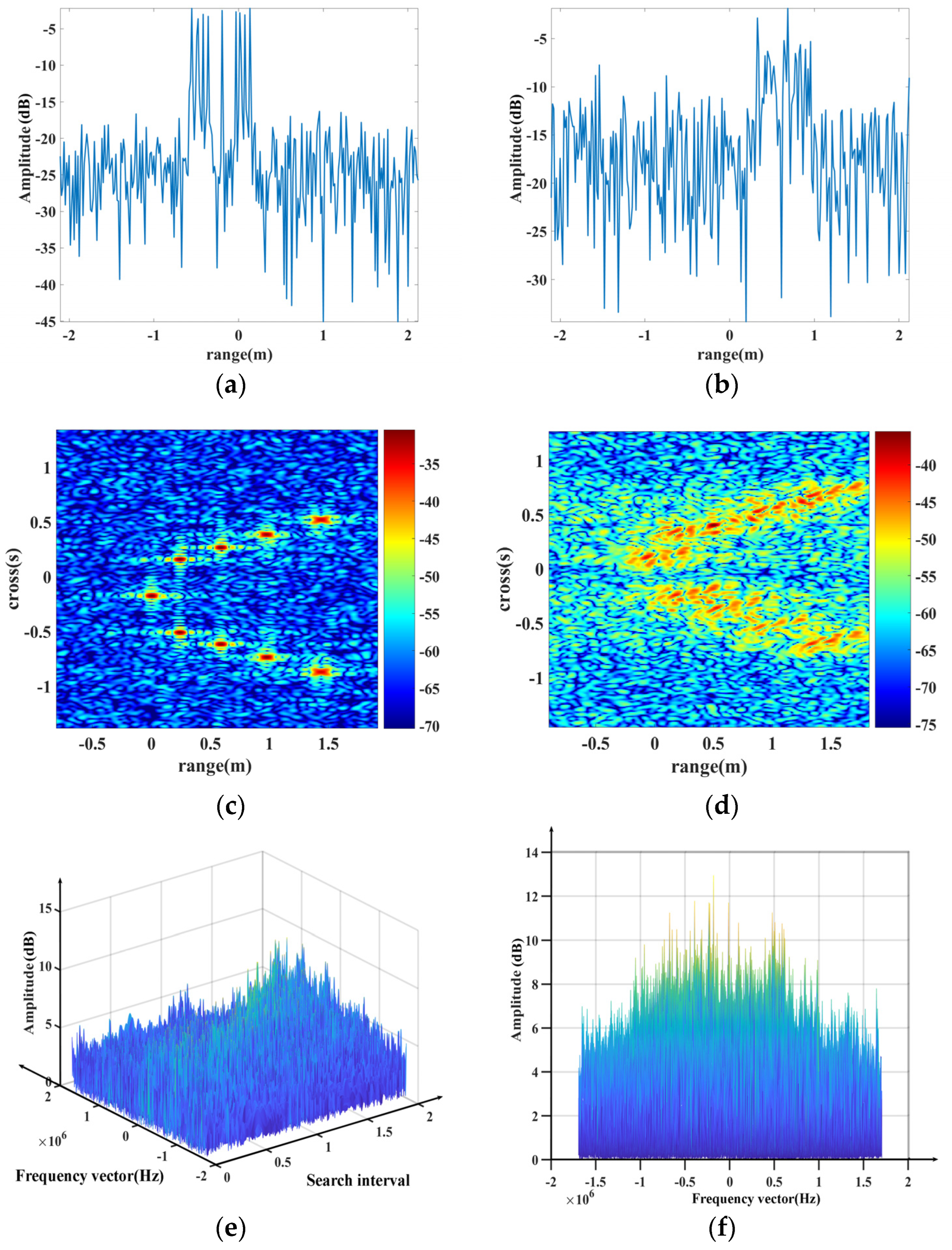
5. Simulation and Analysis
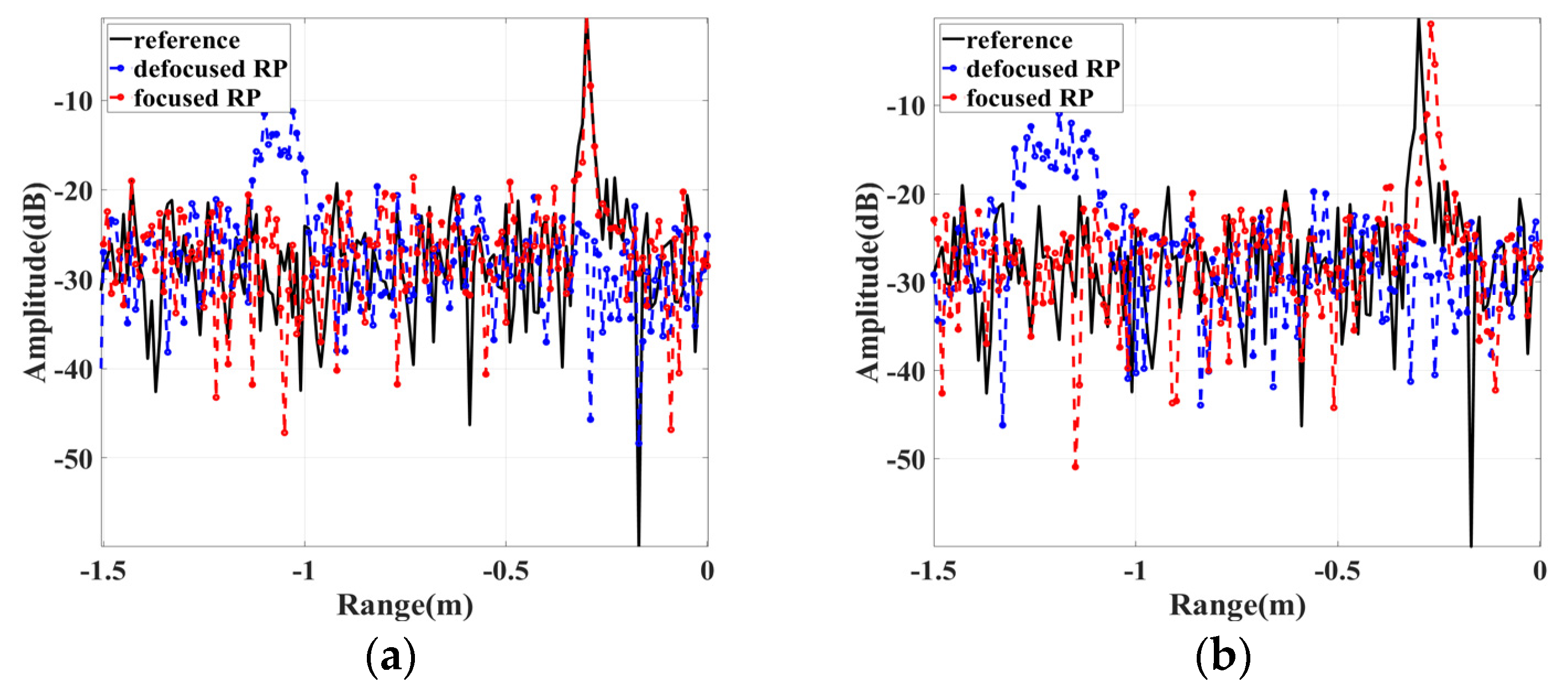
5.1. Validation of the Proposed Algorithm over the Signal Scatter
5.2. Validation of the Proposed Algorithm over the RAM-C
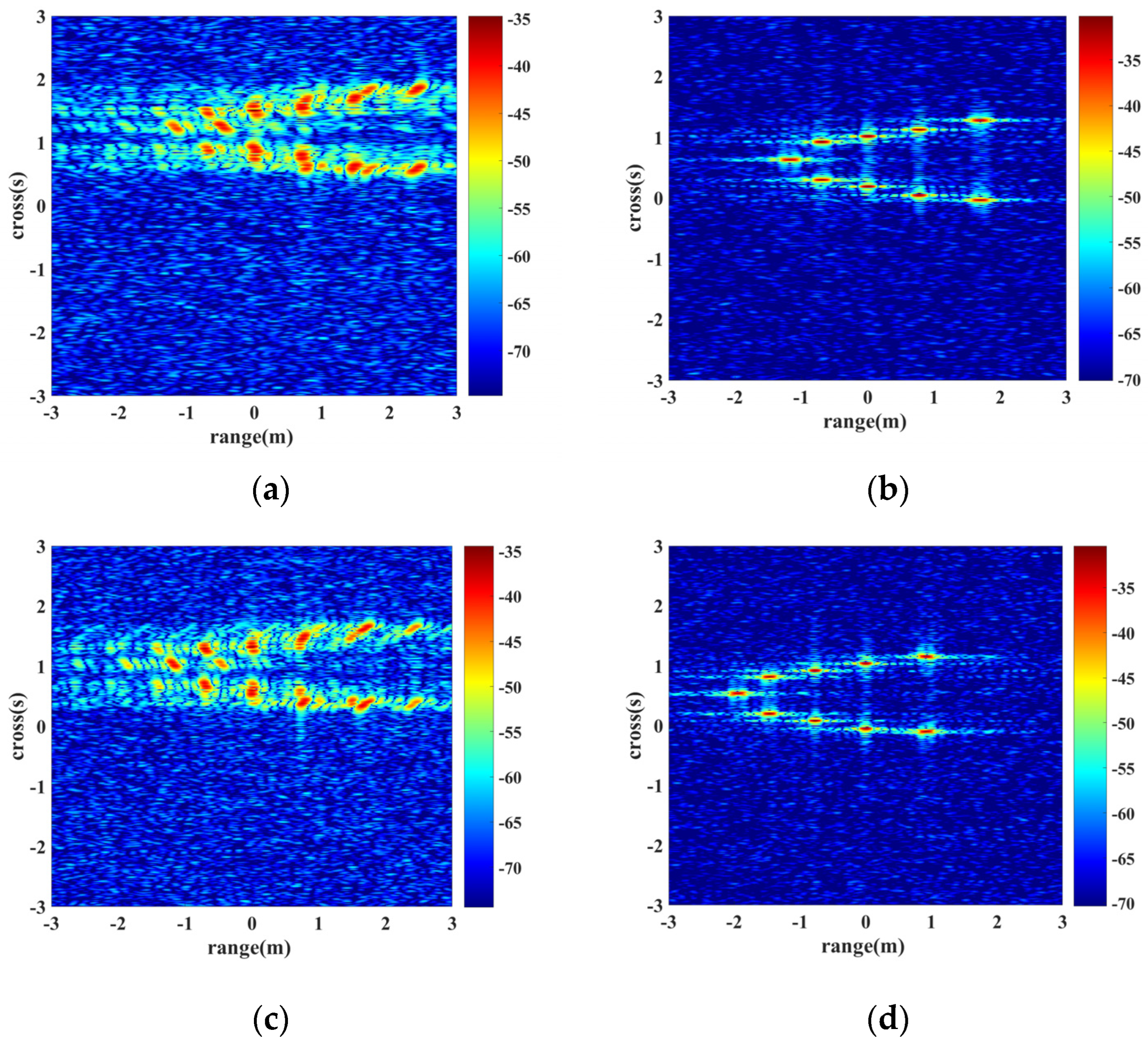
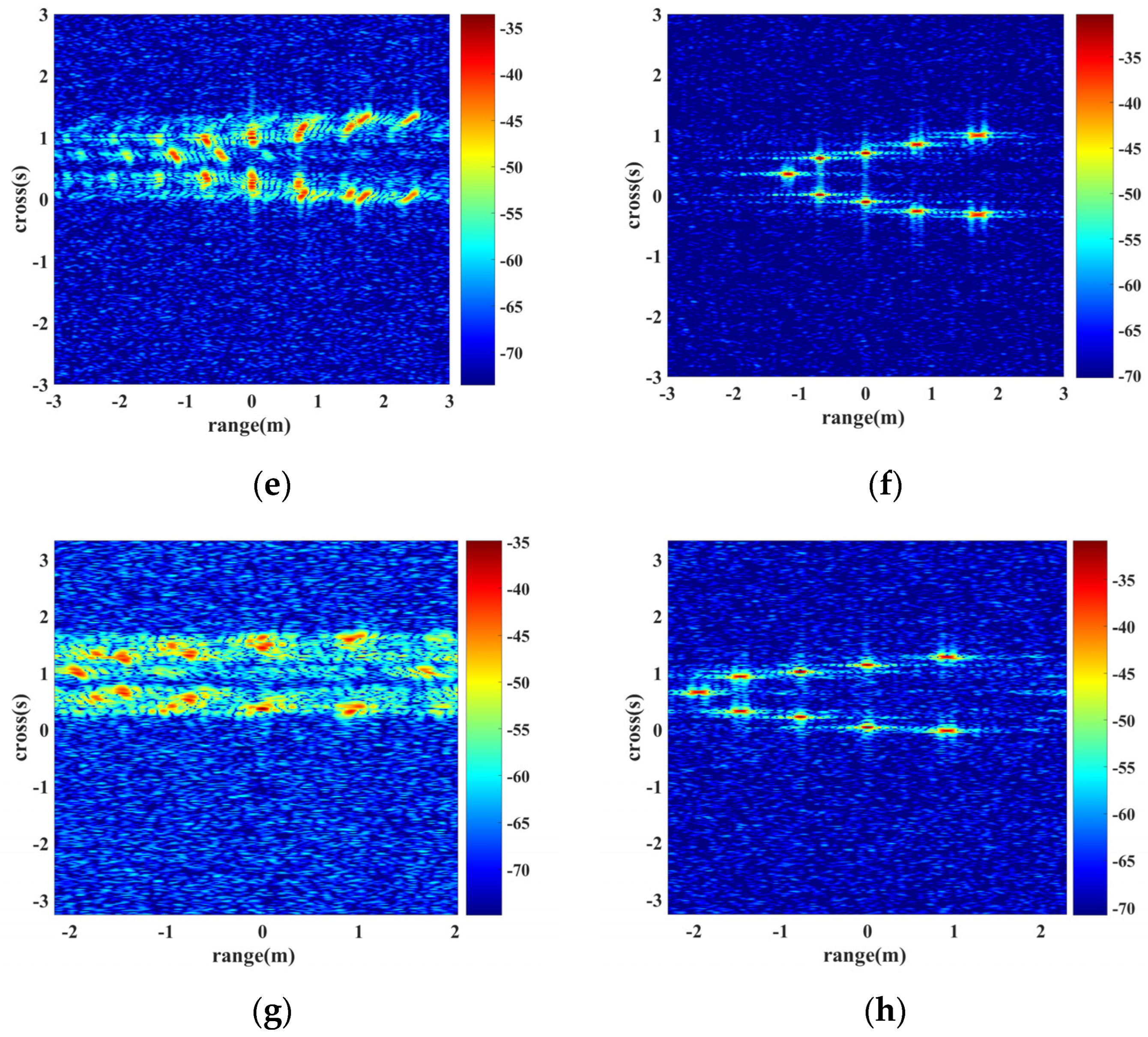
5.3. ISAR Imaging
6. Conclusions
- (1)
- The wideband radar signal inserted into the non-uniform plasma sheath suffers from varied incident depths, reflection intensities and coupled plasma velocities. As a result, the scatter points in different regions of the plasma-sheath-enveloped target have varied reflection intensities and coupled velocities. It induces severe phase error for the wideband radar echo, and causes significantly displacement and broadening for the de-chirp signal, leading to severe 1-D range profile defocusing.
- (2)
- The plasma sheath coupled velocities bring on the primary and secondary phase terms for the de-chirp signal, resulting in the displacement and broadening of the range profile. In this study, the proposed algorithm implemented the range profile focusing procedure by plasma sheath velocity estimation and phase compensation. Further, the induced CLEAN strategy guaranteed that multicomponent LFM signal can be estimated and each scatter has been accurately compensated. Finally, the feasibility and superior performance of the proposed FRFT-CLEAN-based focusing algorithm is demonstrated via simulation results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Li, K.; Liu, Y.; Zhou, Y.; Li, X.; Liu, Y. Study of the influence of time-varying plasma sheath on radar echo signal. IEEE Trans. Plasma Sci. 2017, 68, 3166–3176. [Google Scholar] [CrossRef]
- Li, J.; Gong, T.; Yang, S.; Guo, L.; Cheng, M. Influence of hypersonic turbulence in plasma sheath on synthetic aperture radar imaging. IET Microw. Antennas Propag. 2017, 11, 2223–2227. [Google Scholar]
- Zhang, X.; Liu, Y.; Bai, B.; Li, X.; Shen, F.; Chen, X.Y.; Zhao, L. Establishment of a Wideband Radar Scattering Center Model of a Plasma Sheath. IEEE Access 2019, 7, 140402–140410. [Google Scholar] [CrossRef]
- Swift, C.T.; Beck, F.B.; Thomson, J.; Castellow, S.L. Ram-III S-Band Diagnostic Experiment. ElectroMagn. Syst. 1970. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Li, B.; Descombes, S.; Lanteri, S. An Exponential-Based DGTD Method for Modeling 3-D Plasma-Surrounded Hypersonic Vehicles. IEEE Trans. Antennas Propag. 2020, 68, 3847–3858. [Google Scholar] [CrossRef]
- Hartunian, R.A.; Stewart, G.E.; Fergason, S.D.; Curtiss, T.J.; Seibold, R.W. Causes and Mitigation of Radio Frequency (RF) Blackout during Reentry of Reusable Launch Vehicles; Aerospace Corporation: El Segundo, CA, USA, 2007; pp. 1–103. [Google Scholar]
- Guo, Y.-G.L.L.-X.; Li, J.-T. Hypersonic Vehicle Plasma Sheath and Electromagnetic Characteristics Data. In Manual Beijing China: Science; Science Press: Beijing, China, 2019; pp. 33–60. [Google Scholar]
- Kashiwa, T.; Yoshida, N.; Fukai, I. Transient analysis of a magnetized plasma in three-dimensional space. IEEE Trans. Antennas Propag. 1988, 36, 1096–1105. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Wei, H.; Liu, Y.; Shi, L.; Yao, B.; Li, X. A 3-D total-field/scattered field plane-wave source for the FDTD analysis of reentry plasma sheath. IEEE Trans. Antennas Propag. 2020, 68, 6214–6225. [Google Scholar] [CrossRef]
- Soliman, E.A.; Helaly, A.; Megahed, A.A. Propagation of electromagnetic waves in planar bounded plasma region. Prog. ElectroMagn. Res. 2007, 67, 25–37. [Google Scholar] [CrossRef]
- Bai, B.; Li, X.; Liu, Y.; Xu, J.; Shi, L.; Xie, K. Effects of reentry plasma sheath on the polarization properties of obliquely incident EM waves. IEEE Trans. Antennas Propag. 2014, 42, 3365–3372. [Google Scholar] [CrossRef]
- Kojima, T.; Higashi, T.; Itakura, K. Reflection and transmission of electromagnetic waves obliquely incident upon a moving compressible plasma slab. IEEE Trans. Antennas Propag. 1972, 20, 398–400. [Google Scholar] [CrossRef]
- Laroussi, M.; Roth, J.R. Numerical calculation of the reflection, absorption, and transmission of microwaves by a nonuniform plasma slab. IEEE Trans. Plasma Sci. 1993, 21, 366–372. [Google Scholar] [CrossRef]
- Yang, H.W.; Liu, Y. Numerical analysis of the reflection and absorption of electromagnetic wave in nonuniform magnetized plasma slab. Optik 2012, 123, 371–375. [Google Scholar] [CrossRef]
- Liu, Z.; Bao, W.; Li, X.; Liu, D.; Bai, B. Effects of pressure variation on polarization properties of obliquely incident RF waves in re-entry plasma sheath. IEEE Trans. Plasma Sci. 2015, 43, 3147–3154. [Google Scholar] [CrossRef]
- Lin, T.C.; Sproul, L.K. Influence of reentry turbulent plasma fluctuation on EM wave propagation. Comput. Fluids 2006, 35, 703–714. [Google Scholar] [CrossRef]
- Roberds, N.A.; Young, M.W.; Miller, N.E.; Logemann, C.; Statom, T.K.; Wagnild, R.M. Parasitic Modulation of Microwave Signals by a Hypersonic Plasma Layer. IEEE Trans. Plasma Sci. 2024, 1, 1–10. [Google Scholar] [CrossRef]
- Sotnikov, V.I.; Leboeuf, J.N.; Mudaliar, S. Scattering of electromagnetic waves in the presence of wave turbulence excited by a flow with velocity shear. IEEE Trans. Plasma Sci. 2010, 38, 2208–2218. [Google Scholar] [CrossRef]
- He, G.; Zhan, Y.; Zhang, J.; Ge, N. Characterization of the Dynamic Effects of the Reentry Plasma Sheath on Electromagnetic Wave Propagation. IEEE Trans. Plasma Sci. 2016, 44, 232–238. [Google Scholar] [CrossRef]
- He, G.; Zhan, Y.; Ge, N.; Pei, Y.; Wu, B. Measuring the Time-Varying Channel Characteristics of the Plasma Sheath from the Reflected Signal. IEEE Trans. Plasma Sci. 2014, 42, 3975–3981. [Google Scholar] [CrossRef]
- Sha, Y.; Zhang, H.; Guo, X. Analyses of Electromagnetic Properties of a Hypersonic Object With Plasma Sheath. IEEE Trans. Antennas Propag. 2019, 67, 2470–2481. [Google Scholar] [CrossRef]
- Chen, X.; Shen, F.; Liu, Y.; Ai, W.; Li, X.P. Improved Scattering-Matrix Method and its Application to Analysis of Electromagnetic Wave Reflected by Reentry Plasma Sheath. IEEE Trans. Plasma Sci. 2018, 46, 1755–1767. [Google Scholar] [CrossRef]
- Chen, X.; Shen, F.; Liu, Y.; Li, X.; Ai, W. Radar detection of plasma-covered reentry object based on crossed two-component LFM signa. Appl. Comput. Electromagn. Soc. J. 2018, 33, 665–674. [Google Scholar]
- Ding, Y.; Bai, B.; Gao, H.; Niu, G.; Shen, F.; Liu, Y.; Li, X. An Analysis of Radar Detection on a Plasma Sheath Covered Reentry Target. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4255–4268. [Google Scholar] [CrossRef]
- Ding, Y.; Bai, B.; Gao, H.; Liu, Y.; Li, X.; Zhao, M. Method of Detecting a Target Enveloped by a Plasma Sheath Based on Doppler Frequency Compensation. IEEE Trans. Plasma Sci. 2020, 48, 4103–4111. [Google Scholar] [CrossRef]
- Xie, Y.; Li, X.; Shen, F.; Bai, B.; Liu, Y.; Chen, X.; Shi, L. Analysis of inverse synthetic aperture radar imaging in the presence of time-varying plasma sheath. Plasma Sci. Technol. 2022, 3, 19–32. [Google Scholar] [CrossRef]
- Xie, Y.; Li, X.; Shen, F.; Mao, Z.; Bai, B.; Chen, X. Influence of Plasma Sheath’s Velocity Field on ISAR Imaging of Hypersonic Target. Remote Sens. 2022, 14, 3799. [Google Scholar] [CrossRef]
- Zheng, B.; Jiangting, L.; Lixin, G.; Luo, X. Analyzing the Electromagnetic Scattering Characteristics of a Hypersonic Vehicle Based on the Inhomogeneity Zonal Medium Model. IEEE Trans. Antennas Propag. 2021, 69, 971–982. [Google Scholar]
- Zheng, B.; Jiangting, L.; Lixin, G. ISAR Imaging Analysis of a Hypersonic Vehicle Covered with Plasma Sheath. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]




| Initialization: , and are zero, is the signal of the measured data after mixing with the reference signal. |
| Step 1: Apply the FRFT transform to the signal and obtain energy distribution on the plane using Equation (14). Then estimate the chirp rate and initial frequency of the strongest components through peak search using Equations (16) and (17), respectively. |
| Step 2: Estimate the coupled velocity induced by the plasma using Equation (18), and then construct the compensation function using Equation (19). |
| Step 3: Implement the -th order () FRFT over the signal, and design a proper narrow band-stop filter with center frequency to filter out the strongest component of the signal. |
| Step 4: Conduct the -th order IFRFT over the filtered signal to transform it back to the time domain (called residual signal); |
| Step 5: Subtract residual signal from the signal to extract the strongest component, and then multiply it with the compensation function to achieve the defocus signal . Set and . |
| Step 6: Repeat the above steps until the residual signal energy is under a certain threshold, or else implement the FT over the to obtain a focused range profile. |
| Case | () | () | Error | Before | After | ||
|---|---|---|---|---|---|---|---|
| PSLR (dB) | ISLR (dB) | PSLR (dB) | ISLR (dB) | ||||
| 1 | 5100 | 5183 | 1.63% | −0.8419 | 7.3152 | −8.8674 | −4.4451 |
| 2 | 6800 | 6871 | 1.04% | −0.5857 | 5.2513 | −6.5754 | −4.1100 |
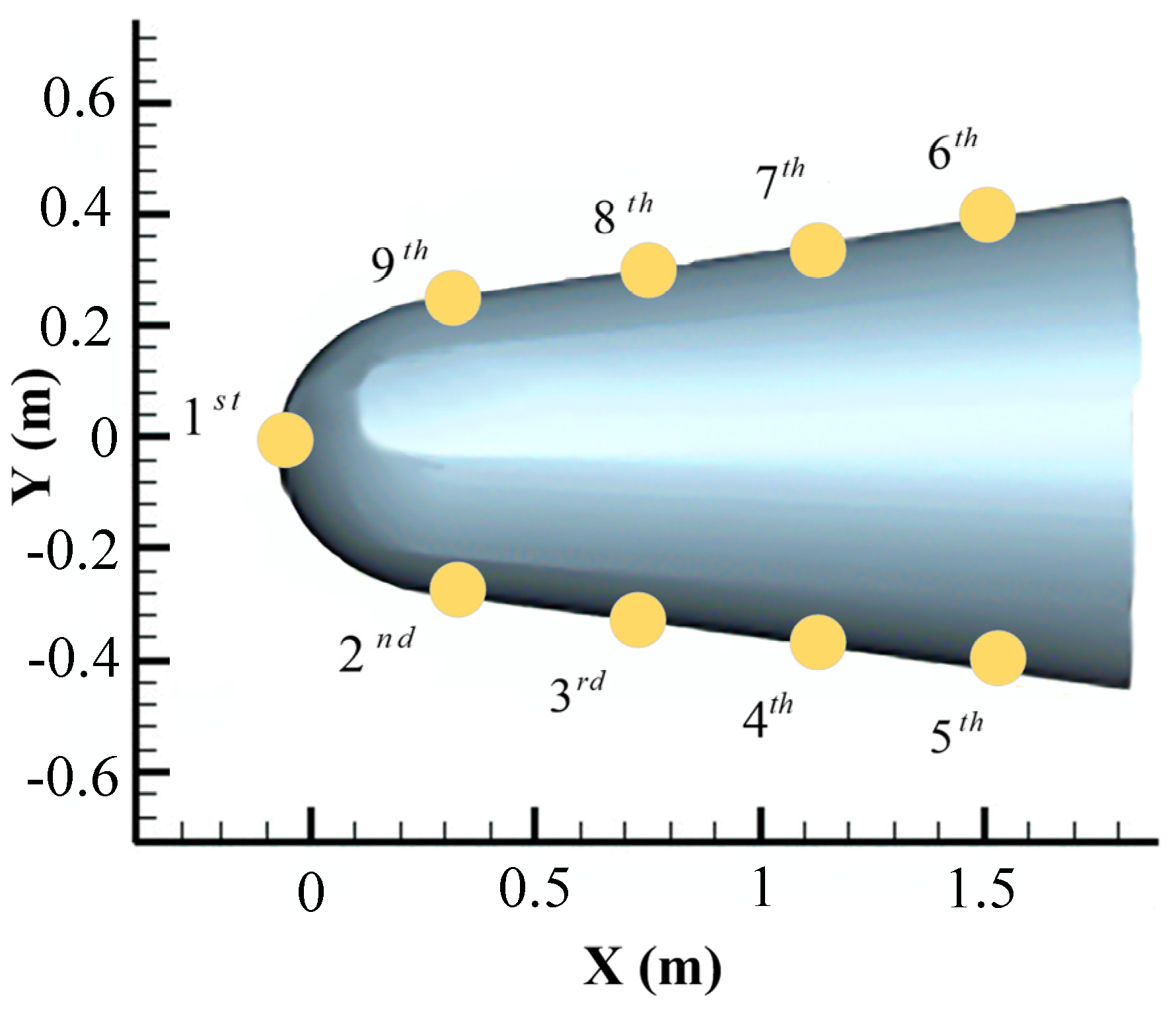
| Scatter | (m−3) | Incident Depth (m) | (dB) | (rad) | (ms−1) |
|---|---|---|---|---|---|
| 1 | 1.74 × 1020 | 0.017 | −5.5 | −1.35 | 6243 |
| 2 | 7.62 × 1018 | 0.053 | −8.7 | 1.04 | 4045 |
| 3 | 4.74 × 1018 | 0.063 | −10.4 | −0.18 | 2098 |
| 4 | 3.28 × 1018 | 0.074 | −11.1 | 0.96 | 1898 |
| 5 | 8.94 × 1017 | 0.093 | −11.5 | −1.24 | 6800 |
| 6 | 9.01 × 1017 | 0.093 | −11.6 | −1.24 | 6800 |
| 7 | 3.27 × 1018 | 0.074 | −11.3 | 0.96 | 1889 |
| 8 | 4.71 × 1018 | 0.063 | −10.5 | −0.19 | 2104 |
| 9 | 7.65 × 1018 | 0.053 | −8.6 | 1.04 | 4051 |
| Scatter | ) | ) | Error (%) | Before | After | ||
|---|---|---|---|---|---|---|---|
| PSLR (dB) | ISLR (dB) | PSLR (dB) | ISLR (dB) | ||||
| 1 | 6243 | 6460 | 3.47 | −0.2442 | 4.7684 | −7.8629 | −3.8451 |
| 2 | 4045 | 4080 | 0.87 | −0.7981 | 3.9968 | −8.2546 | −3.8649 |
| 3 | 2098 | 2175 | 3.67 | −0.3940 | 5.9896 | −6.9665 | −4.5842 |
| 4 | 1898 | 1807 | 4.79 | −0.2874 | 3.5545 | −6.8457 | −4.0987 |
| 5 | 6800 | 7129 | 4.84 | −0.2798 | 5.3415 | −7.9983 | −3.2251 |
| 6 | 6800 | 6493 | 4.51 | −0.3124 | 5.8736 | −8.5645 | −3.7401 |
| 7 | 1889 | 1812 | 4.08 | −0.2983 | 3.7425 | −8.0118 | −3.0644 |
| 8 | 2104 | 2141 | 1.76 | −0.6994 | 3.7624 | −7.9429 | −4.6866 |
| 9 | 4051 | 4082 | 0.77 | −0.6655 | 4.5120 | −8.9895 | −3.1445 |
| Average | 3.20 | −0.4421 | 4.6157 | −7.9374 | −3.8060 | ||
| Scene | RD | Proposed | ||||
|---|---|---|---|---|---|---|
| PSNR (dB) | SSIM (dB) | Time (s) | PSNR (dB) | SSIM (dB) | Time (s) | |
| (50 km, 15 Ma) | 24.9126 | 0.1346 | 2.44 | 29.8316 | 0.3641 | 5.01 |
| (40 km, 15 Ma) | 24.8151 | 0.1291 | 2.76 | 29.9001 | 0.3552 | 4.86 |
| (30 km, 15 Ma) | 24.9552 | 0.1469 | 2.60 | 29.7269 | 0.3502 | 4.77 |
| (30 km, 25 Ma) | 25.0023 | 0.1226 | 2.92 | 29.2487 | 0.3142 | 4.92 |
| Average | 24.9213 | 0.1333 | 2.68 | 29.6768 | 0.3459 | 4.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, F.; Chen, X.; Bai, B.; Liu, Y.; Li, X.; Zhang, Z. Focusing Algorithm of Range Profile for Plasma-Sheath-Enveloped Target. Remote Sens. 2024, 16, 1475. https://doi.org/10.3390/rs16081475
Shen F, Chen X, Bai B, Liu Y, Li X, Zhang Z. Focusing Algorithm of Range Profile for Plasma-Sheath-Enveloped Target. Remote Sensing. 2024; 16(8):1475. https://doi.org/10.3390/rs16081475
Chicago/Turabian StyleShen, Fangfang, Xuyang Chen, Bowen Bai, Yanming Liu, Xiaoping Li, and Zherui Zhang. 2024. "Focusing Algorithm of Range Profile for Plasma-Sheath-Enveloped Target" Remote Sensing 16, no. 8: 1475. https://doi.org/10.3390/rs16081475
APA StyleShen, F., Chen, X., Bai, B., Liu, Y., Li, X., & Zhang, Z. (2024). Focusing Algorithm of Range Profile for Plasma-Sheath-Enveloped Target. Remote Sensing, 16(8), 1475. https://doi.org/10.3390/rs16081475






