Solar Wind Charge-Exchange X-ray Emissions from the O5+ Ions in the Earth’s Magnetosheath
Abstract
:1. Introduction
2. Methods
2.1. SWCX Mechanism
2.2. 3-D Global Hybrid Model
2.3. 3-D Geocoronal Hydrogen Model
2.4. SASAL
3. Results
3.1. Distributions of O6+ Ions and Hydrogen Atoms
3.2. Spectrum of O6+ Ions during SWCX Process
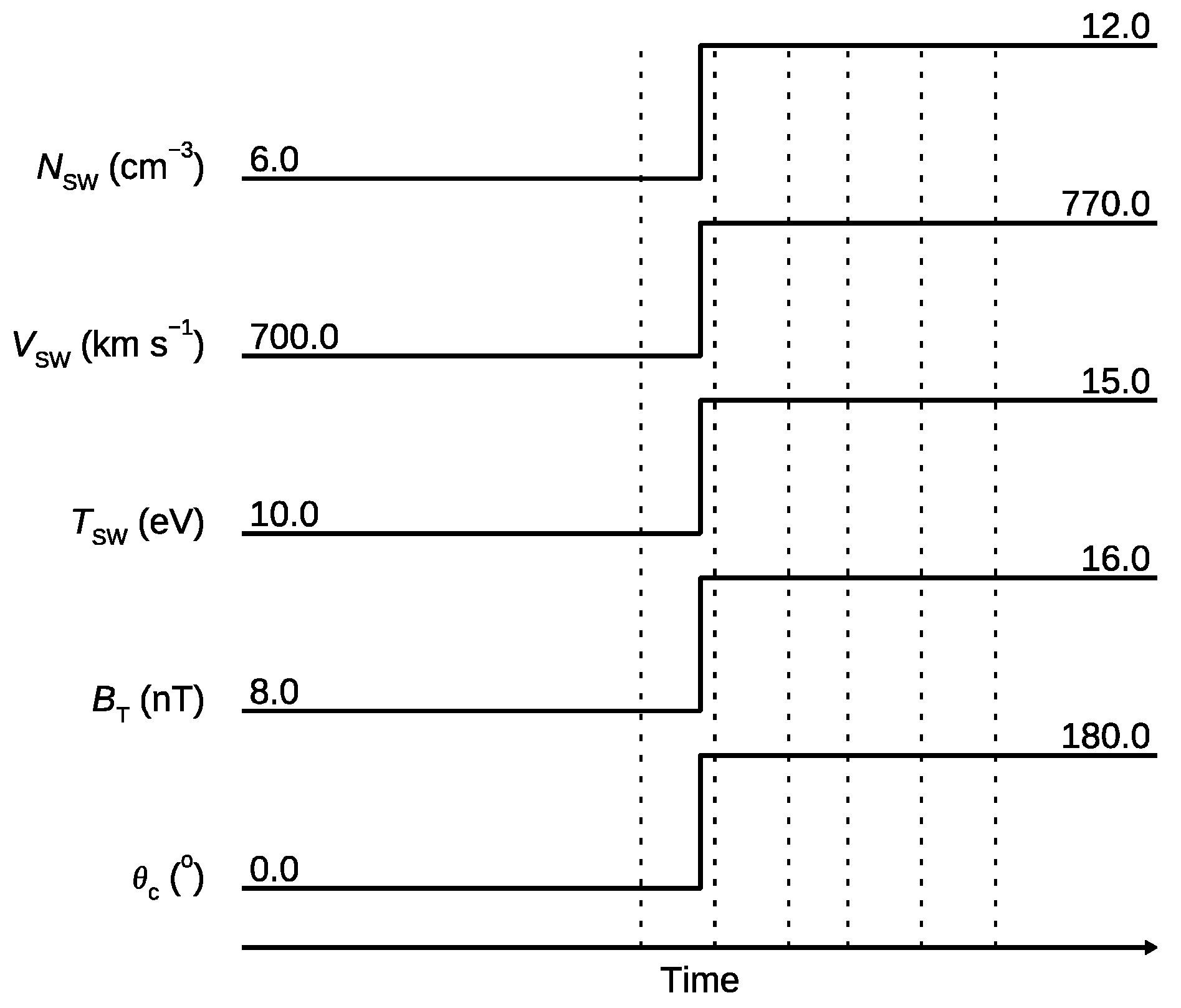
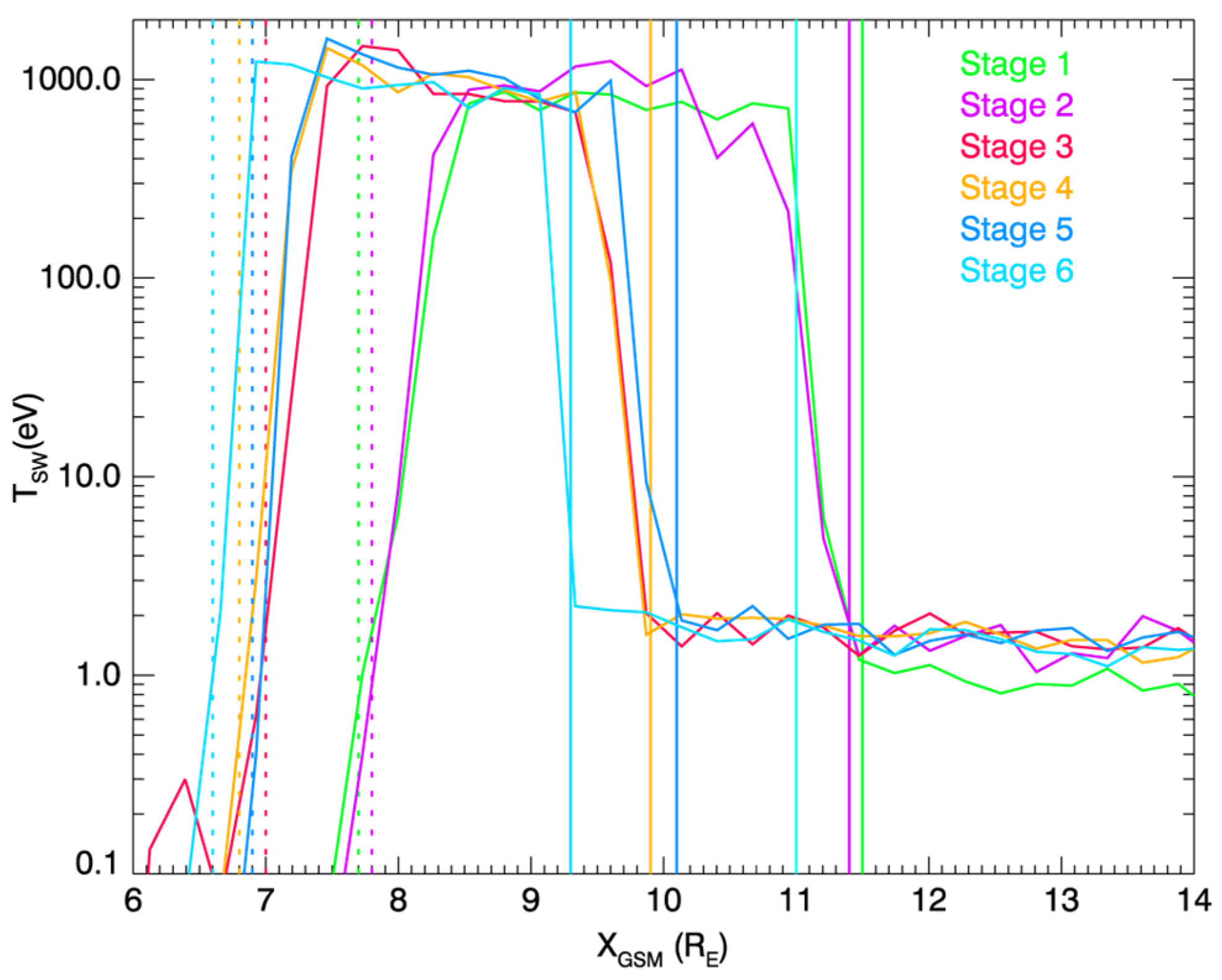
3.3. Effects of Interplanetary Shock Waves on Soft X-ray Emission
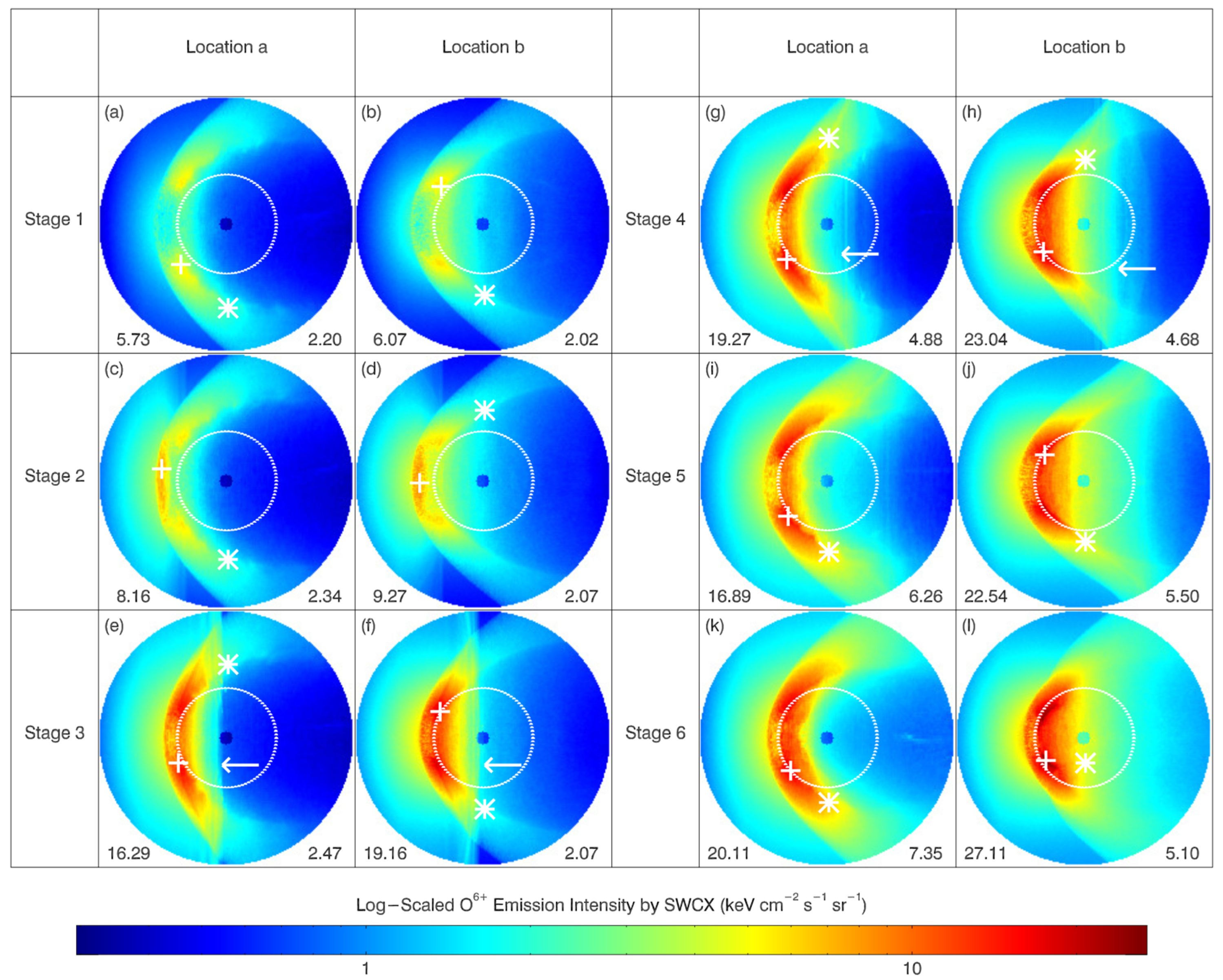
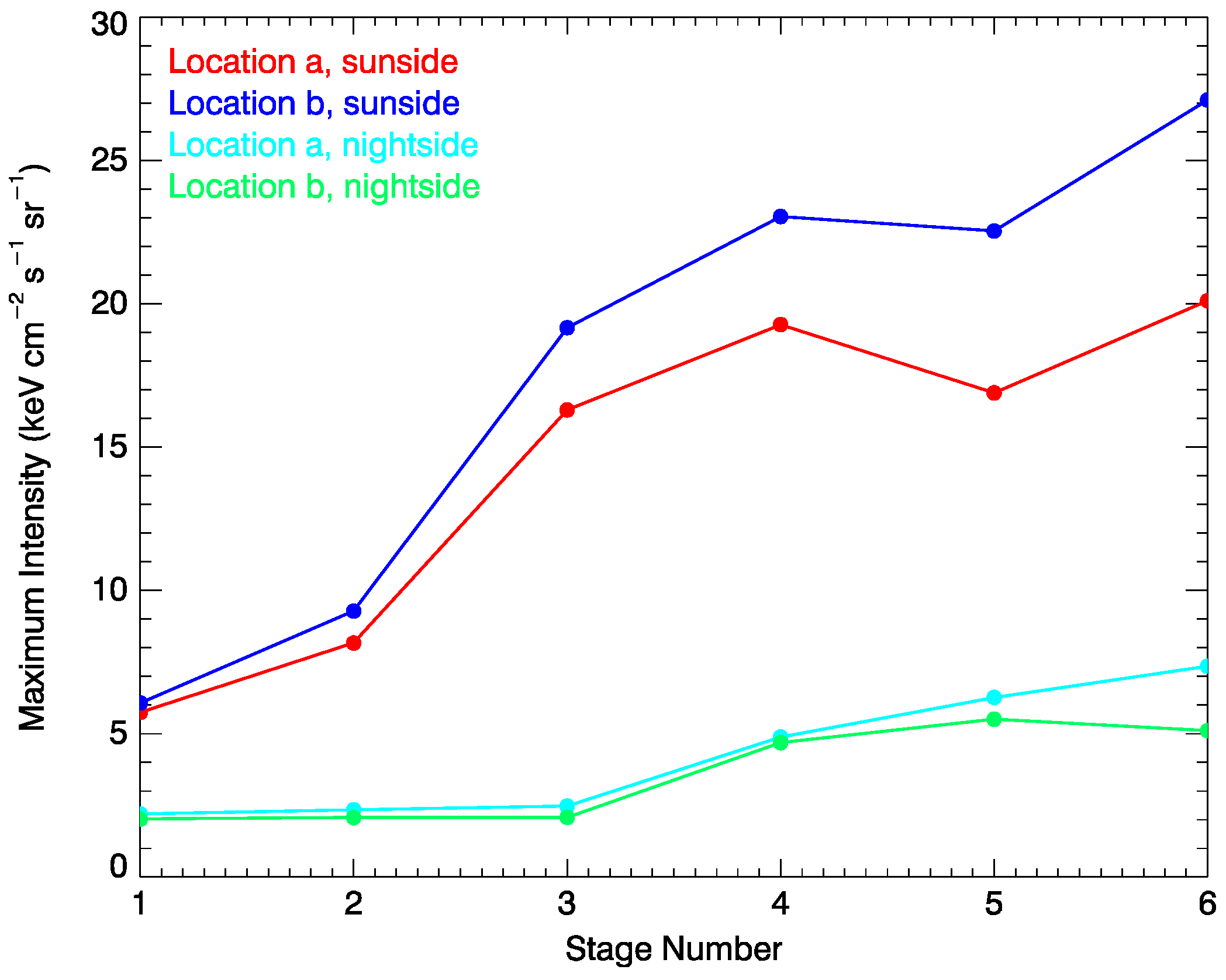
3.4. Emission Intensity Enhancement
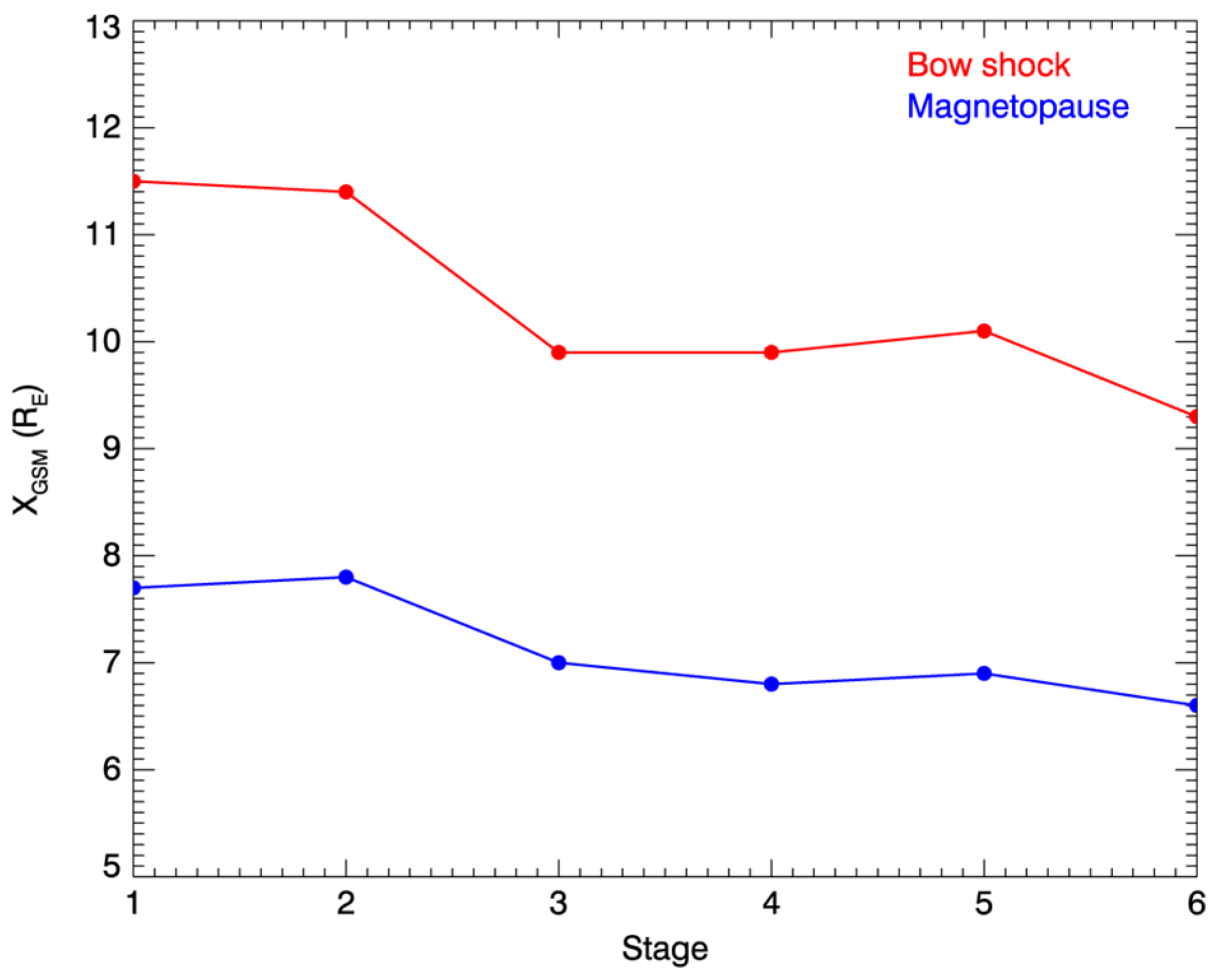
3.5. Bow Shock and Magnetopause Compressions
4. Conclusions
- A global hybrid model is used to simulate the number density, velocity, and temperature distribution of O6+ in the magnetosheath. Then, the SASAL is used to calculate the state distributions of excited O5+* ions, which are generated from the collisions between O6+ ions and hydrogen atoms, to obtain the efficiency factors for the X-ray emissions. Then, the X-ray emission intensities are simulated at 60.0 RE at the dusk side and at the north pole.
- It is found that there are two closed strong emission lines for O5+* at 10.582 nm and 10.583 nm, corresponding to energies of 107.047 eV and 107.040 eV. The efficiency factors of both lines vary significantly with collision speed. All energy states of O5+* ions have almost the same distribution pattern in the simulated images. The strongest emission intensity on the dayside is generated in the cusp region, and the strongest emission intensity on the nightside is in the area near the magnetopause in the magnetosheath. This is because the O6+ density is the highest while the velocity is the lowest in the cusp region where the magnetic field is converging, providing favorable conditions for generating strong emissions.
- During the passage of an IP-TD structure, significant emission intensity enhancement and compressions of both bow shock and magnetopause are observed in the simulations. The passage of the shock in the magnetosheath is clearly shown in the simulated images. The emission intensities simulated at dusk are always stronger than those simulated at the north pole, possibly because the solar wind heavy ions in the magnetosheath are mainly confined to near the equatorial region.
- The emission intensity profiles can be reliably used to extract the location of the bow shock, while the location of the magnetopause is difficult to identify, possibly due to the LOS overlapping effect.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sonett, C.P.; Abrams, I.J. The distant geomagnetic field: 3. Disorder and shocks in the magnetopause. J. Geophys. Res. 1963, 68, 1233–1263. [Google Scholar] [CrossRef]
- Nabert, C.; Glassmeier, K.H.; Plaschke, F. A new method for solving the MHD equations in the magnetosheath. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2013; Volume 31, No. 3; pp. 419–437. [Google Scholar]
- Dimmock, A.P.; Nykyri, K. The statistical mapping of magnetosheath plasma properties based on THEMIS measurements in the magnetosheath interplanetary medium reference frame. J. Geophys. Res. Space Phys. 2013, 118, 4963–4976. [Google Scholar] [CrossRef]
- Omidi, N.; Zhang, H.; Chu, C.; Turner, D. Parametric dependencies of spontaneous hot flow anomalies. J. Geophys. Res. Space Phys. 2014, 119, 9823–9833. [Google Scholar] [CrossRef]
- Breuillard, H.; Le Contel, O.; Chust, T.; Berthomier, M.; Retino, A.; Turner, D.L.; Nakamura, R.; Baumjohann, W.; Cozzani, G.; Catapano, F.; et al. The properties of Lion roars and electron dynamics in mirror mode waves observed by the Magnetospheric MultiScale Mission. J. Geophys. Res. Space Phys. 2018, 123, 93–103. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, T.; Shi, C.; Graham, D.B.; Dunlop, M.W.; He, J.; Tsurutani, B.T.; Wu, D. Ion and electron dynamics in the presence of mirror, electromagnetic ion cyclotron, and whistler waves. Astrophys. J. 2019, 883, 185. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, H.; Zhang, K.; Xia, H.; Qian, C. Local time response of auroral electrojet during magnetically disturbed periods: DMSP and CHAMP coordinated observations. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030624. [Google Scholar] [CrossRef]
- Cravens, T.E. Comet Hyakutake X-ray source: Charge transfer of solar wind heavy ions. Geophys. Res. Lett. 1997, 24, 105–108. [Google Scholar] [CrossRef]
- Paresce, F.; Fahr, H.; Lay, G. A search for interplanetary He II, 304-A emission. J. Geophys. Res. Space Phys. 1981, 86, 10038–10048. [Google Scholar] [CrossRef]
- Lisse, C.M.; Christian, D.J.; Dennerl, K.; Meech, K.J.; Petre, R.; Weaver, H.A.; Wolr, S.J. Charge exchange-induced X-ray emission from Comet C/1999 S4 (LINEAR). Science 2001, 292, 1343–1348. [Google Scholar] [CrossRef]
- Ringuette, R.; Koutroumpa, D.; Kuntz, K.D.; Kaaret, P.; Jahoda, K.; LaRocca, D.; Kounkel, M.; Richardson, J.; Zajczyk, A.; Bluem, J. HaloSat observations of heliospheric solar wind charge exchange. Astrophys. J. 2021, 918, 41. [Google Scholar] [CrossRef]
- Zhou, Y.; Yamasaki, N.Y.; Toriumi, S.; Mitsuda, K. Geocoronal Solar Wind Charge Exchange Process Associated with the 2006-December-13 Coronal Mass Ejection Event. J. Geophys. Res. Space Phys. 2023, 128, e2023JA032069. [Google Scholar] [CrossRef]
- Ishikawa, K.; Ezoe, Y.; Miyoshi, Y.; Terada, N.; Mitsuda, K.; Ohashi, T. Suzaku observation of strong solar-wind charge-exchange emission from the terrestrial exosphere during a geomagnetic storm. Publ. Astron. Soc. Jpn. 2013, 65, 63. [Google Scholar] [CrossRef]
- Ringuette, R.; Kuntz, K.D.; Koutroumpa, D.; Kaaret, P.; LaRocca, D.; Richardson, J. Observations of Magnetospheric Solar Wind Charge Exchange. Astrophys. J. 2023, 955, 139. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Sun, T.R.; Carter, J.A.; Liu, W.H.; Sembay, S.; Zhang, S.N.; Ji, L.; Wang, C. Two methods for separating the magnetospheric solar wind charge exchange soft X-ray emission from the diffuse X-ray background. Earth Planet. Phys. 2023, 8, 119–132. [Google Scholar] [CrossRef]
- Connor, H.K.; Sibeck, D.G.; Collier, M.R.; Baliukin, I.I.; Branduardi-Raymont, G.; Brandt, P.C.; Buzulukova, N.Y.; Collado-Vega, Y.M.; Escoubet, C.P.; Fok, M.-C.; et al. Soft X-ray and ENA Imaging of the Earth’s Dayside Magnetosphere. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028816. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.R.; Wang, C.; Sembay, S.F.; Lopez, R.E.; Escoubet, C.P.; Branduardi-Raymont, G.; Zheng, J.H.; Yu, X.Z.; Guo, X.C.; Dai, L.; et al. Soft X-ray imaging of the magnetosheath and cusps under different solar wind conditions: MHD simulations. J. Geophys. Res. Space 2019, 124, 2435–2450. [Google Scholar] [CrossRef]
- Raab, W.; Branduardi-Raymont, G.; Wang, C.; Dai, L.; Donovan, E.; Enno, G.; Escoubet, P.; Holland, A.; Li, J.; Kataria, D.; et al. SMILE: A joint ESA/CAS mission to investigate the interaction between the solar wind and Earth’s magnetosphere. Proc. SPIE 2016, 9905, 990502-1–990502-9. [Google Scholar] [CrossRef]
- Collier, M.R.; Porter, F.S.; Sibeck, D.G.; Carter, J.A.; Chiao, M.P.; Chornay, D.J.; Cravens, T.; Galeazzi, M.; Keller, J.W.; Koutroumpa, D.; et al. Prototyping a global soft X-ray imaging instrument for heliophysics, planetary science, and astrophysics science. Astron. Nachr. 2012, 333, 378–382. [Google Scholar] [CrossRef]
- Somana, M.R.; Halla, D.J.; Hollanda, A.D.; Burgona, R.; Buggeya, T.; Skottfelta, J.; Sembayb, S.; Drummb, P.; Thornhillb, J.; Readb, A.; et al. The SMILE Soft X-ray Imager (SXI) CCD design and development. J. Instrum. 2018, 13, C01022. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Cravens, T.E. Implications of solar wind composition for cometary X-rays. Astrophys. J. 2000, 544, 558. [Google Scholar] [CrossRef]
- Robertson, I.P.; Collier, M.R.; Cravens, T.E.; Fok, M.-C. X-ray emission from the terrestrial magnetosheath including the cusps. J. Geophys. Res. Space Phys. 2006, 111, A12105. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.Y.; Lu, S.; Perez, J.D.; Lu, Q. Investigation of storm time magnetotail and ion injection using three-dimensional global hybrid simulation. J. Geophys. Res. Space Phys. 2014, 119, 7413–7432. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.Y. Three-dimensional global hybrid simulation of dayside dynamics associated with the quasi-parallel bow shock. J. Geophys. Res. Space Phys. 2005, 110, A12216. [Google Scholar] [CrossRef]
- Swift, D.W. Use of a hybrid code for global-scale plasma simulation. J. Comput. Phys. 1996, 126, 109–121. [Google Scholar] [CrossRef]
- Kivelson, M.G.; Russell, C.T. (Eds.) Introduction to Space Physics; Cambridge University Press: Cambridge, UK, 1995; p. 31. [Google Scholar]
- Lepri, S.T.; Landi, E.; Zurbuchen, T.H. Solar wind heavy ions over solar cycle 23: ACE/SWICS measurements. Astrophys. J. 2013, 768, 94. [Google Scholar] [CrossRef]
- Von Steiger, R.; Zurbuchen, T.H.; McComas, D.J. Oxygen flux in the solar wind: Ulysses observations. Geophys. Res. Lett. 2010, 37, L22101. [Google Scholar] [CrossRef]
- Hodges, R.R., Jr. Monte Carlo simulation of the terrestrial hydrogen exosphere. J. Geophys. Res. Space Phys. 1994, 99, 23229–23247. [Google Scholar] [CrossRef]
- Brinkmann, R.T. Departures from Jeans’ escape rate for H and He in the Earth’s atmosphere. Planet. Space Sci. 1970, 18, 449–478. [Google Scholar] [CrossRef]
- Cole, K.D. Theory of some Quiet Magnetospheric [Phenomena related to the Geomagnetic Tail. Nature 1966, 211, 1385–1387. [Google Scholar] [CrossRef]
- Hodges, R.R., Jr.; Tinsley, B.A. Charge exchange in the Venus ionosphere as the source of the hot exospheric hydrogen. J. Geophys. Res. Space Phys. 1981, 86, 7649–7656. [Google Scholar] [CrossRef]
- Liang, G.Y.; Li, F.; Wang, F.L.; Wu, Y.; Zhong, J.Y.; Zhao, G. X-ray and EUV spectroscopy of various astrophysical and laboratory plasmas: Collisional, photoionization and charge-exchange plasmas. Astrophys. J. 2014, 783, 124. [Google Scholar] [CrossRef]
- Verner, D.A.; Ferland, G.J.; Korista, K.T.; Yakovlev, D.G. Atomic data for astrophysics. II. New analytic fits for photoionization cross sections of atoms and ions. Astrophys. J. 1996, 465, 487. [Google Scholar] [CrossRef]
- Salop, A.; Olson, R.E. Charge exchange between H(1s) and fully stripped heavy ions at low-keV impact energies. Phys. Rev. A 1976, 13, 1312–1320. [Google Scholar] [CrossRef]
- Liang, G.Y.; Zhu, X.L.; Wei, H.G.; Yuan, D.W.; Zhong, J.Y.; Wu, Y.; Hutton, R.; Cui, W.; Cui, X.W.; Zhao, G. Charge-exchange soft X-ray emission of highly charged ions with inclusion of multiple-electron capture. Mon. Not. R. Astron. Soc. 2021, 508, 2194–2203. [Google Scholar] [CrossRef]
- Liang, G.Y.; Sun, T.R.; Lu, H.Y.; Zhu, X.L.; Wu, Y.; Li, S.B.; Wei, H.G.; Yuan, D.W.; Zhong, J.Y.; Cui, W.; et al. X-ray morphology due to charge-exchange emissions used to study the global structure around Mars. Astrophys. J. 2023, 943, 85. [Google Scholar] [CrossRef]
- Kharchenko, V.; Dalgarno, A. Spectra of cometary X rays induced by solar wind ions. J. Geophys. Res. Space Phys. 2000, 105, 18351–18359. [Google Scholar] [CrossRef]
- He, F.; Zhang, X.X.; Wang, X.Y.; Chen, B. EUV emissions from solar wind charge exchange in the Earth’s magnetosheath: Three-dimensional global hybrid simulation. J. Geophys. Res. Space Phys. 2015, 120, 138–156. [Google Scholar] [CrossRef]

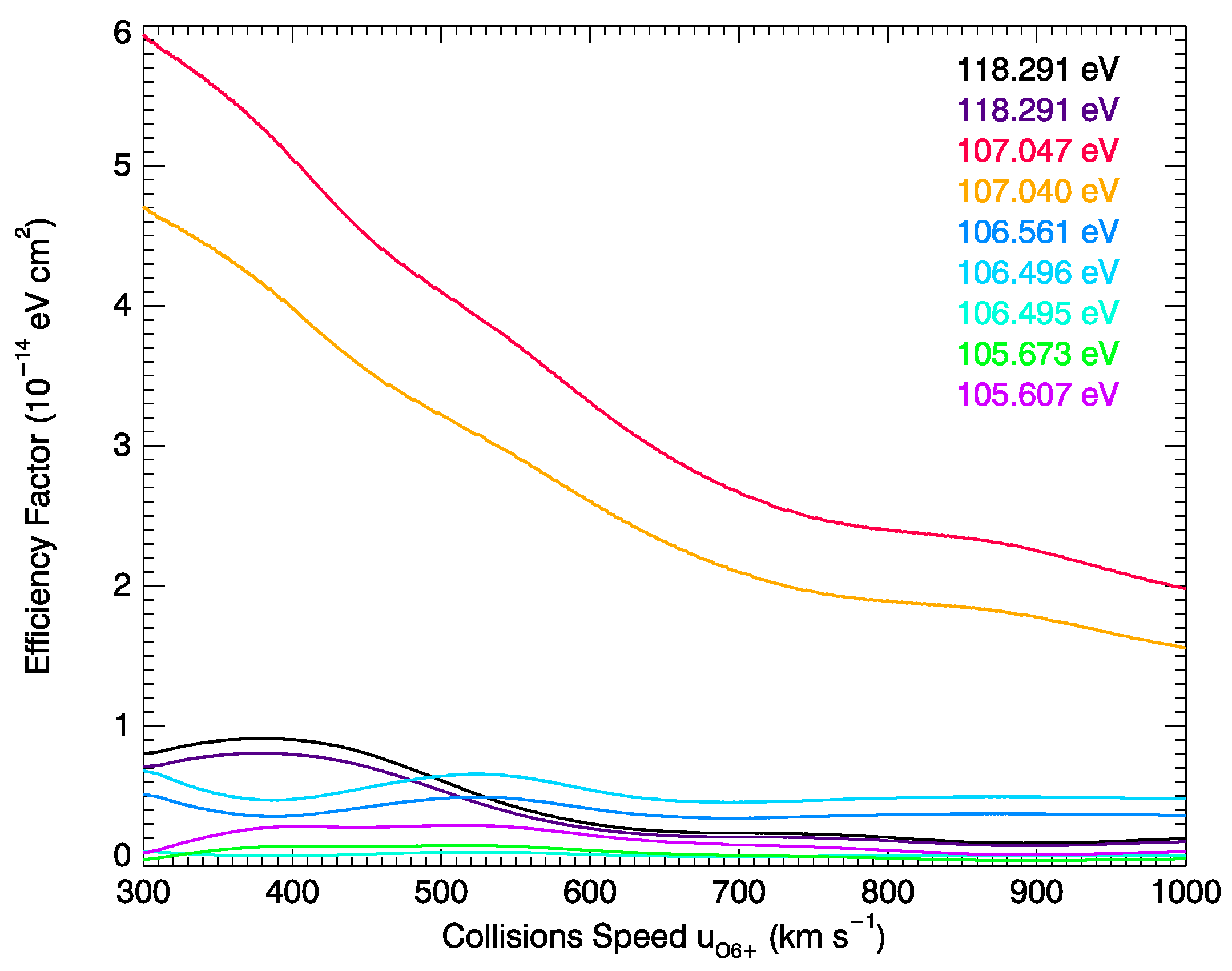
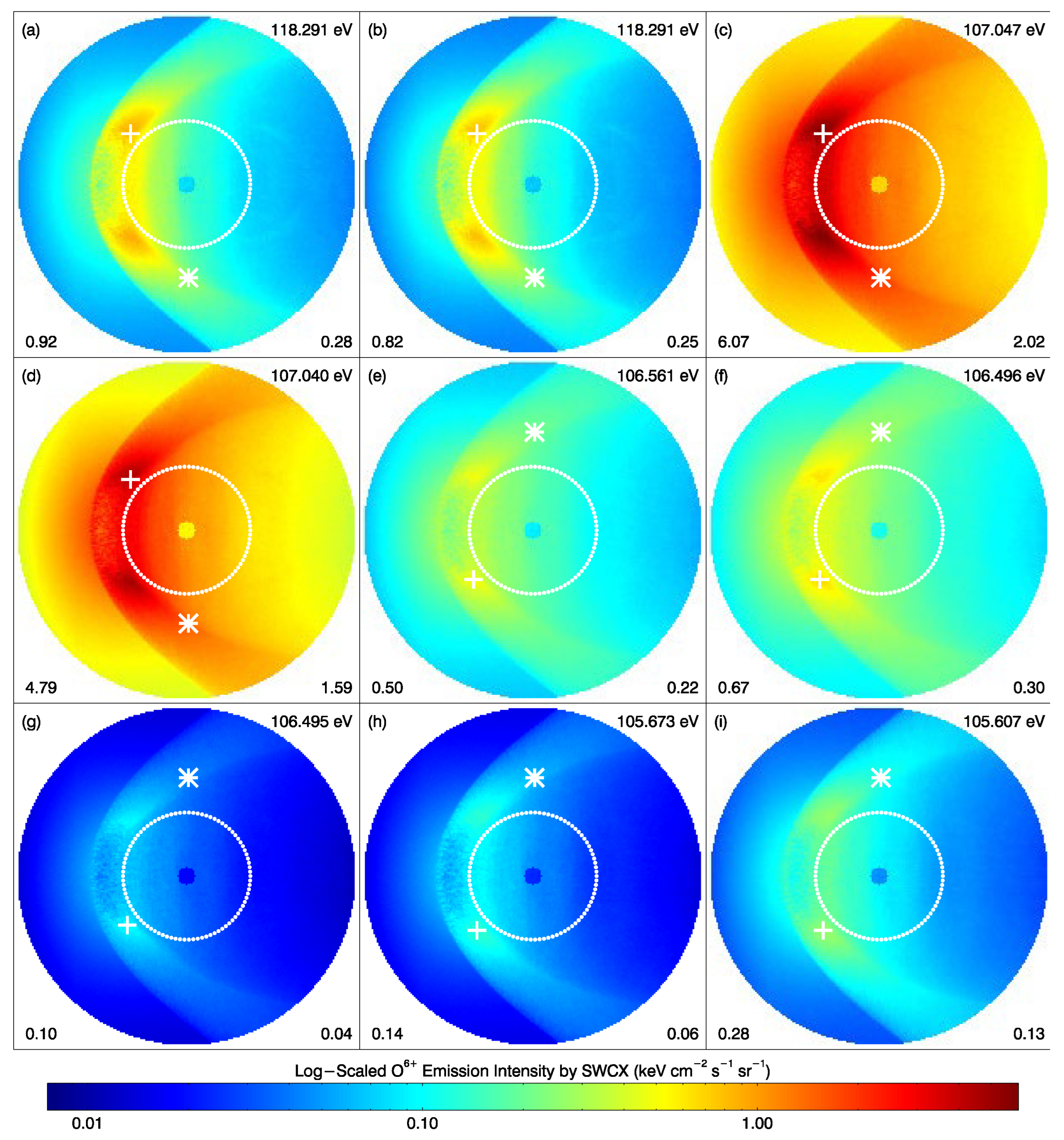
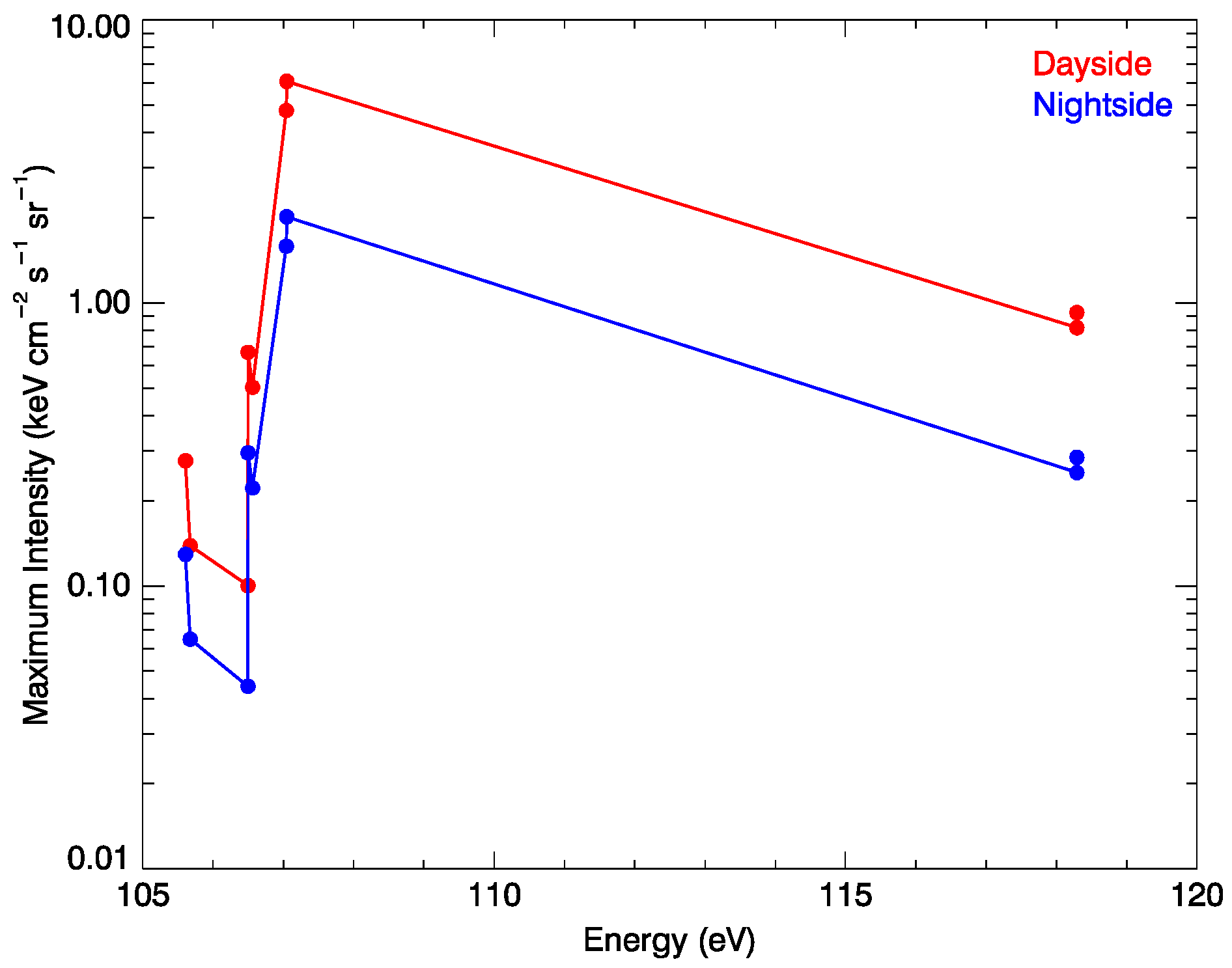

| Number | Energy State | Wavelength (nm) | Energy (eV) |
|---|---|---|---|
| 1 | 1s2 5d 2P1/2 → 1s2 2p 2D3/2 | 10.481 | 118.291 |
| 2 | 1s2 5p 2P1/2 → 1s2 2p 2P3/2 | 10.481 | 118.291 |
| 3 | 1s2 4d 2P1/2 → 1s2 2p 2D3/2 | 11.582 | 107.047 |
| 4 | 1s2 4p 2P1/2 → 1s2 2p 2P3/2 | 11.583 | 107.040 |
| 5 | 1s2 5d 2P3/2 → 1s2 2p 2D5/2 | 11.635 | 106.561 |
| 6 | 1s2 5f 2P1/2 → 1s2 3s 2F5/2 | 11.642 | 106.496 |
| 7 | 1s2 5d 2P1/2 → 1s2 3s 2D5/2 | 11.642 | 106.495 |
| 8 | 1s2 5p 2P3/2 → 1s2 2p 2P1/2 | 11.732 | 105.673 |
| 9 | 1s2 5p 2P1/2 → 1s2 3s 2P1/2 | 11.740 | 105.607 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; He, F.; Zhang, X.-X.; Liang, G.; Wang, X.; Wei, Y. Solar Wind Charge-Exchange X-ray Emissions from the O5+ Ions in the Earth’s Magnetosheath. Remote Sens. 2024, 16, 1480. https://doi.org/10.3390/rs16091480
Zhang Z, He F, Zhang X-X, Liang G, Wang X, Wei Y. Solar Wind Charge-Exchange X-ray Emissions from the O5+ Ions in the Earth’s Magnetosheath. Remote Sensing. 2024; 16(9):1480. https://doi.org/10.3390/rs16091480
Chicago/Turabian StyleZhang, Zhicheng, Fei He, Xiao-Xin Zhang, Guiyun Liang, Xueyi Wang, and Yong Wei. 2024. "Solar Wind Charge-Exchange X-ray Emissions from the O5+ Ions in the Earth’s Magnetosheath" Remote Sensing 16, no. 9: 1480. https://doi.org/10.3390/rs16091480
APA StyleZhang, Z., He, F., Zhang, X.-X., Liang, G., Wang, X., & Wei, Y. (2024). Solar Wind Charge-Exchange X-ray Emissions from the O5+ Ions in the Earth’s Magnetosheath. Remote Sensing, 16(9), 1480. https://doi.org/10.3390/rs16091480








