A UAV-Based Single-Lens Stereoscopic Photography Method for Phenotyping the Architecture Traits of Orchard Trees
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Field and Data Acquisition
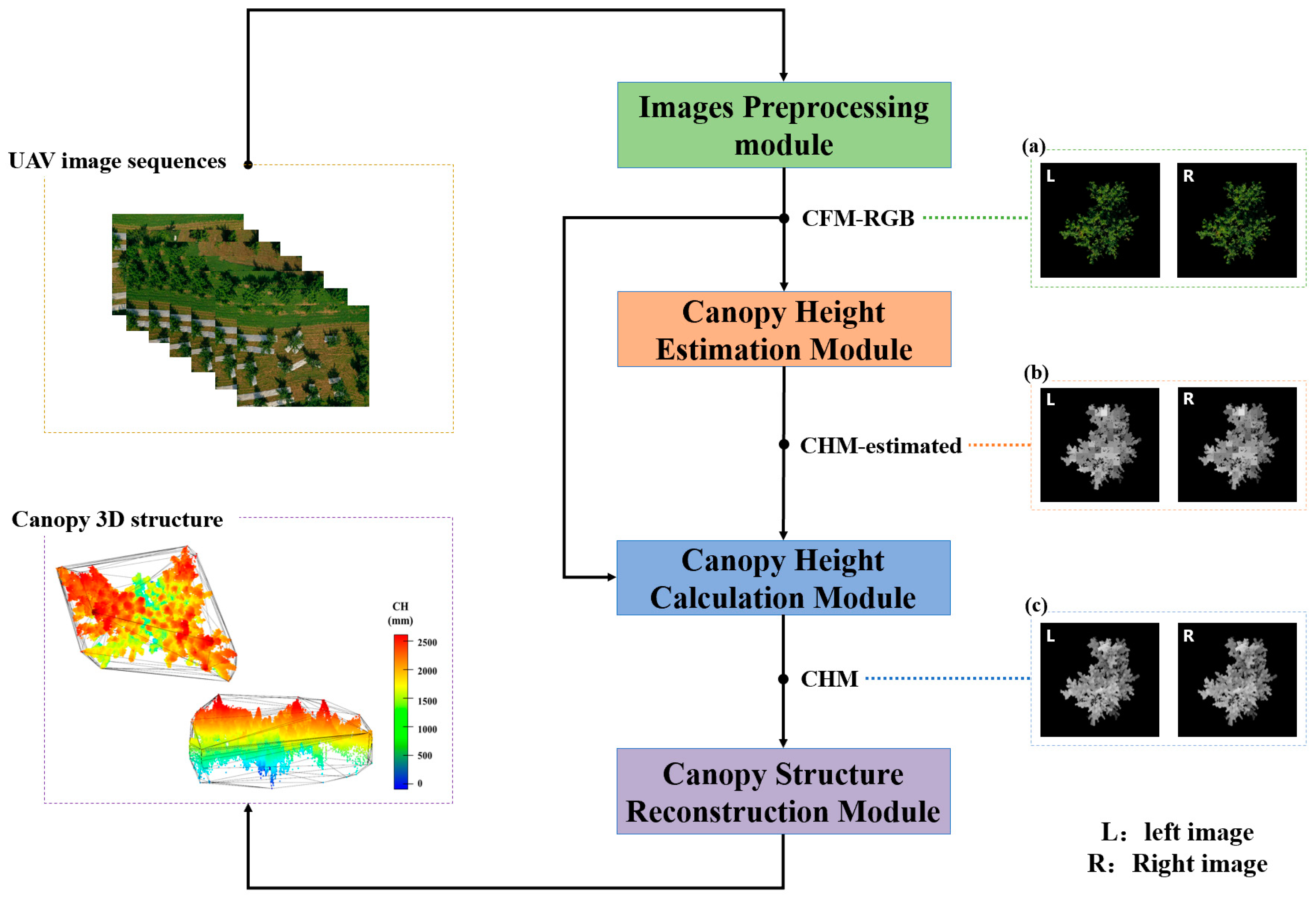
2.2. Algorithm and Methodology
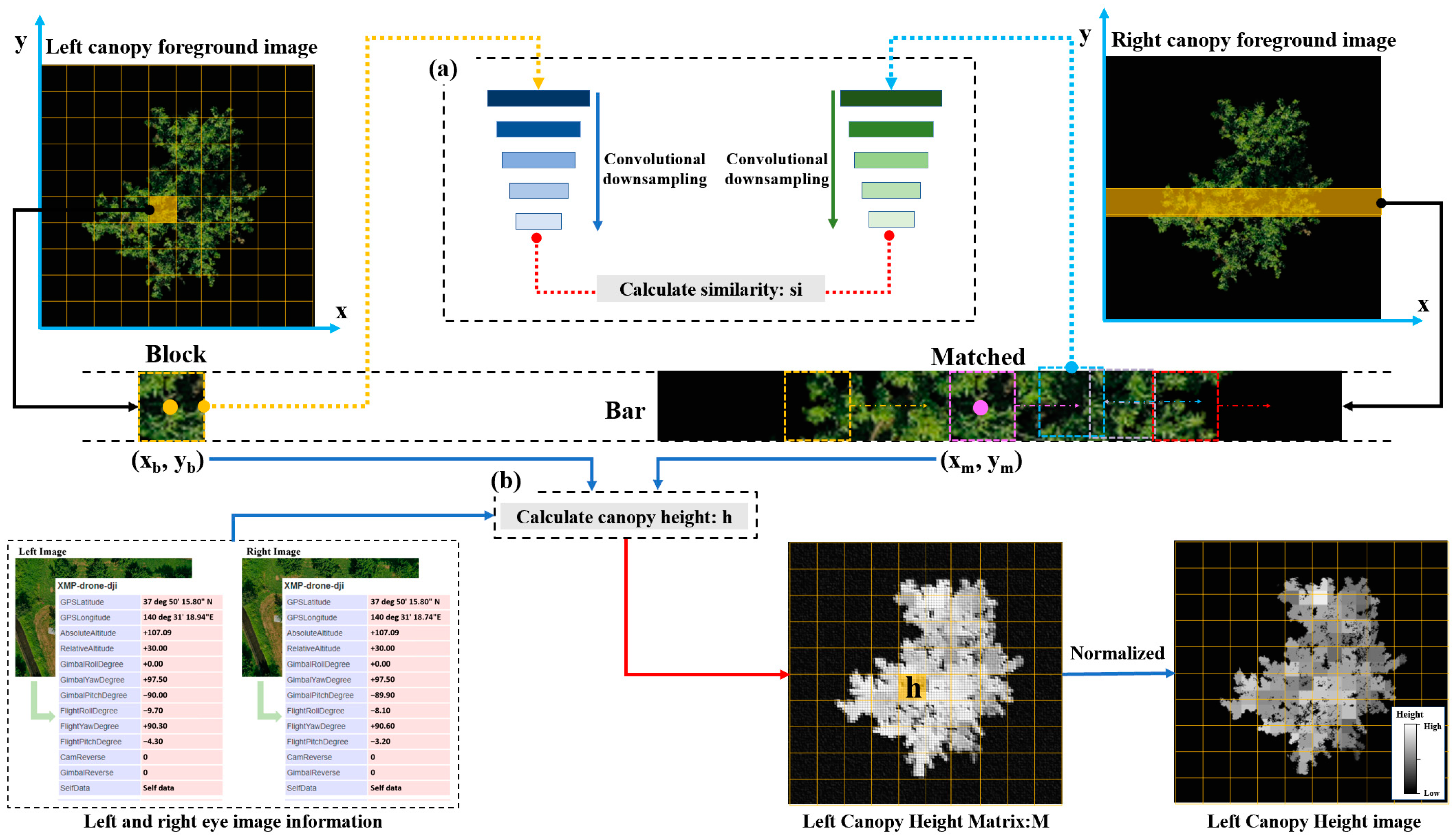
2.2.1. Canopy Height Estimation Module
| Algorithm 1. Similarity calculation process for binocular canopy block matching |
| Input: left eye block: BL, matched right eye block: BR |
| Output: similarity between canopy blocks: si |
| 1: for i ← 1 to 5 do 2: BL ← convolutional_downsampling (BL, kernel size: 3×, step size: 1) 3: BR ← convolutional_downsampling (BR, kernel size: 3×3, step size: 1) 4: end for 5: ML, MR ← high-dimensional feature map of BL, BR, respectively. 6: si = dcos(ML, MR), the cosine distance between ML and MR by Equation (1) |
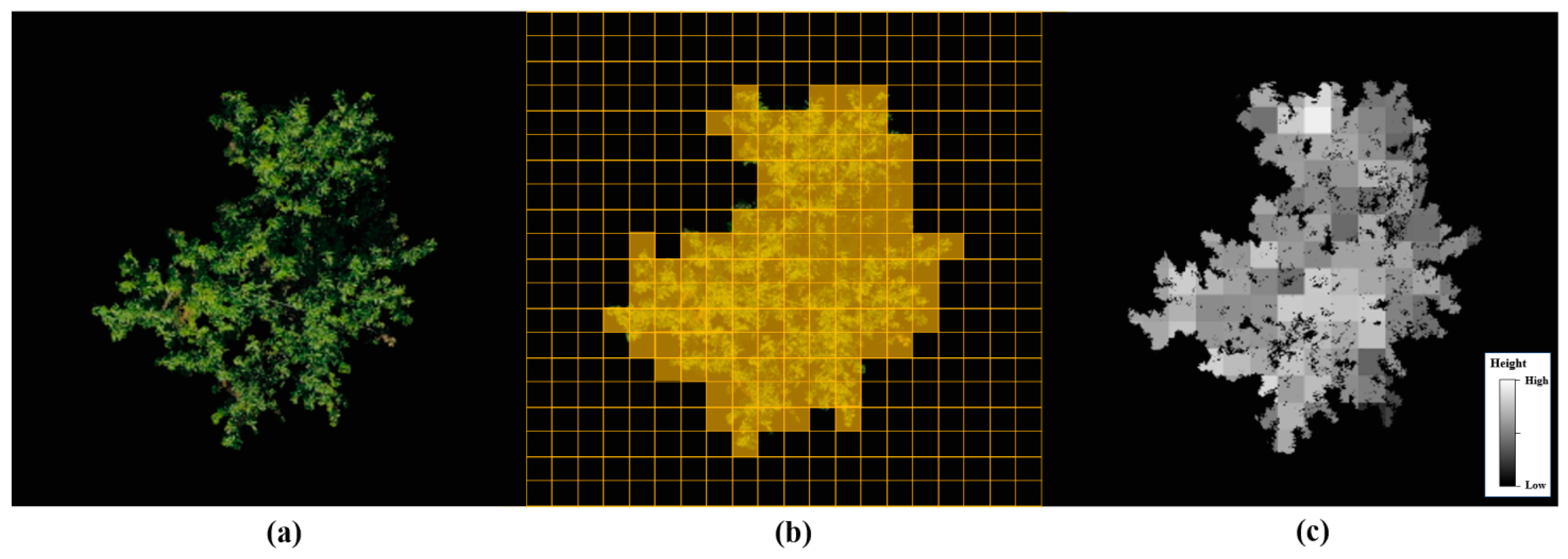
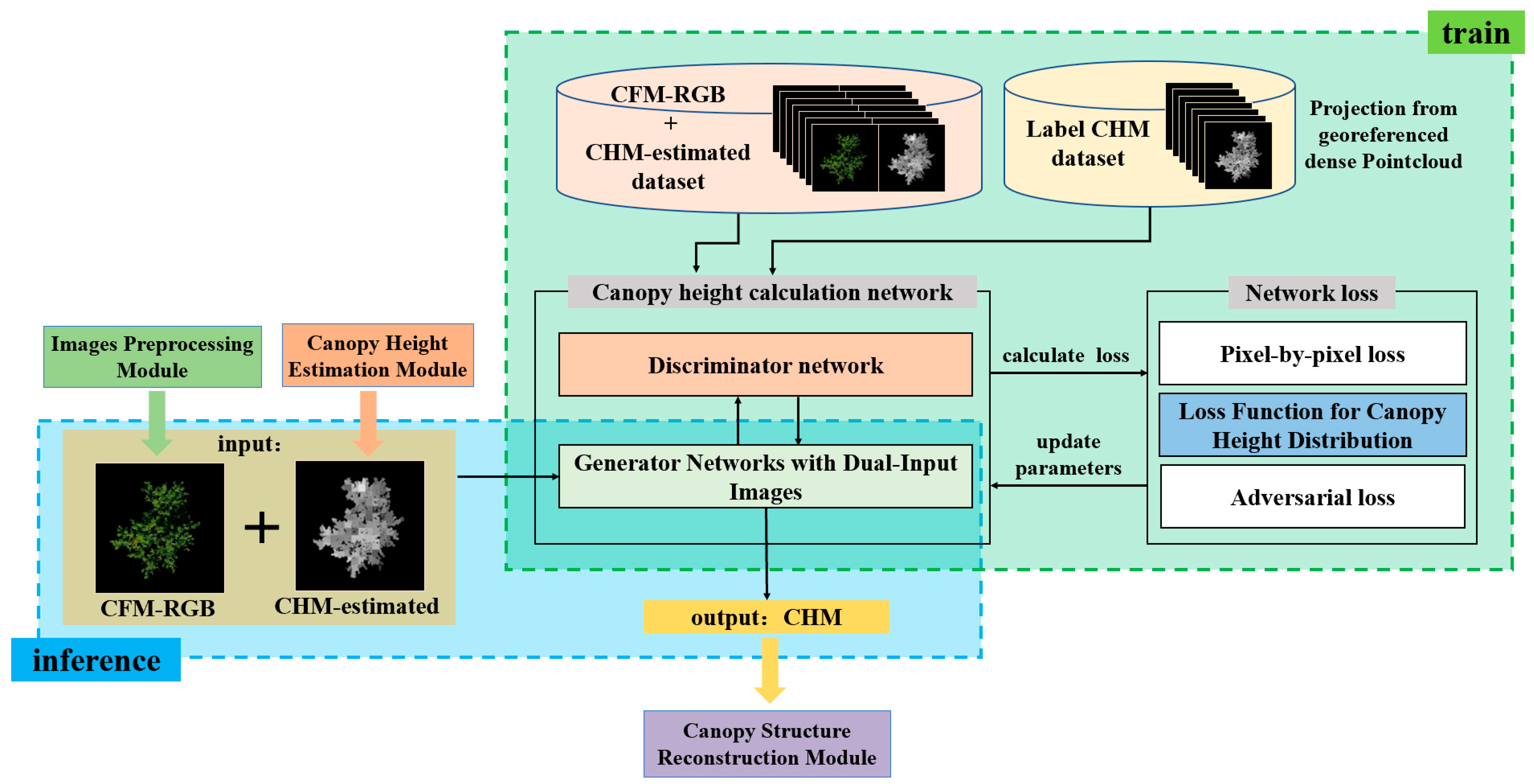
2.2.2. Canopy Height Calculation Module
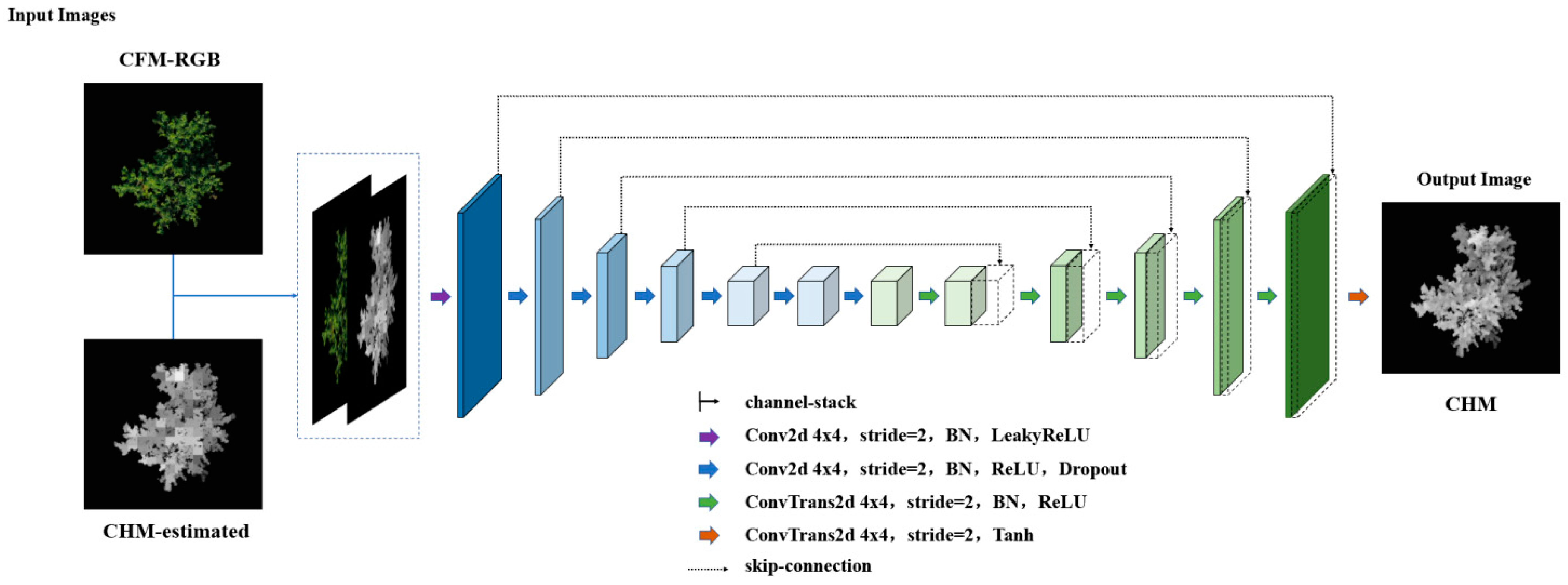
Generator Network with Dual Input Images
Loss Function for Canopy Height Distribution
2.3. Canopy Architecture Traits Extraction
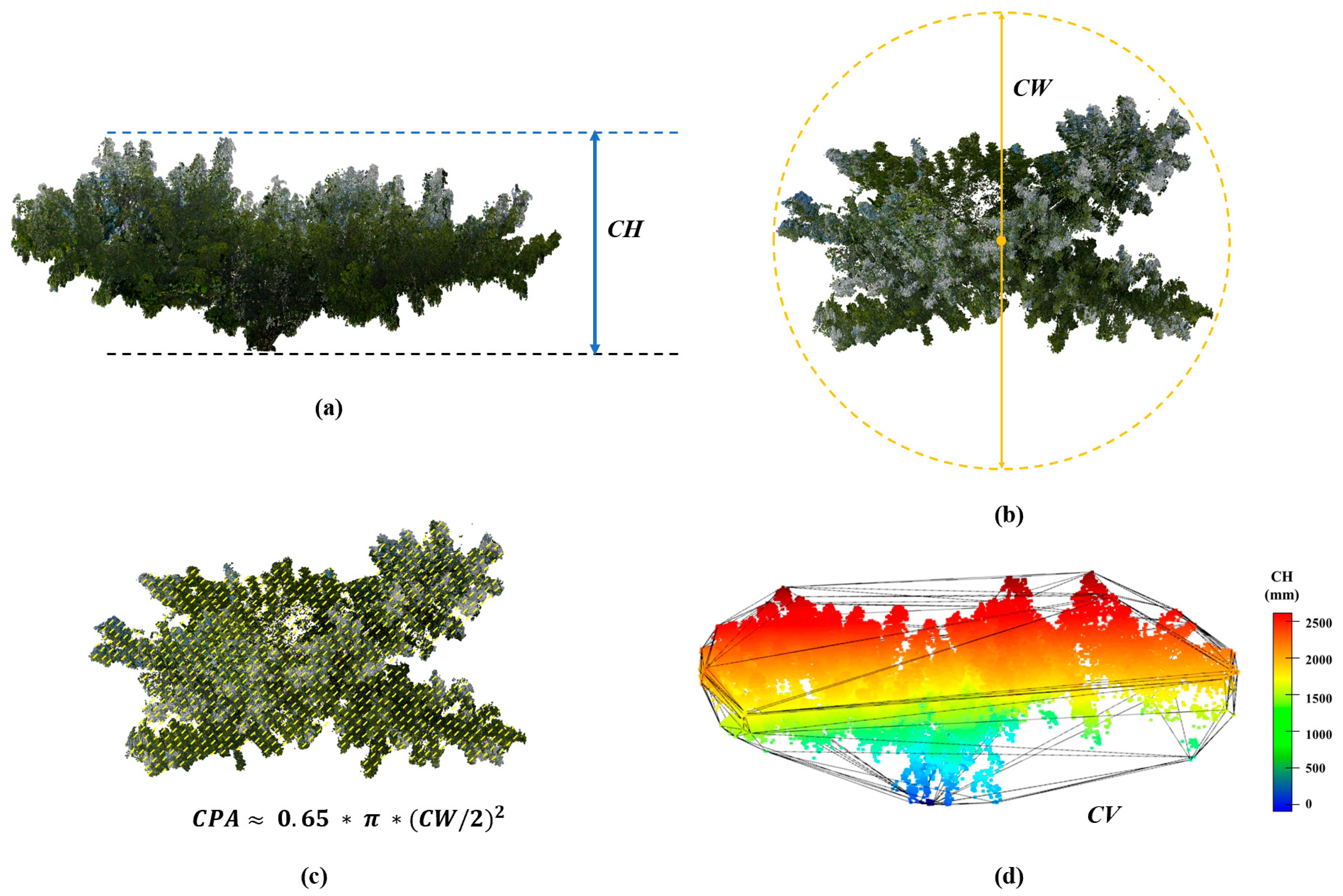
- CH (Canopy Height)—the vertical distance from the highest part of the canopy to the ground, as shown in Figure 11a;
- CW (Canopy Width)—the diameter of the smallest outer circle of the vertical projection of the canopy, as shown in Figure 11b;
- CV (Canopy Volume)—the volume of the 3D convex envelope of the canopy, as shown in Figure 11d.
2.4. Implementation
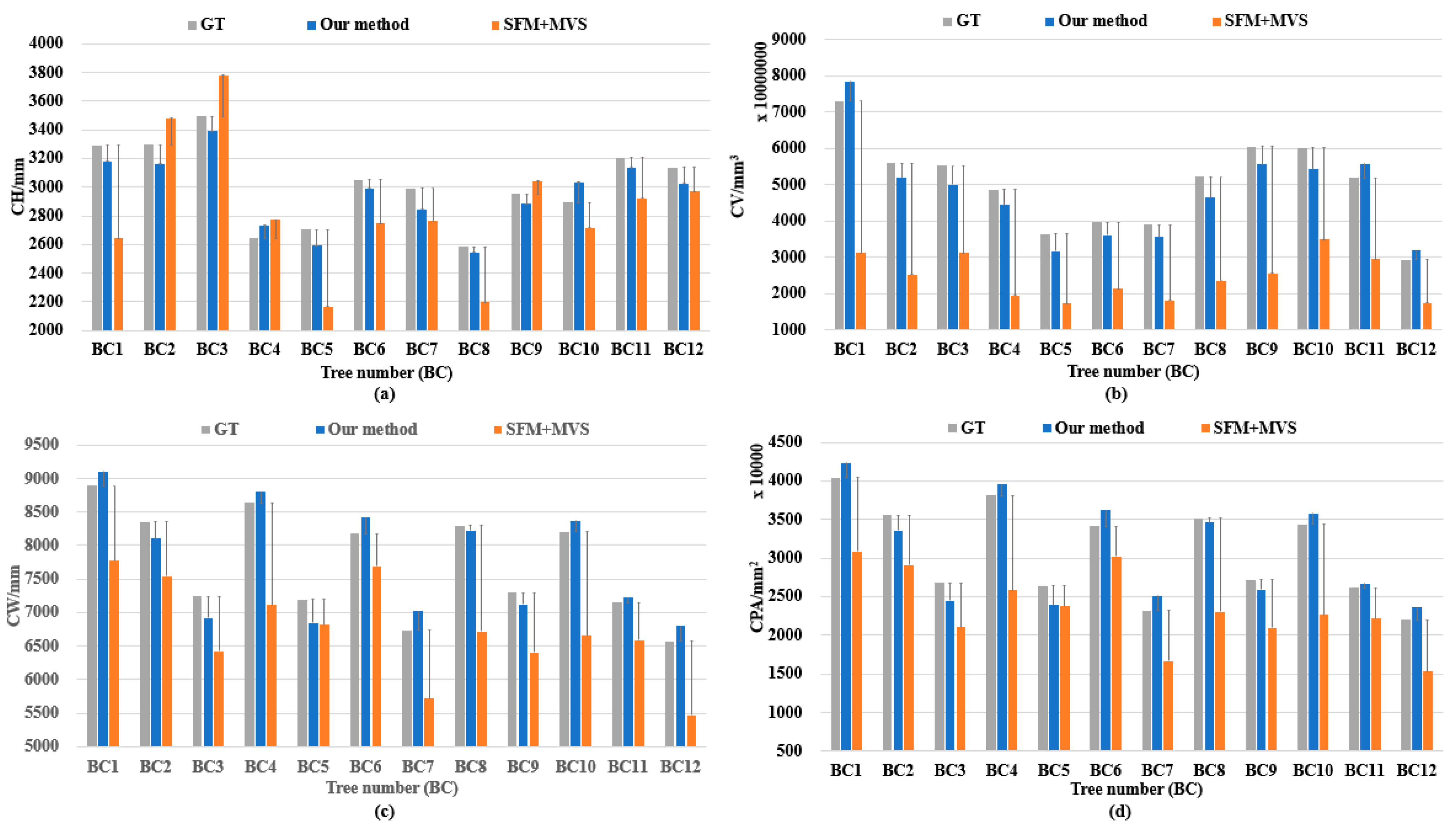
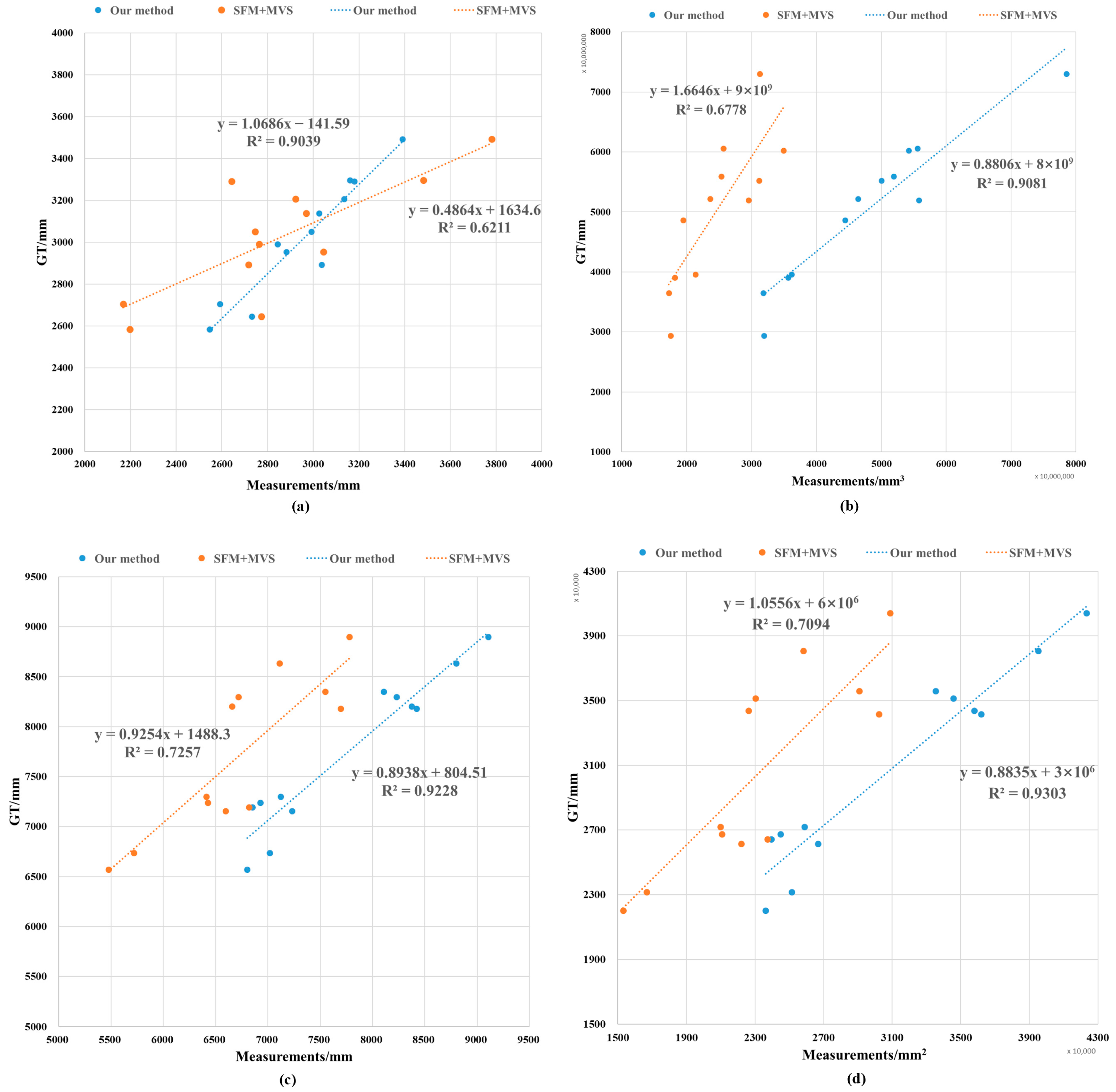
3. Results
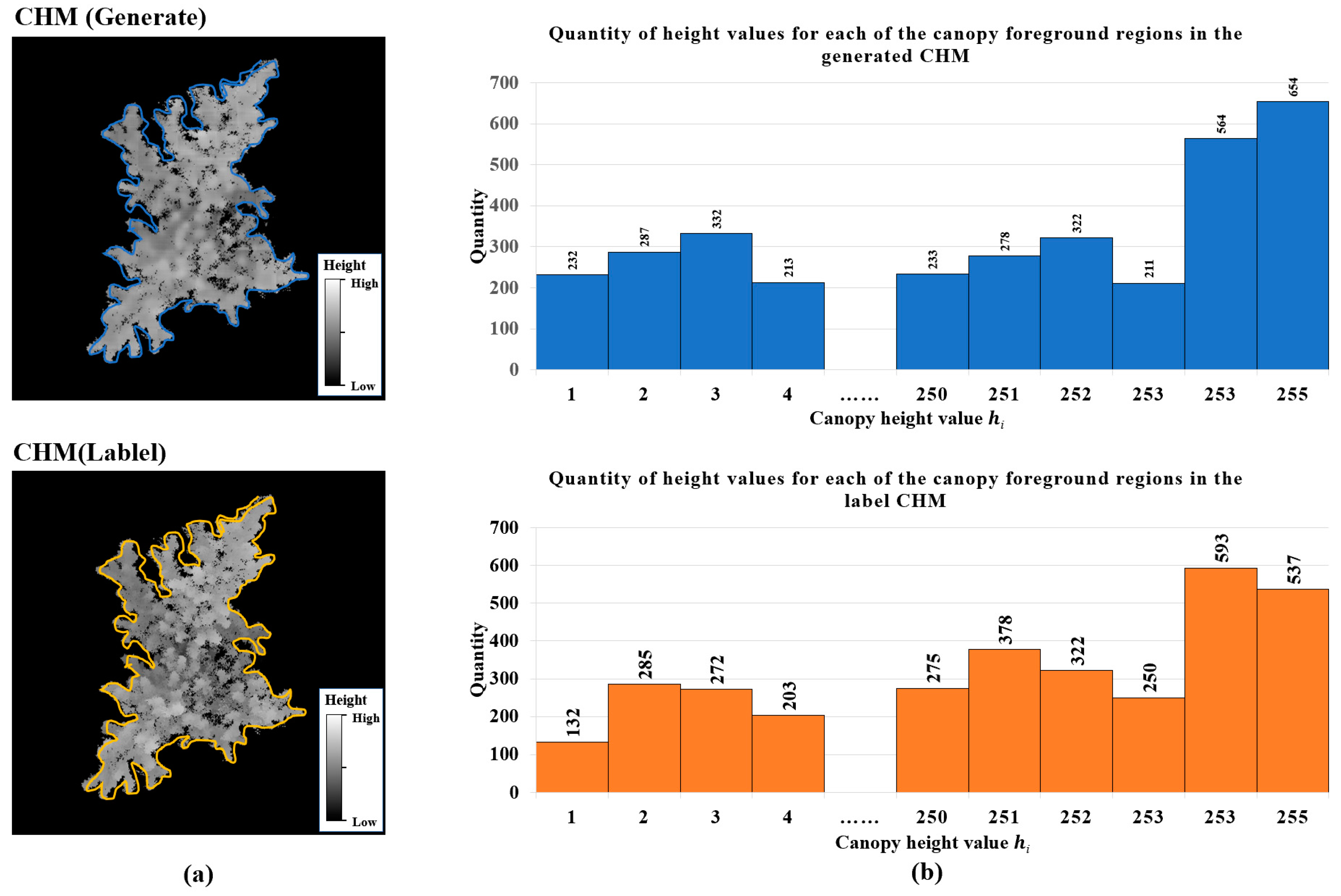
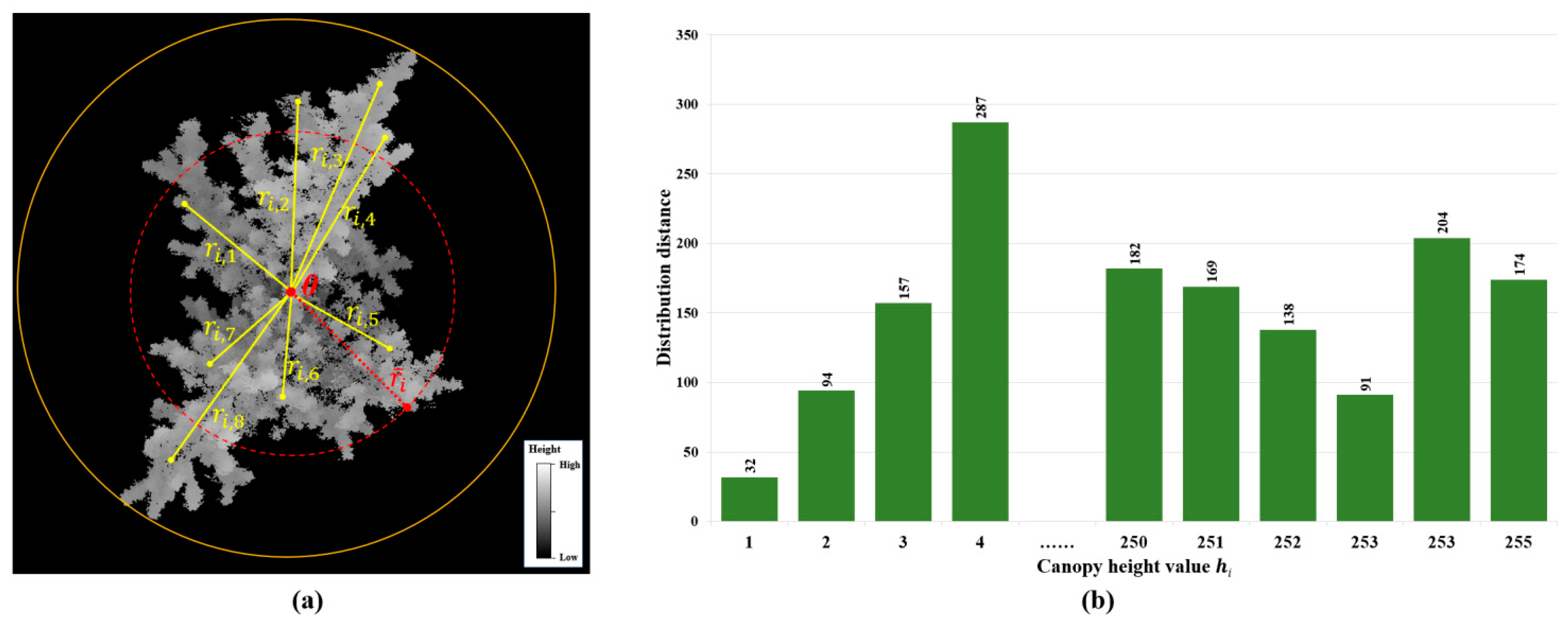
3.1. Validation via Canopy Structure Traits
3.2. Validation
3.3. Reconstruction Efficiency Comparison
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Methodologies of Image-Preprocessing Module and Canopy Structure Reconstruction Module
Appendix A.1.1. Image-Preprocessing Module
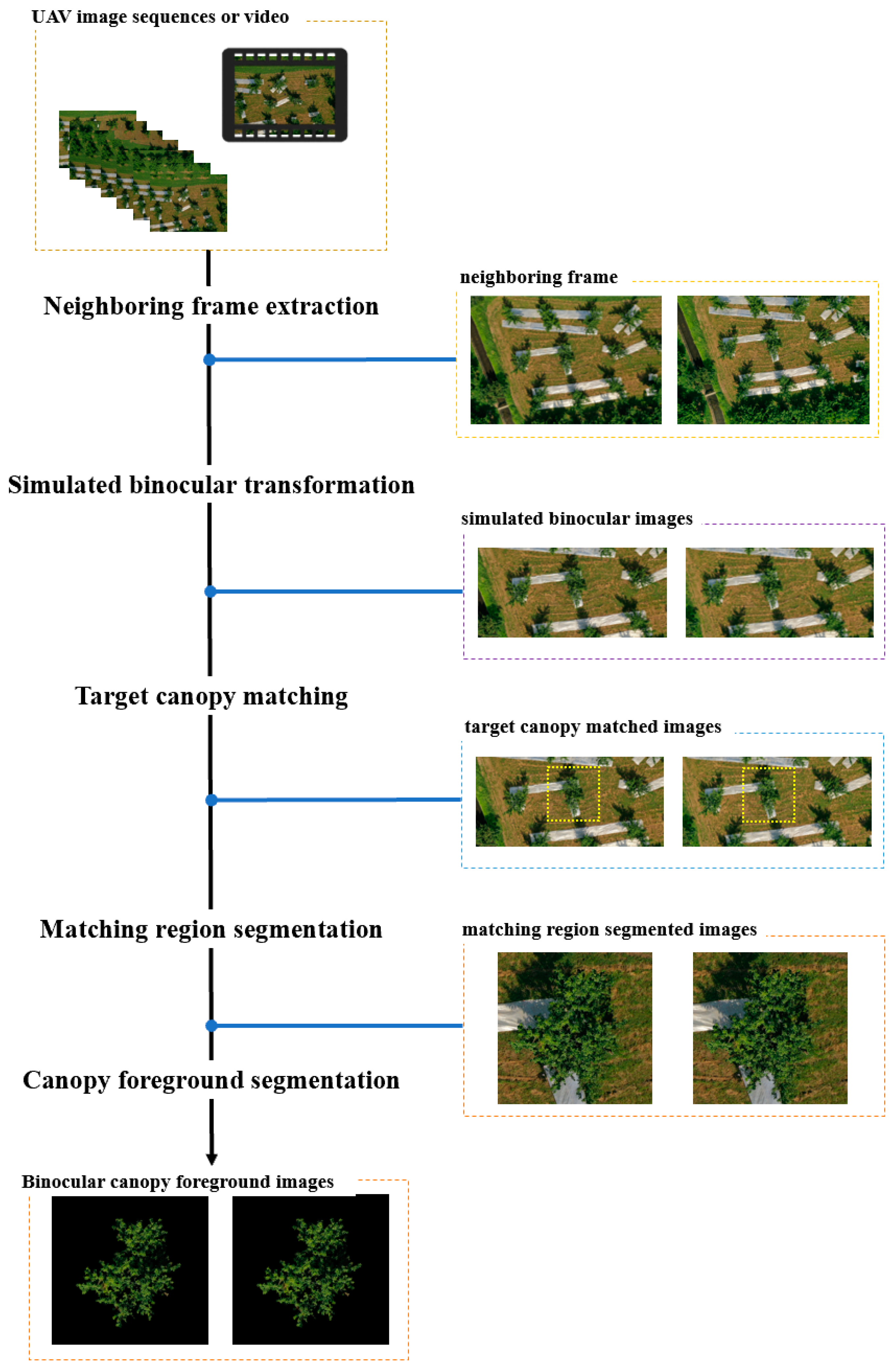
- Neighboring frame extraction: Extract neighboring frame images from UAV aerial videos or image sequences.
- Simulate binocular transformation: Since the UAV trajectory may not be parallel to the camera lens CMOS sensor, it is necessary to convert the adjacent frames into a standard binocular image. This paper provides two transformations for simulating standard binocular photography, and the details of the process are as follows:
- Known camera lens attitude: The attitude of the lens while capturing UAV photographs can be obtained from the UAV aerial photography log. According to the rotation angle α of the horizontal direction of the camera lens, rotate the neighboring frames of the image and crop out the redundant boundaries; thus, the form of the standard binocular image can be obtained.
- Unknown camera lens attitude: If the attitude of the UAV camera lens is unknown, the rotation angle can be calculated based on binocular feature point matching, and the standard binocular image form can be obtained by rotating the neighboring frame images according to the rotation angle and cropping out the redundant boundary.
- Target canopy matching: In this study, we used high-dimensional feature template matching to match the uniform canopy object in the binocular image, and we were able to determine the region of the uniform canopy object in the binocular map.
- Matching region segmentation: The matching region of the same fruit tree canopy in the binocular image is segmented.
- Canopy foreground segmentation: In order to reduce the impact of the ground background region on the subsequent process of fruit tree canopy height estimation, this module uses the foreground segmentation network (in this paper, we use the U2-Net) to realize the separation of the front background of the fruit tree canopy.
Appendix A.1.2. Canopy Structure Reconstruction Module

Appendix A.2. Canopy Structure Parameter Error Rates (Absolute Values) for the Proposed Method, the SFM+MVS Method, and Ground Truth
| CH (mm) | |||||
|---|---|---|---|---|---|
| Tree_Num | GT | Our Method | SFM+MVS | Error_Our Method | Error_SFM+MVS |
| BC1 | 3291.9998 | 3180.4354 | 2643.0954 | 3.389% | 19.712% |
| BC2 | 3296.9971 | 3161.1417 | 3481.7983 | 4.121% | 5.605% |
| BC3 | 3493.9995 | 3389.718 | 3780.952 | 2.985% | 8.213% |
| BC4 | 2644.9966 | 2731.0678 | 2773.5854 | 3.254% | 4.862% |
| BC5 | 2705.9975 | 2592.0667 | 2167.6885 | 4.210% | 19.893% |
| BC6 | 3050.9987 | 2992.4442 | 2744.8381 | 1.919% | 10.035% |
| BC7 | 2990.9973 | 2843.4558 | 2763.0019 | 4.933% | 7.623% |
| BC8 | 2583.9996 | 2546.8567 | 2197.591 | 1.437% | 14.954% |
| BC9 | 2954.9980 | 2882.5761 | 3045.1062 | 2.451% | 3.049% |
| BC10 | 2892.9977 | 3036.5482 | 2716.9824 | 4.962% | 6.084% |
| BC11 | 3206.9969 | 3134.6084 | 2922.3992 | 2.257% | 8.874% |
| BC12 | 3138.9999 | 3024.7864 | 2969.2662 | 3.639% | 5.407% |
| Average | 3.296% | 9.526% | |||
| CV (mm3) | |||||
| Tree_Num | GT | Our Method | SFM+MVS | error_Our Method | error_SFM+MVS |
| BC1 | 72,988,178,184 | 78,534,836,967 | 31,289,459,492 | 7.599% | 57.131% |
| BC2 | 55,946,120,754 | 51,911,611,874 | 25,312,103,772 | 7.211% | 54.756% |
| BC3 | 55,218,551,779 | 50,042,335,368 | 31,180,146,570 | 9.374% | 43.533% |
| BC4 | 48,632,835,775 | 44,404,385,165 | 19,454,252,047 | 8.695% | 59.998% |
| BC5 | 36,500,327,835 | 31,794,054,227 | 17,249,641,227 | 12.894% | 52.741% |
| BC6 | 39,610,631,527 | 36,172,979,005 | 21,360,270,901 | 8.679% | 46.074% |
| BC7 | 39,052,282,765 | 35,616,992,140 | 18,155,816,993 | 8.797% | 53.509% |
| BC8 | 52,181,807,543 | 46,413,451,781 | 23,608,660,174 | 11.054% | 54.757% |
| BC9 | 60,609,531,275 | 55,582,427,180 | 25,678,835,565 | 8.294% | 57.632% |
| BC10 | 60,231,686,918 | 54,224,943,037 | 34,921,278,335 | 9.973% | 42.022% |
| BC11 | 51,930,116,269 | 55,804,523,508 | 29,566,996,423 | 7.461% | 43.064% |
| BC12 | 29,354,802,482 | 31,931,216,927 | 17,505,795,232 | 8.777% | 40.365% |
| Average | 9.067% | 50.465% | |||
| CW (mm) | |||||
| Tree_Num | GT | Our Method | SFM+MVS | error_Our Method | error_SFM+MVS |
| BC1 | 8897.1615 | 9107.1821 | 7778.5201 | 2.361% | 12.573% |
| BC2 | 8349.0019 | 8105.6921 | 7548.2131 | 2.914% | 9.591% |
| BC3 | 7238.9471 | 6925.4361 | 6423.6768 | 4.331% | 11.262% |
| BC4 | 8635.5524 | 8798.5615 | 7110.0029 | 1.888% | 17.666% |
| BC5 | 7194.3135 | 6848.8549 | 6817.7399 | 4.802% | 5.234% |
| BC6 | 8179.3771 | 8419.1807 | 7694.8620 | 2.932% | 5.924% |
| BC7 | 6737.5763 | 7018.0028 | 5716.5546 | 4.162% | 15.154% |
| BC8 | 8297.6803 | 8228.9672 | 6716.7766 | 0.828% | 19.052% |
| BC9 | 7299.5998 | 7120.3661 | 6409.4224 | 2.455% | 12.195% |
| BC10 | 8204.6801 | 8371.931 | 6656.2883 | 2.038% | 18.872% |
| BC11 | 7155.1607 | 7227.6965 | 6593.3290 | 1.014% | 7.852% |
| BC12 | 6569.0604 | 6801.6852 | 5475.4785 | 3.541% | 16.647% |
| Average | 2.772% | 12.669% | |||
| CPA (mm2) | |||||
| Tree_Num | GT | Our Method | SFM+MVS | error_Our Method | error_SFM+MVS |
| BC1 | 40,411,613.06 | 42,341,991.34 | 30,888,526.73 | 4.777% | 23.565% |
| BC2 | 35,585,441.19 | 33,541,574.36 | 29,086,505.21 | 5.744% | 18.263% |
| BC3 | 26,751,863.59 | 24,484,852.43 | 21065,443.24 | 8.474% | 21.256% |
| BC4 | 38,070,053.30 | 39,520,878.15 | 25,807,313.27 | 3.811% | 32.211% |
| BC5 | 26,422,989.60 | 23,946,341.33 | 23,729,254.56 | 9.373% | 10.195% |
| BC6 | 34,154,166.95 | 36,186,193.38 | 30,227,686.49 | 5.950% | 11.496% |
| BC7 | 23,174,513.56 | 25,143,765.19 | 16,682,915.49 | 8.497% | 28.012% |
| BC8 | 35,149,295.93 | 34,569,563.87 | 23,031,649.66 | 1.649% | 34.475% |
| BC9 | 27,202,031.82 | 25,882,599.11 | 20,972,056.82 | 4.850% | 22.903% |
| BC10 | 34,365,806.90 | 35,781,168.46 | 22,618,691.96 | 4.119% | 34.183% |
| BC11 | 26,136,174.62 | 26,668,774.15 | 22,192,832.34 | 2.038% | 15.088% |
| BC12 | 22,029,759.19 | 23,617,628.86 | 15,305,495.50 | 7.208% | 30.524% |
| Average | 5.541% | 23.514% | |||
Appendix A.3. Winter Time Application
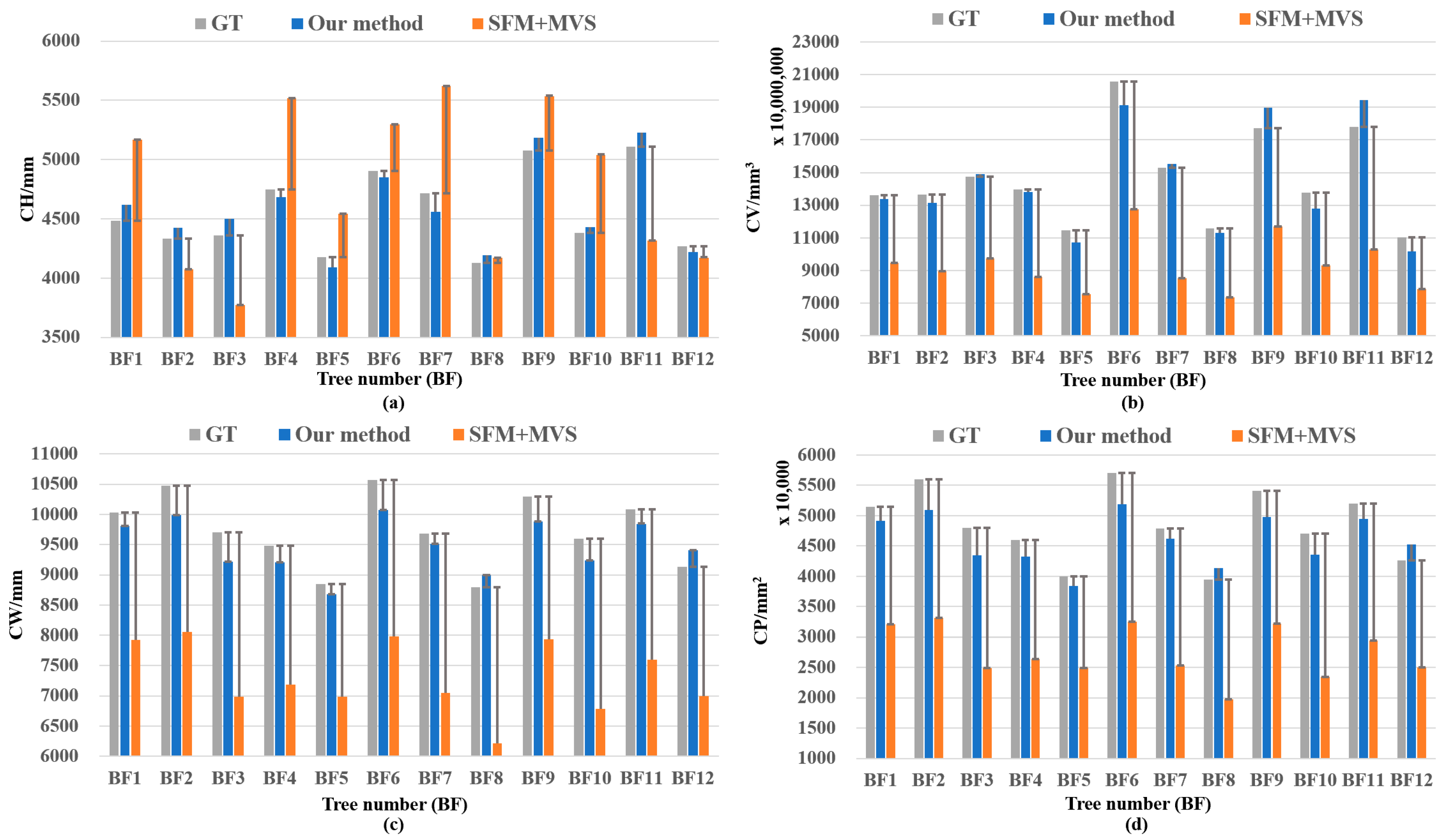

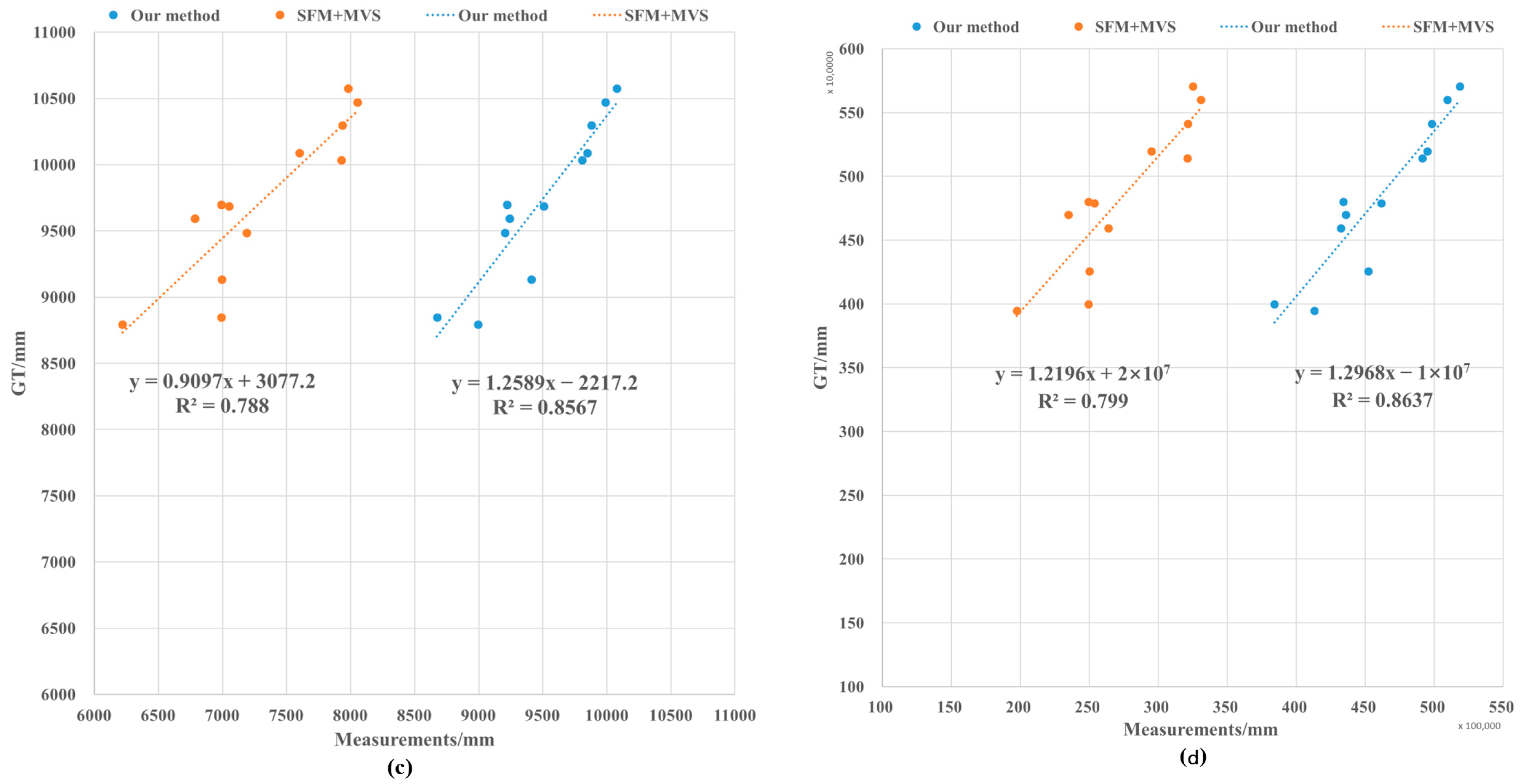
| CH (mm) | |||||
|---|---|---|---|---|---|
| Tree_Num | GT | Our Method | SFM+MVS | Error_Our Method | Error_SFM+MVS |
| BF1 | 4484.98050 | 4618.509 | 5169.901 | 2.977% | 15.271% |
| BF2 | 4331.69937 | 4424.6815 | 4073.0618 | 2.147% | 5.971% |
| BF3 | 4360.79979 | 4502.2321 | 3770.4123 | 3.243% | 13.539% |
| BF4 | 4746.90247 | 4681.1086 | 5517.4742 | 1.386% | 16.233% |
| BF5 | 4175.70496 | 4092.5167 | 4544.5342 | 1.992% | 8.833% |
| BF6 | 4905.89905 | 4851.6634 | 5298.6295 | 1.106% | 8.005% |
| BF7 | 4717.59796 | 4559.8403 | 5621.1942 | 3.344% | 19.154% |
| BF8 | 4128.70026 | 4195.3521 | 4171.5054 | 1.614% | 1.037% |
| BF9 | 5077.59857 | 5185.1781 | 5536.7487 | 2.119% | 9.043% |
| BF10 | 4382.09534 | 4432.1185 | 5041.5632 | 1.142% | 15.049% |
| BF11 | 5107.99408 | 5226.1024 | 4316.4606 | 2.312% | 15.496% |
| BF12 | 4266.70075 | 4217.5366 | 4173.9611 | 1.152% | 2.174% |
| Average | 2.044% | 10.817% | |||
| CV (mm3) | |||||
| Tree_Num | GT | Our Method | SFM+MVS | error_Our Method | error_SFM+MVS |
| BF1 | 136,229,237,885 | 133,655,821,175 | 94,728,440,093 | 1.889% | 30.464% |
| BF2 | 136,613,113,912 | 131,467,520,473 | 89,458,954,398 | 3.766% | 34.517% |
| BF3 | 147,484,106,788 | 148,983,106,913 | 97,456,201,958 | 1.016% | 33.921% |
| BF4 | 139,481,684,081 | 137,920,598,688 | 85,926,643,851 | 1.118% | 38.395% |
| BF5 | 114,622,326,464 | 106,985,450,087 | 75,644,170,444 | 6.662% | 34.006% |
| BF6 | 205,824,240,590 | 191,391,325,177 | 127,680,818,551 | 7.012% | 37.966% |
| BF7 | 152,807,118,136 | 155,486,208,774 | 85,291,725,418 | 1.753% | 44.183% |
| BF8 | 115,944,151,016 | 112,997,614,846 | 73,508,895,423 | 2.541% | 36.600% |
| BF9 | 177,349,329,903 | 189,563,398,636 | 116,836,062,676 | 6.887% | 34.121% |
| BF10 | 137,619,496,656 | 127,814,375,449 | 93,184,910,986 | 7.124% | 32.288% |
| BF11 | 178,161,183,739 | 194,327,302,860 | 102,912,299,940 | 9.074% | 42.236% |
| BF12 | 110,476,314,241 | 101,518,577,788 | 78,535,122,836 | 8.108% | 28.912% |
| Average | 4.746% | 35.634% | |||
| CW (mm) | |||||
| Tree_Num | GT | Our Method | SFM+MVS | error_Our Method | error_SFM+MVS |
| BF1 | 10034.82887 | 9808.0548 | 7927.4768 | 2.260% | 21.000% |
| BF2 | 10472.58835 | 9987.9103 | 8051.3289 | 4.628% | 23.120% |
| BF3 | 9698.44070 | 9220.4719 | 6987.5975 | 4.928% | 27.951% |
| BF4 | 9485.52571 | 9202.128 | 7186.9222 | 2.988% | 24.233% |
| BF5 | 8848.54280 | 8674.1266 | 6989.1535 | 1.971% | 21.014% |
| BF6 | 10574.19065 | 10077.6282 | 7977.6013 | 4.696% | 24.556% |
| BF7 | 9685.14630 | 9508.4412 | 7049.7687 | 1.824% | 27.211% |
| BF8 | 8794.72770 | 8994.9784 | 6217.5931 | 2.277% | 29.303% |
| BF9 | 10297.73217 | 9877.8708 | 7934.2353 | 4.077% | 22.952% |
| BF10 | 9595.50221 | 9238.7074 | 6781.9227 | 3.718% | 29.322% |
| BF11 | 10089.13285 | 9845.3625 | 7600.5276 | 2.416% | 24.666% |
| BF12 | 9132.31919 | 9409.2268 | 6995.2876 | 3.032% | 23.401% |
| Average | 3.235% | 24.894% | |||
| CPA (mm2) | |||||
| Tree_Num | GT | Our Method | SFM+MVS | error_Our Method | error_SFM+MVS |
| BF1 | 51,407,108.77 | 49,109,894.98 | 32,082,868.96 | 4.469% | 37.591% |
| BF2 | 55,990,107.86 | 50,927,517.27 | 33,093,170.3 | 9.042% | 40.895% |
| BF3 | 48,018,331.73 | 43,401,979.28 | 24,926,367.84 | 9.614% | 48.090% |
| BF4 | 45,933,130.88 | 43,229,456.74 | 26,368,724.64 | 5.886% | 42.593% |
| BF5 | 39,971,159.81 | 38,410,923.68 | 24,937,470.29 | 3.903% | 37.611% |
| BF6 | 57,081,780.4 | 51,846,554.61 | 32,489,863.98 | 9.171% | 43.082% |
| BF7 | 47,886,777.1 | 46,155,332.97 | 25,371,899.03 | 3.616% | 47.017% |
| BF8 | 39,486,444.75 | 41,305,081.9 | 19,735,486.28 | 4.606% | 50.020% |
| BF9 | 54,136,032.3 | 49,811,534.49 | 32,137,596.21 | 7.988% | 40.635% |
| BF10 | 47,004,415.65 | 43,573,822.86 | 23,480,584.78 | 7.298% | 50.046% |
| BF11 | 51,964,998.49 | 49,484,212.18 | 29,491,082.82 | 4.774% | 43.248% |
| BF12 | 42,576,053.49 | 45,197,156.4 | 24,981,262.74 | 6.156% | 41.326% |
| Average | 6.377% | 43.513% | |||

| Method | Reconstruction Time | Average Reconstruction Time/Tree | Number of Images Needed for Reconstruction/Picture |
|---|---|---|---|
| SFM+MVS | 01 h:33 m:04 s | 266 s | 130 |
| Our method | 6 m (↓88.7%) | 30 s (↓88.7%) | 24 (↓81.5%) |
References
- Anthony, B.M.; Minas, I.S. Optimizing peach tree canopy architecture for efficient light use, increased productivity and improved fruit quality. Agronomy 2021, 11, 1961. [Google Scholar] [CrossRef]
- Anderson, N.T.; Walsh, K.B.; Wulfsohn, D. Technologies for forecasting tree fruit load and harvest timing—From ground, sky and time. Agronomy 2021, 11, 1409. [Google Scholar] [CrossRef]
- Ortenzi, L.; Violino, S.; Pallottino, F.; Figorilli, S.; Vasta, S.; Tocci, F.; Antonucci, F.; Imperi, G.; Costa, C. Early estimation of olive production from light drone orthophoto, through canopy radius. Drones 2021, 5, 118. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, L.; Liu, P.; Wang, J.; Zhang, X.; Gao, D. Online calculation method of fruit trees canopy volume for precision spray. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2019, 50, 120–129. [Google Scholar]
- Gu, C.; Zhai, C.; Wang, X.; Wang, S. Cmpc: An innovative lidar-based method to estimate tree canopy meshing-profile volumes for orchard target-oriented spray. Sensors 2021, 21, 4252. [Google Scholar] [CrossRef] [PubMed]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Aslan, M.F.; Durdu, A.; Sabanci, K.; Ropelewska, E.; Gültekin, S.S. A comprehensive survey of the recent studies with UAV for precision agriculture in open fields and greenhouses. Appl. Sci. 2022, 12, 1047. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Zarzour, H.; Kechida, A.; Taberkit, A.M. Deep learning techniques to classify agricultural crops through UAV imagery: A review. Neural Comput. Applications 2022, 34, 9511–9536. [Google Scholar] [CrossRef]
- Slavík, M.; Kuželka, K.; Modlinger, R.; Tomášková, I.; Surový, P. UAV laser scans allow detection of morphological changes in tree canopy. Remote Sens. 2020, 12, 3829. [Google Scholar] [CrossRef]
- Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of backpack, handheld, under-canopy UAV, and above-canopy UAV laser scanning for field reference data collection in boreal forests. Remote Sens. 2020, 12, 3327. [Google Scholar] [CrossRef]
- Chisholm, R.A.; Cui, J.; Lum, S.K.; Chen, B.M. UAV LiDAR for below-canopy forest surveys. J. Unmanned Veh. Syst. 2013, 1, 61–68. [Google Scholar] [CrossRef]
- Ghanbari Parmehr, E.; Amati, M. Individual tree canopy parameters estimation using UAV-based photogrammetric and LiDAR point clouds in an urban park. Remote Sens. 2021, 13, 2062. [Google Scholar] [CrossRef]
- Sun, G.; Wang, X.; Yang, H.; Zhang, X. A canopy information measurement method for modern standardized apple orchards based on UAV multimodal information. Sensors 2020, 20, 2985. [Google Scholar] [CrossRef] [PubMed]
- Mu, Y.; Fujii, Y.; Takata, D.; Zheng, B.; Noshita, K.; Honda, K.; Ninomiya, S.; Guo, W. Characterization of peach tree crown by using high-resolution images from an unmanned aerial vehicle. Hortic. Res. 2018, 5, 74. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Fang, Z.; Wu, B.; Liu, S.; Ma, Y.; Pan, Y. Tree Canopy Height Estimation and Accuracy Analysis Based on Uav Remote Sensing Images. The International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2022, 43, 129–134. [Google Scholar]
- Nasiri, V.; Darvishsefat, A.A.; Arefi, H.; Pierrot-Deseilligny, M.; Namiranian, M.; Le Bris, A. Unmanned aerial vehicles (UAV)-based canopy height modeling under leaf-on and leaf-off conditions for determining tree height and crown diameter (case study: Hyrcanian mixed forest). Can. J. For. Res. 2021, 51, 962–971. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T.G.; Mund, J.P.; Greve, K. UAV-based photogrammetric tree height measurement for intensive forest monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
- Hobart, M.; Pflanz, M.; Weltzien, C.; Schirrmann, M. Growth height determination of tree walls for precise monitoring in apple fruit production using UAV photogrammetry. Remote Sens. 2020, 12, 1656. [Google Scholar] [CrossRef]
- Malekabadi, A.J.; Khojastehpour, M.; Emadi, B. Disparity map computation of tree using stereo vision system and effects of canopy shapes and foliage density. Comput. Electron. Agric. 2019, 156, 627–644. [Google Scholar] [CrossRef]
- Ni, Z.; Burks, T.F. 3D dense reconstruction of plant or tree canopy based on stereo vision. Agricultural Engineering International. CIGR J. 2018, 20, 248–260. [Google Scholar]
- Zhang, R.; Lian, S.; Li, L.; Zhang, L.; Zhang, C.; Chen, L. Design and experiment of a binocular vision-based canopy volume extraction system for precision pesticide application by UAVs. Comput. Electronics in Agriculture 2023, 213, 108197. [Google Scholar] [CrossRef]
- Matsuura, Y.; Heming, Z.; Nakao, K.; Qiong, C.; Firmansyah, I.; Kawai, S.; Yamaguchi, Y.; Maruyama, T.; Hayashi, H.; Nobuhara, H. High-precision plant height measurement by drone with RTK-GNSS and single camera for real-time processing. Sci. Rep. 2023, 13, 6329. [Google Scholar] [CrossRef] [PubMed]
- Hirschmuller, H. Accurate and efficient stereo processing by semi-global matching and mutual information. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 807–814. [Google Scholar]
- Hamzah, R.A.; Abd Rahim, R.; Noh, Z.M. Sum of absolute differences algorithm in stereo correspondence problem for stereo matching in computer vision application. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 1, pp. 652–657. [Google Scholar]
- Stateras, D.; Kalivas, D. Assessment of olive tree canopy characteristics and yield forecast model using high resolution UAV imagery. Agriculture 2020, 10, 385. [Google Scholar] [CrossRef]
- Raman, M.G.; Carlos, E.F.; Sankaran, S. Optimization and evaluation of sensor angles for precise assessment of architectural traits in peach trees. Sensors 2022, 22, 4619. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Zhang, C.; Xu, B.; Zhu, Y.; Zhao, F.; Han, S.; Yang, G.; Yang, H. Predicting individual apple tree yield using UAV multi-source remote sensing data and ensemble learning. Comput. Electron. Agric. 2022, 201, 107275. [Google Scholar] [CrossRef]
- Sanz, R.; Llorens, J.; Escolà, A.; Arnó, J.; Planas, S.; Román, C.; Rosell-Polo, J.R. LIDAR and non-LIDAR-based canopy parameters to estimate the leaf area in fruit trees and vineyard. Agric. For. Meteorol. 2018, 260, 229–239. [Google Scholar] [CrossRef]
- Zhu, W.; Sun, Z.; Peng, J.; Huang, Y.; Li, J.; Zhang, J.; Yang, B.; Liao, X. Estimating maize above-ground biomass using 3D point clouds of multi-source unmanned aerial vehicle data at multi-spatial scales. Remote Sens. 2019, 11, 2678. [Google Scholar] [CrossRef]
- Kameyama, S.; Sugiura, K. Estimating tree height and volume using unmanned aerial vehicle photography and SfM technology, with verification of result accuracy. Drones 2020, 4, 19. [Google Scholar] [CrossRef]
- Straffelini, E.; Cucchiaro, S.; Tarolli, P. Mapping potential surface ponding in agriculture using UAV-SfM. Earth Surf. Process. Landf. 2021, 46, 1926–1940. [Google Scholar] [CrossRef]
- Miraki, M.; Sohrabi, H.; Fatehi, P.; Kneubuehler, M. Individual tree crown delin-eation from high-resolution UAV images in broadleaf forest. Ecol. Inform. 2021, 61, 101207. [Google Scholar] [CrossRef]
- Sun, G.; Wang, X.; Ding, Y.; Lu, W.; Sun, Y. Remote measurement of apple orchard canopy information using unmanned aerial vehicle photogrammetry. Agronomy 2019, 9, 774. [Google Scholar] [CrossRef]
- Scalisi, A.; McClymont, L.; Peavey, M.; Morton, P.; Scheding, S.; Un-derwood, J.; Goodwin, I. Detecting, mapping and digitising canopy geometry, fruit number and peel colour in pear trees with different architecture. Sci. Hortic. 2024, 326, 112737. [Google Scholar] [CrossRef]
- López-Granados, F.; Torres-Sánchez, J.; Jiménez-Brenes, F.M.; Arquero, O.; Lovera, M.; de Castro, A.I. An efficient RGB-UAV-based platform for field almond tree phenotyping: 3-D architecture and flowering traits. Plant Methods 2019, 15, 160. [Google Scholar] [CrossRef] [PubMed]




| Method | SFM+MVS | Our Method |
|---|---|---|
| Reconstruction time | 02 h:06 m:04 s | 6 m (↓95.2%) |
| Average reconstruction time/tree | 630 s | 30 s (↓95.2%) |
| Number of images needed for reconstruction/picture | 203 | 24 (↓88.2%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Peng, X.; Bai, T.; Wang, H.; Takata, D.; Guo, W. A UAV-Based Single-Lens Stereoscopic Photography Method for Phenotyping the Architecture Traits of Orchard Trees. Remote Sens. 2024, 16, 1570. https://doi.org/10.3390/rs16091570
Zhang W, Peng X, Bai T, Wang H, Takata D, Guo W. A UAV-Based Single-Lens Stereoscopic Photography Method for Phenotyping the Architecture Traits of Orchard Trees. Remote Sensing. 2024; 16(9):1570. https://doi.org/10.3390/rs16091570
Chicago/Turabian StyleZhang, Wenli, Xinyu Peng, Tingting Bai, Haozhou Wang, Daisuke Takata, and Wei Guo. 2024. "A UAV-Based Single-Lens Stereoscopic Photography Method for Phenotyping the Architecture Traits of Orchard Trees" Remote Sensing 16, no. 9: 1570. https://doi.org/10.3390/rs16091570
APA StyleZhang, W., Peng, X., Bai, T., Wang, H., Takata, D., & Guo, W. (2024). A UAV-Based Single-Lens Stereoscopic Photography Method for Phenotyping the Architecture Traits of Orchard Trees. Remote Sensing, 16(9), 1570. https://doi.org/10.3390/rs16091570










