Four Years of Atmospheric Boundary Layer Height Retrievals Using COSMIC-2 Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Instrumentation and Databases
2.1.1. COSMIC-2
2.1.2. Microwave Radiometers
2.1.3. Ceilometer and Lidar
2.1.4. Radiosondes
2.2. Methodologies to Retrieve ABLH
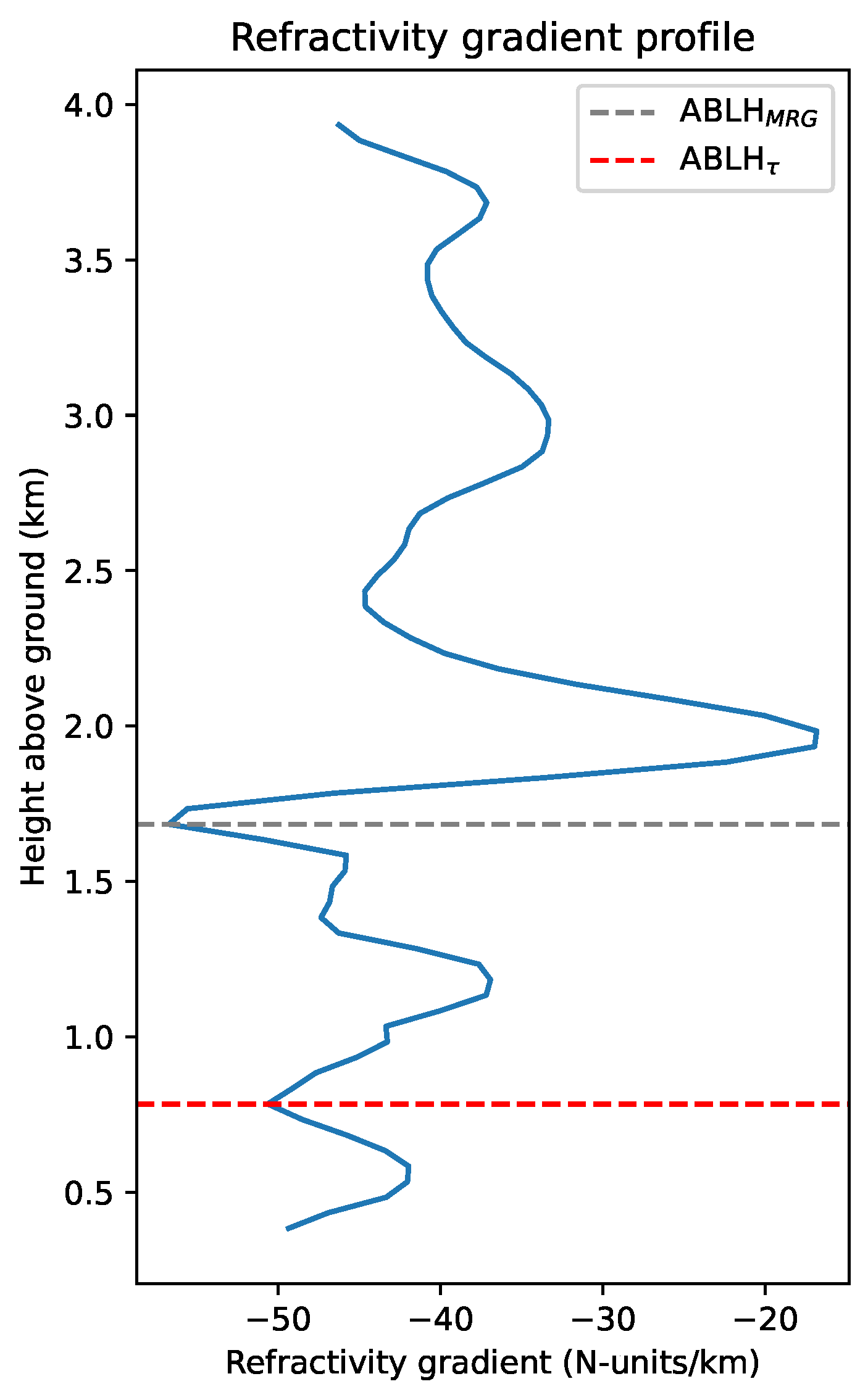
2.2.1. Methods Based on Refractivity
2.2.2. Methods Based on Temperature
2.2.3. Method Based on RCS
2.3. Determination of the Optimum Algorithm for ABLH Retrieval from COSMIC-2 Data
3. Results
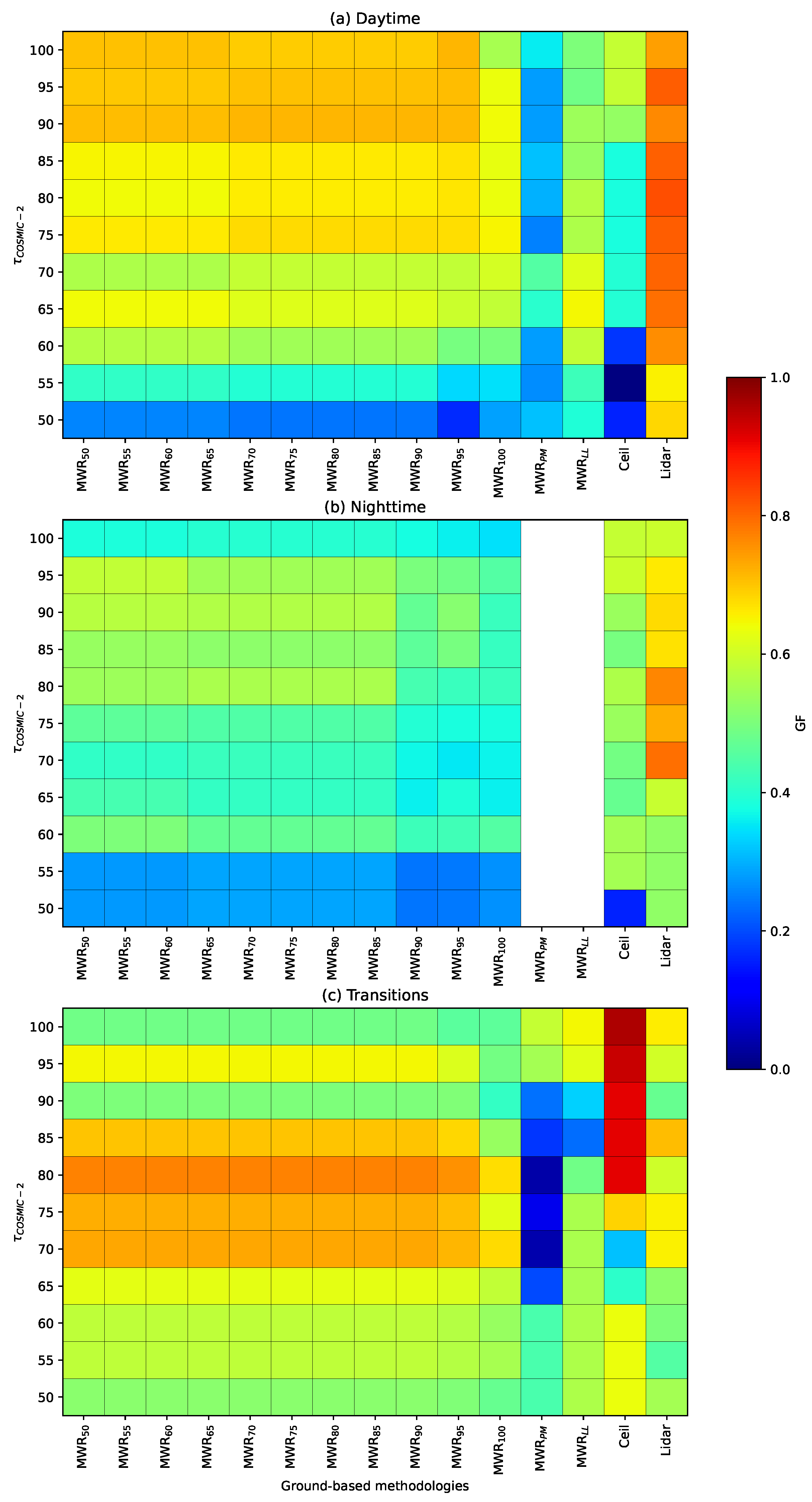
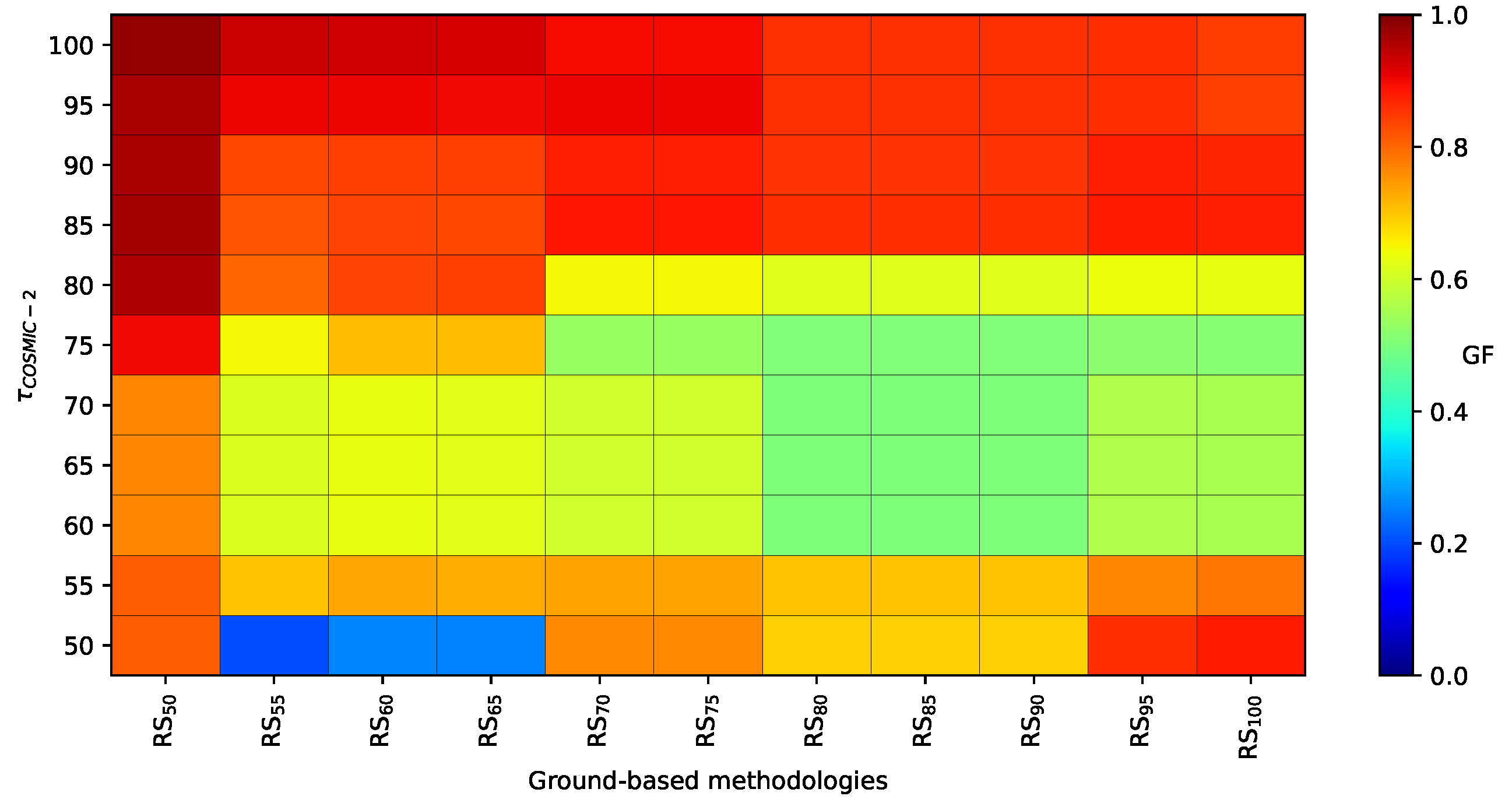
3.1. Tune-Up of the ABLH Retrieval Algorithm
3.1.1. Land Regions
3.1.2. Oceanic Regions
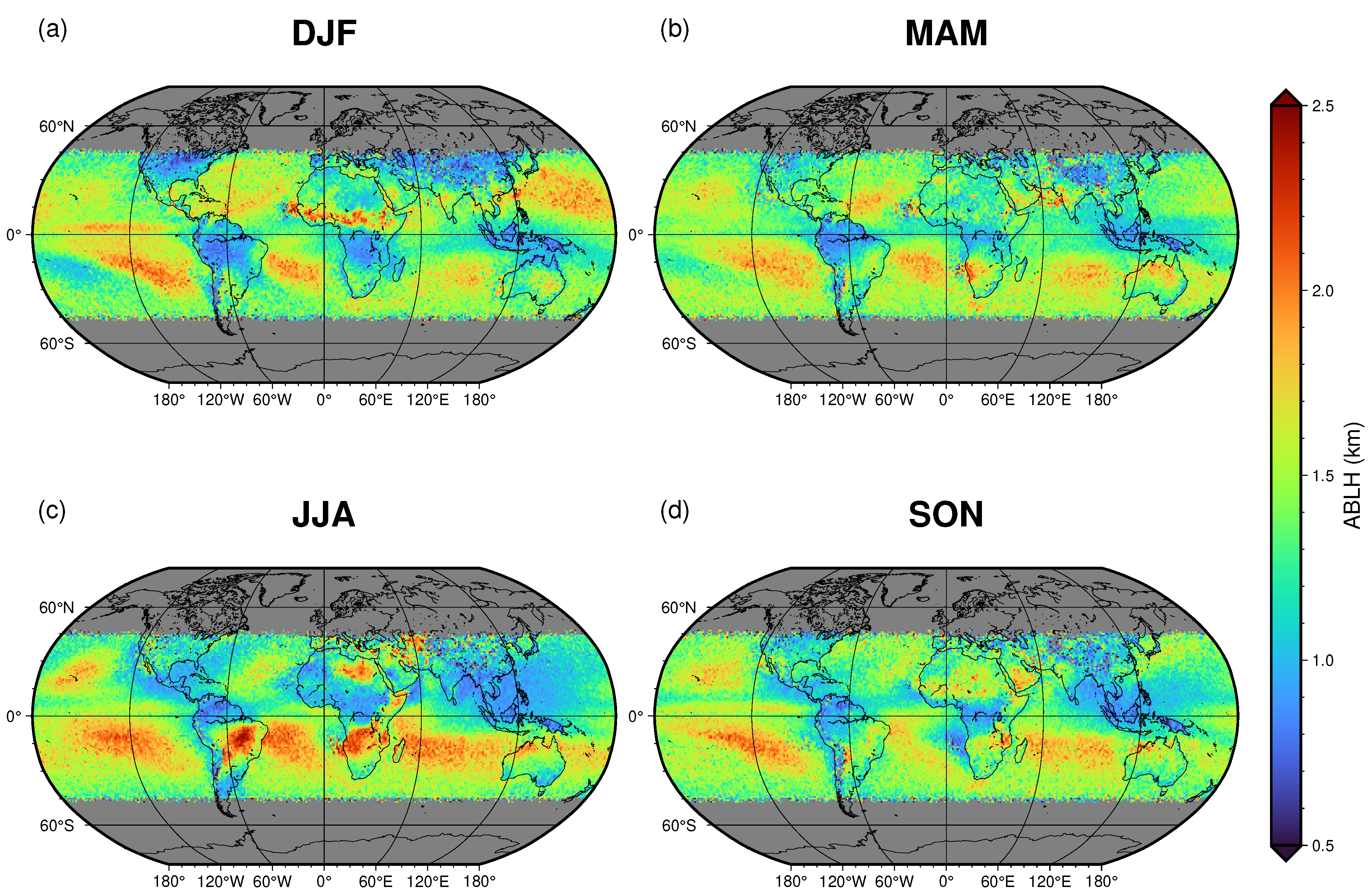
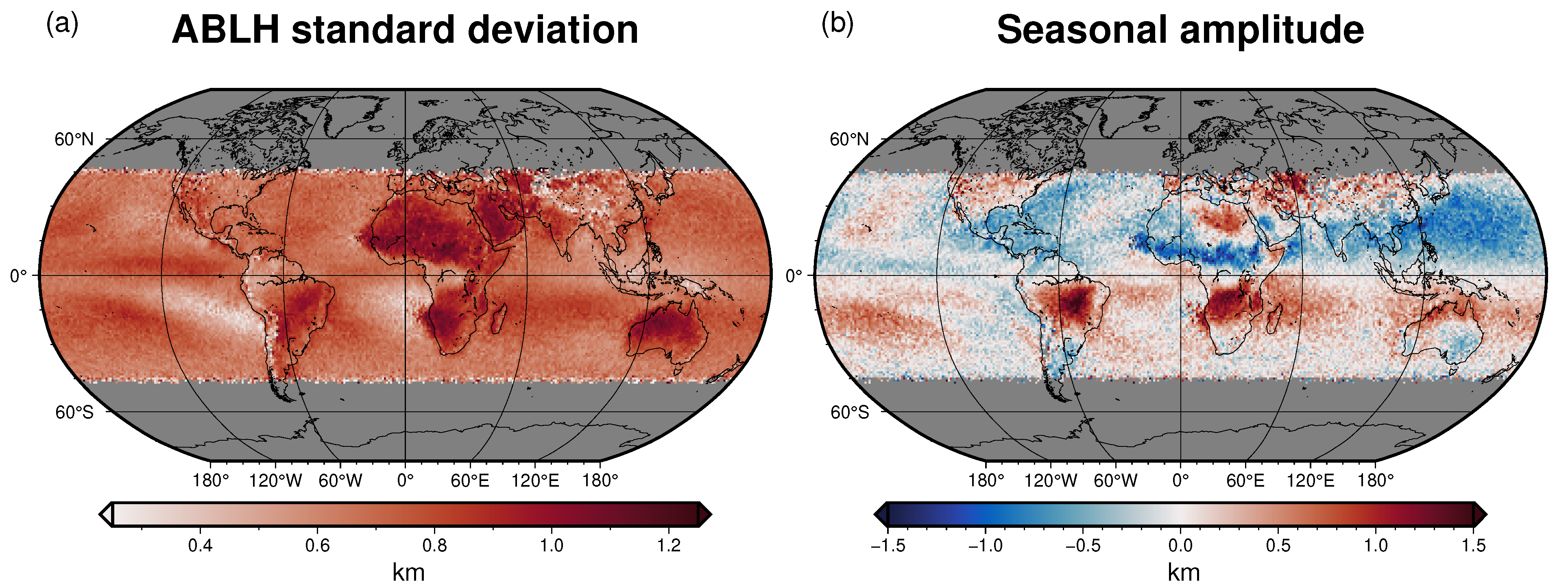
3.2. ABLH Seasonal Fields from Satellite Observations
3.3. ABLH Intradiurnal Fields from Satellite Observations
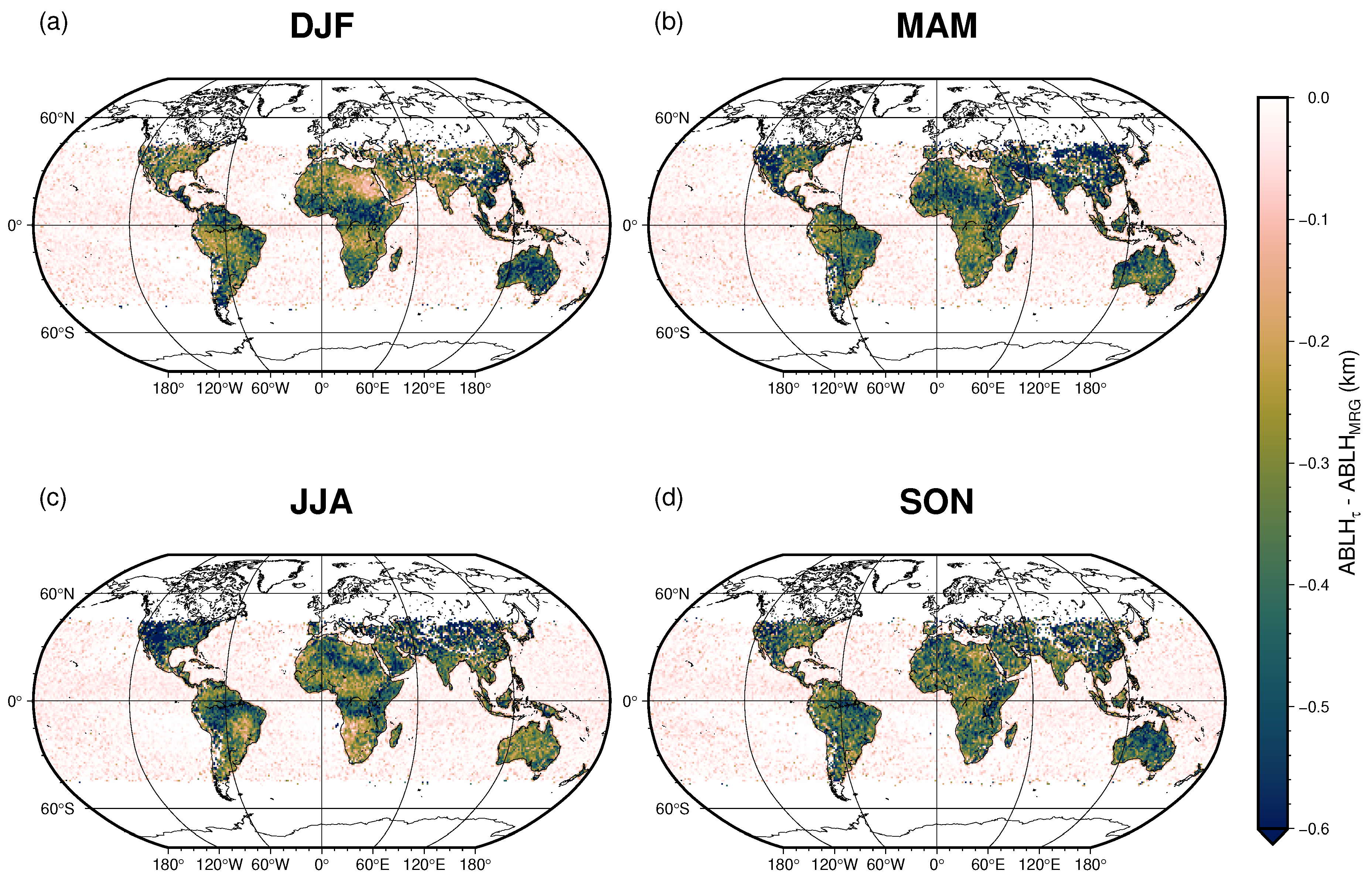
3.4. Comparison of the Proposed Algorithm with MRG Method
4. Discussion
4.1. ABLH Proposed Algorithm
4.2. ABLH Seasonal Fields
4.3. ABLH Intradiurnal Fields
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric Boundary Layer |
| ABLH | Atmospheric Boundary Layer Height |
| ACTRIS | Aerosol, Cloud and Trace Gases Research Infrastructure |
| AGORA | Andalusian Global ObseRvatory of the Atmosphere |
| ALADIN | Atmospheric Laser Doppler Instrument |
| ARM | Atmospheric Radiation Measurement |
| CALIPSO | Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations |
| CBL | Convective Boundary Layer |
| CDAAC | COSMIC Data Analysis and Archive Center |
| COSMIC | Constellation Observing System for Meteorology, Ionosphere and Climate |
| DJF | December, January and February |
| EARLINET | Europea Aerosol Research Lidar Network |
| EaRSLab | Earth Remote Sensing Laboratory |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ENA | Eastern North Atlantic |
| EPCAPE | Eastern Pacific Cloud Aerosol Precipitation Experiment |
| EVASO | EVora Atmospheric Sciences Observatory |
| FT | Free Troposphere |
| GF | Goodness of Fit function |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| ICT | Institute of Earth Sciences |
| IISTA | Andalusian Institute for Earth System Research |
| ITCZ | Intertropical Convergence Zone |
| IVM | Ion Velocity Meter |
| JJA | June, July, and August |
| JPL | Jet Propulsion Laboratory |
| LEO | Low Earth Orbit |
| LSG | Lowest Significant Gradient |
| MAM | March, April, and May |
| MRG | Minimum Refractivity Gradient |
| MWR | Microwave Radiometer |
| NOAA | National Oceanic and Atmospheric Administration |
| NSPO | National Space Organization |
| PAOLI | Portable Aerosol and Cloud Lidar |
| PBL | Planetary Boundary Layer |
| PM | Parcel Method |
| RCS | Range-Corrected Signal |
| RL | Residual Layer |
| RO | Radio Occultation |
| SBL | Stable Boundary Layer |
| SON | September, October, and November |
| SPALINET | Spanish and Portuguese Aerosol Lidar Network |
| SPCZ | South Pacific Convergence Zone |
| TGRS | TriG (GPS, GALILEO and GLONASS) GNSS Radio Occultation System |
| UCAR | University Corporation for Atmospheric Research |
References
- Seibert, P.; Beyrich, F.; Gryning, S.; Joffre, S.; Rasmussen, A.; Tercier, P. Mixing layer depth determination for dispersion modelling. European Commission. In COST Action; European Commission: Brussels, Belgium, 1998. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988; Volume 13. [Google Scholar]
- AMS. Glossary of Meteorology; American Meteorological Society (AMS): Boston, MA, USA, 2000. [Google Scholar]
- Medeiros, B.; Hall, A.; Stevens, B. What controls the mean depth of the PBL? J. Clim. 2005, 18, 3157–3172. [Google Scholar] [CrossRef]
- von Engeln, A.; Teixeira, J. A planetary boundary layer height climatology derived from ECMWF reanalysis data. J. Clim. 2013, 26, 6575–6590. [Google Scholar] [CrossRef]
- Chan, K.M.; Wood, R. The seasonal cycle of planetary boundary layer depth determined using COSMIC radio occultation data. J. Geophys. Res. Atmos. 2013, 118, 12–422. [Google Scholar] [CrossRef]
- Liu, S.; Liang, X.Z. Observed diurnal cycle climatology of planetary boundary layer height. J. Clim. 2010, 23, 5790–5809. [Google Scholar] [CrossRef]
- Palmén, E.; Newton, C.W. Atmospheric Circulation Systems: Their Structure and Physical Interpretation; Academic Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Garratt, J.R. The atmospheric boundary layer. Earth-Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Kotthaus, S.; Bravo-Aranda, J.A.; Collaud Coen, M.; Guerrero-Rascado, J.L.; Costa, M.J.; Cimini, D.; O’Connor, E.J.; Hervo, M.; Alados-Arboledas, L.; Jiménez-Portaz, M.; et al. Atmospheric boundary layer height from ground-based remote sensing: A review of capabilities and limitations. Atmos. Meas. Tech. 2023, 16, 433–479. [Google Scholar] [CrossRef]
- Han, S.; Bian, H.; Tie, X.; Xie, Y.; Sun, M.; Liu, A. Impact of nocturnal planetary boundary layer on urban air pollutants: Measurements from a 250-m tower over Tianjin, China. J. Hazard. Mater. 2009, 162, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Peña, A.; Floors, R.; Sathe, A.; Gryning, S.E.; Wagner, R.; Courtney, M.S.; Larsén, X.G.; Hahmann, A.N.; Hasager, C.B. Ten years of boundary-layer and wind-power meteorology at Høvsøre, Denmark. Bound.-Layer Meteorol. 2016, 158, 1–26. [Google Scholar] [CrossRef]
- Illingworth, A.J.; Cimini, D.; Haefele, A.; Haeffelin, M.; Hervo, M.; Kotthaus, S.; Löhnert, U.; Martinet, P.; Mattis, I.; O’connor, E.; et al. How can existing ground-based profiling instruments improve European weather forecasts? Bull. Am. Meteorol. Soc. 2019, 100, 605–619. [Google Scholar] [CrossRef]
- Barlow, J.; Best, M.; Bohnenstengel, S.I.; Clark, P.; Grimmond, S.; Lean, H.; Christen, A.; Emeis, S.; Haeffelin, M.; Harman, I.N.; et al. Developing a research strategy to better understand, observe, and simulate urban atmospheric processes at kilometer to subkilometer scales. Bull. Am. Meteorol. Soc. 2017, 98, ES261–ES264. [Google Scholar] [CrossRef]
- Vajda, A.; Tuomenvirta, H.; Jokinen, P.; Luomaranta, A.; Makkonen, L.; Tikanmäki, M.; Groenemeijer, P.; Saarikivi, P.; Michaelides, S.; Papadakis, M.; et al. Probabilities of Adverse Weather Affecting Transport in Europe: Climatology and Scenarios up to the 2050s; Ilmatieteen Laitos: Helsinki, Finland, 2011. [Google Scholar]
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Cancillo, M.L.; King, C.W. A wind profiler climatology of boundary layer structure above the boreal forest. J. Geophys. Res. Atmos. 1997, 102, 29083–29100. [Google Scholar] [CrossRef]
- Emeis, S.; Schafer, K.; Munkel, C. Surface-based remote sensing of the mixing-layer height-a review. Meteorol. Z. 2008, 17, 621. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Haeffelin, M.; Kotthaus, S.; Löhnert, U.; Martinet, P.; O’Connor, E.; Walden, C.; Coen, M.C.; Preissler, J. Towards the profiling of the atmospheric boundary layer at European scale—introducing the COST Action PROBE. Bull. Atmos. Sci. Technol. 2020, 1, 23–42. [Google Scholar] [CrossRef]
- Collaud Coen, M.; Praz, C.; Haefele, A.; Ruffieux, D.; Kaufmann, P.; Calpini, B. Determination and climatology of the planetary boundary layer height above the Swiss plateau by in situ and remote sensing measurements as well as by the COSMO-2 model. Atmos. Chem. Phys. 2014, 14, 13205–13221. [Google Scholar] [CrossRef]
- Duncan, J.B., Jr.; Bianco, L.; Adler, B.; Bell, T.; Djalalova, I.V.; Riihimaki, L.; Sedlar, J.; Smith, E.N.; Turner, D.D.; Wagner, T.J.; et al. Evaluating convective planetary boundary layer height estimations resolved by both active and passive remote sensing instruments during the CHEESEHEAD19 field campaign. Atmos. Meas. Tech. 2022, 15, 2479–2502. [Google Scholar] [CrossRef]
- Jordan, N.S.; Hoff, R.M.; Bacmeister, J.T. Validation of Goddard Earth Observing System-version 5 MERRA planetary boundary layer heights using CALIPSO. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, J.; Miao, Y.; Liu, H.; Zhang, Y.; Li, Z.; Zhai, P. Planetary boundary layer height from CALIOP compared to radiosonde over China. Atmos. Chem. Phys. 2016, 16, 9951–9963. [Google Scholar] [CrossRef]
- Flamant, P.; Cuesta, J.; Denneulin, M.L.; Dabas, A.; Huber, D. ADM-Aeolus retrieval algorithms for aerosol and cloud products. Tellus Dyn. Meteorol. Oceanogr. 2008, 60, 273–286. [Google Scholar] [CrossRef]
- Straume, A.G.; Rennie, M.; Isaksen, L.; de Kloe, J.; Marseille, G.J.; Stoffelen, A.; Flament, T.; Stieglitz, H.; Dabas, A.; Huber, D.; et al. ESA’s space-based Doppler wind lidar mission Aeolus–First wind and aerosol product assessment results. EPJ Web Conf. 2020, 237, 01007. [Google Scholar] [CrossRef]
- Abril-Gago, J.; Guerrero-Rascado, J.L.; Costa, M.J.; Bravo-Aranda, J.A.; Sicard, M.; Bermejo-Pantaleón, D.; Bortoli, D.; Granados-Muñoz, M.J.; Rodríguez-Gómez, A.; Muñoz-Porcar, C.; et al. Statistical validation of Aeolus L2A particle backscatter coefficient retrievals over ACTRIS/EARLINET stations on the Iberian Peninsula. Atmos. Chem. Phys. 2022, 22, 1425–1451. [Google Scholar] [CrossRef]
- Abril-Gago, J.; Ortiz-Amezcua, P.; Bermejo-Pantaleón, D.; Andújar-Maqueda, J.; Bravo-Aranda, J.A.; Granados-Muñoz, M.J.; Navas-Guzmán, F.; Alados-Arboledas, L.; Foyo-Moreno, I.; Guerrero-Rascado, J.L. Validation activities of Aeolus wind products on the southeastern Iberian Peninsula. Atmos. Chem. Phys. 2023, 23, 8453–8471. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Xie, F.; Wu, D.; Ao, C.; Mannucci, A.; Kursinski, E. Advances and limitations of atmospheric boundary layer observations with GPS occultation over southeast Pacific Ocean. Atmos. Chem. Phys. 2012, 12, 903–918. [Google Scholar] [CrossRef]
- Ao, C.O.; Waliser, D.E.; Chan, S.K.; Li, J.L.; Tian, B.; Xie, F.; Mannucci, A.J. Planetary boundary layer heights from GPS radio occultation refractivity and humidity profiles. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Ho, S.p.; Peng, L.; Anthes, R.A.; Kuo, Y.H.; Lin, H.C. Marine boundary layer heights and their longitudinal, diurnal, and interseasonal variability in the southeastern Pacific using COSMIC, CALIOP, and radiosonde data. J. Clim. 2015, 28, 2856–2872. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Chen, B.; Zhou, T.; Yan, H.; Jin, H.; Huang, Z.; Zhang, B. Comparisons of PBL heights derived from CALIPSO and ECMWF reanalysis data over China. J. Quant. Spectrosc. Radiat. Transf. 2015, 153, 102–112. [Google Scholar] [CrossRef]
- Von Engeln, A.; Teixeira, J.; Wickert, J.; Buehler, S.A. Using CHAMP radio occultation data to determine the top altitude of the planetary boundary layer. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Basha, G.; Ratnam, M.V. Identification of atmospheric boundary layer height over a tropical station using high-resolution radiosonde refractivity profiles: Comparison with GPS radio occultation measurements. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Fishbach, F. A satellite method for temperature and pressure below 24 km. Bull. Am. Meteorol. Soc 1965, 9, 1. [Google Scholar] [CrossRef]
- Lusignan, B.; Modrell, G.; Morrison, A.; Pomalaza, J.; Ungar, S. Sensing the Earth’s atmosphere with occultation satellites. Proc. IEEE 1969, 57, 458–467. [Google Scholar] [CrossRef]
- Ware, R.; Exner, M.; Feng, D.; Gorbunov, M.; Hardy, K.; Herman, B.; Kuo, Y.; Meehan, T.; Melbourne, W.; Rocken, C.; et al. GPS sounding of the atmosphere from low Earth orbit: Preliminary results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef]
- Kursinski, E.; Hajj, G.; Bertiger, W.; Leroy, S.; Meehan, T.; Romans, L.; Schofield, J.; McCleese, D.; Melbourne, W.; Thornton, C.; et al. Initial results of radio occultation observations of Earth’s atmosphere using the Global Positioning System. Science 1996, 271, 1107–1110. [Google Scholar] [CrossRef]
- Kursinski, E.; Hajj, G.; Schofield, J.; Linfield, R.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Rocken, C.; Anthes, R.; Exner, M.; Hunt, D.; Sokolovskiy, S.; Ware, R.; Gorbunov, M.; Schreiner, W.; Feng, D.; Herman, B.; et al. Analysis and validation of GPS/MET data in the neutral atmosphere. J. Geophys. Res. Atmos. 1997, 102, 29849–29866. [Google Scholar] [CrossRef]
- Fong, C.J.; Wu, B.H.; Yen, N.; Chen, P. Application of FORMOSAT-3/COSMIC mission to global Earth monitoring. In Proceedings of the Space 2005, Long Beach, CA, USA, 30 August–1 September 2005; p. 6774. [Google Scholar]
- Hsu, C.T.; Matsuo, T.; Liu, J.Y. Impact of assimilating the FORMOSAT-3/COSMIC and FORMOSAT-7/COSMIC-2 RO data on the Midlatitude and low-latitude ionospheric specification. Earth Space Sci. 2018, 5, 875–890. [Google Scholar] [CrossRef]
- Ho, S.p.; Anthes, R.A.; Ao, C.O.; Healy, S.; Horanyi, A.; Hunt, D.; Mannucci, A.J.; Pedatella, N.; Randel, W.J.; Simmons, A.; et al. The COSMIC/FORMOSAT-3 radio occultation mission after 12 years: Accomplishments, remaining challenges, and potential impacts of COSMIC-2. Bull. Am. Meteorol. Soc. 2020, 101, E1107–E1136. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 radio occultation constellation: First results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Santosh, M. Estimation of daytime planetary boundary layer height (PBLH) over the tropics and subtropics using COSMIC-2/FORMOSAT-7 GNSS–RO measurements. Atmos. Res. 2022, 279, 106361. [Google Scholar] [CrossRef]
- Qiu, C.; Wang, X.; Li, H.; Zhou, K.; Zhang, J.; Li, Z.; Liu, D.; Yuan, H. A Comparison of Atmospheric Boundary Layer Height Determination Methods Using GNSS Radio Occultation Data. Atmosphere 2023, 14, 1654. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Rocken, C.; Lenschow, D.; Kuo, Y.H.; Anthes, R.; Schreiner, W.; Hunt, D. Observing the moist troposphere with radio occultation signals from COSMIC. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Guo, P.; Kuo, Y.H.; Sokolovskiy, S.; Lenschow, D. Estimating atmospheric boundary layer depth using COSMIC radio occultation data. J. Atmos. Sci. 2011, 68, 1703–1713. [Google Scholar] [CrossRef]
- Tien, J.Y.; Okihiro, B.B.; Esterhuizen, S.X.; Franklin, G.W.; Meehan, T.K.; Munson, T.N.; Robison, D.E.; Turbiner, D.; Young, L.E. Next generation scalable spaceborne GNSS science receiver. In Proceedings of the 2012 international technical meeting of the institute of navigation, Newport Beach, CA, USA, 30 January–1 February 2012; pp. 882–914. [Google Scholar]
- Esterhuizen, S.; Franklin, G.; Hurst, K.; Mannucci, A.; Meehan, T.; Webb, F.; Young, L. TriG-A GNSS precise orbit and radio occultation space receiver. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1442–1446. [Google Scholar]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.G.; Xia-Serafino, W.; Lynch, E. Initial assessment of the COSMIC-2/FORMOSAT-7 neutral atmosphere data quality in NESDIS/STAR using in situ and satellite data. Remote. Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Wee, T.K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R. Inversion and error estimation of GPS radio occultation data. J. Meteorol. Soc. Jpn. Ser. 2004, 82, 507–531. [Google Scholar] [CrossRef]
- Ho, S.p.; Kirchengast, G.; Leroy, S.; Wickert, J.; Mannucci, A.J.; Steiner, A.; Hunt, D.; Schreiner, W.; Sokolovskiy, S.; Ao, C.; et al. Estimating the uncertainty of using GPS radio occultation data for climate monitoring: Intercomparison of CHAMP refractivity climate records from 2002 to 2006 from different data centers. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Ho, S.p.; Hunt, D.; Steiner, A.K.; Mannucci, A.J.; Kirchengast, G.; Gleisner, H.; Heise, S.; von Engeln, A.; Marquardt, C.; Sokolovskiy, S.; et al. Reproducibility of GPS radio occultation data for climate monitoring: Profile-to-profile inter-comparison of CHAMP climate records 2002 to 2008 from six data centers. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wee, T.K. A variational regularization of Abel transform for GPS radio occultation. Atmos. Meas. Tech. 2018, 11, 1947–1969. [Google Scholar] [CrossRef]
- Straume, A.; Schuettemeyer, D.; Von Bismarck, J.; Kanitz, T.; Fehr, T. Aeolus Scientific Calibration and Validation Implementation Plan; European Space Research and Technology Centre: Noordwijk, The Netherlands, 2019. [Google Scholar]
- Basha, G.; Kishore, P.; Ratnam, M.V.; Ravindra Babu, S.; Velicogna, I.; Jiang, J.H.; Ao, C.O. Global climatology of planetary boundary layer top obtained from multi-satellite GPS RO observations. Clim. Dyn. 2019, 52, 2385–2398. [Google Scholar] [CrossRef]
- Rose, T.; Crewell, S.; Löhnert, U.; Simmer, C. A network suitable microwave radiometer for operational monitoring of the cloudy atmosphere. Atmos. Res. 2005, 75, 183–200. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Costa, M.J.; Bortoli, D.; Navas-Guzmán, F.; Alados-Arboledas, L. Microwave radiometer, sun-photometer and GNSS multi-comparison of integrated water vapor in Southwestern Europe. Atmos. Res. 2023, 287, 106698. [Google Scholar] [CrossRef]
- Heese, B.; Flentje, H.; Althausen, D.; Ansmann, A.; Frey, S. Ceilometer lidar comparison: Backscatter coefficient retrieval and signal-to-noise ratio determination. Atmos. Meas. Tech. 2010, 3, 1763–1770. [Google Scholar] [CrossRef]
- Cazorla, A.; Casquero-Vera, J.A.; Román, R.; Guerrero-Rascado, J.L.; Toledano, C.; Cachorro, V.E.; Orza, J.A.G.; Cancillo, M.L.; Serrano, A.; Titos, G.; et al. Near-real-time processing of a ceilometer network assisted with sun-photometer data: Monitoring a dust outbreak over the Iberian Peninsula. Atmos. Chem. Phys. 2017, 17, 11861–11876. [Google Scholar] [CrossRef]
- Althausen, D.; Engelmann, R.; Baars, H.; Heese, B.; Ansmann, A.; Müller, D.; Komppula, M. Portable Raman lidar PollyXT for automated profiling of aerosol backscatter, extinction, and depolarization. J. Atmos. Ocean. Technol. 2009, 26, 2366–2378. [Google Scholar] [CrossRef]
- Salgueiro, V.; Costa, M.J.; Guerrero-Rascado, J.L.; Couto, F.T.; Bortoli, D. Characterization of forest fire and Saharan desert dust aerosols over south-western Europe using a multi-wavelength Raman lidar and Sun-photometer. Atmos. Environ. 2021, 252, 118346. [Google Scholar] [CrossRef]
- Preißler, J.; Wagner, F.; Pereira, S.; Guerrero-Rascado, J. Multi-instrumental observation of an exceptionally strong Saharan dust outbreak over Portugal. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Pappalardo, G.; Amodeo, A.; Apituley, A.; Comeron, A.; Freudenthaler, V.; Linné, H.; Ansmann, A.; Bösenberg, J.; D’Amico, G.; Mattis, I.; et al. EARLINET: Towards an advanced sustainable European aerosol lidar network. Atmos. Meas. Tech. 2014, 7, 2389–2409. [Google Scholar] [CrossRef]
- Sicard, M.; Molero, F.; Guerrero-Rascado, J.L.; Pedrós, R.; Expósito, F.J.; Córdoba-Jabonero, C.; Bolarín, J.M.; Comerón, A.; Rocadenbosch, F.; Pujadas, M.; et al. Aerosol LiDAR intercomparison in the framework of SPALINET—The Spanish LiDAR network: Methodology and results. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 3547–3559. [Google Scholar] [CrossRef]
- Holdridge, D. Balloon-Borne Sounding System (SONDE) Instrument Handbook; Technical Report, DOE Office of Science Atmospheric Radiation Measurement (ARM) Program; U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research: Washington, DC, USA, 2020.
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 37. [Google Scholar]
- Cartwright, K.V. Simpson’s rule cumulative integration with MS Excel and irregularly-spaced data. J. Math. Sci. Math. Educ. 2017, 12, 1–9. [Google Scholar]
- List, R.J. Smithsonian Meteorological Tables; Smithsonian miscellaneous collections; NWS Weather Forecast Offices: Silver Spring, MD, USA, 1951. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- de Arruda Moreira, G.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Foyo-Moreno, I.; Cazorla, A.; Alados, I.; Lyamani, H.; Landulfo, E.; Alados-Arboledas, L. Study of the planetary boundary layer height in an urban environment using a combination of microwave radiometer and ceilometer. Atmos. Res. 2020, 240, 104932. [Google Scholar] [CrossRef]
- Stull, R.B. Meteorology for Scientists and Engineers: A Technical Companion Book with Ahrens’ Meteorology Today; Brooks/Cole: Salt Lake City, UL, USA, 2000. [Google Scholar]
- Holzworth, G.C. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather. Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
- Menut, L.; Flamant, C.; Pelon, J.; Flamant, P.H. Urban boundary-layer height determination from lidar measurements over the Paris area. Appl. Opt. 1999, 38, 945–954. [Google Scholar] [CrossRef]
- Kotthaus, S.; Bravo-Aranda, J.; Collaud Coen, M.; Guerrero-Rascado, J.; Costa, M.J.; Cimini, D.; O’Connor, E.; Maxime, H.; Arboledas, L.; Jiménez-Portaz, M.; et al. Atmospheric boundary layer height from ground-based remote sensing: A review of capabilities and limitations. Atmos. Meas. Tech. Discuss. 2022, 2022, 1–88. [Google Scholar] [CrossRef]
- Granados-Muñoz, M.; Navas-Guzmán, F.; Bravo-Aranda, J.; Guerrero-Rascado, J.; Lyamani, H.; Fernández-Gálvez, J.; Alados-Arboledas, L. Automatic determination of the planetary boundary layer height using lidar: One-year analysis over southeastern Spain. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Renju, R.; Raju, C.S.; Mishra, M.; Mathew, N.; Rajeev, K.; Moorthy, K.K. Atmospheric boundary layer characterization using multiyear ground-based microwave radiometric observations over a tropical coastal station. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 6877–6882. [Google Scholar] [CrossRef]
- Carpenter, T. Thermal Properties of Dry and Saturated Soils. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2019. [Google Scholar]
- Schneider, T.; Bischoff, T.; Haug, G.H. Migrations and dynamics of the intertropical convergence zone. Nature 2014, 513, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Haffke, C.; Magnusdottir, G. The South Pacific Convergence Zone in three decades of satellite images. J. Geophys. Res. Atmos. 2013, 118, 10–839. [Google Scholar] [CrossRef]
- Vincent, D.G. The South Pacific convergence zone (SPCZ): A review. Mon. Weather. Rev. 1994, 122, 1949–1970. [Google Scholar] [CrossRef]
- Klein, S.A.; Hartmann, D.L. The seasonal cycle of low stratiform clouds. J. Clim. 1993, 6, 1587–1606. [Google Scholar] [CrossRef]
- Teixeira, J. Simulation of fog with the ECMWF prognostic cloud scheme. Q. J. R. Meteorol. Soc. 1999, 125, 529–552. [Google Scholar] [CrossRef]
- Geiß, A.; Wiegner, M.; Bonn, B.; Schäfer, K.; Forkel, R.; von Schneidemesser, E.; Münkel, C.; Chan, K.L.; Nothard, R. Mixing layer height as an indicator for urban air quality? Atmos. Meas. Tech. 2017, 10, 2969–2988. [Google Scholar] [CrossRef]
- Milroy, C.; Martucci, G.; Lolli, S.; Loaec, S.; Sauvage, L.; Xueref-Remy, I.; Lavrič, J.V.; Ciais, P.; Feist, D.G.; Biavati, G.; et al. An assessment of pseudo-operational ground-based light detection and ranging sensors to determine the boundary-layer structure in the coastal atmosphere. Adv. Meteorol. 2012, 2012, 929080. [Google Scholar] [CrossRef]
- Toledo, D.; Córdoba-Jabonero, C.; Adame, J.A.; De La Morena, B.; Gil-Ojeda, M. Estimation of the atmospheric boundary layer height during different atmospheric conditions: A comparison on reliability of several methods applied to lidar measurements. Int. J. Remote. Sens. 2017, 38, 3203–3218. [Google Scholar] [CrossRef]
- Barlow, J.F.; Dunbar, T.; Nemitz, E.; Wood, C.R.; Gallagher, M.; Davies, F.; O’Connor, E.; Harrison, R. Boundary layer dynamics over London, UK, as observed using Doppler lidar during REPARTEE-II. Atmos. Chem. Phys. 2011, 11, 2111–2125. [Google Scholar] [CrossRef]
- de Arruda Moreira, G.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Benavent-Oltra, J.A.; Ortiz-Amezcua, P.; Róman, R.; Bedoya-Velásquez, A.E.; Landulfo, E.; Alados-Arboledas, L. Study of the planetary boundary layer by microwave radiometer, elastic lidar and Doppler lidar estimations in Southern Iberian Peninsula. Atmos. Res. 2018, 213, 185–195. [Google Scholar] [CrossRef]
- Tang, G.; Zhang, J.; Zhu, X.; Song, T.; Münkel, C.; Hu, B.; Schäfer, K.; Liu, Z.; Zhang, J.; Wang, L.; et al. Mixing layer height and its implications for air pollution over Beijing, China. Atmos. Chem. Phys. 2016, 16, 2459–2475. [Google Scholar] [CrossRef]
- Seidel, D.J.; Zhang, Y.; Beljaars, A.; Golaz, J.C.; Jacobson, A.R.; Medeiros, B. Climatology of the planetary boundary layer over the continental United States and Europe. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wang, X.; Wang, K. Estimation of atmospheric mixing layer height from radiosonde data. Atmos. Meas. Tech. 2014, 7, 1701–1709. [Google Scholar] [CrossRef]
- Guerrero-Rascado, J.L.; Olmo, F.; Avilés-Rodríguez, I.; Navas-Guzmán, F.; Pérez-Ramírez, D.; Lyamani, H.; Alados Arboledas, L. Extreme Saharan dust event over the southern Iberian Peninsula in september 2007: Active and passive remote sensing from surface and satellite. Atmos. Chem. Phys. 2009, 9, 8453–8469. [Google Scholar] [CrossRef]
- McGrath-Spangler, E.L.; Denning, A.S. Global seasonal variations of midday planetary boundary layer depth from CALIPSO space-borne LIDAR. J. Geophys. Res. Atmos. 2013, 118, 1226–1233. [Google Scholar] [CrossRef]
- Ratnam, M.; Basha, S. A robust method to determine global distribution of atmospheric boundary layer top from COSMIC GPS RO measurements. Atmos. Sci. Lett. 2010, 11, 216–222. [Google Scholar] [CrossRef]
- Bianco, L.; Djalalova, I.; King, C.; Wilczak, J. Diurnal evolution and annual variability of boundary-layer height and its correlation to other meteorological variables in California’s Central Valley. Bound.-Layer Meteorol. 2011, 140, 491–511. [Google Scholar] [CrossRef]
- Brooks, I.M. Finding boundary layer top: Application of a wavelet covariance transform to lidar backscatter profiles. J. Atmos. Ocean. Technol. 2003, 20, 1092–1105. [Google Scholar] [CrossRef]
- Manghnani, V.; Raman, S.; Niyogi, D.S.; Parameswara, V.; Morrison, J.M.; Ramana, S.; Raju, J. Marine boundary-layer variability over the Indian Ocean during INDOEX (1998). Bound.-Layer Meteorol. 2000, 97, 411–430. [Google Scholar] [CrossRef]
- Subrahamanyam, D.B.; Ramachandran, R.; Gupta, K.S.; Mandal, T.K. Variability of mixed-layer heights over the Indian Ocean and central Arabian Sea during INDOEX, IFP-99. Bound.-Layer Meteorol. 2003, 107, 683–695. [Google Scholar] [CrossRef]
- Zeng, X.; Brunke, M.A.; Zhou, M.; Fairall, C.; Bond, N.A.; Lenschow, D.H. Marine atmospheric boundary layer height over the eastern Pacific: Data analysis and model evaluation. J. Clim. 2004, 17, 4159–4170. [Google Scholar] [CrossRef]
- Johnson, R.H.; Ciesielski, P.E. Multiscale variability of the atmospheric boundary layer during DYNAMO. J. Atmos. Sci. 2017, 74, 4003–4021. [Google Scholar] [CrossRef]
- Zhang, C. Double ITCZs. J. Geophys. Res. Atmos. 2001, 106, 11785–11792. [Google Scholar] [CrossRef]
- Meenu, S.; Rajeev, K.; Parameswaran, K.; Suresh Raju, C. Characteristics of the double intertropical convergence zone over the tropical Indian Ocean. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Wood, R.; Bretherton, C.S. Boundary layer depth, entrainment, and decoupling in the cloud-capped subtropical and tropical marine boundary layer. J. Clim. 2004, 17, 3576–3588. [Google Scholar] [CrossRef]
- Niyogi, D. Urban impacts on regional rainfall climatology. In Proceedings of the Ninth International Conference on Urban Climate/12th Symposium on the Urban Environment, Toulouse, France, IAUC and American Meteorological Society, UCP9-7, Toulouse, France, 20–24 July 2015; Available online: http://www.meteo.fr/icuc9/presentations/UCP/UCP9-7.pdf (accessed on 4 February 2024).
- Melecio-Vázquez, D.; González-Cruz, J.; Arend, M.; Han, Z.; Gutierrez, E.; Dempsey, M.; Booth, J. New York metro-area boundary layer catalogue: Boundary layer height and stability conditions from long-term observations. In Proceedings of the Ninth International Conference on Urban Climate/12th Symposium on the Urban Environment, Toulouse, France, IAUC and American Meteorological Society, Toulouse, France, 20–24 July 2015. [Google Scholar]
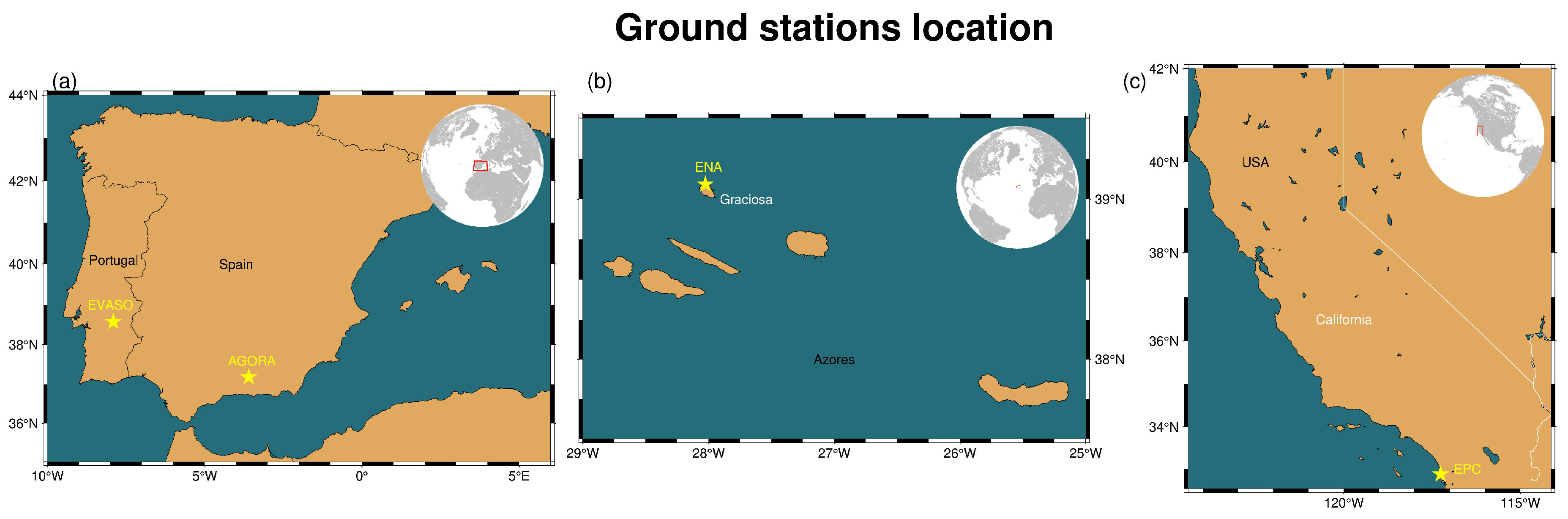


| Facility | Location and Altitude | Instruments |
|---|---|---|
| Andalusian Global Observatory of the Atmosphere | Granada (Spain) | Ceilometer |
| (AGORA) | 37.164°N, 3.605°W, 680 m a.s.l. | MWR |
| Evora Atmospheric Sciences Observatory | Évora (Portugal) | Lidar |
| (EVASO) | 38.568°N, 7.912°W, 293 m a.s.l. | MWR |
| Eastern North Atlantic | Azores (Portugal) | Radiosondes |
| (ENA) | 39.053°N, 28.010°W, 26 m a.s.l. | |
| Eastern Pacific CAPE | La Jolla (California, USA) | Radiosondes |
| (EPC) | 32.897°N, 117.257°W, 7 m a.s.l. |
| Atmospheric Property | Instrument (Variables) | Method | Equations | Section |
|---|---|---|---|---|
| Refractivity (N) | COSMIC-2 satellite (N) MWR (T, , ) Radiosonde (T, p, U) | MRG [28] LSG [45] | (4) (1), (4), (6), (8), (7), (9) (1), (4), (10), (11) | Section 2.2.1 |
| Potential temperature () | MWR (T) Radiosonde (T) | PM [74] Liu and Liang [7] | (12) | Section 2.2.2 |
| Range-corrected signal (RCS) | Ceilometer (RCS) Lidar (RCS) | Gradient [75] | (4) | Section 2.2.3 |
| Surface | Period | (%) | Validation Data Source | GF | n |
|---|---|---|---|---|---|
| Land | Daytime | 82 | Lidar | 0.828 | 21 |
| Nighttime | 68 | Lidar | 0.813 | 18 | |
| Transitions | 98 | Ceilometer | 0.956 | 9 | |
| Ocean | - | 99 | Radiosonde | 0.984 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garnés-Morales, G.; Costa, M.J.; Bravo-Aranda, J.A.; Granados-Muñoz, M.J.; Salgueiro, V.; Abril-Gago, J.; Fernández-Carvelo, S.; Andújar-Maqueda, J.; Valenzuela, A.; Foyo-Moreno, I.; et al. Four Years of Atmospheric Boundary Layer Height Retrievals Using COSMIC-2 Satellite Data. Remote Sens. 2024, 16, 1632. https://doi.org/10.3390/rs16091632
Garnés-Morales G, Costa MJ, Bravo-Aranda JA, Granados-Muñoz MJ, Salgueiro V, Abril-Gago J, Fernández-Carvelo S, Andújar-Maqueda J, Valenzuela A, Foyo-Moreno I, et al. Four Years of Atmospheric Boundary Layer Height Retrievals Using COSMIC-2 Satellite Data. Remote Sensing. 2024; 16(9):1632. https://doi.org/10.3390/rs16091632
Chicago/Turabian StyleGarnés-Morales, Ginés, Maria João Costa, Juan Antonio Bravo-Aranda, María José Granados-Muñoz, Vanda Salgueiro, Jesús Abril-Gago, Sol Fernández-Carvelo, Juana Andújar-Maqueda, Antonio Valenzuela, Inmaculada Foyo-Moreno, and et al. 2024. "Four Years of Atmospheric Boundary Layer Height Retrievals Using COSMIC-2 Satellite Data" Remote Sensing 16, no. 9: 1632. https://doi.org/10.3390/rs16091632
APA StyleGarnés-Morales, G., Costa, M. J., Bravo-Aranda, J. A., Granados-Muñoz, M. J., Salgueiro, V., Abril-Gago, J., Fernández-Carvelo, S., Andújar-Maqueda, J., Valenzuela, A., Foyo-Moreno, I., Navas-Guzmán, F., Alados-Arboledas, L., Bortoli, D., & Guerrero-Rascado, J. L. (2024). Four Years of Atmospheric Boundary Layer Height Retrievals Using COSMIC-2 Satellite Data. Remote Sensing, 16(9), 1632. https://doi.org/10.3390/rs16091632














