High Resolution Ranging with Small Sample Number under Low SNR Utilizing RIP-OMCS Strategy and AHRC l1 Minimization for Laser Radar
Abstract
1. Introduction
- (1)
- Firstly, we introduce an RIP-OMCS strategy. This strategy ensures uniform internal sampling within each channel and coprime sampling among channels, facilitating hardware implementation. This strategy achieves a much smaller sample number while maintaining high-ranging accuracy.
- (2)
- Subsequently, we utilize the cross-correlation function for estimating sampling-time errors. Using the cross-correlation function of the time-domain spectrum of the reference channel and other channels, the asynchronous sampling-time error can be estimated. After compensating for these estimated errors, we perform ranging model registration.
- (3)
- Finally, we reformulate target-range estimation as an optimization problem of sparse representation. This optimization incorporates sparse constraints and AHRC to embody prior information. Through an iterative solving process, AHRC gradually refines, thereby enhancing the accuracy of the solution. AHRC combines the characteristics of the logarithmic penalty function and the arctangent penalty function in different regions. Therefore, AHRC effectively distinguishes the influence of signal and noise when solving the optimization problem. This leads to the reconstruction of a high-resolution range profile and the acquisition of a more accurate target distance while reducing the influence of noise. The proposed method achieves accurate high-resolution ranging under low-SNR, ultra-wide bandwidth, and sub-Nyquist sampling.
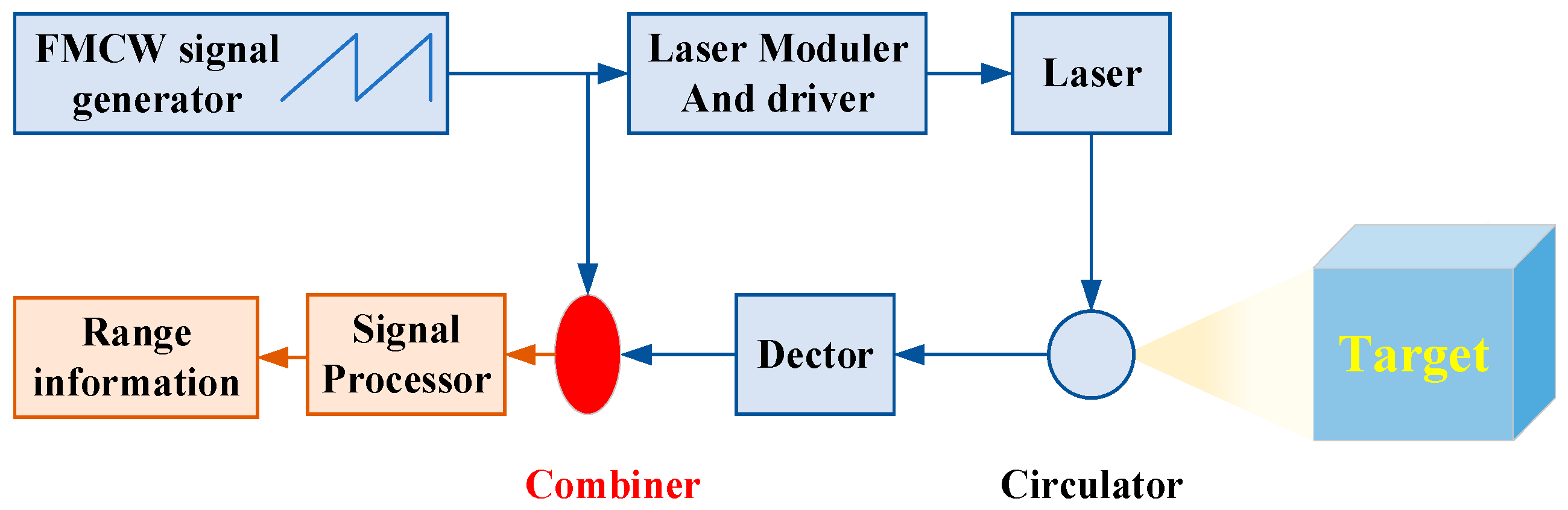
2. Laser-Radar Ranging Model with Small Sample Number Based on Multi-Channel Coprime Sampling
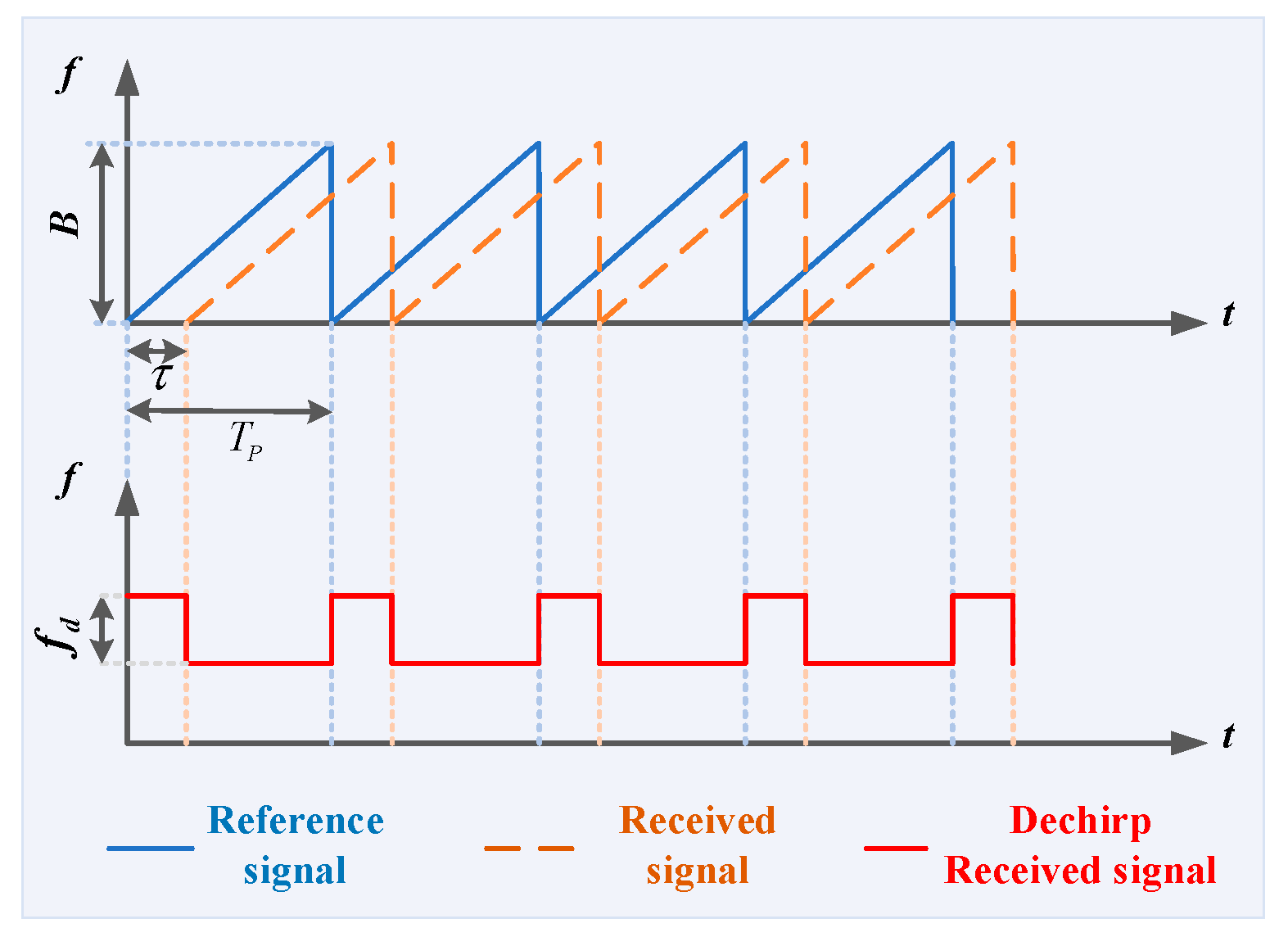
2.1. Mathematical Model of Laser-Radar Ranging
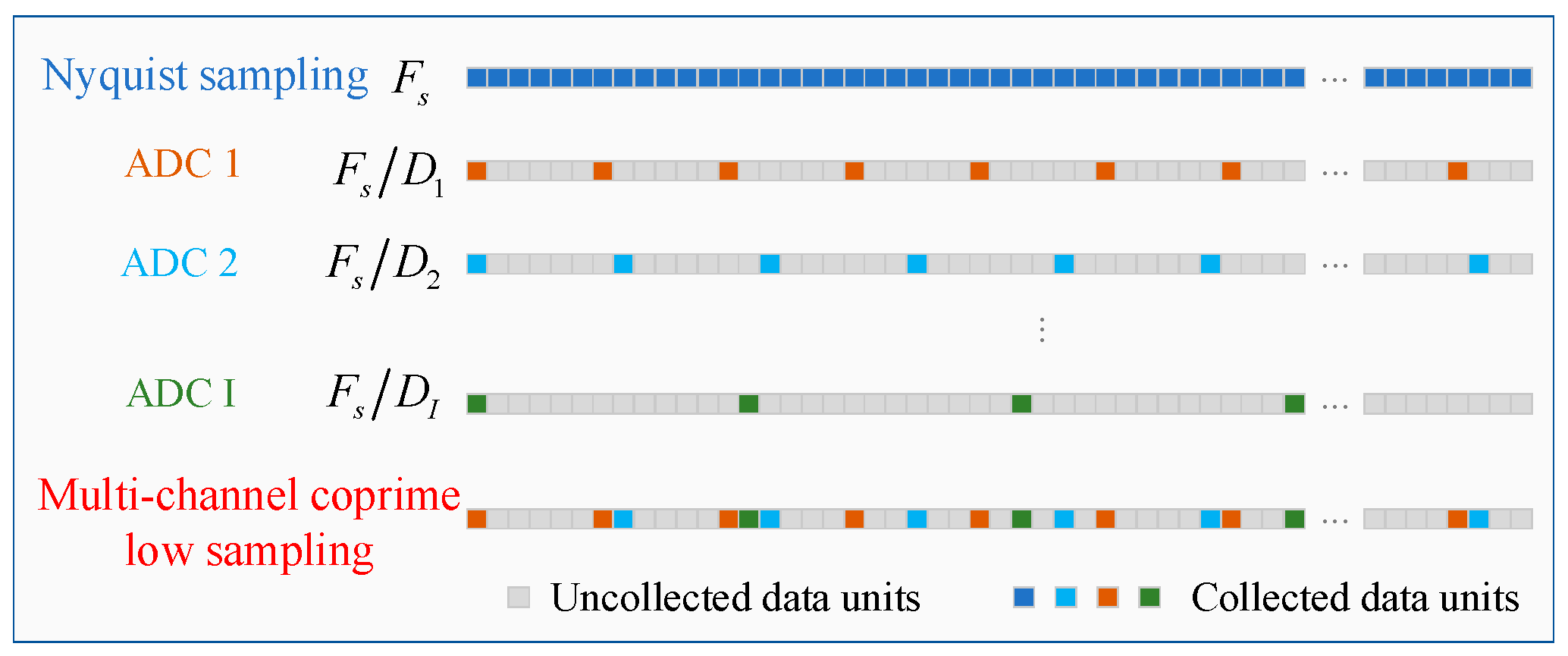
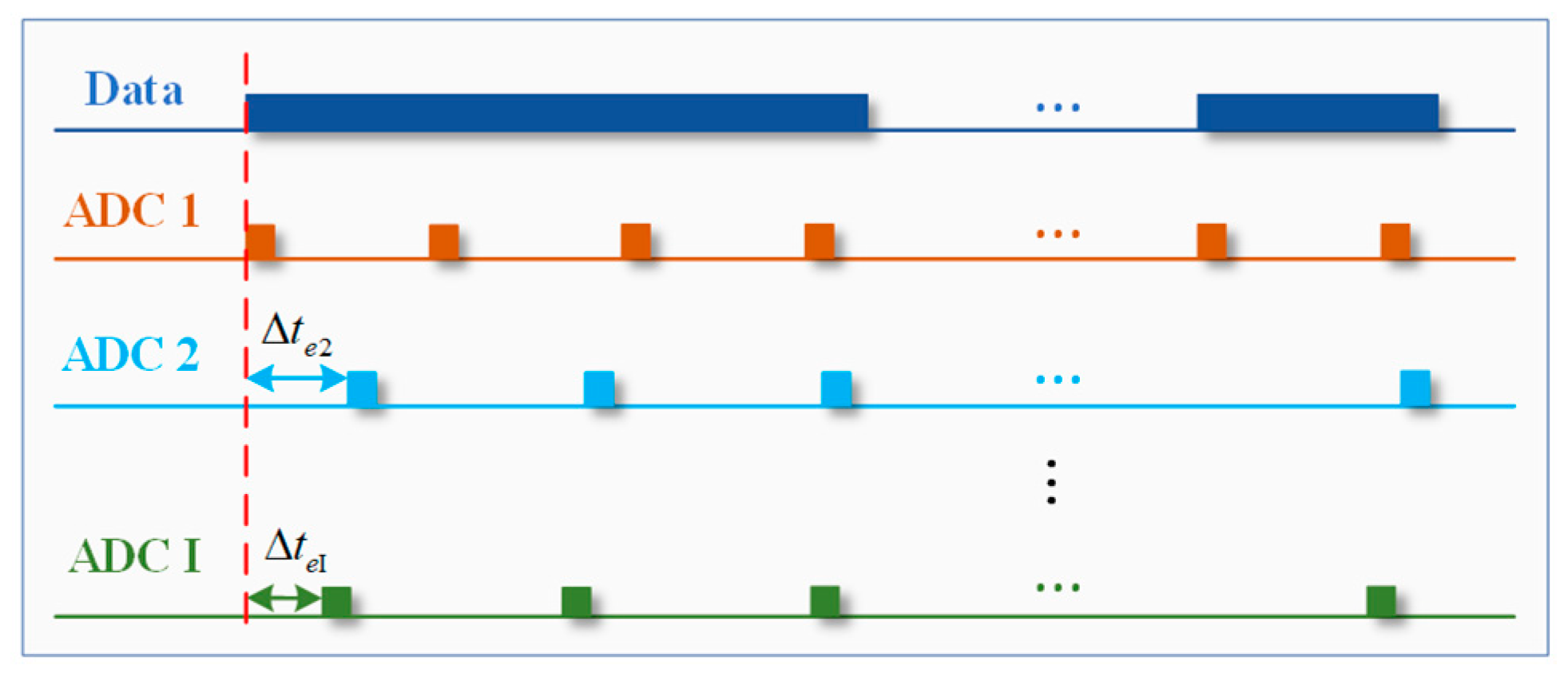
2.2. Ranging Model Based on the Multi-Channel Coprime Low-Sampling Scheme
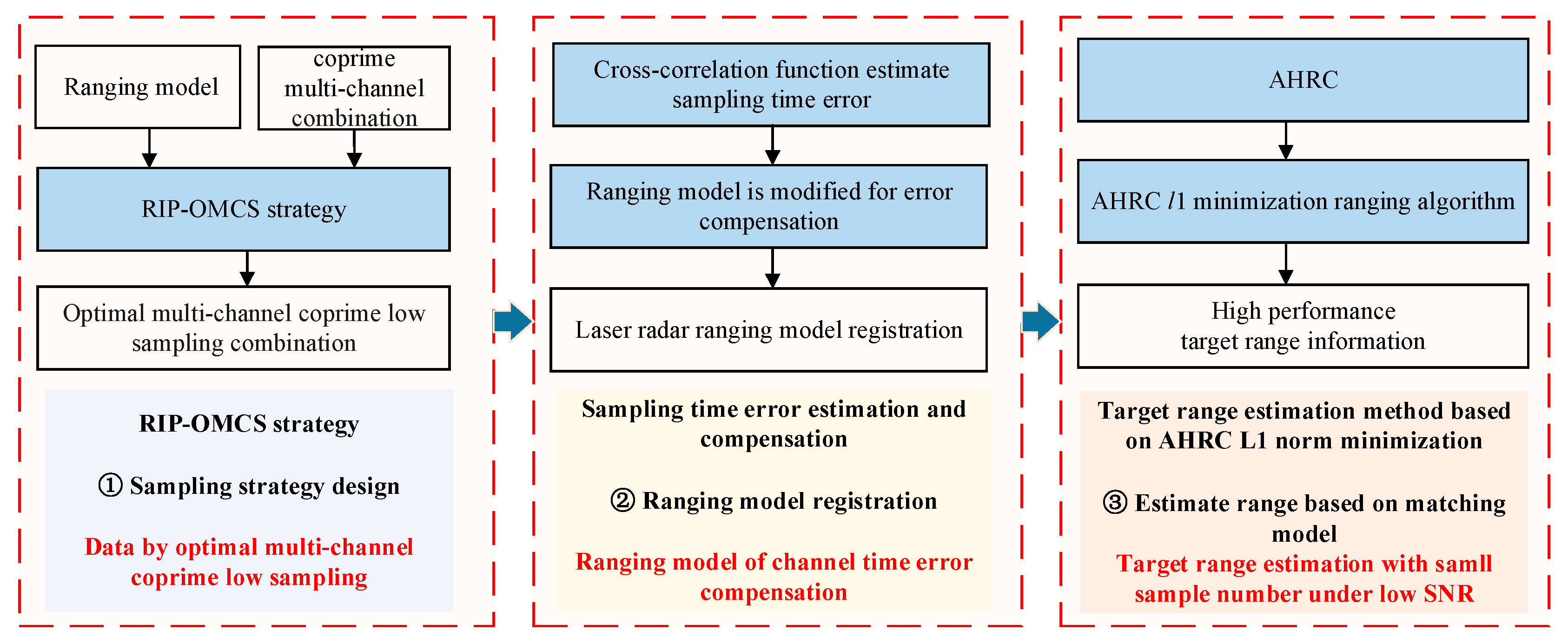
3. High-Resolution Ranging Based on Optimal Multi-Channel Coprime Low-Sampling under Low SNR
- To reduce the overall sample number of the laser-radar system, we propose the RIP-OMCS strategy. This strategy achieves a small overall sample number while maintaining ranging accuracy.
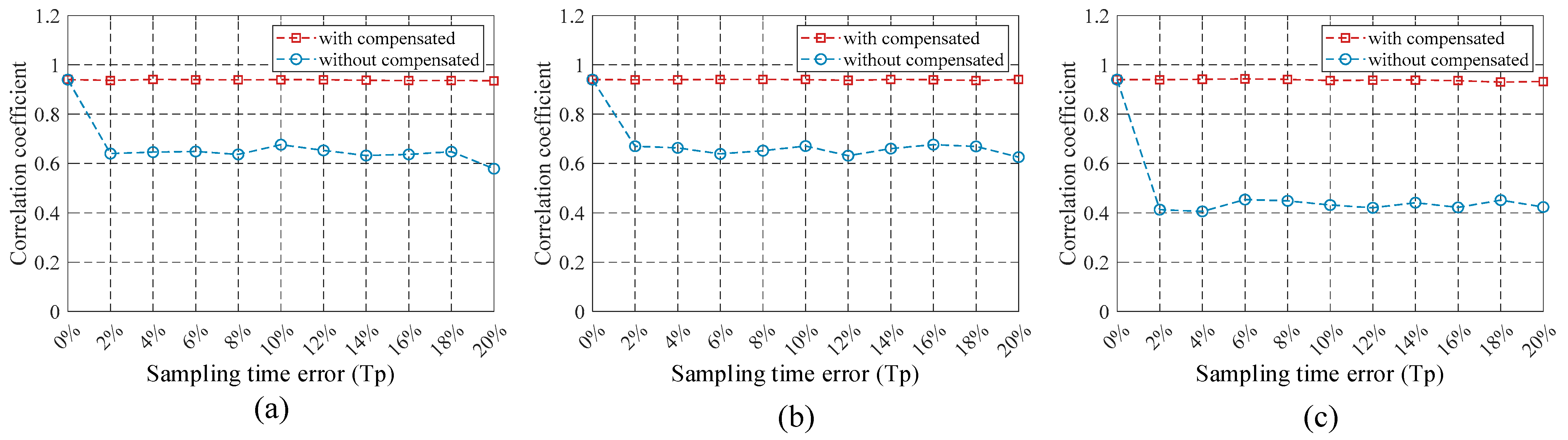
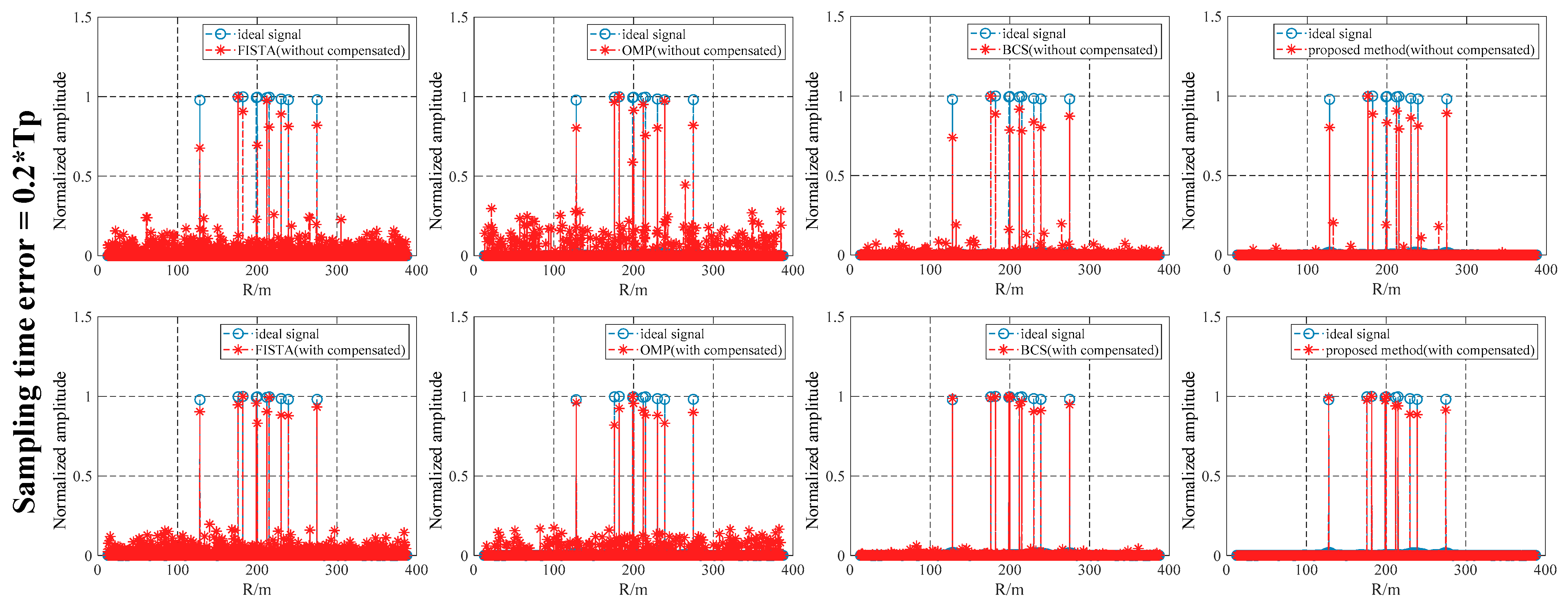
- Addressing the issue of asynchronous sampling-time error, we propose the cross-correlation method to estimate errors. The time error compensation is performed by means of ranging model registration.
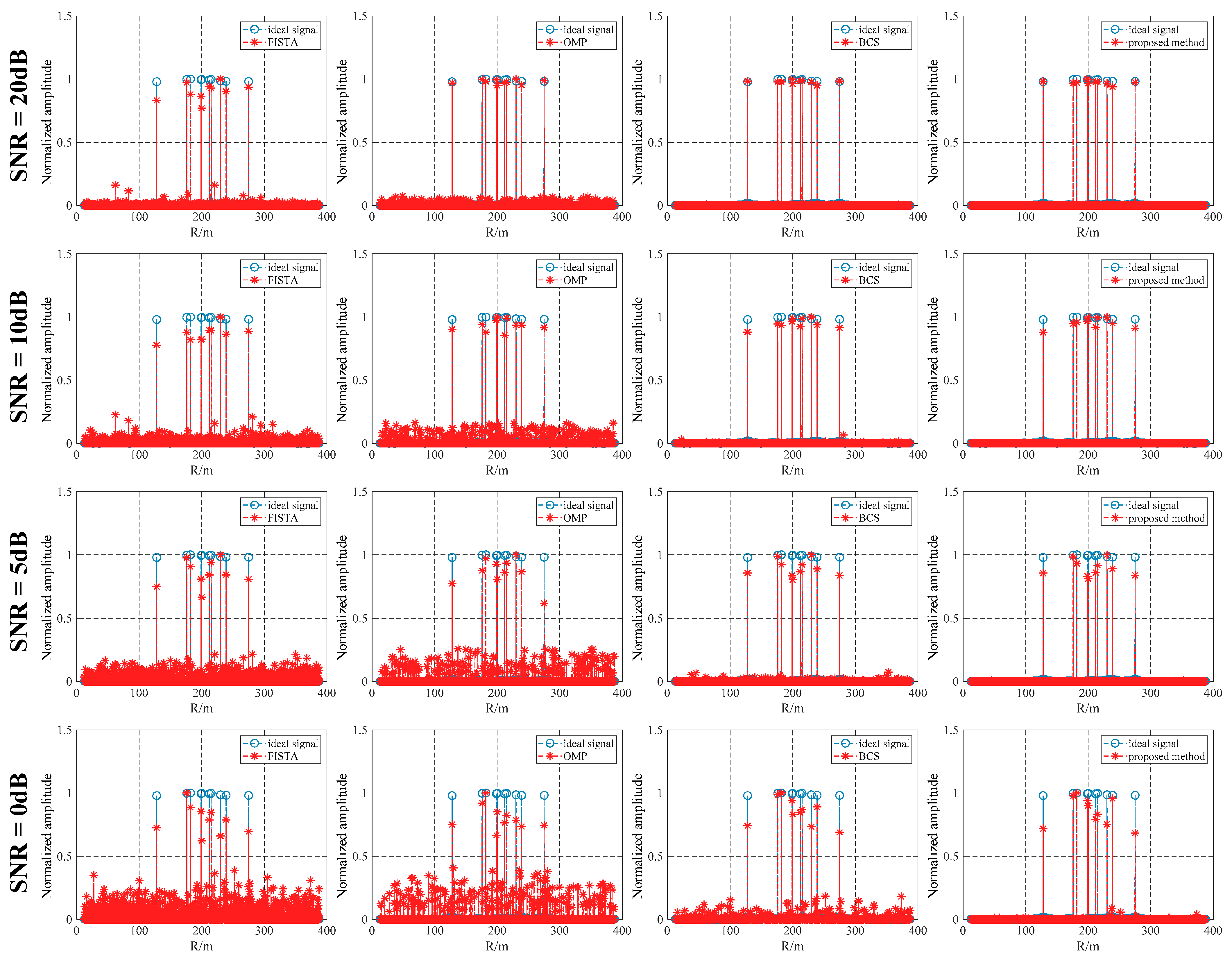
- To tackle the performance limitations of traditional sparse-reconstruction algorithms and the accuracy issues of target-range estimation under low SNR, we introduce a target-range estimation method based on AHRC minimization under a low SNR. AHRC is formulated by combining logarithmic and arctangent penalty functions. This constraint function dynamically imposes precise constraints on the noise and target components, obtaining a high-resolution range profile and enhancing the target-range-estimation accuracy.
3.1. RIP-OMCS Strategy
3.2. Asynchronous Sampling-Time Error Estimation and Compensation
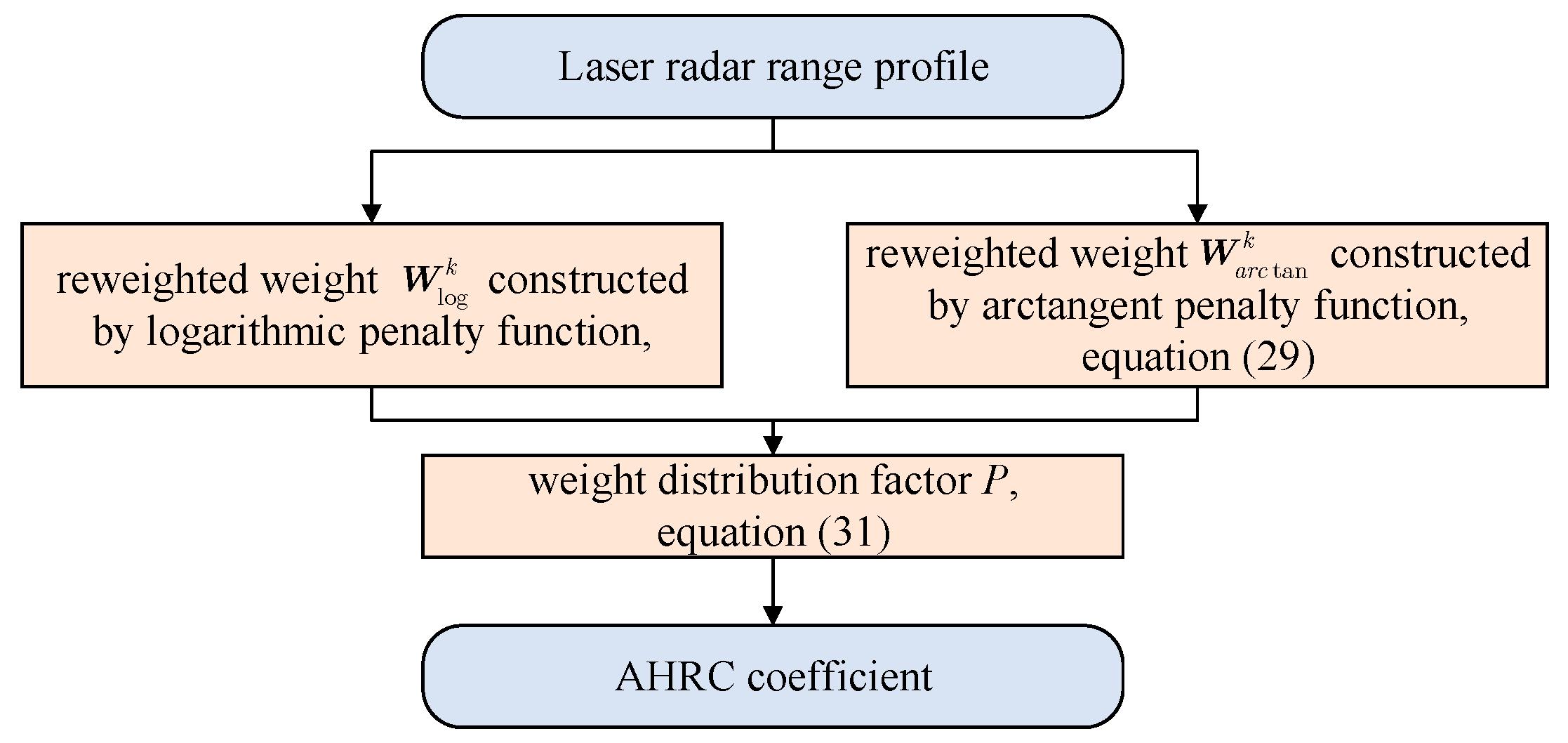
3.3. AHRC Minimization for Target-Range Estimation
3.3.1. AHRC
3.3.2. Statistical Modeling
3.3.3. Solution of the Optimization Problem
4. Discussion
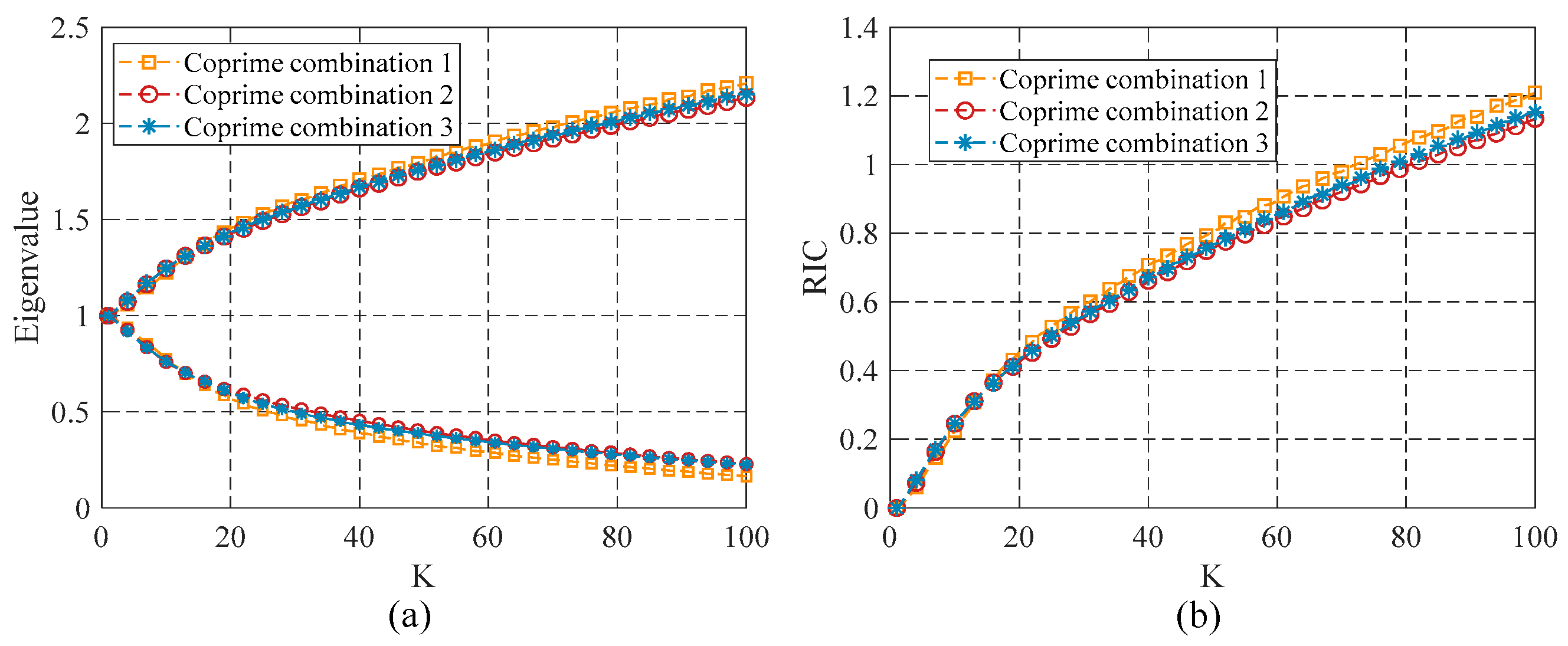
4.1. Performance Analysis of RIP-OMCS
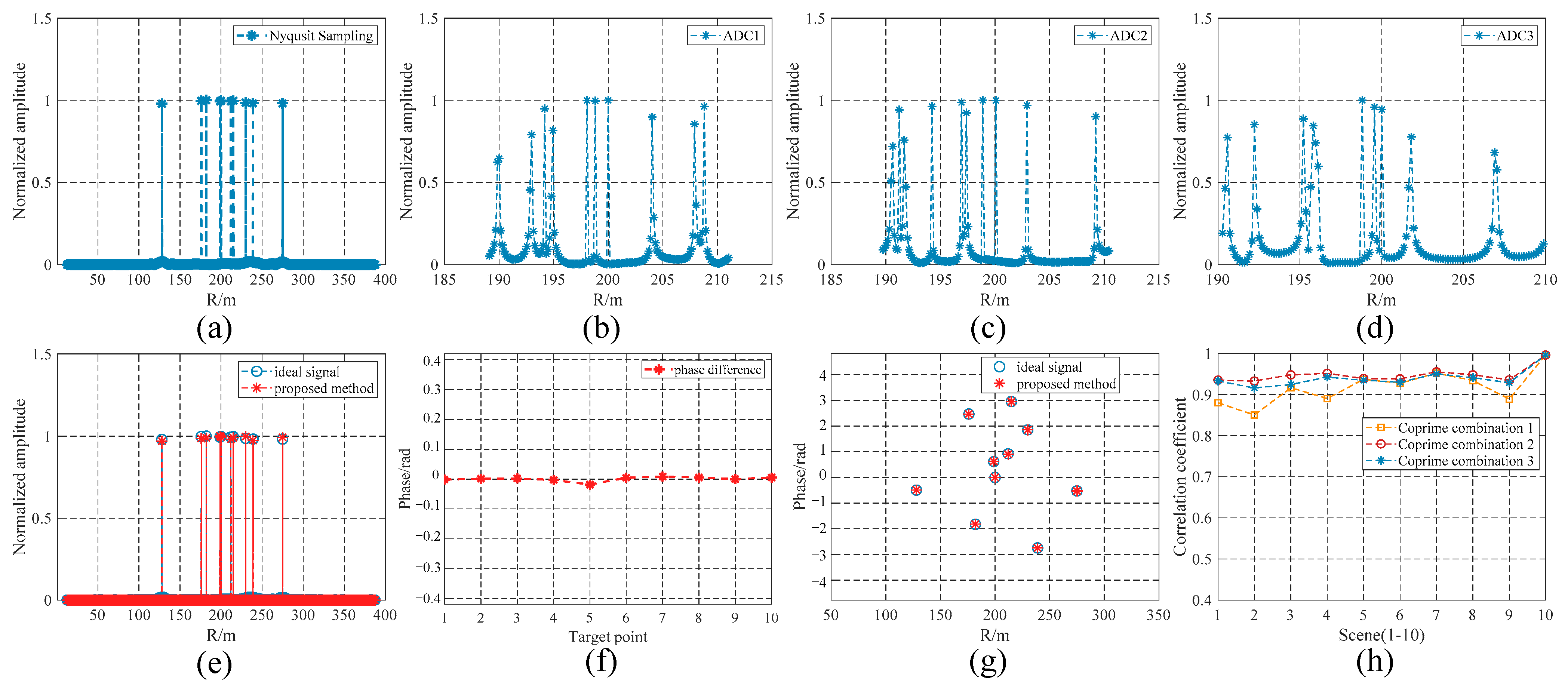
4.2. Performance Analysis of Sampling-Time Error Compensation
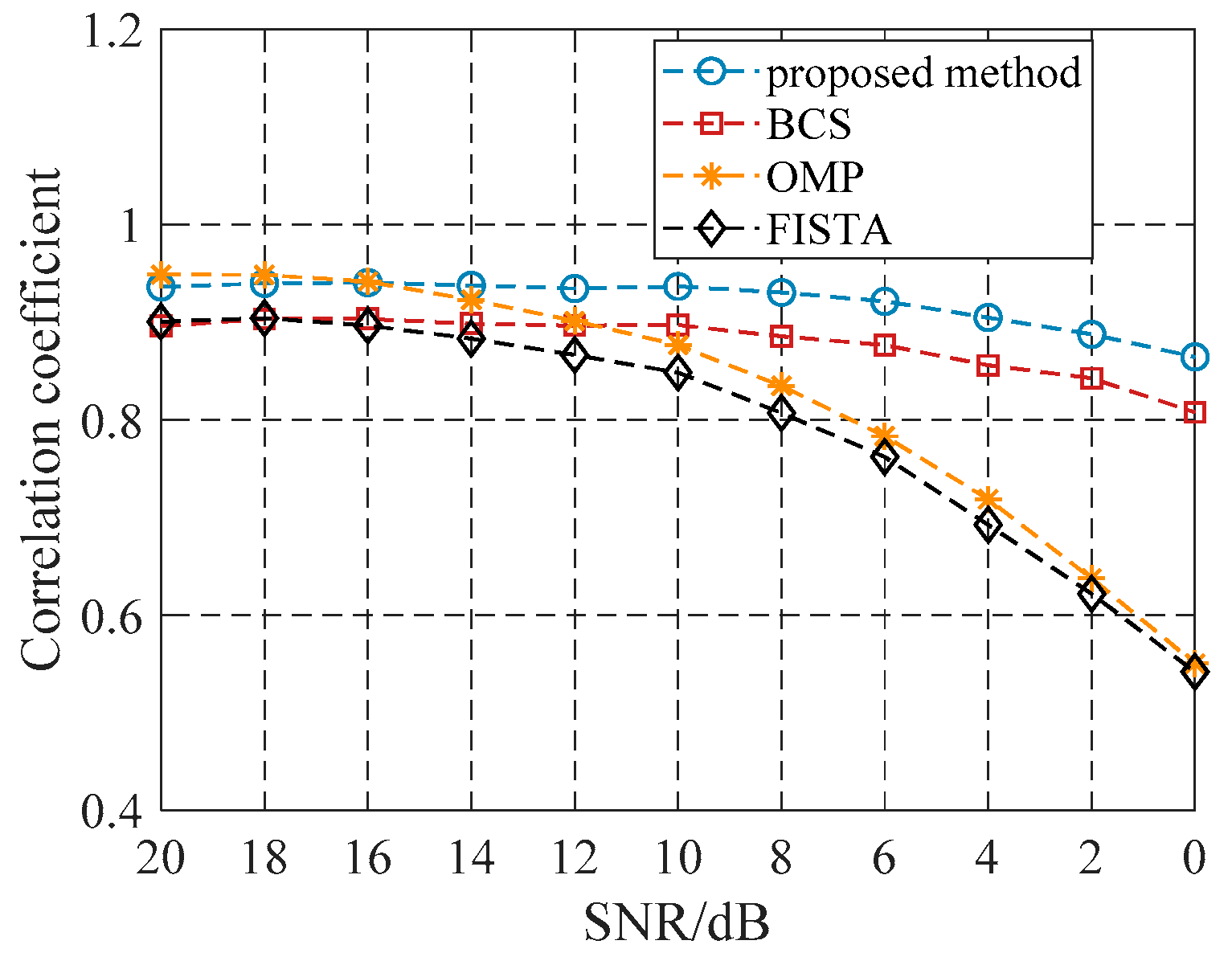
4.3. Performance Analysis of the Proposed Algorithm under Different SNRs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amann, M.-C.; Bosch, T.M.; Lescure, M.; Myllylae, R.A.; Rioux, M. Laser ranging: A critical review of unusual techniques for distance measurement. Opt. Eng. 2001, 40, 10–19. [Google Scholar]
- Lu, Z.; Ge, C.; Wang, Z.; Jia, D.; Yang, T. Basics and developments of frequency modulation continuous wave LiDAR. Opto-Electron. Eng. 2019, 46, 190038-1–190038-14. [Google Scholar]
- Azadbakht, M.; Fraser, C.S.; Khoshelham, K. A Sparsity-Based Regularization Approach for Deconvolution of Full-Waveform Airborne Lidar Data. Remote Sens. 2016, 8, 648. [Google Scholar] [CrossRef]
- Swatantran, A.; Tang, H.; Barrett, T.; DeCola, P.; Dubayah, R. Rapid, High-Resolution Forest Structure and Terrain Mapping over Large Areas using Single Photon Lidar. Sci. Rep. 2016, 6, 28277. [Google Scholar] [CrossRef]
- Pfrunder, A.; Borges, P.V.K.; Romero, A.R.; Catt, G.; Elfes, A. Real-time autonomous ground vehicle navigation in heterogeneous environments using a 3D LiDAR. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2601–2608. [Google Scholar]
- Wang, X.; Guo, L.; Li, Y.; Han, L.; Xu, Q.; Jing, D.; Li, L.; Xing, M. Noise-Robust Vibration Phase Compensation for Satellite ISAL Imaging by Frequency Descent Minimum Entropy Optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Trahan, R.; Nemati, B.; Zhou, H.; Shao, M.; Hahn, I.; Schulze, W. Low-CNR inverse synthetic aperture LADAR imaging demonstration with atmospheric turbulence. Proc. SPIE 2016, 9846, 87–99. [Google Scholar]
- Chen, J.; Li, M.; Xing, M.; Xu, G.; Zhu, Y.; Li, R.; Li, W. Processing of airborne microwave photonic SAR raw data with inaccurate RSF. IEEE J. Miniaturization Air Space Syst. 2023, 4, 86–92. [Google Scholar] [CrossRef]
- Meta, A.; Hoogeboom, P.; Ligthart, L.P. Signal processing for FMCW SAR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3519–3532. [Google Scholar] [CrossRef]
- Pierrottet, D.; Amzajerdian, F.; Petway, L.; Barnes, B.; Lockard, G.; Rubio, M. Linear FMCW laser radar for precision range and vector velocity measurements. MRS Proc. 2008, 1076, 10760406. [Google Scholar] [CrossRef]
- Xi, R.; Ma, D.; Liu, X.; Wang, L.; Liu, Y. Intra-Pulse Frequency Coding Design for a High-Resolution Radar against Smart Noise Jamming. Remote Sens. 2022, 14, 5149. [Google Scholar] [CrossRef]
- Qian, X.; Jiang, W.; Deen, M.J. Single Photon Detectors for Automotive LiDAR Applications: State-of-the-Art and Research Challenges. IEEE J. Sel. Top. Quantum Electron. 2024, 30, 1–20. [Google Scholar] [CrossRef]
- Behroozpour, B.; Sandborn, A.M.; Wu, M.C.; Boser, B.E. Lidar system architectures and circuits. IEEE Commun. Mag. 2017, 55, 135–142. [Google Scholar] [CrossRef]
- Candan, C. A method for fine resolution frequency estimation from three DFT samples. IEEE Signal Process. Lett. 2011, 18, 351–354. [Google Scholar] [CrossRef]
- Aiello, M.; Cataliotti, A.; Nuccio, S. A comparison of spectrum estimation techniques for nonstationary signals in induction motor drive measurements. IEEE Trans. Instrum. Meas. 2005, 54, 2264–2271. [Google Scholar] [CrossRef]
- Bhutani, A.; Marahrens, S.; Gehringer, M.; Göttel, B.; Pauli, M.; Zwick, T. The role of millimeter-waves in the distance measurement accuracy of an FMCW radar sensor. Sensors 2019, 19, 3938. [Google Scholar] [CrossRef]
- Chen, A.; Huang, J.; Qiu, J.; Ke, Y.; Zheng, L.; Chen, X. Signal processing for a FMCW material level measurement system. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 244–247. [Google Scholar]
- Chen, J.; Li, M.; Yu, H.; Xing, M. Full-aperture processing of airborne microwave photonic SAR raw data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Giusti, E.; Cataldo, D.; Bacci, A.; Tomei, S.; Martorella, M. ISAR image resolution enhancement: Compressive sensing versus state-of-the-art super-resolution techniques. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1983–1997. [Google Scholar] [CrossRef]
- Ender, J.H. On compressive sensing applied to radar. Signal Process. 2010, 90, 1402–1414. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.-J.; Xing, M.-D.; Sheng, J.-L.; Guo, R.; Bao, Z. High-resolution ISAR imaging by exploiting sparse apertures. IEEE Trans. Antennas Propag. 2012, 60, 997–1008. [Google Scholar] [CrossRef]
- Xu, G.; Xing, M.-D.; Xia, X.-G.; Zhang, L.; Liu, Y.-Y.; Bao, Z. Sparse regularization of interferometric phase and amplitude for InSAR image formation based on Bayesian representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2123–2136. [Google Scholar] [CrossRef]
- Jiang, N.; Du, H.; Ge, S.; Zhu, J.; Feng, D.; Wang, J.; Huang, X. High-Resolution Azimuth Missing Data SAR Imaging Based on Sparse Representation Autofocusing. Remote Sens. 2023, 15, 3425. [Google Scholar] [CrossRef]
- Huang, D.-r.; Zhang, L.; Xing, M.-D.; Xu, G.; Duan, J.; Bao, Z. Sparse aperture inverse synthetic aperture radar imaging of manoeuvring targets with compensation of migration through range cells. IET Radar Sonar Navig. 2014, 8, 1164–1176. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Qiao, Z. Resolution enhancement for ISAR imaging via improved statistical compressive sensing. EURASIP J. Adv. Signal Process. 2016, 2016, 80. [Google Scholar] [CrossRef]
- Yu, H.; Lan, Y.; Yuan, Z.; Xu, J.; Lee, H. Phase unwrapping in InSAR: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 40–58. [Google Scholar] [CrossRef]
- Yu, H.; Zhou, Y.; Ivey, S.S.; Lan, Y. Large-scale multibaseline phase unwrapping: Interferogram segmentation based on multibaseline envelope-sparsity theorem. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9308–9322. [Google Scholar] [CrossRef]
- Tang, Y.; Qin, B.; Yan, Y.; Wang, L.; Xing, M. High-resolution and wide-swath imaging of the multiple-transmitter-multiple-receiver synthetic aperture ladar system. Infrared Laser Eng. 2016, 45, 0830001. [Google Scholar] [CrossRef]
- Xu, Z.; Qi, S.; Zhang, P. High Accuracy Multi-Antenna Ranging Algorithm and Performance Analysis for FMCW Radar. IEEE Trans. Radar Syst. 2023, 1, 657–668. [Google Scholar] [CrossRef]
- Li, D.; Zhou, K.; Cui, A.; Qiao, M.; Wu, S.; Wang, Y.; Yao, Y.; Wu, J.; Gao, J. Multi-Channel Inverse Synthetic Aperture Ladar Imaging Detection Technology and Experimental Research. Laser Optoelectron. Prog. 2021, 58, 342–353. [Google Scholar]
- Engels, F.; Heidenreich, P.; Wintermantel, M.; Stäcker, L.; Kadi, M.A.; Zoubir, A.M. Automotive radar signal processing: Research directions and practical challenges. IEEE J. Sel. Top. Signal Process. 2021, 15, 865–878. [Google Scholar] [CrossRef]
- Li, Y.; Wang, T.; Huo, T.; Nie, L. A Study on the Range Equation Modeling for Multichannel Medium-Earth-Orbit SAR-GMTI Systems. Remote Sens. 2021, 13, 2734. [Google Scholar] [CrossRef]
- Guo, L.; Xu, Q.; Li, X.; Zeng, X.; Tang, Y.; Xing, M. Multi-channel scan mode and imaging algorithm for synthetic aperture ladar. Optik 2021, 155, 225–232. [Google Scholar] [CrossRef]
- Xu, G.; Liu, Y.; Xing, M. Multi-channel synthetic aperture radar imaging of ground moving targets using compressive sensing. IEEE Access 2018, 6, 66134–66142. [Google Scholar] [CrossRef]
- Yao, Z.; Mauldin, T.; Hefferman, G.; Wei, T. Digitally integrated self-trained predistortion curve finder for passive sweep linearization of semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–5. [Google Scholar] [CrossRef]
- Xu, X.; Chen, Y.; Zhu, K.; Yang, J.; Tan, Z.; Luo, M. Research on FPGA pulse laser ranging method based on deep learning. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Yuan, S.; Yan, X.; Xu, J.; Zhu, W.; Qin, H. Cognitive Imaging Lidar Based on Deep Learning. Acta Photonica Sin. 2021, 50, 1011002. [Google Scholar]
- Liu, B.; Liu, J. A Method of the Realization of High Accuracy in FMCW Ranging System. J. Instrum. 2001, 15, 41–45. [Google Scholar]
- Li, Z.; Zhang, R.; Yang, J.; Xiong, J. Improving Range Precision of LFMCW Radar with Frequency Domain Up-Sampling-Interpolating Method. Telecommun. Eng. 2005, 45, 77–80. [Google Scholar]
- Vasilyev, A.; Satyan, N.; Xu, S.; Rakuljic, G.; Yariv, A. Multiple source frequency-modulated continuous-wave optical reflectometry: Theory and experiment. App. Opt. 2010, 49, 1932–1937. [Google Scholar] [CrossRef]
- Scherr, S.; Ayhan, S.; Fischbach, B.; Bhutani, A.; Pauli, M.; Zwick, T. An efficient frequency and phase estimation algorithm with CRB performance for FMCW radar applications. IEEE Trans. Instrum. Meas. 2015, 64, 1868–1875. [Google Scholar] [CrossRef]
- Xu, Z.; Qi, S.; Zhang, P. A coherent CZT-based algorithm for high-accuracy ranging with FMCW radar. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Zhang, T.; Qu, X.; Zhang, F. The Slight Vibrations Compensation of FMCW Ranging Method Based on Three Light Paths Structure. Spectrosc. Spect. Anal. 2020, 40, 1007–1011. [Google Scholar]
- He, J.; Zhang, Q.; Yang, X.; Luo, Y.; Ji, N. Sampling Technology of ISAIL. Acta Photonica Sin. 2010, 39, 1272–1277. [Google Scholar]
- Zang, B.; Guo, R.; Zhang, L.; Tang, Y.; Xing, M. A Phase Adjustment Algorithm for ISAIL Based on Sparsity. Acta Electonica Sin. 2011, 39, 1272–1277. [Google Scholar]
- Tian, H.; Mao, H.; Liu, Z.; Zeng, Z. Airborne ladar sparse imaging on targets with micro-motions based on inverse synthetic aperture technique. Infrared Laser Eng. 2020, 49, 20200190. [Google Scholar]
- Wu, S.; Ding, L.; Li, P.; Chen, L.; Zhu, Y. Millimeter-Wave SAR Sparse Imaging With 2-D Spatially Pseudorandom Spiral-Sampling Pattern. IEEE Trans. Microw. Theory Tech. 2020, 68, 4672–4683. [Google Scholar] [CrossRef]
- Wang, L.; Ai, Z.; Shi, J.; Wang, J.; Zhang, X.; Yang, J. Low Computational Complexity SAR Imaging Algorithm for Ship Monitoring via 2-D Band-Limited Sparse Fourier Transform. IEEE Sens. J. 2024, 24, 13326–13342. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Wang, F.; Zhang, P.; Li, M. New Point Matching Algorithm Using Sparse Representation of Image Patch Feature for SAR Image Registration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1498–1510. [Google Scholar] [CrossRef]
- Pu, W.; Bao, Y. RPCA-AENet: Clutter Suppression and Simultaneous Stationary Scene and Moving Targets Imaging in the Presence of Motion Errors. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 2339–2352. [Google Scholar] [CrossRef]
- Romero, D.; Ariananda, D.D.; Tian, Z.; Leus, G. Compressive covariance censing: Structure-based compressive sensing beyond sparsity. IEEE Signal Process. Mag. 2016, 33, 78–93. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Tsaig, Y.; Donoho, D.L. Extensions of compressed sensing. Signal Process. 2006, 86, 549–571. [Google Scholar] [CrossRef]
- Wipf, D.; Nagarajan, S. Solving sparse linear inverse problems: Analysis of reweighted L1 and L2 methods. In Proceedings of the Signal Processing with Adaptive Sparse Structured Representations (SPARS), Saint-Malo, France, 6–9 April 2009; pp. 1–7. [Google Scholar]
- Huang, Y.; Liao, G.; Zhang, L.; Xiang, Y.; Li, J.; Nehorai, A. Efficient narrowband RFI mitigation algorithms for SAR systems with reweighted tensor structures. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9396–9409. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yu, H.; Chen, J.; Xing, M.; Hong, W. Sparse synthetic aperture radar imaging from compressed sensing and machine learning: Theories applications and trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Wavelength | 1.55 μm | R0 | 200 m |
| Pulse width | 28 μs | 300 m | |
| Bandwidth | 1 GHz | Fs | 89.3 MHz |
| Parameter | ADC 1 | ADC 2 | ADC 3 | ADC 4 | Downsampling Rate |
|---|---|---|---|---|---|
| Coprime Combination 1 | Fs/11 | Fs/13 | — | — | 16.78% |
| Coprime Combination 2 | Fs/17 | Fs/18 | Fs/19 | — | 16.7% |
| Coprime Combination 3 | Fs/13 | Fs/29 | Fs/37 | Fs/40 | 16.34% |
| 20 dB | 18 dB | 16 dB | 14 dB | 12 dB | 10 dB | 8 dB | 6 dB | 4 dB | 2 dB | 0 dB | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Proposed method | 94% | 94% | 94% | 94% | 93% | 93% | 93% | 92% | 90% | 89% | 86% |
| BCS | 90% | 90% | 90% | 90% | 90% | 90% | 89% | 88% | 86% | 84% | 80% |
| OMP | 95% | 95% | 94% | 92% | 90% | 88% | 83% | 78% | 72% | 64% | 55% |
| FISTA | 90% | 90% | 90% | 88% | 87% | 85% | 81% | 76% | 69% | 62% | 54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, M.; Xing, M.; Gao, Y.; Fu, J.; Wu, Z.; Tang, W. High Resolution Ranging with Small Sample Number under Low SNR Utilizing RIP-OMCS Strategy and AHRC l1 Minimization for Laser Radar. Remote Sens. 2024, 16, 1647. https://doi.org/10.3390/rs16091647
Xue M, Xing M, Gao Y, Fu J, Wu Z, Tang W. High Resolution Ranging with Small Sample Number under Low SNR Utilizing RIP-OMCS Strategy and AHRC l1 Minimization for Laser Radar. Remote Sensing. 2024; 16(9):1647. https://doi.org/10.3390/rs16091647
Chicago/Turabian StyleXue, Min, Mengdao Xing, Yuexin Gao, Jixiang Fu, Zhixin Wu, and Wangshuo Tang. 2024. "High Resolution Ranging with Small Sample Number under Low SNR Utilizing RIP-OMCS Strategy and AHRC l1 Minimization for Laser Radar" Remote Sensing 16, no. 9: 1647. https://doi.org/10.3390/rs16091647
APA StyleXue, M., Xing, M., Gao, Y., Fu, J., Wu, Z., & Tang, W. (2024). High Resolution Ranging with Small Sample Number under Low SNR Utilizing RIP-OMCS Strategy and AHRC l1 Minimization for Laser Radar. Remote Sensing, 16(9), 1647. https://doi.org/10.3390/rs16091647







