Inclined Aerial Image and Satellite Image Matching Based on Edge Curve Direction Angle Features
Abstract
1. Introduction
- (1)
- Long-distance inclined aerial images, which are seriously affected by atmospheric absorption and scattering, have low contrast and low SNR. The above factor makes feature extraction difficult and increases the difficulty of image matching.
- (2)
- The acquisition of aerial images is mobile and flexible, while the revisit cycle of satellite images is long. Therefore, the acquisition time of satellite images is usually several months or even one year earlier than that of aerial images. This leads to a large difference in the same region of aerial and satellite images, and the difficulty of image matching increases.
- (3)
- Different sensors for acquiring aerial and satellite images lead to differences in the gray value of the same scenery, causing difficulties in image matching [36].
- (1)
- The innovative concept of curve direction angle is proposed, defining the direction angle between two pixels and the short curve direction angle formed by several pixels. A long curve can be depicted by several short curve direction angles, which facilitates image matching.
- (2)
- A corner point detection algorithm combined with a bilateral filter considering the difference and distance of the direction angles is designed, and a feature point descriptor with preceding direction angles and successive direction angles as elements is established.
- (3)
- A descriptor comparison algorithm based on direction angles misalignment subtraction is presented, and the index vector of matched direction angles is obtained. A matching similarity computation method that incorporates multiple factors is proposed.
2. Related Work
2.1. Tilt and Resolution Transformations
2.2. Edge Detection
2.3. Contour Extraction
| Algorithm 1: Contour Extraction | |
| Scan the image with a TV raster and perform the following steps for each pixel such that . | |
| Step 1: | If and , then and =. Else if , then and . Otherwise, go to Step 3. |
| Step 2: | Includes Step 2.1 through Step 2.5. |
| Step 2.1: | Starting from , look clockwise around the pixels in the neighborhood of and find a nonzero pixel. Let be the first found nonzero pixel. If no nonzero pixel is found, and go to Step 3. |
| Step 2.2: | and . |
| Step 2.3: | Starting from the next element of the pixel in the counterclockwise order, examine the pixels in the neighborhood of the current pixel counterclockwise to find a nonzero pixel and let the first one be . |
| Step 2.4: | If the pixel is a 0-pixel examined in Step 2.3, then . If the pixel is not a 0-pixel examined in Step 2.3 and , then . |
| Step 2.5: | If ,then go to Step 3; Otherwise, ,, and go to Step 2.3. |
| Step 3: | If , then resume the raster scan from the pixel . The algorithm terminates when the scan reaches the lower right corner of the picture. |
| : the gray value of pixel ; : the sequential number of the border. | |
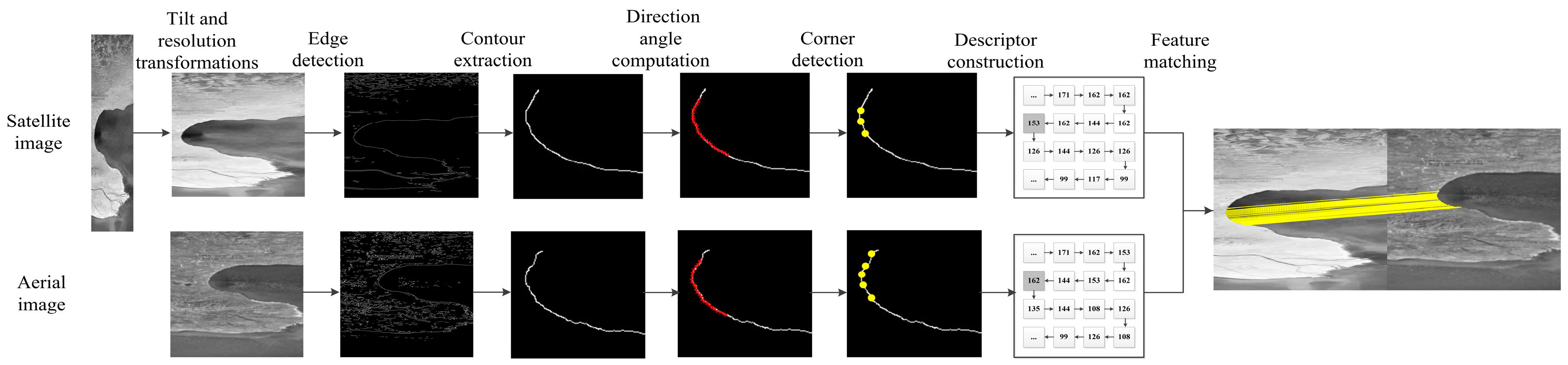
3. Materials and Methods
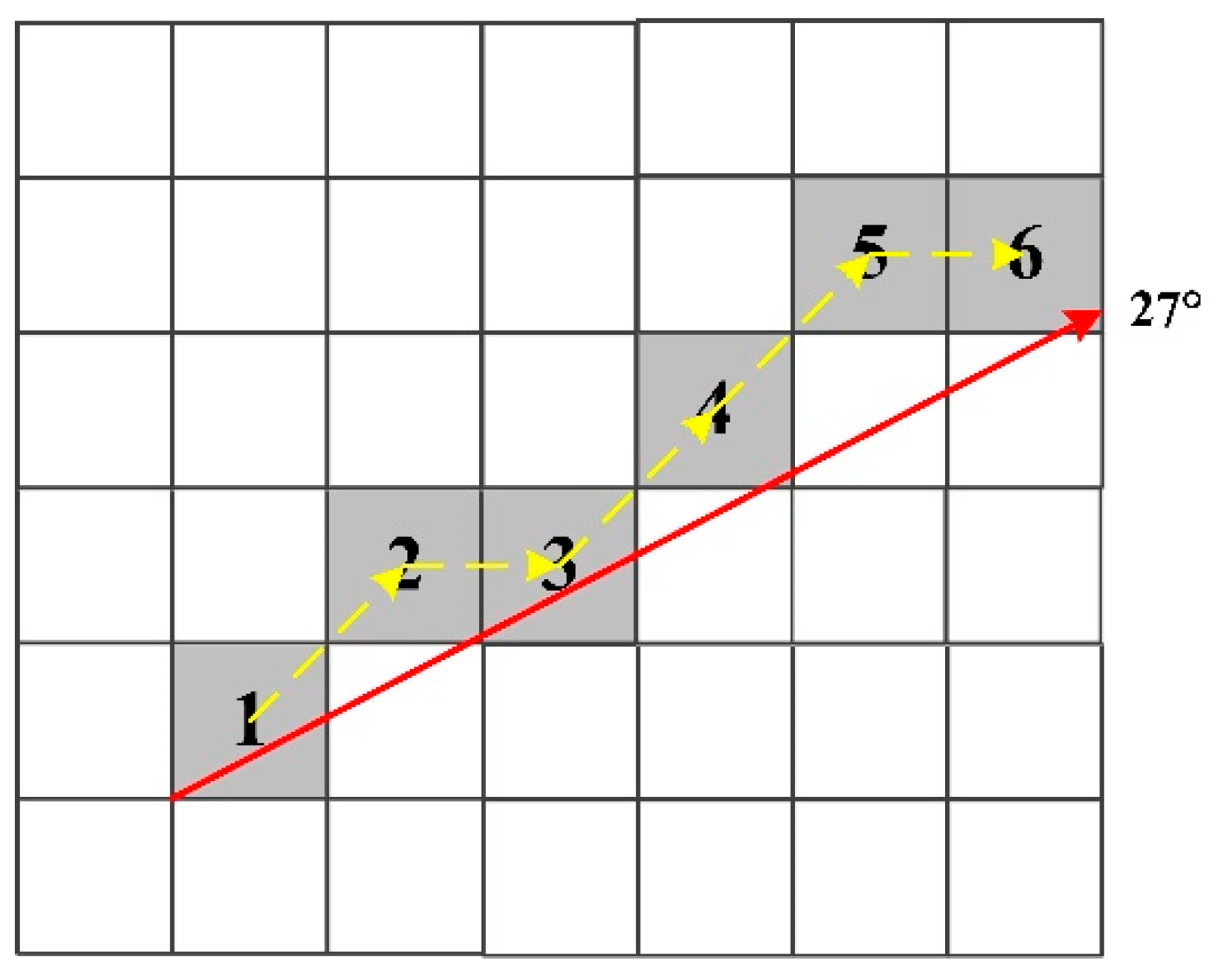
3.1. Curve Direction Angle
3.2. Corner Point Detection
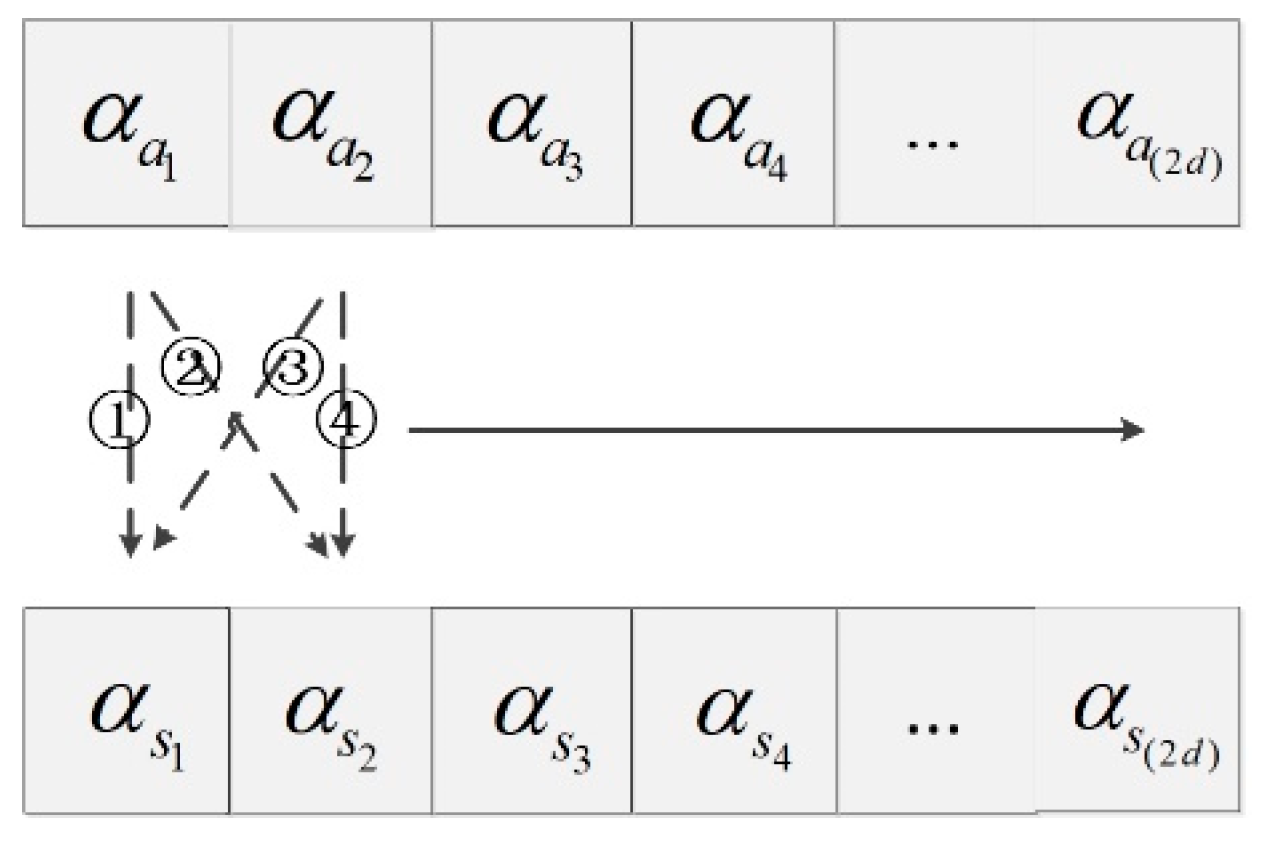
3.3. Descriptor Construction
3.4. Feature Matching
4. Results
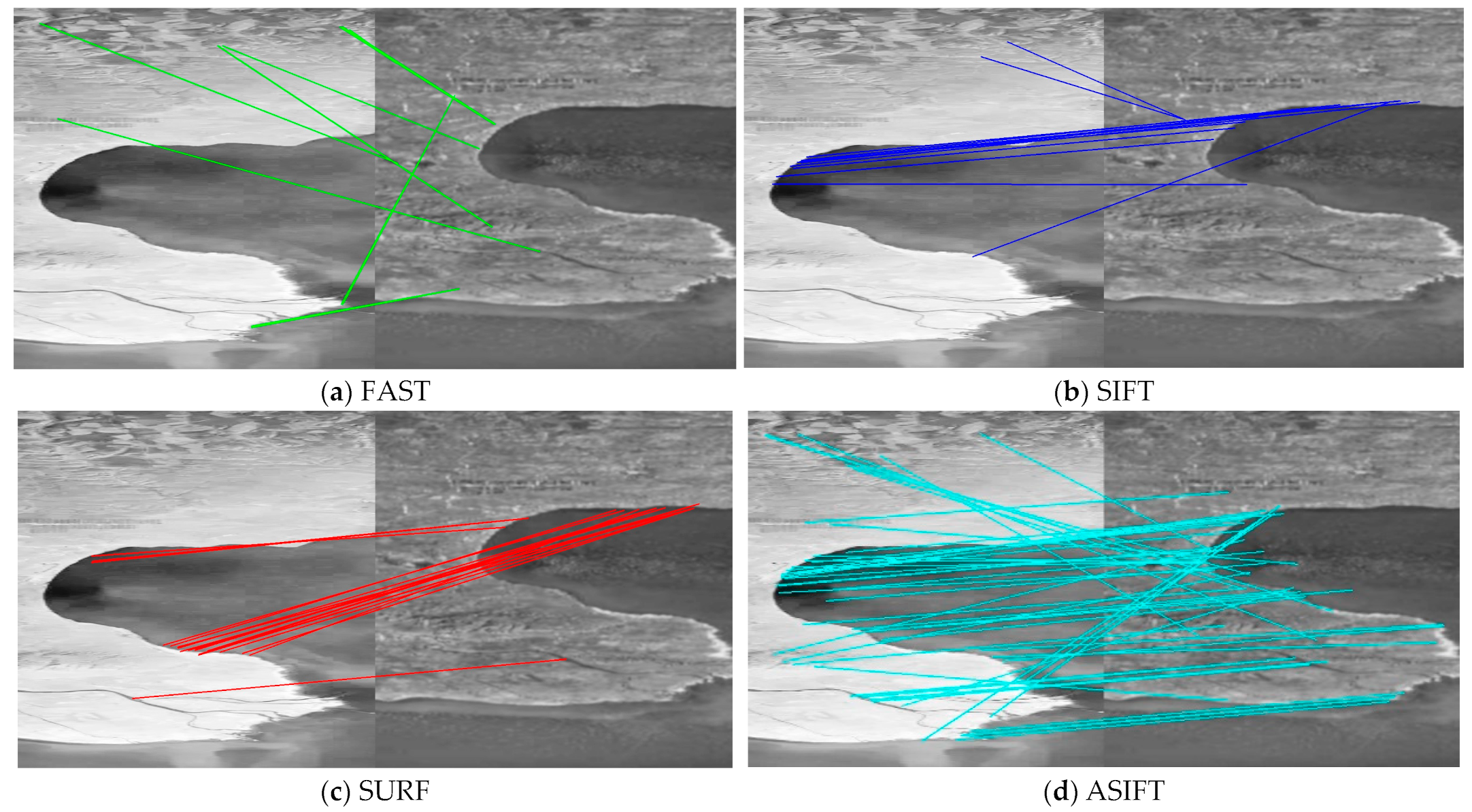
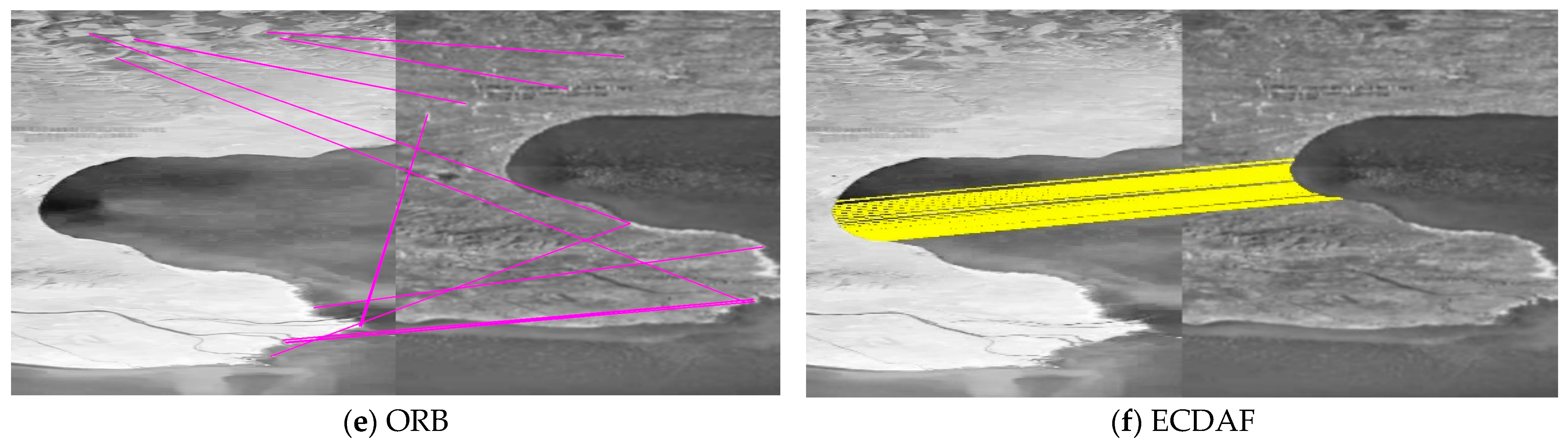
4.1. Qualitative Evaluation
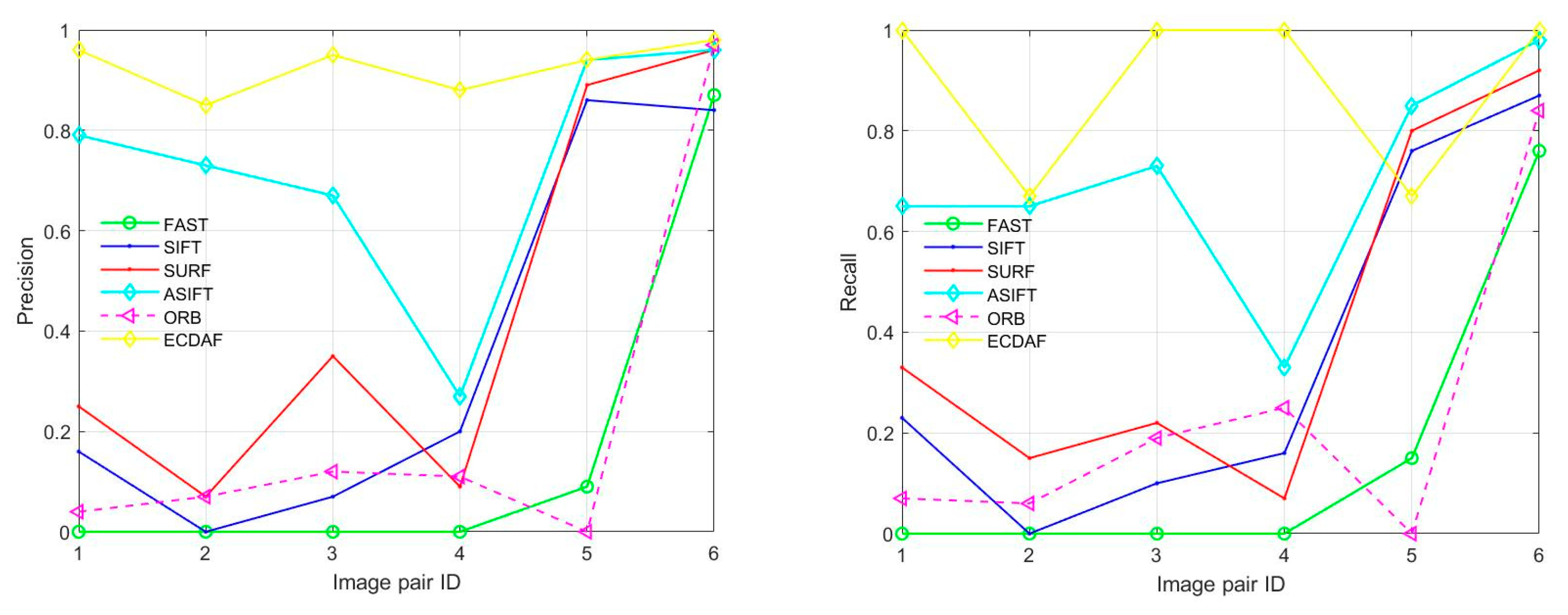
4.2. Precision and Recall
4.3. Running Time
4.4. Parameter Setting
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, H.; Huang, C.; Wang, F.; Song, K.; Yin, Z. Robust semantic template matching using a superpixel region binary descriptor. IEEE Trans. Image Process. 2019, 28, 3061–3074. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Cao, Z.; Yang, J.; Xian, K.; Li, X. Image feature correspondence selection: A comparative study and a new contribution. IEEE Trans. Image Process. 2020, 29, 3506–3519. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector free local feature matching with transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 10–25 June 2021; pp. 8918–8927. [Google Scholar]
- Zhang, H.; Lei, L.; Ni, W.; Cheng, K.; Tang, T.; Wang, P.; Kuang, G. Registration of Large Optical and SAR Images with Non-Flat Terrain by Investigating Reliable Sparse Correspondences. Remote Sens. 2023, 15, 4458. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J.; Zhou, H.; Zhao, J.; Guo, X. Guided locality preserving feature matching for remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4435–4447. [Google Scholar] [CrossRef]
- Feng, R.; Shen, H.; Bai, J.; Li, X. Advances and opportunities in remote sensing image geometric registration: A systematic review of state-of-the-art approaches and future research directions. IEEE Geosci. Remote Sens. Mag. 2021, 9, 120–142. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Tian, J.; Yuille, A.; Tu, Z. Robust point matching via vector field consensus. IEEE Trans. Image Process. 2014, 23, 1706–1721. [Google Scholar] [CrossRef]
- He, J.; Jiang, X.; Hao, Z.; Zhu, M.; Gao, W.; Liu, S. LPHOG: A Line Feature and Point Feature Combined Rotation Invariant Method for Heterologous Image Registration. Remote Sens. 2023, 15, 4548. [Google Scholar] [CrossRef]
- Sommervold, O.; Gazzea, M.; Arghandeh, R. A Survey on SAR and Optical Satellite Image Registration. Remote Sens. 2023, 15, 850. [Google Scholar] [CrossRef]
- Bellavia, F. SIFT matching by context exposed. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 2445–2457. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Qiao, P.; Lv, X.; Li, J.; Du, T.; Cai, Y. Image Registration Algorithm for Remote Sensing Images Based on Pixel Location Information. Remote Sens. 2023, 15, 436. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Pang, S.; Ge, J.; Hu, L.; Guo, K.; Zheng, Y.; Zheng, C.; Zhang, W.; Liang, J. RTV-SIFT: Harnessing Structure Information for Robust Optical and SAR Image Registration. Remote Sens. 2023, 15, 4476. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L. Surf: Speeded up robust features. In Proceedings of the Computer Vision—ECCV 2006, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Yao, G.; Cui, J.; Deng, K.; Zhang, L. Robust harris corner matching based on the quasi-homography transform and self-adaptive window for wide-baseline stereo images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 559–574. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the Computer Vision—ECCV 2006, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Michael, C.; Vincent, L.; Christoph, S.; Pascal, F. BRIEF: Binary robust independent elementary features. In Proceedings of the Computer Vision—ECCV 2010, Heraklion, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Ethan, R.; Vincent, R.; Kurt, K.; Gary, B. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Yu, G.; Morel, J. ASIFT: An algorithm for fully affine invariant comparison. Image Process. 2011, 1, 11–38. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Hu, Z. MSLD: A robust descriptor for line matching. Pattern Recognit. 2009, 42, 941–953. [Google Scholar] [CrossRef]
- Zhang, L.; Koch, R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency. J. Vis. Commun. Image Represent. 2013, 24, 794–805. [Google Scholar] [CrossRef]
- Wang, L.; Neumann, U.; You, S. Wide-baseline image matching using line signatures. In Proceedings of the 2009 IEEE International Conference on Computer Vision (ICCV), Kyoto, Japan, 29 September–2 October 2009; pp. 1311–1318. [Google Scholar]
- López, J.; Santos, R.; Fdez-Vidal, X.; Pardo, X. Two-view line matching algorithm based on context and appearance in low-textured images. Pattern Recognit. 2015, 48, 2164–2184. [Google Scholar] [CrossRef]
- Lourakis, M.; Halkidis, S.; Orphanoudakis, S. Matching disparate views of planar surfaces using projective invariants. Image Vis. Comput. 2000, 18, 673–683. [Google Scholar] [CrossRef]
- Fan, B.; Wu, F.; Hu, Z. Robust line matching through line-point invariants. Pattern Recognit. 2012, 45, 794–805. [Google Scholar] [CrossRef]
- Zhu, H.; Jiao, L.; Ma, W.; Liu, F.; Zhao, W. A novel neural network for remote sensing image matching. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2853–2865. [Google Scholar] [CrossRef]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A. MatchNet: Unifying feature and metric learning for patch-based matching. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3279–3286. [Google Scholar]
- Quan, D.; Liang, X.; Wang, S.; Wei, S.; Li, Y.; Huyan, N.; Jiao, L. AFD-Net: Aggregated feature difference learning for cross-spectral image patch matching. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3017–3026. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-Net: A trainable CNN for joint description and detection of local features. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8084–8093. [Google Scholar]
- Ma, W.; Zhang, J.; Wu, Y.; Jiao, L.; Zhu, H.; Zhao, W. A novel two-step registration method for remote sensing images based on deep and local features. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4834–4843. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, W.; Yan, W.; Xiang, D.; Wu, J.; Yang, X.; Bian, H. Registration of multimodal remote sensing image based on deep fully convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3028–3042. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Huang, Y. A Rotation-Invariant Optical and SAR Image Registration Algorithm Based on Deep and Gaussian Features. Remote Sens. 2021, 13, 2628. [Google Scholar] [CrossRef]
- Uss, M.; Vozel, B.; Lukin, V.; Chehdi, K. Exhaustive search of correspondences between multimodal remote sensing images using convolutional neural network. Sensors 2022, 22, 1231–1247. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Jiang, J.; Zhao, J.; Guo, X. LMR: Learning a two-class classifier for mismatch removal. IEEE Trans. Image Process. 2019, 28, 4045–4059. [Google Scholar] [CrossRef]
- Quan, D.; Wei, H.; Wang, S.; Gu, Y.; Hou, B.; Jiao, L. A novel coarse-to-fine deep learning registration framework for multimodal remote sensing images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5108316. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Wan, Y.; Liu, X.; Yan, X.; Li, J. Multi-modal remote sensing image matching considering co-occurrence filter. IEEE Trans. Image Process. 2022, 31, 2584–2597. [Google Scholar] [CrossRef]
- Richard, H.; Andrew, Z. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 36–58. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Bao, P.; Zhang, L.; Wu, X. Canny edge detection enhancement by scale multiplication. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1485–1490. [Google Scholar] [CrossRef]
- Xu, Q.; Varadarajan, S.; Chakrabarti, C.; Karam, L. A distributed canny edge detector: Algorithm and FPGA implementation. IEEE Trans. Image Process. 2014, 23, 2944–2960. [Google Scholar] [CrossRef]
- Suzuki, S.; Abe, K. Topological structural analysis of digitized binary images by border following. Comput. Vis. Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Bian, J.; Lin, W.; Liu, Y.; Zhang, L.; Yeung, S.; Cheng, M.; Reid, I. GMS: Grid–based motion statistics for fast, ultra–robust feature correspondence. In Proceedings of the 2017 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5183–5192. [Google Scholar]










| Scene | Azimuth Angle | Pitch Angle | Flight Altitude | Imaging Distance |
|---|---|---|---|---|
| Forests | 39.16° | 71.38° | 12.23 km | 38.3 km |
| Hills | 48.49° | 56.31° | 13.98 km | 25.2 km |
| Farmland | 68.62° | 75.25° | 8.15 km | 32.0 km |
| Lake | 79.84° | 78.69° | 8.57 km | 43.7 km |
| Buildings | 27.91° | 65.93° | 8.42 km | 20.5 km |
| Flyover | 43.38° | 53.27° | 8.93 km | 14.9 km |
| Scene | FAST | SIFT | SURF | ASIFT | ORB | ECDAF |
|---|---|---|---|---|---|---|
| Forests | (0.00, 0.00) | (16.7, 22.8) | (25.0, 32.8) | (79.1, 65.2) | (4.50, 7.22) | (96.0, 100) |
| Hills | (0.00, 0.00) | (0.00, 0.00) | (7.10, 15.3) | (73.2, 65.1) | (7.10, 5.92) | (85.0, 66.7) |
| Farmland | (0.00, 0.00) | (7.70, 10.4) | (35.0, 21.7) | (66.6, 72.9) | (12.5, 18.9) | (95.3, 100) |
| Lake | (0.00, 0.00) | (20.0, 15.8) | (9.10, 6.80) | (26.9, 32.6) | (11.1, 24.6) | (88.0, 100) |
| Buildings | (9.10, 15.3) | (85.7, 76.2) | (89.6, 80.3) | (93.9, 85.4) | (0.00, 0.00) | (93.7, 66.7) |
| Flyover | (87.5, 75.6) | (84.0, 86.9) | (96.5, 91.9) | (95.8, 97.8) | (96.9, 83.7) | (98.0, 100) |
| Scene (ID) | FAST | SIFT | SURF | ASIFT | ORB | ECDAF |
|---|---|---|---|---|---|---|
| Forests (1) | 2.83 | 9.11 | 2.71 | 98.85 | 0.69 | 12.37 |
| Hills (2) | 1.34 | 9.44 | 2.85 | 142.3 | 0.66 | 20.81 |
| Farmland (3) | 0.61 | 4.56 | 2.72 | 53.61 | 0.65 | 7.72 |
| Lake (4) | 0.64 | 3.99 | 1.67 | 22.19 | 0.62 | 4.19 |
| Buildings (5) | 1.63 | 6.41 | 2.54 | 88.24 | 0.68 | 10.15 |
| Flyover (6) | 3.22 | 8.36 | 3.19 | 103.8 | 0.83 | 18.92 |
| Number | Parameter | Value | Number | Parameter | Value |
|---|---|---|---|---|---|
| 1 | 35 | 5 | 12.4 | ||
| 2 | 4.1 | 6 | 3 | ||
| 3 | 28 | 7 | 6.6 | ||
| 4 | 8 | 8 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, C.; Ding, Y.; Sun, C.; Yuan, G.; Zhang, H. Inclined Aerial Image and Satellite Image Matching Based on Edge Curve Direction Angle Features. Remote Sens. 2025, 17, 268. https://doi.org/10.3390/rs17020268
Wang H, Liu C, Ding Y, Sun C, Yuan G, Zhang H. Inclined Aerial Image and Satellite Image Matching Based on Edge Curve Direction Angle Features. Remote Sensing. 2025; 17(2):268. https://doi.org/10.3390/rs17020268
Chicago/Turabian StyleWang, Hao, Chongyang Liu, Yalin Ding, Chao Sun, Guoqin Yuan, and Hongwen Zhang. 2025. "Inclined Aerial Image and Satellite Image Matching Based on Edge Curve Direction Angle Features" Remote Sensing 17, no. 2: 268. https://doi.org/10.3390/rs17020268
APA StyleWang, H., Liu, C., Ding, Y., Sun, C., Yuan, G., & Zhang, H. (2025). Inclined Aerial Image and Satellite Image Matching Based on Edge Curve Direction Angle Features. Remote Sensing, 17(2), 268. https://doi.org/10.3390/rs17020268





