The Surface Heat Flow of Mars at the Noachian–Hesperian Boundary
Abstract
1. Introduction
2. Background
3. Thrust Faults Used for the Analysis
4. HPEs Abundances and Heat Production
5. Crustal Model
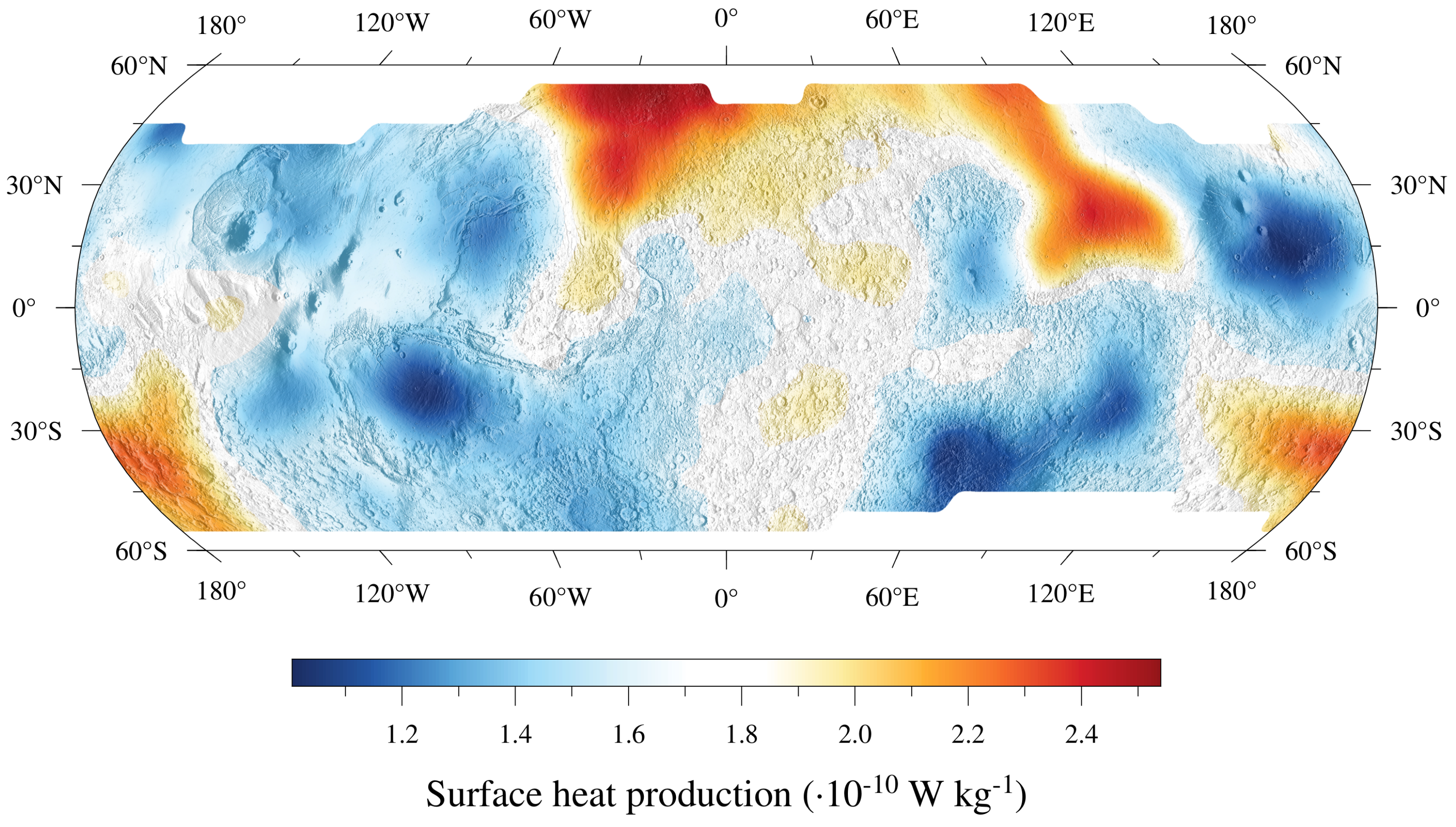
6. Regional Heat Flows and Crustal HPE Abundances at the Noachian–Hesperian Boundary
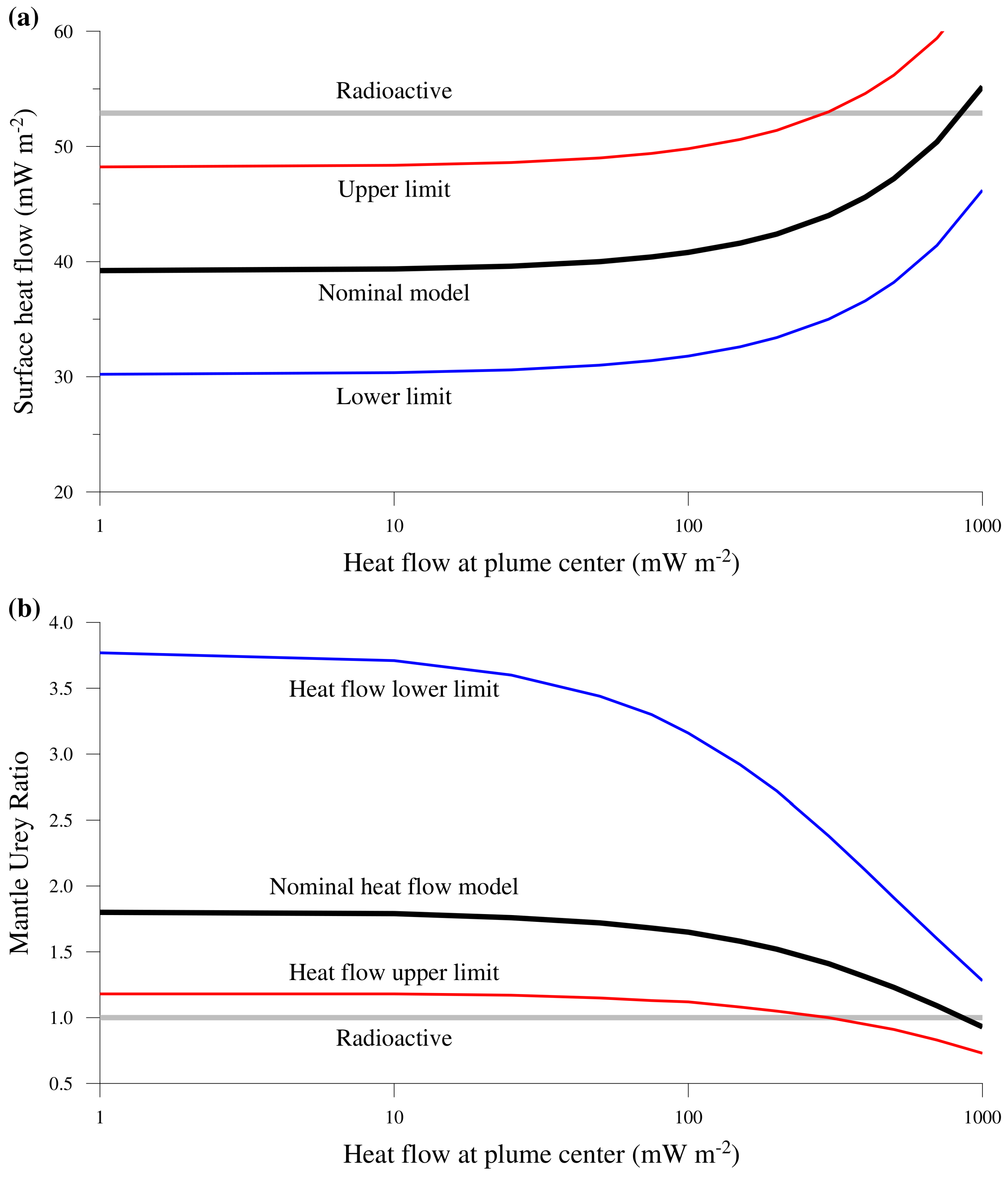
7. Building a Global Heat Flow Model for 3.7 Ga
7.1. Heat Flow Model Based on Thrust Fault Depths (Mars “Without Plumes”)
7.2. Global Heat Flow Model with Large Plumes
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Solomon, S.C.; Aharonson, O.; Aurnou, J.M.; Banerdt, W.B.; Carr, M.H.; Dombard, A.J.; Frey, H.V.; Golombek, M.P.; Hauck, S.A., 2nd; Head, J.W., 3rd; et al. New perspectives on ancient Mars. Science 2005, 307, 1214–1220. [Google Scholar] [CrossRef]
- Carr, M.H.; Head, J.W. Geologic history of Mars. Earth Planet. Sci. Lett. 2010, 294, 185–203. [Google Scholar] [CrossRef]
- Fassett, C.I.; Head, J.W. Sequence and timing of conditions on early Mars. The timing of martian valley network activity: Constraints from buffered crater counting. Icarus 2011, 211, 1204–1214. [Google Scholar] [CrossRef]
- Ramirez, R.M.; Craddock, R.A. The geological and climatological case for a warmer and wetter early Mars. Nat. Geosci. 2018, 11, 230–237. [Google Scholar] [CrossRef]
- Mangold, N.; Adeli, S.; Conway, S.; Ansan, V.; Langlais, B. A chronology of early Mars climatic evolution from impact crater degradation. J. Geophys. Res. 2012, 117, E04003. [Google Scholar] [CrossRef]
- Bibring, J.-P.; Langevin, Y.; Mustard, J.F.; Poulet, F.; Arvidson, R.; Gendrin, A.; Gondet, B.; Mangold, N.; Pinet, P.; Forget, F.; et al. Global mineralogical and aqueous Mars history derived from OMEGA/Mars express data. Science 2006, 312, 400–404. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Mustard, J.F.; Murchie, S.L.; Bibring, J.-P.; Meunier, A.; Fraeman, A.A.; Langevin, Y. Subsurface water and clay mineral formation during the early history of Mars. Nature 2011, 479, 53–60. [Google Scholar] [CrossRef]
- Baratoux, D.; Toplis, M.J.; Monnereau, M.; Sautter, V. The petrological expression of early Mars volcanism. J. Geophys. Res. 2013, 118, 59–64. [Google Scholar] [CrossRef]
- Wilson, J.H.; Mustard, J.F. Exposures of olivine-rich rocks in the vicinity of Ares Vallis: Implications for Noachian and Hesperian volcanism. J. Geophys. Res. 2013, 118, 916–929. [Google Scholar] [CrossRef]
- McSween, H.Y. Petrology on Mars. Am. Mineral. 2015, 100, 2380–2395. [Google Scholar] [CrossRef]
- Citron, R.I.; Manga, M.; Hemingway, D.J. Timing of oceans on Mars from shoreline deformation. Nature 2018, 555, 643–646. [Google Scholar] [CrossRef]
- Ruiz, J. The early heat loss evolution of Mars and their implications for internal and environmental history. Sci. Rep. 2014, 4, 4338. [Google Scholar] [CrossRef] [PubMed]
- Milbury, C.; Schubert, G.; Raymond, C.A.; Smrekar, S.E.; Langlais, B. The history of Mars’ dynamo as revealed by modelling magnetic anomalies near Tyrrhenus Mons and Syrtis Major. J. Geophys. Res. 2012, 117, E10007. [Google Scholar]
- Langlais, B.; Thébault, E.; Quesnel, E.; Mangold, N.A. Late Martian Dynamo Cessation Time 3.77 Gy Ago. Lunar Planet. Sci. Conf. 2012, 43, 1231. [Google Scholar]
- Steele, S.C.; Fu, R.R.; Muxworthy, A.R.; Volk, M.W.R.; Collins, G.S.; North, T.L.; Davison, T.M. Taleomagnetic evidence for a long-lived, potentially reversing martian dynamo at 3.9 Ga. Sci. Adv. 2023, 9, eade9071. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Anderson, F.S.; Andrews-Hanna, J.; Carter, J.; Catling, D.C.; Christensen, P.R.; Cohen, B.; Dressing, C.D.; Edwards, C.S.; Elkins-Tanton, L.T.; et al. The sustainability of habitability on terrestrial planets: Insights, questions, and needed measurements from Mars for understanding the evolution of Earth-like worlds. J. Geophys. Res. Planets 2016, 121, 1927–1961. [Google Scholar] [CrossRef]
- Solomon, S.C.; Head, J.W. Heterogeneities in the thickness of the elastic lithosphere of Mars: Constraints on heat flow and internal dynamics. J. Geophys. Res. 1990, 95, 11073–11083. [Google Scholar] [CrossRef]
- Anderson, S.; Grimm, R.E. Rift processes at the Valles Marineris, Mars: Constraints from gravity on necking and rate-depending strength evolution. J. Geophys. Res. 1998, 103, 11113–11124. [Google Scholar]
- McGovern, P.J.; Solomon, S.C.; Smith, D.E.; Zuber, M.T.; Simons, M.; Wieczorek, M.A.; Phillips, R.J.; Neumann, G.A.; Aharonson, O.; Head, J.W. Correction to Localized gravity/topography admittance and correlation spectra on Mars: Implications for regional and global evolution. J. Geophys. Res. 2004, 109, E07007. [Google Scholar] [CrossRef]
- Grott, M.; Hauber, E.; Werner, S.C.; Kronberg, P.; Neukum, G. High heat flux on ancient Mars: Evidence from rift flank uplift at Coracis Fossae. Geophys. Res. Lett. 2005, 32, L21201. [Google Scholar] [CrossRef]
- Ruiz, J.; McGovern, P.J.; Tejero, R. The early thermal and magnetic state of the cratered highlands of Mars. Earth Planet. Sci. Lett. 2006, 241, 2–10. [Google Scholar] [CrossRef]
- Ruiz, J.; McGovern, P.J.; Jiménez-Díaz, A.; López, V.; Williams, J.; Hahn, B.C.; Tejero, R. The thermal evolution of Mars as constrained by paleo-heat flows. Icarus 2011, 15, 508–517. [Google Scholar] [CrossRef]
- Schultz, R.A.; Watters, T.R. Forward mechanical modeling of the Amenthes Rupes thrust fault on Mars. Geophys. Res. Lett. 2001, 28, 4659–4662. [Google Scholar] [CrossRef]
- Grott, M.; Hauber, E.; Werner, S.C.; Kronberg, P.; Neukum, G. Mechanical mod- eling of thrust faults in the Thaumasia region, Mars, and implications for the Noachian heat flux. Icarus 2007, 186, 517–526. [Google Scholar] [CrossRef]
- Ruiz, J.; Fernández, C.; Gomez-Ortiz, D.; Dohm, J.M.; López, V.; Tejero, R. Ancient heat flow, crustal thickness, and lithospheric mantle rheology in the Amenthes region, Mars. Earth Planet. Sci. Lett. 2008, 270, 1–12. [Google Scholar] [CrossRef]
- Ruiz, J.; Williams, J.-P.; Dohm, J.M.; Fernández, C.; López, V. Ancient heat flows and crustal thickness at Warrego rise, Thaumasia Highlands, Mars: Implications for a stratified crust. Icarus 2009, 203, 47–57. [Google Scholar] [CrossRef]
- Mueller, K.; Vida, A.; Robbins, S.; Golombek, M.; West, C. Fault and fold growth of the Amenthes uplift: Implications for Late Noachian crustal rheology and heat flow on Mars. Earth Planet. Sci. Lett. 2014, 408, 100–109. [Google Scholar] [CrossRef]
- Egea-González, I.; Jiménez-Díaz, A.; Parro, L.M.; Lopez, V.; Williams, J.P.; Ruiz, J. Thrust fault modeling and Late-Noachian lithospheric structure of the circum-Hellas region, Mars. Icarus 2017, 288, 53–68. [Google Scholar] [CrossRef]
- Herrero-Gil, A.; Egea-González, I.; Ruiz, J.; Romeo, I. Structural modeling of lobate scarps in the NW margin of Argyre impact basin, Mars. Icarus 2019, 319, 367–380. [Google Scholar] [CrossRef]
- Smith, D.; Zuber, M.T.; Frey, H.V.; Garvin, J.B.; Head, J.W.; Muhleman, D.O.; Pettengill, G.H.; Phillips, R.J.; Solomon, S.C.; Zwally, H.J.; et al. Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars. J. Geophys. Res. 2001, 106, 23689–23722. [Google Scholar] [CrossRef]
- Gwinner, K.; Scholten, F.; Preusker, F.; Elgner, S.; Roatsch, T.; Spiegel, M.; Schmidt, R.; Oberst, J.; Jaumann, R.; Heipke, C. Topography of Mars from global mapping by HRSC high-resolution digital terrain models and orthoimages: Characteristics and performance. Earth Planet. Sci. Lett. 2010, 294, 506–519. [Google Scholar] [CrossRef]
- Watters, T.R.; Robinson, M.S. Lobate scarps and the Martian crustal dichotomy. J. Geophys. Res. 1999, 104, 18981–18990. [Google Scholar] [CrossRef]
- Tanaka, K.L.; Robbins, S.J.; Fortezzo, C.M.; Skinner, J.A., Jr.; Hare, T.M. The digital global geologic map of Mars: Chronostratigraphic ages, topographic and crater morphologic characteristics, and updated resurfacing history. Planet. Space Sci. 2014, 95, 11–24. [Google Scholar] [CrossRef]
- Herrero-Gil, A.; Egea-González, I.; Jiménez-Díaz, A.; Rivas-Dorado, S.; Parro, L.M.; Fernández, C.; Ruiz, J.; Romeo, I. Lithospheric contraction concentric to Tharsis: Structural modeling of large thrust faults between Thaumasia highlands and Aonia Terra, Mars. J. Struct. Geol. 2023, 177, 104983. [Google Scholar] [CrossRef]
- Atkins, R.M.; Byrne, P.L.; Wegmann, K.W. Morphometry and timing of major crustal shortening structures on Mars. Lunar Planet. Sci. 2019, 50, 2132. [Google Scholar]
- Parro, L.M.; Jiménez-Díaz, A.; Mansilla, F.; Ruiz, J. Present-day heat flow model of Mars. Nat. Sci. Rep. 2017, 7, 45629. [Google Scholar] [CrossRef] [PubMed]
- Boynton, W.V.; Taylor, G.J.; Evans, L.G.; Reedy, R.C.; Starr, R.; Janes, D.M.; Kerry, K.E.; Drake, D.M.; Kim, K.J.; Williams, R.M.S.; et al. Concentration of H, Si, Cl, K, Fe, and Th in the low and mid latitude regions of Mars. J. Geophys. Res. 2007, 112, E12S99. [Google Scholar]
- Hahn, B.C.; McLennan, S.M.; Klein, E.C. Martian surface heat production and crustal heat flow from Mars Odyssey gamma-ray spectrometry. Geophys. Res. Lett. 2011, 38, L14203. [Google Scholar] [CrossRef]
- Rani, A.; Basu Sarbadhikari, A.; Hood, D.R.; Gasnault, O.; Nambiar, S.; Karunatillake, S. Consolidated chemical provinces on Mars: Implications for geologic interpretations. Geophys. Res. Lett. 2022, 49, e2022GL099235. [Google Scholar] [CrossRef]
- Meyer, C. Mars Meteorite Compendium; Lyndon B. Johnson Space Center, NASA: Houston, TX, USA, 2003. [Google Scholar]
- Herrero-Gil, A.; Ruiz, J.; Romeo, I. 3D modeling of planetary lobate scarps: The case of Ogygis Rupes, Mars. Earth Planet Sci. Lett. 2020a, 532, 116004. [Google Scholar] [CrossRef]
- Herrero-Gil, A.; Ruiz, J.; Romeo, I. Lithospheric contraction on Mars: A 3D model of the Amenthes thrust fault system. J. Geophys. Res. Planets 2020b, 125, e2019JE006201. [Google Scholar] [CrossRef]
- Taylor, G.J.; Boynton, W.V.; Brückner, J.; Wänke, H.; Dreibus, G.; Kerry, K.E.; Keller, J.M.; Reedy, R.C.; Evans, L.G.; Starr, R.D.; et al. Bulk composition and early differ- entiation of Mars. J. Geophys. Res. 2006, 111, E03S10. [Google Scholar]
- Wieczorek, M.A.; Broquet, A.; McLennan, S.M.; Rivoldini, A.; Golombek, M.; Antonangeli, D.; Beghein, C.; Giardini, D.; Gudkova, T.; Gyalay, S.; et al. InSight constraints on the global character of the Martian crust. J. Geophys. Res. Planets 2022, 127, e2022JE007298. [Google Scholar] [CrossRef]
- Jellinek, A.M.; Johnson, C.L.; Schubert, G. Constraints on the elastic thickness, heat flow, and melt production at early Tharsis from topography and magnetic field observations. J. Geophys. Res. 2008, 113, E09004. [Google Scholar] [CrossRef]
- Ranalli, G. Rheology of the lithosphere in space and time. Geol. Soc. Spec. Publ. 1997, 121, 19–37. [Google Scholar] [CrossRef]
- Frey, H.V. Impact constraints on, and a chronology for, major events in early Mars history. J. Geophys. Res. 2006, 111, E08S91. [Google Scholar] [CrossRef]
- Broquet, A.; Wieczorek, M.A. The gravitational signature of Martian volcanoes. J. Geophys. Res. Planets 2019, 124, 2054–2086. [Google Scholar] [CrossRef]
- Watters, T.R.; Schultz, R.A.; Robinson, M.S.; Cook, A.C. The mechanical and thermal structure of Mercury’s early lithosphere. Geophys. Res. Lett. 2002, 29, 37-1–37-4. [Google Scholar] [CrossRef]
- Taylor, S.R.; McLennan, S.M. Planetary Crusts: Their Composition, Origin and Evolution; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- McLennan, S.M. Large-ion lithophile element fractionation during the early differentiation of Mars and the composition of the Martian primitive mantle. Meteor. Planet. Sci. 2003, 38, 895–904. [Google Scholar] [CrossRef]
- Van Schmus, W.R. Natural radioactivity of the crust and mantle. In Global Earth Physics: A Handbook of Physical constants. AGU Reference Shelf 1; Ahrens, T.J., Ed.; American Geophysical Union: Washington, DC, USA, 1995; pp. 283–291. [Google Scholar]
- Zuber, M.T.; Solomon, S.C.; Phillips, R.J.; Smith, D.E.; Tyler, G.L.; Aharonson, O.; Balmino, G.; Banerdt, W.B.; Head, J.W.; Johnson, C.L.; et al. Nternal structure and early thermal evolution of Mars from Mars Global Surveyor. Science 2000, 287, 1788–1793. [Google Scholar] [CrossRef]
- Neumann, G.A.; Zuber, M.T.; Wieczorek, M.A.; McGovern, P.J.; Lemoine, F.G.; Smith, D.E. The crustal structure of Mars from gravity and topography. J. Geophys. Res. 2004, 109, E08002. [Google Scholar] [CrossRef]
- Genova, A.; Goossens, S.; Lemoine, F.G.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus 2016, 272, 228–245. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Beuthe, M.; Rivoldini, A.; Van Hoolst, T. Hydrostatic interfaces in bodies with nonhydrostatic lithospheres. J. Geophys. Res. Planets 2019, 124. [Google Scholar] [CrossRef]
- Caristan, Y. he transition from high temperature creep to fracture in Mary- land diabase. J. Geophys. Res. 1982, 87, 6781–6790. [Google Scholar] [CrossRef]
- Parmentier, E.M.; Zuber, M.T. Early evolution of Mars with mantle compositional stratification or hydrothermal crustal cooling. J. Geophys. Res. 2007, 112, E02007. [Google Scholar] [CrossRef]
- Andrews-Hanna, J.C.; Phillips, R.J.; Zuber, M.T. Meridiani Planum and the global hydrology of Mars. Nature 2007, 446, 163–165. [Google Scholar] [CrossRef]
- Beardsmore, G.R.; Cull, J.P. Crustal Heat Flow: A Guide to Measurement and Modelling; Cambridge University Press: Cambridge, UK, 2001; p. 324. [Google Scholar]
- Kieffer, H.H.; Martin, T.Z.; Peterfreund, A.; Jakosky, B.M.; Miner, E.; Palluconi, F.D. Thermal and albedo mapping of Mars during the Viking primary mission. J. Geophys. Res. 1977, 82, 4249–4291. [Google Scholar] [CrossRef]
- Norman, M.D. The composition and thickness of the crust of Mars estimated from rare Earth elements and neodymium-isotopic compositions of martian meteorites. Meteor. Planet. Sci. 1999, 34, 439–449. [Google Scholar] [CrossRef]
- Norman, M.D. hickness and composition of the martian crust revisited: Implications of an ultradepleted mantle with Nd isotopic composition like that of QUE94201. Lunar Planet. Sci. 2002, 33, 1175. [Google Scholar]
- Grott, M. Late crustal growth on Mars: Evidence from lithospheric extension. Geophys. Res. Lett. 2005, 32, L23201. [Google Scholar] [CrossRef]
- Werner, S.C. The global martian volcanic evolutionary history. Icarus 2009, 201, 44–68. [Google Scholar] [CrossRef]
- Carr, M.H. Volcanism on Mars. J. Geophys. Res. 1973, 78, 4049–4062. [Google Scholar] [CrossRef]
- McKenzie, D.; Barnett, D.; Yuan, D.-N. The relationship between martian gravity and topography. Earth Planet. Sci. Lett. 2002, 195, 1–16. [Google Scholar] [CrossRef]
- Wenzel, M.J.; Manga, M.; Jellinek, M. Tharsis as a consequence of Mars’ dichotomy and layered mantle. Geophys. Res. Lett. 2004, 31, L04702. [Google Scholar] [CrossRef]
- Belleguic, V.; Lognonne, P.; Wieczorek, M. Constraints on the martian lithosphere from gravity and topography data. J. Geophys. Res. 2005, 110, E11005. [Google Scholar] [CrossRef]
- Cohen, B.E.; Mark, D.F.; Cassata, W.S.; Lee, M.R.; Tomkinson, T.; L, C. Smith Taking the pulse of Mars via dating of a plume-fed volcano. Nat. Commun. 2017, 8, 640. [Google Scholar] [CrossRef]
- Day, J.M.D.; Tait, K.T.; Moynier, F.; Neal, C.R.; Liu, Y.; Udry, A. Martian magmatism from plume metasomatized mantle. Nat. Commun. 2018, 9, 4799. [Google Scholar] [CrossRef] [PubMed]
- Grott, M.; Breuer, D. On the spatial variability of the martian elastic lithosphere thickness: Evidence for mantle plumes? J. Geophys. Res. 2008, 115, E03005. [Google Scholar] [CrossRef]
- Lee, C.-T.; Keller, D.; Dasgupta, R.; Siebach, K.; McGovern, P.; Borchardt, J.; Zhang, J. Crustal thickness effects on chemical differentiation and hydrology on Mars. Earth Planet. Sci. Lett. 2025, 651, 119155. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Poli, S. Experimentally based water budgets for dehydrating slabs and consequences for arc magma generation. Earth Planet. Sci. Lett. 1998, 163, 361–379. [Google Scholar] [CrossRef]
- Wänke, H.; Dreibus, G. Chemical composition and accretion history of terrestrial planets. Philos. Trans. R. Soc. Lond. 1988, 325, 545–557. [Google Scholar]
- Drilleau, M.; Samuel, H.; Garcia, R.F.; Rivoldini, A.; Perrin, C.; Michaut, C.; Wieczorek, M.; Tauzin, B.; Connolly, J.A.D.; Meyer, P.; et al. Marsquake locations and 1-D seismic models for Mars from InSight data. J. Geophys. Res. Planets 2022, 127, e2021JE007067. [Google Scholar] [CrossRef] [PubMed]
- Samuel, H.; Drilleau, M.; Rivoldini, A.; Xu, Z.; Huang, Q.; Garcia, R.F.; Lekić, V.; Irving, J.C.E.; Badro, J.; Lognonné, P.; et al. Geophysical evidence for an enriched molten silicate layer above Mars’s core. Nature 2023, 622, 717–718. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Huang, D.; Durán, C.; Sossi, P.A.; Giardini, D.; Murakami, M. Evidence for a liquid silicate layer atop the Martian core. Nature 2023, 622, 718–723. [Google Scholar] [CrossRef]
- Hernández-Montenegro, J.D.; Asimow, P.D.; Herzberg, C.T. Estimating primary magmas from Mars with PRIMARSMELT: Implications for the petrogenesis of some Martian rocks and the thermal evolution of Mars. J. Geophys. Res. Planets 2024, 129, e2024JE008508. [Google Scholar] [CrossRef]
- McGovern, P.J.; Schubert, G. Thermal evolution of the Earth: Effects of volatile exchange between atmosphere and interior. Earth Planet. Sci. Lett. 1989, 96, 27–37. [Google Scholar] [CrossRef]
- Sandu, C.; Kiefer, W.S. Degassing history of Mars and the lifespan of its magnetic dynamo. Geophys. Res. Lett. 2012, 39, L03201. [Google Scholar] [CrossRef]

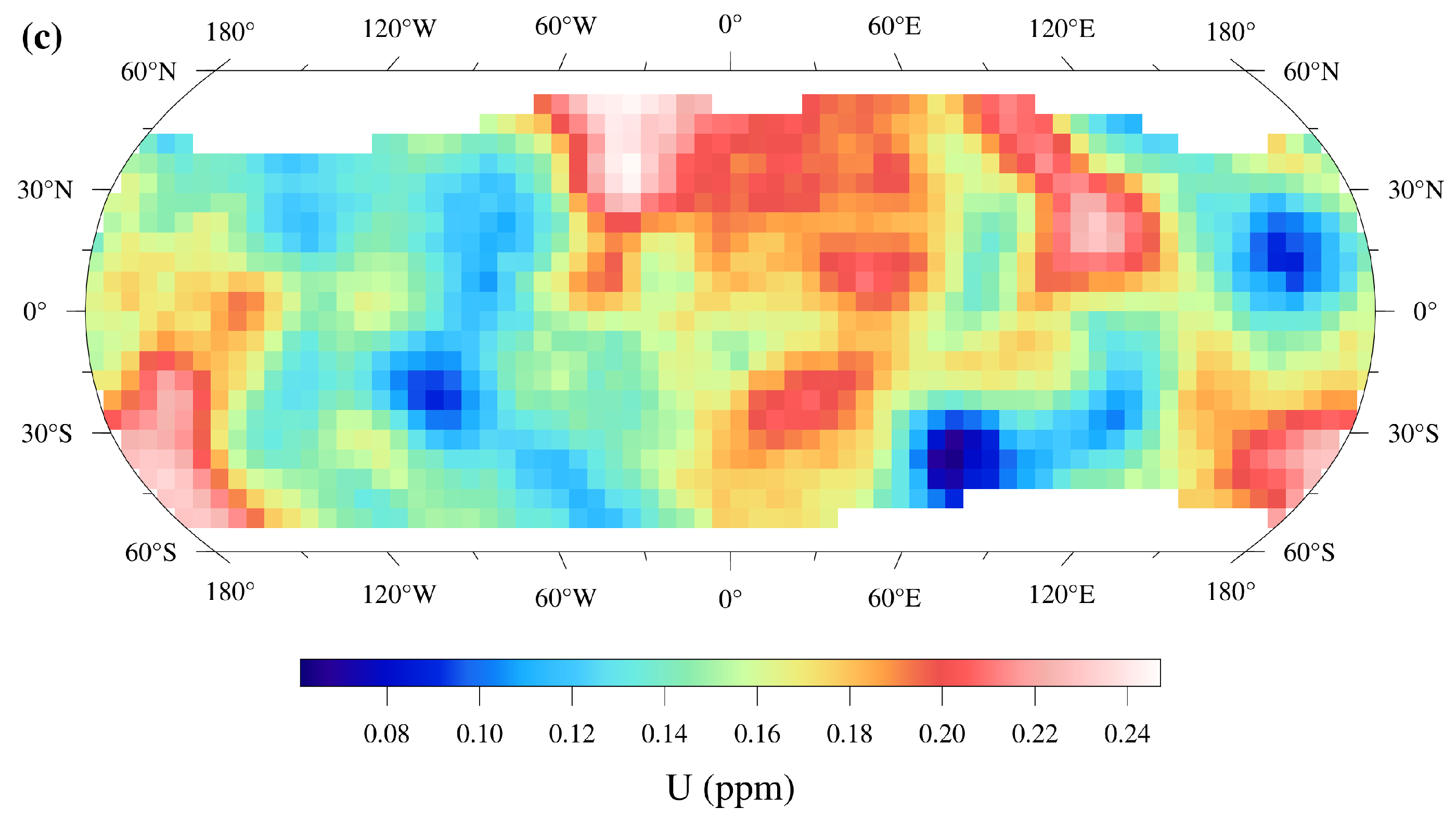
| Thrust | BDT Depth (km) a | H (W ) b | F (mW ) | b (km) c | |
|---|---|---|---|---|---|
| 1. Warrego W | 17–21 | 0.46 | 53.1–43.9 | 98.78 | 1.18–0.98 |
| 2. Warrego E | 21–27 | 0.45 | 43.8–35.8 | 94.56 | 1.04–0.85 |
| 3. Amenthes Rupes | 20–24 | 0.45 | 45.8–35.2 | 58.03 | 1.76–1.35 |
| 4. Ogygis Rupes | 17–18 | 0.39 | 52.6–49.8 | 73.48 | 1.82–1.72 |
| 5. Phrixi Rupes | 16–19 | 0.43 | 56.0–47.7 | 78.58 | 1.67–1.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz, J.; Parro, L.M.; Egea-González, I.; Romeo, I.; Álvarez-Lozano, J.; Jiménez-Díaz, A. The Surface Heat Flow of Mars at the Noachian–Hesperian Boundary. Remote Sens. 2025, 17, 274. https://doi.org/10.3390/rs17020274
Ruiz J, Parro LM, Egea-González I, Romeo I, Álvarez-Lozano J, Jiménez-Díaz A. The Surface Heat Flow of Mars at the Noachian–Hesperian Boundary. Remote Sensing. 2025; 17(2):274. https://doi.org/10.3390/rs17020274
Chicago/Turabian StyleRuiz, Javier, Laura M. Parro, Isabel Egea-González, Ignacio Romeo, Julia Álvarez-Lozano, and Alberto Jiménez-Díaz. 2025. "The Surface Heat Flow of Mars at the Noachian–Hesperian Boundary" Remote Sensing 17, no. 2: 274. https://doi.org/10.3390/rs17020274
APA StyleRuiz, J., Parro, L. M., Egea-González, I., Romeo, I., Álvarez-Lozano, J., & Jiménez-Díaz, A. (2025). The Surface Heat Flow of Mars at the Noachian–Hesperian Boundary. Remote Sensing, 17(2), 274. https://doi.org/10.3390/rs17020274






