Downscaling Method for Crop Yield Statistical Data Based on the Standardized Deviation from the Mean of the Comprehensive Crop Condition Index
Highlights
- A downscaling method using the standardized deviation of the CCCI was proposed to effectively transform crop yield statistics from administrative units to the pixel level.
- The spatial heterogeneity of crop growth was expressed through the spatiotemporal dynamic weights of CCCI, and the spatial variation in crop yield was effectively reflected.
- This method provides reliable spatialized yield data to support crop yield predictions, climate change impact assessments, and precision agriculture applications at large scales.
- Spatialized crop yield results could expand training samples for pixel-level yield predictions, overcoming the challenge of limited ground-truth data in agricultural remote sensing research.
Abstract
1. Introduction
2. Data Preparation and Processing
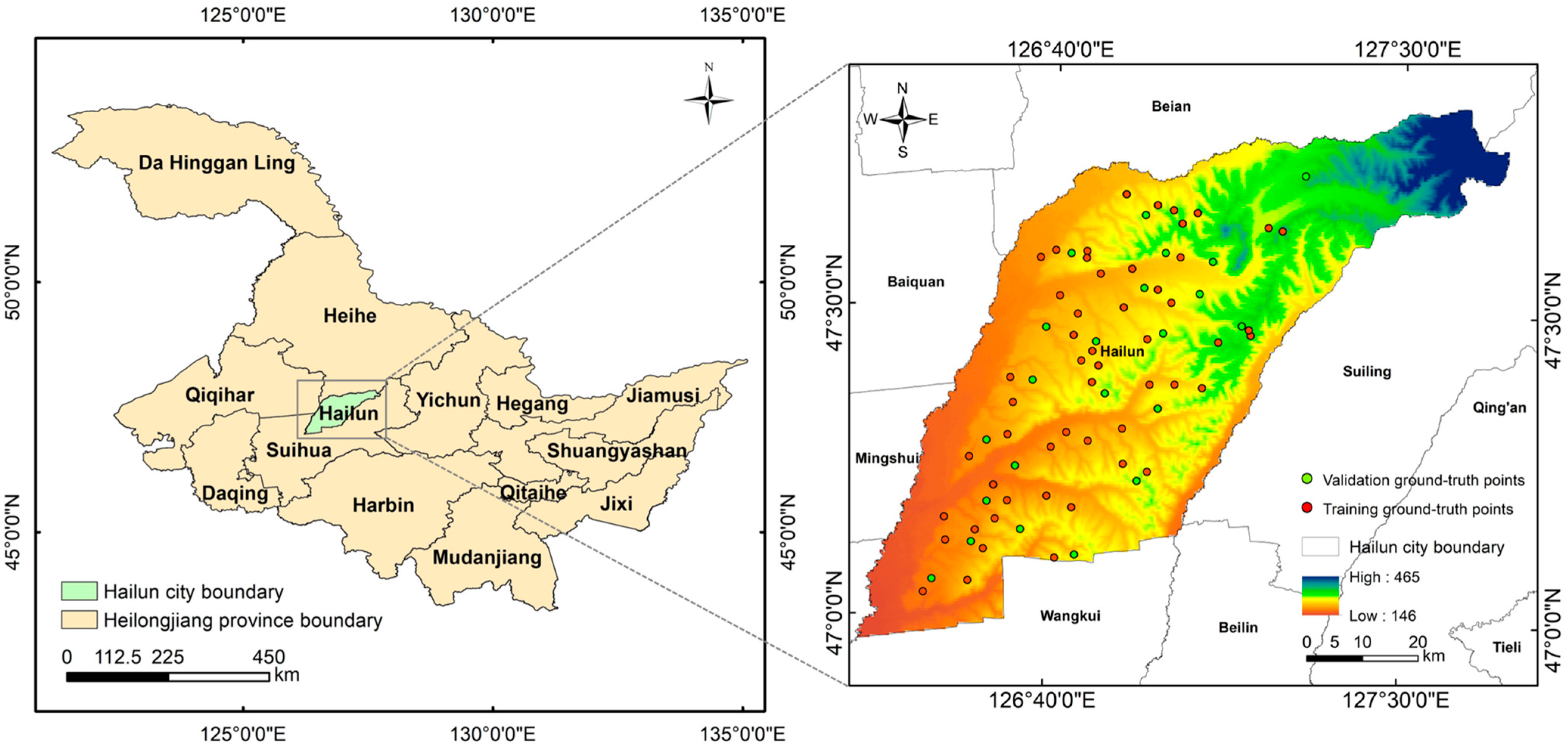
2.1. Study Area
2.2. Remote Sensing Data Acquisition and Preprocessing
2.3. Remote Sensing Inversion of Crop Condition Parameters
2.3.1. Inversion of Crop Condition Parameters Based on the SNAP Model
2.3.2. Acquisition of Net Primary Production (NPP) Based on MODIS and Sentinel-2 Remote Sensing Data
2.4. Crop Growth Parameters and Ground-Truth Crop Yield Data
2.5. Other Data
3. Research Methods
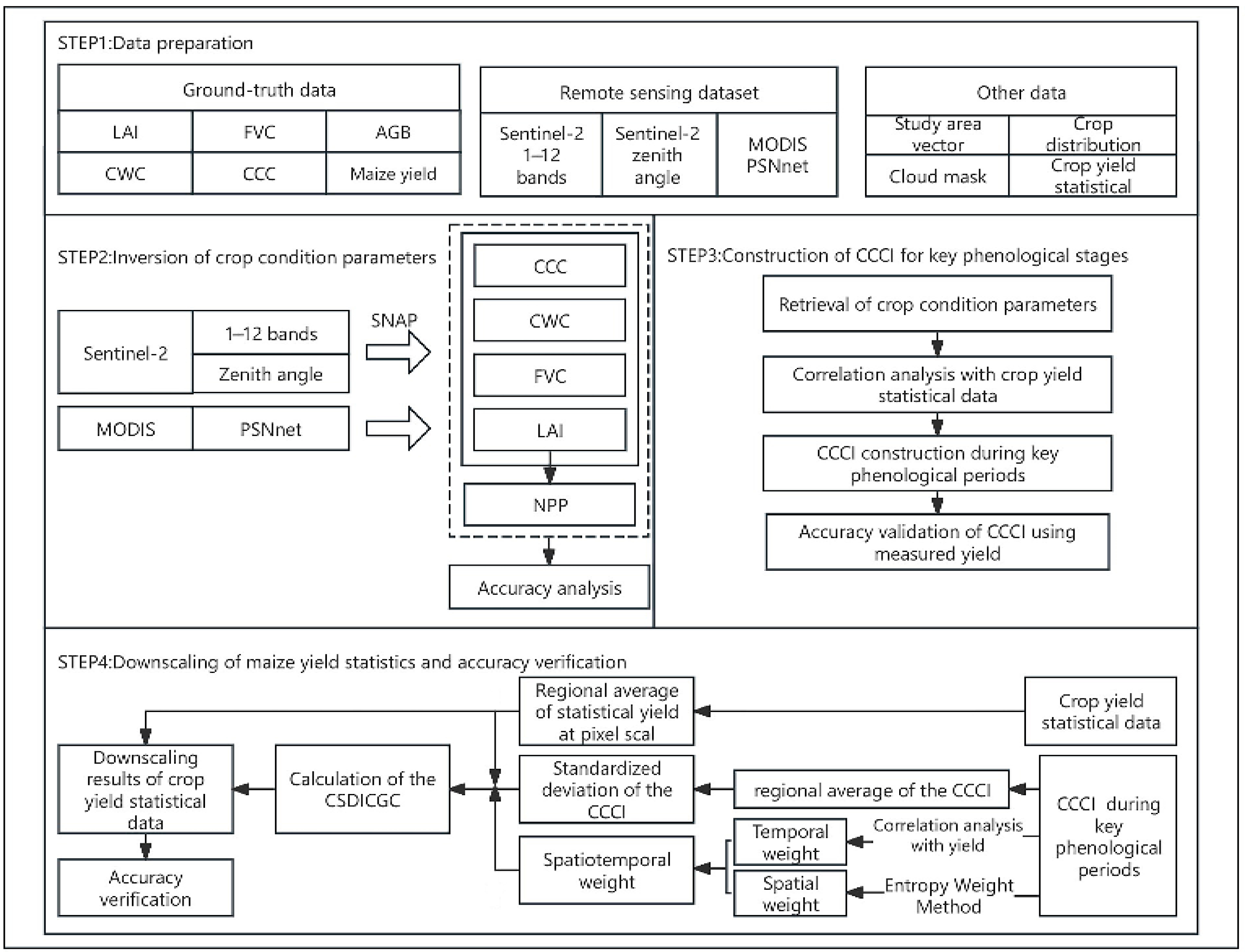
3.1. Technical Route
3.2. Main Research Process
3.2.1. Comprehensive Crop Condition Index for Key Phenological Stages
- (1)
- Correlation Analysis between Crop Condition Parameters During Key Phenological Stages and Statistical Yield
- (2)
- Construction of the CCCI for Key Phenological Stages Based on the Determination Method of Normalized Regression Coefficient Weights
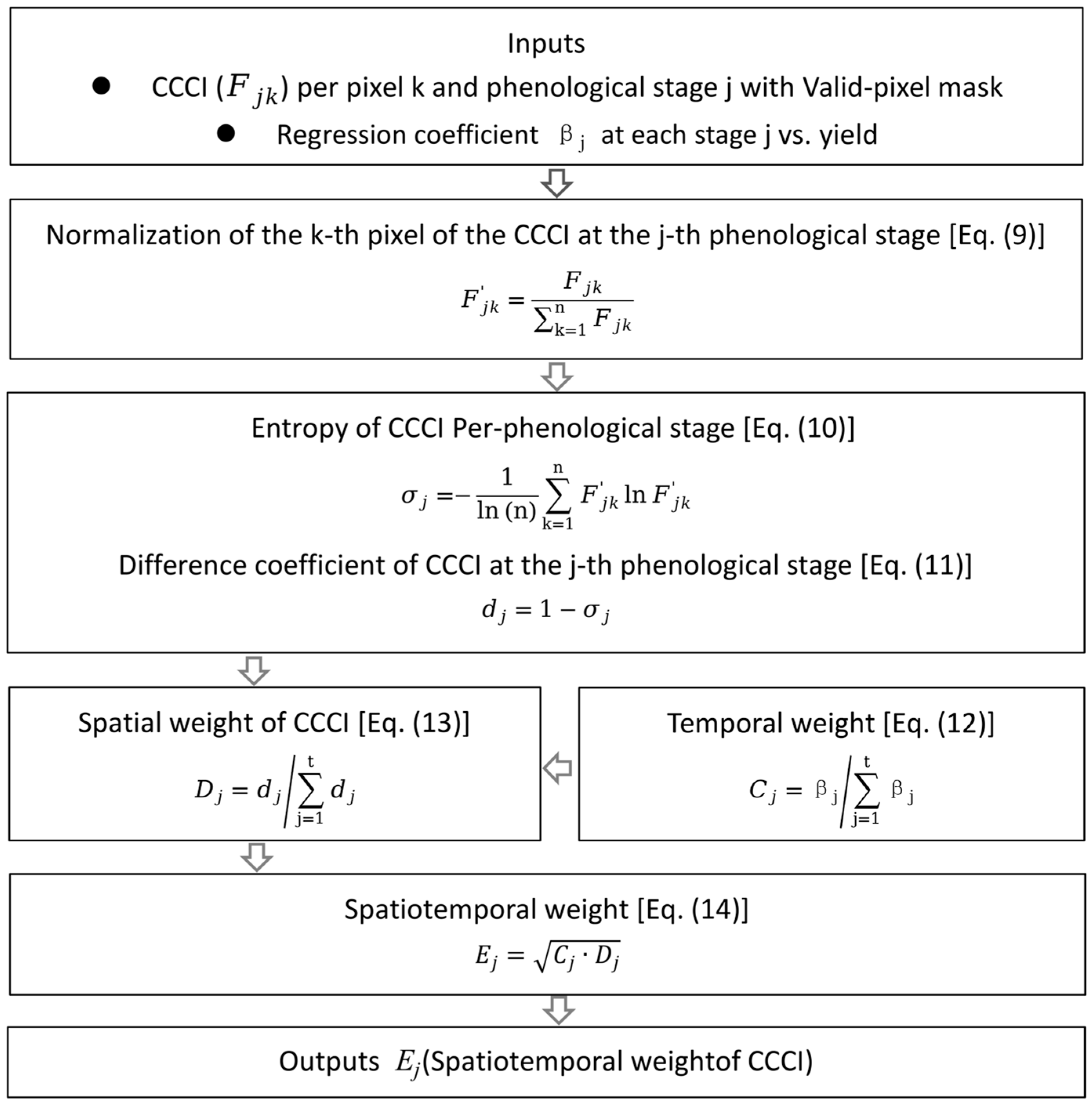
3.2.2. Calculation of the Comprehensive Spatial Difference Index of Crop Growth Conditions (CSDICGC)
- (1)
- Determination of the Temporal Weight Coefficient of the CCCI During Key Phenological Stages
- (2)
- Calculation of the Difference Coefficient of the CCCI
- (3)
- Calculation of the Spatiotemporal Weights of the CCCI
- (a)
- Temporal Weight Calculation
- (b)
- Calculation of the Spatial Weights of the CCCI
- (c)
- Comprehensive Spatiotemporal Weight Calculation
- (4)
- Calculation of the Comprehensive Spatial Difference Index of Crop Growth Conditions (CSDICGC)
- (a)
- Calculation of the Regional Average CCCI for Key Phenological Stages
- (b)
- Standardized Deviation of the CCCI
- (c)
- Calculation of the CSDICGC
3.2.3. Downscaling of Maize Yield Statistics
3.2.4. Accuracy Verification
- (1)
- Accuracy Validation Based on Ground-Truth Data
- (2)
- Regional Validation Crop Yield Statistics
4. Results and Analysis
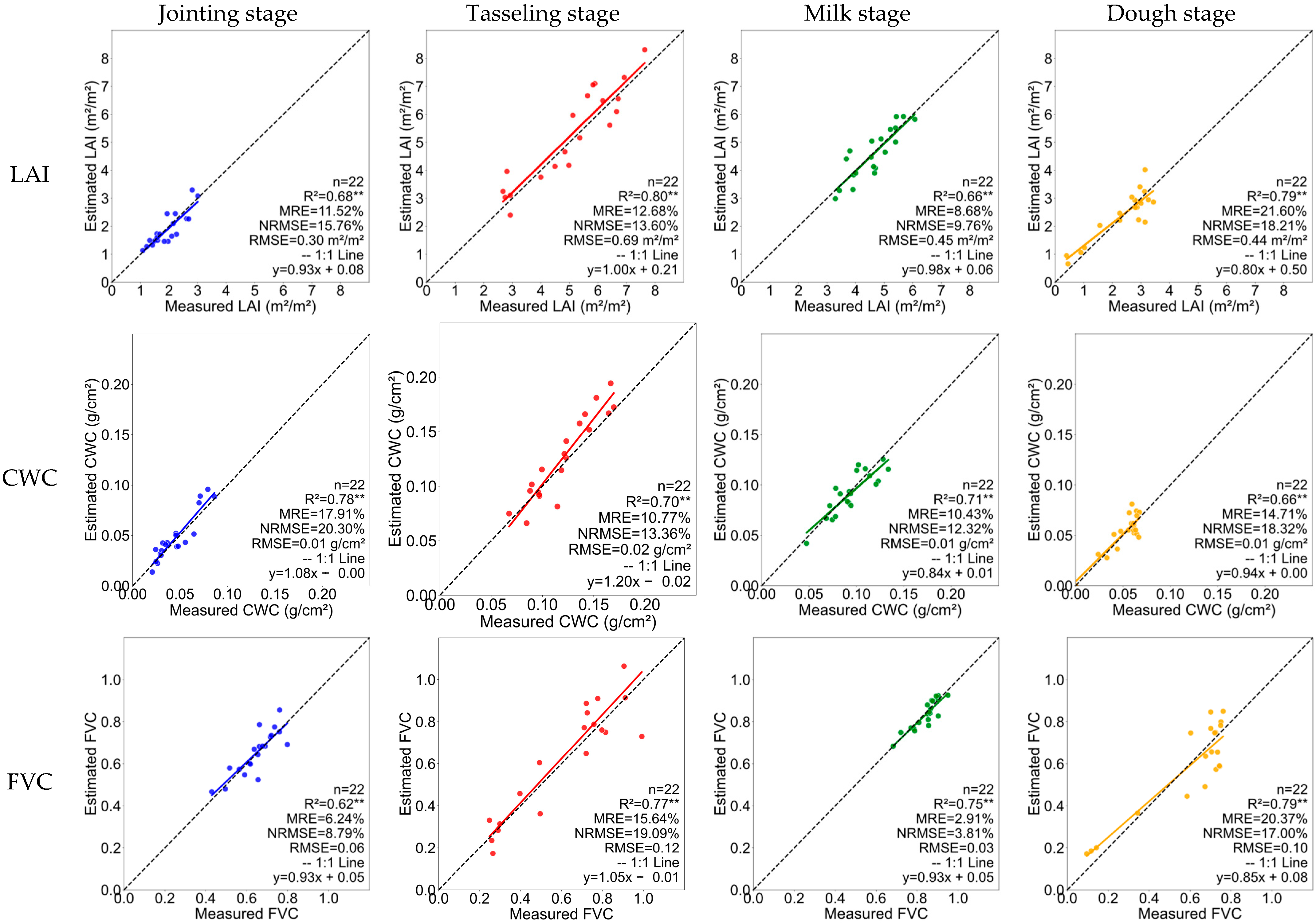
4.1. Verification of the Inversion Results and Precision of the Main Growth Period Parameters
4.2. Construction of the CCCI for Key Phenological Stages
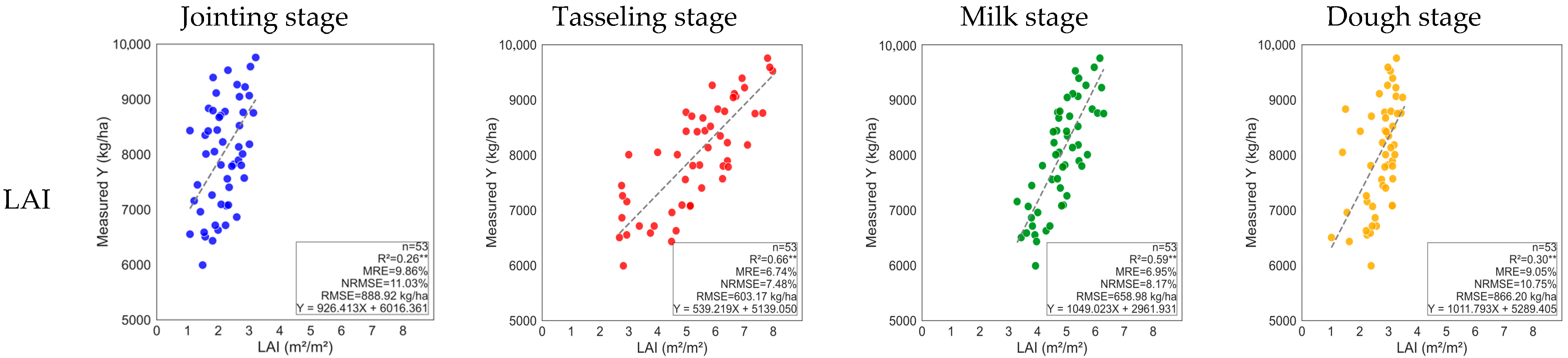
4.2.1. Correlation Analysis Between Crop Condition Parameters in Key Phenological Periods and Crop Yield
4.2.2. Determination of Weights for Crop Condition Parameters in Key Phenological Periods
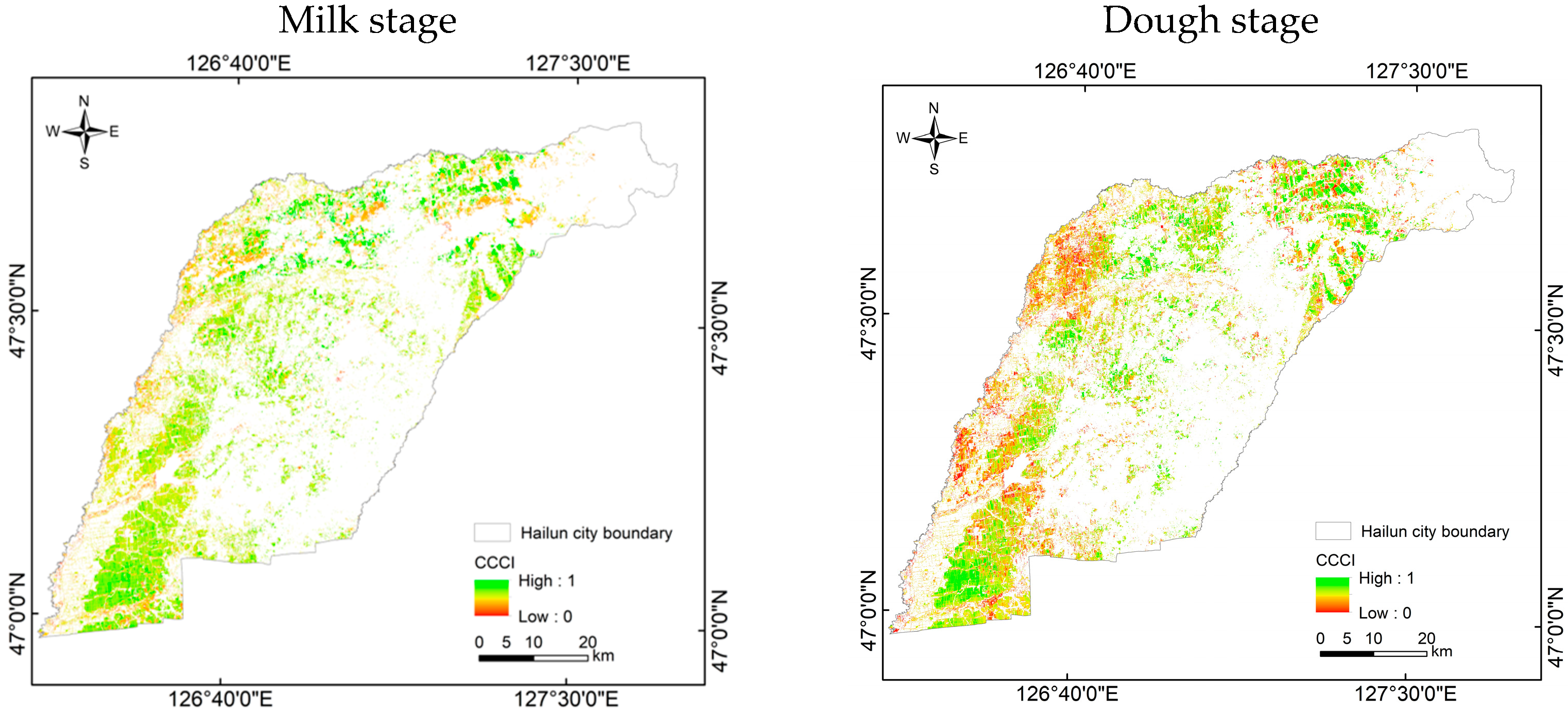
4.2.3. Construction of the CCCI for Key Phenological Periods
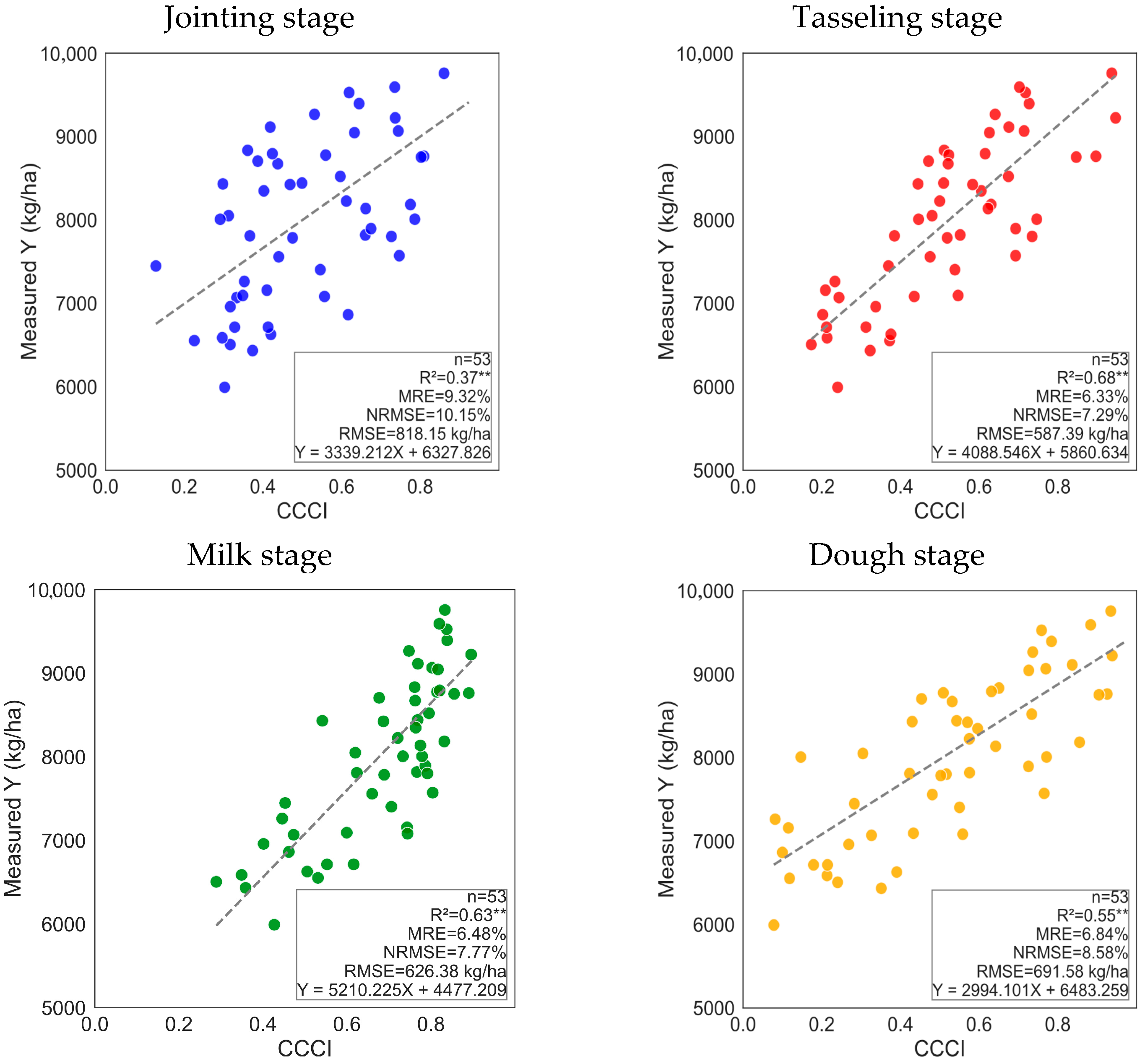
4.2.4. Accuracy Verification of the CCCI for Key Phenological Stages
4.3. Calculations Based on the CSDICGC
4.3.1. Calculation of the Time Weight for the CCCI During Key Phenological Periods
4.3.2. Calculation of Spatial Weights for the CCCI During Key Phenological Periods
4.3.3. Calculation of Spatiotemporal Dynamic Weight Coefficients for the CCCI During Key Phenological Periods
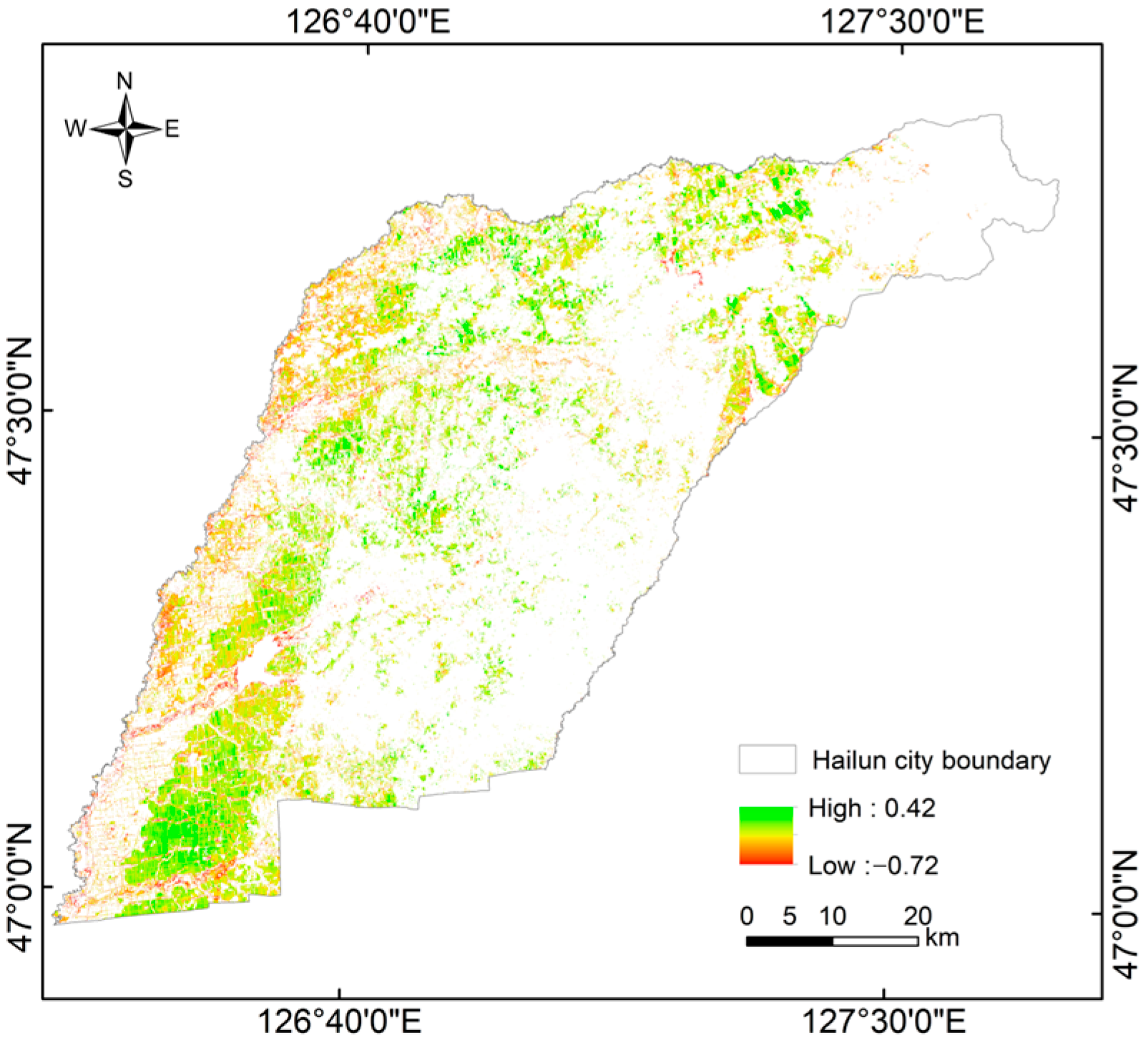
4.3.4. Calculation of the CSDICGC
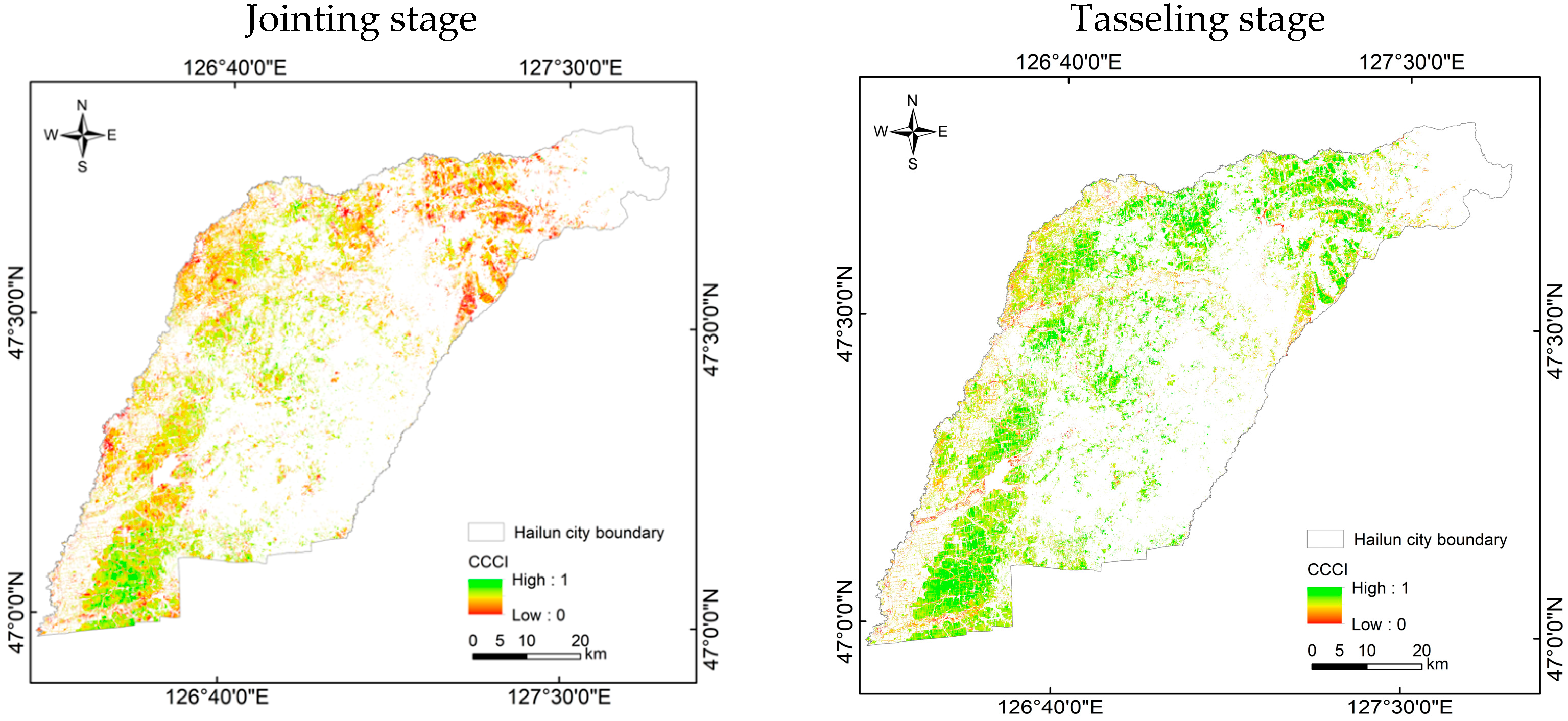
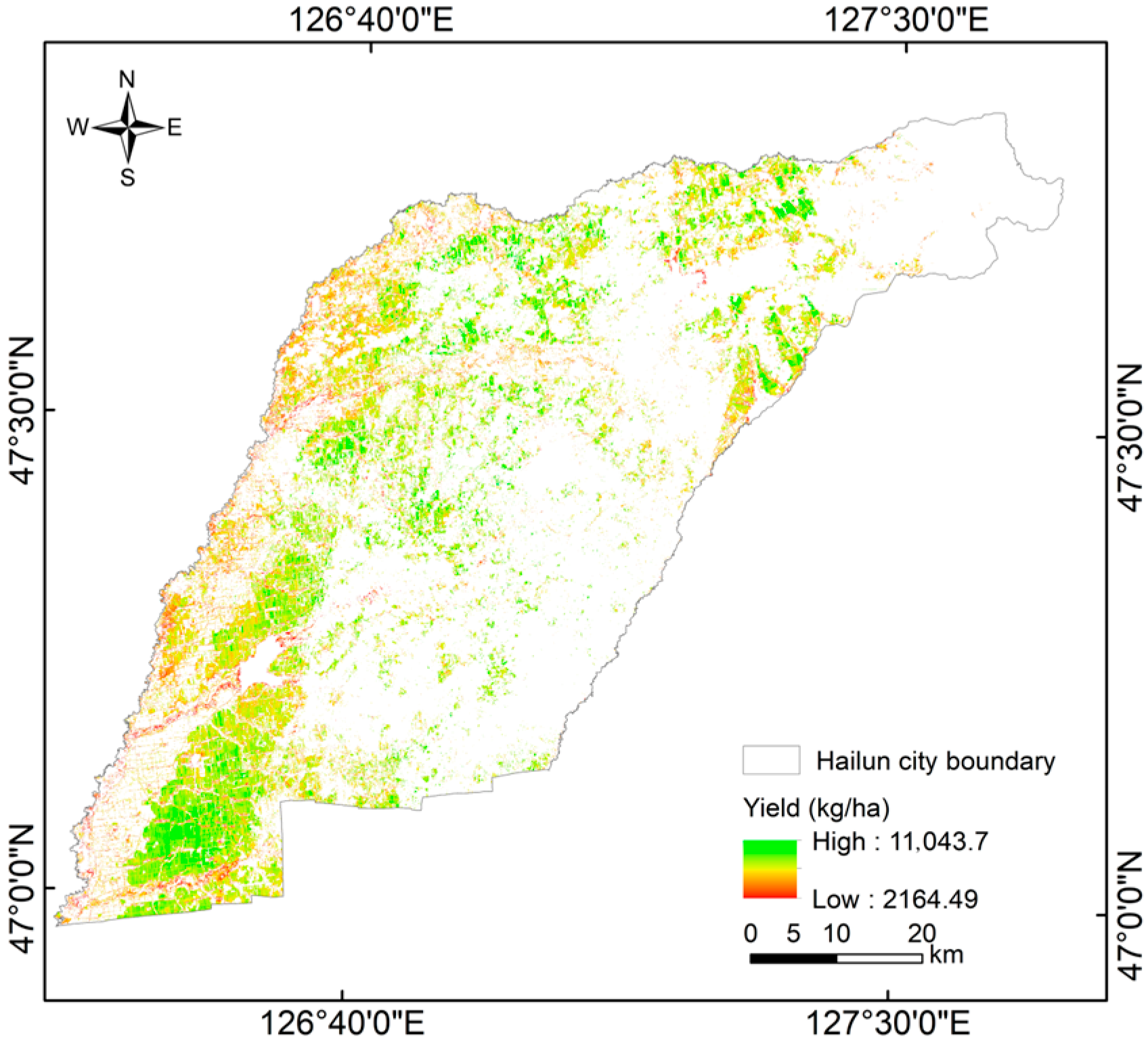
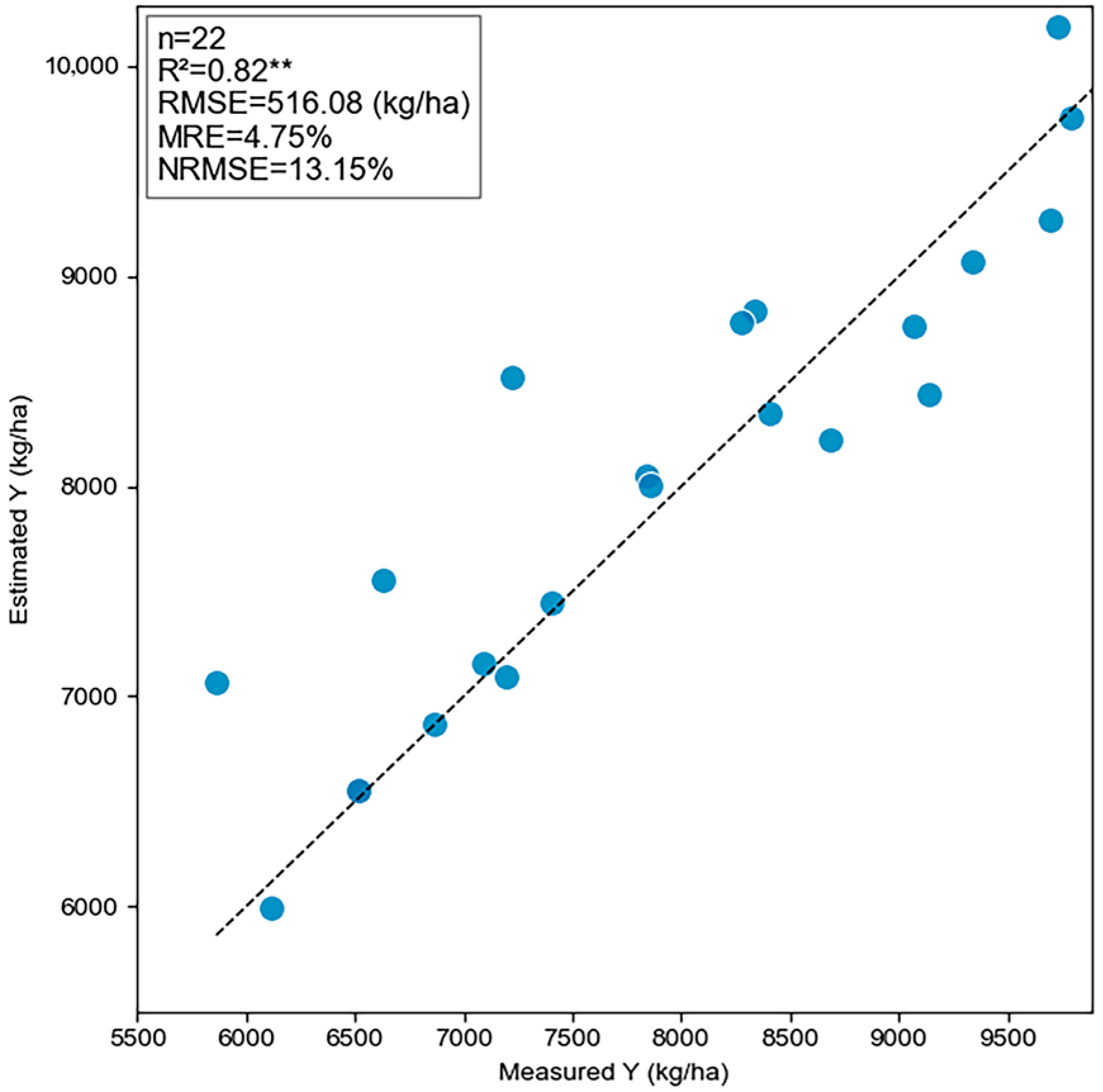
4.4. Downscaling and Accuracy Analysis of Regional Maize Yield Statistical Data
5. Discussion
5.1. Limitations and Improvements of This Study
5.2. Innovations of This Study
- (1)
- A method for constructing the CCCI for key phenological periods based on the normalized regression coefficient weight determination method was outlined.
- (2)
- A method for expressing the spatial heterogeneity of crop growth status using temporally and spatially dynamic weights of the CCCI was proposed.
- (3)
- A downscaling method for crop yield statistical data based on the CSDICGC was proposed.
5.3. Application Prospects of This Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Soltani, A.; Galeshi, S.; Attarbashi, M.R.; Taheri, A.H. Comparison of two methods for estimating parameters of harvest index increase during seed growth. Field Crop. Res. 2004, 89, 369–378. [Google Scholar] [CrossRef]
- Deng, X.; Gibson, J.; Wang, P. Management of trade-offs between cultivated land conversions and land productivity in Shandong Province. J. Clean. Prod. 2017, 142, 767–774. [Google Scholar] [CrossRef]
- Khan, M.R.; de Bie, C.A.J.M.; van Keulen, H.; Smaling, E.M.A.; Real, R. Disaggregating and mapping crop statistics using hypertemporal remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 36–46. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Q.; Liu, Y.; Li, J.; Ren, W. Index System and Transferring Methods to Build the National Society and Economy Grid Database. J. Geo-Inf. Sci. 2011, 13, 573–578. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Spatial distribution of China grain output based on land use and population density. Trans. Chin. Soc. Agric. Eng. 2012, 28, 1–8. (In Chinese) [Google Scholar] [CrossRef]
- Fan, Y.; Shi, P.; Gu, Z.; Li, X.A. Method of Data Gridding from Administration Cell to Gridding Cell. Sci. Geogr. Sin. 2004, 24, 105–108. [Google Scholar] [CrossRef]
- Liu, X.H.; Kyriakidis, P.C.; Goodchild, M.F. Population-density estimation using regression and area-to-point residual kriging. Int. J. Geogr. Inf. Sci. 2008, 22, 431–447. [Google Scholar] [CrossRef]
- Yue, W.; Gao, J.; Yang, X. Estimation of Gross Domestic Product Using Multi-Sensor Remote Sensing Data: A Case Study in Zhejiang Province, East China. Remote Sens. 2014, 6, 7260–7275. [Google Scholar] [CrossRef]
- You, L.; Wood, S. Assessing the spatial distribution of crop areas using a cross-entropy method. Int. J. Appl. Earth Obs. Geoinf. 2005, 7, 310–323. [Google Scholar] [CrossRef]
- Monfreda, C.; Rarnankutty, N.; Foley, J.A. Farming the planet: Geographic distribution of crop areas, yields, physiological types and netprimary production in the year 2000. Glob. Biogeochem. Cycles 2008, 22, GB1022. [Google Scholar] [CrossRef]
- Potter, P.; Ramankutty, N.; Bennett, E.M.; Donner, S.D. Characterizing the Spatial Patterns of Global Fertilizer Application and Manure Production. Earth Interact. 2010, 14, 1–22. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Zhu, X.; Shi, P.; Pan, Y. Development of a gridded dataset of annual irrigation water withdrawal in China. In Proceedings of the 2012 First International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Shanghai, China, 2–4 August 2012; IEEE: New York, NY, USA, 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Van Ittersum, M.K.; Cassman, K.G.; Grassini, P.; Wolf, J.; Tittonell, P.; Hochman, Z. Yield gap analysis with local to global relevance—A review. Field Crop. Res. 2013, 143, 4–17. [Google Scholar] [CrossRef]
- Woittiez, L.S.; van Wijk, M.T.; Slingerland, M.; van Noordwijk, M.; Giller, K.E. Yield gaps in oil palm: A quantitative review of contributing factors. Eur. J. Agron. 2017, 83, 57–77. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Shen, Y.; Stricevic, R.; Pei, H.; Sun, H.; Amiri, E.; Penas, A.; del Rio, S. Evaluation of the FAO AquaCrop Model for Winter Wheat on the North China Plain under Deficit Irrigation from Field Experiment to Regional Yield Simulation. Agric. Water Manag. 2014, 135, 61–72. [Google Scholar] [CrossRef]
- Shi, S.; Chen, Y.; Li, Z. Spatial simulation of per unit area yield of maize by statistics based on regionalization and multiple regression analysis. J. Anhui Agric. Sci. 2011, 39, 3193–3195. (In Chinese) [Google Scholar]
- You, L.; Wood, S.; Wood-Sichra, U.; Wu, W. Generating global crop distribution maps: From census to grid. Agric. Syst. 2014, 127, 53–60. [Google Scholar] [CrossRef]
- You, L.; Wood, S. An Entropy Approach to Spatial Disaggregation of Agricultural Production. Agric. Syst. 2006, 90, 329–347. [Google Scholar] [CrossRef]
- Xiao, G.; Zhu, X.; Hou, C.; Liu, Y.; Xu, K. A Spatialization Method for Grain Yield Statistical Data: A Study on Winter Wheat of Shandong Province, China. Agron. J. 2019, 111, 1892–1903. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Xu, E. Spatialization of Actual Grain Crop Yield Coupled with Cultivation Systems and Multiple Factors: From Survey Data to Grid. Agronomy 2020, 10, 675. [Google Scholar] [CrossRef]
- Zhao, X.; Jin, T.; Dong, W.; Liu, M.; Liu, Q.; Liu, E. Spatialization of Spring Maize Yield Area in Northeast China Based on Multiple Linear Regression. Chin. J. Agrometeorol. 2023, 44, 1022–1031. (In Chinese) [Google Scholar] [CrossRef]
- Pei, J.i.e.; Zou, Y.; Liu, Y.; He, Y.; Tan, S.; Wang, T.; Huang, J. Downscaling Administrative-Level Crop Yield Statistics to 1 km Grids Using Multisource Remote Sensing Data and Ensemble Machine Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 14437–14453. [Google Scholar] [CrossRef]
- Ji, G.; Liao, S.; Yue, Y.; Hou, P.; Yang, X. Spatial distribution of grain yield based on different sample scales and partitioning schemes and its error correction. Trans. Chin. Soc. Agric. Eng. 2015, 31, 272–278. (In Chinese) [Google Scholar]
- Spaeth, S.C.; Randall, H.C.; Sinclair, T.R.; Vendeland, J.S. Stability of soybean harvest index. Agron. J. 1984, 76, 482–486. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Hatfield, J.L.; Jackson, T.J.; Akhmedov, B.; Prueger, J.; Stern, A. Crop condition and yield simulations using Landsat and MODIS. Remote Sens. Environ. 2004, 92, 548–559. [Google Scholar] [CrossRef]
- Dempewolf, J.; Adusei, B.; Becker-Rehef, I.; Hansen, M.; Potapov, P.; Khan, A.; Barker, B. Wheat Yield Forecasting for Punjab Province from Vegetation Index Time Series and Historic Crop Statistics. Remote Sens. 2014, 6, 9653–9675. [Google Scholar] [CrossRef]
- Mkhabela, M.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. For. Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using Terra and Aqua MODIS reflectance data. Remote Sens. Environ. 2007, 106, 39–58. [Google Scholar]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Clerici, N.; Valbuena Calderón, C.A.; Posada, J.M. Fusion of Sentinel-1A and Sentinel-2A data for land cover mapping: A case study in the lower Magdalena region, Colombia. J. Maps 2017, 13, 718–726. [Google Scholar] [CrossRef]
- Hemmerling, J.; Pflugmacher, D.; Hostert, P. Mapping Temperate Forest Tree Species Using Dense Sentinel-2 Time Series. Remote Sens. Environ. 2021, 267, 112743. [Google Scholar] [CrossRef]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations—Application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Kganyago, M.; Mhangara, P.; Alexandridis, T.; Laneve, G.; Ovakoglou, G.; Mashiyi, N. Validation of sentinel-2 leaf area index lai product derived from snap toolbox and its comparison with global lai products in an African semiarid agricultural landscape. Remote Sens. Lett. 2020, 11, 883–892. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.M.; Zhang, X.; Yan, Y.; Zhu, J.; Zheng, H.; Zhou, K.; Yao, X.; Tian, Y.; Zhu, Y.; et al. Improved Estimation of Leaf Chlorophyll Content of Row Crops from Canopy Reflectance Spectra through Minimizing Canopy Structural Effects and Optimizing Off-Noon Observation Time. Remote Sens. Environ. 2020, 248, 111985. [Google Scholar] [CrossRef]
- Wang, B.; Jia, K.; Liang, S.; Xie, X.; Wei, X.; Zhao, X.; Yao, Y.; Zhang, X. Assessment of Sentinel-2 MSI spectral band reflectance for estimating fractional vegetation cover. Remote Sens. 2018, 10, 1927. [Google Scholar] [CrossRef]
- He, L.; Wang, R.; Mostovoy, G.; Liu, J.; Chen, J.; Shang, J.; Liu, J.; McNairn, H.; Powers, J. Crop Biomass Mapping Based on Ecosystem Modeling at Regional Scale Using High Resolution Sentinel-2 Data. Remote Sens. 2021, 13, 806. [Google Scholar] [CrossRef]
- Peng, D.; Huang, J.; Li, C.; Liu, L.; Huang, W.; Wang, F.; Yang, X. Modelling paddy rice yield using MODIS data. Agric. For. Meteorol. 2014, 184, 107–116. [Google Scholar] [CrossRef]
- Pearse, G.D.; Watt, M.S.; Morgenroth, J. Comparison of optical LAI measurements under diffuse and clear skies after correcting for scattered radiation. Agric. For. Meteorol. 2016, 221, 61–70. [Google Scholar] [CrossRef]
- Sun, Y.; He, Q.; Zhou, G.; Song, Y. Response of grain quality to plant growth dynamics in summer maize as influenced by sowing dates and weather factors. Ind. Crops Prod. 2025, 231, 121210. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, W.; Rezaei, E.E.; Li, J.; Sun, Z.; Zhang, J. The Optimal Phenological Phase of Maize for Yield Prediction with High-Frequency UAV Remote Sensing. Remote Sens. 2022, 14, 1559. [Google Scholar] [CrossRef]
- Ren, Y.; Li, Q.; Du, X.; Zhang, Y.; Wang, H.; Shi, G.; Wei, M. Analysis of Corn Yield Prediction Potential at Various Growth Phases Using a Process-Based Model and Deep Learning. Plants 2023, 12, 446. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Liu, Q.Z.; Zhang, S.Y.; Chen, X.G.; Ji, Y.D.; Liu, F.G.; Pulatov, A.; Feng, P.Y. Response of Wheat and Maize Growth-Yields to Meteorological and Agricultural Droughts Based on Standardized Precipitation Evapotranspiration Indexes and Soil Moisture Deficit Indexes. Agric. Water Manag. 2022, 266, 107566. [Google Scholar] [CrossRef]
- Rinaldi, M.; Losavio, N.; Flagella, Z. Evaluation and application of the OILCROP–sun model for sunflower in southern Italy. Agric. Syst. 2003, 78, 17–30. [Google Scholar] [CrossRef]
- He, J.; Zhao, Y.; He, P.; Yu, M.; Zhu, Y.; Cao, W.; Zhang, X.; Tian, Y. Rice Yield Prediction Based on Simulation Zone Partitioning and Dual-Variable Hierarchical Assimilation. Remote Sens. 2025, 17, 386. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, L.; Zhou, X.; Zhu, Y.; Cao, W.; Qiu, X.; Cheng, T.; Tian, Y. Integrating remote sensing information with crop model to monitor wheat growth and yield based on simulation zone partitioning. Precis. Agric. 2017, 19, 55–78. [Google Scholar] [CrossRef]
- Jiang, H.; Wei, X.; Chen, Z.; Zhu, M.; Yao, Y.; Zhang, X.; Jia, K. Influence of different soil reflectance schemes on the retrieval of vegetation LAI and FVC from PROSAIL in agriculture region. Comput. Electron. Agric. 2023, 212, 108165. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Kang, Y.; Özdoğan, M. Corn yield prediction and uncertainty analysis based on remotely sensed variables using a Bayesian neural network approach. Remote Sens. Environ. 2021, 259, 112408. [Google Scholar] [CrossRef]
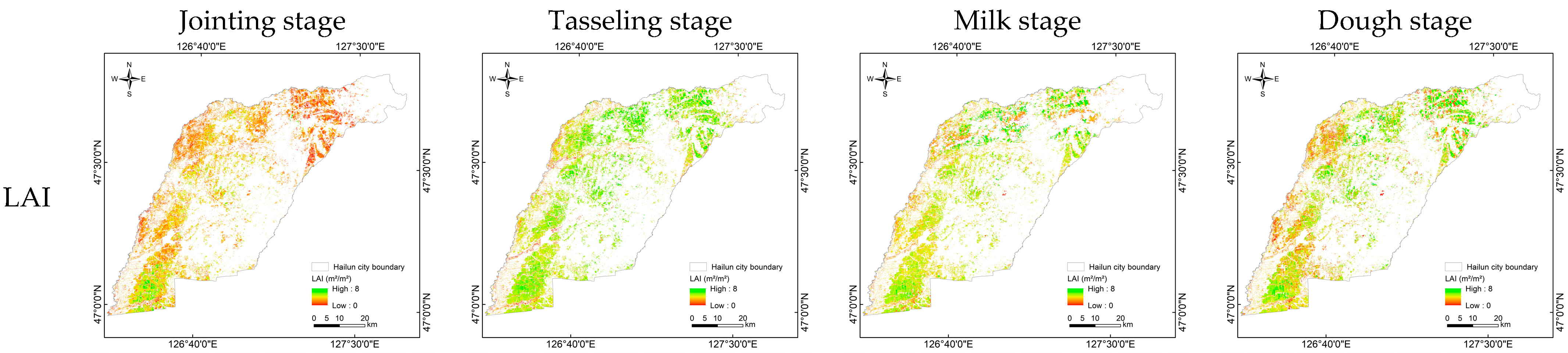


| Number | Stage | Phenological Stage Description |
|---|---|---|
| 1 | 20 May–8 June | Sowing stage–Emergence stage |
| 2 | 9 June–29 June | Emergence stage–Three-leaf stage |
| 3 | 30 June–19 July | Three-leaf stage–Seven-leaf stage (Jointing stage) |
| 4 | 20 July–1 August | Seven-leaf stage (Jointing stage)–Tasseling stage |
| 5 | 1 August–5 September | Tasseling stage–Grain filling (Milk stage) |
| 6 | 5 September–30 September | Grain filling (Milk stage)–Physiological maturity stage |
| Number | Image Date | Crop Condition Parameter Names |
|---|---|---|
| 1 | 20230702 | LAI, CCC, CWC, FVC |
| 2 | 20230806 | LAI, CCC, CWC, FVC |
| 3 | 20230828 | LAI, CCC, CWC, FVC |
| 4 | 20230912 | LAI, CCC, CWC, FVC |
| Number | Date of Ground Survey | Main Ground Observation Parameters | Phenological Period Description |
|---|---|---|---|
| 1 | 20230702 | LAI, CCC, CWC, FVC, AGB | Jointing stage |
| 2 | 20230806 | LAI, CCC, CWC, FVC, AGB | Tasseling stage |
| 3 | 20230828 | LAI, CCC, CWC, FVC, AGB | Milk stage |
| 4 | 20230912 | LAI, CCC, CWC, FVC, AGB | Dough stage |
| 5 | 20231002 | ground-truth maize yield | Physiological maturity |
| Phenological Period Description | LAI | CWC | FVC | CCC | NPP |
|---|---|---|---|---|---|
| Jointing stage | 0.1976 | 0.1412 | 0.2317 | 0.1681 | 0.2614 |
| Tasseling stage | 0.2183 | 0.1757 | 0.1842 | 0.2110 | 0.2108 |
| Milk stage | 0.2045 | 0.1894 | 0.2079 | 0.1856 | 0.2126 |
| Dough stage | 0.2175 | 0.1723 | 0.1741 | 0.1479 | 0.2882 |
| Weighting Index | Jointing Stage | Tasseling Stage | Milk Stage | Dough Stage |
|---|---|---|---|---|
| Regression coefficient between CCCI and yield | 3339.212 | 4088.546 | 5210.225 | 2994.101 |
| Temporal weight | 0.21 | 0.26 | 0.34 | 0.19 |
| Weighting Index | Jointing Stage | Tasseling Stage | Milk Stage | Dough Stage |
|---|---|---|---|---|
| Coefficient of variation | 0.0257 | 0.0770 | 0.0440 | 0.0367 |
| Spatial weight | 0.14 | 0.42 | 0.24 | 0.20 |
| Weighting Index | Jointing Stage | Tasseling Stage | Milk Stage | Dough Stage |
|---|---|---|---|---|
| Spatiotemporal dynamic weight | 0.17 | 0.34 | 0.30 | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, K.; Ren, J.; Bu, X.; Zhao, H. Downscaling Method for Crop Yield Statistical Data Based on the Standardized Deviation from the Mean of the Comprehensive Crop Condition Index. Remote Sens. 2025, 17, 3408. https://doi.org/10.3390/rs17203408
Luo K, Ren J, Bu X, Zhao H. Downscaling Method for Crop Yield Statistical Data Based on the Standardized Deviation from the Mean of the Comprehensive Crop Condition Index. Remote Sensing. 2025; 17(20):3408. https://doi.org/10.3390/rs17203408
Chicago/Turabian StyleLuo, Ke, Jianqiang Ren, Xiangxin Bu, and Hongwei Zhao. 2025. "Downscaling Method for Crop Yield Statistical Data Based on the Standardized Deviation from the Mean of the Comprehensive Crop Condition Index" Remote Sensing 17, no. 20: 3408. https://doi.org/10.3390/rs17203408
APA StyleLuo, K., Ren, J., Bu, X., & Zhao, H. (2025). Downscaling Method for Crop Yield Statistical Data Based on the Standardized Deviation from the Mean of the Comprehensive Crop Condition Index. Remote Sensing, 17(20), 3408. https://doi.org/10.3390/rs17203408





