Modulation of Typical Three-Dimensional Targets on the Echo Waveform Using Analytical Formula
Abstract
Highlights
- Derive the formula of waveform modulated by three typical three-dimensional targets without constraint of position and attitude.
- Reveal the modulation of shape, size, position, and attitude of three-dimensional targets on waveform through qualitative and mathematical analysis.
- The derived analytical expression for the three-dimensional target laser pulse echo waveform simplifies the simulation process and facilitates the inversion of target’s features, such as size and attitude.
- The investigated typical three-dimensional targets exhibit close resemblance to satellite main bodies, European architectural roofs, and canopies. Investigation into their modulation mechanisms on laser echo waveforms thereby promotes the application of full-waveform LiDAR across multiple remote sensing domains, including mapping, building identification, deep-space exploration, and space debris removal.
Abstract
1. Introduction
- (I)
- Derive the formula of waveform modulated by three typical 3D targets, namely, a rectangular prism, a regular hexagonal prism, and a cone, without constraint of position and attitude. Such formula has not been reported before.
- (II)
- Reveal the modulation of shape, size, position, and attitude of 3D targets on waveform; the effect of target size has not been investigated before.
- (III)
- Build the experimental platform to measure the echo waveform modulated by 3D target and examine the validity of derived formula of the echo waveform.
- (IV)
- 3D shapes chosen in this paper are typical structural model of targets such as main body of satellite, roof of European building, canopy, and space debris.
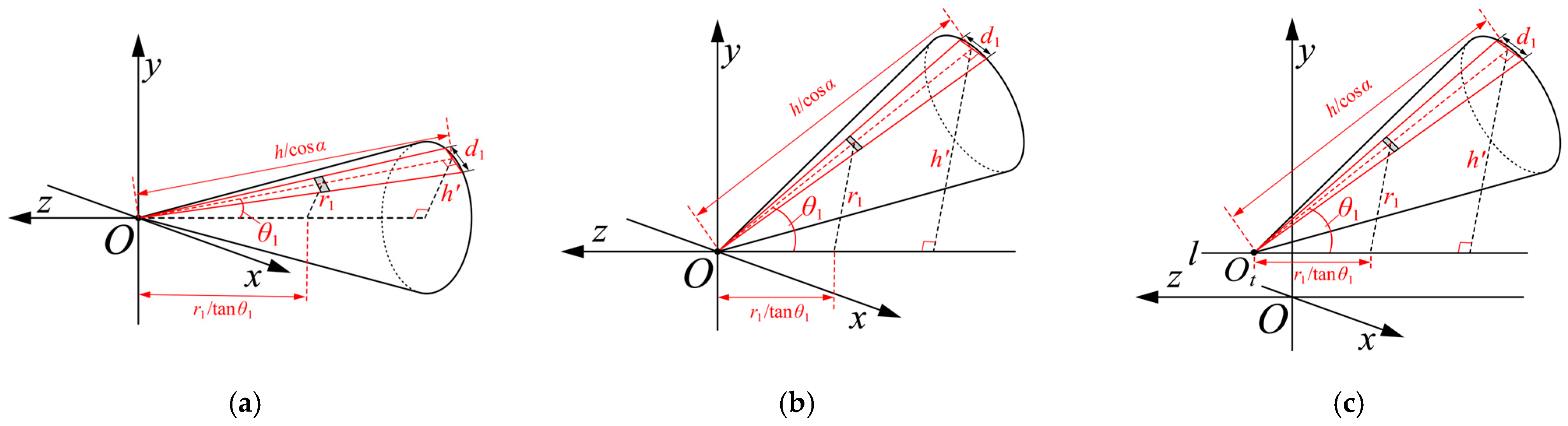
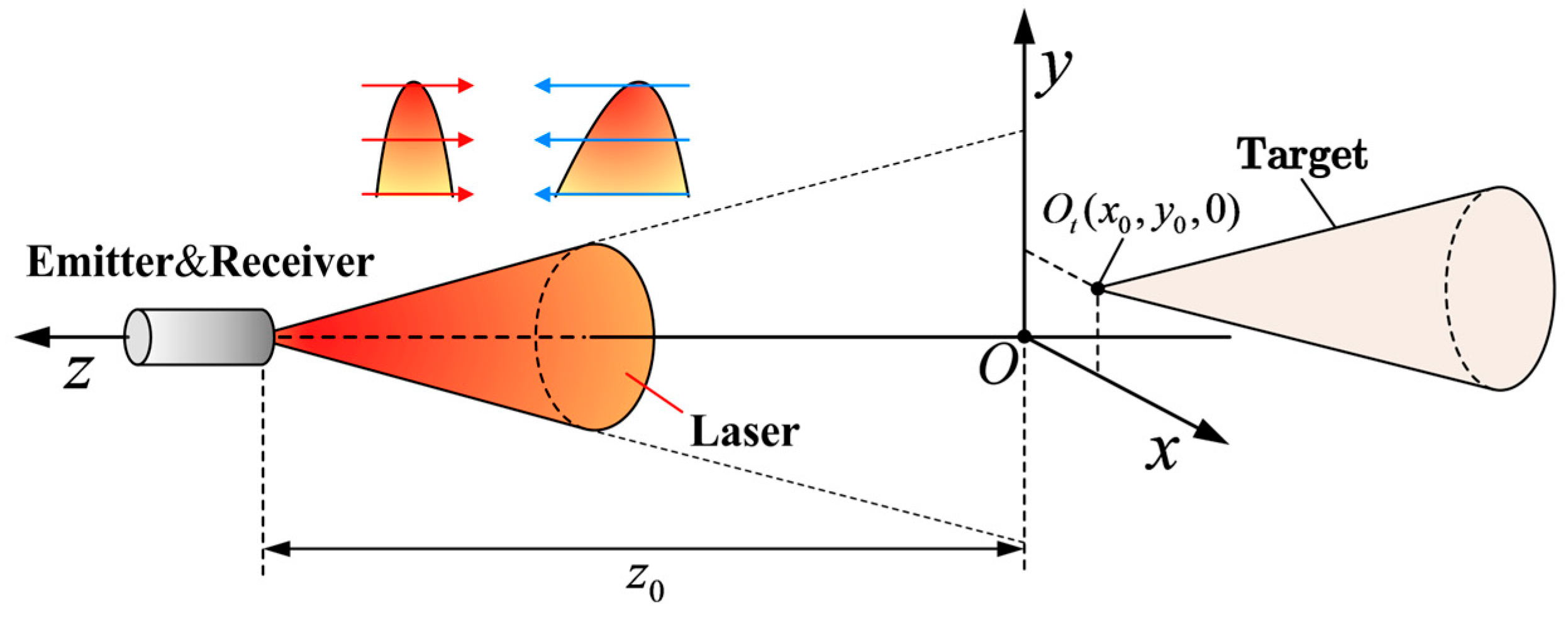
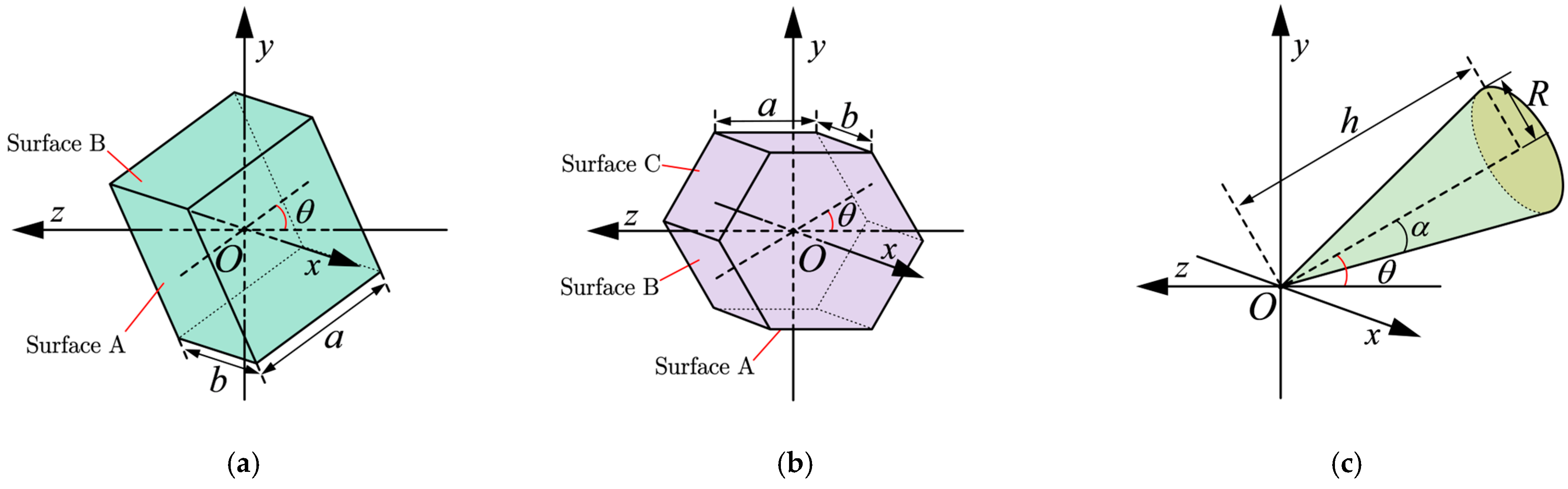
2. Formula Derivation
- Rectangular prism:
- Regular Hexagonal Prism:
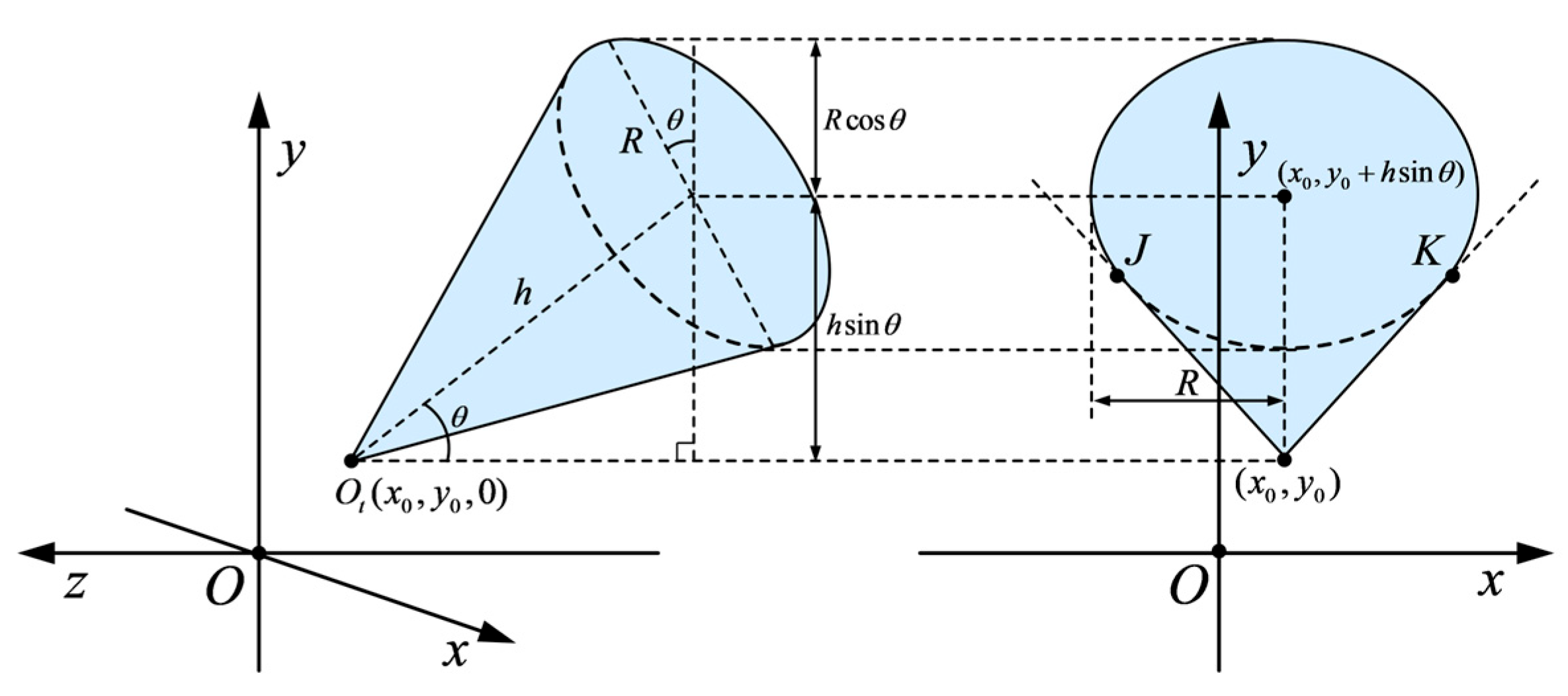
- Cone:
3. Simulation Process and Experimental Validation
3.1. Simulation Modeling
3.2. Experimental Validation and Comparison
4. Results and Analysis
4.1. Non-Rotated
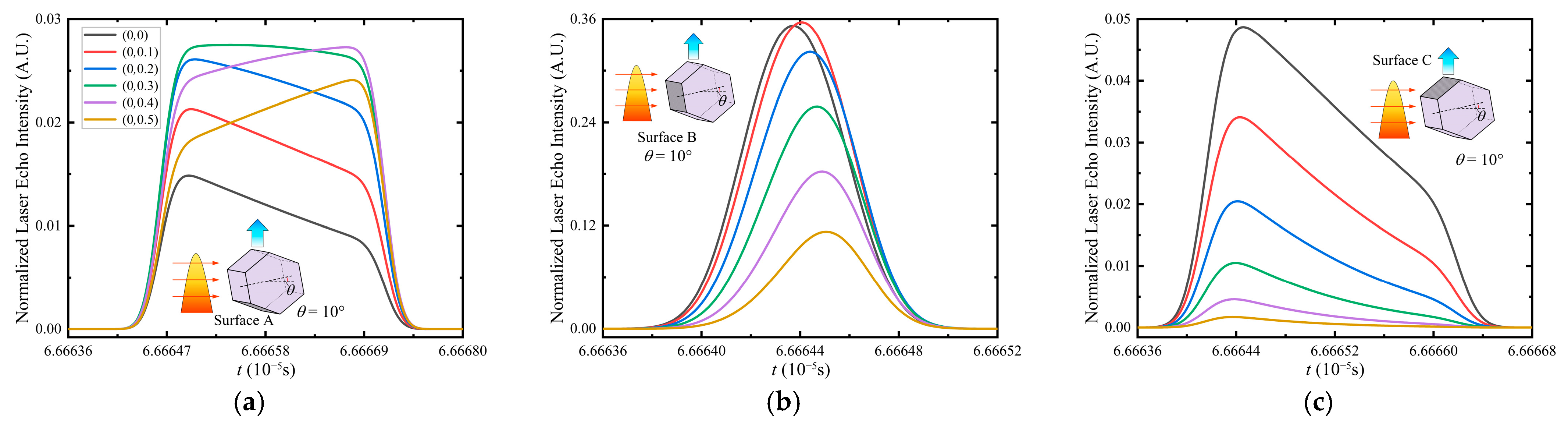
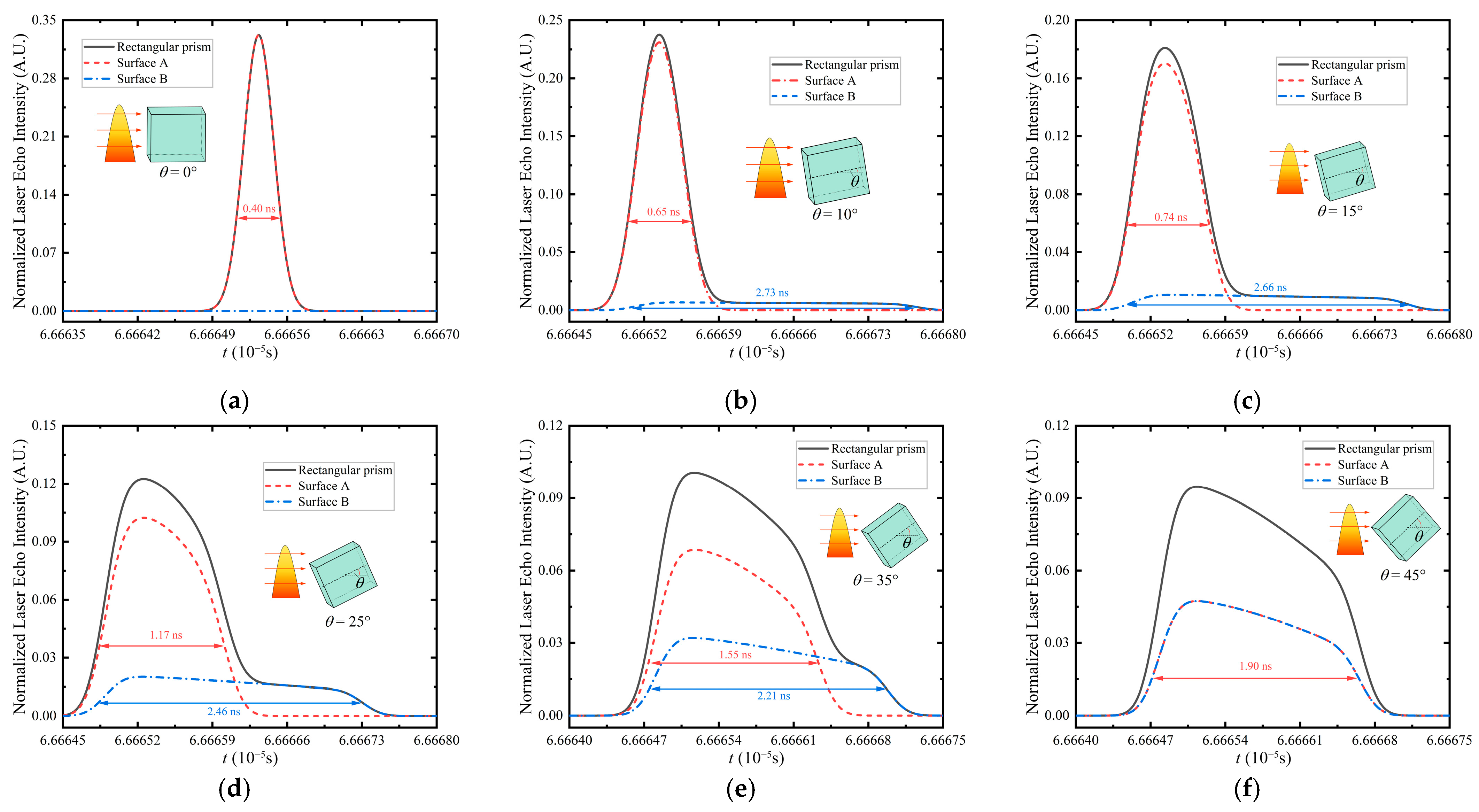
4.1.1. Prisms
- Rectangular Prisms
- Regular hexagonal prism.
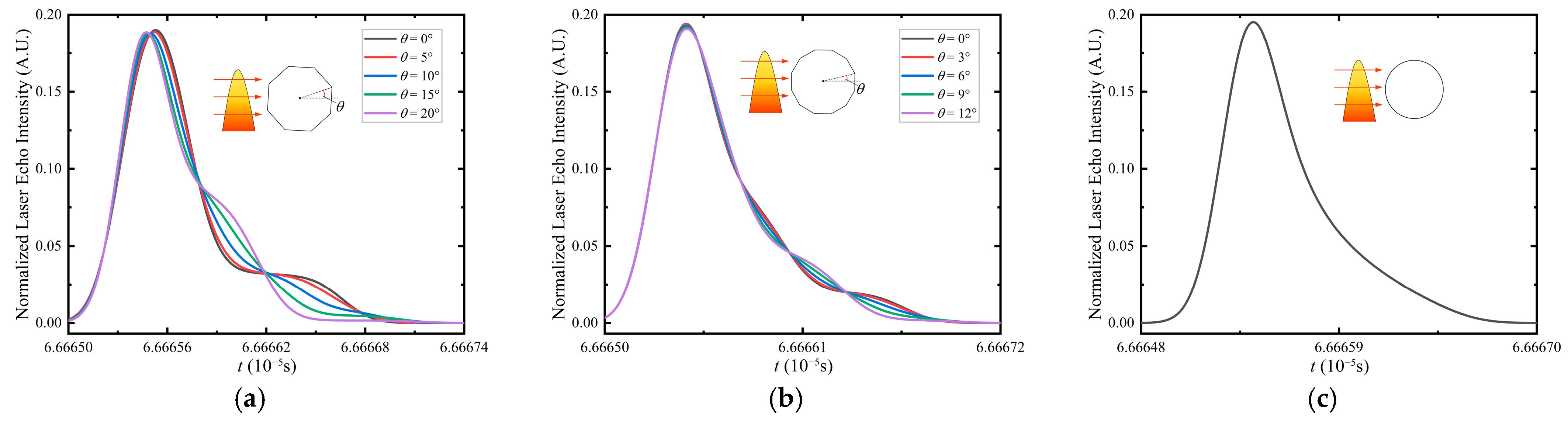
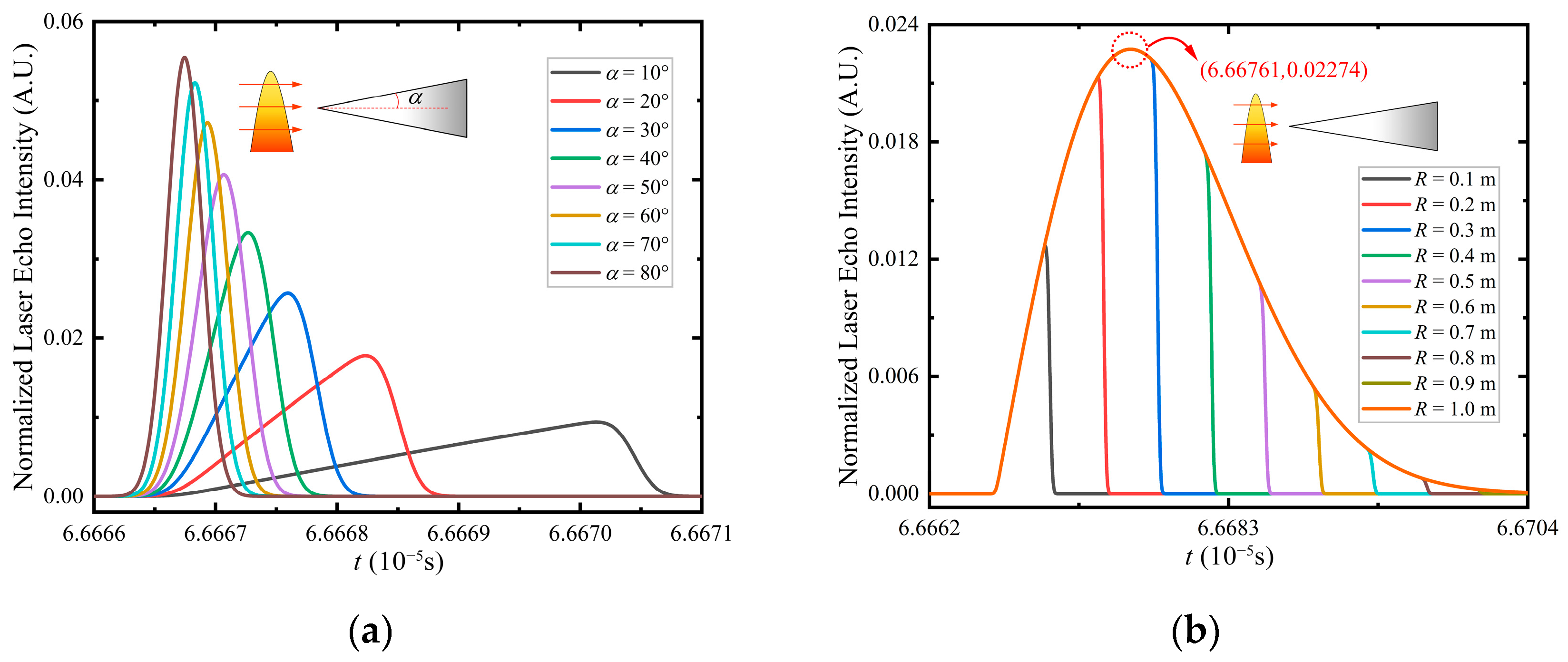
4.1.2. Cone
- Influence of bottom radius on echo waveform.
4.2. Rotated
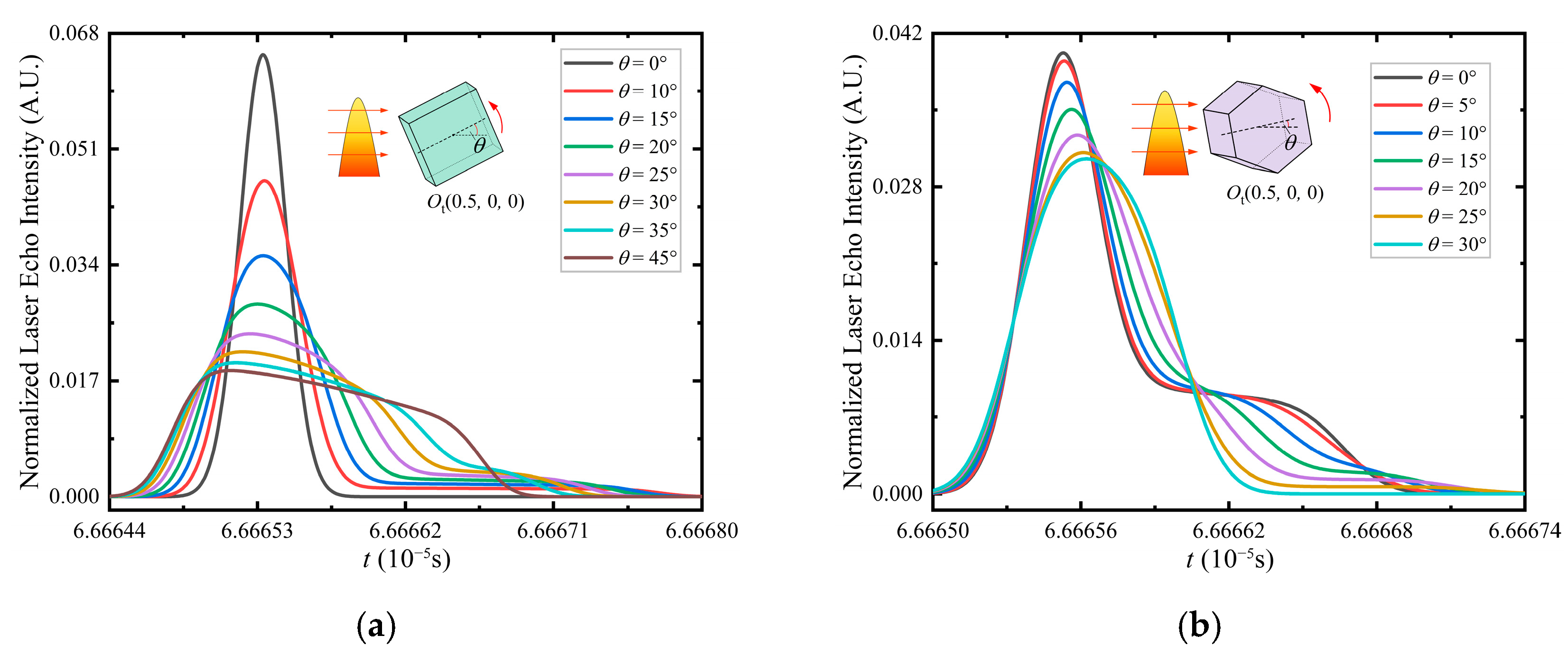
4.2.1. Prisms
- Rectangular prism.
- Regular hexagonal prism.
4.2.2. Cone
- Influence of rotation angle on the variation in modulated echo waveform.
- Influence of target size under rotated condition.
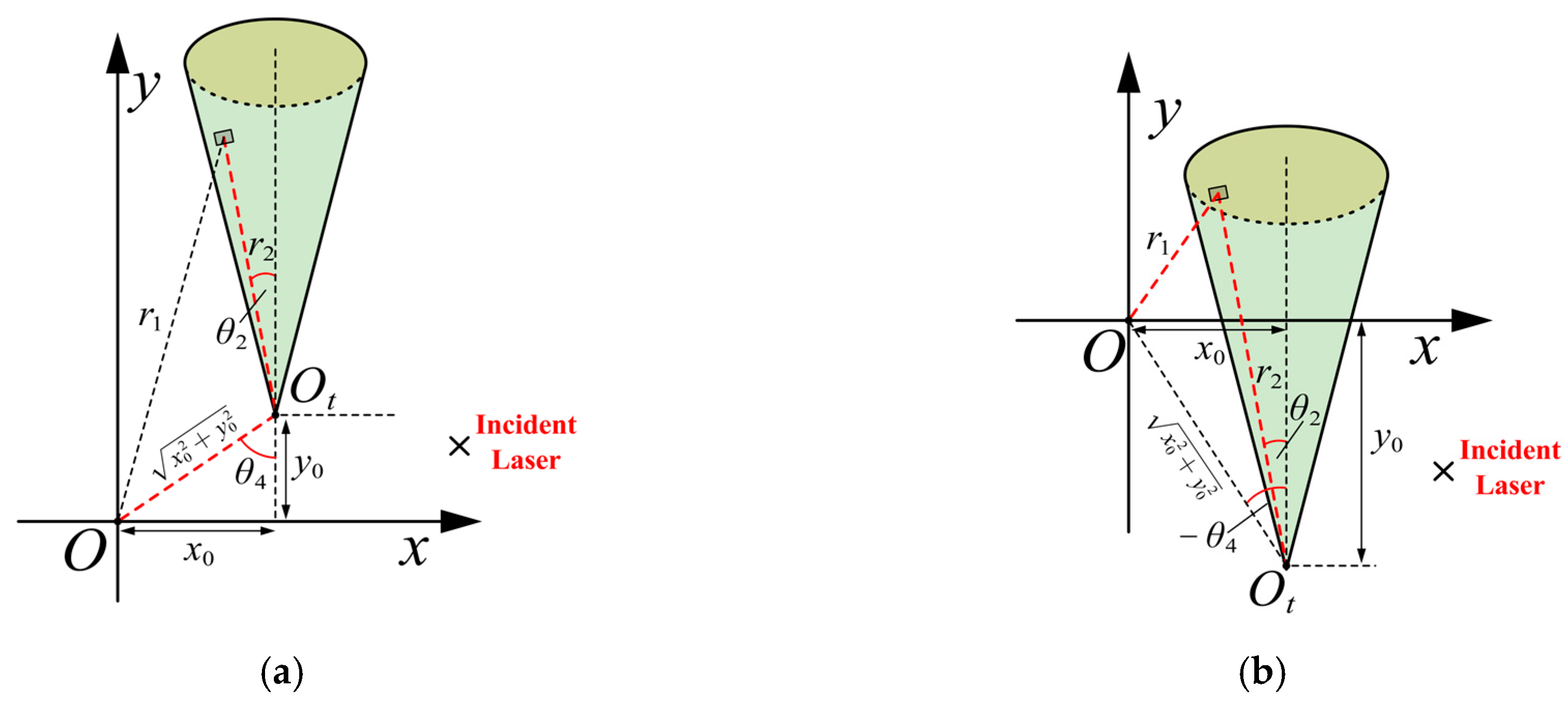
4.3. Position
4.3.1. Prisms
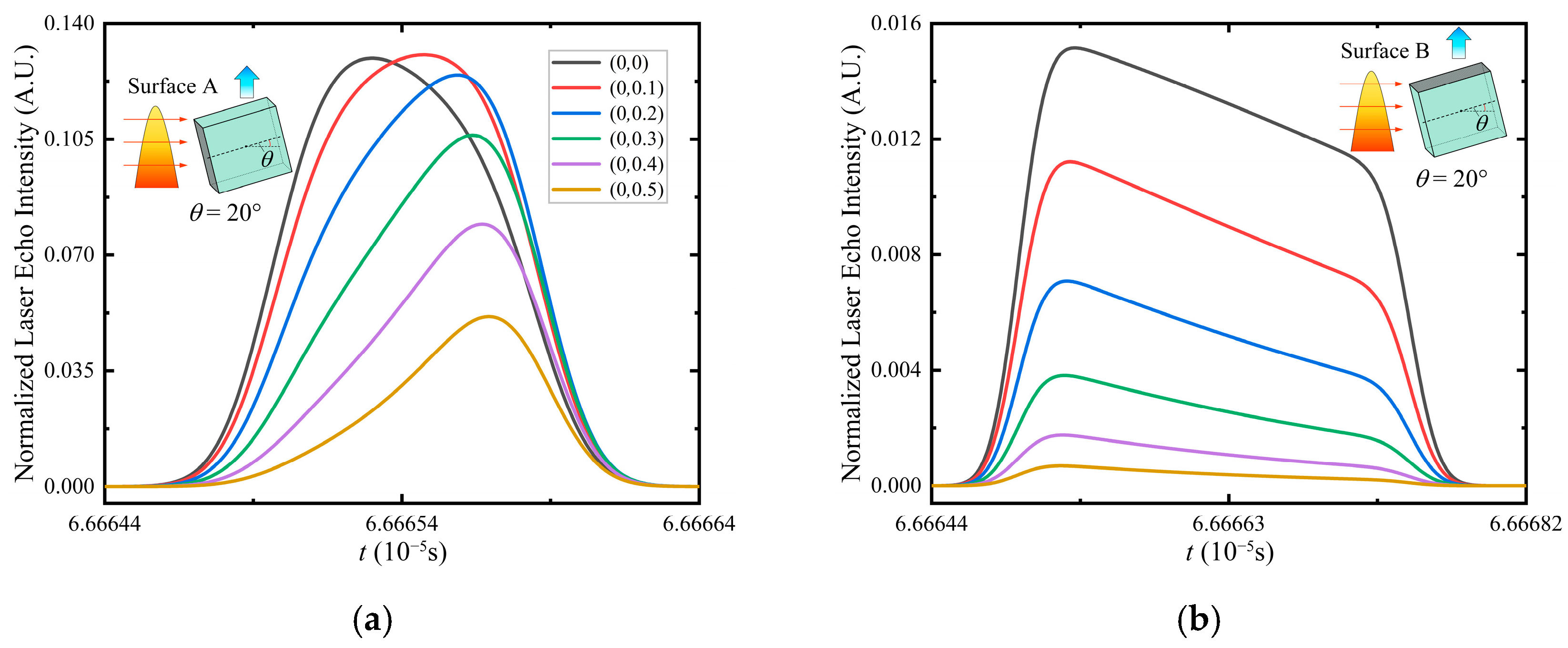
- Dependence of echo waveform on target’s-coordinate.
- Dependence of echo waveform on target’s-coordinate.
4.3.2. Cone
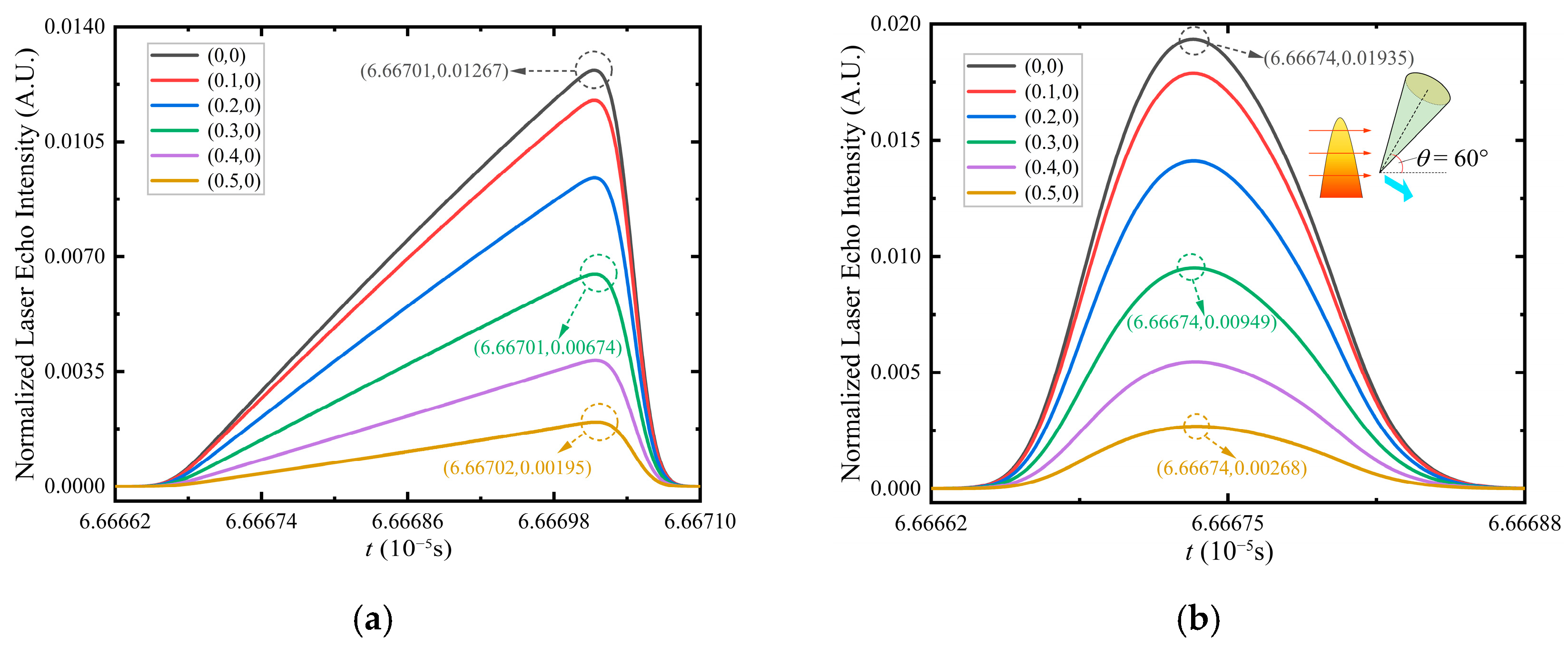
- Dependence of echo waveform on target’s -coordinate.
- Dependence of echo waveform on target’s -coordinate.
5. Discussion
5.1. Target Discrimination
5.2. Inversion of Target Characteristic Parameters
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Blair, J.B.; Hofton, M.A. Modeling laser altimeter return waveforms over complex vegetation using high-resolution elevation data. Geophys. Res. Lett. 1999, 26, 2509–2512. [Google Scholar] [CrossRef]
- Guo, Y.L.; Hu, Y.H.; Fang, J.J.; Xu, S.L.; Zhang, X.Y. Research status and development trend of LiDAR super resolution imaging technology. J. Radars 2025, 3, 2095–2283X. [Google Scholar]
- Zhang, X.Y.; Shan, L.Q.; Fang, J.J.; Guo, R.; Xu, S.L.; Wang, Y.C.; Guo, Y.L.; Yang, X.; Han, F.; Hu, Y.H. Super-resolution Imaging Using Reflective Tomography LiDAR over 10 km. Adv. Imaging 2025, 2, 051002. [Google Scholar] [CrossRef]
- Li, Y.H.; Wu, Z.S. Target recognition using subnanosecond pulse laser range profiles. Opt. Express 2010, 18, 16788–16796. [Google Scholar] [CrossRef] [PubMed]
- Hao, Q.; Cheng, Y.; Cao, J.; Zhang, F.H.; Zhang, X.M.; Yu, H.Y. Analytical and numerical approaches to study echo laser pulse profile affected by target and atmospheric turbulence. Opt. Express 2016, 24, 25026–25042. [Google Scholar] [CrossRef]
- Steinvall, O. A review of laser range profiling for target recognition. Encycl. Mod. Opt. 2018, 4, 474–495. [Google Scholar]
- Xu, X.B.; Zhang, H.; Luo, M.Z.; Tan, Z.Y.; Zhang, M.; Yang, H.; Li, Z.H. Research on target echo characteristics and ranging accuracy for laser radar. Infrared Phys. Technol. 2019, 96, 330–339. [Google Scholar] [CrossRef]
- Hu, Y.H.; Hou, A.H.; Ma, Q.L.; Zhao, N.X.; Xu, S.L.; Fang, J.J. Analytical formula to investigate the modulation of sloped targets using LiDAR waveform. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5700512. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitizing airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-Waveform Topographic Lidar: State-of-the-Art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Park, S.; Jung, H.; Lee, S.; Kim, E. Mapping Forest Vertical Structure in Sogwang-ri Forest from Full-Waveform Lidar Point Clouds Using Deep Neural Network. Remote Sens. 2021, 13, 3736. [Google Scholar] [CrossRef]
- Zhao, G.P.; Arturo, S.; Kati, L.; Sun, C.L.; Fei, L.K. Hyperspectral and Full-Waveform LiDAR Improve Mapping of Tropical Dry Forest’s Successional Stages. Remote Sens. 2021, 13, 3830. [Google Scholar] [CrossRef]
- Nicolas, D.; Dennis, L.M. Bridging the Gap: Comprehensive Boreal Forest Complexity Mapping through LVIS Full-Waveform LiDAR, Single-Year and Time Series Landsat Imagery. Remote Sens. 2023, 15, 5274. [Google Scholar]
- Canuto, M.A.; Estrada-Belli, F.; Garrison, T.G. Ancient lowland Maya complexity as revealed by airborne laser scanning of northern Guatemala. Science 2018, 361, 6409. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Wang, X.Y.; Guo, H.D. Airborne and spaceborne remote sensing for archaeological and cultural heritage applications: A review of the century (1907–2017). Remote Sens. Environ. 2019, 232, 111280. [Google Scholar] [CrossRef]
- Inomata, T.; Triadan, D.; López, V.A.V. Monumental architecture at aguada Fénix and the rise of Maya civilization. Nature 2020, 582, 7813. [Google Scholar] [CrossRef]
- Bachagha, N.; Wang, X.Y.; Luo, L.; Li, L.; Khatteli, H.; Lasaponara, R. Remote sensing and GIS techniques for reconstructing the military fort system on the Roman boundary (Tunisian section) and identifying archaeological sites. Remote Sens. Environ. 2020, 236, 111418. [Google Scholar] [CrossRef]
- Hovi, A.; Korpela, I. Real and simulated waveform-recording LiDAR data in juvenile boreal forest vegetation. Remote Sens. Environ. 2014, 140, 665–678. [Google Scholar] [CrossRef]
- András, Z.; Anke, S.; Adam, K.; Deák, B.; Werner, M.; Ágnes, V.; Balázs, S.; Norbert, P. Categorizing Grassland Vegetation with Full-Waveform Airborne Laser Scanning: A Feasibility Study for Detecting Natura 2000 Habitat Types. Remote Sens. 2014, 6, 8056–8087. [Google Scholar]
- Dargie, G.C.; Lewis, S.L.; Lawson, I.T.; Mitchard, E.T.A.; Page, S.E.; Bocko, Y.E.; Ifo, S.A. Age, extent and carbon storage of the central Congo Basin peatland complex. Nature 2017, 542, 86–90. [Google Scholar] [CrossRef]
- Pablo, C.; Luis, A.R. A Full-Waveform Airborne Laser Scanning Metric Extraction Tool for Forest Structure Modelling. Do Scan Angle and Radio-metric Correction Matter. Remote Sens. 2020, 12, 292. [Google Scholar]
- Sumnall, M.J.; Hill, R.A.; Hinsley, S.A. Towards Forest Condition Assessment: Evaluating Small-Footprint Full-Waveform Airborne Laser Scanning Data for Deriving Forest Structural and Compositional Metrics. Remote Sens. 2022, 14, 5081. [Google Scholar] [CrossRef]
- Steinvall, O.; Chevalier, T.; Grönwall, C. Simulation and modeling of laser range profiling and imaging of small surface vessels. Opt. Eng. 2014, 53, 013109. [Google Scholar] [CrossRef]
- Steinvall, O.; Tulldahl, M. Laser range profiling for small target recognition. Opt. Eng. 2017, 56, 031206. [Google Scholar] [CrossRef]
- Steinvall, O.; Tulldahl, M.; Berglund, F.; Allard, L. Laser profiling for airborne target classification. In Proceedings of the SPIE, 23nd Laser Radar Technology and Applications, Orlando, FL, USA, 7–12 May 2018; Volume 10636, p. 1063602. [Google Scholar]
- Ma, H.; Song, J.L.; Wang, J.D. Forest canopy LAI and vertical FAVD profile inversion from airborne full-waveform LiDAR data based on a radiative transfer model. Remote Sens. 2015, 7, 1897–1914. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.; Yin, T.G.; Lauret, N. Discrete anisotropic radiative transfer (DART 5) for modeling airborne and satellite spectroradiometer and LIDAR acquisitions of natural and urban landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.; Yin, T.G.; Lauret, N.; Grau, E.; Rubio, J.; Cook, B.D.; Morton, D.C.; Sun, G.Q. Simulation of satellite, airborne and terrestrial LiDAR with DART (I): Waveform simulation with quasi-Monte Carlo ray tracing. Remote Sens. Environ. 2016, 184, 418–435. [Google Scholar] [CrossRef]
- Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the impact of discrete-return lidar system and survey characteristics over young conifer and broadleaf forests. Remote Sens. Environ. 2010, 115, 2798–2809. [Google Scholar] [CrossRef]
- Pang, Y.; Lefsky, M.; Sun, G.; Ranson, J. Impact of footprint diameter and off-nadir pointing on the precision of canopy height estimates from spaceborne lidar. Remote Sens. Environ. 2011, 115, 2798–2809. [Google Scholar] [CrossRef]
- Calders, K.; Lewis, P.; Disney, M.; Verbesselt, J.; Herold, M. Investigating assumptions of crown archetypes for modelling LiDAR returns. Remote Sens. Environ. 2013, 134, 39–49. [Google Scholar] [CrossRef]
- Ristorcelli, T.; Hamoir, D.; Briottet, X. Simulating space lidar waveforms from smaller-footprint airborne laser scanner data for vegetation observation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 534–538. [Google Scholar] [CrossRef]
- North, P.R.J.; Rosette, J.A.B.; Suárez, J.C.; Los, S.O. A Monte Carlo radiative transfer model of satellite waveform LiDAR. Int. J. Remote Sens. 2010, 31, 1343–1358. [Google Scholar] [CrossRef]
- Wu, J.Y.; Van Aardt, J.A.N.; Gregory, P.A. Comparison of signal deconvolution algorithms based on small-footprint LiDAR waveform simulation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 6. [Google Scholar] [CrossRef]
- Zhou, G.Q.; Long, S.H.; Xu, J.S.; Zhou, S.; Song, B.; Deng, R.H.; Wang, C. Comparison analysis of five waveform decomposition algorithms for the airborne LiDAR echo signal. IEEE Trans. Geosci. Remote Sens. 2021, 14, 7869–7880. [Google Scholar] [CrossRef]
- Steinvall, O. Effects of target shape and reflection on laser radar cross sections. Appl. Opt. 2000, 39, 4381–4391. [Google Scholar] [CrossRef]
- Johnson, S.E. Effect of target surface orientation on the range precision of laser detection and ranging systems. J. Appl. Remote Sens. 2009, 3, 033564. [Google Scholar] [CrossRef]
- Hu, Y.H.; Hou, A.H.; Zhang, X.Y.; Han, F.; Zhao, N.X.; Xu, S.L.; Ma, Q.L.; Gu, Y.L.; Dong, X.; Fang, J.J. Assessment of lateral structural details of targets using principles of full-waveform light detection and ranging. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5704116. [Google Scholar] [CrossRef]
- Hu, Y.H.; Zhang, X.Y.; Hou, A.H.; Xu, S.L.; Gu, Y.L.; Lu, H.B.; Ma, Q.L.; Zhao, N.X.; Fang, J.J. Laser echo waveform modulation modelling from lateral structure using a mathematical formula. Int. J. Remote Sens. 2023, 44, 2382–2399. [Google Scholar] [CrossRef]
- Wang, Y.X.; Fang, J.J.; Xu, S.L.; Zhang, X.Y.; Ma, S.J.; Guo, Y.L.; Shan, L.Q.; Hu, Y.H. Intelligent shape discrimination and multi-dimensional feature parameter inversion of target based on laser echo waveform. Chin. J. Lasers 2025, 53, 2. [Google Scholar]
- Stysley, P.R.; Coyle, D.B.; Clarke, G.B.; Frese, E.; Blalock, G.; Morey, P.; Kay, R.B.; Poulios, D.; Hersh, M. Laser production for NASA’s Global Ecosystem Dynamics Investigation (GEDI) lidar. In Proceedings of the SPIE, 21nd Laser Radar Technology and Applications, Baltimore, MD, USA, 17–21 April 2016; Volume 9832, p. 983207. [Google Scholar]
- Zhang, X.Y.; Hu, Y.H.; Shen, S.Y.; Fang, J.J.; Wang, Y.C.; Liu, Y.F.; Han, F. Kilometer-level laser reflective tomography experiment and debris barycenter estimation. Acta Phys. Sin. 2022, 71, 114205. [Google Scholar] [CrossRef]
- Bai, J.; Niu, Z.; Huang, Y.R.; Bi, K.Y.; Fu, Y.W.; Gao, S.; Wu, M.Q.; Wang, L. Full-waveform hyperspectral LiDAR data decomposition via ranking central locations of natural target echoes (Rclonte) at different wavelengths. Remote Sens. Environ. 2024, 310, 114227. [Google Scholar] [CrossRef]
- Zhang, F.X.; Wang, X.; Wang, L.G.; Mo, F.; Zhao, L.P.; Yang, X.M.; Lv, X.; Xie, J.F. A Satellite Full-Waveform Laser Decomposition Method for Forested Areas Based on Hidden Peak Detection and Adaptive Genetic Optimization. Remote Sens. 2025, 17, 701. [Google Scholar] [CrossRef]
- Keller, U. Ultrafast Lasers: A Comprehensive Introduction to Fundamental Principles with Practical Applications; Springer: Cham, Switzerland, 2021; pp. 555–556. [Google Scholar]
- Zhu, J.H.; Yin, T.H.; Guo, W.; Zhang, B.B.; Zhou, Z.M. An underwater target azimuth trajectory enhancement approach in BTR. Appl. Acoust. 2025, 230, 110373. [Google Scholar] [CrossRef]
- Xu, Z.; Fan, C.Y.; Huang, X.T. MIMO radar waveform design for multipath exploitation. IEEE Trans. Signal Process. 2021, 69, 5359. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, B.; Ai, W.H.; Xie, Z.; Zhu, J.H. Radar transceiver design for extended targets based on optimal linear detector. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6070–6082. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Q.; Fei, T.Y. A robust joint frequency spectrum and power allocation strategy in a coexisting radar and communication system. Chin. J. Aeronaut. 2024, 37, 393–409. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Q.; Zhang, L.; Liu, B.B.; Xu, H.X. Joint power, bandwidth, and subchannel allocation in a UAV-assisted DFRC network. IEEE Internet Things J. 2025, 12, 11633. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Q.; Liu, B.B. Joint customer assignment, power allocation, and subchannel allocation in a UAV-based joint radar and communication network. IEEE Internet Things J. 2024, 11, 29643. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Hemispherical reflectance, | 1 |
| Total power, | 1 (A. U.) |
| Range between the laser emitter and target, | 10 km |
| Laser divergence angle, | 0.1 mrad |
| Laser wavelength, | 1064 nm |
| Width, | 0.2 ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, X.; Xu, S.; Han, F.; Xia, Y.; Fang, J.; Hu, Y. Modulation of Typical Three-Dimensional Targets on the Echo Waveform Using Analytical Formula. Remote Sens. 2025, 17, 3419. https://doi.org/10.3390/rs17203419
Wang Y, Zhang X, Xu S, Han F, Xia Y, Fang J, Hu Y. Modulation of Typical Three-Dimensional Targets on the Echo Waveform Using Analytical Formula. Remote Sensing. 2025; 17(20):3419. https://doi.org/10.3390/rs17203419
Chicago/Turabian StyleWang, Yongxiang, Xinyuan Zhang, Shilong Xu, Fei Han, Yuhao Xia, Jiajie Fang, and Yihua Hu. 2025. "Modulation of Typical Three-Dimensional Targets on the Echo Waveform Using Analytical Formula" Remote Sensing 17, no. 20: 3419. https://doi.org/10.3390/rs17203419
APA StyleWang, Y., Zhang, X., Xu, S., Han, F., Xia, Y., Fang, J., & Hu, Y. (2025). Modulation of Typical Three-Dimensional Targets on the Echo Waveform Using Analytical Formula. Remote Sensing, 17(20), 3419. https://doi.org/10.3390/rs17203419







