Estimating Winter Wheat Canopy Chlorophyll Content Through the Integration of Unmanned Aerial Vehicle Spectral and Textural Insights
Abstract
1. Introduction
2. Materials and Methods
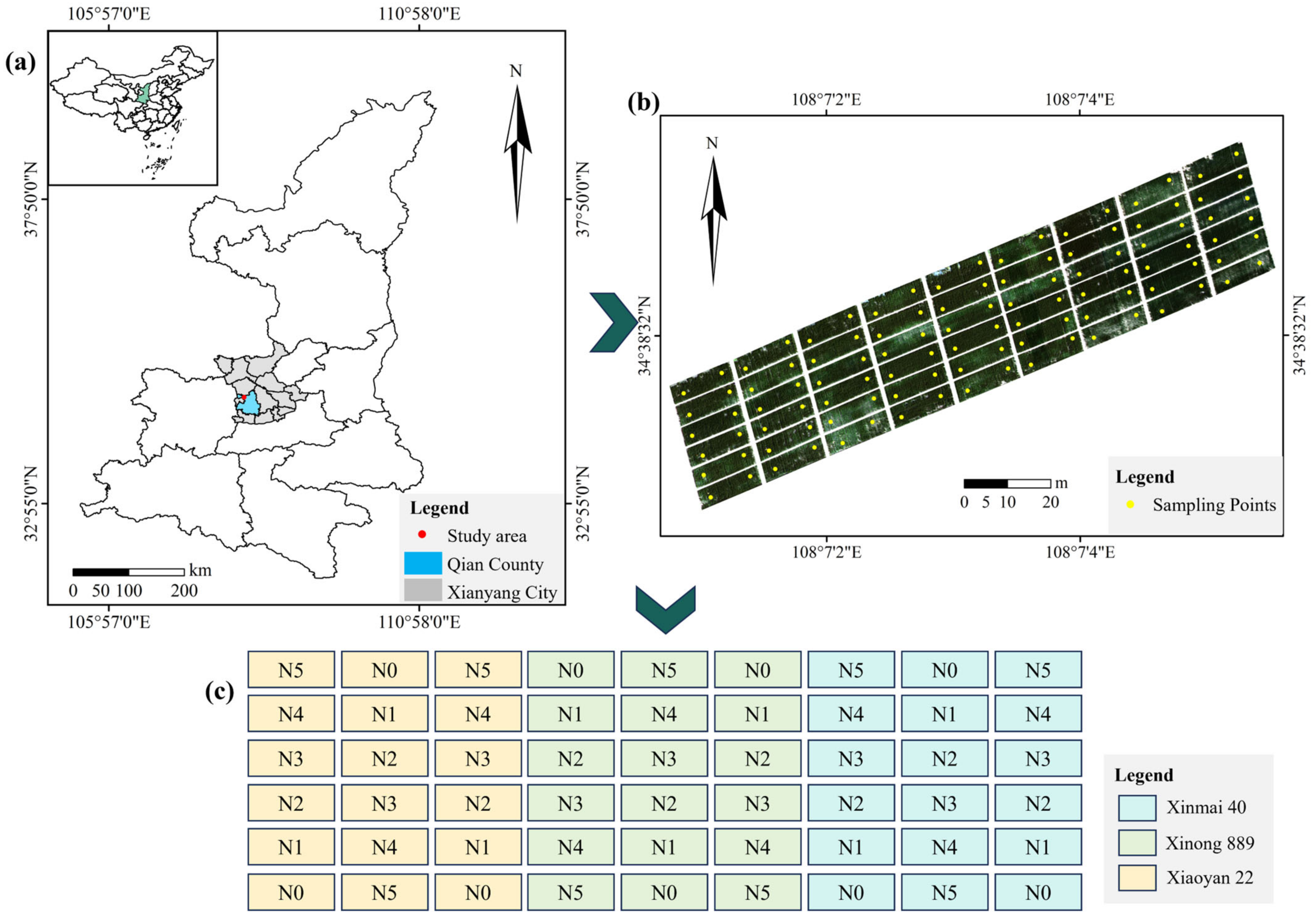
2.1. Location of the Study Area and Experimental Design
2.2. Data Acquisition
2.2.1. UAV Image Data Collection and Preprocessing
2.2.2. Collecting Relative Canopy Chlorophyll Content
2.3. Image Feature Extraction
2.3.1. Vegetation Index Extraction
2.3.2. Texture Feature Extraction
2.4. Modeling Approaches
2.5. Model Evaluation Criteria
3. Results
3.1. Statistical Analysis of RCCC
3.2. Analysis of Input Parameters
3.2.1. Selection of Optimal TIs
3.2.2. Correlation Analysis Between VIs and RCCC
3.3. The Estimation of RCCC
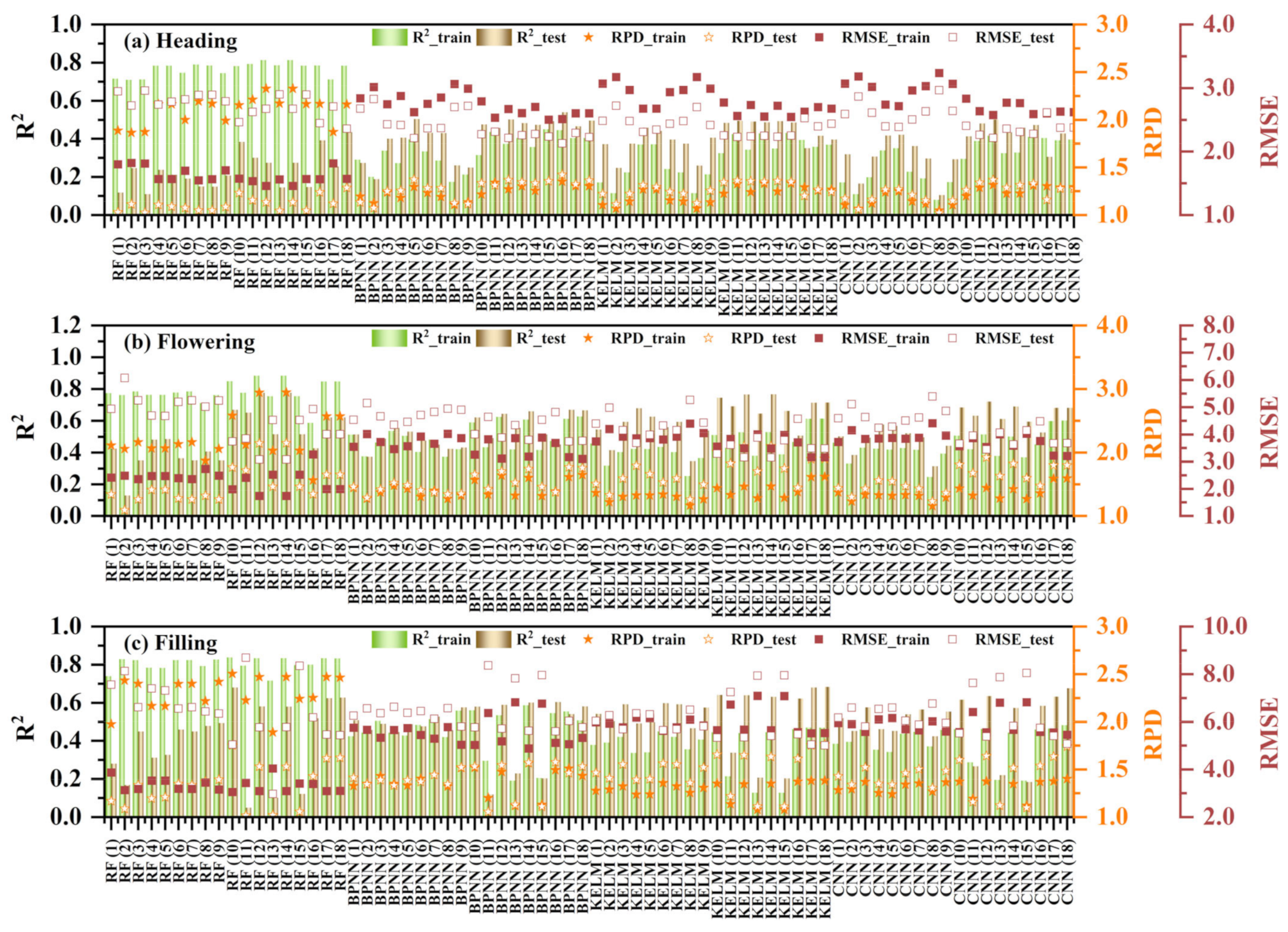
3.3.1. The Univariate Regression of RCCC
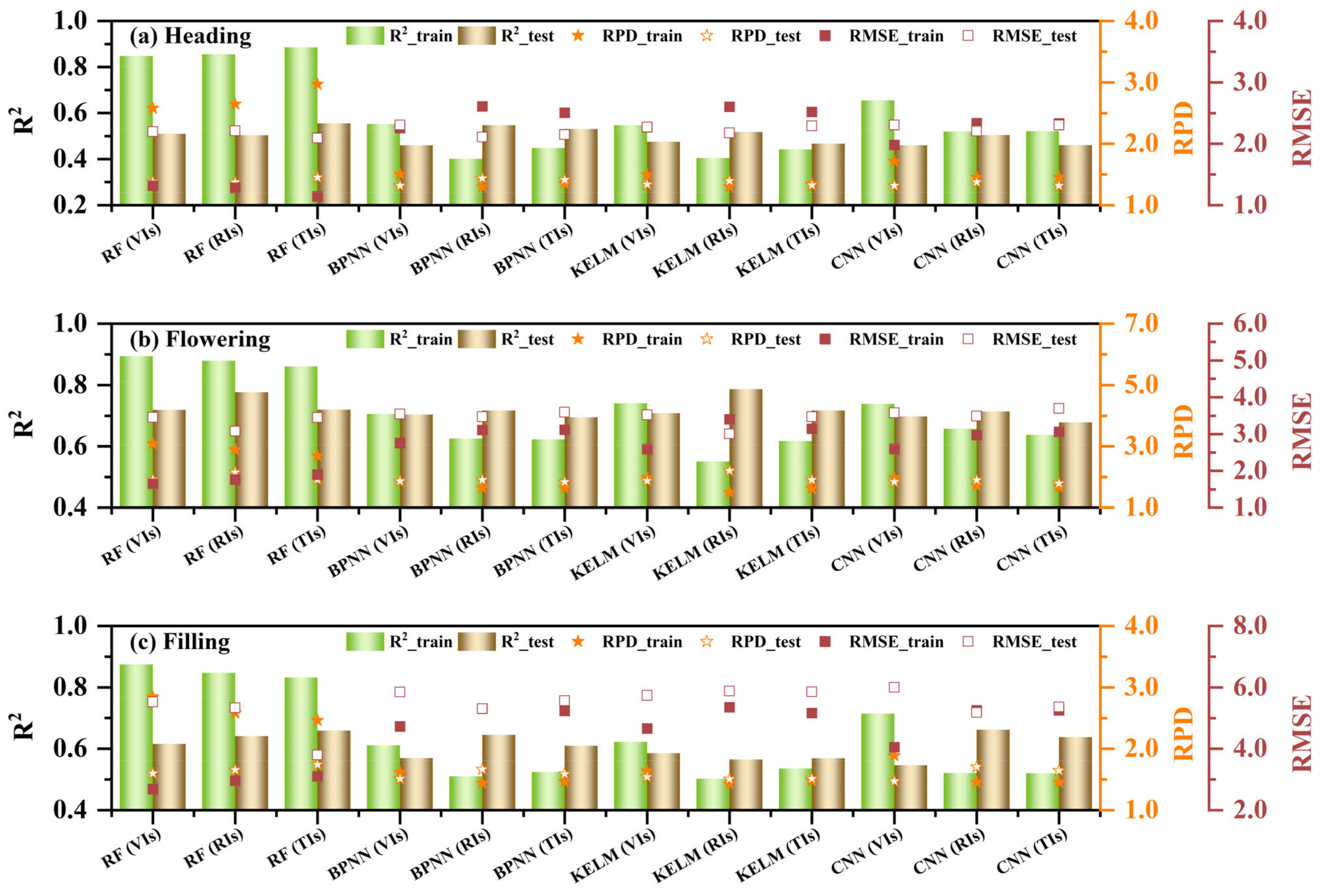
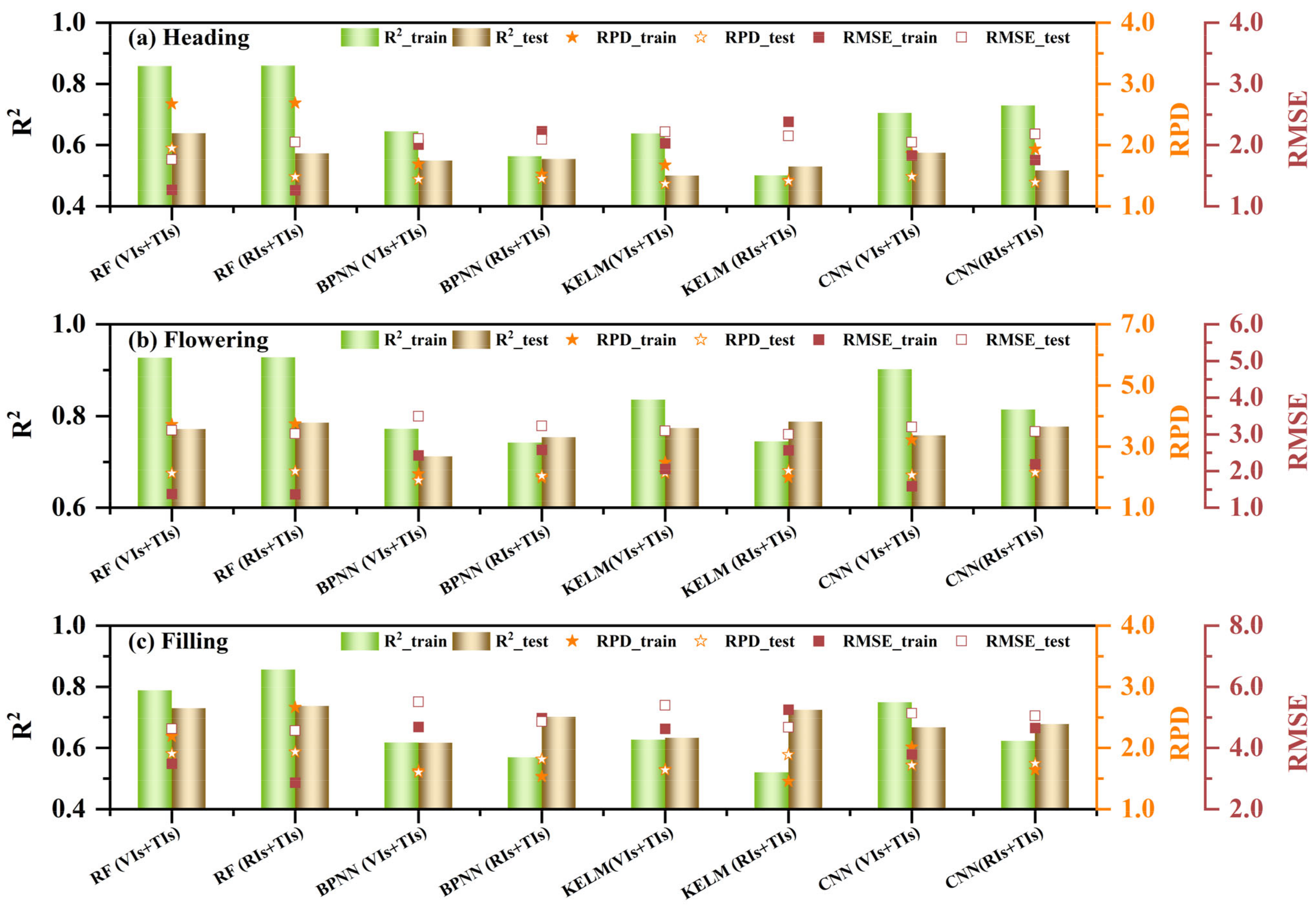
3.3.2. The Multivariate Regression of RCCC
4. Discussion
4.1. Analysis of Univariate Regression and Outstanding Variable
4.2. Improvement of RCCC Estimation Through Multivariate Regression and Texture Indices
4.3. Model Adaptability and Optimal Mapping of RCCC
4.4. Limitations and Future Perspectives
5. Conclusions
- (1)
- Vegetation indices based on red-edge bands with high sensitivity (LCI720, NDRE720, RECI720) and texture indices with multi-spatial information (DTI, RTI, NDTI) were critical in estimating RCCC. Univariate regression models were reasonable for the flowering and filling stages, while the outstanding multivariate models, which incorporate multiple features, captured more complex relationships and outperformed univariate models, achieving an R² increase of 0.35% to 69.55% compared to the optimal univariate models.
- (2)
- The RF model demonstrated outstanding performance in both univariate and multivariate regressions. Among all models, the RF model based on RIS+TIS during the flowering stage exhibited the best performance (R²_train = 0.93, RMSE_train = 1.36, RPD_train = 3.74, R²_test = 0.79, RMSE_test = 3.01, RPD_test = 2.20). With more variables, BPNN, KELM, and CNN models better leverage the advantages of neural networks, thus improving training performance.
- (3)
- Compared to using single-type features for RCCC estimation, the combination of vegetation indices and texture indices increased from 0.16% to 40.70% in the R² values of some models. Integrating spectral and texture information from UAV multispectral images effectively estimates the RCCC of winter wheat in this study area, providing valuable information for winter wheat management. However, future work should expand the applicability of the estimation models developed in this study.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Khaledi-Alamdari, M.; Majnooni-Heris, A.; Fakheri-Fard, A.; Russo, A. Probabilistic climate risk assessment in rainfed wheat yield: Copula approach using water requirement satisfaction index. Agric. Water Manag. 2023, 289, 108542. [Google Scholar] [CrossRef]
- Korotkova, I.V.; Chaika, T.O.; Romashko, T.P.; Chetveryk, O.O.; Rybalchenko, A.M.; Barabolia, O.V. Emmer wheat productivity formation depending on pre-sowing seed treatment method in organic and traditional technology cultivation. Regul. Mech. Biosyst. 2023, 14, 41–47. [Google Scholar] [CrossRef]
- Hema, K.; Yogita, N.; Nitin, D.; Swapna, C. Design of Spectral Absorbance-Based Electronic Reader for Chlorophyll Measurement. SSRG Int. J. Electr. Electron. Eng. 2023, 10, 46–55. [Google Scholar] [CrossRef]
- Cartelat, A.; Zoran, G.C.; Goulas, Y.; Sylvie, M.; Caroline, L.; Prioul, J.L.; Aude, B.; Jeuffroy, M.H.; Philippe, G.; Giovanni, A.; et al. Optically assessed contents of leaf polyphenolics and chlorophyll as indicators of nitrogen deficiency in wheat (Triticum aestivum L.). Field Crops Res. 2005, 91, 35–49. [Google Scholar] [CrossRef]
- Goulas, Y.; Zoran, G.C.; Cartelat, A.; Moya, I. Dualex: A new instrument for field measurements of epidermal ultraviolet absorbance by chlorophyll fluorescence. Appl. Opt. 2004, 43, 4488–4496. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; He, P.; Zhang, Y.; Liu, H.; Chang, H.; Xu, X. Modelling of crop chlorophyll content based on Dualex. Trans. Chin. Soc. Agric. Eng. 2015, 31, 191–197. [Google Scholar]
- Raffaele, C.; Fabio, C.; Simone, P.; Stefano, P. Chlorophyll estimation in field crops: An assessment of handheld leaf meters and spectral reflectance measurements. J. Agric. Sci. 2015, 153, 876–890. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Xiao, Y.; Shi, X.; Zeng, Y. Diversity Analysis of Chlorophyll, Flavonoid, Anthocyanin, and Nitrogen Balance Index of Tea Based on Dualex. Phyton-Int. J. Exp. Bot. 2021, 90, 1549–1558. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. A Review on Unmanned Aerial Vehicle Remote Sensing: Platforms, Sensors, Data Processing Methods, and Applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- Qi, H.; Bingyu, Z.; Zeyu, W.; Liang, Y.; Jianwen, L.; Leidi, W.; Tingting, C.; Yubin, L.; Lei, Z. Estimation of Peanut Leaf Area Index from Unmanned Aerial Vehicle Multispectral Images. Sensors 2020, 20, 6732. [Google Scholar] [CrossRef]
- Luo, S.; Jiang, X.; He, Y.; Li, J.; Jiao, W.; Zhang, S.; Xu, F.; Han, Z.; Sun, J.; Yang, J.; et al. Multi-dimensional variables and feature parameter selection for aboveground biomass estimation of potato based on UAV multispectral imagery. Front. Plant Sci. 2022, 13, 948249. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Wang, W.; Zhang, Q.; Li, D.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Baret, F.; Liu, S.; et al. Estimation of Nitrogen Nutrition Status in Winter Wheat From Unmanned Aerial Vehicle Based Multi-Angular Multispectral Imagery. Front. Plant Sci. 2019, 10, 1601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yi, Y.; Wang, L.; Zhang, X.; Chen, S.; Su, Z.; Zhang, S.; Xue, Y. Estimation of the Bio-Parameters of Winter Wheat by Combining Feature Selection with Machine Learning Using Multi-Temporal Unmanned Aerial Vehicle Multispectral Images. Remote Sens. 2024, 16, 469. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, Y.; Ren, Y.; Zhang, Z.; Geng, H. Prediction of Chlorophyll Content in Multi-Temporal Winter Wheat Based on Multispectral and Machine Learning. Front. Plant Sci. 2022, 13, 896408. [Google Scholar] [CrossRef]
- Wang, Y.; Lola, S.; Poblete, T.; Victoria, G.-D.; Dongryeol, R.; Pablo, J.Z.T. Evaluating the role of solar-induced fluorescence (SIF) and plant physiological traits for leaf nitrogen assessment in almond using airborne hyperspectral imagery. Remote Sens. Environ. 2022, 279, 113141. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Li, C.; Li, Z.; Wang, Y.; Feng, H.; Xu, B. Estimation of Winter Wheat Above-Ground Biomass Using Unmanned Aerial Vehicle-Based Snapshot Hyperspectral Sensor and Crop Height Improved Models. Remote Sens. 2017, 9, 708. [Google Scholar] [CrossRef]
- Zhang, A.; Yin, S.; Wang, J.; He, N.; Chai, S.; Pang, H. Grassland Chlorophyll Content Estimation from Drone Hyperspectral Images Combined with Fractional-Order Derivative. Remote Sens. 2023, 15, 5623. [Google Scholar] [CrossRef]
- Qian, B.; Ye, H.; Huang, W.; Xie, Q.; Pan, Y.; Xing, N.; Ren, Y.; Guo, A.; Jiao, Q.; Lan, Y. A sentinel-2-based triangular vegetation index for chlorophyll content estimation. Agric. For. Meteorol. 2022, 13, 925986. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, L.; Zhang, Q.; Huang, C.; Yi, X.; Chen, X.; Hou, T.; Lv, X.; Zhang, Z. Cotton Yield Estimation Based on Vegetation Indices and Texture Features Derived From RGB Image. Front. Plant Sci. 2019, 166, 105026. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Li, J.; Guo, X.; Wang, S.; Lu, J. Estimating biomass of winter oilseed rape using vegetation indices and texture metrics derived from UAV multispectral images. Comput. Electron. Agric. 2024, 14, 1265. [Google Scholar] [CrossRef]
- Li, W.; Pan, K.; Liu, W.; Xiao, W.; Ni, S.; Shi, P.; Chen, X.; Li, T. Monitoring Maize Canopy Chlorophyll Content throughout the Growth Stages Based on UAV MS and RGB Feature Fusion. Agriculture 2024, 14, 1265. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, S.; Jia, X.; Qi, L.; Liu, S.; Lu, H.; Wang, C.; Liu, W.; Zhao, X.; He, L.; et al. Estimating Relative Chlorophyll Content in Rice Leaves Using Unmanned Aerial Vehicle Multi-Spectral Images and Spectral–Textural Analysis. Agronomy 2023, 13, 1541. [Google Scholar] [CrossRef]
- Wang, T.; Gao, M.; Cao, C.; You, J.; Zhang, X.; Shen, L. Winter wheat chlorophyll content retrieval based on machine learning using in situ hyperspectral data. Comput. Electron. Agric. 2022, 193, 106728. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.; Meng, H.; Miao, H.; Jiang, S.; Chang, Q. UAV Hyperspectral Data Combined with Machine Learning for Winter Wheat Canopy SPAD Values Estimation. Remote Sens. 2023, 15, 4658. [Google Scholar] [CrossRef]
- Feng, Z.; Guan, H.; Yang, T.; He, L.; Duan, J.; Song, L.; Wang, C.; Feng, W. Estimating the canopy chlorophyll content of winter wheat under nitrogen deficiency and powdery mildew stress using machine learning. Comput. Electron. Agric. 2023, 211, 107989. [Google Scholar] [CrossRef]
- Cai, Y.L.; Yanying, M.; Hao, W.; Dan, W. Hyperspectral Estimation Models of Winter Wheat Chlorophyll Content Under Elevated CO2. Front. Plant Sci. 2021, 12, 642917. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Xiang, Y.; Tang, Z.; Huang, X.; Shi, H.; Sun, T.; Yang, W.; Cui, S.; Chen, G.; et al. Estimation of Winter Wheat Chlorophyll Content Based on Wavelet Transform and the Optimal Spectral Index. Agronomy 2024, 14, 1309. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Shi, B.; Chang, Q. Estimation of Winter Wheat Plant Nitrogen Concentration from UAV Hyperspectral Remote Sensing Combined with Machine Learning Methods. Remote Sens. 2023, 15, 2831. [Google Scholar] [CrossRef]
- Zoran, G.C.; Guillaume, M.; Naïma Ben, G.; Gwendal, L. A new optical leaf-clip meter for simultaneous non-destructive assessment of leaf chlorophyll and epidermal flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef]
- Zhang, C.; Xue, Y. Estimation of Biochemical Pigment Content in Poplar Leaves Using Proximal Multispectral Imaging and Regression Modeling Combined with Feature Selection. Sensors 2023, 24, 217. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Parida, P.K.; Somasundaram, E.; Krishnan, R.; Radhamani, S.; Sivakumar, U.; Parameswari, E.; Raja, R.; Shri Rangasami, S.R.; Sangeetha, S.P.; Gangai Selvi, R. Unmanned Aerial Vehicle-Measured Multispectral Vegetation Indices for Predicting LAI, SPAD Chlorophyll, and Yield of Maize. Agriculture 2024, 14, 1110. [Google Scholar] [CrossRef]
- Qiao, L.; Tang, W.; Gao, D.; Zhao, R.; An, L.; Li, M.; Sun, H.; Song, D. UAV-based chlorophyll content estimation by evaluating vegetation index responses under different crop coverages. Comput. Electron. Agric. 2022, 196, 106775. [Google Scholar] [CrossRef]
- Wasonga, D.O.; Yaw, A.; Kleemola, J.; Alakukku, L.; Mäkelä, P.S.A. Red-Green-Blue and Multispectral Imaging as Potential Tools for Estimating Growth and Nutritional Performance of Cassava under Deficit Irrigation and Potassium Fertigation. Remote Sens. 2021, 13, 598. [Google Scholar] [CrossRef]
- An, L.; Tang, W.; Qiao, L.; Zhao, R.; Sun, H.; Li, M.; Zhang, Y.; Zhang, M.; Li, X. Estimation of chlorophyll distribution in banana canopy based on RGB-NIR image correction for uneven illumination. Comput. Electron. Agric. 2022, 202, 107358. [Google Scholar] [CrossRef]
- Maccioni, A.; Agati, G.; Mazzinghi, P. New vegetation indices for remote measurement of chlorophylls based on leaf directional reflectance spectra. J. Photochem. Photobiol. B Biol. 2001, 61, 52–61. [Google Scholar] [CrossRef]
- Palanisamy, S.; Latha, K.; Pazhanivelan, S.; Ramalingam, K.; Karthikeyan, G.; Sudarmanian, N.S. Spatial prediction of leaf chlorophyll content in cotton crop using drone-derived spectral indices. Curr. Sci. 2023, 123, 1473–1480. [Google Scholar] [CrossRef]
- Ma, W.; Han, W.; Zhang, H.; Cui, X.; Zhai, X.; Zhang, L.; Shao, G.; Niu, Y.; Huang, S. UAV multispectral remote sensing for the estimation of SPAD values at various growth stages of maize under different irrigation levels. Comput. Electron. Agric. 2024, 227, 109566. [Google Scholar] [CrossRef]
- Liu, X.; Du, R.; Xiang, Y.; Chen, J.; Zhang, F.; Shi, H.; Tang, Z.; Wang, X. Estimating Winter Canola Aboveground Biomass from Hyperspectral Images Using Narrowband Spectra-Texture Features and Machine Learning. Plants 2024, 13, 2978. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Gao, W.; Zhang, Y.; Hou, X. Improving lake chlorophyll-a interpreting accuracy by combining spectral and texture features of remote sensing. Environ. Sci. Pollut. Res. 2023, 30, 83628–83642. [Google Scholar] [CrossRef]
- Fawagreh, K.; Gaber, M.M.; Elyan, E. Random forests: From early developments to recent advancements. Syst. Sci. Control. Eng. 2014, 2, 602–609. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, X. Artificial Intelligence Random Forest Algorithm and the Application. In Proceedings of the 2020 International Conference on Data Processing Techniques and Applications for Cyber-Physical Systems, Laibin, China, 11–12 December 2020; Springer: Singapore, 2021; pp. 205–213. [Google Scholar]
- Rumelhart, D.E.; McClelland, J.L. Parallel Distributed Processing, Volume 1: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar] [CrossRef]
- Li, J.; Cheng, J.-h.; Shi, J.-y.; Huang, F. Brief Introduction of Back Propagation (BP) Neural Network Algorithm and Its Improvement. In Proceedings of the Advances in Computer Science and Information Engineering, Zhengzhou, China, 19–20 May 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2, pp. 553–558. [Google Scholar]
- Wythoff, B.J. Backpropagation neural networks: A tutorial. Chemom. Intell. Lab. Syst. 1993, 18, 115–155. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Xu, H. Performance Enhancement of Kernel Extreme Learning Machine Using Whale Optimization Algorithm in Fruit Image Classification. In Proceedings of the 2023 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, Australia, 4–7 September 2023; pp. 1–6. [Google Scholar]
- Wang, Z.; Chen, S.; Guo, R.; Li, B.; Feng, Y. Extreme learning machine with feature mapping of kernel function. IET Image Process. 2020, 14, 2495–2502. [Google Scholar] [CrossRef]
- Indolia, S.; Goswami, A.K.; Mishra, S.P.; Asopa, P. Conceptual Understanding of Convolutional Neural Network- A Deep Learning Approach. Procedia Comput. Sci. 2018, 132, 679–688. [Google Scholar] [CrossRef]
- Lindsay, G. Convolutional Neural Networks as a Model of the Visual System: Past, Present, and Future. J. Cogn. Neurosci. 2021, 33, 2017–2031. [Google Scholar] [CrossRef]
- Cong, S.; Zhou, Y. A review of convolutional neural network architectures and their optimizations. Artif. Intell. Rev. 2022, 56, 1905–1969. [Google Scholar] [CrossRef]
- Dini, R.; Dedy Dwi, P.; Suhartono, S. Input selection in support vector regression for univariate time series forecasting. AIP Conf. Proc. 2019, 2194, 020105. [Google Scholar] [CrossRef]
- Ali, S.; Simit, R. Mapping red edge-based vegetation health indicators using Landsat TM data for Australian native vegetation cover. Earth Sci. Inform. 2018, 11, 545–552. [Google Scholar] [CrossRef]
- Jesús, D.; Jochem, V.; Luis, A.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Anatoly, A.G. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Ziqi, L.; Bin, H.; Xingwen, Q. Potential of texture from SAR tomographic images for forest aboveground biomass estimation. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102049. [Google Scholar] [CrossRef]
- Huanbo, Y.; Yaohua, H.; Zhouzhou, Z.; Yichen, Q.; Kaili, Z.; Taifeng, G.; Jun, C. Estimation of Potato Chlorophyll Content from UAV Multispectral Images with Stacking Ensemble Algorithm. Agronomy 2022, 12, 2318. [Google Scholar] [CrossRef]
- Iqbal, H.S. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Bin, C.; Qian, Z.; Wenjiang, H.; Xiaoyu, S.; Huichun, Y.; Xuliang, Z. A New Integrated Vegetation Index for the Estimation of Winter Wheat Leaf Chlorophyll Content. Remote Sens. 2019, 11, 974. [Google Scholar] [CrossRef]
- Hu, J.; Feng, H.; Wang, Q.; Shen, J.; Wang, J.; Liu, Y.; Feng, H.; Yang, H.; Guo, W.; Qiao, H.; et al. Pretrained Deep Learning Networks and Multispectral Imagery Enhance Maize LCC, FVC, and Maturity Estimation. Remote Sens. 2024, 16, 784. [Google Scholar] [CrossRef]
- Qi, S.; Quanjun, J.; Xiaojin, Q.; Liangyun, L.; Xinjie, L.; Huayang, D. Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations. Remote Sens. 2021, 13, 470. [Google Scholar] [CrossRef]
- Ding, S.; Jing, J.; Dou, S.; Zhai, M.; Zhang, W. Citrus Canopy SPAD Prediction under Bordeaux Solution Coverage Based on Texture- and Spectral-Information Fusion. Agriculture 2023, 13, 1701. [Google Scholar] [CrossRef]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image Quality Assessment: Unifying Structure and Texture Similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2567–2581. [Google Scholar] [CrossRef]
- Dong, Y.; Zheng, B.; Liu, H.; Zhang, Z.; Fu, Z. Symmetric mean and directional contour pattern for texture classification. Electron. Lett. 2021, 57, 918–920. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Liu, X.; Guanter, L.; Liu, L.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.; Du, S.; Gastellu-Etchegorry, J.-P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2019, 231, 110772. [Google Scholar] [CrossRef]
- Fu, Z.; Jiang, J.; Gao, Y.; Krienke, B.; Wang, M.; Zhong, K.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Wheat Growth Monitoring and Yield Estimation based on Multi-Rotor Unmanned Aerial Vehicle. Remote Sens. 2020, 12, 508. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Zhang, J.; Guo, Y.; Yang, X.; Yu, G.; Bai, X.; Chen, J.; Chen, Y.; Shi, L.; et al. Improving estimation of maize leaf area index by combining of UAV-based multispectral and thermal infrared data: The potential of new texture index. Comput. Electron. Agric. 2023, 214, 108294. [Google Scholar] [CrossRef]
- Xingjiao, Y.; Huo, X.; Pi, Y.; Wang, W.Y.; Fan, K.; Qian, L.; Wang, W.; Hu, X. Estimate Leaf Area Index and Leaf Chlorophyll Content in Winter-Wheat Using Image Texture and Vegetation Indices Derived from Multi-Temporal RGB Images; Research Square: Durham, NC, USA, 2023. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2019, 20, 611–629. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Sun, Y.; Zhao, Y.; Zhuang, H.; Ban, W.; Chen, Y.; Fu, E.; Chen, S.; Liu, J.; et al. Combining Spectral and Texture Features of UAS-Based Multispectral Images for Maize Leaf Area Index Estimation. Remote Sens. 2022, 14, 331. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. III.3-Theory of the Backpropagation Neural Network *. In Neural Networks for Perception; Academic Press: Cambridge, MA, USA, 1992; pp. 65–93. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y.; Chen, Y.; Qiao, X.; Qian, W. Water Chlorophyll a Estimation Using UAV-Based Multispectral Data and Machine Learning. Drones 2023, 7, 2. [Google Scholar] [CrossRef]
- Krichen, M. Convolutional Neural Networks: A Survey. Computers 2023, 12, 151. [Google Scholar] [CrossRef]
- Luo, F.; Liu, G.; Guo, W.; Chen, G.; Xiong, N. ML-KELM: A Kernel Extreme Learning Machine Scheme for Multi-Label Classification of Real Time Data Stream in SIoT. IEEE Trans. Netw. Sci. Eng. 2021, 9, 1044–1055. [Google Scholar] [CrossRef]
| Year | Variety | Date | Growth Stage Description |
|---|---|---|---|
| 2023–2024 | Xiaoyan22, Xinong889, and Xinmai40 | 28 April | Heading Stage |
| 15 May | Flowering Stage | ||
| 24 May | Filling Stage |
| Definition | Calculation Formula | References |
|---|---|---|
| Normalized pigment chlorophyll ratio index (NPCI) | [30] | |
| Visible-band difference vegetation index (VDVI) | [31] | |
| Normalized difference vegetation index (NDVI) | [32] | |
| Green normalized difference vegetation index (GNDVI) | [32] | |
| Green chlorophyll index (GCI) | [33] | |
| Simple ratio (SR) | [34] | |
| Modified simple ratio (MSR) | [35] | |
| Red-edge simple ratio (RESR720) | [36] | |
| Red-edge simple ratio (RESR750) | [36] | |
| Leaf chlorophyll index (LCI720) | [30] | |
| Leaf chlorophyll index (LCI750) | [30] | |
| Normalized difference red-edge (NDRE720) | [37] | |
| Normalized difference red-edge (NDRE750) | [37] | |
| Red-edge chlorophyll index (RECI720) | [38] | |
| Red-edge chlorophyll index (RECI750) | [38] |
| Definition | Calculation Formula | References |
|---|---|---|
| Difference texture index (DTI) | [40] | |
| Ratio texture index (RTI) | [40] | |
| Normalized difference texture index (NDTI) | [40] |
| Dataset | Growth Stage | Sample Numbers | Range | Mean | Standard Deviation | Coefficient of Variation/% |
|---|---|---|---|---|---|---|
| Training set | Heading | 81 | 37.31~53.59 | 44.50 | 3.39 | 7.62% |
| Flowering | 81 | 27.62~53.80 | 43.61 | 5.11 | 11.71% | |
| Filling | 81 | 16.72~49.95 | 30.38 | 7.64 | 25.14% | |
| Testing set | Heading | 27 | 37.59~52.12 | 43.51 | 3.03 | 6.97% |
| Flowering | 27 | 29.59~54.81 | 43.14 | 6.61 | 15.33% | |
| Filling | 27 | 17.81~49.96 | 32.48 | 8.83 | 27.18% |
| Stages | Texture Feature | Correlation Coefficient (r) | |||||
|---|---|---|---|---|---|---|---|
| Blue | Green | Red | RE720 | RE750 | NIR | ||
| Heading | Mean (mean) | −0.32 ** | −0.39 ** | −0.38 ** | −0.42 ** | −0.17 | −0.07 |
| Variance (var) | −0.14 | −0.22 * | −0.18 | −0.16 | −0.07 | −0.03 | |
| Homogeneity (hom) | 0.24 * | 0.22 * | 0.22 * | 0.27 ** | 0.06 | 0.12 | |
| Contrast (con) | −0.20 * | −0.25 * | −0.15 | −0.28 ** | −0.21 * | −0.16 | |
| Dissimilarity (dis) | −0.24 * | −0.24 * | −0.21 * | −0.29 ** | −0.17 | −0.16 | |
| Entropy (ent) | −0.21 * | −0.26 ** | −0.24 * | −0.27 ** | −0.01 | 0.03 | |
| Second moment (sm) | 0.18 | 0.22 * | 0.23 * | 0.24 * | 0.01 | −0.03 | |
| Correlation (corr) | 0.02 | −0.04 | 0.08 | −0.06 | −0.11 | −0.01 | |
| Flowering | Mean (mean) | −0.32 ** | −0.43 ** | −0.54 ** | −0.32 ** | 0.24 * | −0.03 |
| Variance (var) | 0.03 | −0.27 ** | −0.09 | −0.235 * | −0.15 | −0.09 | |
| Homogeneity (hom) | −0.05 | 0.10 | −0.02 | 0.09 | 0.04 | −0.02 | |
| Contrast (con) | 0.08 | −0.23 * | −0.02 | −0.17 | −0.11 | −0.03 | |
| Dissimilarity (dis) | 0.06 | −0.15 | 0.01 | −0.13 | −0.08 | −0.01 | |
| Entropy (ent) | 0.03 | −0.02 | −0.06 | −0.05 | 0.01 | −0.04 | |
| Second moment (sm) | −0.02 | 0.03 | 0.02 | 0.05 | 0.03 | 0.06 | |
| Correlation (corr) | −0.10 | 0.00 | −0.03 | −0.03 | −0.12 | −0.17 | |
| Filling | Mean (mean) | −0.23 * | −0.2 ** | −0.48 ** | −0.17 | 0.46 ** | 0.53 ** |
| Variance (var) | 0.00 | −0.09 | −0.26 ** | −0.10 | 0.05 | 0.08 | |
| Homogeneity (hom) | −0.02 | 0.04 | 0.14 | −0.08 | −0.05 | −0.07 | |
| Contrast (con) | 0.01 | −0.02 | −0.23 * | 0.04 | 0.24 * | 0.28 ** | |
| Dissimilarity (dis) | 0.02 | −0.03 | −0.19 * | 0.07 | 0.19 * | 0.22 * | |
| Entropy (ent) | 0.02 | −0.03 | −0.13 | −0.06 | 0.09 | 0.07 | |
| Second moment (sm) | −0.01 | 0.03 | 0.11 | 0.07 | −0.10 | −0.04 | |
| Correlation (corr) | 0.13 | 0.09 | 0.04 | −0.04 | 0.00 | 0.01 | |
| VIs | Heading | Flowering | Filling |
|---|---|---|---|
| NPCI | −0.46 ** | −0.69 ** | −0.65 ** |
| VDVI | −0.36 ** | −0.60 ** | −0.63 ** |
| NDVI | 0.48 ** | 0.69 ** | 0.64 ** |
| GNDVI | 0.62 ** | 0.72 ** | 0.60 ** |
| GCI | 0.60 ** | 0.69 ** | 0.62 ** |
| SR | 0.51 ** | 0.69 ** | 0.70 ** |
| MSR | 0.48 ** | 0.69 ** | 0.64 ** |
| RESR720 | −0.32 ** | −0.53 ** | −0.58 ** |
| RESR750 | −0.42 ** | −0.65 ** | −0.62 ** |
| LCI720 | 0.59 ** | 0.77 ** | 0.69 ** |
| LCI750 | 0.65 ** | 0.73 ** | 0.50 ** |
| NDRE720 | 0.61 ** | 0.78 ** | 0.70 ** |
| NDRE750 | 0.65 ** | 0.69 ** | 0.36 ** |
| RECI720 | 0.59 ** | 0.75 ** | 0.70 ** |
| RECI750 | 0.65 ** | 0.69 ** | 0.35 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, H.; Zhang, R.; Song, Z.; Chang, Q. Estimating Winter Wheat Canopy Chlorophyll Content Through the Integration of Unmanned Aerial Vehicle Spectral and Textural Insights. Remote Sens. 2025, 17, 406. https://doi.org/10.3390/rs17030406
Miao H, Zhang R, Song Z, Chang Q. Estimating Winter Wheat Canopy Chlorophyll Content Through the Integration of Unmanned Aerial Vehicle Spectral and Textural Insights. Remote Sensing. 2025; 17(3):406. https://doi.org/10.3390/rs17030406
Chicago/Turabian StyleMiao, Huiling, Rui Zhang, Zhenghua Song, and Qingrui Chang. 2025. "Estimating Winter Wheat Canopy Chlorophyll Content Through the Integration of Unmanned Aerial Vehicle Spectral and Textural Insights" Remote Sensing 17, no. 3: 406. https://doi.org/10.3390/rs17030406
APA StyleMiao, H., Zhang, R., Song, Z., & Chang, Q. (2025). Estimating Winter Wheat Canopy Chlorophyll Content Through the Integration of Unmanned Aerial Vehicle Spectral and Textural Insights. Remote Sensing, 17(3), 406. https://doi.org/10.3390/rs17030406





