Estimating Olive Tree Density in Delimited Areas Using Sentinel-2 Images

Abstract

The objective of this study is to develop a method for estimating the density of olive trees in delimited plots using low-resolution images from the Sentinel-2 satellite. This approach is particularly relevant in certain regions where high-resolution orthophotos, which are often costly and not always available, cannot be accessed. This study focuses on the Extremadura region in Spain, where 48,530 olive plots were analysed. Data from Sentinel-2’s multispectral bands were obtained for each plot, and a Random Forest Regression (RFR) model was used to correlate these values with the number of olive trees, previously counted from orthophotos using machine learning object detection techniques. The results show that the proposed method can predict olive tree density within an acceptable error margin, which is especially useful for distinguishing plots with a density greater than 300 olive trees per hectare—a key criterion for allocating agricultural subsidies in the region. Although the accuracy of the model is not optimal, an average error of ±15.04 olive trees per hectare makes it a viable tool for practical applications where extreme precision is not required. The developed method may also be extrapolated to other cases and crop types, such as fruit trees or forest masses, offering an efficient solution for annual density estimates without relying on costly aerial images. Future research could enhance the accuracy of the model by grouping plots according to additional characteristics, such as tree size or plantation type.

1. Introduction

Precision agriculture has emerged as an essential tool for optimising productivity and sustainability in the agricultural sector. Within this field, remote sensing stands out for its ability to quickly and efficiently obtain accurate and up-to-date data over large geographical areas. Satellite imagery, such as that provided by the Sentinel-2 mission, enables farmers and agricultural managers to monitor and analyse the status of their crops at regular intervals. This facilitates the early detection of issues such as water stress, pests, and diseases, allowing for corrective measures to be implemented before these issues escalate and significantly impact production. Additionally, remote sensing is crucial for regulatory compliance and verification of conditions for receiving agricultural subsidies and grants, as it provides objective, verifiable data on cultivated areas and management practises. These advantages make remote sensing an indispensable tool for modern agriculture, promoting both economic efficiency and environmental sustainability.

The application of remote sensing together with machine learning techniques has been used for various purposes and crops for many years. Numerous crop classification systems rely on satellite imagery. For instance, some studies, such as [1,2], focus on classifying crops from a single cloud-free image. Others, like [3], use multiple images to create a Normalised Difference Vegetation Index (NDVI) time series, which is then used for further classification with random forests, utilising 21 images from the Landsat-8 satellite. In similar studies, such as [4], temporal series approaches in China were tested using different sensor datasets, evaluated with random forests and support vector machines. In [5], crop classification using multitemporal images with a combination of the 12 spectral bands of Sentinel-2 (https://sentiwiki.copernicus.eu/web/sentinel-2, accessed on 31 October 2024) was shown to provide better results than using individual bands or a single image. Other studies, such as [6], have also demonstrated the effectiveness of using all 12 bands in a time series. Furthermore, articles like [7] recommend the use of all 12 bands for optimal performance over individual bands. Some studies incorporate phenological features from time series to improve performance, as shown by [8,9], indicating that the use of these complete datasets offers marginally higher accuracy than red, near-infrared (NIR), and shortwave infrared (SWIR) spectroscopy.

On the other hand, the analysis of aerial images—whether from aeroplanes, drones, or unmanned aerial vehicles (UAVs)—in agriculture offers numerous advantages that are transforming crop management and resource efficiency. Orthophotos, with their high resolution, enable the identification and monitoring of various land features, such as crop distribution, the presence of weeds, the status of agricultural infrastructure (roads, irrigation channels), and problem areas affected by pests or diseases. Their high spatial resolution makes possible, for instance, the detailed identification and counting of trees within a plot with high accuracy. This detection capability facilitates better planning and management of agricultural activities, such as pruning, irrigation, and fertilisation. Public administrations and agricultural management agencies also benefit from aerial image analysis technology for tree counting. Accurate tree counts are essential for the fair and efficient distribution of agricultural subsidies and grants. These grants are often based on specific criteria, such as cultivated area and planting density. Accurate data on the number of trees in each plot allow for authorities to verify applicants’ eligibility and accurately calculate the subsidy amounts. However, one of the major drawbacks of using these images is the cost associated with conducting continuous flights to capture these data. In many regions, flights are not conducted annually due to high costs, which can limit the availability of up-to-date data. Despite this drawback, orthophotos or high-resolution images remain an invaluable tool in modern agriculture, providing a solid foundation for decision-making and the optimisation of agricultural practises.

Continuous advances in remote sensing technologies and machine learning algorithms have significantly improved the accuracy and efficiency of tree detection from aerial images. Among the most effective approaches are the integration of laser imaging detection and ranging (LiDAR) with aerial images, the use of UAV-derived Canopy Height Models (CHM), and methods based on Convolutional Neural Networks (CNN). The most common object detection methods [10] are two-stage detectors and one-stage detectors. In the two-stage method, the first stage involves preprocessing to generate object region proposals (without classification), and in the second stage, each region is classified as a possible object. This type of detector is accurate, but is computationally slower. In the one-stage method, object classification is performed directly without preprocessing, making it faster and less computationally costly than the two-stage approach. The most widely used one-stage detection technique is You Only Look Once (YOLO) [11], with successful results shown in [12,13] for tree detection in static images.

For example, in [14], machine learning methods are used that incorporate UAV data from hyperspectral sensors and LiDAR to accurately classify forest tree species, improving forest inventory and ecological sustainability. In [15], photogrammetry and UAV-based hyperspectral images are also used to effectively detect and classify individual trees in boreal forests, as well as for the automatic detection and delineation of tree crowns from passive remote sensing images. Ref. [16] achieved good results in forestry analysis applied to endangered tree species. Ref. [17] used CNN-based methods combined with high-spatial-resolution RGB images from UAVs, achieving an average accuracy of 92% with processing times of less than 30 s; and in [18], a similar approach reported an accuracy average of 91.58%. In [19], a deep neural network was used for large-scale spatial tree density estimation from remote sensing images, with a relative mean absolute error of 16.72% and a mean squared error of 77.96. Specifically applied to olive tree counting, Ref. [20] used very high-spatial-resolution remote sensing images, distinguishing them from other land cover classes and counting valid spots within a predefined size range.

Satellite images, mainly from Sentinel-2, have been frequently used for classifying tree species in forests and large areas, as described in [21,22,23,24] or [25]. However, no studies have been found in the literature using Sentinel-2 images to identify the number or density of trees in a specific area. The reason is that the low resolution of these images (1 pixel equals 100 m²) renders them unsuitable for identifying objects or the size of a tree.

The motivation for this study was to assess the feasibility of estimating the approximate number of olive trees in a plot using only Sentinel-2 images. This approach is of particular interest for agencies responsible for agricultural management, which requires olive density control in plots at times when high-resolution orthophotos are unavailable, whereas Sentinel-2 images can be obtained continuously. Furthermore, the administrative allocation of subsidies to plots based on density is typically performed in value ranges, so extreme precision in these values is not required. Keeping annual updates of olive plot density values leads to considerable cost savings by reducing the need for field inspections.

The following approach was used in this research: the spectral band information from Sentinel-2 images for plots with tree plantations provided us with the data that can relate these values to the number of trees in the plot. By focusing on specific and well-defined plantations, such as olive groves, which exhibit a significant contrast between the trees and the soil, we aimed to study the direct relationship between Sentinel-2 band values in an area and the number of planted olive trees, evaluating whether they fell within an acceptable error margin. To support this theory, data from olive plots were used in this study according to two methodologies: (a) from Sentinel-2 images for the phenological year, calculating the mean value of each of the Sentinel-2 bands for an olive plot, as explained in Section 2.1 (b) from aerial images, performing an accurate count of olive trees in the same plots using object detection techniques, as described in Section 2.2. Section 2.3 describes how a neural network was created to predict the number of olive trees in a plot based on the average band values of the plot. Section 3 describes the direct relationship between the data from olive plots using techniques (a) and (b), which are verified with experimental data, and then analyses the results. Section 4 outlines the study conclusions.

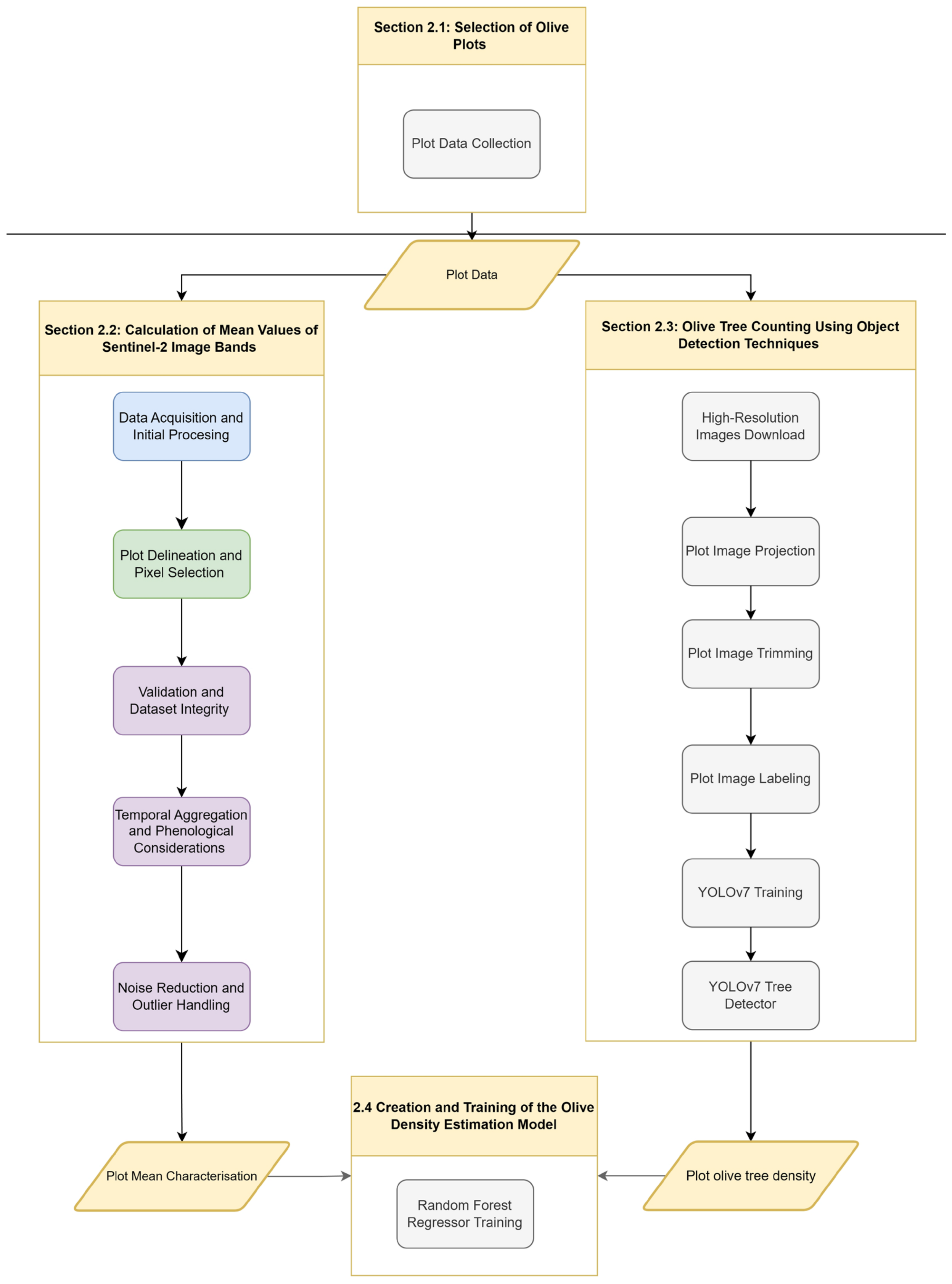
2. Materials and Methods

The objective of this study was to establish the relationship between the values provided by the Sentinel-2 satellite for olive plots and the density of olive trees present in these plots. We hypothesised that by using data from Sentinel-2 satellite images and calculating the average of all bands within an olive plot, it would be possible to estimate the number of olive trees in the plot within an acceptable error margin. To validate this hypothesis, the following processes were carried out, as described in the subsequent subsections (showed in Figure 1): selection of olive plots for the study in a specific area, calculation of average band values from Sentinel-2 images for the identified plots, automatic counting of olive trees in the plots using object detection techniques on aerial images for the selected plots, and development of a neural network that integrated these data in the training process to predict the number of olive trees in a plot based solely on Sentinel-2 images. It should be noted that this experiment was conducted in a delimited region with olive plantations of varied but not excessively different planting layouts. That is, in the selected region, the cultivation method was typically similar in rows of varying widths, without clusters of vines, but with varied densities and orientations and uniform soil treatment.

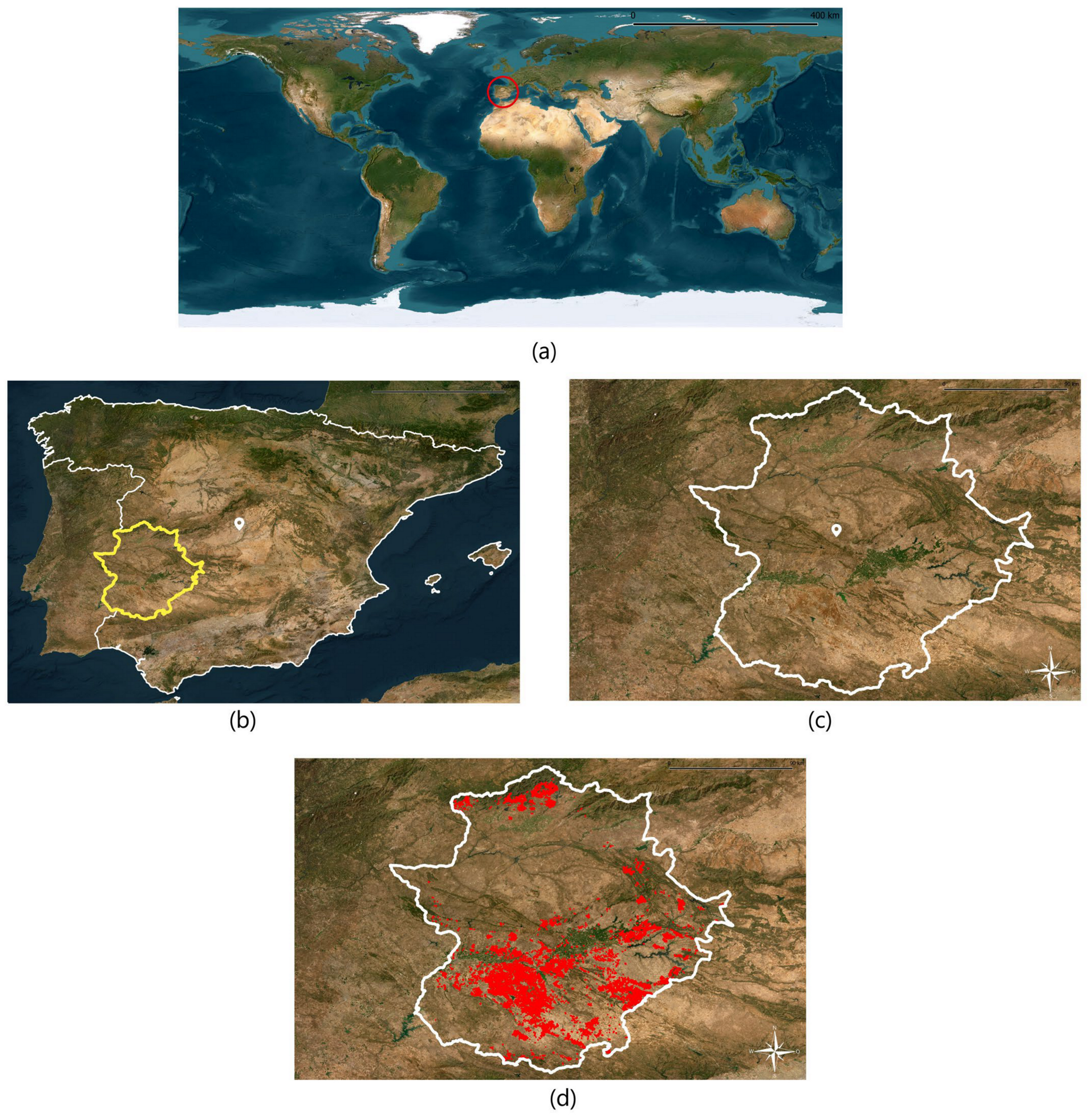
2.1. Selection of Olive Plots

The first step was to select a representative set of olive plots located in the Extremadura region, Spain, at coordinates (DMS) 38°40′0″N, 6°10′0″W (Figure 2). This region has an average temperature of 17.9 °C, an annual average precipitation of 456 mm, and an average humidity of 59.08%. The highest elevation included in this study was 1112 metres above sea level (MASL), and the lowest was 150 MASL. The choice of this region was based on its high number of olive trees, providing a substantial dataset, with similar planting methods and layouts, consistent soil treatment, homogeneous soil characteristics, and similar climate.

In our database, the total number of olive plots is 53,041, covering a total area of 59,528 hectares. For this study, as mentioned earlier, olive plantations with a similar pattern were selected, referring to those with an orderly layout where each olive tree is clearly separated from the others, maintaining a variable but defined distance between them. This layout is found in two types of olive plantations: traditional plantations and intensive plantations.

Traditional plantations are characterised by larger distances between trees, resulting in a more spaced-out distribution, while intensive plantations reduce these distances to optimise production, although without causing tree overlaps. Due to these overlaps, all plots characterised by super-intensive plantations, also known as hedgerow plantations (olive trees very close to each other), were excluded from this study, removing a total of 1311 plots. Additionally, to avoid potential artificial fluctuations in the calculated data caused by crop irrigation, only rainfed plantations were selected, excluding 3200 plots corresponding to irrigated systems. However, the remaining plots vary in size, providing a diverse dataset for analysis. The total number of plots included in this study is 48,530 (downloadable from https://doi.org/10.5281/zenodo.14017071). Data collection was conducted using the graphical delimitations of the geographic information system (GIS) declarations from the Junta de Extremadura, which categorises these areas as olive plots.

The Extremadura region has aerial surveys with orthophotos from 2022. The phenological year 2022 was chosen to link the orthophoto images with the Sentinel-2 images. The plots identified as olive in 2022 in Extremadura and used for this study, in total 48,530, with an average surface area of 1.25 hectares, are marked in red in Figure 2d and cover an area of 56,051 hectares.

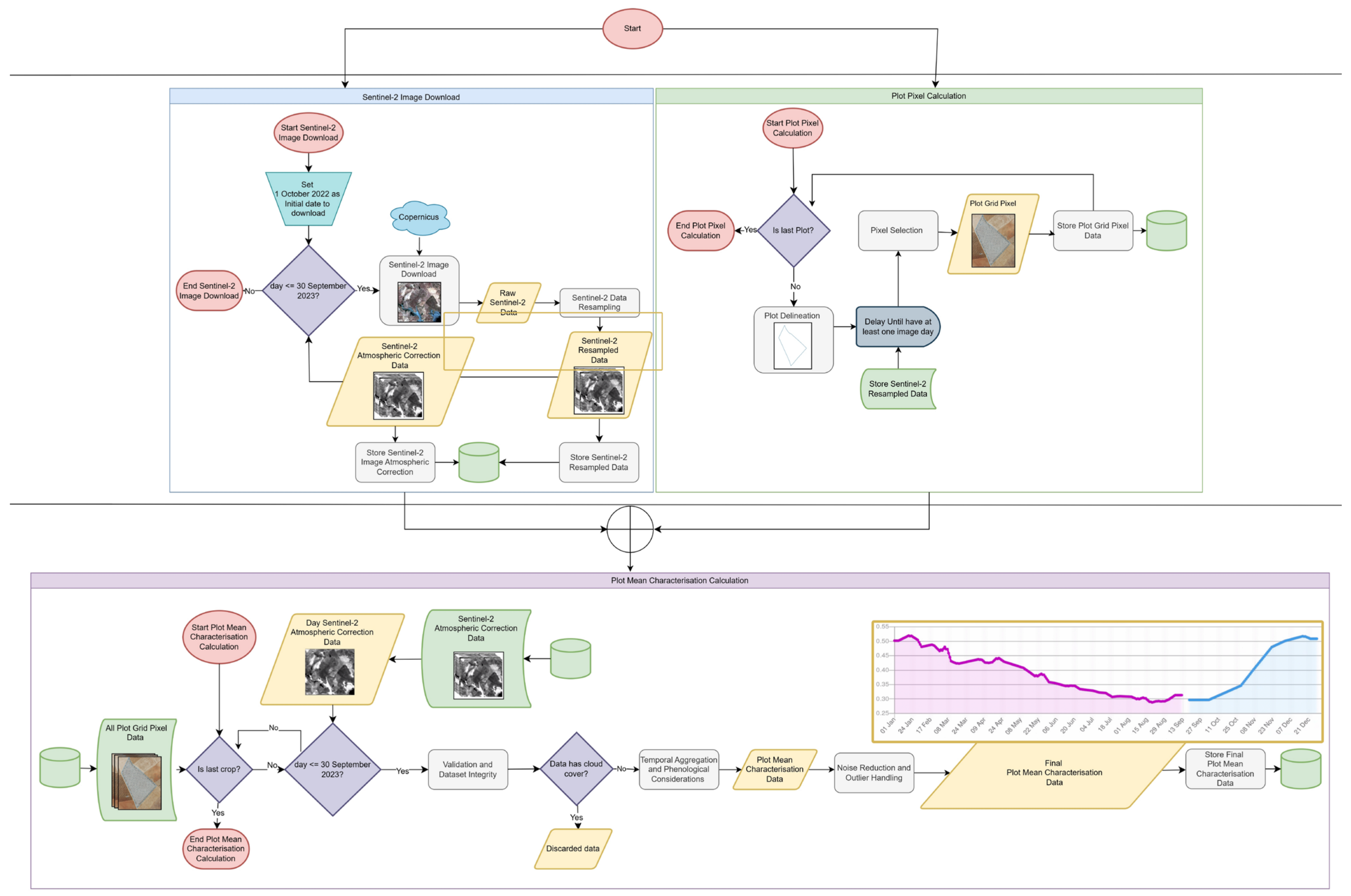
2.2. Calculation of Mean Values of Sentinel-2 Image Bands

The main objective of this method was to extract, process, and analyse the spectral information within each olive grove plot to calculate mean reflectance values for all Sentinel-2 bands. These values, referred to as Plot Mean Characterisation (PMC), serve as the foundation for subsequent density estimation analysis. The following are the summarised phases related to the calculation of the values of Sentinel-2 image bands. These steps are presented concisely here, but for a more detailed understanding of the processes, readers are encouraged to consult [6].

(1)

Data Acquisition and Initial Processing

Sentinel-2 images for the phenological year 2022, from 1 October 2022 to 30 September 2023 (a total of 61 images per plot), were downloaded via the Copernicus API (https://scihub.copernicus.eu/, accessed on 23 July 2024) for the 48,530 plots identified as olive groves. This dataset spans the entire phenological cycle of olive trees, ensuring a comprehensive capture of spectral changes throughout the year.

The Sentinel-2 mission provides multispectral data at varying resolutions (10 m, 20 m, and 60 m) across 12 bands. For this study, all bands were resampled to a uniform resolution of 10 × 10 m using bilinear interpolation to ensure consistency in spatial analysis. The raw reflectance data were pre-processed to normalise values between 0 and 1, correcting for variations due to atmospheric interference and sensor inconsistencies.

To address challenges related to atmospheric distortions and cloud cover, the Sen2Cor v2.12 atmospheric correction tool was employed. This tool removes the influence of atmospheric water vapour, aerosols, and ozone, ensuring that the reflectance values used in the analysis accurately represent the surface properties of the plots. Additionally, cloud masking was applied using both Sen2Cor outputs and proprietary algorithms tailored for detecting and interpolating cloud-contaminated pixels. These algorithms relied on temporal consistency checks across the 61 images to flag anomalies and interpolate missing data. These data, once are processed, are stored in the database.

(2)

Plot Delineation and Pixel Selection

Each plot’s spatial boundaries were defined using georeferenced polygons provided by local administrative datasets. It is necessary to have, at least, one day’s image of Sentinel-2 to perform the matching between Sentinel-2-pixel images and plot pixels. These polygons were overlaid on Sentinel-2 images to extract the corresponding pixels for each plot. Since plot boundaries often include edge pixels that may partially fall outside the plot, these pixels were excluded to avoid introducing spectral noise from adjacent areas, as shown in Figure 3. This refinement ensures that the PMC accurately represents the spectral characteristics of the olive grove. Every plot grid calculated is stored in the database.

The process for aligning plot boundaries with Sentinel-2-pixel grids leveraged tools such as Python-based geospatial libraries. The methodologies applied ensured precise identification and extraction of plot-specific spectral data, as detailed in [26].

(3)

Validation and Dataset Integrity

Images of plots with incomplete data due to persistent cloud cover or other missing values were flagged and excluded from the analysis to maintain dataset integrity. The final dataset consisted of 48,530 plots with complete PMC values, ensuring robustness and reliability for subsequent machine learning applications.

(4)

Temporal Aggregation and Phenological Considerations

The Sentinel-2 images were collected across a full phenological year to account for seasonal variations in olive tree reflectance. For each plot, mean reflectance values were calculated for all 12 bands at each of the 61 time points. To reduce noise and enhance the reliability of the dataset, a temporal averaging process was applied, which involved computing the mean reflectance values across all 61 images for each band. This approach smooths out anomalies caused by short-term environmental changes, such as rain or cloud shadows, while preserving the overall spectral signature of the plot.

(5)

Noise Reduction and Outlier Handling

One of the critical challenges in working with low-resolution imagery is managing noise and outliers. Outliers were identified based on deviations from expected reflectance ranges for olive trees, using statistical thresholds and domain-specific knowledge. For instance, reflectance values outside the typical range for olive trees in the near-infrared (NIR) band were flagged and excluded. Additional filtering processes ensured that only high-quality data contributed to the PMC calculations.

The resulting PMC dataset is not merely a static representation of spectral data, but a dynamic foundation for advanced agricultural monitoring. By incorporating temporal and spatial dimensions, the PMC captures nuanced variations that reflect the phenological and environmental conditions of each plot. This comprehensive dataset enables scalable analysis, offering a cost-effective alternative to high-resolution orthophotos while maintaining sufficient accuracy for density estimation.

Moreover, this method establishes a framework that can be extended to other agricultural applications. For example, the methodology could be adapted to monitor crop health, identify stress factors, or estimate biomass in other perennial crops. The robust preprocessing pipeline, combined with Sentinel-2’s frequent revisit time, provides an operationally viable solution for large-scale agricultural analysis.

By systematically calculating the PMC for each plot, this study bridges the gap between remote sensing data and actionable agricultural insights. The detailed preprocessing steps (shown in Figure 4), combined with the integration of phenological and spatial considerations, ensure that the PMC serves as a reliable input for machine learning models aimed at density estimation. The PMC values for the 48,530 plots are available for download at: https://doi.org/10.5281/zenodo.14017108.

2.3. Olive Tree Counting Using Object Detection Techniques

To achieve the objective of the study, it was essential to previously have the density of olive trees per hectare of each enclosure, since these values would serve as a reference for the training of the model and the subsequent validation of the estimated densities. However, in the region of Extremadura, there is no official or systematic record of counting olive trees, given that this practice is not carried out regularly in the area. This lack of direct data forced a specific process to be implemented to obtain this information accurately.

The purpose of this process was to automatically count the existing olive trees in the selected plots (the same 48,530 plots mentioned in the previous section). To achieve this, a total of 435 aerial images of the Extremadura region from 2022 (https://pnoa.ign.es/web/portal/pnoa-imagen/productos-a-descarga, accessed on 23 May 2024), taken between June and July, with a combined size of 923.7 GB, were used. These orthophotos were downloaded in high-quality GeoTIFF format with georeferencing data, necessary to determine the coordinates of each image point, crop the image according to the plot boundary, and link it to subsequent geospatial analyses. Using the boundary data from the GIS graphical declarations from the Junta de Extremadura for olive plots, a coordinate projection was made to crop the plot area from the corresponding orthophoto image. In this way, the specific area of each olive plot in the image was accurately identified. This process is similar to the projection in Sentinel-2 images described in [6]. To perform the counting, the first step was to generate a neural network with the ability to detect the object olive tree. Once this system was generated, it was used for large-scale counting across all olive plots in Extremadura.

The YOLOv7 object detection system [11] with the neural network characteristics described in [27,28] was used to generate a model capable of detecting and counting the number of olive trees in the provided images. The use of this object detection algorithm instead of other segmentation-based methods, as employed in [29], is justified by the characteristics of the olive plots selected for this study. These plots correspond to traditional and intensive plantations, where the trees are arranged in an orderly manner with sufficient spacing between them, which prevents overlap. This configuration allows for the individual detection of trees, as each one can be clearly and accurately identified without encountering overlapping tree crowns, entire trees overlapping each other, or unions between crowns of nearby trees.

In this context, where the tree distribution is uniform and there are no complex structures or dense planting patterns like in super-intensive plantations (also known as hedgerow plantations), the use of a single-stage detection model such as YOLOv7 is particularly suitable. It is important to clarify that YOLOv7 was applied exclusively to the high-resolution orthophotos, as these provide the necessary spatial detail to individually detect olive trees within the plots. Sentinel-2 images, with their resolution of 10 × 10 m, lack the granularity required for such object detection tasks. Thus, orthophotos were indispensable for generating the accurate tree counts necessary for subsequent density calculations and model training. If our dataset included super-intensive olive plots, which create “hedgerow plantations”, the use of segmentation methods would be essential for accurate detection. While the method performs effectively in traditional and intensive plantations, its application to super-intensive systems or irregular planting patterns presents challenges. Super-intensive plantations, characterised by dense and overlapping trees, may require segmentation-based approaches to accurately delineate individual trees. Similarly, irregularly spaced plantations would necessitate additional training data to capture variability in tree distributions and ensure robust model performance.

For the training process, images and labels of objects classified as olive trees were provided to the model via manual labelling using the LabelImg (https://github.com/HumanSignal/labelImg, accessed on 5 July 2024) tool, as shown in the example in Figure 5. This software allows for the creation of labels for images in various formats, such as “YOLO”, “CreateML”, and “PascalVOC”. In this format, a TXT file is created that will contain one line for each tagged object. Each line follows the format of “class”, “x-center”, “y-center”, “box-width”, and “box-height”. This way, when training YOLO, it knows exactly where the identified object is located. Thus, for each plot with its corresponding PNG images, a TXT file was generated, with the image labelled with olives marked by a square. The YOLO neural network configuration file “yolov7-e6e.yaml” (https://github.com/WongKinYiu/yolov7/blob/main/cfg/training/yolov7-e6e.yaml, accessed on 16 September 2024) and weights “yolov7-e6e.pt” (https://github.com/WongKinYiu/yolov7/releases/download/v0.1/yolov7-e6e.pt, accessed on 16 September 2024), which have demonstrated better performance than their competitors in tree detection processes [30], were used, with images of 1280 × 1280 pixels and 50 training epochs. Considering YOLO’s configuration, from the yolov7-e6e.yaml file, the parameter nc, corresponding to the number of classes, must be changed to as many classes as we wanted to train and identify. In this case, since we only wanted to detect olive, nc had the value of 1. Depth_multiple and width_multiple parameters are scalars used to control the model size by adjusting the number of layers (depth) and channels (width) proportionally. Values of 1.0 indicate the default full-size YOLOv7 model. The default configuration of the YOLOv7 neural network architecture is based on two main components: the backbone and the head. The backbone serves as the foundation of the network, responsible for extracting features from the input image. It processes the image through multiple layers of convolution, downsampling, and feature aggregation, gradually capturing patterns ranging from simple edges to complex shapes. The depth and width of this backbone are determined by parameters such as depth_multiple and width_multiple, which allow for the upscaling model to adjust to different computational needs. As features flow through the backbone, they are passed to the head, the second key component. The head is where the network refines these features and generates predictions. It processes information from different stages of the backbone using operations such as upsampling, concatenation, and feature fusion. By combining features at different resolutions, the head balances spatial detail and semantic depth, allowing for accurate detection of objects of all sizes. Specialised layers, such as SPPCSPC, help to further aggregate and refine features for final predictions. These predictions include bounding boxes, class probabilities, and confidence scores. To help the network detect objects of various sizes, the architecture uses anchors, which are predefined bounding box dimensions. Anchors act as templates, giving the model a starting point for detecting objects at different scales. Each anchor is associated with a specific feature map resolution, ensuring that smaller anchors focus on detecting small objects in high-resolution maps, while larger anchors are used in lower-resolution maps for larger objects. In each test, after completing the labelling stages, the images (along with their labels) were divided into three sets, training, validation, and testing, in proportions of 70%, 15%, and 15%, respectively, as suggested by the algorithm.

To achieve appropriate olive tree detection, models were incrementally generated by increasing the number of labelled trees as input examples until the improvement in accuracy over the previous model became minimal. As shown in

Table 1. Generation of olive tree detection models by incrementally providing approximately 1000 labelled olive trees in each test.

Model	Plots	Olives	Precision	Recall	mAP@0.5	mAP@0.5:0.95
1	25	1102	0.131	0.279	0.0937	0.174
2	32	2032	0.156	0.192	0.149	0.035
3	41	3031	0.331	0.386	0.266	0.0559
4	50	4105	0.353	0.445	0.297	0.0614
5	56	5090	0.466	0.626	0.511	0.134
6	68	6082	0.488	0.651	0.515	0.134
7	83	7249	0.518	0.622	0.525	0.145
8	86	8055	0.546	0.596	0.544	0.181
9	93	9042	0.645	0.527	0.545	0.183
10	49	10,055	0.671	0.557	0.587	0.193
11	97	11,060	0.707	0.597	0.6155	0.226
12	98	12,063	0.723	0.634	0.682	0.246
13	108	13,044	0.767	0.597	0.67	0.247
14	113	14,085	0.804	0.721	0.698	0.258
15	133	15,014	0.846	0.836	0.823	0.288
16	142	16,004	0.857	0.848	0.859	0.292
17	159	17,013	0.865	0.851	0.896	0.315

, approximately 1000 additional labelled olive trees were provided for each partial model in each test. This process was repeated until the improvements showed a logarithmic progression, with minimal gains relative to the substantial effort required for manual labelling.

The evaluation process was conducted iteratively, with approximately 1000 additional trees labelled in each training step. Metrics such as precision, recall, and mAPs were tracked after 50 epochs per iteration. Initially, rapid improvements were observed during models 1–5, with significant relative gains: precision increased by 0.335, recall by 0.347, and mAP@0.5 by 0.4173. Between models 6–13, the rate of improvement slowed, with precision increasing by 0.279, recall by 0.054, and mAP@0.5 by 0.155. During the saturation phase (models 14–17), the improvements became marginal, particularly between models 15–17, where precision increased by just 0.019, recall by 0.015, and mAP@0.5 by 0.073. At the stopping point (models 16–17), minimal improvements were recorded: precision increased by only 0.008 (0.8%), and recall increased by 0.037 (0.3%).

Comparatively, labelling work between models 13–15 (+1970 labelled olives) yielded significant metric gains, including a 0.079 improvement in precision and a 0.239 increase in recall, making the effort worthwhile. However, between models 15–17 (+1999 labelled olives), the gains were smaller, with a precision increase of just 0.019 and recall of 0.015. With these minimal improvements it was decided to conclude this process and select model #17 as the olive tree counting detection model, achieving a high accuracy rate of 0.865, which can be considered very reliable.

In summary, the model selected for large-scale olive tree counting (model #17) achieved, after 50 epochs, an accuracy of 0.865, a recall of 0.851, an mAP@0.5 of 0.896, and an mAP@0.5:0.95 of 0.315, with the learning curves shown in Figure 6. To obtain this model, 17,013 olive trees were manually labelled across 159 plots (approximately 118 hectares), which were randomly selected from the 48,530 olive plots stored in our system’s database.

Finally, this olive tree model (model #17) was used to perform large-scale identification of olive trees in the remaining 48,371 plots (an example is shown in Figure 7). The result stored in the database is the olive density, which is the plot area divided by the corresponding number of olive trees. This process required approximately 26 days of computation.

This count of olive trees is a key element in the entire study, as it is essential for calculating the density (olive trees/area) for each of the 48,371 plots. As previously explained, this process of counting and calculating density is not routinely conducted in Extremadura; therefore, no ground-truth data exist for these plots. This absence highlights the critical role of the counting and density calculation process described earlier. Recognising that any error in the initial count could directly impact the quality and reliability of the developed model, we requested feedback from the Junta de Extremadura to validate our approach.

The validation was conducted using the “field verification” system, wherein personnel physically visit plots to count olive trees on-site. To ensure representativeness, feedback was obtained for a diverse subset of plots, covering a range of tree densities (low, medium, and high). Additionally, this validation process allowed us to assess error patterns more closely, identifying that errors were minimal in homogeneous plots and slightly higher in regions with irregular planting. This independent verification confirmed the reliability of our counting method, with an average error difference of 12.37 olive trees per hectare. The observed accuracy highlights the robustness of the developed model, even when applied to diverse field conditions. Such accuracy is well within acceptable ranges for practical applications in agricultural monitoring and subsidy management. Furthermore, this level of precision supports the validity of using our model as a cost-effective alternative to traditional field-based measurements. The supporting data and comparisons can be found in the annex uploaded (available for download at https://doi.org/10.5281/zenodo.14524441). By exclusively using YOLOv7 on orthophotos, we ensured the reliability of the tree count data, which are a critical input for training the regression model applied to Sentinel-2 data. This separation of data sources and methodologies was essential for the success of this study.

2.4. Creation and Training of the Olive Density Estimation Model

The main objective of this study was to infer olive tree density within a plot using only data from Sentinel-2 images. For the 48,530 olive plots, we had Sentinel-2 image data (obtained as described in Section 2.2) and the number of olive trees in each of these plots (obtained from orthophotos as described in Section 2.3), as well as the area of each plot. Using these data, the aim was to identify a correlation between olive density and the PMC of the plots. The Random Forest (RF) algorithm, which has been shown to outperform other machine learning algorithms applied in similar domains [31,32,33], was used for this purpose. Specifically, the random forest regressor (RFR) algorithm provided by the Python library “scikit-learn” (https://scikit-learn.org/1.5/modules/generated/sklearn.ensemble.RandomForestRegressor.html, accessed on 16 September 2024) was chosen, as it is specially designed for regression problems like this one. This type of algorithm uses multiple decision trees to improve prediction capability and reduce the risk of overfitting. Each decision tree is trained with a random sample of data, and the predictions from all trees are averaged to produce the final result. The hyperparameters used for the algorithm are those proposed by [31], where optimisations are performed with Grid Search, with a RFR of 100 n_estimators and a max_depth of 20.

The model was provided with all values from the 12 Sentinel-2 bands stored in the PMC. Although other experimental approaches could have been explored, such as selecting indices (NDVI, NWDI, etc.) or specific band combinations, previous experiments (such as [34]) have shown that models perform better when more raw data are provided, as the model itself is responsible for weighting the information.

For training, the data (Sentinel images, number of olive trees, and plot area) from the 48,530 plots were divided into training sets based on [35], which suggests that, for datasets with a sample size between 100 and 1,000,000, the optimal split is 70% for training and 30% for testing. To ensure the presence of sufficient data that were not biassed by training, the test set was further divided into 15% validation and 15% test sets (https://www.v7labs.com/blog/train-validation-test-set, accessed on 2 September 2024), with the validation set used during training and the test set used for model evaluation. From the 41,250 plots in the train and validation divisions, the PMC values for each of the Sentinel-2 bands for all available dates during the phenological year 2022, from 1 October 2022 to 30 September 2023, were collected, along with the number of olive trees obtained through the process described in Section 2.3.

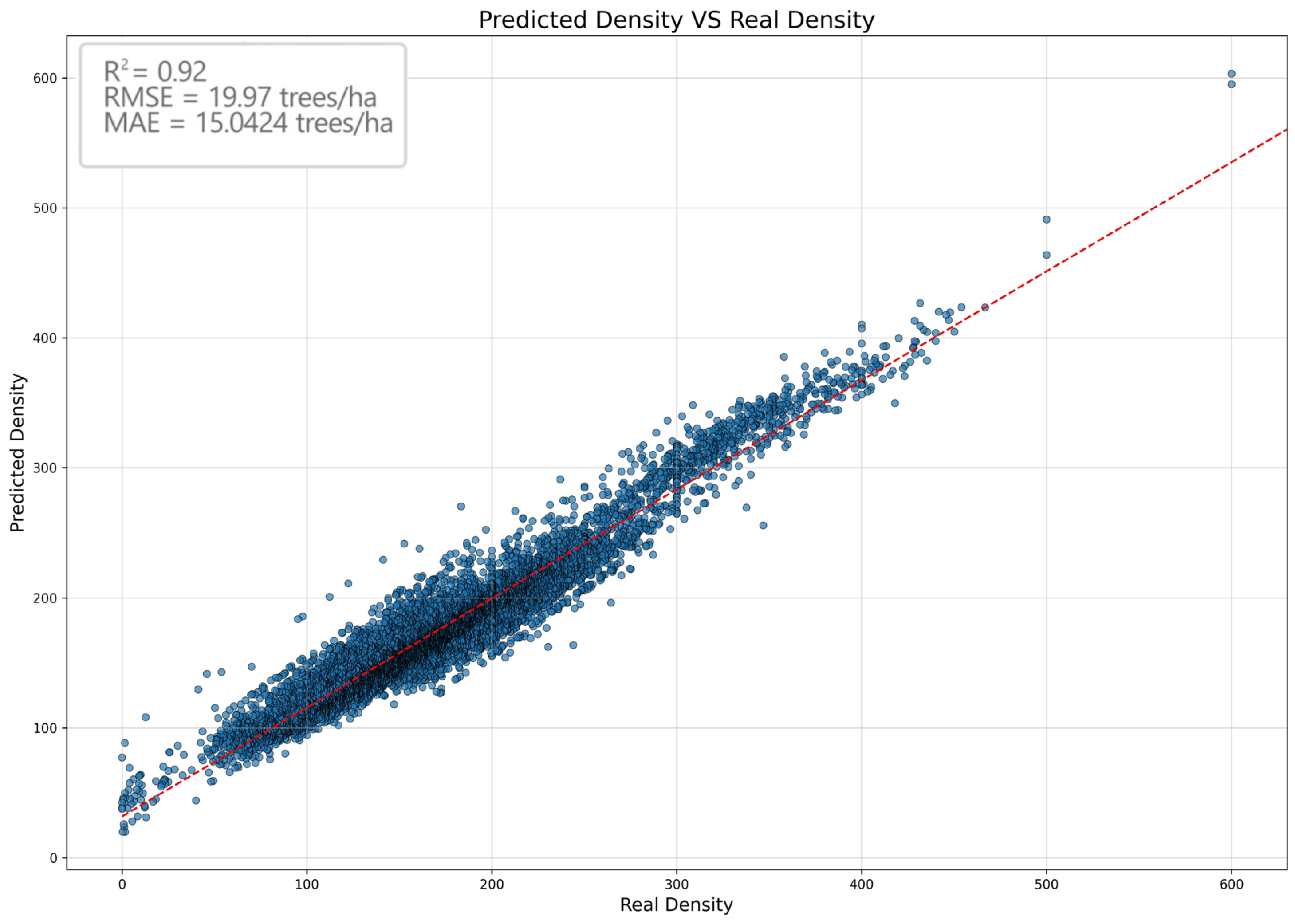
3. Results and Discussion

The experimental results involved using RFR with PMC data (mean values from the 61 images with the 12 Sentinel-2 bands) and olive density found in the 41,250 plots. The main objective of the study was to examinate the degree of concordance between the PMC value and the predicted number of olive trees. The following average results were obtained for the tests:

-

Mean Squared Error (MSE): 2283.3388: This metric measures the average of squared errors, that is, the difference between predicted and actual values squared. Squaring the errors magnifies them, giving more weight to larger errors and thus penalising them more heavily.

-

Root Mean Squared Error (RMSE): 47.7842: RMSE helps interpret MSE in the same units as the target variable, aiding in understanding the magnitude of errors (by taking the square root of the MSE). Like MSE, RMSE penalises larger errors.

-

Mean Absolute Error (MAE): 28.9256: This metric calculates the average of absolute errors, i.e., the absolute difference between the predicted and actual values without penalising large prediction errors. This makes MAE more robust and provides a more realistic interpretation of the overall performance of the model, especially in the presence of outliers.

-

R-squared (R²): 0.8105: This metric measures the proportion of variance in the target variable that can be explained by the independent variables of the model. An R² value close to 1 indicates that the model effectively expresses the correlation between the input data and the predicted values.

The interpretation of these metrics can focus on olive tree density within plots, as this value is critical for many administrative agencies when granting subsidies. For example, in the case of the Junta de Extremadura, special subsidies are available when density exceeds 300 olive trees per hectare. The plots studied had densities below 2400 trees per hectare (ol/ha), but only 6817 exceeded the density of 300 ol/ha (14%). Within this context, the MSE value of 2283.3388 was within an acceptable range, indicating a good model fit. It should be noted that MSE does not share the same scale as the actual data and is sensitive to large errors, especially outliers, such as the 14% of plots with densities above 300 ol/ha. The RMSE of 47.7842 indicates that predictions do not significantly deviate at this density range. The resulting MAE of 28.9256 ol/ha indicates an average deviation of 1.20% of the maximum density (2400 ol/ha), which is acceptable given that most values are below 300 ol/ha, and this metric does not penalise large errors. The difference of 18.85 ol/ha between RMSE and MAE suggests the presence of outliers. Due to these outliers, MAE should be considered the more important metric because it provides a better representation of the real average error value. The R² metric, with a value of 0.8105, suggests that the model captures most of the data’s trends. These metrics indicate that there is a correlation between the values calculated and provided by Sentinel-2, as well as the plot area in hectares, with the density of the plots.

The test set, previously separated as 15% of our total data (Section 2.4), included a total of 7280 plots, which were used to evaluate how the system performs with data it had not seen before, as these plots were not part of the training or validation processes. This test set allowed us to assess the model’s ability to make accurate predictions on completely independent data. The data used for testing are very diverse, where the randomly selected enclosures have a real density between 0 and 700 and an area between 0.01 ha and 78.63 ha (Table OliveAreaRangeTable available for download at https://doi.org/10.5281/zenodo.14614777, and data are represented in Figure 8).

It is important to highlight that olive tree densities show significant variability across all area ranges, with the most pronounced variation observed in smaller plots (0–5 hectares). In these small areas, real densities range widely from 0 to 600 trees per hectare, while the median density typically falls between 140 and 180 trees per hectare. Given this variability, it becomes essential to incorporate plantation area as a variable during both model training and subsequent predictions. This approach can help establish a more robust correlation not only between spectral indices (PMC) and density, but also with plantation size, ultimately improving the accuracy and reliability of density estimations across different plot scales.

For each plot in the test set, the Random Forest Regressor (RFR) model was provided with the plot area and all relevant data associated with the plot obtained from Sentinel-2. The input data included the PMC values extracted from the Sentinel-2 images (Section 2.2). The goal was to predict the tree density for each plot using only these characteristics.

Once the RFR model generated tree density predictions for the plots, these predictions were compared to the actual density values calculated using the YOLOv7 system, as described and validated in Section 2.3. YOLOv7 provided an accurate count of the olive trees by processing high-resolution aerial images of the plots. By dividing the total number of trees detected using YOLOv7 by the area of each plot, the actual tree density was obtained for comparison.

The results of the direct comparison between the predicted density (RFR) and the actual density (YOLOv7) are shown in the scatter plot in Figure 9. The attached table (downloadable at https://doi.org/10.5281/zenodo.14017156) contains, for the 7280 analysed enclosures, all the values between their prediction and their actual density.

Upon analysing the prediction results for the 7280 plots, comparing the density predicted by the RFR model and the density obtained using YOLOv7, an RMSE of 19.97 trees/ha and an MAE of 15.0424 trees/ha were obtained, with an R² of 0.92. These values demonstrate a strong relationship between the predicted and observed densities, suggesting that the model can make accurate and satisfactory predictions. These values were an improvement over the model training metrics, suggesting that the model had successfully learned the general patterns from the training data and was capable of generalising well with real data. Consultations with officials from the payment agency in Extremadura indicated that these values are highly acceptable for determining plot density and allocating the relevant economic subsidies.

When applying an error threshold of 15 ol/ha, a total of 4470 plots (61.4% of the plots) met this criterion. For plots with an error between 15 and 30 ol/ha, there were 1700 plots (23.35%). Plots with an error greater than 30 ol/ha numbered 1110 (15.25%).

The dataset was categorised into 100-hectare ranges to explore potential improvements in our model. The data are presented in

Table 2. Dataset divided into 100-hectare ranges, showing the trends in model predictions across different olive plantation real density intervals (0–100, 100–200, 200–400, and 400–700 trees per hectare) with low, aperture, close, high aperture, and high values.

Real Density Range	Low	Aperture (Q1)	Close (Median)	High Aperture (Q3)	High
0–100	20.02607737	91.53829665	100.63791	111.7480847	185.9161699
100–200	94.37370502	129.4377352	153.1214327	173.1675677	270.48398
200–300	154.322933	201.6940327	217.7084302	238.5834046	336.4272699
300–400	255.9488633	308.8662211	325.5536854	344.8509101	389.2324947
400–500	349.8323968	373.2557864	382.5139817	399.8740504	426.781692
500–600	463.8554844	470.6864178	477.5173513	484.3482847	491.1792182
600–700	595.0706677	597.1009745	599.1312812	601.161588	603.1918948

and are visualised with a boxplot in Figure 10.

The findings reveal different patterns across various density ranges. In the low-density categories, those from 0 to 100 hectares, there is greater variation, with broader interquartile ranges and more spread-out values. This points to a higher level of uncertainty in predictions for sparse olive orchards, where the spectral data may be more irregular or difficult to differentiate, possibly due to lower plot sizes. As the density increases (200–400 trees per hectare), the predictions become more consistent, with narrower interquartile ranges and values that align more closely with actual measurements. This shows that the model is more reliable for moderately dense plantations, where the spectral data are more consistent.

In the highest-density ranges (400–700 trees per hectare), the prediction variability significantly drops, with narrower interquartile ranges and fewer extreme values. This suggests that the model performs more reliably and accurately in densely planted orchards, where the spectral and spatial patterns are clearer and more easily detected.

This analysis demonstrates the model’s strong performance in moderate- to high-density plantations, but also highlights higher prediction uncertainty in areas with lower tree density. These results underline the need to account for density-related factors when evaluating model performance and suggest opportunities for further refinement of predictive models in the future.

Based on these data, the performance of the model can be considered especially satisfactory, as the majority of predictions (61.4%) fell within the 15 ol/ha error threshold. This indicates that the model is sufficiently accurate to meet the operational and accuracy requirements set for density estimation in this context.

4. Conclusions

This study successfully develops a method to estimate olive tree density within a plot using only Sentinel-2 images, despite their relatively low resolution. The proposed approach is particularly useful in situations where high-resolution orthophotos are unavailable for accurate tree counting, primarily due to budget constraints that prevent periodic flights.

The method is suitable for applications where absolute precision is not required, allowing for a margin of error below 15.04 trees per hectare (ol/ha). This makes it a viable solution for agencies and organisations that need annual olive density estimates, especially in situations where plots with densities of over 300 ol/ha need to be distinguished, as is the case for certain administrative subsidies managed in Extremadura, Spain.

Although this study focuses on olive groves, the approach could potentially be extrapolated to other types of fruit trees, forest masses, or woodlands, where tree identification and counting follow similar patterns and where the plantations and trees are clearly separated from each other, as is typically observed in traditional or intensive olive plantation systems. In these types of plantations, the trees are arranged in an orderly manner with sufficient spacing between them, ensuring that each tree can be individually distinguished. The novelty of this work lies in the first-time application of Sentinel-2 data and Random Forest Regression to estimate olive tree density at the plot level. Previous studies have focused on broader tasks, such as crop classification or vegetation health monitoring, but not on tree density estimation for specific crops. This targeted practical application addresses a relevant real-world gap. Additionally, this method provides an efficient alternative for performing this procedure annually without relying on orthophoto flights.

It is important to note that the primary goal of this study was to establish a relationship between the satellite image data of olive plots and the actual density of these plots, rather than experimentally identifying the most suitable algorithms to achieve this. While the technique employed, RFR, successfully achieved highly suitable values, other algorithms should be tested if the objective is to achieve possible improvements, such as having lower error deviations.

We have clarified that the method presented in this study is specifically designed for traditional and intensive plantations, where the orderly distribution of olive trees allows for effective tree detection using YOLOv7 applied to orthophotos. However, the method’s performance is not directly transferable to super-intensive plantations (hedgerows) or plots with irregularly spaced trees. To apply the methodology to such scenarios, significant adaptations would be required, including the use of segmentation algorithms to address overlapping crowns and denser planting patterns.

It must also be recognised that the experimentation carried out in this study is deliberately focused on a specific and partial case: olive groves in traditional and intensive plantation systems within the Extremadura region. While this provides strong evidence for the method’s efficacy in such contexts, it is only the beginning of its potential applications. Future research could explore its broader utility across diverse agricultural systems and environmental scenarios.

Although the primary objective of this study was to estimate olive tree density using the Random Forest Regressor algorithm and data provided by Sentinel-2, there are areas where tree detection could be improved. One such area is the previously mentioned implementation of segmentation algorithms, which offer a more precise approach in complex situations, such as identifying trees in forests, trees hidden under others (sub-canopy trees), overlapping trees, or those trees that are close to each other. The use of segmentation techniques would address the limitations presented by the YOLOv7 model, such as those mentioned previously. By implementing these algorithms, not only could detection be improved in denser or more irregular olive groves, but it would also open the possibility of applying this approach to other types of plantations, such as fruit trees or forests, where tree distribution patterns are less uniform and more complex to analyse.

Thus, segmentation would act as a complementary tool for tree detection, mitigating the weaknesses of the current approach and expanding the range of scenarios in which the methodology could be successfully applied.

Additionally, incorporating LiDAR (Light Detection and Ranging) data could be a game changer. LiDAR technology provides precise three-dimensional information about the structure of vegetation and the terrain, which could significantly enhance tree detection accuracy, especially in complex or dense environments where traditional remote sensing methods face challenges.

To increase the model’s accuracy and improve its applicability, additional experiments should be conducted to analyse plots considering specific factors such as terrain slope and predominant orientation, as these elements can significantly influence tree growth by affecting sunlight, water, and resource availability.

It is also important to note that certain complementary data, such as green cover, could not be considered in this study due to unavailability from the sources used. However, its inclusion could represent a significant turning point in future work, as this information would improve model accuracy in various aspects, such as providing a more detailed view of vegetation in plots, facilitating differentiation between real olive trees and other elements that may introduce noise into the data, such as the overgrowth of grasses or weeds. Such growth can generate anomalous values or overestimations in metrics derived from Sentinel-2 images and incorrect density predictions. Grouping cases with similar characteristics could lead to more accurate predictions with smaller error margins, further optimising the proposed method.

The methodological framework established here is adaptable and opens avenues for diverse applications. By refining the method and adapting it to new contexts, such as irregularly spaced trees or high-density plantations, researchers can expand its applicability to meet the challenges of modern precision agriculture and environmental monitoring.

In addition to subsidy allocation, this method offers broader practical applications in agricultural and environmental contexts. For instance, it could enable early detection of plantation anomalies, such as tree mortality, disease outbreaks, or stress caused by water scarcity. This information could support timely interventions to prevent further damage or loss. Moreover, annual density monitoring may help optimise resource distribution, such as water or fertilisers, or guide replanting efforts to increase productivity. Furthermore, the method could contribute to post-catastrophe assessments by rapidly evaluating damage caused by extreme weather events, fires, or droughts.