Towards the Optimization of TanSat-2: Assessment of a Large-Swath Methane Measurement
Abstract
:1. Introduction
2. Data and Methods
2.1. Satellite Measurement Configuration
2.1.1. Pseudo XCH4 Measurements Setup
2.1.2. XCH4 Error Scenarios
2.1.3. Large-Swath Orbits and Tansat-2 Elliptical Orbit
2.2. Observation System Simulation Experiments
3. Results
3.1. Control Experiment
3.2. Monthly and Weekly a Posteriori Flux Estimates
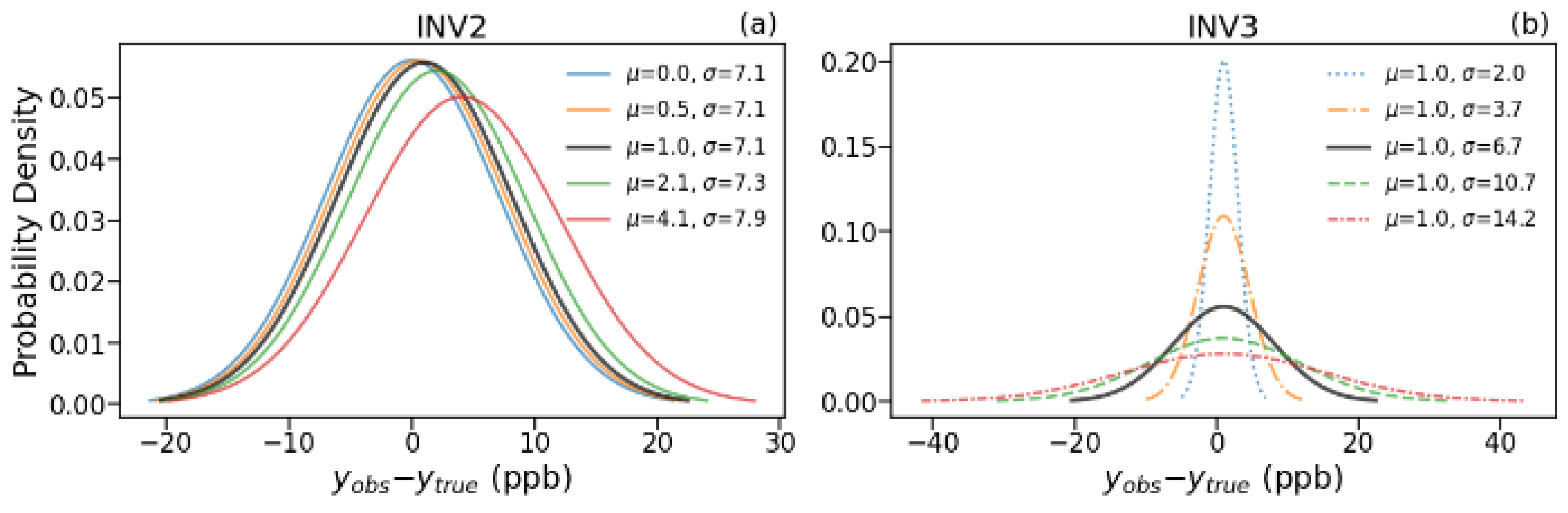
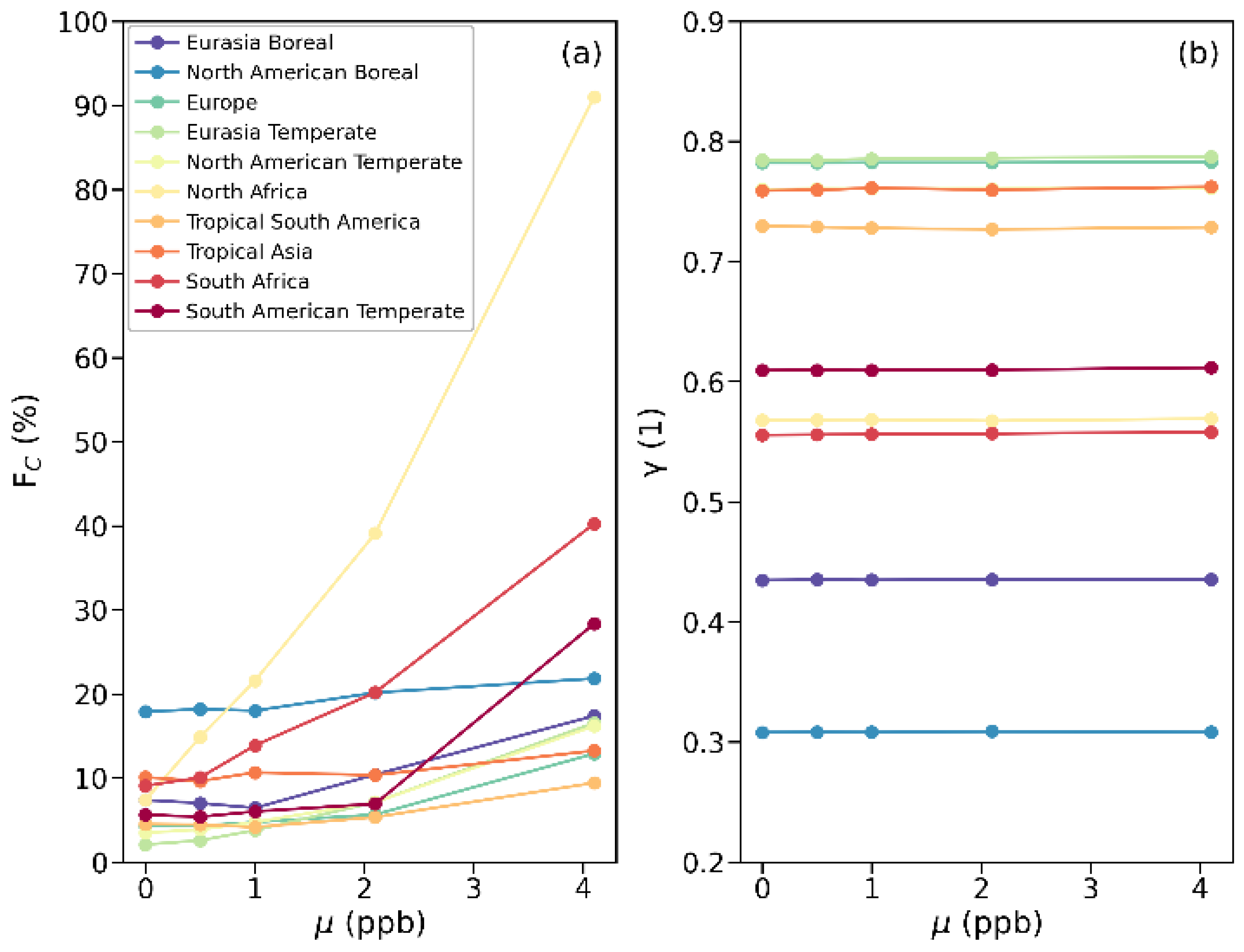
3.3. Sensitivity of a Posteriori Flux Estimates to Systematic Errors
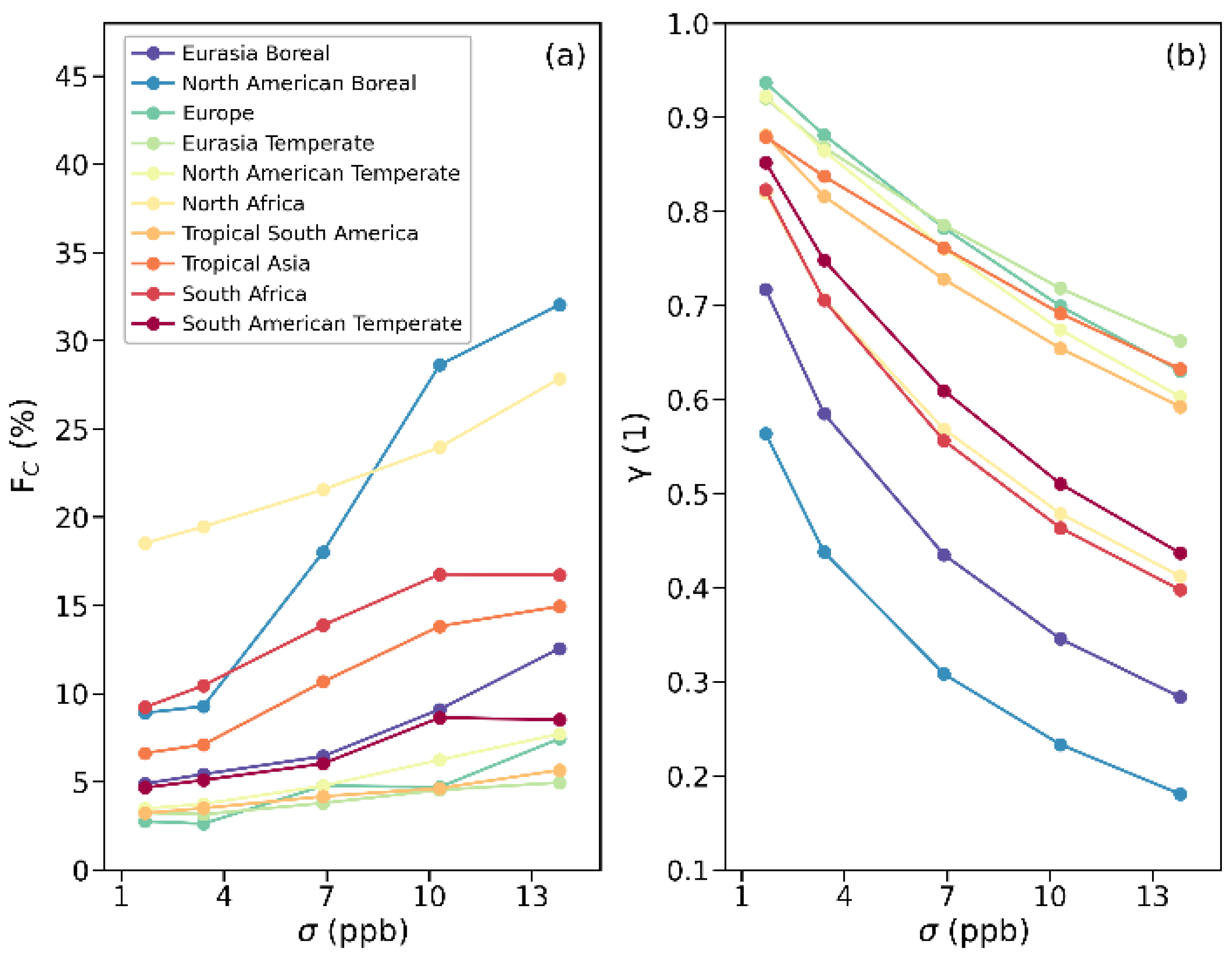
3.4. Sensitivity of Inverted Fluxes to Random Errors
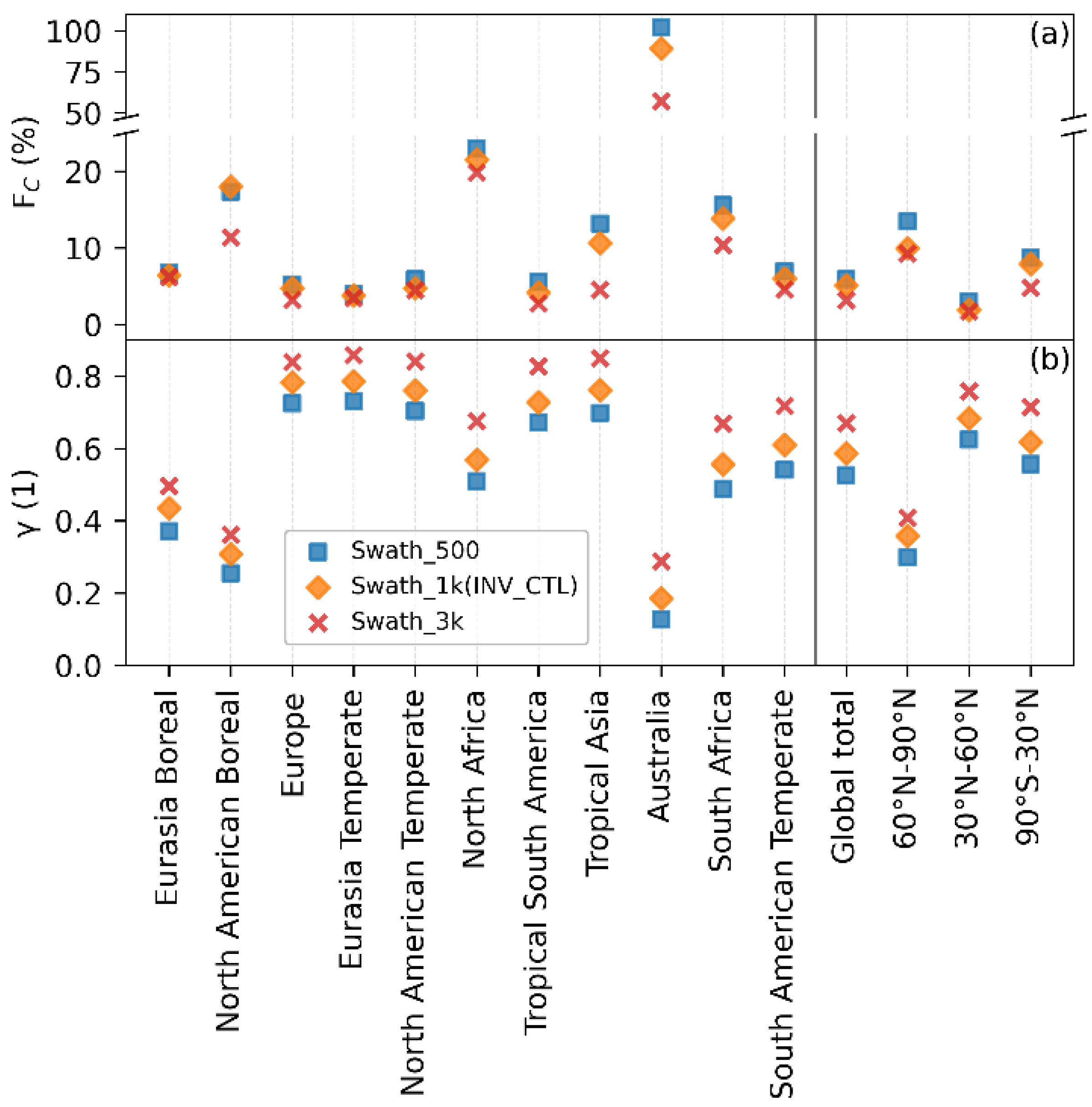
3.5. Sensitivity of Inverted Fluxes to Swath Width
3.6. Elliptical Medium Earth Orbit for TanSat-2
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, S.; Lin, X.; Thompson, R.L.; Xi, Y.; Liu, G.; Hauglustaine, D.; Lan, X.; Poulter, B.; Ramonet, M.; Saunois, M.; et al. Wetland Emission and Atmospheric Sink Changes Explain Methane Growth in 2020. Nature 2022, 612, 477–482. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Parker, R.J.; Lunt, M.F.; Bösch, H. Methane Emissions Are Predominantly Responsible for Record-Breaking Atmospheric Methane Growth Rates in 2020 and 2021. Atmos. Chem. Phys. 2023, 23, 4863–4880. [Google Scholar] [CrossRef]
- Palmer, P.I.; Feng, L.; Lunt, M.F.; Parker, R.J.; Bösch, H.; Lan, X.; Lorente, A.; Borsdorff, T. The Added Value of Satellite Observations of Methane Forunderstanding the Contemporary Methane Budget. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20210106. [Google Scholar] [CrossRef]
- Jacob, D.J.; Varon, D.J.; Cusworth, D.H.; Dennison, P.E.; Frankenberg, C.; Gautam, R.; Guanter, L.; Kelley, J.; McKeever, J.; Ott, L.E.; et al. Quantifying Methane Emissions from the Global Scale down to Point Sources Using Satellite Observations of Atmospheric Methane. Atmos. Chem. Phys. 2022, 22, 9617–9646. [Google Scholar] [CrossRef]
- UNEP. United Nations Environment Programme/Climate and Clean Air Coalition. Global Methane Assessment: 2030 Baseline Report; UNEP: Nariobi, Kenya, 2022. [Google Scholar]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noël, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY: Mission Objectives and Measurement Modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef]
- Yokota, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global Concentrations of CO2 and CH4 Retrieved from GOSAT: First Preliminary Results. Sola 2009, 5, 160–163. [Google Scholar] [CrossRef]
- Imasu, R.; Matsunaga, T.; Nakajima, M.; Yoshida, Y.; Shiomi, K.; Morino, I.; Saitoh, N.; Niwa, Y.; Someya, Y.; Oishi, Y.; et al. Greenhouse Gases Observing SATellite 2 (GOSAT-2): Mission Overview. Prog. Earth Planet. Sci. 2023, 10, 33. [Google Scholar] [CrossRef]
- Lu, X.; Jacob, D.J.; Zhang, Y.; Maasakkers, J.D.; Sulprizio, M.P.; Shen, L.; Qu, Z.; Scarpelli, T.R.; Nesser, H.; Yantosca, R.M.; et al. Global Methane Budget and Trend, 2010–2017: Complementarity of Inverse Analyses Using in Situ (GLOBALVIEWplus CH4 ObsPack) and Satellite (GOSAT) Observations. Atmos. Chem. Phys. 2021, 21, 4637–4657. [Google Scholar] [CrossRef]
- Qu, Z.; Jacob, D.J.; Bloom, A.A.; Worden, J.R.; Parker, R.J.; Boesch, H. Inverse Modeling of 2010–2022 Satellite Observations Shows That Inundation of the Wet Tropics Drove the 2020–2022 Methane Surge. Proc. Natl. Acad. Sci. USA 2024, 121, e2402730121. [Google Scholar] [CrossRef] [PubMed]
- Stavert, A.; Saunois, M.; Canadell, J.; Poulter, B.; Jackson, R.; Regnier, P.; Lauerwald, R.; Raymond, P.; Allen, G.; Patra, P.; et al. Regional Trends and Drivers of the Global Methane Budget. Glob. Chang. Biol. 2022, 28, 182–200. [Google Scholar] [CrossRef]
- Yin, Y.; Chevallier, F.; Ciais, P.; Bousquet, P.; Saunois, M.; Zheng, B.; Worden, J.; Bloom, A.A.; Parker, R.J.; Jacob, D.J.; et al. Accelerating Methane Growth Rate from 2010 to 2017: Leading Contributions from the Tropics and East Asia. Atmos. Chem. Phys. 2021, 21, 12631–12647. [Google Scholar] [CrossRef]
- Zhang, Y.; Jacob, D.J.; Lu, X.; Maasakkers, J.D.; Scarpelli, T.R.; Sheng, J.-X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Chang, J.; et al. Attribution of the Accelerating Increase in Atmospheric Methane during 2010–2018 by Inverse Analysis of GOSAT Observations. Atmos. Chem. Phys. 2021, 21, 3643–3666. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Zhu, S.; Parker, R.J.; Liu, Y. Tropical Methane Emissions Explain Large Fraction of Recent Changes in Global Atmospheric Methane Growth Rate. Nat. Commun. 2022, 13, 1378. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Butz, A.; Hasekamp, O.; aan de Brugh, J.; Schneider, A.; Wu, L.; Hase, F.; Kivi, R.; Wunch, D.; et al. Methane Retrieved from TROPOMI: Improvement of the Data Product and Validation of the First 2 Years of Measurements. Atmos. Meas. Tech. 2021, 14, 665–684. [Google Scholar] [CrossRef]
- Gao, M.; Xing, Z.; Vollrath, C.; Hugenholtz, C.H.; Barchyn, T.E. Global Observational Coverage of Onshore Oil and Gas Methane Sources with TROPOMI. Sci. Rep. 2023, 13, 16759. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Jacob, D.J.; Gautam, R.; Omara, M.; Scarpelli, T.R.; Lorente, A.; Zavala-Araiza, D.; Lu, X.; Chen, Z.; Lin, J. National Quantifications of Methane Emissions from Fuel Exploitation Using High Resolution Inversions of Satellite Observations. Nat. Commun. 2023, 14, 4948. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Gautam, R.; Pandey, S.; Omara, M.; Maasakkers, J.D.; Sadavarte, P.; Lyon, D.; Nesser, H.; Sulprizio, M.P.; Varon, D.J.; et al. Quantifying Methane Emissions from the Largest Oil-Producing Basin in the United States from Space. Sci. Adv. 2020, 6, eaaz5120. [Google Scholar] [CrossRef] [PubMed]
- Nesser, H.; Jacob, D.J.; Maasakkers, J.D.; Lorente, A.; Chen, Z.; Lu, X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Winter, M.; et al. High-Resolution US Methane Emissions Inferred from an Inversion of 2019 TROPOMI Satellite Data: Contributions from Individual States, Urban Areas, and Landfills. Atmos. Chem. Phys. 2024, 24, 5069–5091. [Google Scholar] [CrossRef]
- Hamburg, S.; Gautam, R.; Zavala-Araiza, D. MethaneSAT—A New Tool Purpose-Built to Measure Oil and Gas Methane Emissions from Space. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 31 October 2022; SPE: Abu Dhabi, United Arab Emirates, 2022; p. D011S007R002. [Google Scholar]
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.; Yang, D.; Yin, Z.; Gu, S.; Tian, L.; Lu, N.; et al. The TanSat Mission: Preliminary Global Observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Cai, Z.; Chen, X.; Yao, L.; Lu, D. First Global Carbon Dioxide Maps Produced from TanSat Measurements. Adv. Atmos. Sci. 2018, 35, 621–623. [Google Scholar] [CrossRef]
- Ran, Y. TanSat: A New Star in Global Carbon Monitoring from China. Sci. Bull. 2019, 64, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Boesch, H.; Liu, Y.; Somkuti, P.; Cai, Z.; Chen, X.; Di Noia, A.; Lin, C.; Lu, N.; Lyu, D.; et al. Toward High Precision XCO2 Retrievals From TanSat Observations: Retrieval Improvement and Validation Against TCCON Measurements. J. Geophys. Res. Atmos. 2020, 125, e2020JD032794. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Liu, Y.; Boesch, H.; Yao, L.; Di Noia, A.; Cai, Z.; Lu, N.; Lyu, D.; Wang, M.; Wang, J.; et al. A New TanSat XCO2 Global Product towards Climate Studies. Adv. Atmos. Sci. 2021, 38, 8–11. [Google Scholar] [CrossRef]
- Yao, L.; Yang, D.; Liu, Y.; Wang, J.; Liu, L.; Du, S.; Cai, Z.; Lu, N.; Lyu, D.; Wang, M.; et al. A New Global Solar-Induced Chlorophyll Fluorescence (SIF) Data Product from TanSat Measurements. Adv. Atmos. Sci. 2021, 38, 341–345. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, F.; Liu, Y.; Yang, D.; Wu, M.; He, W.; Wang, J.; Wang, J.; Ju, W.; Chen, J.M. Global Terrestrial Ecosystem Carbon Flux Inferred from TanSat XCO2 Retrievals. J. Remote Sens. 2022, 2022, 9816536. [Google Scholar] [CrossRef]
- Yang, D.; Hakkarainen, J.; Liu, Y.; Ialongo, I.; Cai, Z.; Tamminen, J. Detection of Anthropogenic CO2 Emission Signatures with TanSat CO2 and with Copernicus Sentinel-5 Precursor (S5P) NO2 Measurements: First Results. Adv. Atmos. Sci. 2023, 40, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Saunois, M.; Martinez, A.; Poulter, B.; Zhang, Z.; Raymond, P.; Regnier, P.; Canadell, J.G.; Jackson, R.B.; Patra, P.K.; Bousquet, P.; et al. Global Methane Budget 2000–2020. In Earth System Science Data Discussions; Copernicus Publications: Göttingen, Germany, 2024; pp. 1–147. [Google Scholar] [CrossRef]
- Houweling, S.; Bergamaschi, P.; Chevallier, F.; Heimann, M.; Kaminski, T.; Krol, M.; Michalak, A.M.; Patra, P. Global Inverse Modeling of CH4 Sources and Sinks: An Overview of Methods. Atmos. Chem. Phys. 2017, 17, 235–256. [Google Scholar] [CrossRef]
- Balasus, N.; Jacob, D.J.; Lorente, A.; Maasakkers, J.D.; Parker, R.J.; Boesch, H.; Chen, Z.; Kelp, M.M.; Nesser, H.; Varon, D.J. A Blended TROPOMI+GOSAT Satellite Data Product for Atmospheric Methane Using Machine Learning to Correct Retrieval Biases. Atmos. Meas. Tech. 2023, 16, 3787–3807. [Google Scholar] [CrossRef]
- Qu, Z.; Jacob, D.J.; Shen, L.; Lu, X.; Zhang, Y.; Scarpelli, T.R.; Nesser, H.; Sulprizio, M.P.; Maasakkers, J.D.; Bloom, A.A.; et al. Global Distribution of Methane Emissions: A Comparative Inverse Analysis of Observations from the TROPOMI and GOSAT Satellite Instruments. Atmos. Chem. Phys. 2021, 21, 14159–14175. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Hachmeister, J.; Vanselow, S.; Reuter, M.; Buschmann, M.; Bovensmann, H.; Burrows, J.P. Advances in Retrieving XCH4 and XCO from Sentinel-5 Precursor: Improvements in the Scientific TROPOMI/WFMD Algorithm. Atmos. Meas. Tech. 2023, 16, 669–694. [Google Scholar] [CrossRef]
- Chevallier, F.; Bréon, F.; Rayner, P.J. Contribution of the Orbiting Carbon Observatory to the Estimation of CO2 Sources and Sinks: Theoretical Study in a Variational Data Assimilation Framework. J. Geophys. Res. 2007, 112, 2006JD007375. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Guerlet, S.; Dils, B.; Aben, I.; Armante, R.; Bergamaschi, P.; Blumenstock, T.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparison and Quality Assessment of near-Surface-Sensitive Satellite-Derived CO2 and CH4 Global Data Sets. Remote Sens. Environ. 2015, 162, 344–362. [Google Scholar] [CrossRef]
- Aben, I.; Hasekamp, O.; Hartmann, W. Uncertainties in the Space-Based Measurements of CO2 Columns Due to Scattering in the Earth’s Atmosphere. J. Quant. Spectrosc. Radiat. Transf. 2007, 104, 450–459. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Vidot, J.; Aben, I. CH4 Retrievals from Space-based Solar Backscatter Measurements: Performance Evaluation against Simulated Aerosol and Cirrus Loaded Scenes. J. Geophys. Res. 2010, 115, 2010JD014514. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- von Clarmann, T.; Degenstein, D.A.; Livesey, N.J.; Bender, S.; Braverman, A.; Butz, A.; Compernolle, S.; Damadeo, R.; Dueck, S.; Eriksson, P.; et al. Overview: Estimating and Reporting Uncertainties in Remotely Sensed Atmospheric Composition and Temperature. Atmos. Meas. Tech. 2020, 13, 4393–4436. [Google Scholar] [CrossRef]
- Kiefer, M.; von Clarmann, T.; Funke, B.; García-Comas, M.; Glatthor, N.; Grabowski, U.; Kellmann, S.; Kleinert, A.; Laeng, A.; Linden, A.; et al. IMK/IAA MIPAS Temperature Retrieval Version 8: Nominal Measurements. Atmos. Meas. Tech. 2021, 14, 4111–4138. [Google Scholar] [CrossRef]
- Dils, B.; Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Parker, R.; Guerlet, S.; Aben, I.; Blumenstock, T.; Burrows, J.P.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparative Validation of GHG-CCI SCIAMACHY/ENVISAT and TANSO-FTS/GOSAT CO2 and CH4 Retrieval Algorithm Products with Measurements from the TCCON. Atmos. Meas. Tech. 2014, 7, 1723–1744. [Google Scholar] [CrossRef]
- Reuter, M.; Buchwitz, M.; Schneising, O.; Noël, S.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Di Noia, A.; Anand, J.; Parker, R.J.; et al. Ensemble-Based Satellite-Derived Carbon Dioxide and Methane Column-Averaged Dry-Air Mole Fraction Data Sets (2003–2018) for Carbon and Climate Applications. Atmos. Meas. Tech. 2020, 13, 789–819. [Google Scholar] [CrossRef]
- Parker, R.J.; Webb, A.; Boesch, H.; Somkuti, P.; Barrio Guillo, R.; Di Noia, A.; Kalaitzi, N.; Anand, J.S.; Bergamaschi, P.; Chevallier, F.; et al. A Decade of GOSAT Proxy Satellite CH4 Observations. Earth System Science Data 2020, 12, 3383–3412. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Martinez-Velarte, M.C.; Landgraf, J. Accounting for Surface Reflectance Spectral Features in TROPOMI Methane Retrievals. Atmos. Meas. Tech. 2023, 16, 1597–1608. [Google Scholar] [CrossRef]
- The International GEOS-Chem User Community Geoschem/Geos-Chem: GEOS-Chem 12.5.0 2019. Available online: https://zenodo.org/records/3403111 (accessed on 13 November 2019).
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Feng, L.; Liu, Y.; Wang, J.; Yang, D. Decadal Methane Emission Trend Inferred from Proxy GOSAT XCH4 Retrievals: Impacts of Transport Model Spatial Resolution. Adv. Atmos. Sci. 2022, 39, 1343–1359. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.; Boesch, H.; Dance, S. Estimating Surface CO2 Fluxes from Space-Borne CO2 Dry Air Mole Fraction Observations Using an Ensemble Kalman Filter. Atmos. Chem. Phys. 2009, 9, 2619–2633. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Bösch, H.; Parker, R.J.; Webb, A.J.; Correia, C.S.C.; Deutscher, N.M.; Domingues, L.G.; Feist, D.G.; Gatti, L.V.; et al. Consistent Regional Fluxes of CH4 and CO2 Inferred from GOSAT Proxy XCH4: XCO2 Retrievals, 2010–2014. Atmos. Chem. Phys. 2017, 17, 4781–4797. [Google Scholar] [CrossRef]
- Gurney, K.; Law, R.; Denning, S.; Rayner, P.; Baker, D.; Bousquet, P.; Bruhwiler, L.; Chen, Y.-H.; Ciais, P.; Fan, S.-M.; et al. Towards Robust Regional Estimates of CO2 Sources and Sinks Using Atmospheric Transport Models. Nature 2002, 415, 626–630. [Google Scholar] [CrossRef]
- Wu, K.; Yang, D.; Liu, Y.; Cai, Z.; Zhou, M.; Feng, L.; Palmer, P.I. Evaluating the Ability of the Pre-Launch TanSat-2 Satellite to Quantify Urban CO2 Emissions. Remote Sens. 2023, 15, 4904. [Google Scholar] [CrossRef]
- Lunt, M.F.; Palmer, P.I.; Feng, L.; Taylor, C.M.; Boesch, H.; Parker, R.J. An Increase in Methane Emissions from Tropical Africa between 2010 and 2016 Inferred from Satellite Data. Atmos. Chem. Phys. 2019, 19, 14721–14740. [Google Scholar] [CrossRef]
- Lunt, M.F.; Palmer, P.I.; Lorente, A.; Borsdorff, T.; Landgraf, J.; Parker, R.J.; Boesch, H. Rain-Fed Pulses of Methane from East Africa during 2018–2019 Contributed to Atmospheric Growth Rate. Environ. Res. Lett. 2021, 16, 024021. [Google Scholar] [CrossRef]
- Zhang, Z.; Poulter, B.; Feldman, A.; Ying, Q.; Ciais, P.; Peng, S.; Li, X. Recent Intensification of Wetland Methane Feedback. Nat. Clim. Chang. 2023, 13, 430–433. [Google Scholar] [CrossRef]
- Merbold, L.; Scholes, R.; Acosta, M.; Beck, J.; Bombelli, A.; Fiedler, B.; Grieco, E.; Helmschrot, J.; Hugo, W.; Kasurinen, V.; et al. Opportunities for an African Greenhouse Gas Observation System. Reg. Environ. Chang. 2021, 21, 104. [Google Scholar] [CrossRef]
- Nickless, A.; Scholes, R.J.; Vermeulen, A.; Beck, J.; Lopez-Ballesteros, A.; Ardö, J.; Karstens, U.; Rigby, M.L.; Kasurinen, V.; Pantazatou, K.; et al. Greenhouse Gas Observation Network Design for Africa. Tellus B 2020, 72, 1–30. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, T.; Yao, L.; Guo, D.; Fan, M.; Ren, X.; Li, M.; Wu, K.; Wang, J.; Cai, Z.; et al. Toward Establishing a Low-Cost UAV Coordinated Carbon Observation Network (LUCCN): First Integrated Campaign in China. Adv. Atmos. Sci. 2024, 41, 1–7. [Google Scholar] [CrossRef]
- Zhao, T.; Yang, D.; Guo, D.; Wang, Y.; Yao, L.; Ren, X.; Fan, M.; Cai, Z.; Wu, K.; Liu, Y. Low-Cost UAV Coordinated Carbon Observation Network: Carbon Dioxide Measurement with Multiple UAVs. Atmos. Environ. 2024, 332, 120609. [Google Scholar] [CrossRef]
- Rößger, N.; Sachs, T.; Wille, C.; Boike, J.; Kutzbach, L. Seasonal Increase of Methane Emissions Linked to Warming in Siberian Tundra. Nat. Clim. Chang. 2022, 12, 1031–1036. [Google Scholar] [CrossRef]
- Smith, S.; O’Neill, B.; Isaksen, K.; Noetzli, J.; Romanovsky, V. The Changing Thermal State of Permafrost. Nat. Rev. Earth Environ. 2022, 3, 10–23. [Google Scholar] [CrossRef]






| Reference Dataset | Period | TCCON Version | Mean Bias 1 (ppb) | Relative Bias 1 (ppb) | Precision 1 (ppb) | Reference |
|---|---|---|---|---|---|---|
| GOSAT OCFP/SRFP 2 | 2009.04–2011.04 | GGG2014 | 0.4/−2.5 | 6.0/3.0 | 18.1/14.9 | Dils et al. (2014) [41] |
| GOSAT OCPR/SRPR 2 | 2009.04–2011.04 | GGG2014 | 7.0/3.1 | 2.7/4.2 | 14.0/14.6 | Dils et al. (2014) [41] |
| Ensemble satellite-derived XCH4_EMMA data 3,6 (SCIAMCHY and GOSAT) | 2003–2018 | GGG2014 | −2.0 | 5.0 | 17.4 | Reuter et al. (2020) [42] |
| GOSAT-UoL proxy v9.0 4 | 2009.04–2019.12 | GGG2014 | 0.0 | 3.89 | 13.72 | Parker et al. (2020) [43] |
| GOSAT-UoL proxy v9.0 5 | 2019 | GGG2014 | −1.0 | 2.9 | / | Qu et al. (2021) [32] |
| TROPOMI-SRON v1.03 5 | 2019 | GGG2014 | −2.7 | 6.7 | / | Qu et al. (2021) [32] |
| TROPOMI-SRON uncorrected | 2018.03–2020.12 | GGG2014 | −14.6 | 9.5 | 12.7 | Lorente et al. (2023) [44] |
| TROPOMI-SRON v19_446 | 2018.03–2020.12 | GGG2014 | −5.3 | 5.1 | 11.9 | Lorente et al. (2023) [44] |
| TROPOMI-WFMD v1.8 6 | 2017.10–2022.04 | GGG2014 | / | 5.2 | 12.4 | Schneising et al. (2023) [33] |
| A blended TROPOMI and GOSAT 7 | 2018–2021 | GGG2020 | −2.9 | 4.4 | 11.9 | Balasus et al. (2023) [31] |
| Experiments | Swath Width (km) | Temporal Resolution | Observation Error | (ppb) | |
|---|---|---|---|---|---|
| (ppb) | (ppb) | ||||
| INV_CTL | 1000 | 1-week | 1.0 ± 0.9 | 6.9 ± 1.6 | 1.0 ± 7.1 |
| INV1_mon | / 1 | 1-month | / | / | / |
| INV2_no_bias | / | / | 0.0 ± 0.0 | / | 0.0 ± 7.1 |
| INV2_low_bias | / | / | 0.5 ± 0.5 | / | 0.5 ± 7.1 |
| INV2_high_bias | / | / | 2.1 ± 1.8 | / | 2.1 ± 7.3 |
| INV2_ext_bias | / | / | 4.1 ± 3.6 | / | 4.1 ± 7.9 |
| INV3_low_unc | / | / | / | 1.7 ± 0.4 | 1.0 ± 2.0 |
| INV3_re_low_unc | / | / | / | 3.4 ± 0.8 | 1.0 ± 3.7 |
| INV3_high_unc | / | / | / | 10.3 ± 2.5 | 1.0 ± 10.7 |
| INV3_ext_unc | / | / | / | 13.8 ± 3.3 | 1.0 ± 14.2 |
| INV4_sw_500 | 500 | / | 1.0 ± 0.9 | 6.9 ± 1.6 | 1.0 ± 7.1 |
| INV4_sw_3k | 3000 | / | 1.1 ± 0.9 | 7.1 ± 1.4 | 1.1 ± 7.3 |
| INV5_elliptical_1.5k | 1500 | 1.3 ± 1.0 | 6.9 ± 1.6 | 1.5 ± 7.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Yang, D.; Feng, L.; Tian, L.; Liu, Y.; Cao, J.; Wu, K.; Cai, Z.; Palmer, P.I. Towards the Optimization of TanSat-2: Assessment of a Large-Swath Methane Measurement. Remote Sens. 2025, 17, 543. https://doi.org/10.3390/rs17030543
Zhu S, Yang D, Feng L, Tian L, Liu Y, Cao J, Wu K, Cai Z, Palmer PI. Towards the Optimization of TanSat-2: Assessment of a Large-Swath Methane Measurement. Remote Sensing. 2025; 17(3):543. https://doi.org/10.3390/rs17030543
Chicago/Turabian StyleZhu, Sihong, Dongxu Yang, Liang Feng, Longfei Tian, Yi Liu, Junji Cao, Kai Wu, Zhaonan Cai, and Paul I. Palmer. 2025. "Towards the Optimization of TanSat-2: Assessment of a Large-Swath Methane Measurement" Remote Sensing 17, no. 3: 543. https://doi.org/10.3390/rs17030543
APA StyleZhu, S., Yang, D., Feng, L., Tian, L., Liu, Y., Cao, J., Wu, K., Cai, Z., & Palmer, P. I. (2025). Towards the Optimization of TanSat-2: Assessment of a Large-Swath Methane Measurement. Remote Sensing, 17(3), 543. https://doi.org/10.3390/rs17030543






