Hybrid Deterministic Sensing Matrix for Compressed Drone SAR Imaging and Efficient Reconstruction of Subsurface Targets
Abstract
:1. Introduction
- Hybrid sensing matrix: Initially, a chirp sensing matrix is designed to efficiently sample or sense chirp signals. Most of the currently operational SAR systems adopt chirp-based LFM signals. This makes the use of chirp-based sensing matrix particularly useful, as they preserve a good correlation with the incoming signals reflected from targets. Then, this paper proposes a hybrid deterministic sensing matrix that combines the chirp-based deterministic matrix and the stochastic random weights. The proposed matrix achieves improved recovery performance for sparse SAR targets, significantly reducing memory and computational burden.
- Efficient data recovery: The method addresses the limitations of conventional random and deterministic matrices, demonstrating superior performance in processing speed and recovery accuracy. By enabling efficient target recovery under high-clutter environments, the method supports lightweight drone SAR missions that are constrained by processing capacity and memory storage.
- Optimized for drone SAR applications: Tailored for lightweight drone platforms, the method ensures high-resolution imaging and effective detection of buried targets in cluttered environments. This property is highly desirable when the number of significant targets are limited and sparsely distributed in high-resolution SAR images. Field tests using a custom-built drone SAR platform validate that the method effectively recovers buried targets.
2. Compressive Sensing and SAR: An Overview
2.1. Compressive Sensing Theory
2.2. Chirp Sensing Matrix
2.3. Performance Metric and Problem Formulation
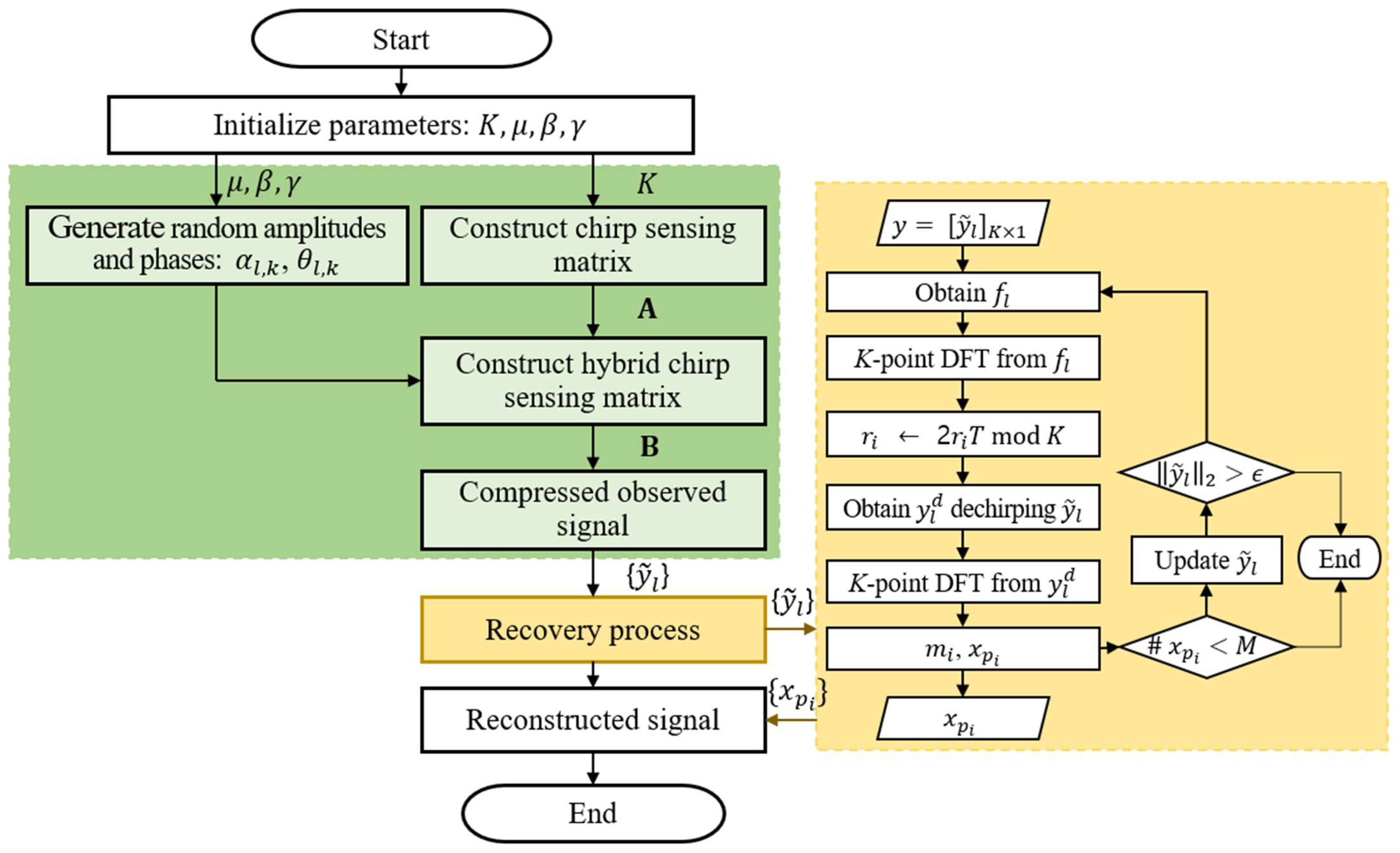
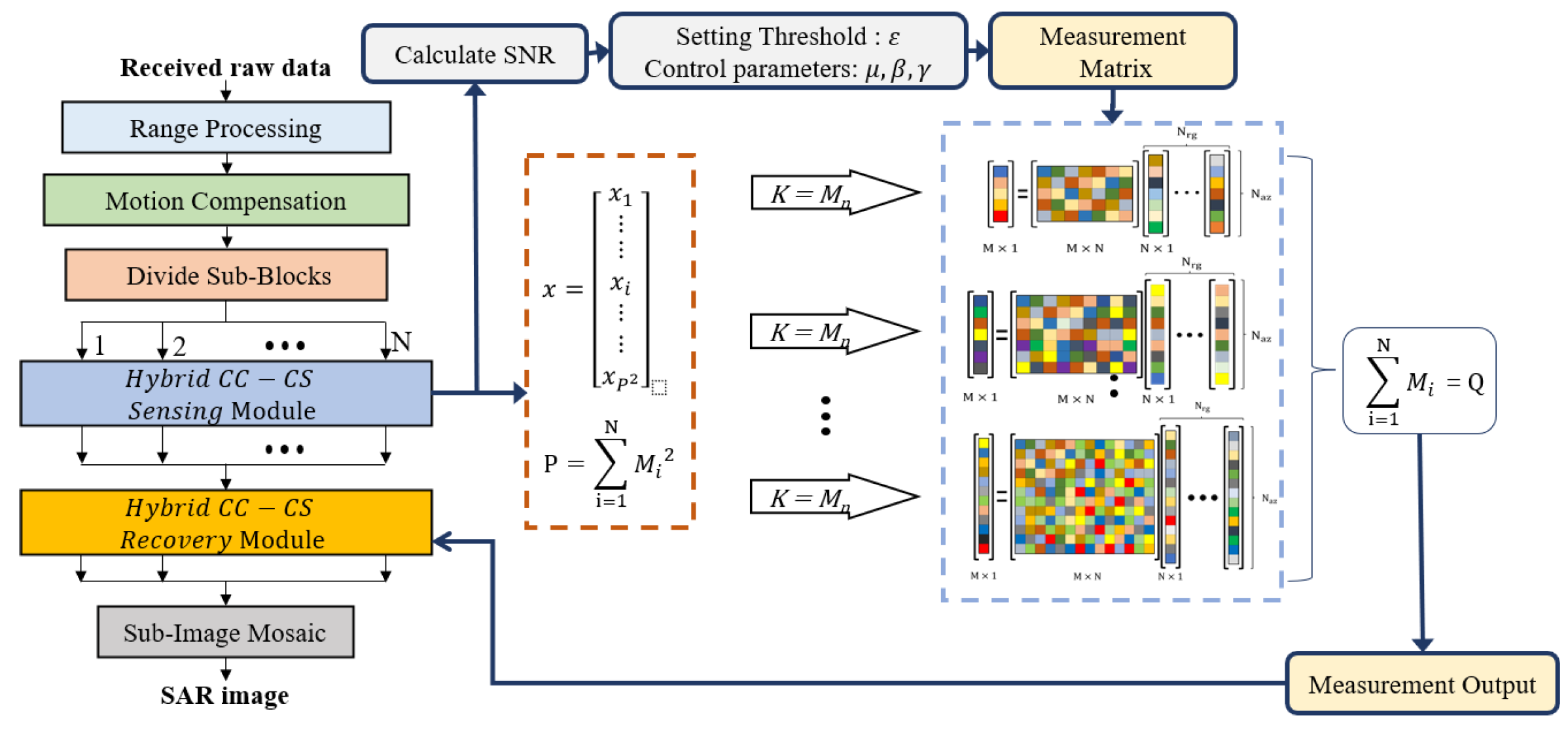
3. Proposed Hybrid CC-CS
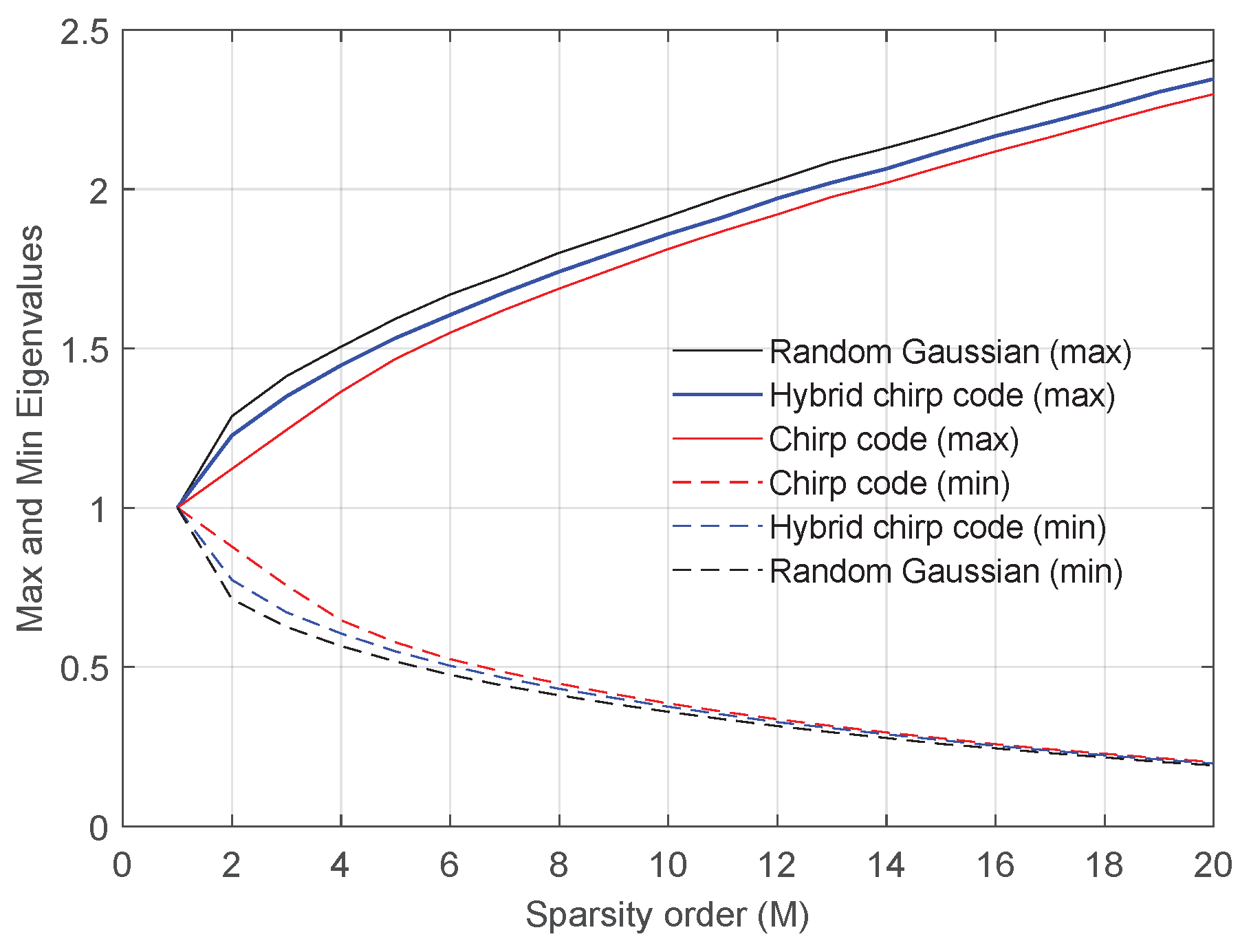
3.1. RIP Conditions
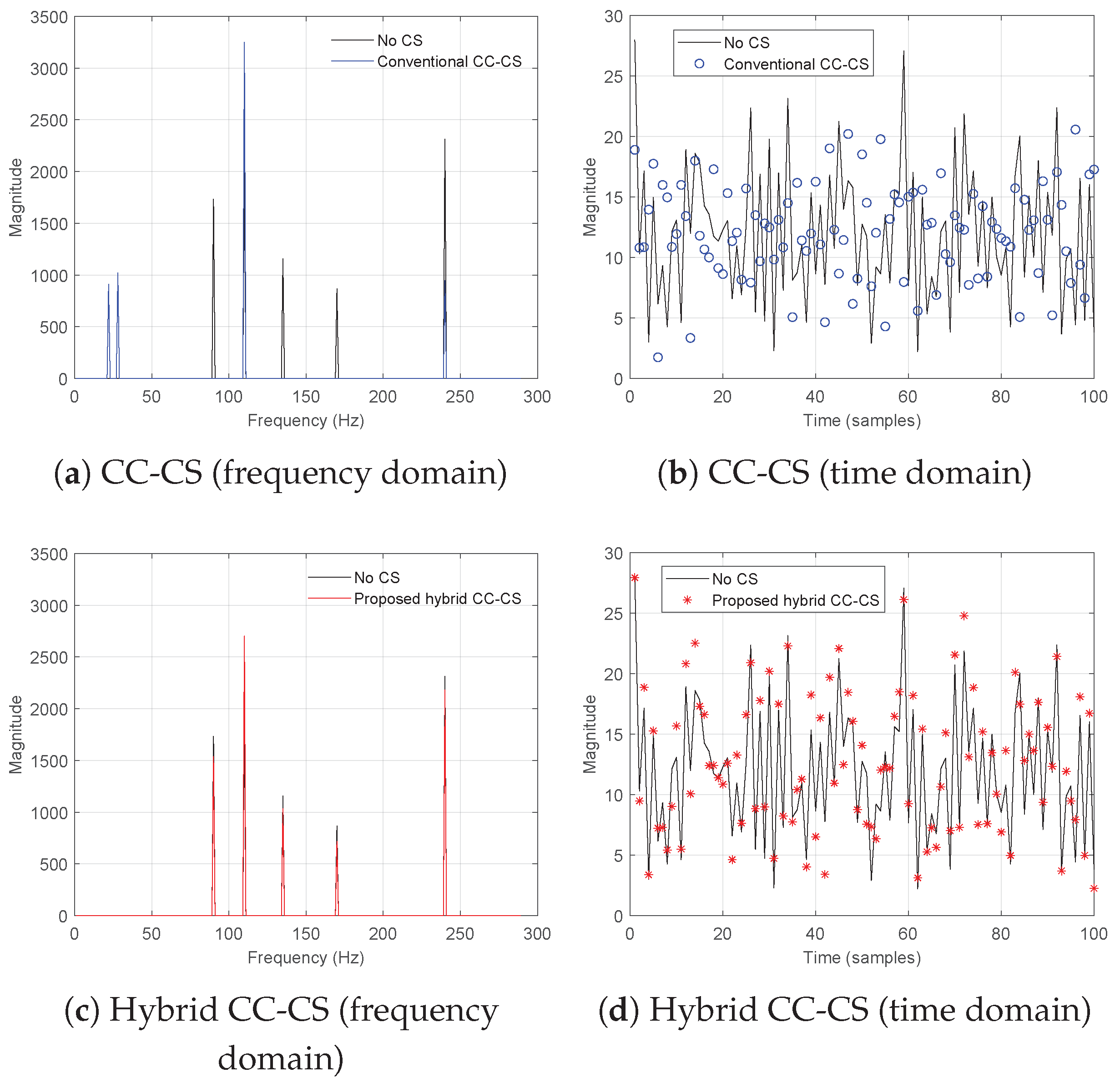
3.2. Hybrid CC-CS Reconstruction Performance
4. SAR Imaging Based on Proposed Sensing Matrix
4.1. SAR Imaging Using Undersampled Data
| Algorithm 1: Proposed hybrid CC-CS for fast SAR imaging |
1: Input: , , K, , 3: For to M do 4: Construct the concatenated sensing matrix: . 5: Compute the compressed measurement matrix: . 6: Compute from using (20) and take the K-point DFT. 7: Find the peak location in the frequency spectrum as mod K. 8: Obtain by dechirping : . 9: Take the K-point DFT of . 10: Find the peak position to , recover the corresponding value . 11: Update : for . 12: If , go to step 14. 13: end for 14: Obtain using . 15: Output: |
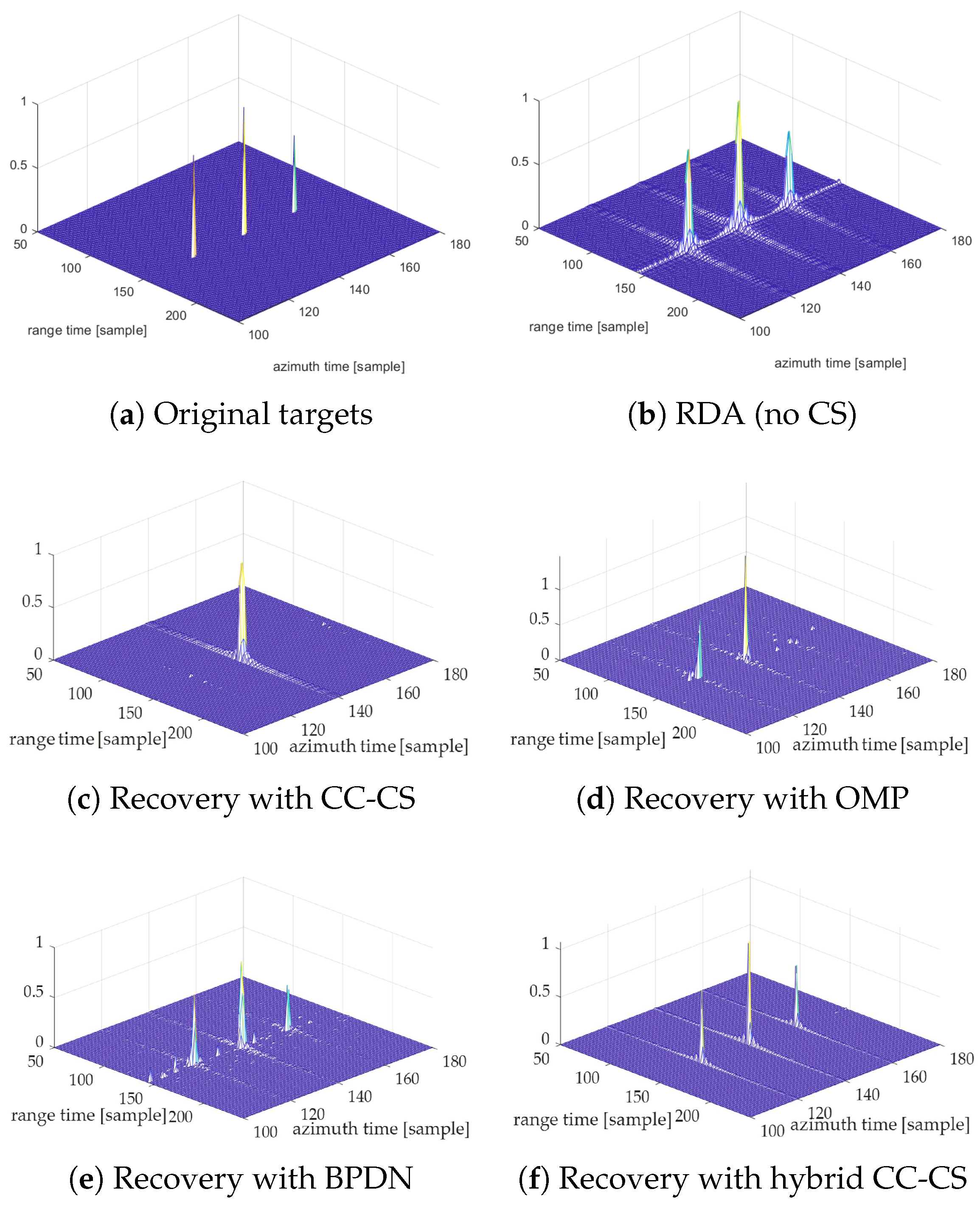
4.2. Modeling and Simulations for SAR Imaging
- RDA (no CS): The standard RDA is applied to the received echo signal without CS.
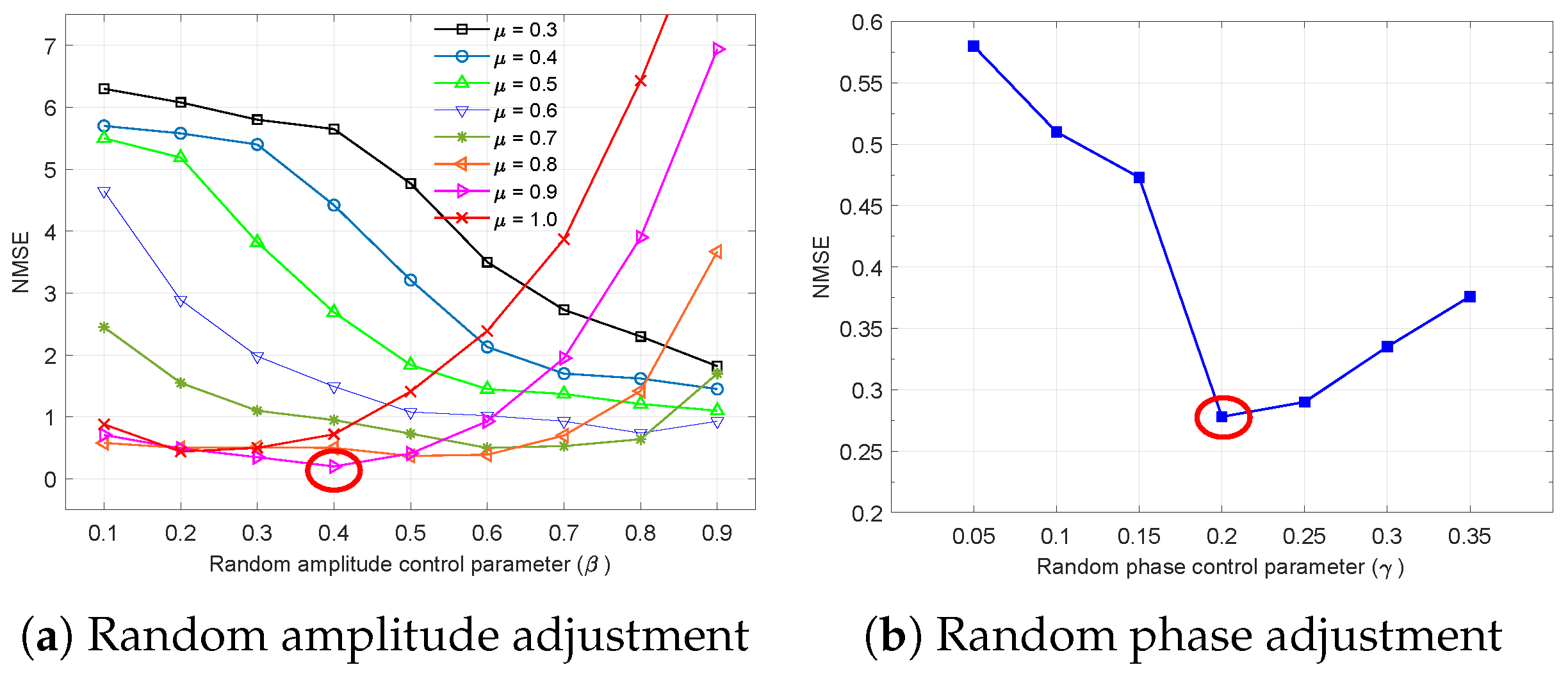
4.3. Control Parameter Optimization for SAR Signal Processing
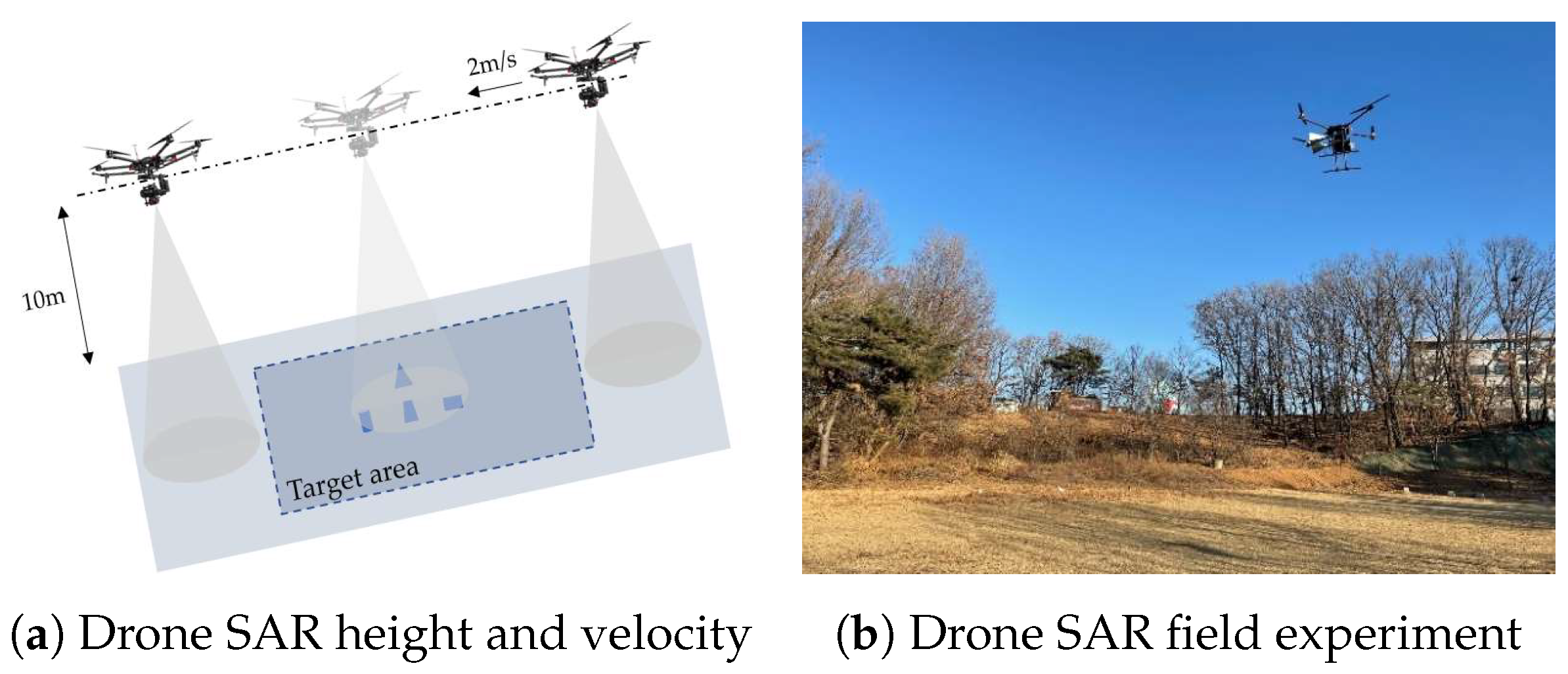
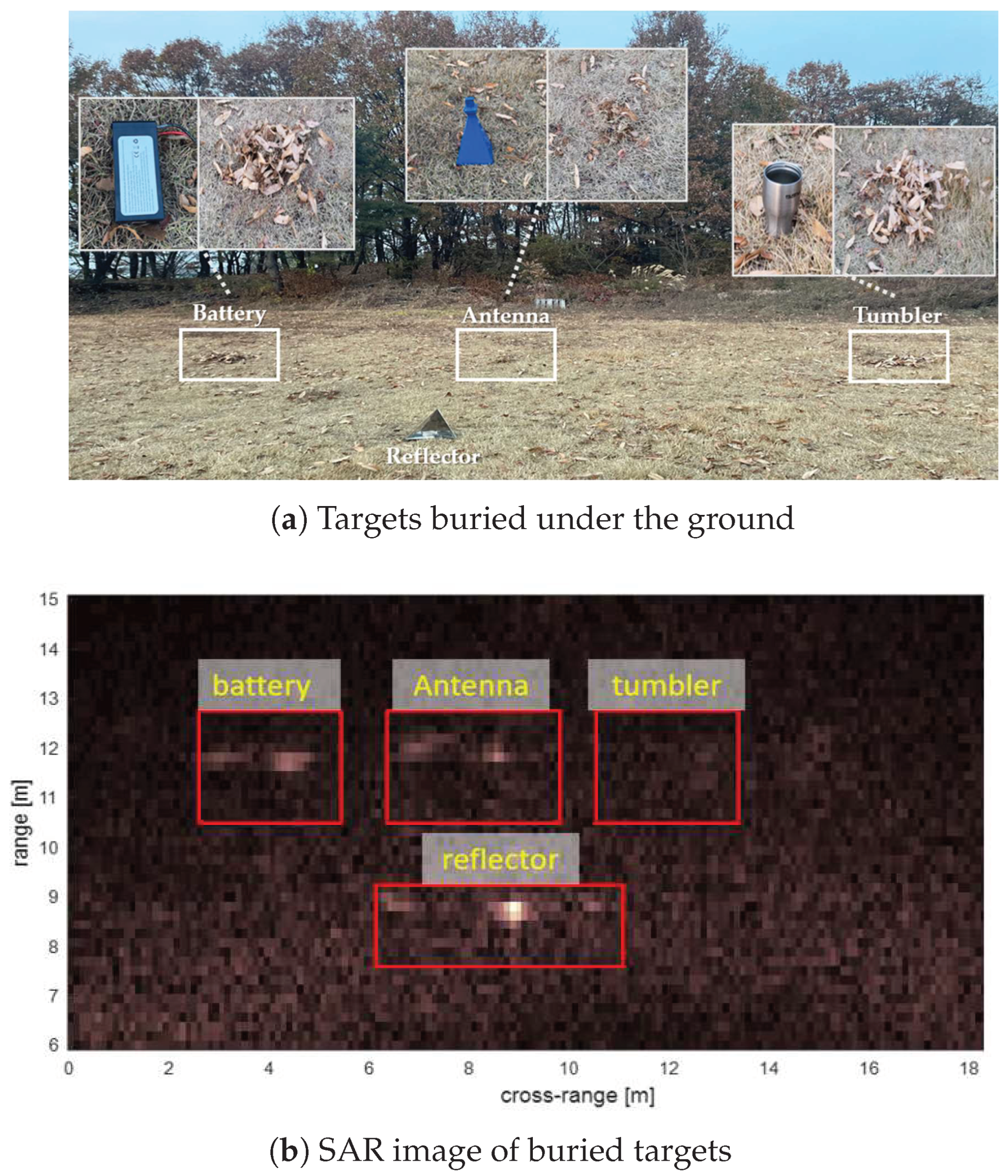
5. Experimental SAR Imaging and Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery from Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Gill, P.R.; Wang, A.; Molnar, A. The In-Crowd Algorithm for Fast Basis Pursuit Denoising. IEEE Trans. Signal Process. 2011, 59, 4595–4605. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message passing algorithms for compressed sensing: I. motivation and construction. In Proceedings of the 2010 IEEE Information Theory Workshop on Information Theory (ITW), Cairo, Egypt, 6–8 January 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message passing algorithms for compressed sensing: II. analysis and validation. In Proceedings of the 2010 IEEE Information Theory Workshop on Information Theory (ITW), Cairo, Egypt, 6–8 January 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery from Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L. Orthogonal Matching Pursuit for Sparse Signal Recovery with Noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J. Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Li, P.; Shim, B. Recovery of Sparse Signals via Generalized Orthogonal Matching Pursuit: A New Analysis. IEEE Trans. Signal Process. 2016, 64, 1076–1089. [Google Scholar] [CrossRef]
- DeVore, R.A. Deterministic Constructions of Compressed Sensing Matrices. J. Complex. 2007, 23, 918–925. [Google Scholar] [CrossRef]
- Patel, V.M.; Easley, G.R.; Healy, D.M.; Chellappa, R. Compressed Synthetic Aperture Radar. IEEE J. Sel. Topics Signal Process. 2010, 4, 244–254. [Google Scholar] [CrossRef]
- Samadi, S.; Çetin, M.; Masnadi-Shirazi, M. Sparse representation-based synthetic aperture radar imaging. IET Radar Sonar Navig. 2011, 5, 182–193. [Google Scholar] [CrossRef]
- Aberman, K.; Eldar, Y.C. Sub-Nyquist SAR via Fourier Domain Range-Doppler Processing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6228–6244. [Google Scholar] [CrossRef]
- Yang, H.; Chen, C.; Chen, S.; Xi, F. Sub-Nyquist SAR via Quadrature Compressive Sampling with Independent Measurements. Remote Sens. 2019, 11, 472. [Google Scholar] [CrossRef]
- Yang, J.; Jin, T.; Huang, X. Compressed Sensing Radar Imaging with Magnitude Sparse Representation. IEEE Access 2019, 7, 29722–29733. [Google Scholar] [CrossRef]
- Song, S.; Dai, Y.; Jin, T.; Wang, X.; Hua, Y.; Zhou, X. An Effective Image Reconstruction Enhancement Method with Convolutional Reweighting for Near-Field SAR. IEEE Antenna Wirel. Propag. Lett. 2024, 23, 2486–2490. [Google Scholar] [CrossRef]
- Choi, J.; Lee, W. Drone SAR Image Compression Based on Block Adaptive Compressive Sensing. Remote Sens. 2021, 13, 3947. [Google Scholar] [CrossRef]
- Pournaghshband, R.; Modarres-Hashemi, M. A Novel Block Compressive Sensing Algorithm for SAR Image Formation. Signal Process. 2023, 210, 109053. [Google Scholar] [CrossRef]
- Wu, J.; Feng, D.; Wang, J.; Huang, X. SAR Imaging from Azimuth Missing Raw Data via Sparsity Adaptive StOMP. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4501605. [Google Scholar] [CrossRef]
- Bi, H.; Feng, J.; Jin, S.; Yang, W.; Xu, W. Mixed-Norm Regularization-Based Polarimetric Holographic SAR 3-D Imaging. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4002305. [Google Scholar] [CrossRef]
- Gilbert, A.; Indyk, P. Sparse Recovery Using Sparse Matrices. Proc. IEEE 2010, 98, 937–947. [Google Scholar] [CrossRef]
- Liu, X.J.; Xia, S.T.; Fu, F.W. Reconstruction Guarantee Analysis of Basis Pursuit for Binary Measurement Matrices in Compressed Sensing. IEEE Trans. Inf. Theory 2017, 63, 2922–2932. [Google Scholar] [CrossRef]
- Çetin, M.; Stojanović, I.; Önhon, N.O.; Varshney, K.; Samadi, S.; Karl, W.C.; Willsky, A.S. Sparsity-Driven Synthetic Aperture Radar Imaging: Reconstruction, autofocusing, moving targets, and compressed sensing. IEEE Signal Process. Mag. 2014, 31, 27–40. [Google Scholar] [CrossRef]
- Calderbank, R.; Howard, S.D.; Jafarpour, S. Construction of a Large Class of Deterministic Sensing Matrices That Satisfy a Statistical Isometry Property. IEEE J. Sel. Topics Signal Process. 2010, 4, 358–374. [Google Scholar] [CrossRef]
- Amini, A.; Marvasti, F. Deterministic Construction of Binary, Bipolar, and Ternary Compressed Sensing Matrices. IEEE Trans. Inf. Theory 2011, 57, 2360–2370. [Google Scholar] [CrossRef]
- Dimakis, A.G.; Smarandache, R.; Vontobel, P.O. LDPC Codes for Compressed Sensing. IEEE Trans. Inf. Theory 2012, 58, 3093–3114. [Google Scholar] [CrossRef]
- Li, S.; Gao, F.; Ge, G.; Zhang, S. Deterministic Construction of Compressed Sensing Matrices via Algebraic Curves. IEEE Trans. Inf. Theory 2012, 58, 5035–5041. [Google Scholar] [CrossRef]
- Mohades, M.M.; Kahaei, M.H. General Approach for Construction of Deterministic Compressive Sensing Matrices. IET Signal Process. 2019, 13, 321–329. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Ren, H. Deterministic Construction of Compressed Sensing Measurement Matrix with Arbitrary Sizes via QC-LDPC and Arithmetic Sequence Sets. Electronics 2023, 12, 2063. [Google Scholar] [CrossRef]
- Yu, N.Y.; Li, Y. Deterministic Construction of Fourier-Based Compressed Sensing Matrices Using an Almost Difference Set. EURASIP J. Adv. Signal Process. 2013, 2013, 155. [Google Scholar] [CrossRef]
- Xu, G.; Xu, Z. Compressed Sensing Matrices from Fourier Matrices. IEEE Trans. Inf. Theory 2015, 61, 469–478. [Google Scholar] [CrossRef]
- Hanumanthu, S.; Kumar P, R. Deterministic Compressed Sensing LFM Radar for Range-Doppler Estimation of Multiple Moving Targets. Measurement 2022, 187, 110315. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, Y.; Chen, S. Image Parallel Block Compressive Sensing Scheme Using DFT Measurement Matrix. Multimed. Tools Appl. 2023, 82, 21561–21583. [Google Scholar] [CrossRef]
- Li, S.; Ge, G. Deterministic Construction of Sparse Sensing Matrices via Finite Geometry. IEEE Trans. Signal Process. 2014, 62, 2850–2859. [Google Scholar] [CrossRef]
- Bryant, D.; Colbourn, C.J.; Horsley, D.; Ó Catháin, P. Compressed Sensing with Combinatorial Designs: Theory and Simulations. IEEE Trans. Inf. Theory 2017, 63, 4850–4859. [Google Scholar] [CrossRef]
- Lu, W.; Dai, T.; Xia, S.T. Binary Matrices for Compressed Sensing. IEEE Trans. Signal Process. 2018, 66, 77–85. [Google Scholar] [CrossRef]
- Lotfi, M.; Vidyasagar, M. A Fast Noniterative Algorithm for Compressive Sensing Using Binary Measurement Matrices. IEEE Trans. Signal Process. 2018, 66, 4079–4089. [Google Scholar] [CrossRef]
- Tong, F.; Li, L.; Peng, H.; Yang, Y. Deterministic Constructions of Compressed Sensing Matrices from Unitary Geometry. IEEE Trans. Inf. Theory 2021, 67, 5548–5561. [Google Scholar] [CrossRef]
- Applebaum, L.; Howard, S.D.; Searle, S.; Calderbank, R. Chirp Sensing Codes: Deterministic Compressed Sensing Measurements for Fast Recovery. Appl. Comput. Harmon. Anal. 2009, 26, 283–290. [Google Scholar] [CrossRef]
- Xu, Q.; Sheng, Z.; Fang, Y.; Zhang, L. Measurement Matrix Optimization for Compressed Sensing System with Constructed Dictionary via Takenaka–Malmquist Functions. Sensors 2021, 21, 1229. [Google Scholar] [CrossRef] [PubMed]
- Pllaha, T.; Tirkkonen, O.; Calderbank, R. Binary Subspace Chirps. IEEE Trans. Inf. Theory 2022, 68, 7735–7752. [Google Scholar] [CrossRef]
- Liu, J.; Mallick, M.; Lian, F.; Han, C.; Sheng, M.; Yao, X. General Similar Sensing Matrix Pursuit: An Efficient and Rigorous Reconstruction Algorithm to Cope with Deterministic Sensing Matrix with High Coherence. Signal Process. 2015, 114, 150–163. [Google Scholar] [CrossRef]
- Obermeier, R.; Martinez-Lorenzo, J.A. Sensing Matrix Design via Mutual Coherence Minimization for Electromagnetic Compressive Imaging Applications. IEEE Trans. Comput. Imag. 2017, 3, 217–229. [Google Scholar] [CrossRef]
- Gu, Z.; Zhou, Z.; Yang, Y.; Adhikary, A.R.; Cai, X. Deterministic Compressed Sensing Matrices from Sequences with Optimal Correlation. IEEE Access 2019, 7, 16704–16710. [Google Scholar] [CrossRef]
- Soumekh, M. SAR-ECCM Using Phase-Perturbed LFM Chirp Signals and DRFM Repeat Jammer Penalization. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 191–205. [Google Scholar] [CrossRef]
- Akhtar, J. Orthogonal Block Coded ECCM Schemes Against Repeat Radar Jammers. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1218–1226. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, J.; Li, C.; Zhu, D. Orthogonal Anti-Jamming Waveform Design with Extended Doppler Tolerance Based on the LFM-PC Signal. Digit. Signal Process. 2022, 122, 103334. [Google Scholar] [CrossRef]
- Schuerger, J.; Garmatyuk, D. Multifrequency OFDM SAR in Presence of Deception Jamming. EURASIP J. Adv. Signal Process. 2010, 2010, 451851. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S.; So, H.C. Deceptive Jamming Suppression with Frequency Diverse MIMO Radar. Signal Process. 2015, 113, 9–17. [Google Scholar] [CrossRef]
- Yu, L.; Barbot, J.P.; Zheng, G.; Sun, H. Compressive Sensing with Chaotic Sequence. IEEE Signal Process. Lett. 2010, 17, 731–734. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, X.; Yang, Q.; Zhai, W.; Shi, X.; Yang, Q.; Kang, X. High-Resolution SAR/ISAR Imaging with Chaotic Noise Signals. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 13–16 November 2017; pp. 372–375. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, F.; Dong, Y.; Zhao, Z.; Wang, Y.; Yan, M. Chaotic Phase-Coded Waveforms with Space-Time Complementary Coding for MIMO Radar Applications. IEEE Access 2018, 6, 42066–42083. [Google Scholar] [CrossRef]
- Pralon, L.; Beltrao, G.; Barreto, A.; Cosenza, B. On the Analysis of PM/FM Noise Radar Waveforms Considering Modulating Signals with Varied Stochastic Properties. Sensors 2021, 21, 1727. [Google Scholar] [CrossRef] [PubMed]
- Šipoš, D.; Gleich, D. A Lightweight and Low-Power UAV-Borne Ground Penetrating Radar Design for Landmine Detection. Sensors 2020, 20, 2234. [Google Scholar] [CrossRef]
- Noviello, C.; Esposito, G.; Catapano, I.; Soldovieri, F. Multilines Imaging Approach for Mini-UAV Radar Imaging System. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3507105. [Google Scholar] [CrossRef]
- García-Fernández, M.; Álvarez Narciandi, G.; Álvarez López, Y.; Las-Heras Andrés, F. Improvements in GPR-SAR Imaging Focusing and Detection Capabilities of UAV-Mounted GPR Systems. ISPRS J. Photogramm. Remote Sens. 2022, 189, 128–142. [Google Scholar] [CrossRef]
- Grathwohl, A.; Stelzig, M.; Kanz, J.; Fenske, P.; Benedikter, A.; Knill, C.; Ullmann, I.; Hajnsek, I.; Moreira, A.; Krieger, G.; et al. Taking a Look Beneath the Surface: Multicopter UAV-Based Ground-Penetrating Imaging Radars. IEEE Microw. Mag. 2022, 23, 32–46. [Google Scholar] [CrossRef]
- Barnawi, A.; Kumar, K.; Kumar, N.; Thakur, N.; Alzahrani, B.; Almansour, A. Unmanned Ariel Vehicle (UAV) Path Planning for Area Segmentation in Intelligent Landmine Detection Systems. Sensors 2023, 23, 7264. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Fernandez, M.; Alvarez-Lopez, Y.; Las Heras, F. Autonomous Airborne 3D SAR Imaging System for Subsurface Sensing: UWB-GPR on Board a UAV for Landmine and IED Detection. Remote Sens. 2019, 11, 2357. [Google Scholar] [CrossRef]
- Schartel, M.; Burr, R.; Schoeder, P.; Rossi, G.; Hügler, P.; Mayer, W.; Waldschmidt, C. Radar-Based Altitude over Ground Estimation of UAVs. In Proceedings of the 2018 11th German Microwave Conference (GeMiC), Freiburg, Germany, 12–14 March 2018; pp. 103–106. [Google Scholar] [CrossRef]
- Başpınar, O.O.; Omuz, B.; Öncü, A. Detection of the Altitude and On-the-Ground Objects Using 77-GHz FMCW Radar Onboard Small Drones. Drones 2023, 7, 86. [Google Scholar] [CrossRef]
- García-Fernández, M.; Álvarez Narciandi, G.; Álvarez López, Y.; Las-Heras, F. Array-Based Ground Penetrating Synthetic Aperture Radar on Board an Unmanned Aerial Vehicle for Enhanced Buried Threats Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5104218. [Google Scholar] [CrossRef]
- García-Fernández, M.; Álvarez Narciandi, G.; Laviada, J.; Álvarez López, Y.; Las-Heras, F. Towards Real-Time Processing for UAV-Mounted GPR-SAR Imaging Systems. ISPRS J. Photogramm. Remote Sens. 2024, 212, 1–12. [Google Scholar] [CrossRef]
- Li, C.K.; Zhang, F. Eigenvalue Continuity and Gersgorin’s Theorem. Electron. J. Linear Algebra 2019, 35, 619–625. [Google Scholar] [CrossRef]



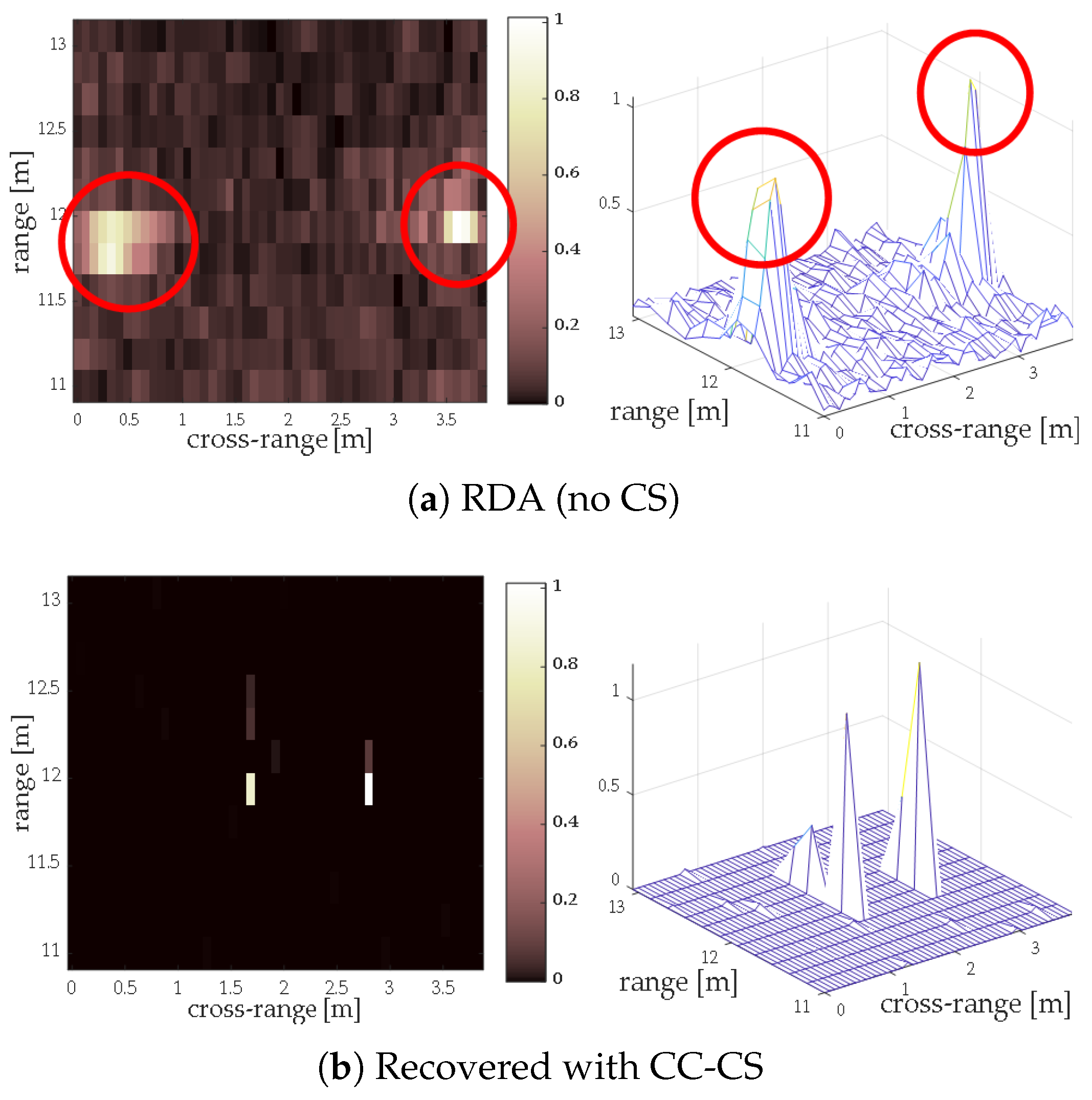
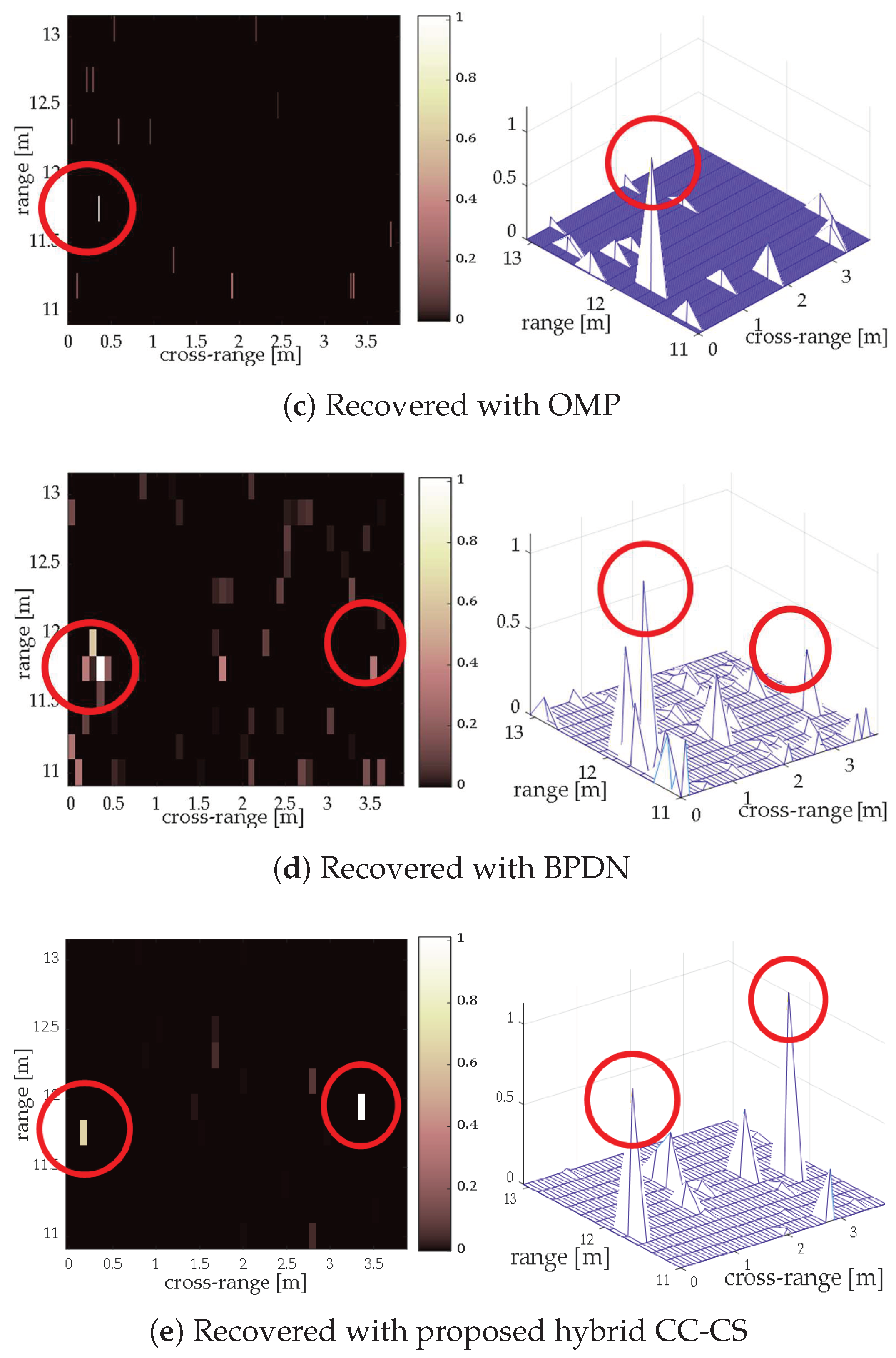
| Parameter | Value |
|---|---|
| Bandwidth | 60 MHz |
| Center frequency | 5.3 GHz |
| Payload velocity | 150 m/s |
| PRF | 150 Hz |
| Sampling rate | 70 MHz |
| Slant range | 20 km |
| Number of targets | 3 |
| Algorithm | Runtime (s) | Recovery |
|---|---|---|
| RDA (no CS) | 0.10 | Success |
| CC-CS | 0.24 | Fail |
| OMP | 0.48 | Fail |
| BPDN | 2.60 | Success |
| Hybrid CC-CS | 0.36 | Success |
| Parameter | Value |
|---|---|
| Altitude | 10 m |
| Bandwidth | 800 MHz |
| Center frequency | 5.6 GHz |
| Payload velocity | 2.0 m/s |
| PRF | 25 Hz |
| Transmit power | 30 dBm |
| Sampling rate | 1.0 MHz |
| 3 dB bandwidth | 13° |
| Number of targets | 3 |
| Algorithm | Times [s] | Recovery |
|---|---|---|
| RDA (no loss) | 0.1 | Success |
| CC-CS | 0.12 | Fail |
| OMP | 0.28 | Fail |
| BPDN | 0.8 | Fail |
| Hybrid CC-CS | 0.13 | Success |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, H.-J.; Lee, H.; Choi, J.; Lee, W. Hybrid Deterministic Sensing Matrix for Compressed Drone SAR Imaging and Efficient Reconstruction of Subsurface Targets. Remote Sens. 2025, 17, 595. https://doi.org/10.3390/rs17040595
Jo H-J, Lee H, Choi J, Lee W. Hybrid Deterministic Sensing Matrix for Compressed Drone SAR Imaging and Efficient Reconstruction of Subsurface Targets. Remote Sensing. 2025; 17(4):595. https://doi.org/10.3390/rs17040595
Chicago/Turabian StyleJo, Hwi-Jeong, Heewoo Lee, Jihoon Choi, and Wookyung Lee. 2025. "Hybrid Deterministic Sensing Matrix for Compressed Drone SAR Imaging and Efficient Reconstruction of Subsurface Targets" Remote Sensing 17, no. 4: 595. https://doi.org/10.3390/rs17040595
APA StyleJo, H.-J., Lee, H., Choi, J., & Lee, W. (2025). Hybrid Deterministic Sensing Matrix for Compressed Drone SAR Imaging and Efficient Reconstruction of Subsurface Targets. Remote Sensing, 17(4), 595. https://doi.org/10.3390/rs17040595






