Analysis of Instantaneous Doppler Positioning Performance Based on LEO Satellite Ephemeris Errors
Abstract
1. Introduction
2. Doppler Positioning Mathematical Model
3. Doppler Positioning Error Simulation Strategy
3.1. Satellite Clock Bias
3.2. Ionospheric Error
3.3. Tropospheric Error
3.4. Earth Rotation Effect
4. Experiment Design
5. Results and Discussion
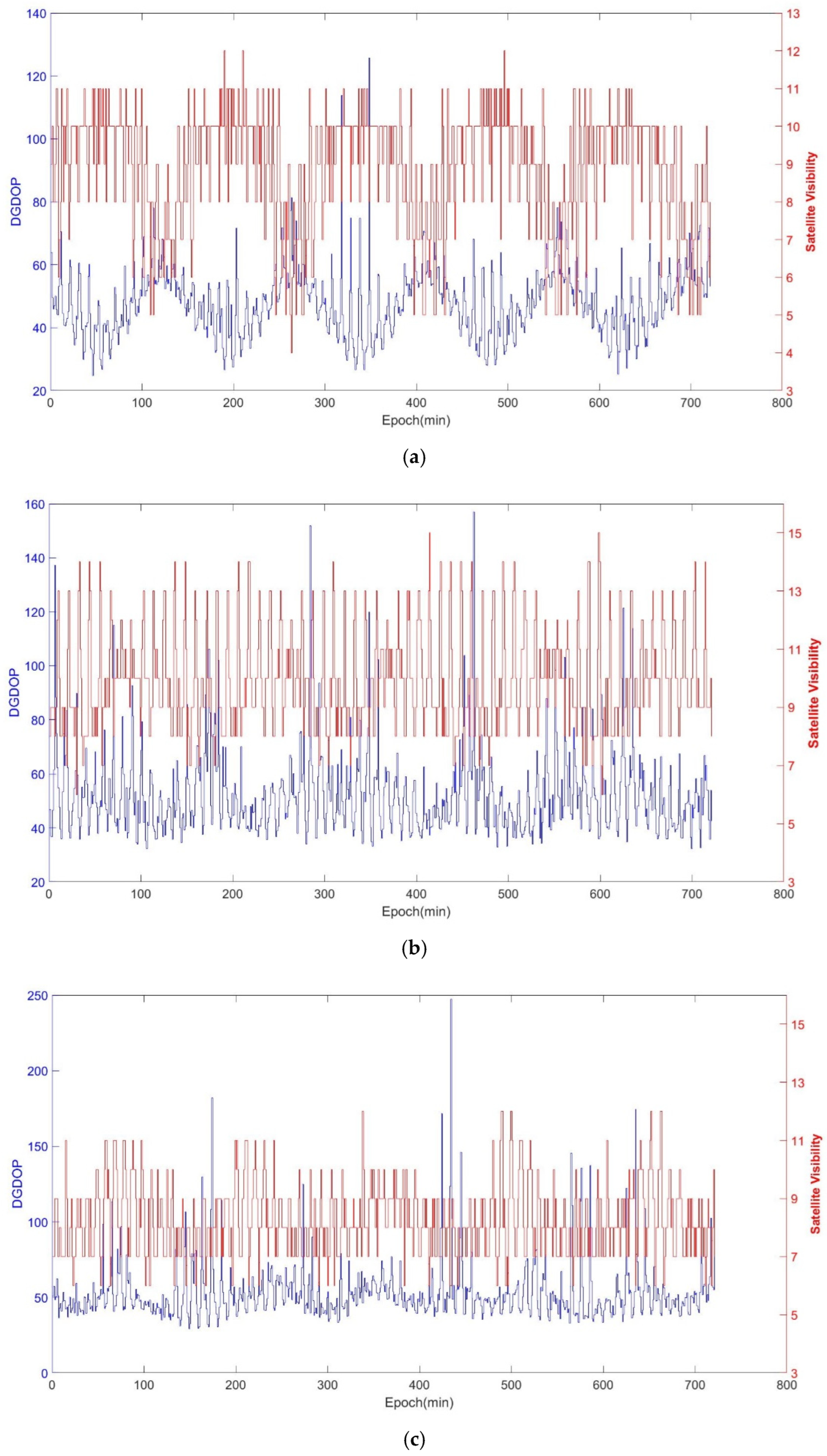
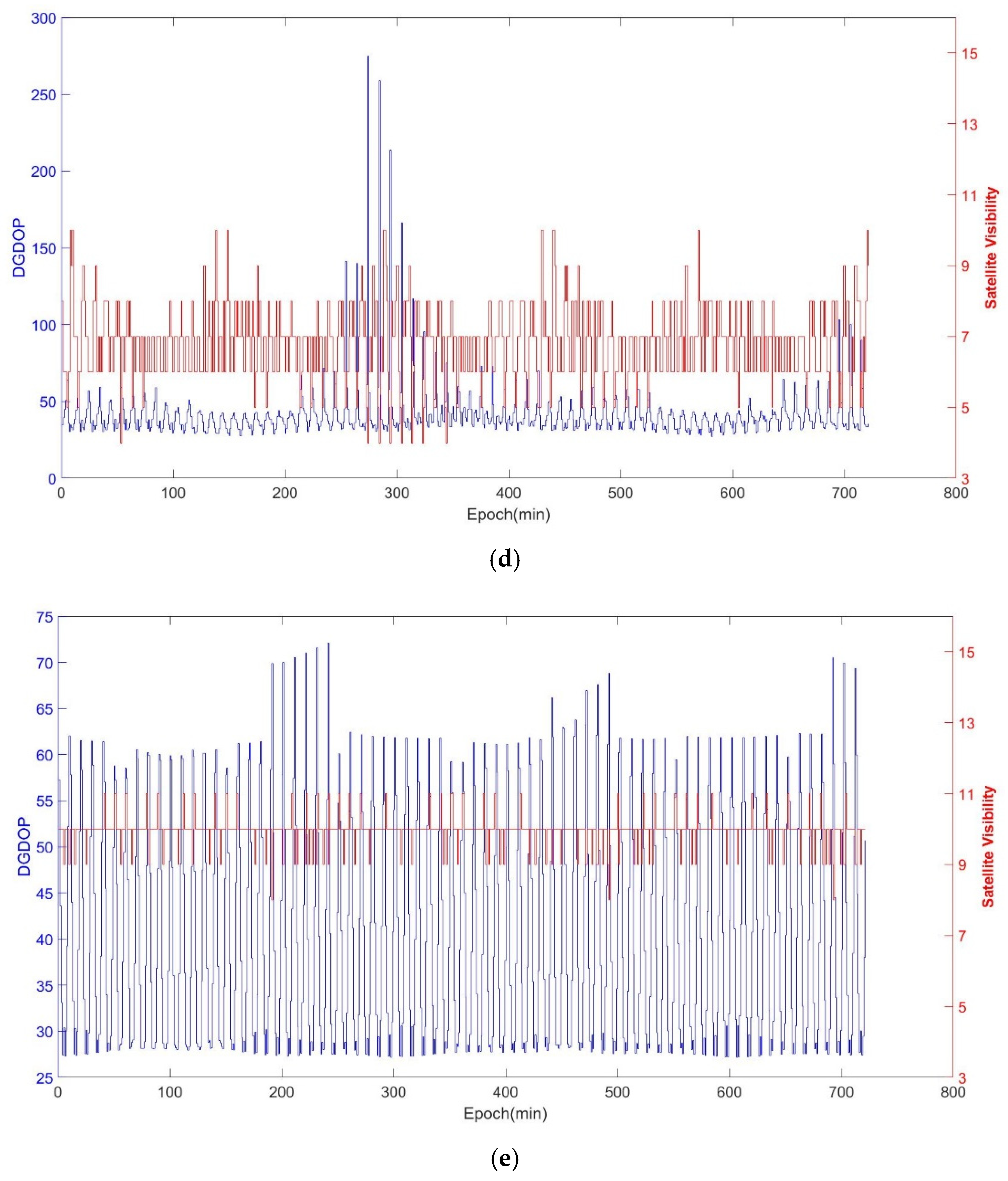
5.1. Number of Visible Satellites and DGDOP
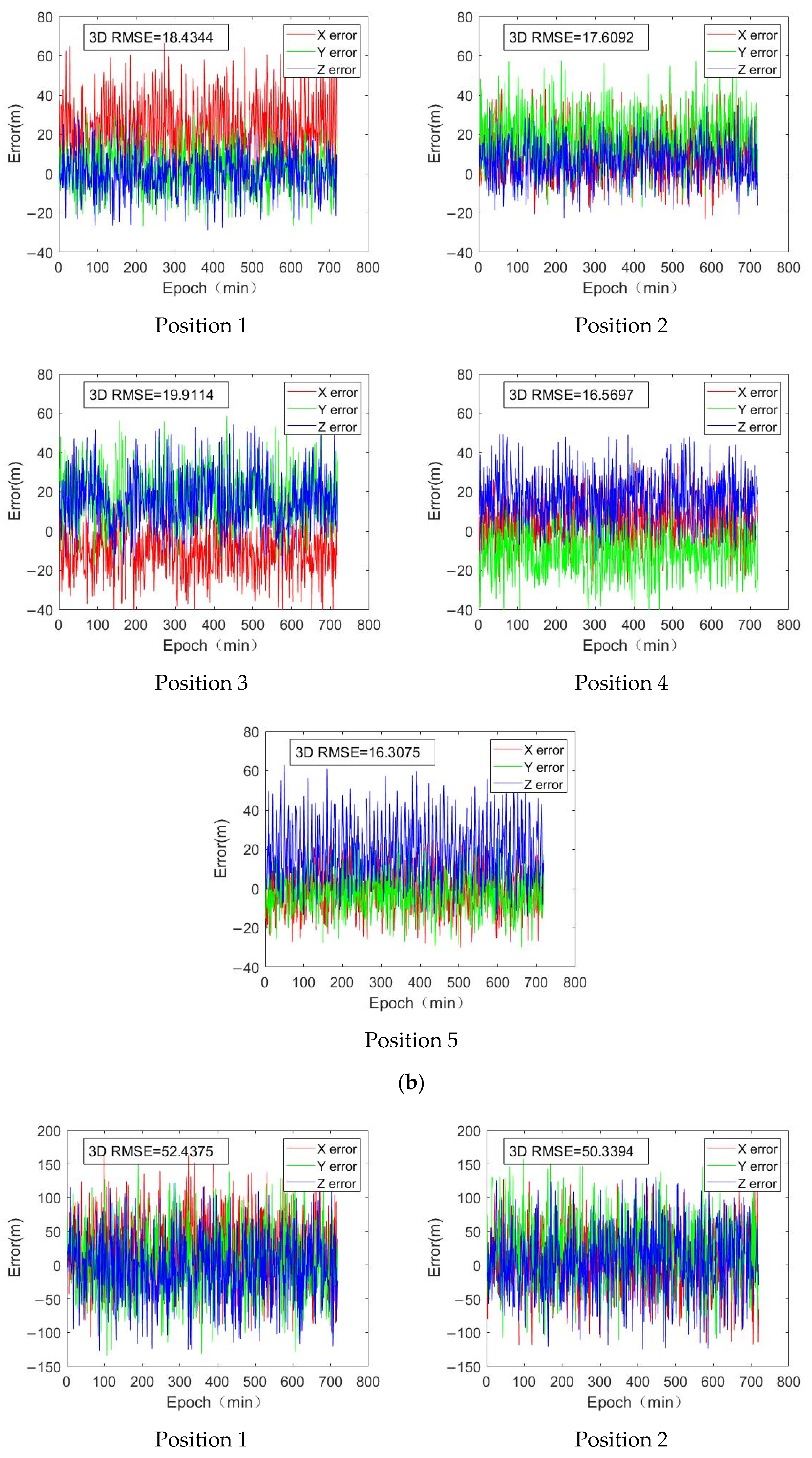
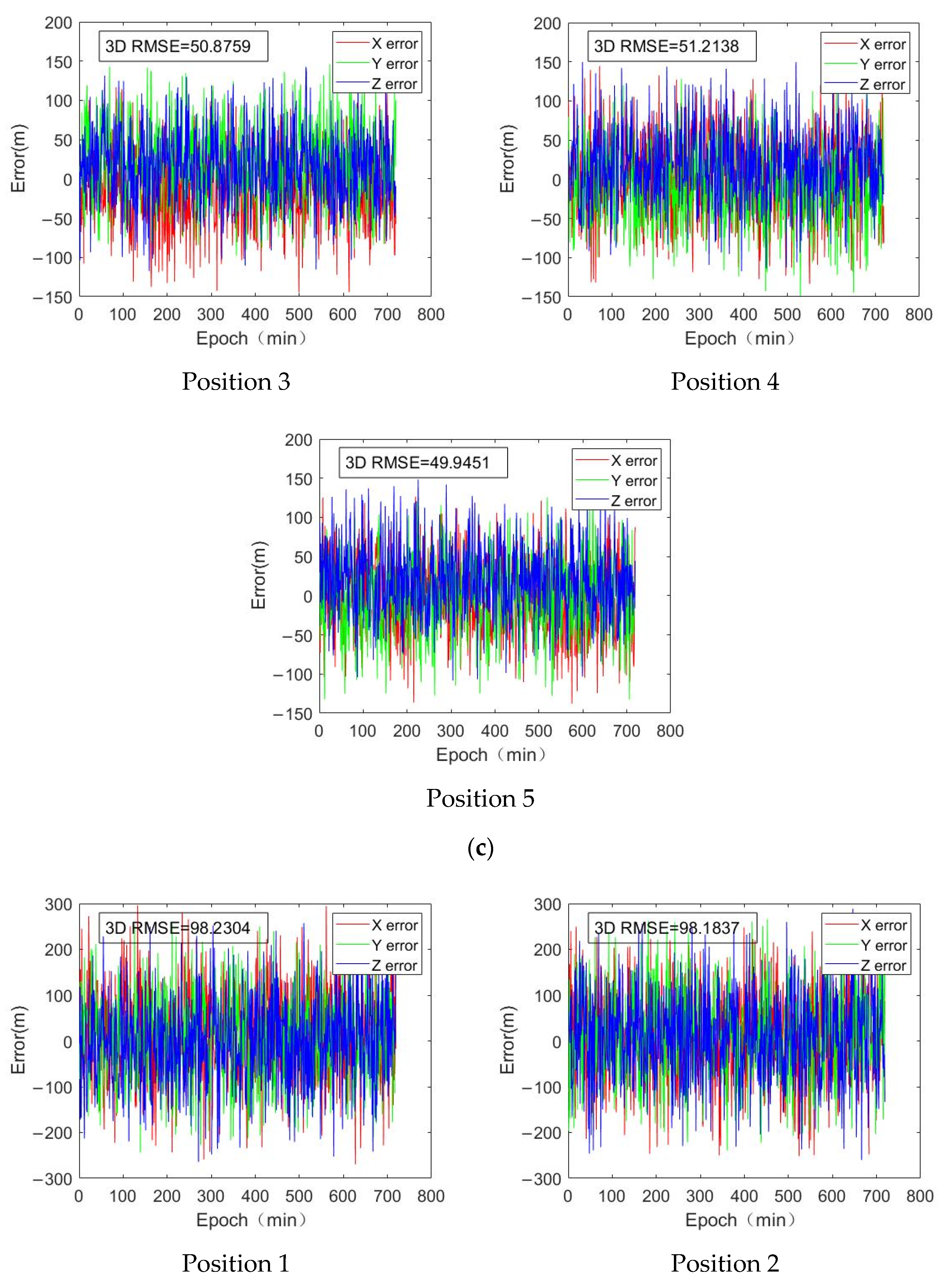
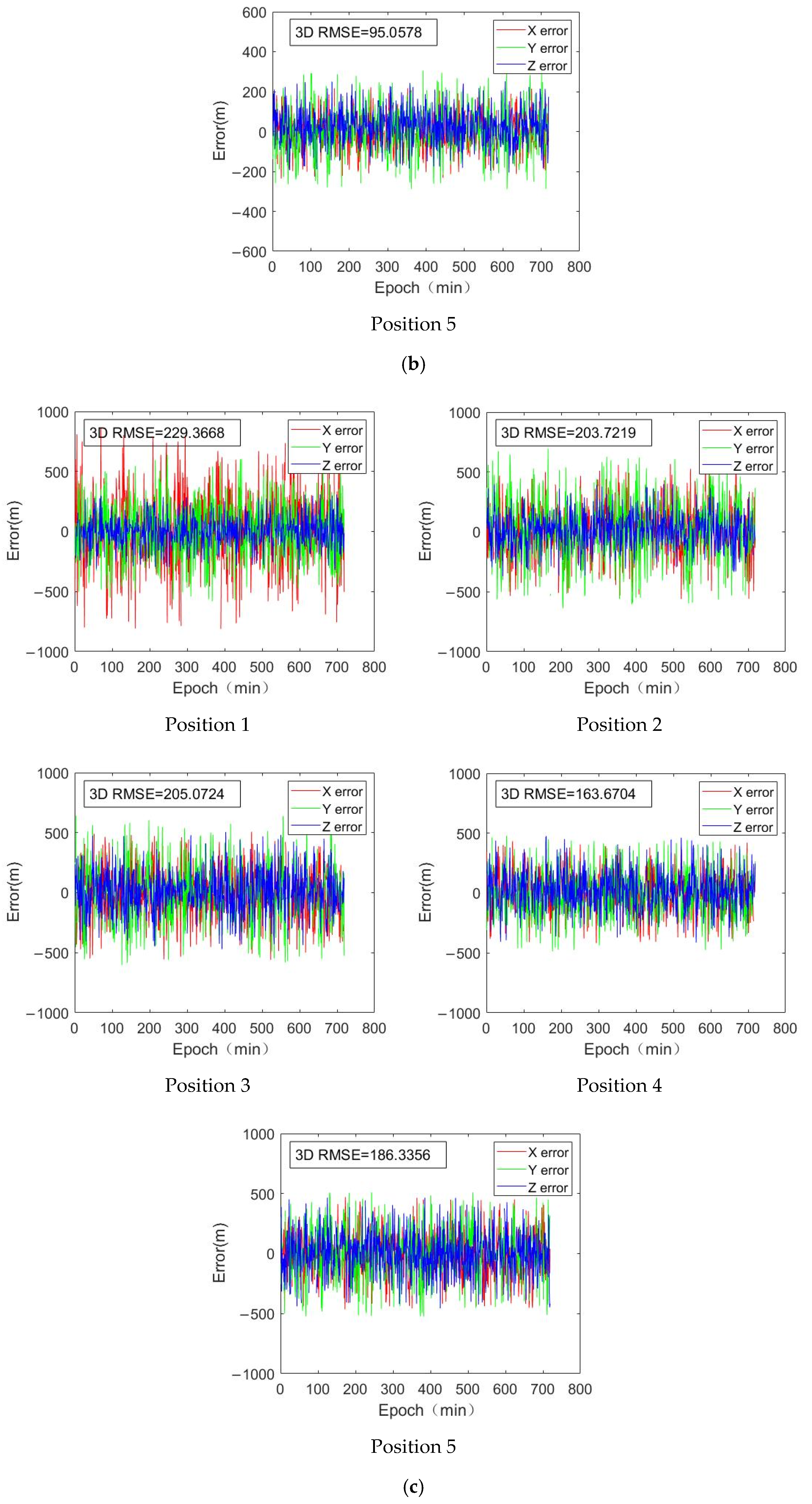
5.2. The Impact of Satellite Orbit Errors on Positioning
5.3. The Impact of Satellite Velocity on Positioning
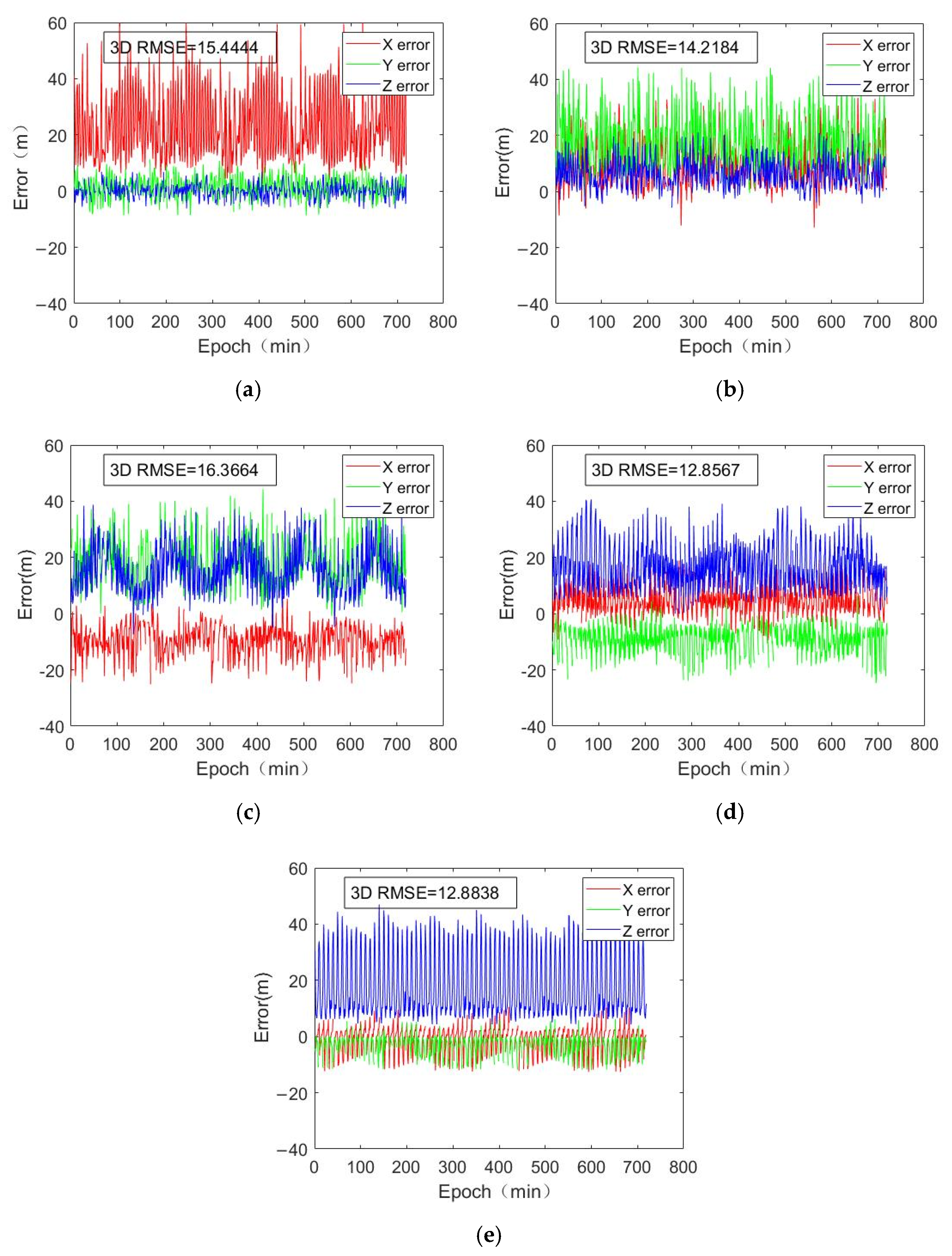
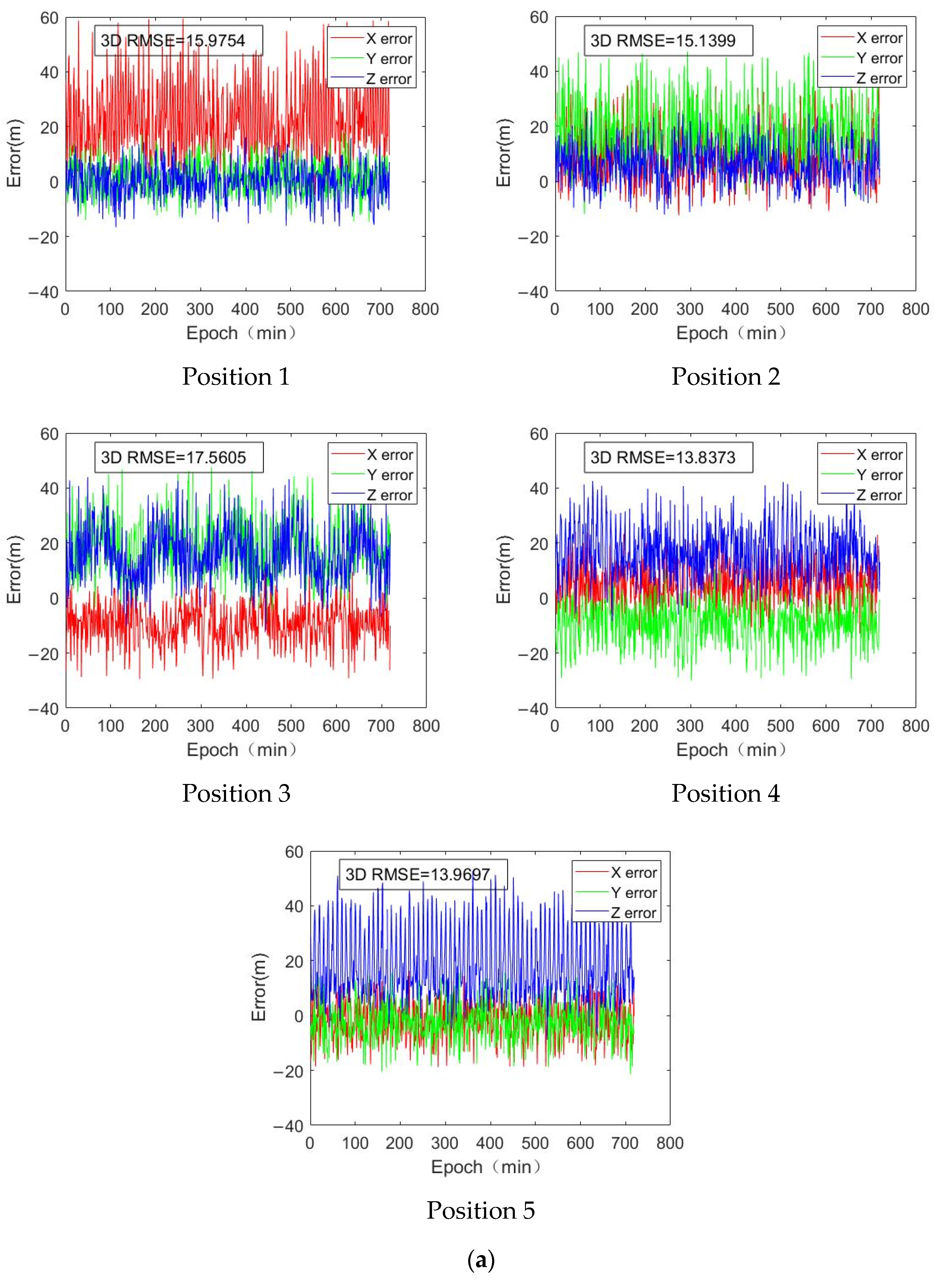
5.4. Normal Positioning Error
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Xia, F.; Xu, C. Modeling and Simulation of GNSS Navigation Messages Based on MWORKS. Softw. Guide 2023, 10, 11–18+253. [Google Scholar]
- Ge, Y.; Xue, L.; Li, J. Analysis of the development trends of US Army PNT capabilities. Navig. Position. Timing 2019, 6, 12–18. [Google Scholar]
- Liu, H.; Fang, S.; Fan, Y.; Ma, S. Review of navigation via signals of opportunity. J. Ordnance Equip. Eng. 2022, 7, 78–86+158. [Google Scholar]
- Li, M.; Huang, T.; Li, W.; Zhao, Q. Overview of Low Earth Orbit (LEO) Navigation Augmentation Technology. J. Geomat. 2024, 49. [Google Scholar] [CrossRef]
- Guo, F.; Yang, Y.; Ma, F.; Zhu, Y.; Liu, H.; Zhang, X. Instantaneous velocity determination and positioning using Doppler shift from a LEO constellation. Satell. Navig. 2023, 4, 9. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Zhang, X.; Cheng, Y. Research and Simulation of Single Star Positioning Algorithm Based on Low Earth Orbit Satellite. In Proceedings of the China Satellite Navigation Academic Annual Conference, Harbin, China, 23–25 May 2018. [Google Scholar]
- Deng, Z.; Gao, H.; Wang, L. Mutiple-scene Doppler Locating Method forLEO Satellite Navigation System. Radio Eng. 2017, 47, 49–53. [Google Scholar]
- Qin, H.; Zhang, Y.; Shi, G.; Wang, D. Doppler positioning technology based on Globalstar signals of opportunity. J. Beijing Univ. Aeronaut. Astronaut. 2023, 1–10. [Google Scholar] [CrossRef]
- Qin, H.; Tan, Z.; Cong, L.; Zhao, C. Positioning technology based on IRIDIUM signals of opportunity. J. Beijing Univ. Aeronaut. Astronaut. 2019, 9, 1691–1699. [Google Scholar] [CrossRef]
- Qin, H.; Tan, Z.; Cong, L.; Zhao, C. Positioning technology based on ORBCOMM signals of opportunity. J. Beijing Univ. Aeronaut. Astronaut. 2020, 11, 1999–2006. [Google Scholar] [CrossRef]
- Qin, H.; Zhang, Y. Positioning technology based on starlink signal of opportunity. J. Navig. Position. 2023, 1, 67–73. [Google Scholar] [CrossRef]
- Liang, J. Investigation on Iridium STL Positioning Method. Doctoral Dissertation, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Fan, H. Effect of Low Earth Orbit Enhancement Constellation on GNSS Precise Point Positioning. Doctoral Dissertation, Taiyuan University of Technology, Taiyuan, China, 2023. [Google Scholar]
- Jiang, X.; Chen, X.; Ma, M.; Wang, Y.; Liang, R.; Yang, Z. Comparative Evaluation of Navigation Enhancement Performanceof Typical LEO Satellite Systems; GNSS World of China: Beijing, China, 2021. [Google Scholar]
- Xu, G.; Xu, Y. GPS Theory, Algorithms and Applications; Tsinghua University Press: Beijing, China, 2017. [Google Scholar]
- Khairallah, N.; Kassas, Z.M. Ephemeris closed-loop tracking of LEO satellites with pseudorange and Doppler measurements. In Proceedings of the 34th international technical meeting of the satellite division of the Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 2544–2555. [Google Scholar]
- Zhou, Q. Beidou Navigation Enhancement Simulation Research Based on LEO Constellation. Doctoral Dissertation, Shandong University of Technology, Zibo, China, 2022. [Google Scholar]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Xie, X. Analysis and discussion on the use of NBCORS system RTK technology for real estate surveying. Zhejiang Land Resour. 2015, 7, 2. [Google Scholar]
- Zhang, Y.; Li, Z.; Shi, C.; Jing, G. Doppler Positioning Performance of LEO Mega Constellation. Space-Integr.-Ground Inf. Netw. 2024, 5, 84–94. [Google Scholar]
- Bao, R.; Tang, C.; Hu, X.; Zhou, S.; Cao, Y.; Yang, Y. Study on the Accuracy Evaluation of BeiDou Broadcast Ionospheric Model. J. Beijing Univ. Aeronaut. Astronaut. 2023. [Google Scholar] [CrossRef]
- Nava, B.; Coisson, P.; Radicella, S.M. A new version of the nequick ionosphere electron density model. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Yu, X. The Key Technology Research on the High Precise Monitoring Management for Vehicle safety Operation Based on GNSS. Doctoral Dissertation, China University of Mining and Technology, Xuzhou, China, 2017. [Google Scholar]






| Constellation Parameter | Constellation 1 | Constellation 2 | Constellation 3 |
|---|---|---|---|
| Total number of satellites | 100 | 100 | 100 |
| Number of orbital planes | 10 | 10 | 10 |
| Orbital inclination | 60° | 30° | 89° |
| Orbital altitude | 700 km | 800 km | 1200 km |
| Downlink frequency | 1575.42 MHz | 1575.42 MHz | 1575.42 MHz |
| Reference Location | Longitude | Latitude |
|---|---|---|
| Location 1 | 0° | 0° |
| Location 2 | 60°E | 20°N |
| Location 3 | 120°E | 40°N |
| Location 4 | 60°W | 60°N |
| Location 5 | 120°W | 80°N |
| Simulation Content | Simulation Strategy |
|---|---|
| Satellite orbit error rate | Setting orbit errors of different magnitudes |
| Satellite velocity error rate | Setting velocity errors of different magnitudes |
| Satellite clock error rate | Frequency stability model |
| Ionospheric delay rate | NeQuickG model |
| Tropospheric delay rate | Improved Saastamoinen model |
| Earth’s rotation effect rate | Sagnac error model |
| DGDOP | Average Number of Visible Satellites | ||
|---|---|---|---|
| Average Value | Standard Deviation | ||
| Location 1 | 48.16 | 10.91 | 8.8 |
| Location 2 | 52.00 | 14.78 | 9.8 |
| Location 3 | 52.60 | 18.84 | 8.2 |
| Location 4 | 41.47 | 18.3 | 6.8 |
| Location 5 | 40.26 | 12.45 | 9.9 |
| X-Direction | Y-Direction | Z-Direction | 3D RMSE | ||
|---|---|---|---|---|---|
| Location 1 | RMSE | 41.3328 | 23.8425 | 15.8652 | 29.0320 |
| Standard deviation | 34.8105 | 24.0485 | 16.1289 | ||
| Location 2 | RMSE | 28.0432 | 35.4720 | 19.9301 | 28.5301 |
| Standard deviation | 26.4041 | 30.6704 | 18.9930 | ||
| Location 3 | RMSE | 25.9708 | 33.4784 | 28.0182 | 29.3275 |
| Standard deviation | 24.2338 | 29.1070 | 23.7010 | ||
| Location 4 | RMSE | 20.5185 | 25.1312 | 27.5027 | 24.5560 |
| Standard deviation | 20.5542 | 24.4429 | 21.1868 | ||
| Location 5 | RMSE | 22.5759 | 24.5714 | 31.4949 | 26.4912 |
| Standard deviation | 22.9293 | 25.2090 | 26.2346 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Chen, M.; Li, W.; Li, Y.; Lv, W.; Zhou, W.; Shen, Y.; Li, X.; Yu, J. Analysis of Instantaneous Doppler Positioning Performance Based on LEO Satellite Ephemeris Errors. Remote Sens. 2025, 17, 620. https://doi.org/10.3390/rs17040620
Shi X, Chen M, Li W, Li Y, Lv W, Zhou W, Shen Y, Li X, Yu J. Analysis of Instantaneous Doppler Positioning Performance Based on LEO Satellite Ephemeris Errors. Remote Sensing. 2025; 17(4):620. https://doi.org/10.3390/rs17040620
Chicago/Turabian StyleShi, Xingyu, Mingjian Chen, Wanli Li, Yuxing Li, Wei Lv, Wenlong Zhou, Yang Shen, Xueqing Li, and Jiashu Yu. 2025. "Analysis of Instantaneous Doppler Positioning Performance Based on LEO Satellite Ephemeris Errors" Remote Sensing 17, no. 4: 620. https://doi.org/10.3390/rs17040620
APA StyleShi, X., Chen, M., Li, W., Li, Y., Lv, W., Zhou, W., Shen, Y., Li, X., & Yu, J. (2025). Analysis of Instantaneous Doppler Positioning Performance Based on LEO Satellite Ephemeris Errors. Remote Sensing, 17(4), 620. https://doi.org/10.3390/rs17040620





