High-Resolution Reconstruction of Total Organic Carbon Content in Lake Sediments Using Hyperspectral Imaging
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sample Collection
2.3. Geochemical and Physical Analysis
2.4. VNIR Hyperspectral Scanning
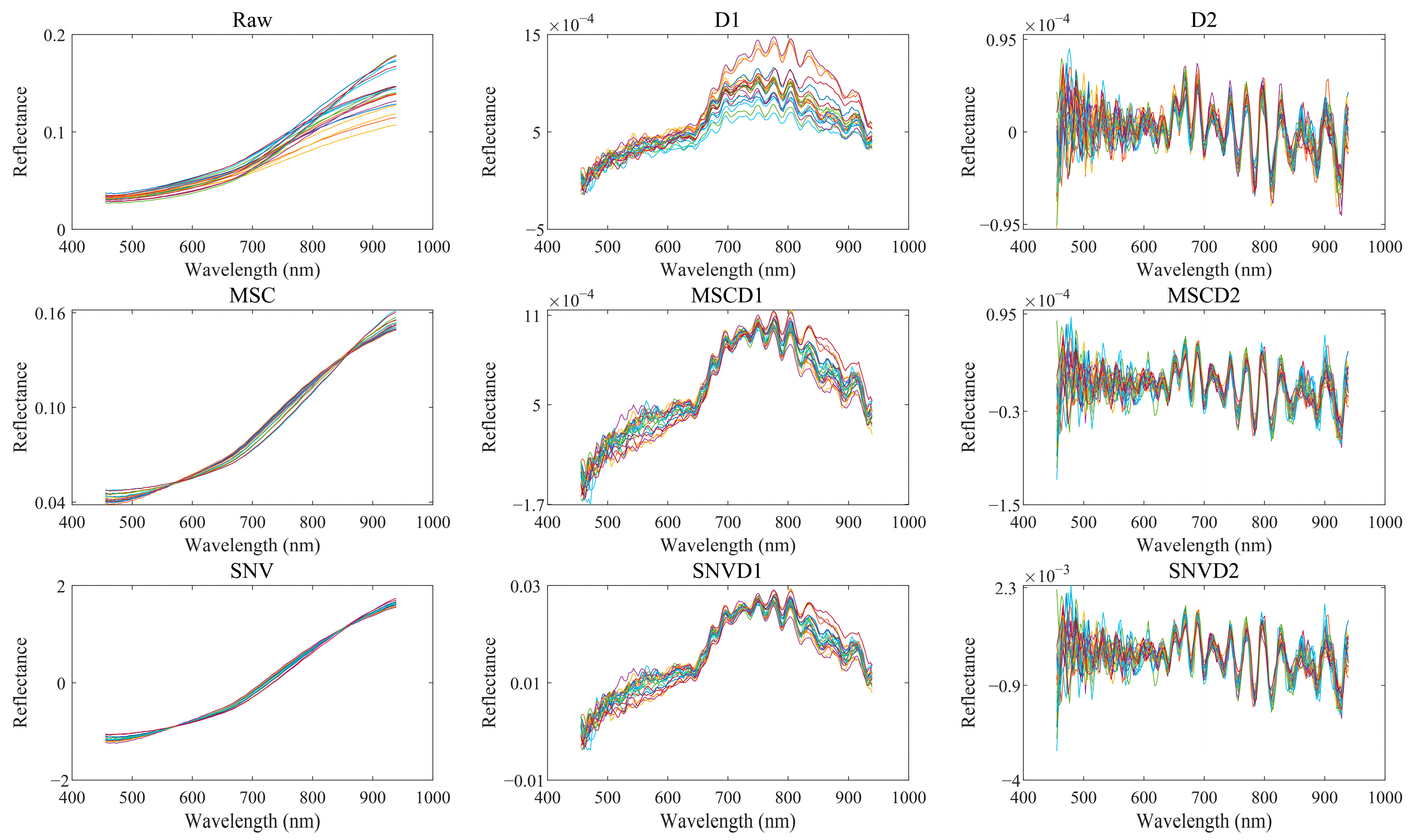
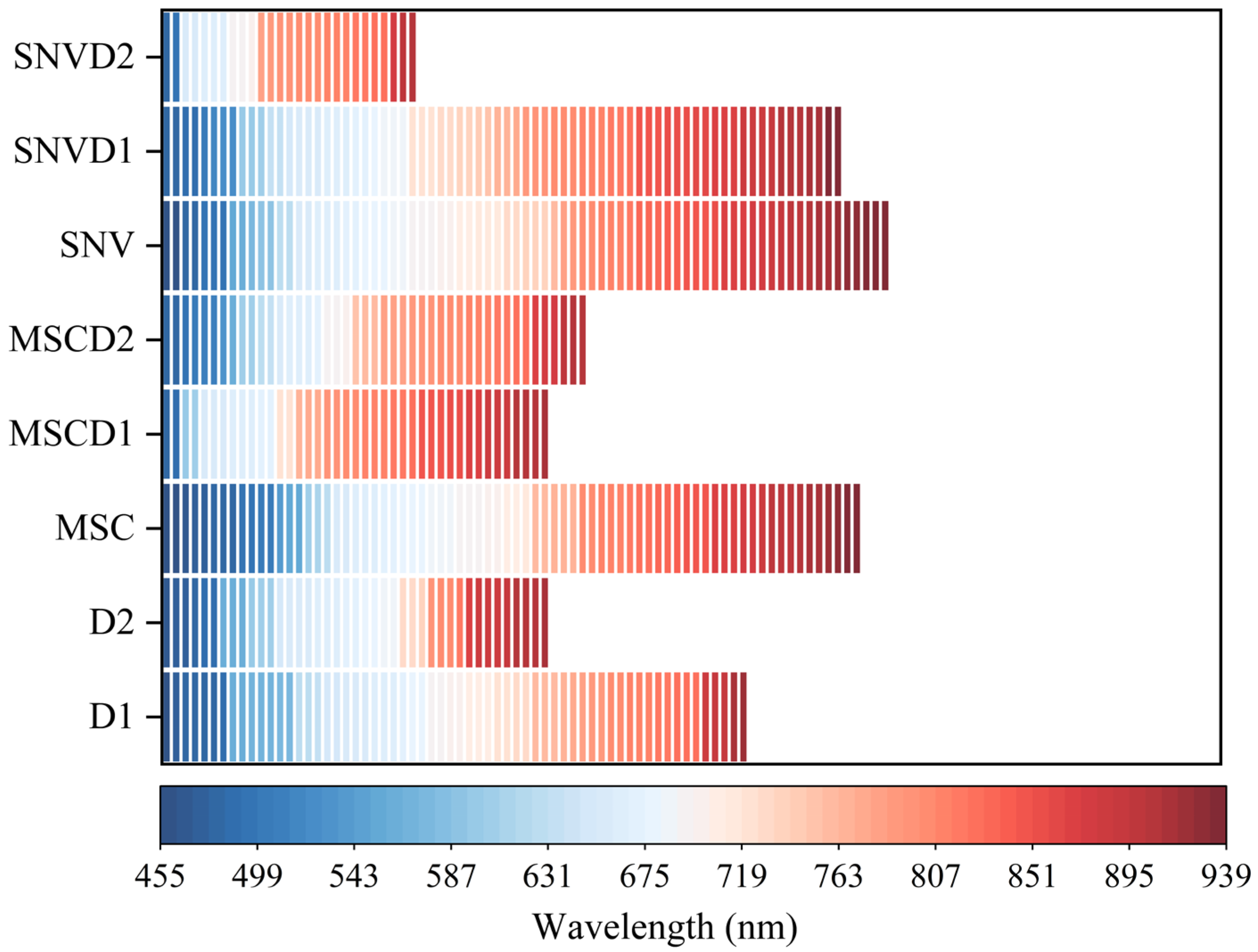
2.5. Spectral Preprocessing
2.6. Partial Least-Squares Regression
2.7. Band Selection
2.8. Sediment Chronology and Time Series Analysis
3. Results and Discussion
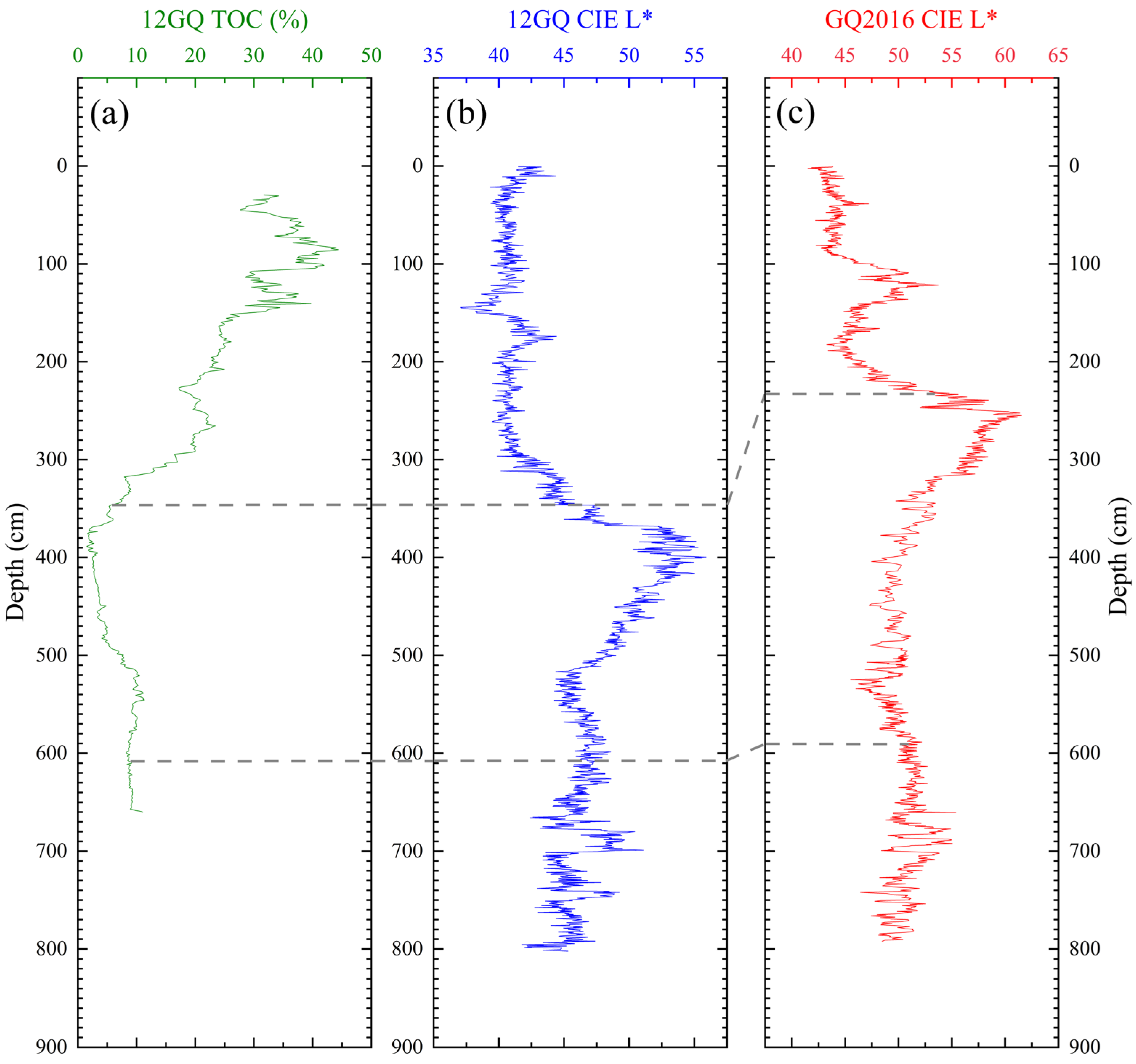
3.1. Chronology
3.2. Spectral Characterization and Preprocessing Results
3.3. Estimation Model of TOC
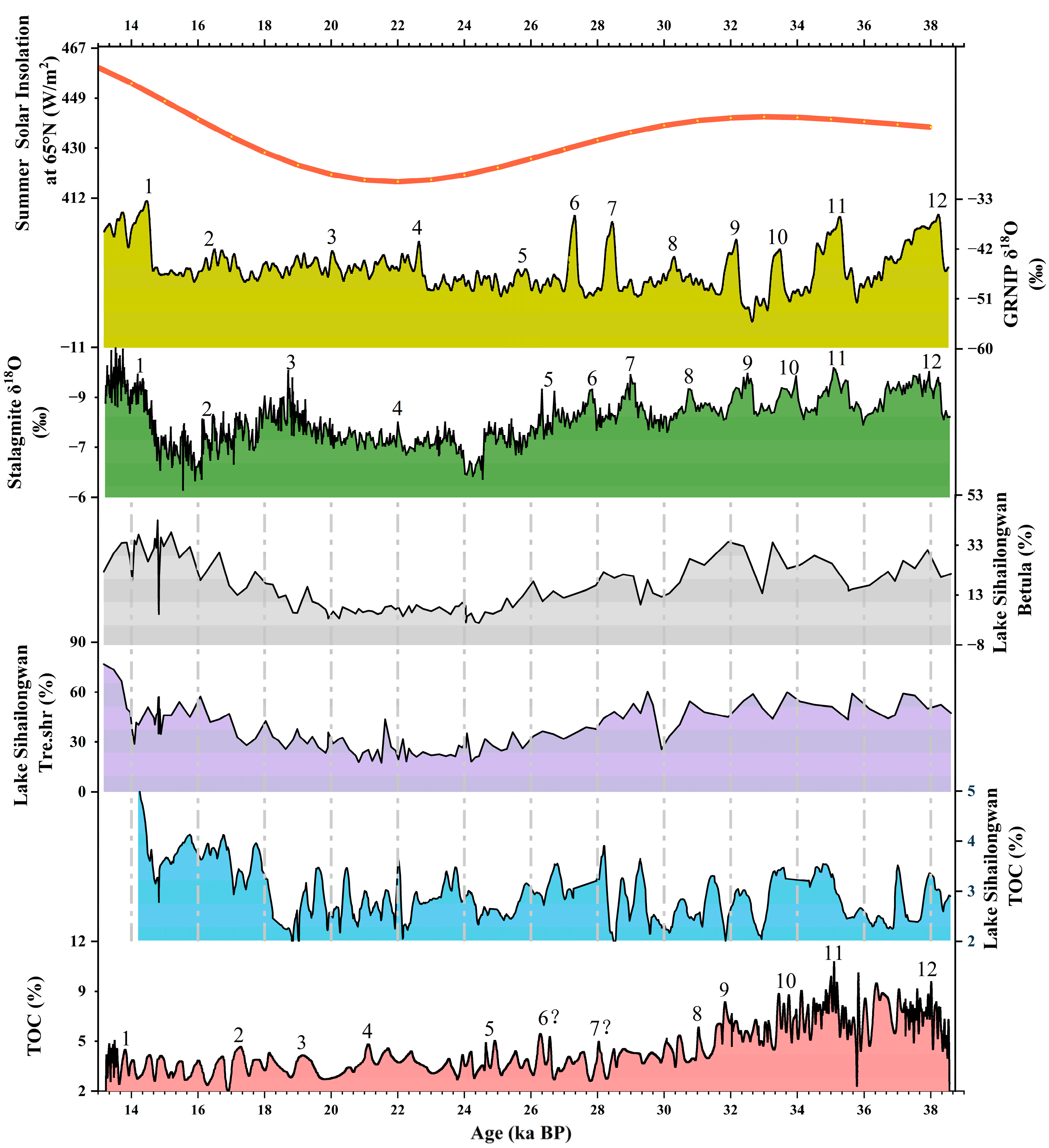
3.4. The Reconstruction of TOC Using the PLSR Model and Its Comparison with the Global Paleoclimate Records
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TOC | total organic carbon |
| PLSR | partial least-squares regression |
| VNIR | visible and near-infrared |
| SWIR | short-wavelength infrared |
| GA | genetic algorithm |
| D2 | Savitzky–Golay second derivative |
| SNV | standard normal variate |
| MSC | multiplicative scatter correction |
| D1 | Savitzky–Golay first derivative |
| SNVD1 | standard normal variate + Savitzky–Golay first derivative |
| SNVD2 | standard normal variate + Savitzky–Golay second derivative |
| MSCD1 | multiplicative scatter correction + Savitzky–Golay first derivative |
| MSCD2 | multiplicative scatter correction + Savitzky–Golay second derivative |
| ANN | artificial neural network |
| SVM | support vector machine |
| RF | random forest |
References
- Jiang, S.W.; Zhou, X.; Li, Z.B.; Tu, L.Y.; Chen, A.Z.; Liu, X.Q.; Ding, M.; Zhang, G.C. Increased effective radiative forcing enhanced the modulating effect of Pacific Decadal Oscillation on late Little Ice Age precipitation in the Jiang-Huai region, China. Clim. Dyn. 2023, 61, 4173–4183. [Google Scholar] [CrossRef]
- Larocque-Tobler, I.; Filipiak, J.; Tylmann, W.; Bonk, A.; Grosjean, M. Comparison between chironomid-inferred mean-August temperature from varved Lake Zabinskie (Poland) and instrumental data since 1896 AD. Quat. Sci. Rev. 2015, 111, 35–50. [Google Scholar] [CrossRef]
- Randsalu-Wendrup, L.; Conley, D.J.; Carstensen, J.; Snowball, I.; Jessen, C.; Fritz, S.C. Ecological Regime Shifts in Lake Kalksjon, Sweden, in Response to Abrupt Climate Change Around the 8.2 ka Cooling Event. Ecosystems 2012, 15, 1336–1350. [Google Scholar] [CrossRef]
- Van Daele, M.; Moernaut, J.; Silversmit, G.; Schmidt, S.; Fontijn, K.; Heirman, K.; Vandoorne, W.; De Clercq, M.; Van Acker, J.; Wolff, C.; et al. The 600 yr eruptive history of Villarrica Volcano (Chile) revealed by annually laminated lake sediments. Geol. Soc. Am. Bull. 2014, 126, 481–498. [Google Scholar] [CrossRef]
- Zhou, X.; Zhan, T.; Tan, N.; Tu, L.Y.; Smol, J.P.; Jiang, S.W.; Zeng, F.M.; Liu, X.Y.; Li, X.Z.; Liu, G.X.; et al. Inconsistent patterns of Holocene rainfall changes at the East Asian monsoon margin compared to the core monsoon region. Quat. Sci. Rev. 2023, 301, 107952. [Google Scholar] [CrossRef]
- Lian, Z.L.; Jiang, Z.J.; Huang, X.P.; Liu, S.L.; Zhang, J.P.; Wu, Y.C. Labile and recalcitrant sediment organic carbon pools in the Pearl River Estuary, southern China. Sci. Total Environ. 2018, 640–641, 1302–1311. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Feng, J.M.; Li, X.Y.; Liu, H.J.; Wang, X.Z. Composition, distribution, and source of organic carbon in surface sediments of Erhai Lake, China. Sci. Total Environ. 2023, 858, 159983. [Google Scholar] [CrossRef]
- Gmitrowicz-Iwan, J.; Kusmierz, S.; Ligeza, S.; Pranagal, J.; Szafran, T. The overlooked carbon cache: Unveiling organic carbon storage in small floodplain lake sediments under humid continental climate changes. Ecol. Indic. 2024, 165, 112224. [Google Scholar] [CrossRef]
- Cao, Y.M.; Peng, J.; Zhou, S.Q.; Chen, X. Impacts of climate warming and atmospheric deposition on recent shifts in chironomid communities in two alpine lakes, eastern China. Environ. Res. 2024, 246, 118133. [Google Scholar] [CrossRef]
- Valinia, S.; Futter, M.N.; Cosby, B.J.; Rosén, P.; Fölster, J. Simple Models to Estimate Historical and Recent Changes of Total Organic Carbon Concentrations in Lakes. Environ. Sci. Technol. 2015, 49, 386–394. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.J.; Wu, D.; Niu, L.L.; Ma, X.Y.; Li, Y.M.; Hillman, A.L.; Abbott, M.B.; Zhou, A.F. Contrasting ecosystem responses to climatic events and human activity revealed by a sedimentary record from Lake Yilong, southwestern China. Sci. Total Environ. 2021, 783, 146922. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Hu, T.P.; Liu, W.J.; Mao, Y.; Shi, M.M.; Xu, A.; Su, Y.W.; Li, X.Y.; Xing, X.L.; Qi, S.H. Modern lake sedimentary record of PAHs and OCPs in a typical karst wetland, south China: Response to human activities and environmental changes. Environ. Pollut. 2021, 291, 118173. [Google Scholar] [CrossRef] [PubMed]
- Lynch, K.L.; Horgan, B.H.; Munakata-Marr, J.; Hanley, J.; Schneider, R.J.; Rey, K.A.; Spear, J.R.; Jackson, W.A.; Ritter, S.M. Near-infrared spectroscopy of lacustrine sediments in the Great Salt Lake Desert: An analog study for Martian paleolake basins. J. Geophys. Res.-Planets 2015, 120, 599–623. [Google Scholar] [CrossRef]
- Sorrel, P.; Jacq, K.; Van Exem, A.; Escarguel, G.; Dietre, B.; Debret, M.; McGowan, S.; Ducept, J.; Gauthier, E.; Oberhänsli, H. Evidence for centennial-scale Mid-Holocene episodes of hypolimnetic anoxia in a high-altitude lake system from central Tian Shan (Kyrgyzstan). Quat. Sci. Rev. 2021, 252, 106748. [Google Scholar] [CrossRef]
- Meyer-Jacob, C.; Michelutti, N.; Paterson, A.M.; Monteith, D.; Yang, H.D.; Weckström, J.; Smol, J.P.; Bindler, R. Inferring Past Trends in Lake Water Organic Carbon Concentrations in Northern Lakes Using Sediment Spectroscopy. Environ. Sci. Technol. 2017, 51, 13248–13255. [Google Scholar] [CrossRef]
- Ghanbari, H.; Antoniades, D. Convolutional neural networks for mapping of lake sediment core particle size using hyperspectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102906. [Google Scholar] [CrossRef]
- Ghanbari, H.; Jacques, O.; Adaïmé, M.É.; Gregory-Eaves, I.; Antoniades, D. Remote Sensing of Lake Sediment Core Particle Size Using Hyperspectral Image Analysis. Remote Sens. 2020, 12, 3850. [Google Scholar] [CrossRef]
- Jacq, K.; Giguet-Covex, C.; Sabatier, P.; Perrette, Y.; Fanget, B.; Coquin, D.; Debret, M.; Arnaud, F. High-resolution grain size distribution of sediment core with hyperspectral imaging. Sediment. Geol. 2019, 393–394, 105536. [Google Scholar] [CrossRef]
- Zander, P.D.; Zarczynski, M.; Tylmann, W.; Rainford, S.K.; Grosjean, M. Seasonal climate signals preserved in biochemical varves: Insights from novel high-resolution sediment scanning techniques. Clim. Past 2021, 17, 2055–2071. [Google Scholar] [CrossRef]
- Butz, C.; Grosjean, M.; Fischer, D.; Wunderle, S.; Tylmann, W.; Rein, B. Hyperspectral imaging spectroscopy: A promising method for the biogeochemical analysis of lake sediments. J. Appl. Remote Sens. 2015, 9, 096031. [Google Scholar] [CrossRef]
- Van Exem, A.; Debret, M.; Copard, Y.; Vannière, B.; Sabatier, P.; Marcotte, S.; Laignel, B.; Reyss, J.-L.; Desmet, M. Hyperspectral core logging for fire reconstruction studies. J. Paleolimnol. 2017, 59, 297–308. [Google Scholar] [CrossRef]
- Jacq, K.; Perrette, Y.; Fanget, B.; Sabatier, P.; Coquin, D.; Martinez-Lamas, R.; Debret, M.; Arnaud, F. High-resolution prediction of organic matter concentration with hyperspectral imaging on a sediment core. Sci. Total Environ. 2019, 663, 236–244. [Google Scholar] [CrossRef]
- Aymerich, I.F.; Oliva, M.; Giralt, S.; Martin-Herrero, J. Detection of Tephra Layers in Antarctic Sediment Cores with Hyperspectral Imaging. PLoS ONE 2016, 11, e0146578. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, L.G.; Zhan, T.; Huang, W.; Zhou, X.Y.; Hao, Q.Z.; Wang, Y.H.; He, X.Q.; Zhao, C.; Zhang, J.; et al. Time-transgressive onset of the Holocene Optimum in the East Asian monsoon region. Earth Planet. Sci. Lett. 2016, 456, 39–46. [Google Scholar] [CrossRef]
- Chai, R.S.; Cao, H.J.; Huang, Q.Y.; Xie, L.H.; Yang, F.; Yin, H.B. Temporal and environmental factors drive community structure and function of methanotrophs in volcanic forest soils. J. For. Res. 2023, 35, 2. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.Y.; Zhan, T.; Oyebanji, D.B.; Zhang, J.X.; Tu, L.Y.; Jiang, S.W. Low-latitude forcing on 4.2 ka event indicated by records in the Asian monsoon region. Glob. Planet. Change 2024, 235, 104401. [Google Scholar] [CrossRef]
- Carneiro, L.M.; do Rosário Zucchi, M.; de Jesus, T.B.; da Silva Júnior, J.B.; Hadlich, G.M. δ13C, δ15N and TOC/TN as indicators of the origin of organic matter in sediment samples from the estuary of a tropical river. Mar. Pollut. Bull. 2021, 172, 112857. [Google Scholar] [CrossRef]
- Jiang, S.W.; Zhou, X.; Zhan, T.; Tu, L.Y.; Liu, X.Y.; Cui, S.K.; Liu, X.Q.; Chen, A.Z.; Zhang, G.C.; Shen, Y.A. Increased radiocarbon age offset of crater lake sediments linked to cool-dry intervals during the past 40,000 yr. Catena 2024, 238, 107881. [Google Scholar] [CrossRef]
- Dotto, A.C.; Dalmolin, R.S.D.; ten Caten, A.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Peng, X.T.; Shi, T.Z.; Song, A.H.; Chen, Y.Y.; Gao, W.X. Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods. Remote Sens. 2014, 6, 2699–2717. [Google Scholar] [CrossRef]
- Qiao, X.X.; Wang, C.; Feng, M.C.; Yang, W.D.; Ding, G.W.; Sun, H.; Liang, Z.Y.; Shi, C.C. Hyperspectral estimation of soil organic matter based on different spectral preprocessing techniques. Spectrosc. Lett. 2017, 50, 156–163. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-Trending of near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Geladi, P.; Macdougall, D.; Martens, H. Linearization and Scatter-Correction for near-Infrared Reflectance Spectra of Meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627. [Google Scholar] [CrossRef]
- Jamshidi, B.; Minaei, S.; Mohajerani, E.; Ghassernian, H. Reflectance Vis/NIR spectroscopy for nondestructive taste characterization of Valencia oranges. Comput. Electron. Agric. 2012, 85, 64–69. [Google Scholar] [CrossRef]
- Sampaio, P.S.; Soares, A.; Castanho, A.; Almeida, A.S.; Oliveira, J.; Brites, C. Optimization of rice amylose determination by NIR-spectroscopy using PLS chemometrics algorithms. Food Chem. 2018, 242, 196–204. [Google Scholar] [CrossRef]
- Wang, X.; Esquerre, C.; Downey, G.; Henihan, L.; O’Callaghan, D.; O’Donnell, C. Development of chemometric models using Vis-NIR and Raman spectral data fusion for assessment of infant formula storage temperature and time. Innov. Food Sci. Emerg. Technol. 2021, 67, 102551. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, J.; Wang, Y.X.; Liu, B.P.; Ding, J.; Mao, X.J.; Zhang, J.; Hu, H.T.; Li, J. Study on discrimination of white tea and albino tea based on near-infrared spectroscopy and chemometrics. J. Sci. Food Agric. 2014, 94, 1026–1033. [Google Scholar] [CrossRef]
- Kuang, B.Y.; Tekin, Y.; Mouazen, A.M. Comparison between artificial neural network and partial least squares for on-line visible and near infrared spectroscopy measurement of soil organic carbon, pH and clay content. Soil Tillage Res. 2015, 146, 243–252. [Google Scholar] [CrossRef]
- Knox, N.M.; Grunwald, S.; McDowell, M.L.; Bruland, G.L.; Myers, D.B.; Harris, W.G. Modelling soil carbon fractions with visible near-infrared (VNIR) and mid-infrared (MIR) spectroscopy. Geoderma 2015, 239, 229–239. [Google Scholar] [CrossRef]
- Gomez, C.; Coulouma, G. Importance of the spatial extent for using soil properties estimated by laboratory VNIR/SWIR spectroscopy: Examples of the clay and calcium carbonate content. Geoderma 2018, 330, 244–253. [Google Scholar] [CrossRef]
- Stevens, A.; Udelhoven, T.; Denis, A.; Tychon, B.; Lioy, R.; Hoffmann, L.; van Wesemael, B. Measuring soil organic carbon in croplands at regional scale using airborne imaging spectroscopy. Geoderma 2010, 158, 32–45. [Google Scholar] [CrossRef]
- Jacq, K.; Debret, M.; Fanget, B.; Coquin, D.; Sabatier, P.; Pignol, C.; Arnaud, F.; Perrette, Y. Theoretical Principles and Perspectives of Hyperspectral Imaging Applied to Sediment Core Analysis. Quaternary 2022, 5, 28. [Google Scholar] [CrossRef]
- Sawant, S.; Manoharan, P. Hyperspectral band selection based on metaheuristic optimization approach. Infrared Phys. Technol. 2020, 107, 103295. [Google Scholar] [CrossRef]
- Yang, P.M.; Hu, J.; Hu, B.F.; Luo, D.F.; Peng, J. Estimating Soil Organic Matter Content in Desert Areas Using In Situ Hyperspectral Data and Feature Variable Selection Algorithms in Southern Xinjiang, China. Remote Sens. 2022, 14, 5221. [Google Scholar] [CrossRef]
- Barman, B.; Patra, S. Variable precision rough set based unsupervised band selection technique for hyperspectral image classification. Knowl.-Based Syst. 2020, 193, 105414. [Google Scholar] [CrossRef]
- Lin, Y.K.; Gao, J.X.; Tu, Y.J.; Zhang, Y.X.; Gao, J. Estimating low concentration heavy metals in water through hyperspectral analysis and genetic algorithm-partial least squares regression. Sci. Total Environ. 2024, 916, 170225. [Google Scholar] [CrossRef]
- Bao, Y.L.; Meng, X.T.; Ustin, S.; Wang, X.; Zhang, X.L.; Liu, H.J.; Tang, H.T. Vis-SWIR spectral prediction model for soil organic matter with different grouping strategies. Catena 2020, 195, 104703. [Google Scholar] [CrossRef]
- Leardi, R. Application of genetic algorithm-PLS for feature selection in spectral data sets. J. Chemom. 2000, 14, 643–655. [Google Scholar] [CrossRef]
- Leardi, R.; Gonzalez, A.L. Genetic algorithms applied to feature selection in PLS regression: How and when to use them. Chemom. Intell. Lab. Syst. 1998, 41, 195–207. [Google Scholar] [CrossRef]
- Reimer, P.J.; Austin, W.E.N.; Bard, E.; Bayliss, A.; Blackwell, P.G.; Bronk Ramsey, C.; Butzin, M.; Cheng, H.; Edwards, R.L.; Friedrich, M.; et al. The IntCal20 Northern Hemisphere Radiocarbon Age Calibration Curve (0–55 cal kBP). Radiocarbon 2020, 62, 725–757. [Google Scholar] [CrossRef]
- Stuiver, M.; Reimer, P.J. Extended 14C Data Base and Revised CALIB 3.0 14C Age Calibration Program. Radiocarbon 1993, 35, 215–230. [Google Scholar] [CrossRef]
- Maarten, B.; Christen, J.A. Flexible paleoclimate age-depth models using an autoregressive gamma process. Bayesian Anal. 2011, 6, 457–474. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave-Propagation and Sampling Theory 1. Complex Signal and Scattering in Multilayered Media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Mann, M.E.; Lees, J.M. Robust estimation of background noise and signal detection in climatic time series. Clim. Change 1996, 33, 409–445. [Google Scholar] [CrossRef]
- Vaughan, S.; Bailey, R.J.; Smith, D.G. Detecting cycles in stratigraphic data: Spectral analysis in the presence of red noise. Paleoceanography 2011, 26. [Google Scholar] [CrossRef]
- Thomson, D.J. Spectrum estimation and harmonic analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef]
- Li, M.S.; Hinnov, L.; Kump, L. Acycle: Time-series analysis software for paleoclimate research and education. Comput. Geosci. 2019, 127, 12–22. [Google Scholar] [CrossRef]
- Galvão, L.S.; Vitorello, Í. Variability of Laboratory Measured Soil Lines of Soils from Southeastern Brazil. Remote Sens. Environ. 1998, 63, 166–181. [Google Scholar] [CrossRef]
- Jia, N.; Li, L.; Guo, H.; Xie, M.Y. Important role of Fe oxides in global soil carbon stabilization and stocks. Nat. Commun. 2024, 15, 10318. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Guo, L.; Sun, X.R.; Fu, P.; Shi, T.Z.; Dang, L.N.; Chen, Y.Y.; Linderman, M.; Zhang, G.L.; Zhang, Y.; Jiang, Q.H.; et al. Mapping soil organic carbon stock by hyperspectral and time-series multispectral remote sensing images in low-relief agricultural areas. Geoderma 2021, 398, 115118. [Google Scholar] [CrossRef]
- Meng, X.T.; Bao, Y.L.; Liu, J.G.; Liu, H.J.; Zhang, X.L.; Zhang, Y.; Wang, P.; Tang, H.T.; Kong, F.C. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Sun, W.C.; Liu, S.; Zhang, X.; Li, Y. Estimation of soil organic matter content using selected spectral subset of hyperspectral data. Geoderma 2022, 409, 115653. [Google Scholar] [CrossRef]
- Sola, I.; González-Audícana, M.; Álvarez-Mozos, J. Validation of a Simplified Model to Generate Multispectral Synthetic Images. Remote Sens. 2015, 7, 2942–2951. [Google Scholar] [CrossRef]
- Jian, Z.M.; Wang, Y.; Dang, H.W.; Lea, D.W.; Liu, Z.Y.; Jin, H.Y.; Yin, Y.Q. Half-precessional cycle of thermocline temperature in the western equatorial Pacific and its bihemispheric dynamics. Proc. Natl. Acad. Sci. USA 2020, 117, 7044–7051. [Google Scholar] [CrossRef] [PubMed]
- Braun, H.; Christl, M.; Rahmstorf, S.; Ganopolski, A.; Mangini, A.; Kubatzki, C.; Roth, K.; Kromer, B. Possible solar origin of the 1,470-year glacial climate cycle demonstrated in a coupled model. Nature 2005, 438, 208–211. [Google Scholar] [CrossRef]
- Berger, A.; Loutre, M.F. Insolation values for the climate of the last 10 million years. Quat. Sci. Rev. 1991, 10, 297–317. [Google Scholar] [CrossRef]
- Mingram, J.; Stebich, M.; Schettler, G.; Hu, Y.Q.; Rioual, P.; Nowaczyk, N.; Dulski, P.; You, H.T.; Opitz, S.; Liu, Q.; et al. Millennial-scale East Asian monsoon variability of the last glacial deduced from annually laminated sediments from Lake Sihailongwan, NE China. Quat. Sci. Rev. 2018, 201, 57–76. [Google Scholar] [CrossRef]
- Rasmussen, S.O.; Andersen, K.K.; Svensson, A.M.; Steffensen, J.P.; Vinther, B.M.; Clausen, H.B.; Siggaard-Andersen, M.L.; Johnsen, S.J.; Larsen, L.B.; Dahl-Jensen, D.; et al. A new Greenland ice core chronology for the last glacial termination. J. Geophys. Res.-Atmos. 2006, 111, D06102. [Google Scholar] [CrossRef]
- Dykoski, C.A.; Edwards, R.L.; Cheng, H.; Yuan, D.X.; Cai, Y.J.; Zhang, M.L.; Lin, Y.S.; Qing, J.M.; An, Z.S.; Revenaugh, J. A high-resolution, absolute-dated Holocene and deglacial Asian monsoon record from Dongge Cave, China. Earth Planet. Sci. Lett. 2005, 233, 71–86. [Google Scholar] [CrossRef]
- Wang, Y.J.; Cheng, H.; Edwards, R.L.; Kong, X.G.; Shao, X.H.; Chen, S.T.; Wu, J.Y.; Jiang, X.Y.; Wang, X.F.; An, Z.S. Millennial- and orbital-scale changes in the East Asian monsoon over the past 224,000 years. Nature 2008, 451, 1090–1093. [Google Scholar] [CrossRef] [PubMed]
- Cui, S.K.; Zhou, X.; Tu, L.Y.; Liu, X.Y.; Zhan, T.; Jiang, S.W.; Oyebanji, D.B.; Qiao, Y.S.; Liu, X.Q.; Xue, H.P.; et al. Inconsistent Hydroclimate Responses in Different Parts of the Asian Monsoon Region during Heinrich Stadials. Lithosphere 2022, 2022, 1507045. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhou, X.; Zhan, T.; Zhou, X.Y.; Wu, H.B.; Jiang, S.W.; Tu, L.Y.; Oyebanji, D.; Shen, Y.A. Pollen evidence for a wet Younger Dryas in northern NE China. Catena 2023, 220, 106667. [Google Scholar] [CrossRef]
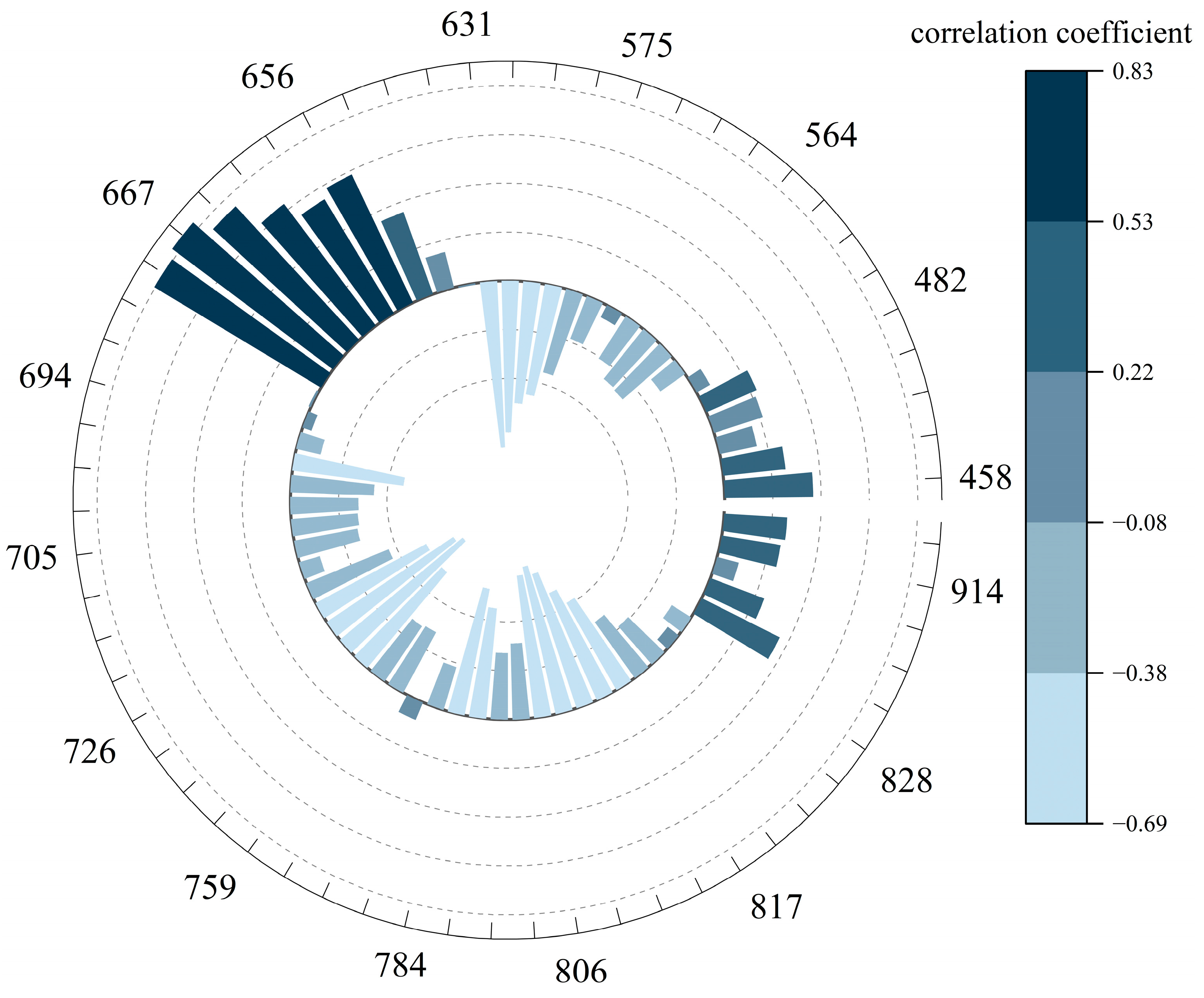



| Number | Max (%) | Min (%) | Mean (%) | |
|---|---|---|---|---|
| Dataset | 260 | 11.27 | 1.51 | 6.06 |
| Calibration set | 182 | 11.27 | 1.51 | 6.12 |
| Validation set | 78 | 11.18 | 1.66 | 5.93 |
| Preprocessing Methods | Abbreviations | Reference |
|---|---|---|
| Standard normal variate | SNV | [32] |
| Multiplicative scatter correction | MSC | [33] |
| Savitzky–Golay first derivatives | D1 | [34] |
| Savitzky–Golay second derivatives | D2 | [34] |
| Standard normal variate + Savitzky–Golay first derivatives | SNVD1 | [35] |
| Standard normal variate + Savitzky–Golay second derivatives | SNVD2 | [36] |
| Multiplicative scatter correction + Savitzky–Golay first derivatives | MSCD1 | [37] |
| Multiplicative scatter correction + Savitzky–Golay second derivatives | MSCD2 | [38] |
| D1 | D2 | MSC | MSCD1 | MSCD2 | SNV | SNVD1 | SNVD2 | |
|---|---|---|---|---|---|---|---|---|
| Calibration set R | 0.95 | 0.95 | 0.94 | 0.93 | 0.94 | 0.90 | 0.92 | 0.93 |
| Validation set R | 0.93 | 0.94 | 0.93 | 0.92 | 0.92 | 0.90 | 0.92 | 0.92 |
| Validation set RMSE (%) | 1.09 | 0.99 | 1.14 | 1.14 | 1.10 | 1.27 | 1.21 | 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Zhou, X.; Zhao, H.; Zhang, G.; Chen, Y.; Jiang, S.; Zhan, T.; Tu, L. High-Resolution Reconstruction of Total Organic Carbon Content in Lake Sediments Using Hyperspectral Imaging. Remote Sens. 2025, 17, 706. https://doi.org/10.3390/rs17040706
Lin X, Zhou X, Zhao H, Zhang G, Chen Y, Jiang S, Zhan T, Tu L. High-Resolution Reconstruction of Total Organic Carbon Content in Lake Sediments Using Hyperspectral Imaging. Remote Sensing. 2025; 17(4):706. https://doi.org/10.3390/rs17040706
Chicago/Turabian StyleLin, Xuening, Xin Zhou, Hongfei Zhao, Guangcheng Zhang, Yiyan Chen, Shiwei Jiang, Tao Zhan, and Luyao Tu. 2025. "High-Resolution Reconstruction of Total Organic Carbon Content in Lake Sediments Using Hyperspectral Imaging" Remote Sensing 17, no. 4: 706. https://doi.org/10.3390/rs17040706
APA StyleLin, X., Zhou, X., Zhao, H., Zhang, G., Chen, Y., Jiang, S., Zhan, T., & Tu, L. (2025). High-Resolution Reconstruction of Total Organic Carbon Content in Lake Sediments Using Hyperspectral Imaging. Remote Sensing, 17(4), 706. https://doi.org/10.3390/rs17040706






