A Geometric Calibration Method for Spaceborne Single-Photon Lasers That Integrates Laser Detectors and Corner Cube Retroreflectors
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Experimental Data
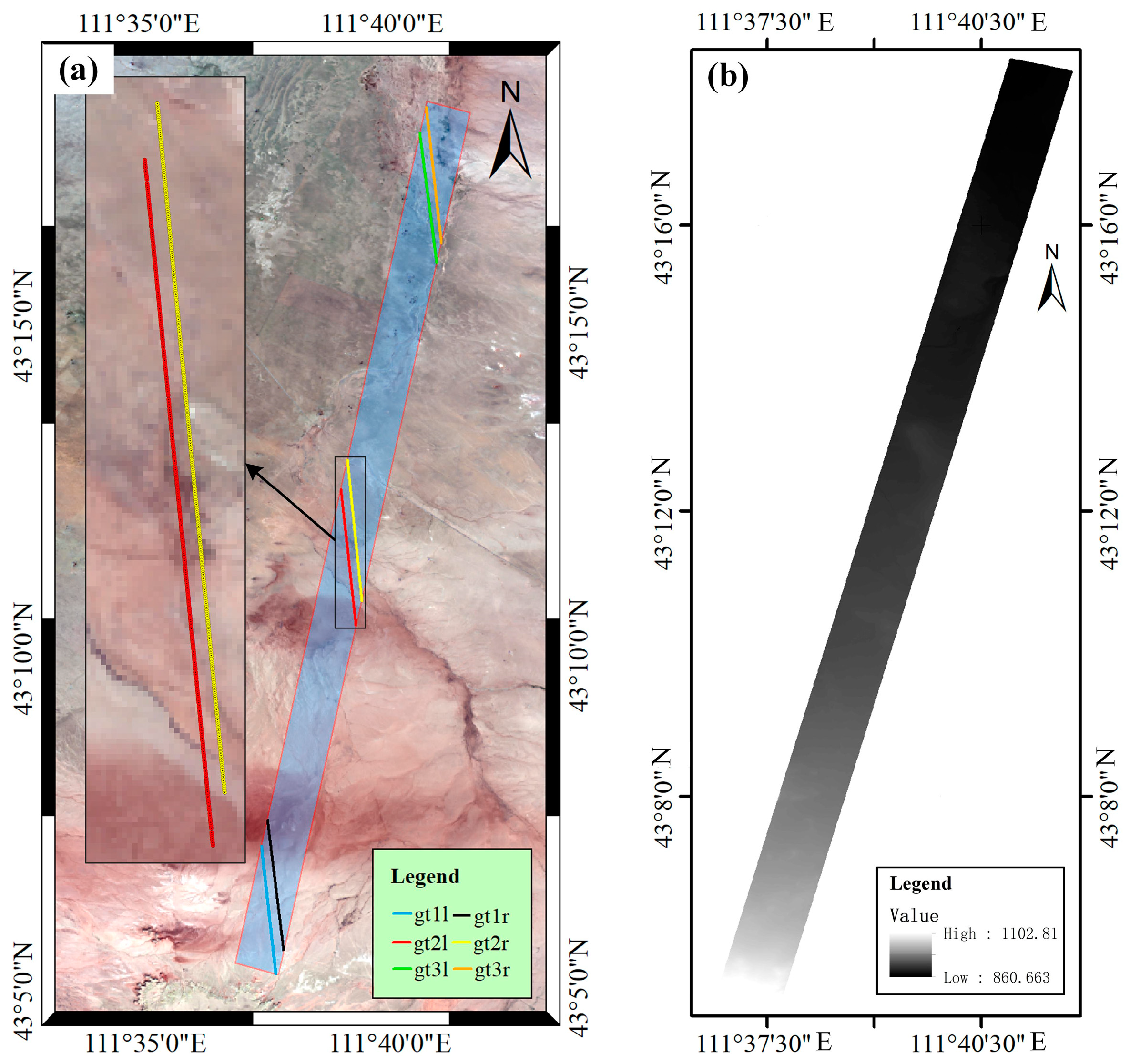
2.1.1. Study Area
2.1.2. Experimental Data
- ATLAS Single-Photon Laser Data
- 2.
- High-Precision DSM
2.2. Methodology
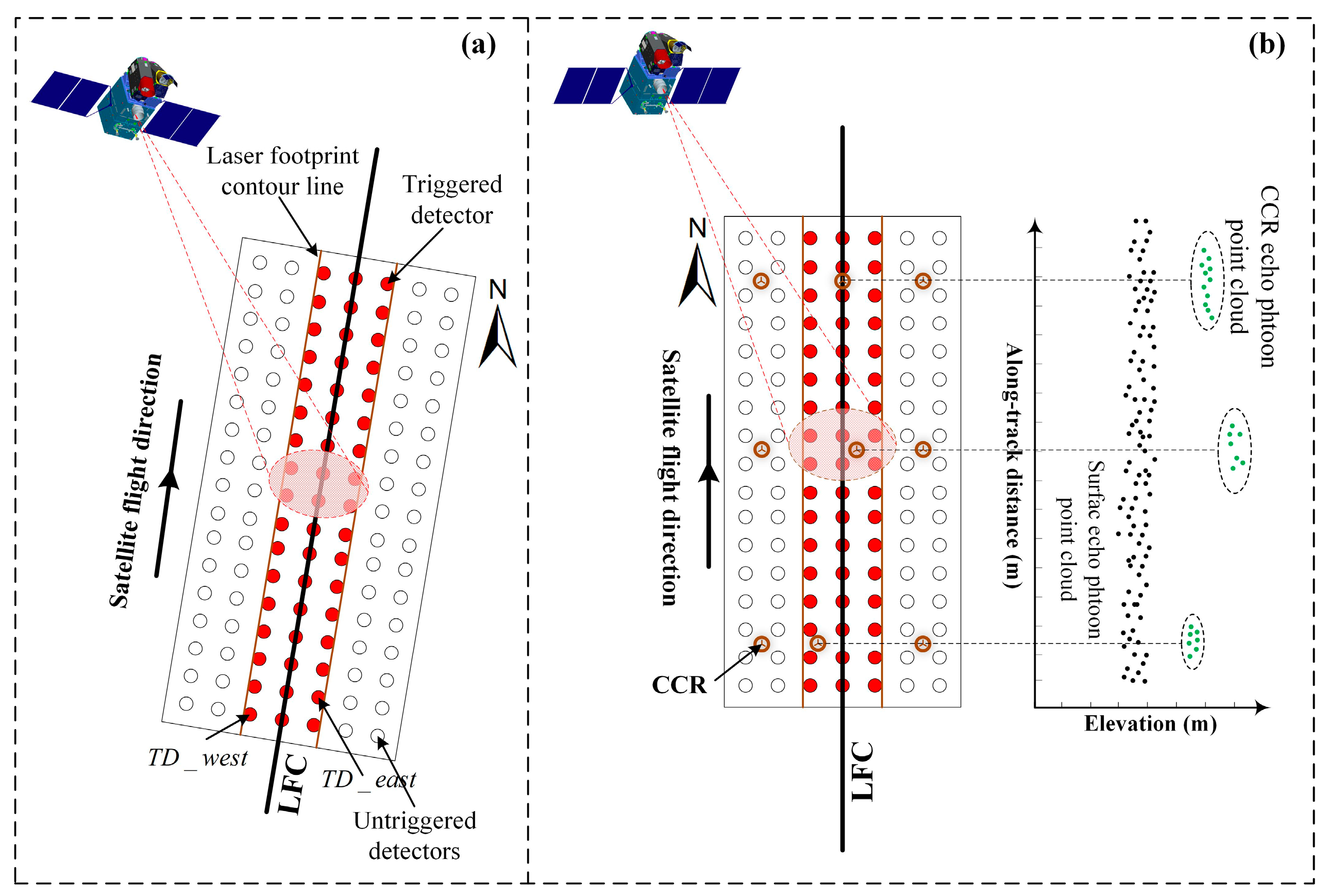
2.2.1. Construction of an LFC Model Based on Detectors
2.2.2. Development of an Accurate Laser Footprint Centroid Positioning Model Using CCRs and Detectors
- Identification of Triggered CCRs and Matching of CCR Photon Clouds
- 2.
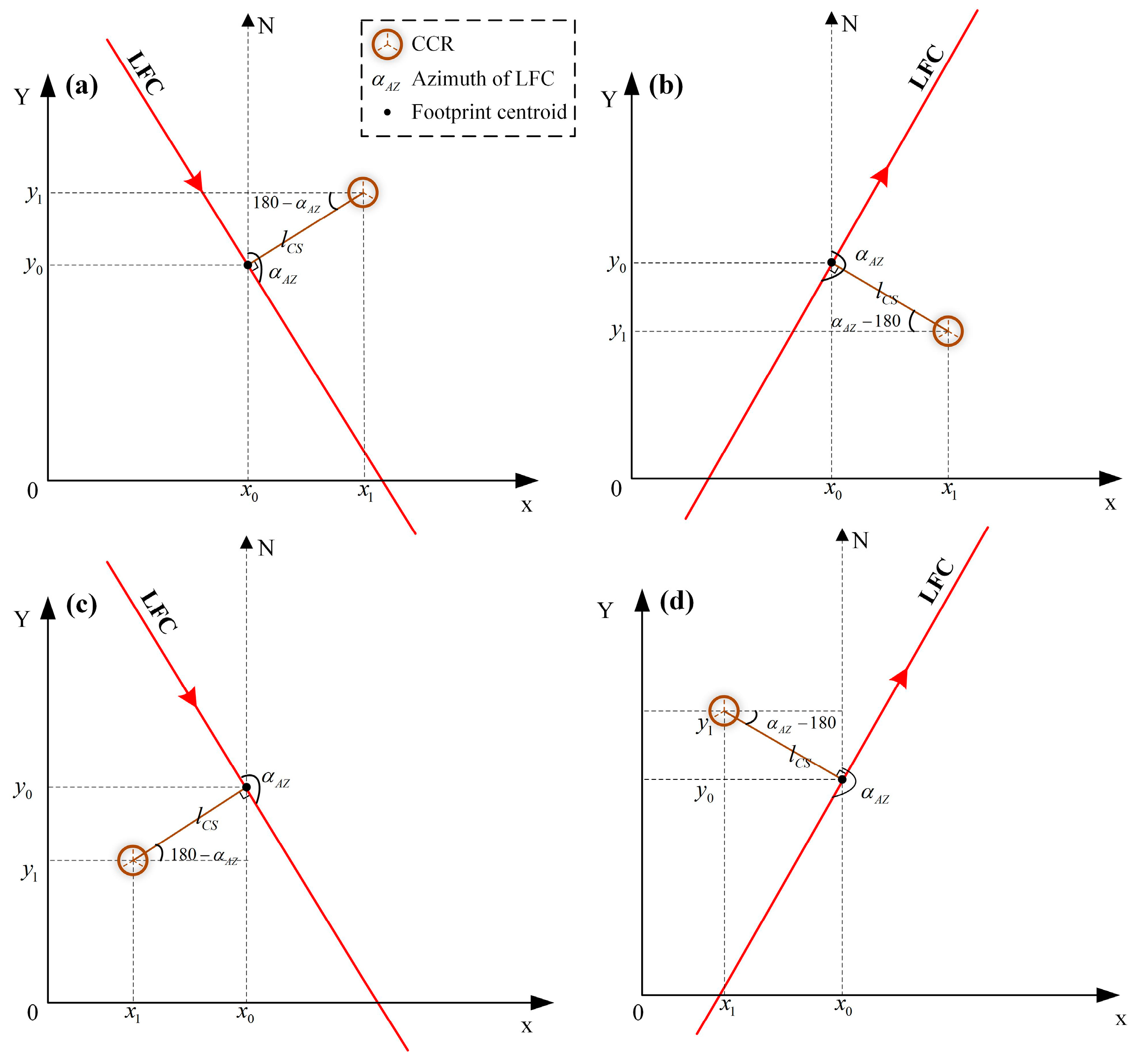
- Precise Positioning of Laser Footprint Centroids Based on the LFC Azimuth
- (a)
- CCR located east of the LFC with azimuth between 0° and 180°:
- (b)
- CCR located east of the LFC with azimuth between 180° and 360°:
- (c)
- CCR located west of the LFC with azimuth between 0° and 180°:
- (d)
- CCR located west of the LFC with azimuth between 180° and 360°:
- CCR located east of the LFC:
- CCR located west of the LFC:
- CCR located on the LFC:
2.2.3. Establishment of a Geometric Calibration Model for a Spaceborne Single-Photon Laser
3. Results
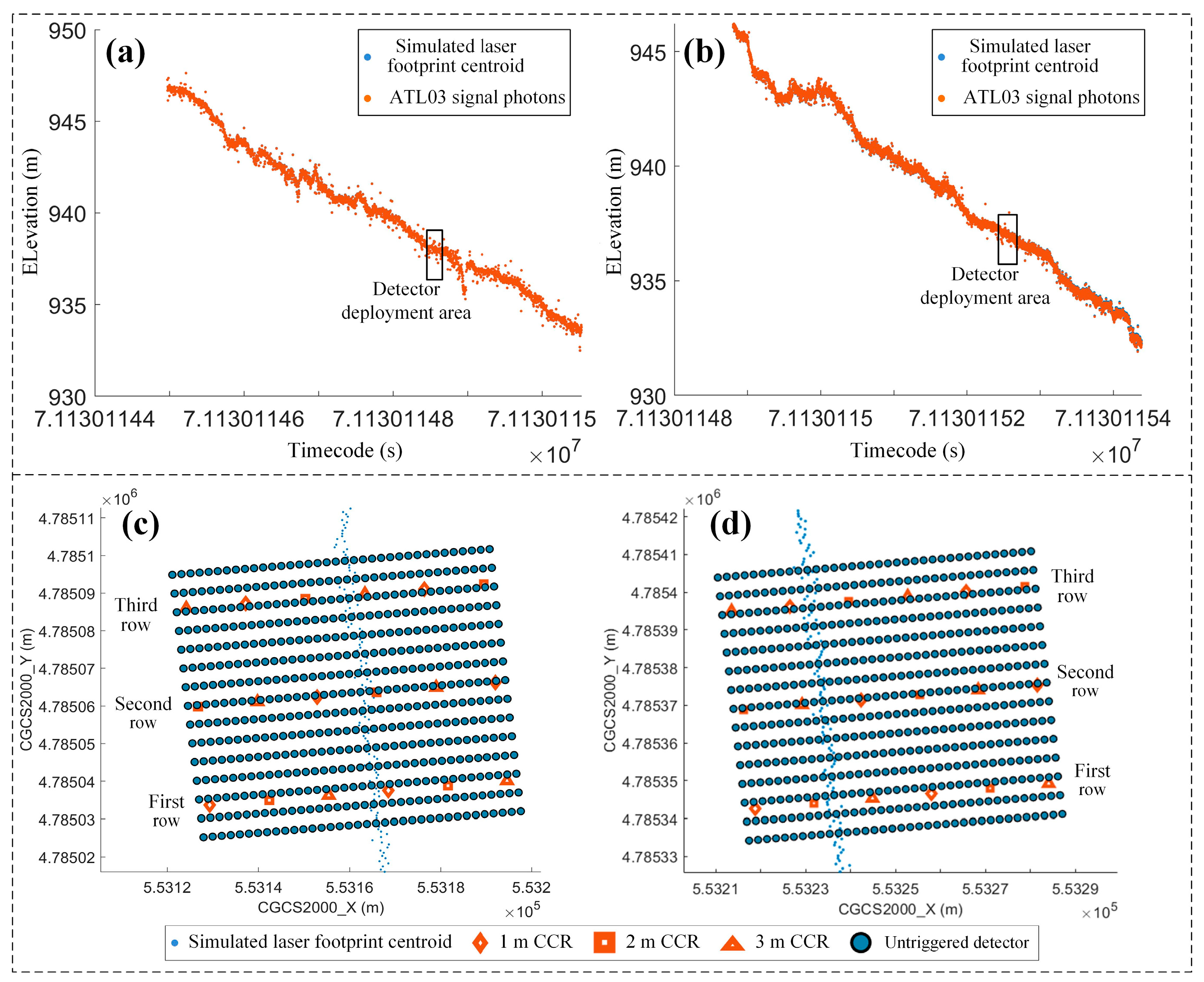
3.1. Simulation of Calibration Data for Spaceborne Single-Photon Lasers
- Simulation of Laser Pointing Angles and Footprint Centroids
- 2.
- Simulation of the Detectors and CCRs
- 3.
- Simulation of Ground-Triggered Detectors
- 4.
- Simulation of Ground and CCR Echo Photon Clouds
3.2. Precise Positioning of Laser Footprint Centroids Through the Integration of Detectors and CCRs
- 1.
- Extraction of the LFC Based on the Detectors
- 2.
- Precise Positioning of Laser Footprint Centroids Integrated with CCRs
3.3. Geometric Calibration of a Spaceborne Single-Photon Laser
4. Discussion
4.1. Deployment Scheme for Detectors and CCRs
4.1.1. Deployment Range of Detector and CCR Arrays
4.1.2. CCR Placement Strategies
- Along-Track Spacing of CCRs
- 2.
- Across-Track Spacing of CCRs
- 3.
- CCR Deployment Height and Scheme
4.1.3. Detector Placement Strategies
4.1.4. Integrated Deployment Strategies for Detectors and CCRs
4.2. Comparison with Other Methods
4.3. Limitations and Suggestions
5. Conclusions
- (1)
- Simulation experiments using ATLAS data demonstrate that the proposed CMDC method can be used to effectively determine the LFC and accurately identify the positions of the centroids of spaceborne single-photon laser footprints by integrating triggered CCRs.
- (2)
- By employing precisely positioned laser footprint centroids as ground control points, the calibration of ATLAS beams gt2l and gt2r was achieved, with a pointing angle accuracy of approximately 1 arcsec and a ranging accuracy better than 2.1 cm. These results robustly validate the efficacy of the CMDC method.
- (3)
- An effective integrated deployment scheme for detectors and CCRs is one of the critical prerequisites for implementing the CMDC method. The following deployment parameters are recommended: a minimum deployment range of × 70 m (along track × across track), a detector deployment spacing of × 2.0 m (along-track × across-track), a CCR deployment spacing of × m (along track × across track), and CCR heights of 1.0, 2.0, and 3.0 m.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Description | Product | Data Fields | Data Directory |
|---|---|---|---|
| Laser emission time | ATL03 | delta_time | /gtx/heights |
| Photon coordinates | lat_ph, lon_ph, h_ph | ||
| Laser time of flight | ATL02 | ph_tof | /atlas/pcex/altimetry/s_w/photons |
| Satellite orbit time | delta_time | /atlas/housekeeping/position_velocity | |
| Satellite orbit data | x_eci_pos, y_eci_pos, z_eci_pos | ||
| Satellite attitude time | ATL02 | delta_time | /atlas/housekeeping/pointing |
| Satellite attitude quaternion | q_sc_i2b_1, q_sc_i2b_2, q_sc_i2b_3, q_sc_i2b_4 |
| Row Number | CCR Number | gt2l | gt2r | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Latitude (°) | Longitude (°) | Elevation (m) | Height (m) | Latitude (°) | Longitude (°) | Elevation (m) | Height (m) | ||
| First row | #1 | 43.20157 | 111.65459 | 938.13 | 1.0 | 43.20159 | 111.65485 | 938.11 | 1.0 |
| #2 | 43.20158 | 111.65475 | 939.16 | 2.0 | 43.20160 | 111.65501 | 939.10 | 2.0 | |
| #3 | 43.20159 | 111.65491 | 940.07 | 3.0 | 43.20161 | 111.65517 | 940.24 | 3.0 | |
| #4 | 43.20160 | 111.65507 | 938.14 | 1.0 | 43.20162 | 111.65533 | 938.21 | 1.0 | |
| #5 | 43.20161 | 111.65523 | 939.21 | 2.0 | 43.20163 | 111.65549 | 939.18 | 2.0 | |
| #6 | 43.20162 | 111.65539 | 940.20 | 3.0 | 43.20164 | 111.65565 | 940.17 | 3.0 | |
| Second row | #7 | 43.20180 | 111.65456 | 939.12 | 2.0 | 43.20182 | 111.65482 | 938.96 | 2.0 |
| #8 | 43.20181 | 111.65472 | 940.04 | 3.0 | 43.20183 | 111.65498 | 940.03 | 3.0 | |
| #9 | 43.20182 | 111.65488 | 937.99 | 1.0 | 43.20184 | 111.65514 | 938.12 | 1.0 | |
| #10 | 43.20184 | 111.65504 | 939.14 | 2.0 | 43.20185 | 111.65530 | 939.29 | 2.0 | |
| #11 | 43.20185 | 111.65521 | 940.10 | 3.0 | 43.20186 | 111.65546 | 940.15 | 3.0 | |
| #12 | 43.20186 | 111.65537 | 938.14 | 1.0 | 43.20187 | 111.65562 | 938.09 | 1.0 | |
| Third row | #13 | 43.20204 | 111.65453 | 940.01 | 3.0 | 43.20206 | 111.65479 | 940.04 | 3.0 |
| #14 | 43.20205 | 111.65469 | 938.21 | 1.0 | 43.20207 | 111.65495 | 938.02 | 1.0 | |
| #15 | 43.20206 | 111.65485 | 938.98 | 2.0 | 43.20208 | 111.65511 | 939.02 | 2.0 | |
| #16 | 43.20207 | 111.65501 | 940.09 | 3.0 | 43.20209 | 111.65527 | 940.00 | 3.0 | |
| #17 | 43.20208 | 111.65518 | 938.20 | 1.0 | 43.20210 | 111.65543 | 938.03 | 1.0 | |
| #18 | 43.20209 | 111.65534 | 938.94 | 2.0 | 43.20212 | 111.65560 | 939.13 | 2.0 | |
References
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; Dimarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, 97–116. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W. The Ice, Cloud, and Land Elevation Satellite–2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Amy Neuenschwander, K.P. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2018, 221, 247–259. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Ma, L.; Hurtt, G.; Tang, H.; Lamb, R.; Lister, A.; Chini, L.; Dubayah, R.; Armston, J.; Campbell, E.; Duncanson, L. Spatial heterogeneity of global forest aboveground carbon stocks and fluxes constrained by spaceborne lidar data and mechanistic modeling. Glob. Change Biol. 2023, 29, 3378–3394. [Google Scholar] [CrossRef]
- Wang, R.; Lu, Y.; Lu, D.; Li, G. Improving extraction of forest canopy height through reprocessing ICESat-2 ATLAS and GEDI data in sparsely forested plain regions. GISci. Remote Sens. 2024, 61, 2396807. [Google Scholar] [CrossRef]
- Huang, Q.; McMillan, M.; Muir, A.; Phillips, J.; Slater, T. Multipeak retracking of radar altimetry waveforms over ice sheets. Remote Sens. Environ. 2024, 303, 114020. [Google Scholar] [CrossRef]
- Robel, A.A.; Sim, S.J.; Meyer, C.; Siegfried, M.R.; Gustafson, C.D. Contemporary ice sheet thinning drives subglacial groundwater exfiltration with potential feedbacks on glacier flow. Sci. Adv. 2023, 9, 33. [Google Scholar] [CrossRef]
- Kossieris, S.; Tsiakos, V.; Tsimiklis, G.; Amditis, A. Inland Water Level Monitoring from Satellite Observations: A Scoping Review of Current Advances and Future Opportunities. Remote Sens. 2024, 16, 1181. [Google Scholar] [CrossRef]
- Liu, C.; Hu, R.; Wang, Y.; Lin, H.; Wu, D.; Dai, Y.; Zhu, Y.; Liu, Z.; Yang, D.; Zhang, Q. Integrating ICESat-2 laser altimeter observations and hydrological modeling for enhanced prediction of climate-driven lake level change. J. Hydrol. 2023, 626, 130304. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, S.; Deng, R.; Huang, Y.; Ye, H.; Xu, Z.; Zeng, K. Mapping Ultrahigh-Spatial-Resolution Bathymetry for a Wide Range of Coastal Optically Shallow Waters Without in Situ Bathymetric Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Wang, E.; Li, D.; Wang, Z.; Cao, W.; Zhang, J.; Wang, J.; Zhang, H. Pixel-level bathymetry mapping of optically shallow water areas by combining aerial RGB video and photogrammetry. Geomorphology 2024, 449, 109049. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Thomas, T.C.; Pennington, T.A.; Rebold, T.W.; Nicholas, J.B.; Rowlands, D.D.; Gardner, A.S.; Bae, S. ICESat-2 Pointing Calibration and Geolocation Performance. Earth Space Sci. 2020, 8, e2020EA001494. [Google Scholar] [CrossRef]
- Yi, H.; Li, S.; Ma, Y.; Huang, K.; Zhou, H.; Shi, G.Y. On-orbit calibration of satellite laser altimeters based on footprint detection. Acta Phys. Sin. 2017, 66, 134206. [Google Scholar] [CrossRef]
- Magruder, L.A.; Suleman, M.A.; Schutz, B.E. ICESat laser altimeter measurement time validation system. Meas. Sci. Technol. 2003, 14, 1978–1985. [Google Scholar] [CrossRef][Green Version]
- Magruder, L.A.; Schutz, B.E.; Silverberg, E.C. Laser pointing angle and time of measurement verification of the ICESat laser altimeter using a ground-based electro-optical detection system. J. Geod. 2003, 77, 148–154. [Google Scholar] [CrossRef]
- Tang, X.M.; Xie, J.F.; Mo, F.; Dou, X.H.; Li, X.; Li, S.N.; Li, S.; Huang, G.H.; Fu, X.K.; Liu, R.; et al. GF-7 dual-beam laser altimeter on-orbit geometric calibration and test verification. Acta Geod. Cartogr. Sin. 2003, 77, 148–154. [Google Scholar]
- Xie, J.; Tang, X.; Mo, F.; Tang, H.; Wang, Z.; Wang, X.; Liu, Y.; Tian, S.; Liu, R.; Xia, X. In-orbit geometric calibration and experimental verification of the ZY3-02 laser altimeter. Photogramm. Rec. 2018, 33, 341–362. [Google Scholar] [CrossRef]
- Tang, X.M.; Xie, J.F.; Fu, X.K.; Mo, F.; Li, S.N.; Dou, X.H. ZY3-02 Laser Altimeter On-orbit Geometrical Calibration and Test. Acta Geod. Cartogr. Sin. 2017, 46, 714–723. [Google Scholar]
- Tang, X.; Xie, J.; Gao, X.; Mo, F.; Feng, W.; Liu, R. The In-Orbit Calibration Method Based on Terrain Matching with Pyramid-Search for the Spaceborne Laser Altimeter. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1053–1062. [Google Scholar] [CrossRef]
- Nan, Y.; Feng, Z.; Liu, E.; Li, B. Iterative Pointing Angle Calibration Method for the Spaceborne Photon-Counting Laser Altimeter Based on Small-Range Terrain Matching. Remote Sens. 2019, 11, 2158. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.; Ma, Y.; Liu, X.; Yang, J.; Yu, D. A new terrain matching method for estimating laser pointing and ranging systematic biases for spaceborne photon-counting laser altimeters. ISPRS J. Photogramm. Remote Sens. 2022, 188, 220–236. [Google Scholar] [CrossRef]
- Schenk, T.; Csatho, B.; Neumann, T. Assessment of ICESat-2’s Horizontal Accuracy Using Precisely Surveyed Terrains in McMurdo Dry Valleys, Antarctica. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Filin, S. Calibration of spaceborne laser Altimeters-an algorithm and the site selection problem. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1484–1492. [Google Scholar] [CrossRef]
- Xie, J.; Liu, R.; Tang, X.; Yang, X.; Zeng, J.; Mo, F.; Mei, Y. A Geometric Calibration Method Without a Field Site of the GF-7 Satellite Laser Relying on a Surface Mathematical Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Carabajal, C.C.; Rowlands, D.D. Enhanced geolocation of spaceborne laser altimeter surface returns: Parameter calibration from the simultaneous reduction of altimeter range and navigation tracking data. J. Geodyn. 2002, 34, 447–475. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Rowlands, D.D.; Williams, T.A.; Sirota, M. Reduction of ICESat systematic geolocation errors and the impact on ice sheet elevation change detection. Geophys. Res. Lett. 2005, 32, 312–321. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Rowlands, D.D.; Mccarthy, J.J.; Pavlis, D.E.; Stoneking, E. Spaceborne Laser-Altimeter-Pointing Bias Calibration from Range Residual Analysis. J. Spacecraft Rockets 2000, 37, 374–384. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Pavlis, D.E.; Lemoine, F.G.; Neumann, G.A.; Luthcke, S.B. The use of laser altimetry in the orbit and attitude determination of Mars Global Surveyor. Geophys. Res. Lett. 1999, 26, 1191–1194. [Google Scholar] [CrossRef]
- Bae, S.; Helgeson, B.; James, M.; Magruder, L.; Sipps, J.; Luthcke, S.; Thomas, T. Performance of ICESat-2 Precision Pointing Determination. Earth Space Sci. 2020, 8, e2020EA001478. [Google Scholar] [CrossRef]
- Tokunaga, M. Accuracy verification of DSM obtained from UAV using commercial software. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar] [CrossRef]
- Magruder, L.; Brunt, K.; Neumann, T.; Klotz, B.; Alonzo, M. Passive ground-based optical techniques for monitoring the on-orbit ICESat-2 altimeter geolocation and footprint diameter. Earth Space Sci. 2021, 8, e2020EA001414. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M.; Alonzo, M. Early ICESat-2 on-orbit Geolocation Validation Using Ground-Based Corner Cube Retro-Reflectors. Remote Sens. 2020, 12, 3653. [Google Scholar] [CrossRef]
- Krystek, M.; Anton, M. A weighted total least-squares algorithm for fitting a straight line. Meas. Sci. Technol. 2007, 18, 3438. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Xie, J.; Liu, R.; Mo, F.; Tang, H.; Jiao, H.; Mei, Y.; Yang, C. Pointing Bias Calibration of Gaofen-7 Laser Altimeter Based on Single Laser Footprint Image. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, V-2-2020, 113–119. [Google Scholar] [CrossRef]
- Xie, J.; Tang, X.; Mo, F.; Li, G.; Zhu, G.; Wang, Z.; Fu, X.; Gao, X.; Dou, X. ZY3-02 Laser Altimeter Footprint Geolocation Prediction. Sensors 2017, 17, 2165. [Google Scholar] [CrossRef]
- Liu, R.; Tang, X.; Xie, J.; Ma, R.; Yang, X.; Mo, F.; Lv, X. A Full-Link Simulation Method for Satellite Single-Photon LiDARs. IEEE Geosci. Remote Sens. Lett. 2023, 21, 1–5. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Yin, T.; Wang, C.; Lauret, N.; Regaieg, O.; Xi, X.; Gastellu-Etchegorry, J.P. Comprehensive LiDAR simulation with efficient physically-based DART-Lux model (I): Theory, novelty, and consistency validation. Remote Sens. Environ. 2022, 272, 112952. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, W.J. High Precision Attitude Determination Method for Star Camera Based on UKF. Acta Photonica Sin. 2020, 49, 146–153. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, C.; Zhu, G.; Wang, Z. Rapid Precision Orbit Determination Based on Dual-Frequency GPS Receiver for ZY3-02 Satellite. J. Geod. Geodyn. 2018, 38, 73–77. [Google Scholar] [CrossRef]
- Fricker, H.A.; Ridgway, J.R.; Minster, J.B.; Yi, D.; Bentley, C. The Algorithm Theoretical Basis Document for Tidal Corrections; Goddard Space Flight Center: Greenbelt, MD, USA; National Aeronautics and Space Administration: Washington, DC, USA, 2012. Available online: https://ntrs.nasa.gov/api/citations/20130013632/downloads/20130013632.pdf (accessed on 20 February 2025).
- Petrov, L.; Luthcke, S. Revision of the Atmospheric Delay Correction for ICESat-2 Laser Altimeter Ranges; National Aeronautics and Space Administration: Washington, DC, USA, 2013. Available online: https://ntrs.nasa.gov/citations/20180006782 (accessed on 20 February 2025).
- Magruder, L.A.; Webb, C.E.; Urban, T.J.; Silverberg, E.C.; Schutz, B.E. ICESat Altimetry Data Product Verification at White Sands Space Harbor. IEEE Trans. Geosci. Remote Sens. 2006, 45, 147–155. [Google Scholar] [CrossRef]
- Xie, J.; Liu, R.; Yang, X.; Mo, F.; Zhang, F.; Liu, L. On-orbit geometric calibration of satellite laser altimeters using infrared detectors and corner-cube retroreflectors. Int. J. Digit. Earth 2023, 16, 2067–2088. [Google Scholar] [CrossRef]



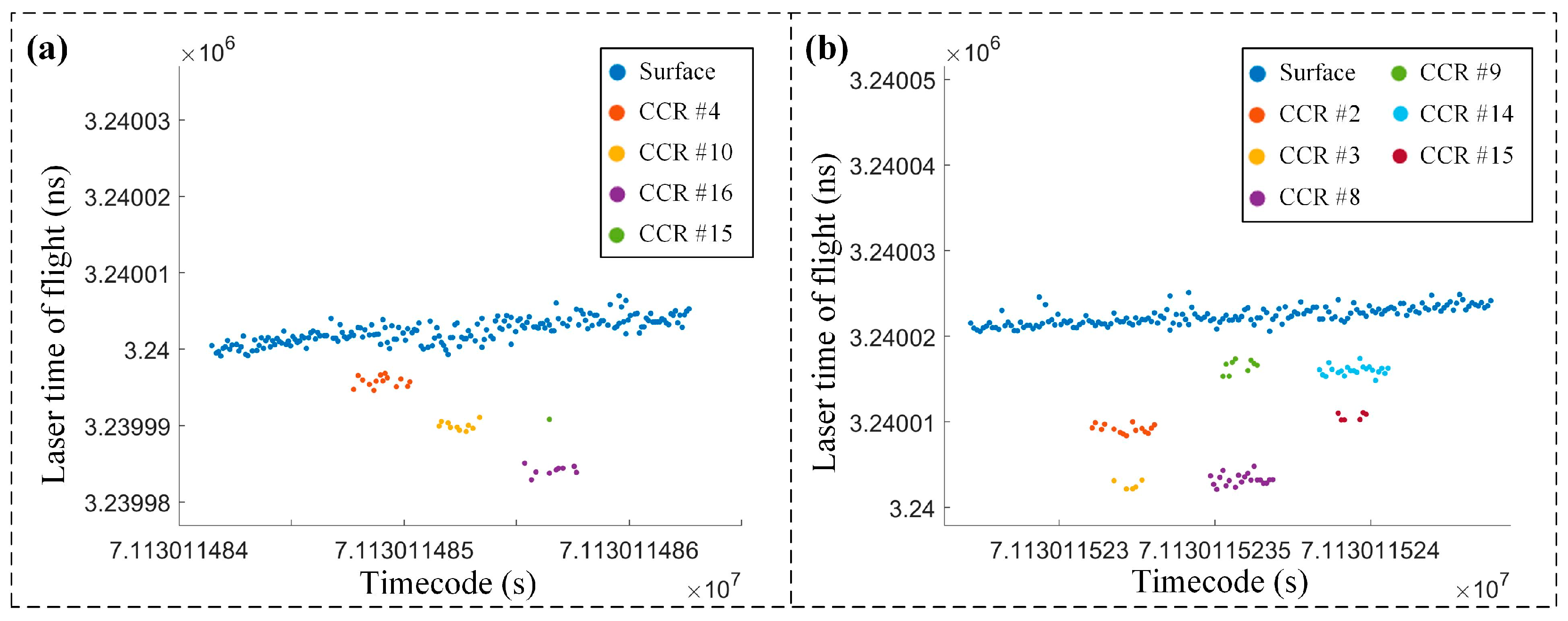


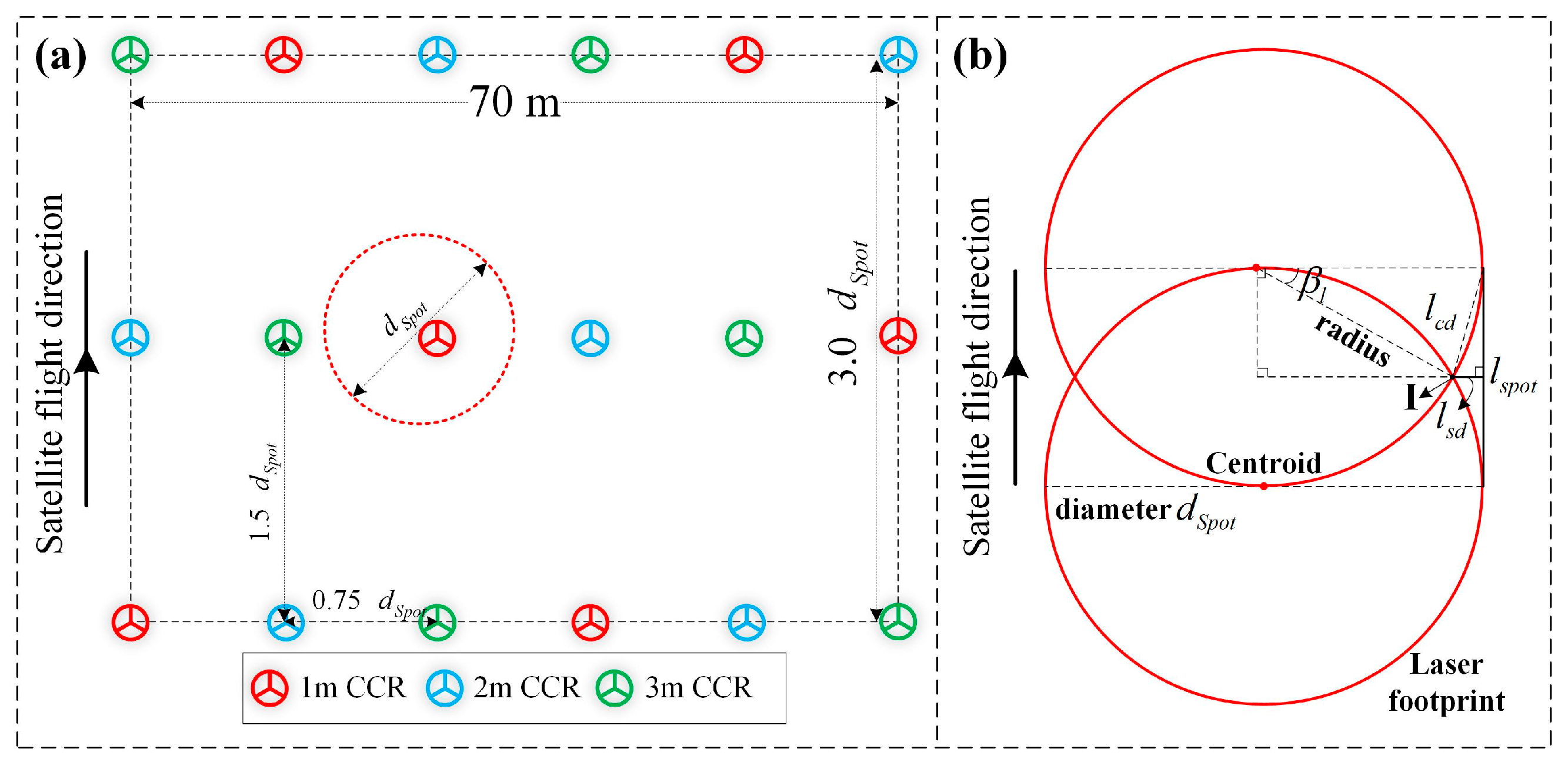
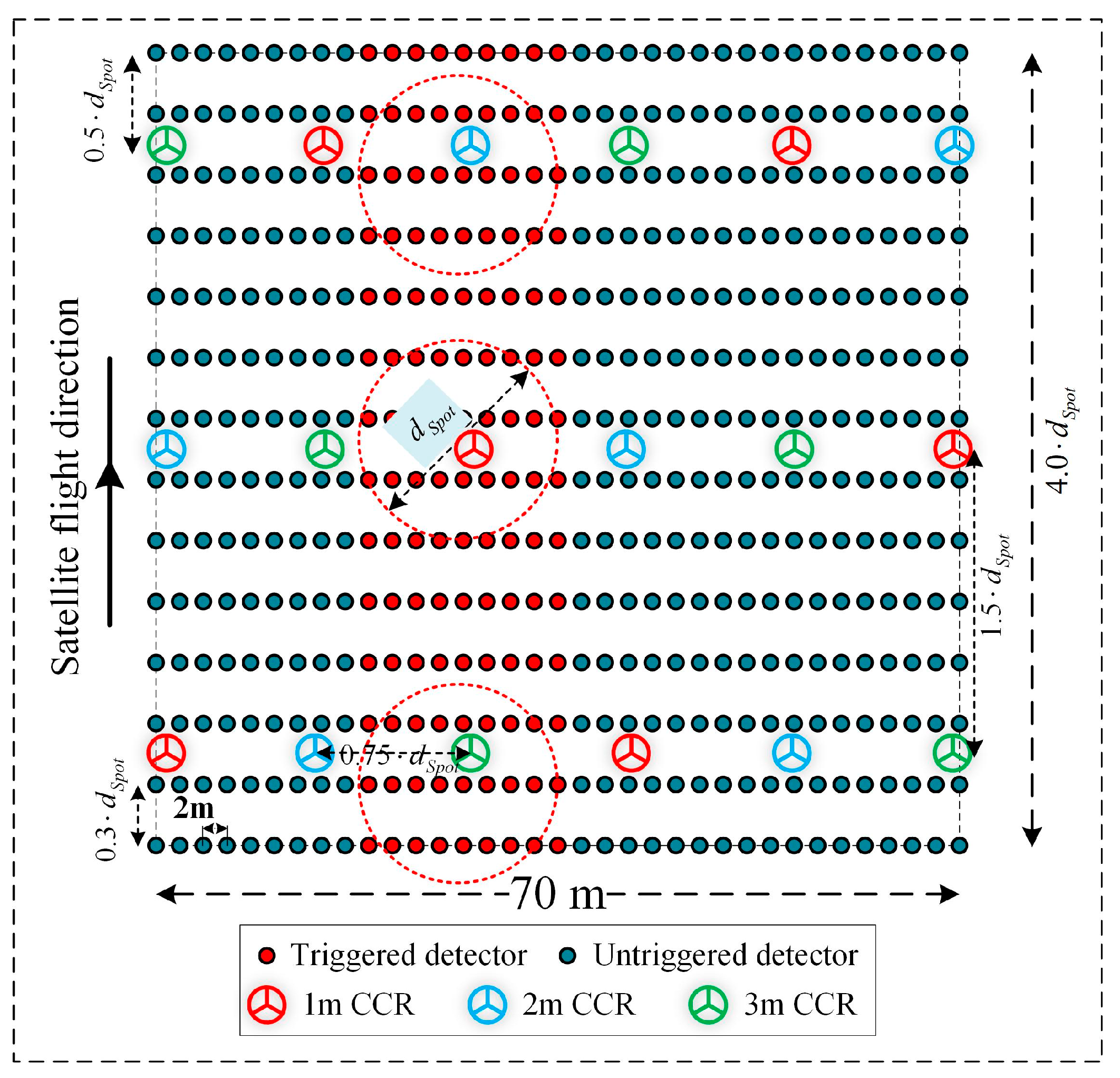
| Beam | Parameter Type | (°) | (°) | (°) | (m) |
|---|---|---|---|---|---|
| gt2l | Initial value | 90.0 | 90.0 | 0.0 | 0.0 |
| True value | 90.294300 | 89.867501 | 0.322752 | −2.308 | |
| gt2r | Initial value | 90.0 | 90.0 | 0.0 | 0.0 |
| True value | 90.580559 | 89.867789 | 0.595424 | 9.237 |
| Beam | Timecode (s) | Latitude (°) | Longitude (°) | Elevation (m) | CCR Number | (m) |
|---|---|---|---|---|---|---|
| gt2l | 71,130,114.84896 | 43.19902 | 111.65414 | 937.92 | # 4 | 1.79 |
| 71,130,114.85246 | 43.19925 | 111.65410 | 937.74 | # 10 | 2.27 | |
| 71,130,114.85646 | 43.19949 | 111.65407 | 937.71 | # 16 | 2.76 | |
| gt2r | 71,130,115.23206 | 43.20178 | 111.65503 | 937.02 | # 2 | 5.02 |
| 71,130,115.23206 | 43.20178 | 111.65503 | 937.02 | # 3 | 8.10 | |
| 71,130,115.23586 | 43.20201 | 111.65500 | 937.30 | # 8 | 5.03 | |
| 71,130,115.23586 | 43.20201 | 111.65500 | 937.30 | # 9 | 8.10 | |
| 71,130,115.23946 | 43.20225 | 111.65497 | 936.98 | # 14 | 5.03 | |
| 71,130,115.23946 | 43.20225 | 111.65497 | 936.98 | # 15 | 8.09 |
| Calibration Type | Laser Pointing Angle and Ranging Error | Difference | ||||
|---|---|---|---|---|---|---|
| (°) | (°) | (m) | (’’) | (’’) | (m) | |
| Initial value | 90.0 | 90.0 | 0.0 | - | - | - |
| True value | 90.294300 | 89.867501 | −2.308 | - | - | - |
| No error | 90.294198 | 89.867426 | −2.01 | −0.3672 | −0.27 | 0.028 |
| Attitude error | 90.294098 | 89.867235 | −2.01 | −0.7272 | −0.9576 | 0.028 |
| Orbital error | 90.294198 | 89.867426 | −2.002 | −0.3672 | −0.27 | 0.036 |
| Timing error | 90.294204 | 89.867427 | −2.01 | −0.3456 | −0.2664 | 0.028 |
| Atmospheric error | 90.294198 | 89.867426 | −2.003 | −0.3672 | −0.27 | 0.035 |
| Tidal error | 90.294198 | 89.867426 | −2.01 | −0.3672 | −0.27 | 0.028 |
| Total error | 90.294104 | 89.867236 | −2.017 | −0.7056 | −0.954 | 0.021 |
| Calibration Type | Laser Pointing Angle and Ranging Error | Difference | ||||
|---|---|---|---|---|---|---|
| (°) | (°) | (m) | (’’) | (’’) | (m) | |
| Initial value | 90.0 | 90.0 | 0.0 | - | - | - |
| True value | 90.580559 | 89.867789 | 9.237 | - | - | - |
| No error | 90.580599 | 89.867733 | 9.259 | 0.1440 | −0.2016 | 0.022 |
| Attitude error | 90.580482 | 89.867509 | 9.259 | −0.2772 | −1.0080 | 0.022 |
| Orbital error | 90.580599 | 89.867733 | 9.264 | 0.1440 | −0.2016 | 0.027 |
| Timing error | 90.580597 | 89.867733 | 9.259 | 0.1368 | −0.2016 | 0.022 |
| Atmospheric error | 90.580599 | 89.867733 | 9.265 | 0.1440 | −0.2016 | 0.028 |
| Tidal error | 90.580599 | 89.867733 | 9.259 | 0.1440 | −0.2016 | 0.022 |
| Total error | 90.580479 | 89.867509 | 9.256 | −0.2880 | −1.0080 | 0.019 |
| Type | Maximum Along Track Error (m) | Maximum Across Track Error (m) | Total Error (m) |
|---|---|---|---|
| Pointing error | 20 | 20 | 29 |
| Orbital error | 150 | 8 | 150 |
| Attitude error | 15 | 15 | 18 |
| Total error | 185 | 43 | 197 |
| Beam Type | Calibration Type | Laser Pointing Angle and Ranging Error | Difference | ||||
|---|---|---|---|---|---|---|---|
| (°) | (°) | (m) | (’’) | (’’) | (m) | ||
| gt2l | True value | 90.294300 | 89.867501 | −2.308 | - | - | - |
| Terrain matching | 90.293721 | 89.866602 | - | −2.0844 | −3.2364 | - | |
| CMCD | 90.294104 | 89.867236 | −2.017 | −0.7056 | -0.9540 | 0.021 | |
| gt2r | True value | 90.580559 | 89.867789 | 9.237 | - | - | - |
| Terrain matching | 90.580100 | 89.866947 | - | −1.6524 | −3.0312 | - | |
| CMCD | 90.580479 | 89.867509 | 9.256 | −0.2880 | −1.0080 | 0.019 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Xie, J.; Mo, F.; Yang, X.; Jiang, Z.; Hong, L. A Geometric Calibration Method for Spaceborne Single-Photon Lasers That Integrates Laser Detectors and Corner Cube Retroreflectors. Remote Sens. 2025, 17, 773. https://doi.org/10.3390/rs17050773
Liu R, Xie J, Mo F, Yang X, Jiang Z, Hong L. A Geometric Calibration Method for Spaceborne Single-Photon Lasers That Integrates Laser Detectors and Corner Cube Retroreflectors. Remote Sensing. 2025; 17(5):773. https://doi.org/10.3390/rs17050773
Chicago/Turabian StyleLiu, Ren, Junfeng Xie, Fan Mo, Xiaomeng Yang, Zhiyu Jiang, and Liang Hong. 2025. "A Geometric Calibration Method for Spaceborne Single-Photon Lasers That Integrates Laser Detectors and Corner Cube Retroreflectors" Remote Sensing 17, no. 5: 773. https://doi.org/10.3390/rs17050773
APA StyleLiu, R., Xie, J., Mo, F., Yang, X., Jiang, Z., & Hong, L. (2025). A Geometric Calibration Method for Spaceborne Single-Photon Lasers That Integrates Laser Detectors and Corner Cube Retroreflectors. Remote Sensing, 17(5), 773. https://doi.org/10.3390/rs17050773









