Accuracy Evaluation of Multi-Technique Combination Nonlinear Terrestrial Reference Frame and EOP Based on Singular Spectrum Analysis
Abstract
:1. Introduction
2. Methodology
2.1. Singular Spectrum Analysis
2.2. Least Squares Fitting
3. Time-Varying Periodic Signal Extraction
3.1. Data
3.2. Data Preprocessing
3.3. Comparison of Least Squares Fitting and SSA
3.4. SSA Results
4. Establishment of a Nonlinear Terrestrial Reference Frame and EOP Based on SSA
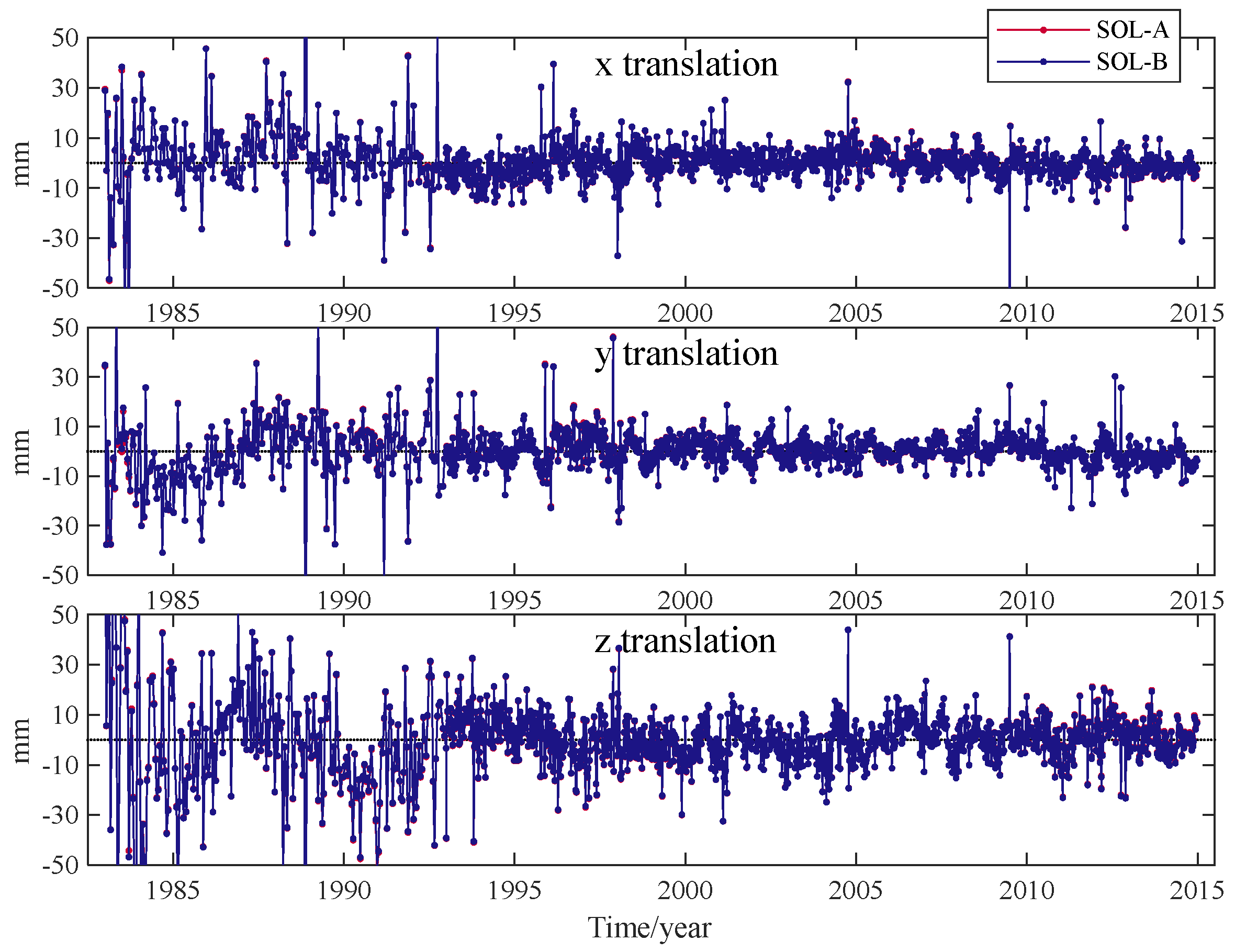
4.1. The Result Analysis of Datum Definition
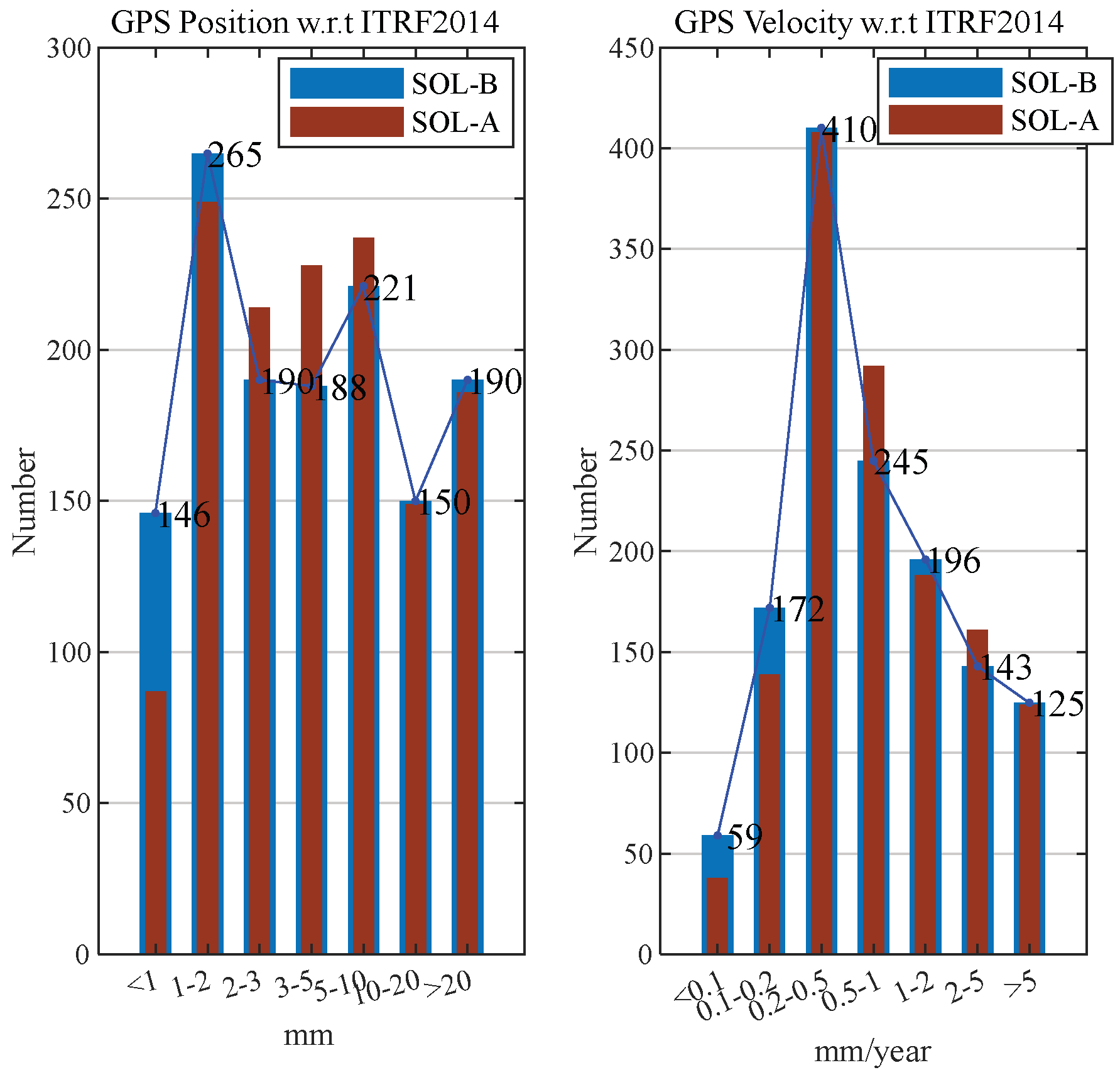
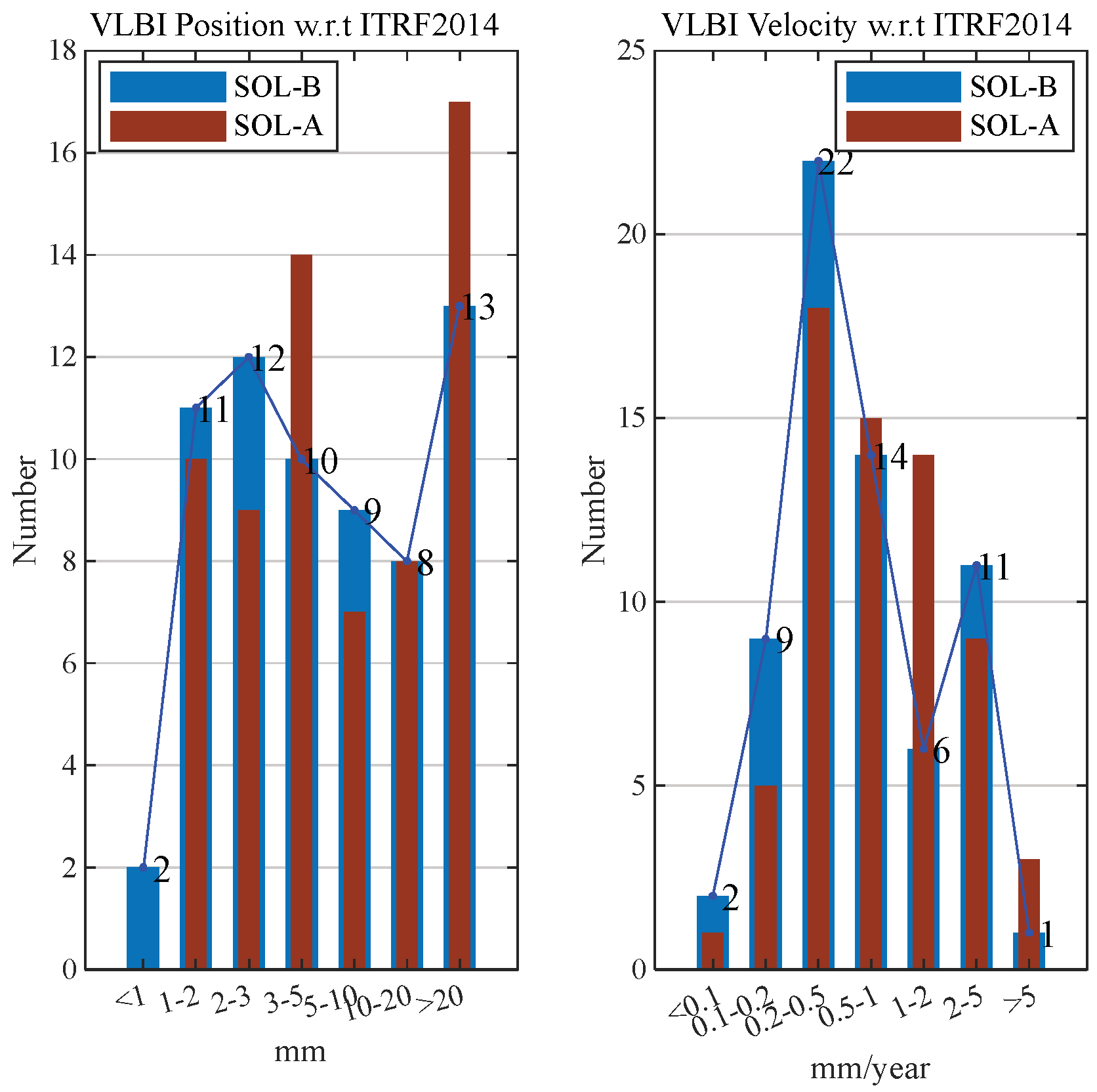
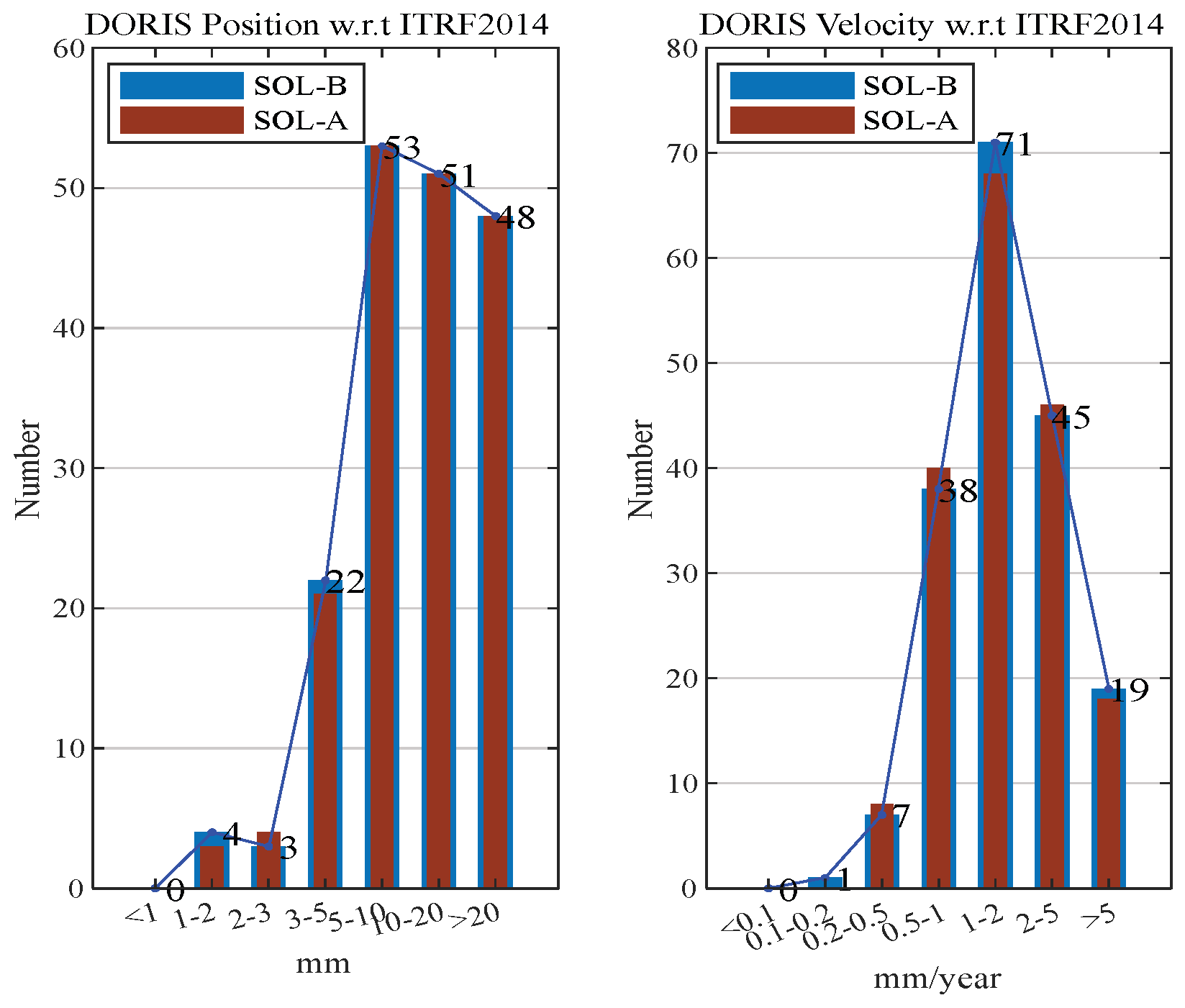
4.2. Accuracy Evaluation of Coordinates and Velocities
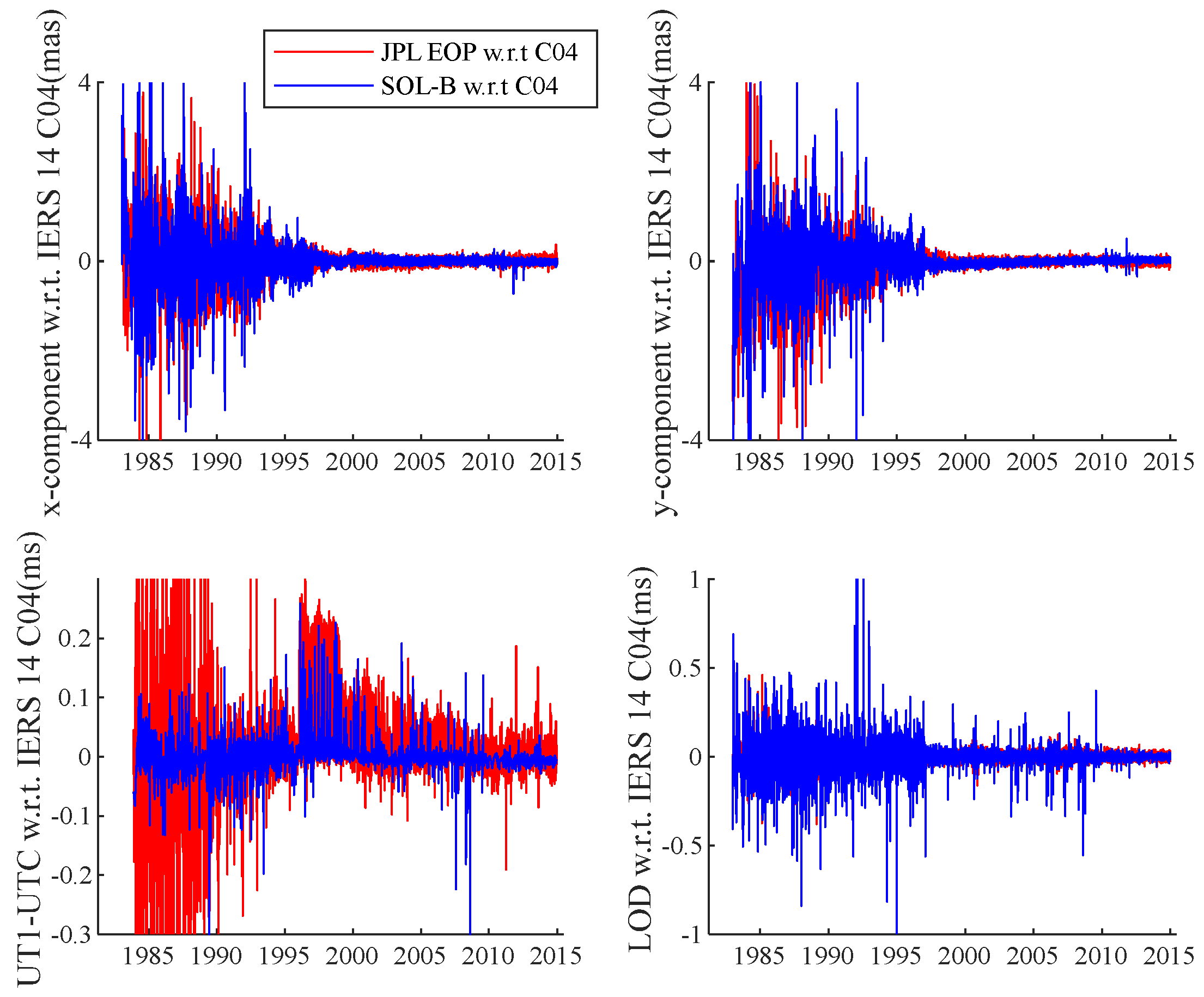
4.3. EOP Result Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, S.; Zhu, W.; Xiong, F.; Gao, J. Construction of mm-level terrestrial reference frame. Chin. J. Geophys. 2009, 52, 2704–2711. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the international terrestrial reference frame modeling non-linear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef]
- He, B.; Wang, X.Y.; Hu, X.G.; Zhao, Q.H. Combination of terrestrial reference frames based on space geodetic techniques in SHAO: Methodology and main issues. Res. Astron. Astrophys. 2017, 17, 089. [Google Scholar] [CrossRef]
- Liu, J.N.; Wei, N.; Shi, C. Current Status and Prospects of the International Earth Reference Framework (ITRF). Nat. J. 2013, 35, 243–250. [Google Scholar]
- Ray, J.; Altamimi, Z.; Collilieux, X.; Dam, T.V. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Wu, X.; Collilieux, X.; Altamimi, Z.; Vermeersen, B.L.A.; Gross, R.S.; Fukumori, I. Accuracy of the international terrestrial reference frame origin and earth expansion. Geophys. Res. Lett. 2011, 38, L13304. [Google Scholar] [CrossRef]
- Seitz, M.; Bloßfeld, M.; Angermann, D.; Seitz, F. DTRF2014: DGFI-TUM’s ITRS realization 2014. Adv. Space Res. 2022, 69, 2391–2420. [Google Scholar] [CrossRef]
- Wu, X.; Abbondanza, C.; Altamimi, Z.; Chin, T.M.; Collilieux, X.; Gross, R.S.; Heflin, M.B.; Jiang, Y.; Parker, J.W. Kalref—A kalman filter and time series approach to the international terrestrial reference frame realization. J. Geophys. Res. 2015, 120, 3775–3802. [Google Scholar] [CrossRef]
- Cheng, P.; Cheng, Y.; Bei, J. The Current Status and Tendency of China Millimeter Coordinate Frame Implementation and Maintenance. Acta Geod. Cartogr. Sin. 2017, 46, 1327–1335. [Google Scholar]
- Collilieux, X.; van Dam, T.; Ray, J.; Coulot, D.; Métivier, L.; Altamimi, Z. Strategies to mitigate aliasing of loading signals while estimating gps frame parameters. J. Geod. 2012, 86, 1–14. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef]
- Jiang, W.P.; Li, Z.; Wei, N.; Liu, J. Methods and prospects for the establishment of a millimeter-scale earth reference frame. Geomat. Surv. Mapp. 2016, 41, 1–6. [Google Scholar]
- Ray, J.; Griffiths, J.; Collilieux, X.; Rebischung, P. Subseasonal GNSS positioning errors. Geophys. Res. Lett. 2013, 40, 5854–5860. [Google Scholar] [CrossRef]
- Rudenko, S.; Bloßfeld, M.; Müller, H.; Dettmering, D.; Angermann, D.; Seitz, M. Evaluation of DTRF2014, ITRF2014, and JTRF2014 by precise orbit determination of SLR satellites. IEEE Trans. Geosci. Remote Sens. 2017, 56, 3148–3158. [Google Scholar] [CrossRef]
- Seitz, M.; Angermann, D.; Bloßfeld, M.; Drewes, H.; Gerstl, M. The 2008 DGFI realization of the ITRS: DTRF2008. J. Geod. 2012, 86, 1097–1123. [Google Scholar] [CrossRef]
- Angermann, D.; Drewes, H.; Gerstl, M.; Krügel, M.; Meisel, B. DGFI Combination Methodology for ITRF2005 Computation. In Geodetic Reference Frames; Springer: Berlin/Heidelberg, Germany, 2009; pp. 11–16. [Google Scholar]
- Gross, R.; Abbondanza, C.; Chin, M.; Heflin, M.; Parker, J. JTRF2020: Results and Next Steps. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 23–28 April 2023; p. EGU23-2117. [Google Scholar] [CrossRef]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Physica D 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Chen, Q.; Dam, T.V.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from gps time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Tang, W.J. The periodic item detection in GPS time series based on singular spectrum analysis. Urban Geotech. Investig. Surv. 2018, 165, 86–90. [Google Scholar]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Physica D 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Physica D 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Rangelova, E.; Sideris, M.G.; Kim, J.W. On the capabilities of the multi-channel singular spectrum method for extracting the main periodic and non-periodic variability from weekly GRACE data. J. Geodyn. 2012, 54, 64–78. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Y.Y.; Wu, S.; Zhang, K. An enhanced singular spectrum analysis method for constructing nonsecular model of GPS site movement. J. Geophys. Res. Solid Earth 2016, 121, 2193–2211. [Google Scholar] [CrossRef]
- Jiang, W.P.; Zhou, X. Effect of the span of Australian GPS coordinate time series in establishing an optimal noise model. Sci. China Earth Sci. 2015, 58, 523–539. [Google Scholar] [CrossRef]
- Perfetti, N. Detection of station coordinate discontinuities within the Italian GPS fiducial network. J. Geod. 2006, 80, 381–396. [Google Scholar] [CrossRef]
- Williams, S.D.P. Offsets in global positioning system time series. J. Geophys. Res. 2003, 108, 2310. [Google Scholar] [CrossRef]
- Altamimi, Z.; Boucher, C.; Gambis, D. Long-term stability of the terrestrial reference frame. Adv. Space Res. 2005, 36, 342–349. [Google Scholar] [CrossRef]
- Altamimi, Z.; Métivier, L.; Collilieux, X. ITRF2008 plate motion model. J. Geophys. Res. Atmos. 2012, 117, 47–56. [Google Scholar] [CrossRef]
- Vitti, A. SIGSEG: A tool for the detection of position and velocity discontinuities in geodetic time-series. GPS Solut. 2012, 16, 405–410. [Google Scholar] [CrossRef]
- Bruni, S.; Zerbini, S.; Raicich, F.; Errico, M.; Santi, E. Detecting discontinuities in GNSS coordinate time series with STARS: Case study, the Bologna and Medicina GPS sites. J. Geod. 2014, 88, 1203–1214. [Google Scholar] [CrossRef]
- Rodionov, S.N. A sequential algorithm for testing climate regime shifts. Geophys. Res. Lett. 2004, 31, L09204. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Jing, Y. Offset detection in GPS position time series with colored noise. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 745–751. [Google Scholar]
- Rosner, B. Percentage points for a generalized ESD many-outlier procedure. Technometrics 1983, 25, 165–172. [Google Scholar] [CrossRef]
- Li, Q.; Wang, X.; Feng, J. Research on the detection method of station coordinate time series jumps and its impact on the Terrestrial Reference Frame. Sci. Surv. Mapp. 2021, 46, 38–46. [Google Scholar] [CrossRef]





| Datum Parameters | WRMS | |
|---|---|---|
| SOL-A | SOL-B | |
| X-component (mm) | 4.2890 | 4.2600 |
| Y-component (mm) | 4.3400 | 4.3370 |
| Z-component (mm) | 7.4360 | 7.4350 |
| Scale SLR (ppb) | 0.8480 | 0.8110 |
| Scale VLBI (ppb) | 1.1250 | 1.0931 |
| Coordinate Accuracy Level (mm) | Percentage of Stations (%) | Velocity Accuracy Level (mm/year) | Percentage of Stations (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GPS | VLBI | SLR | DORIS | GPS | VLBI | SLR | DORIS | ||
| <1 | 10.8 | 3.1 | 0 | 0 | <0.1 | 4.4 | 3.1 | 0 | 0 |
| (1, 2) | 19.6 | 16.9 | 1.6 | 2.2 | (0.1, 0.2) | 12.7 | 13.8 | 0 | 0.6 |
| (2, 3) | 14.1 | 18.5 | 5.6 | 1.7 | (0.2, 0.5) | 30.4 | 33.8 | 11.3 | 3.9 |
| (3, 5) | 13.9 | 15.4 | 9.7 | 12.2 | (0.5, 1) | 18.1 | 21.5 | 27.4 | 21.0 |
| (5, 10) | 16.4 | 13.8 | 18.5 | 29.3 | (1, 2) | 14.5 | 9.2 | 12.9 | 39.1 |
| (10, 20) | 11.1 | 12.3 | 19.4 | 28.2 | (2, 5) | 10.6 | 16.9 | 25.0 | 24.9 |
| >20 | 14.1 | 20.0 | 45.1 | 26.5 | >5 | 9.3 | 1.5 | 23.4 | 10.5 |
| EOP Parameters | WRMS | ||
|---|---|---|---|
| SOL-A | SOL-B | JPL EOP | |
| x-component of Polar Motion (mas) | 0.0578 | 0.0564 | 1.8540 |
| y-component of Polar Motion (mas) | 0.0595 | 0.0576 | 3.1290 |
| UT1-UTC (ms) | 0.0104 | 0.0103 | 0.0295 |
| LOD (ms) | 0.0112 | 0.0109 | 0.0049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, X.; Li, Y. Accuracy Evaluation of Multi-Technique Combination Nonlinear Terrestrial Reference Frame and EOP Based on Singular Spectrum Analysis. Remote Sens. 2025, 17, 821. https://doi.org/10.3390/rs17050821
Li Q, Wang X, Li Y. Accuracy Evaluation of Multi-Technique Combination Nonlinear Terrestrial Reference Frame and EOP Based on Singular Spectrum Analysis. Remote Sensing. 2025; 17(5):821. https://doi.org/10.3390/rs17050821
Chicago/Turabian StyleLi, Qiuxia, Xiaoya Wang, and Yabo Li. 2025. "Accuracy Evaluation of Multi-Technique Combination Nonlinear Terrestrial Reference Frame and EOP Based on Singular Spectrum Analysis" Remote Sensing 17, no. 5: 821. https://doi.org/10.3390/rs17050821
APA StyleLi, Q., Wang, X., & Li, Y. (2025). Accuracy Evaluation of Multi-Technique Combination Nonlinear Terrestrial Reference Frame and EOP Based on Singular Spectrum Analysis. Remote Sensing, 17(5), 821. https://doi.org/10.3390/rs17050821






