Improved Method for the Retrieval of Extinction Coefficient Profile by Regularization Techniques
Abstract
:1. Introduction
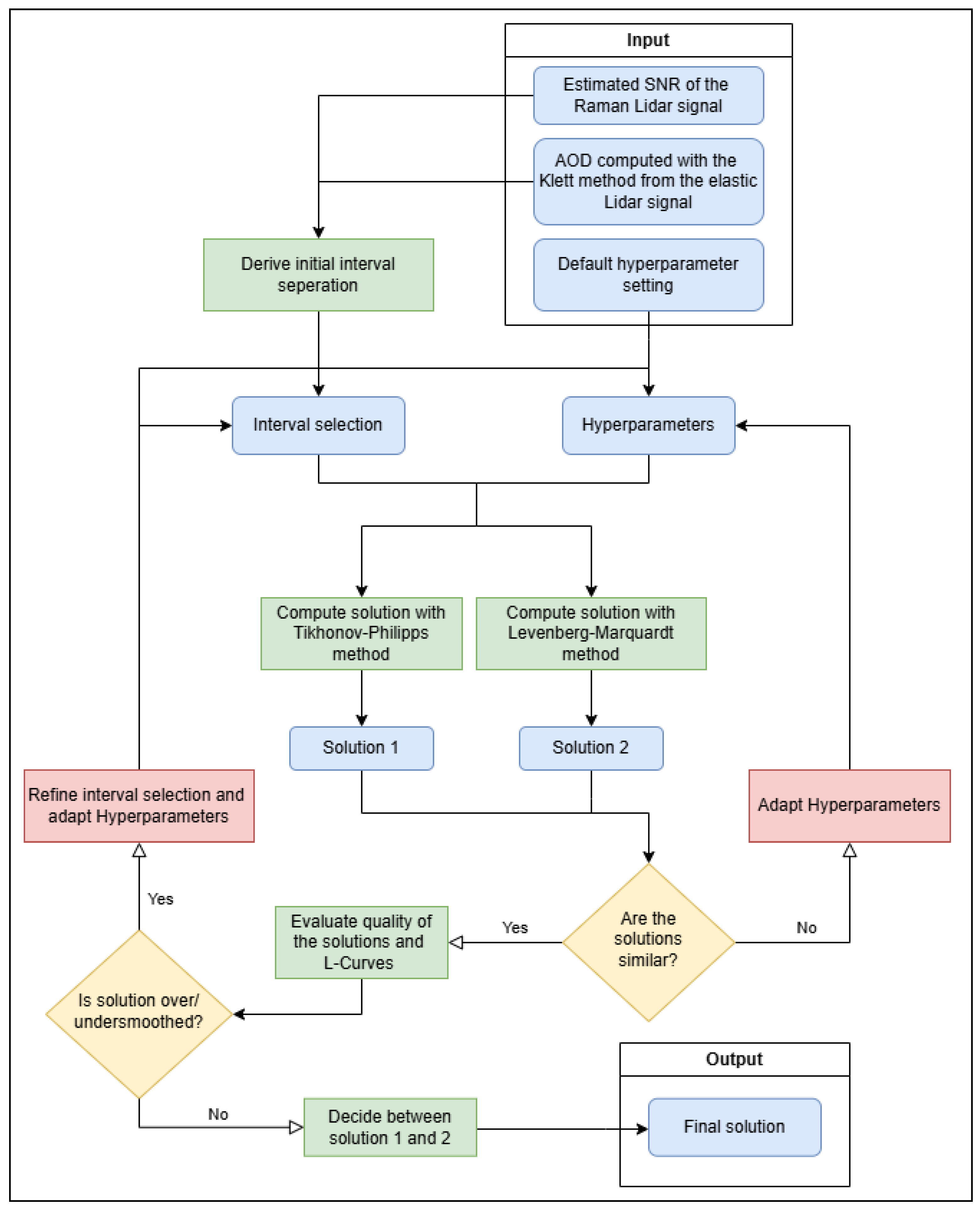
2. Methods and Algorithms
- Tikhonov–Phillips method (a) and variable Levenberg–Marquardt method (b) over the entire interval of interest
- Tikhonov–Phillips method (a) and variable Levenberg–Marquardt method (b) over part-intervals, which are determined by splitting the interval (SI) by a priori heuristically well-structured experiences;
- Tikhonov–Phillips method (a) and variable Levenberg–Marquardt method (b) with an a posteriori SI suggested in Pornsawad et al. [16].
2.1. Basic Algorithm
2.2. Algorithms for Splitting the Data (SI)
- Based on the noise of the data, choose an interval separation such that every single interval has approximately the same noise level.
- Based on the cumulative sum of the extinction solution from Klett’s method, consisting of the backscatter coefficient and the Lidar ratio (LR), determine an interval separation such thatis constant for every . That is, in every part-interval, there may be the same amount of information (extinction).
- Output: Regularized discrete derivative X.
- Set .
- For , compute the regularized derivative of Y in with a regularization method and the L-curve parameter choice rule. Store the regularization parameter and its corresponding curvature of the L-curve.
- Set . Store as the final solution over .
- Set and restart at (2) until .
2.3. Appropriate Shifting of the Data
2.4. The Levenberg–Marquardt Method with Variable Step Width
3. Results
3.1. Sensitivity Quantification
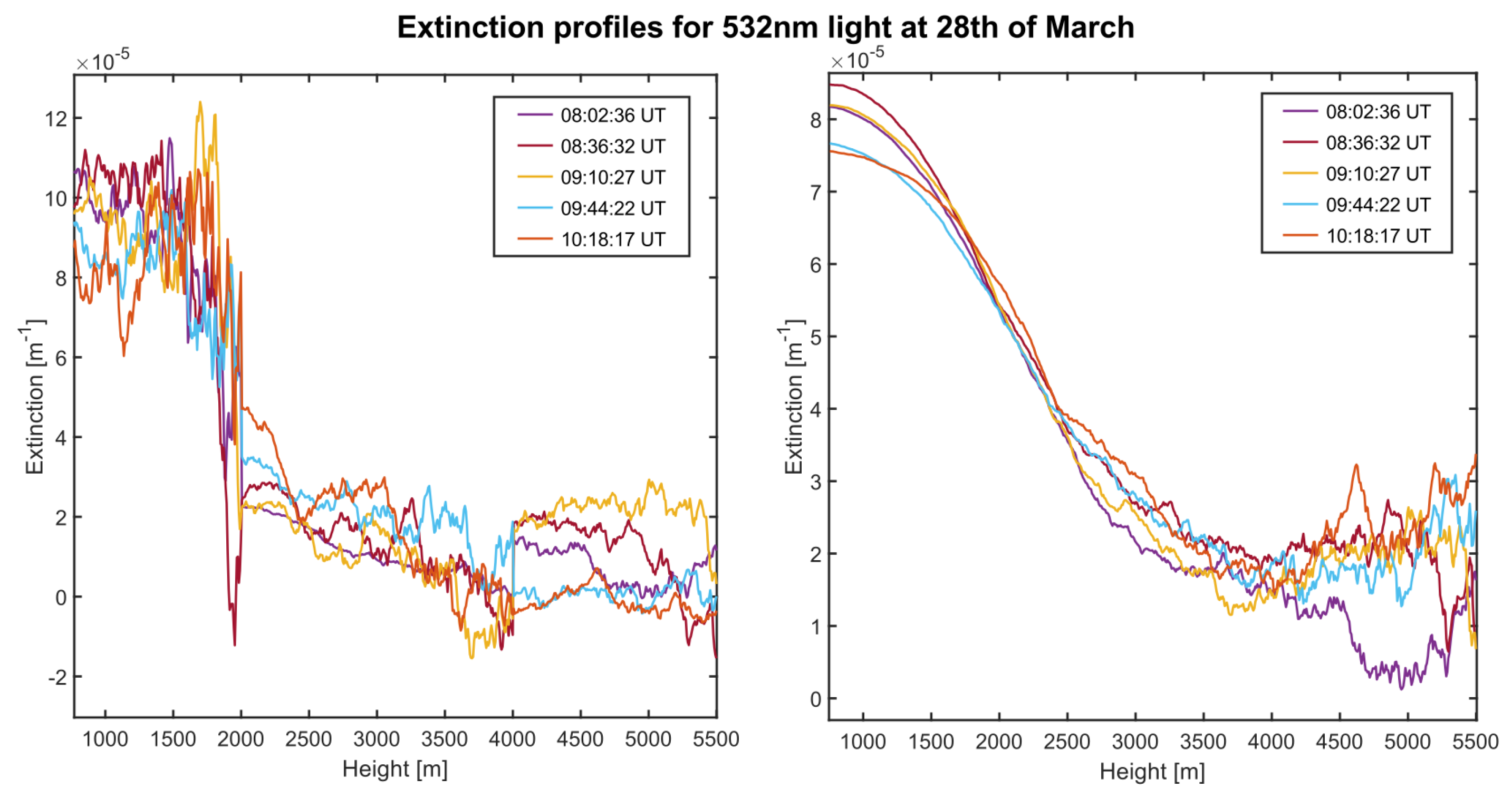
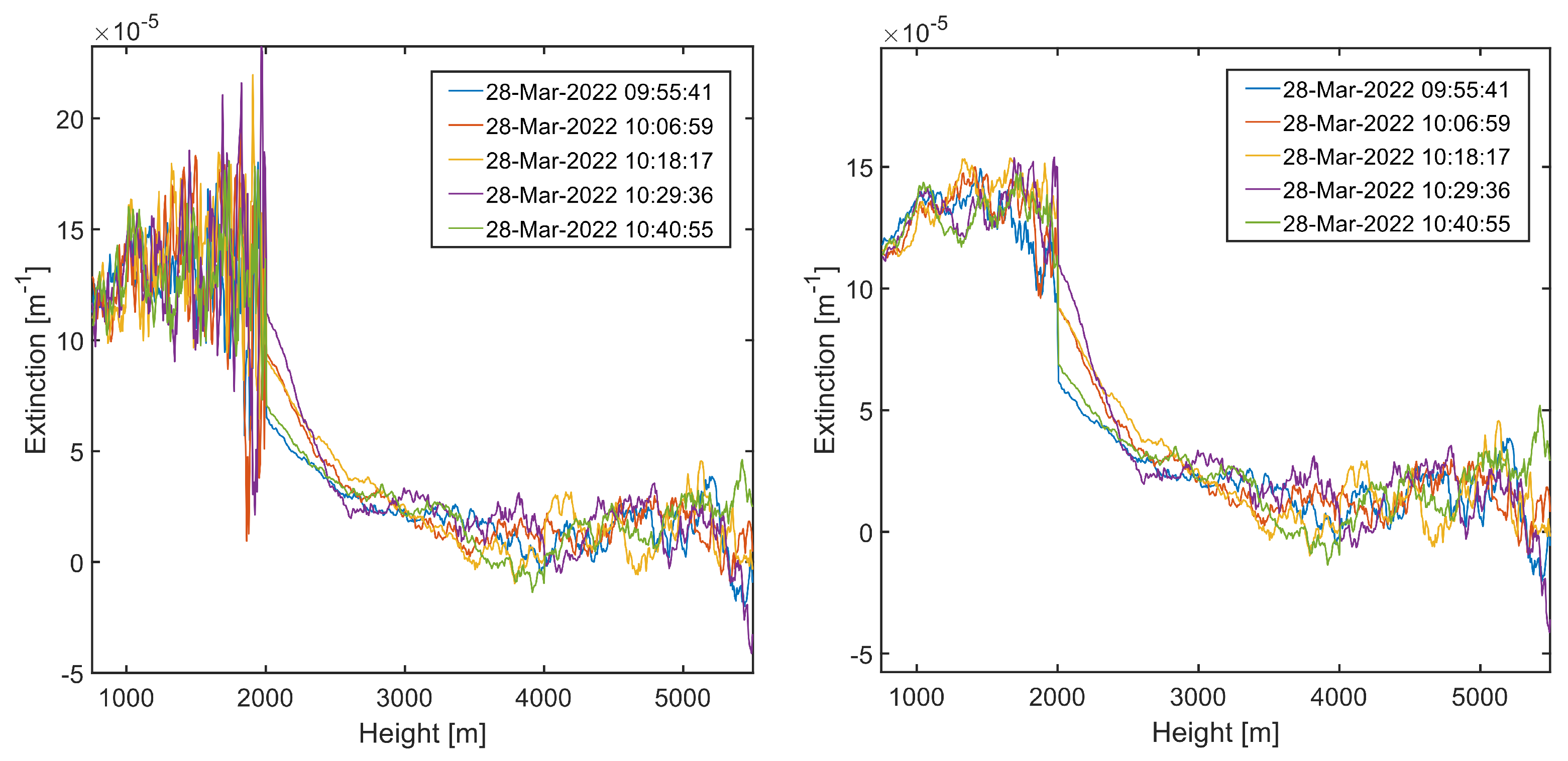
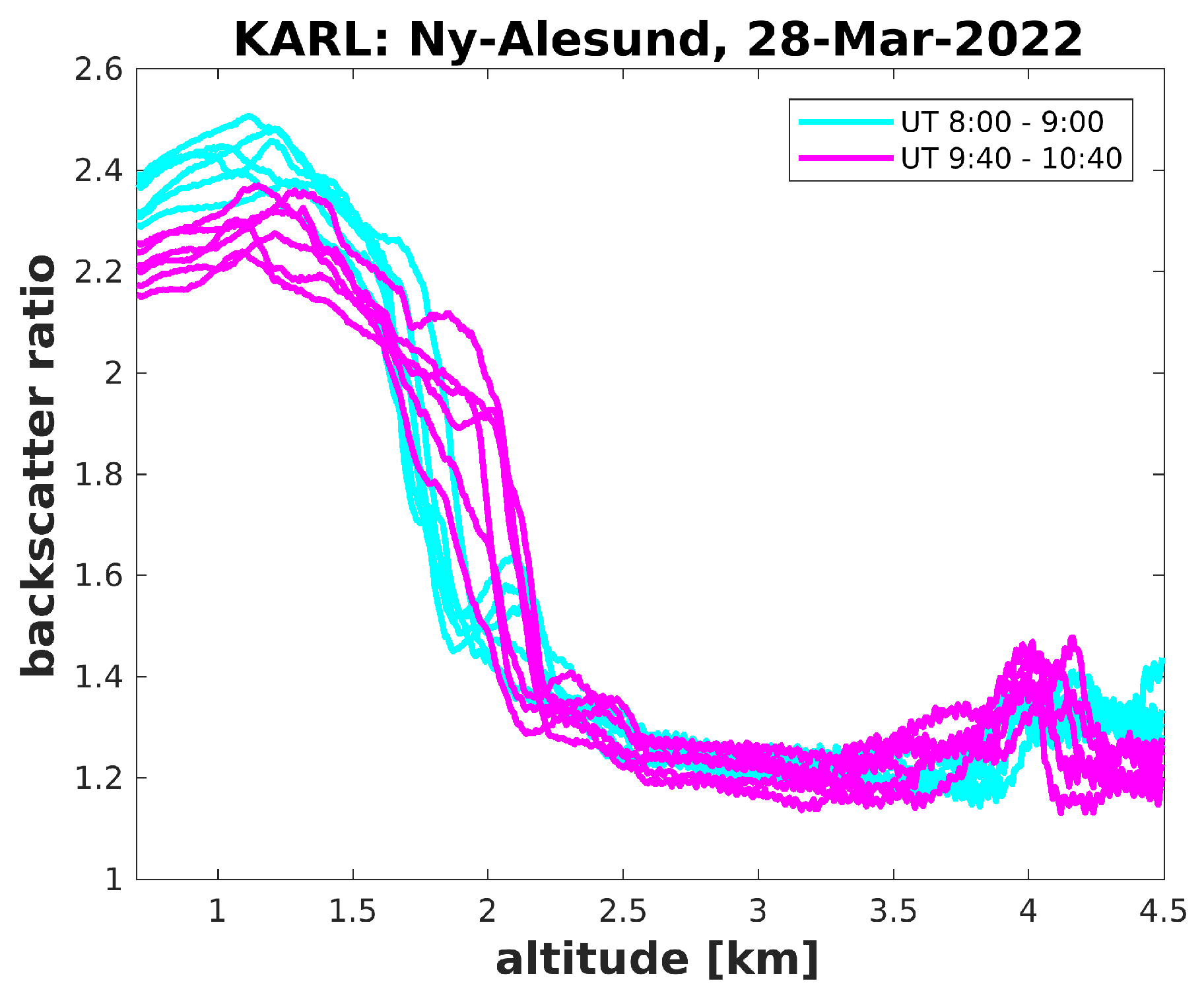
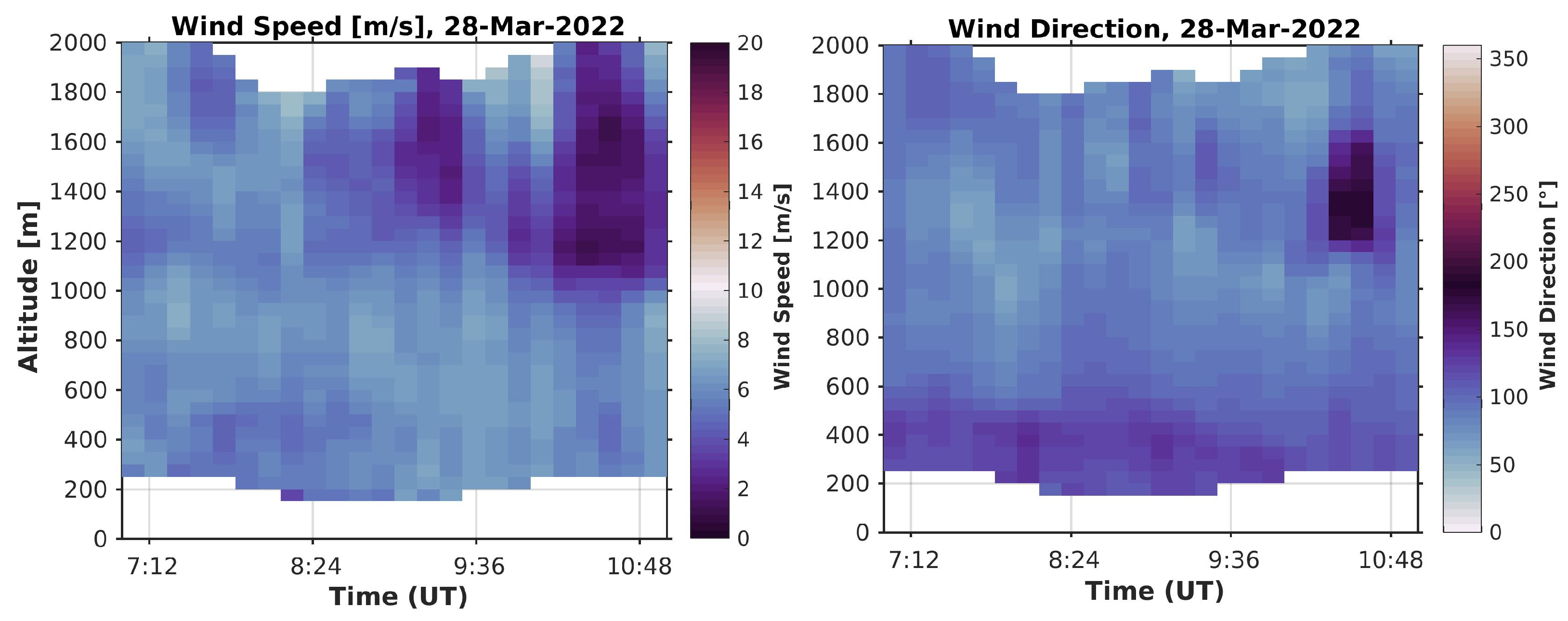
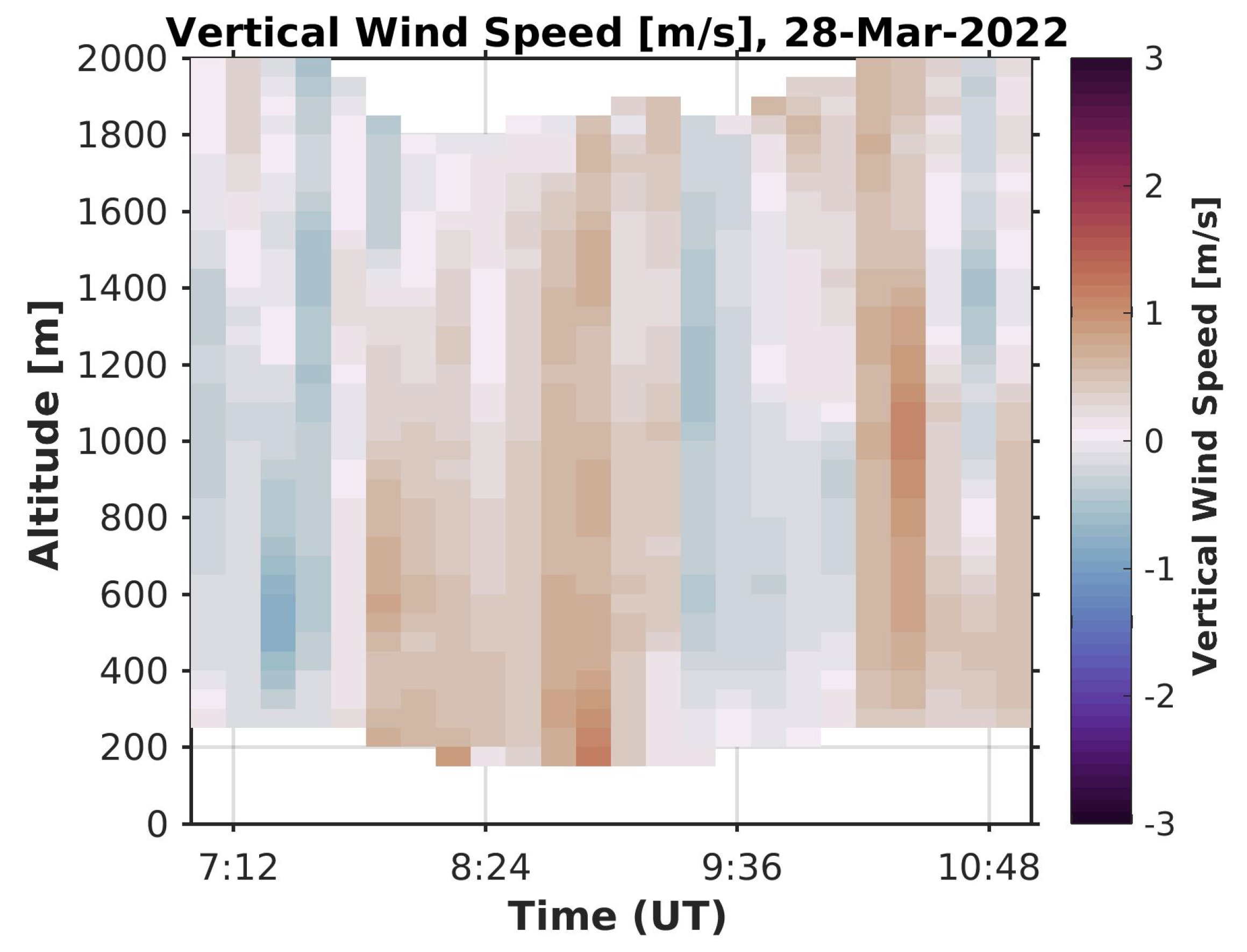
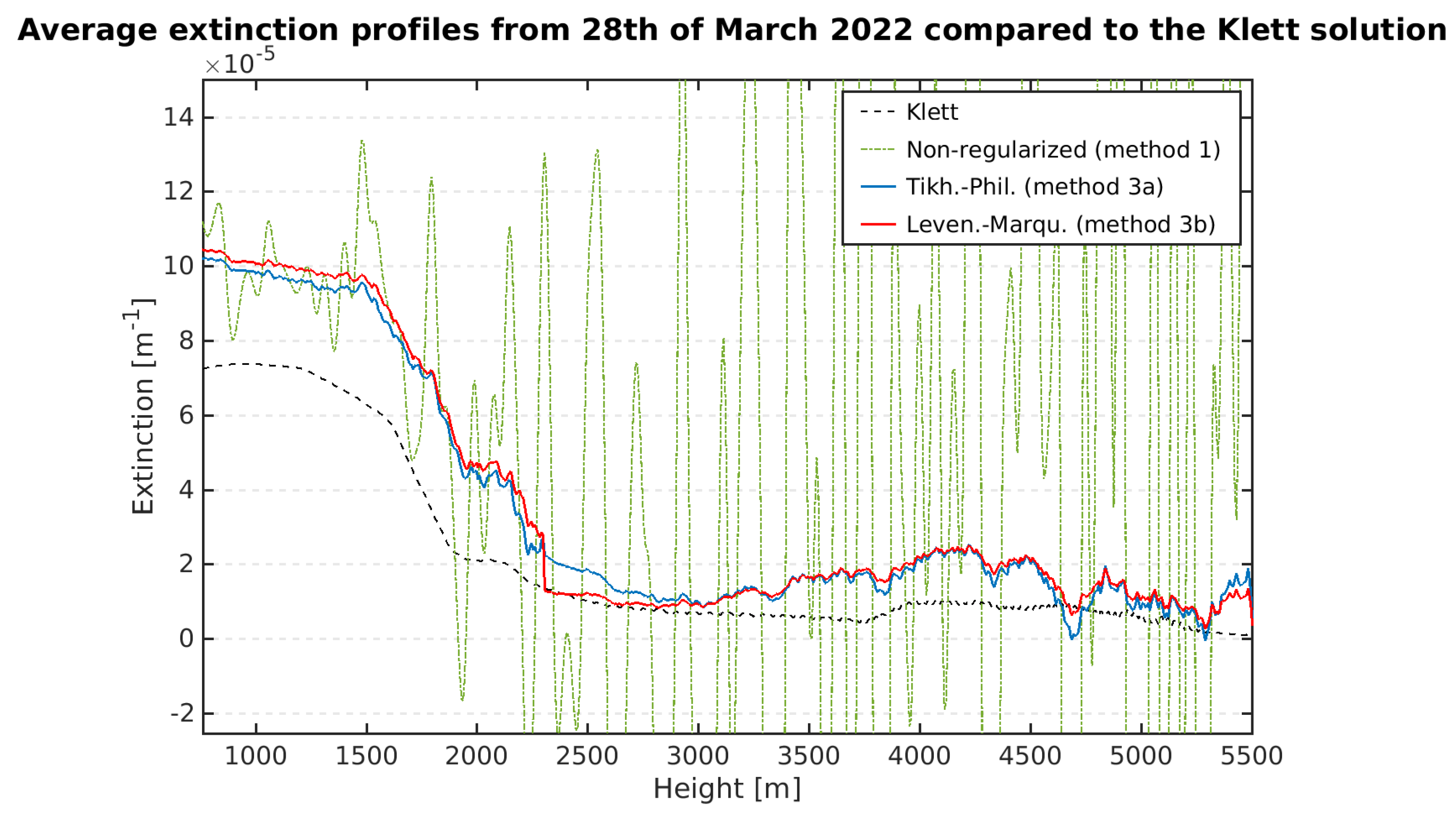
3.2. Analysis of Data from 28 March 2022
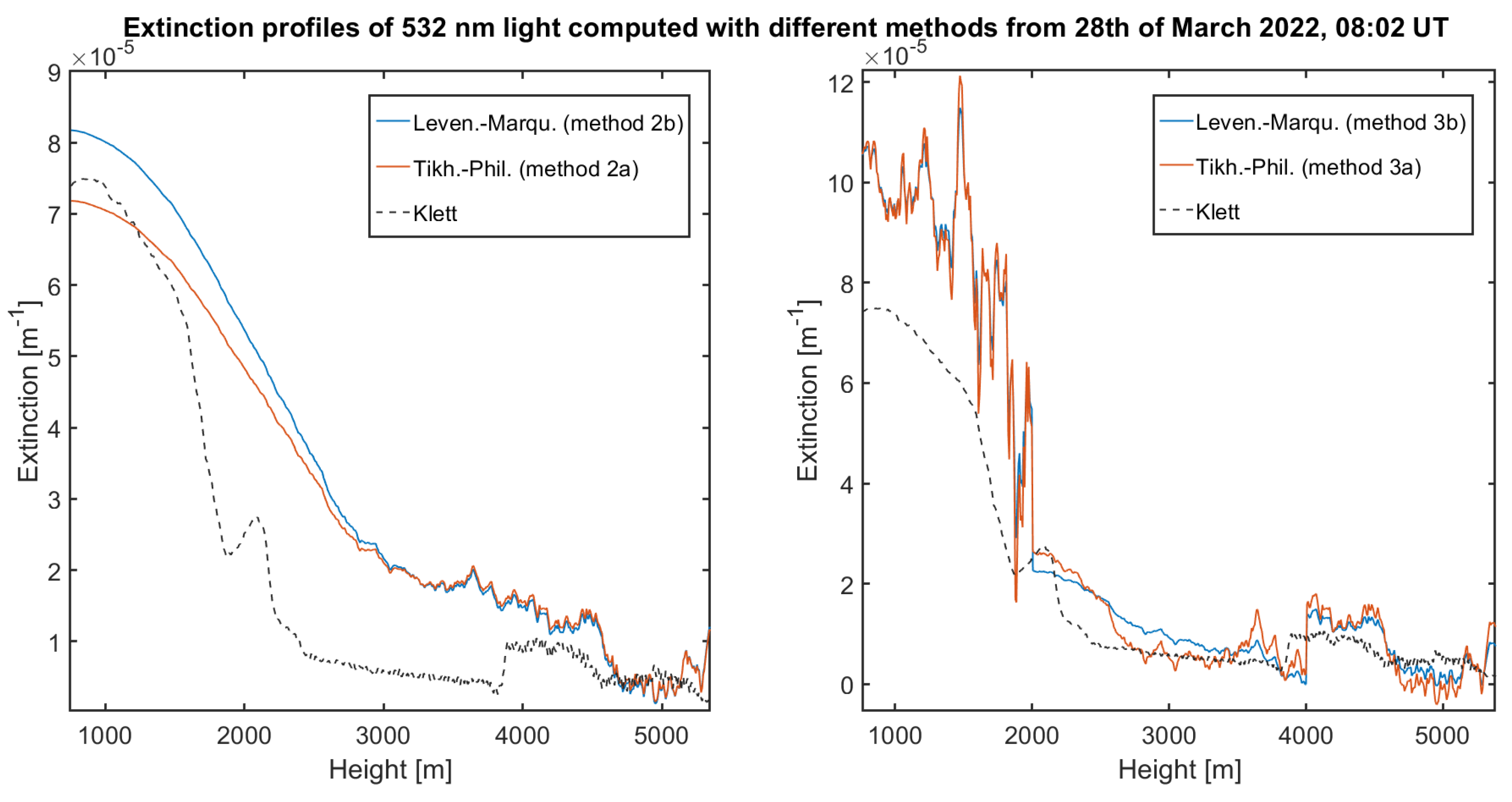
3.2.1. Comparison of the Tikhonov–Phillips and Levenberg–Marquardt Methods
3.2.2. Comparison with a Doppler Wind Lidar
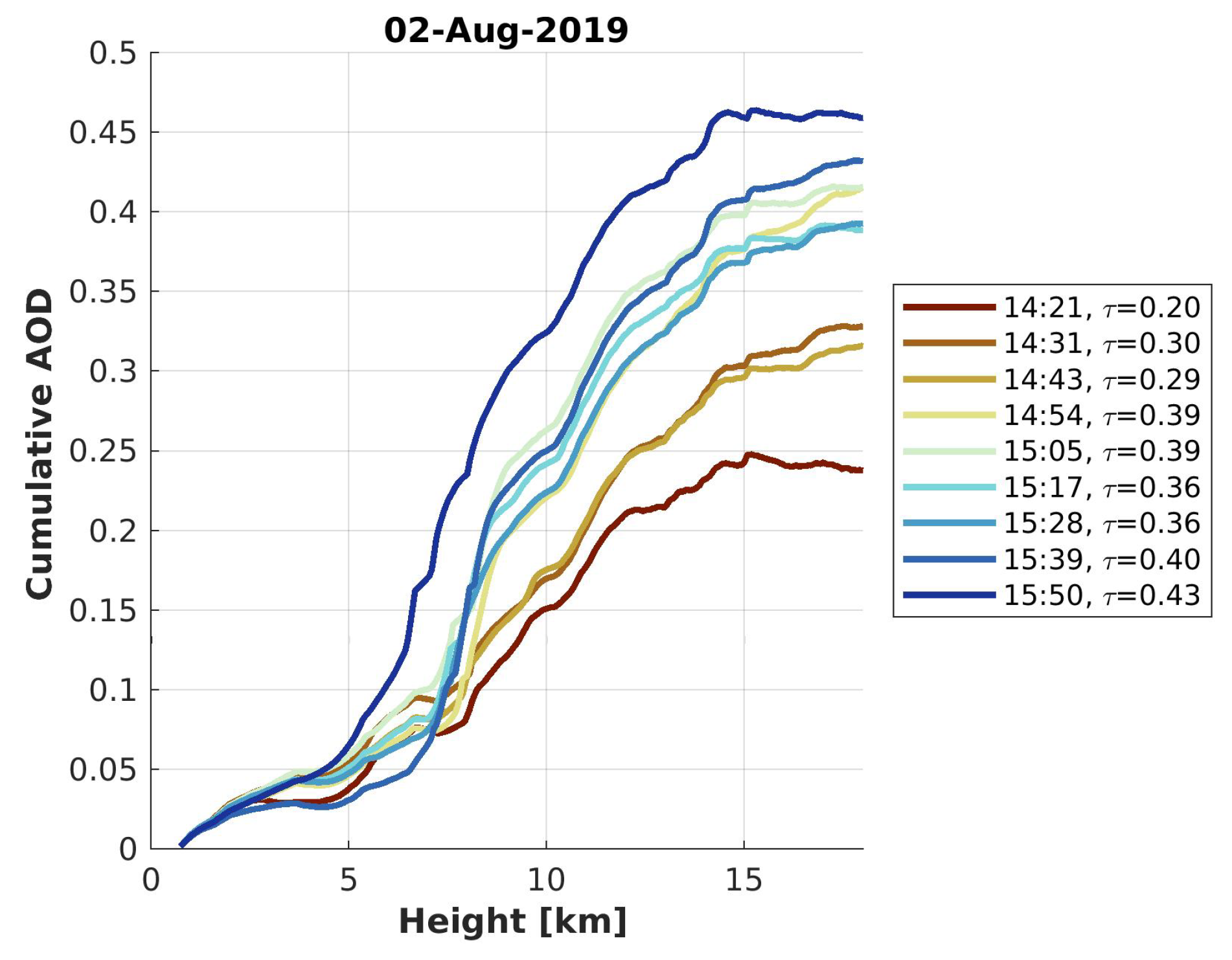
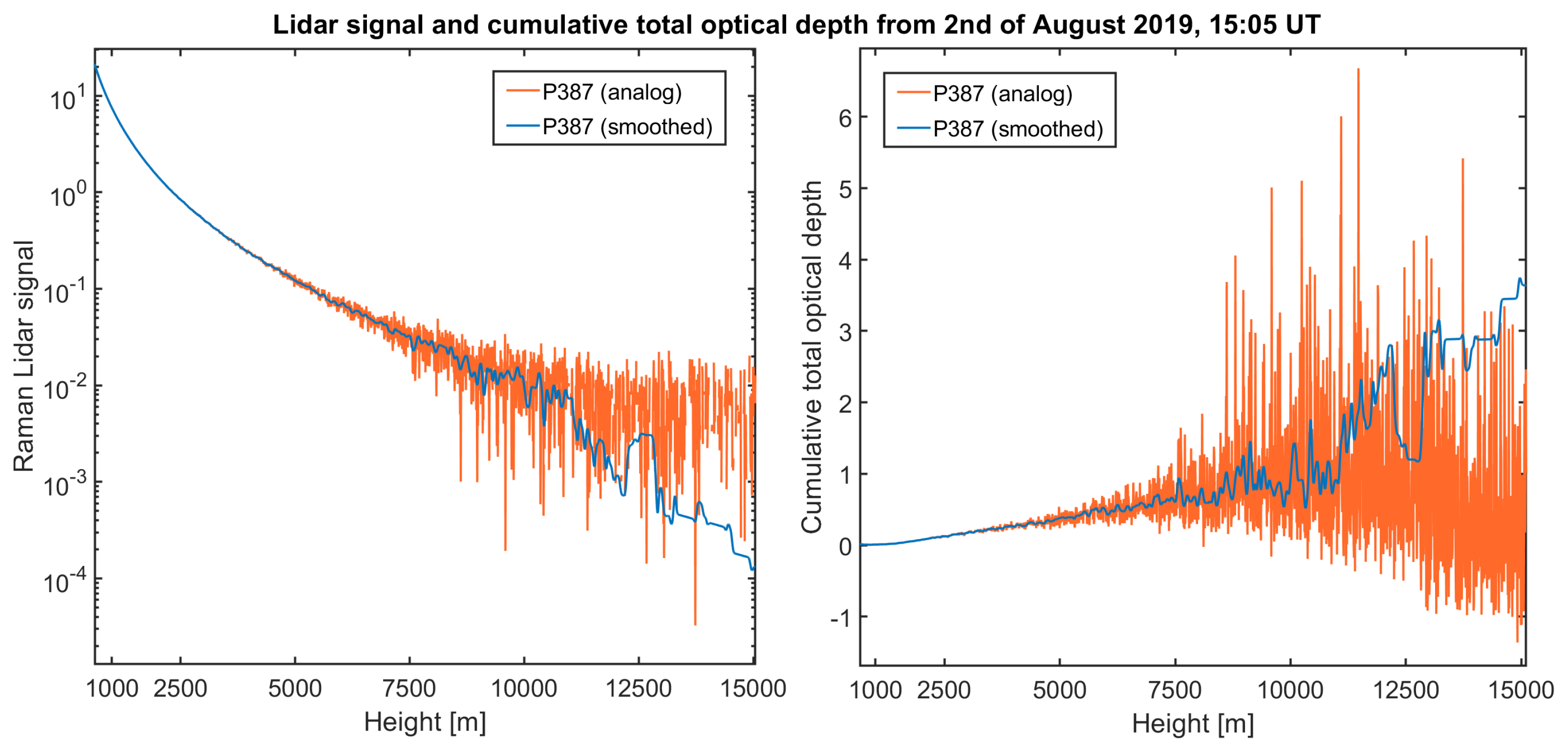
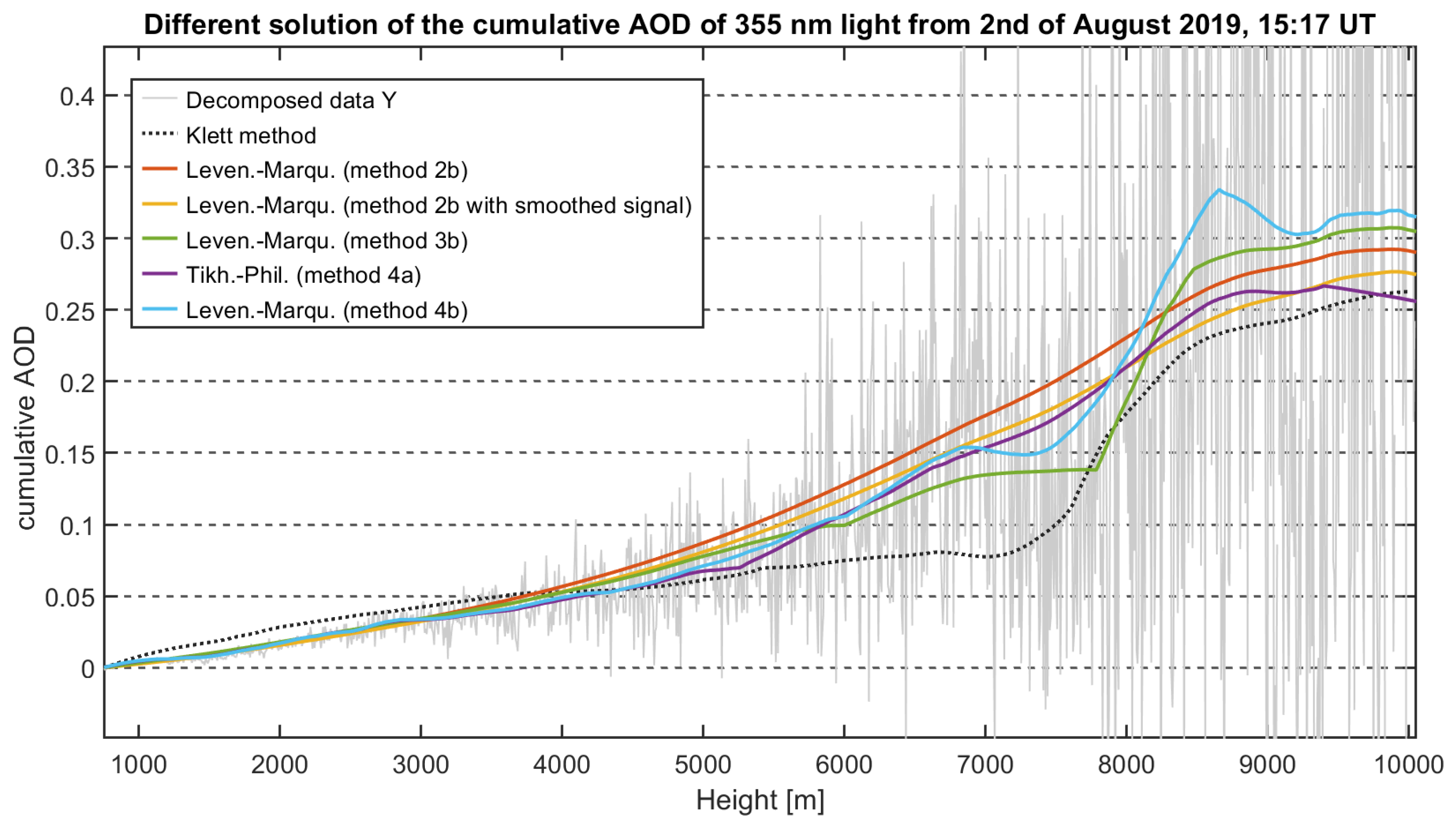
3.3. Analysis of Data from 2 August 2019
- To prevent over-smoothing, it is recommended to use SI. This separation of the intervals needs attention as too narrow intervals (too little information content) may lead to non-physical results. In Figure 13, the solutions with a posteriori SI show few altitudes, in which the cumulative AOD shows a decrease with altitude, corresponding to a negative extinction. This can happen if the information content in the interval is too small compared with the noise. Regularized solutions (of the extinction) are not restricted to positive semi-definite values.
- Although the Levenberg–Marquardt and Tikhonov–Phillips regularization might produce a similar result over a fixed interval, the solution can differ if the a posteriori SI is used. In this case study, only the Levenberg–Marquardt method was able to give meaningful results in combination with the a posteriori SI. Hence, it is in general good to have both regularization techniques in hand.
- An interval split according to Klett’s solution is promising and produces, in this case, the best-regularized solution.
- A pre-smoothing of the Lidar data does not clearly improve the range for a valid retrieval of the extinction coefficient and is therefore not necessary.
3.4. Analysis of Data from 18 October 2021
4. Discussion
4.1. Discussion of Case Studies
4.2. Discussion of Method Adaptions
4.3. Utilizing Klett’s Solution to Derive an A Priori SI
- Compute a regularized Ansmann solution of the extinction based on SI with Klett’s solution.
- Use the regularized extinction profile to update the Lidar ratio assumption for Klett’s algorithm. Compute a possible improved Klett’s solution for the backscatter and extinction coefficients with the updated Lidar ratio.
- Repeat the above steps until the regularized extinction from Ansmann’s algorithm and the extinction from Klett’s algorithm are arbitrarily equal.
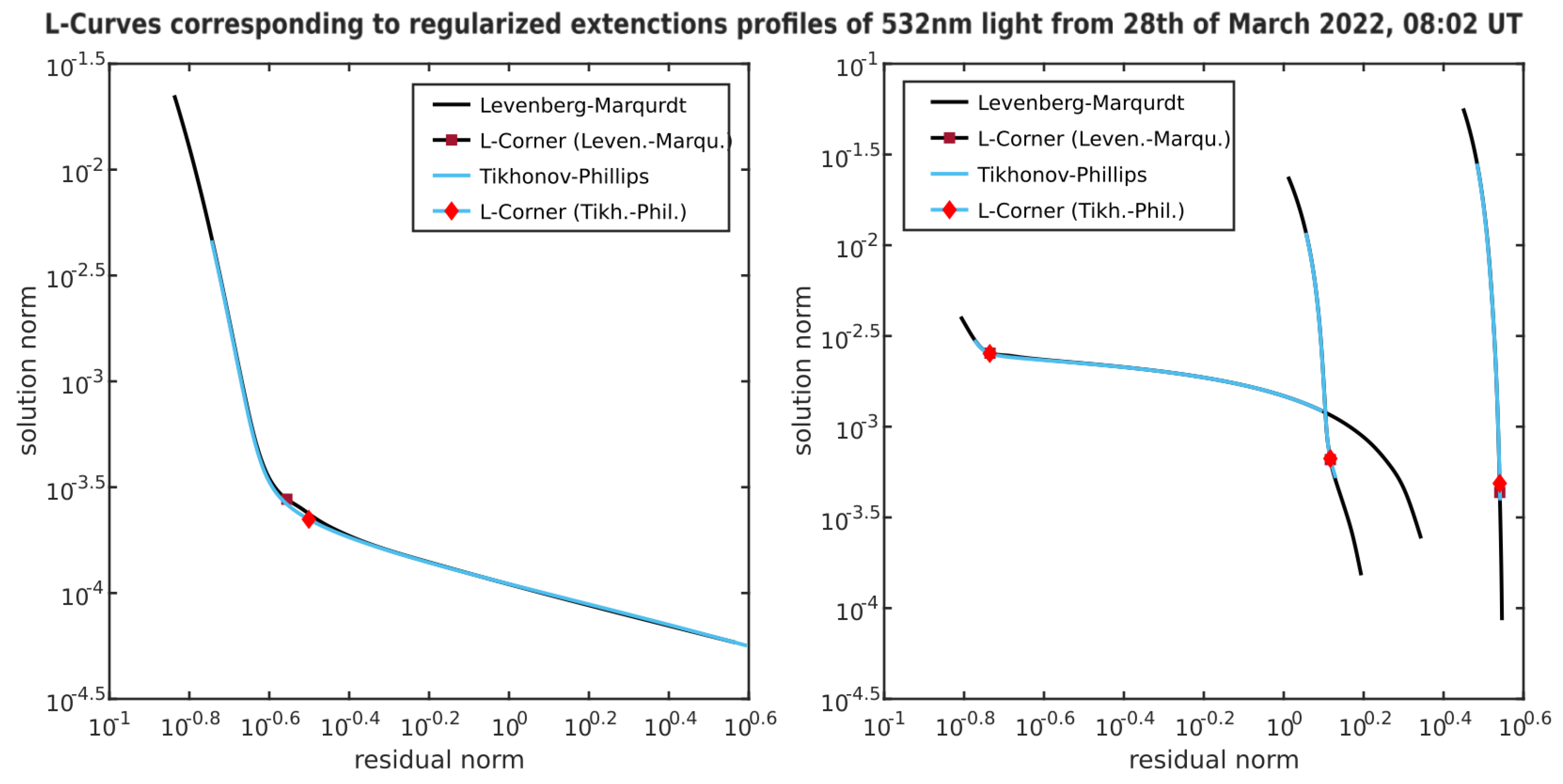
4.4. Discussion of Parameter Choice by L-Curve
5. Conclusions
- The retrieval of the extinction from Raman Lidar data is ill-posed. The main difficulty occurs at the determination of the derivative of the Lidar signal with respect to the altitude. Hence, regularization provides an adequate tool to handle this class of problems.
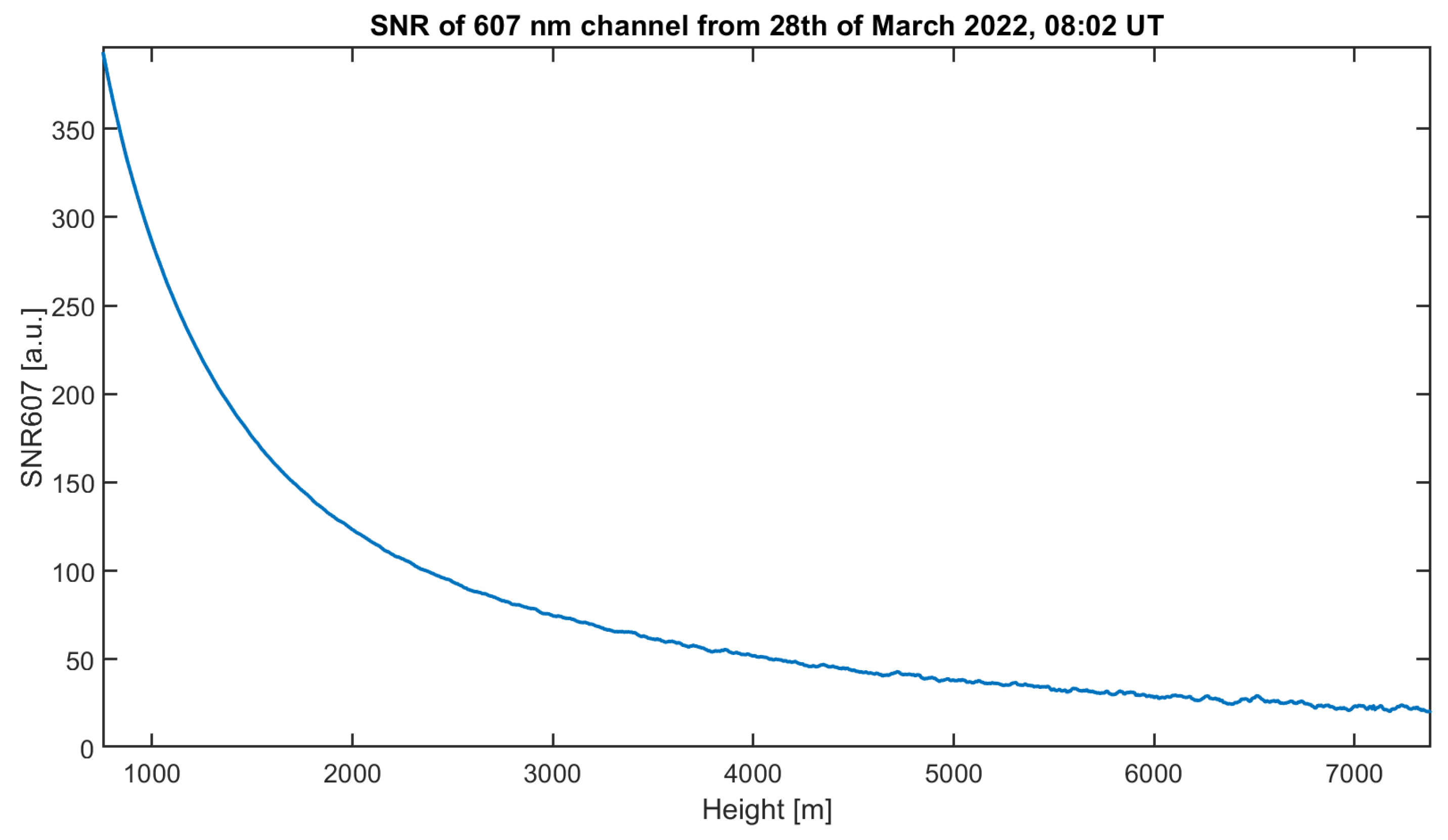
- In principle, all presented methods work. The retrieval of a trustful extinction coefficient is possible into altitudes, which are clearly higher compared with the traditional non-regularized solution. As a rule of thumb, only half of the signal-to-noise ratio is necessary for our approaches. If the SNR of the Lidar data is very good, only a very small regularization parameter will be found, and the regularized and non-regularized solutions are basically identical.
- The regularized solution depends on several hyperparameters, which need some attention to obtain best results. Two important ones are the regularization parameter and the interval separation for finding a solution. As the regularization parameter depends on the noise level and seems to be adjusted to the part of a signal with the worst quality (the upper end of each interval), very large intervals present a solution, which is too smooth. Contrarily, in very narrow intervals, it may be difficult to find an optimal regularization parameter, as the corresponding L-curve was oddly shaped.
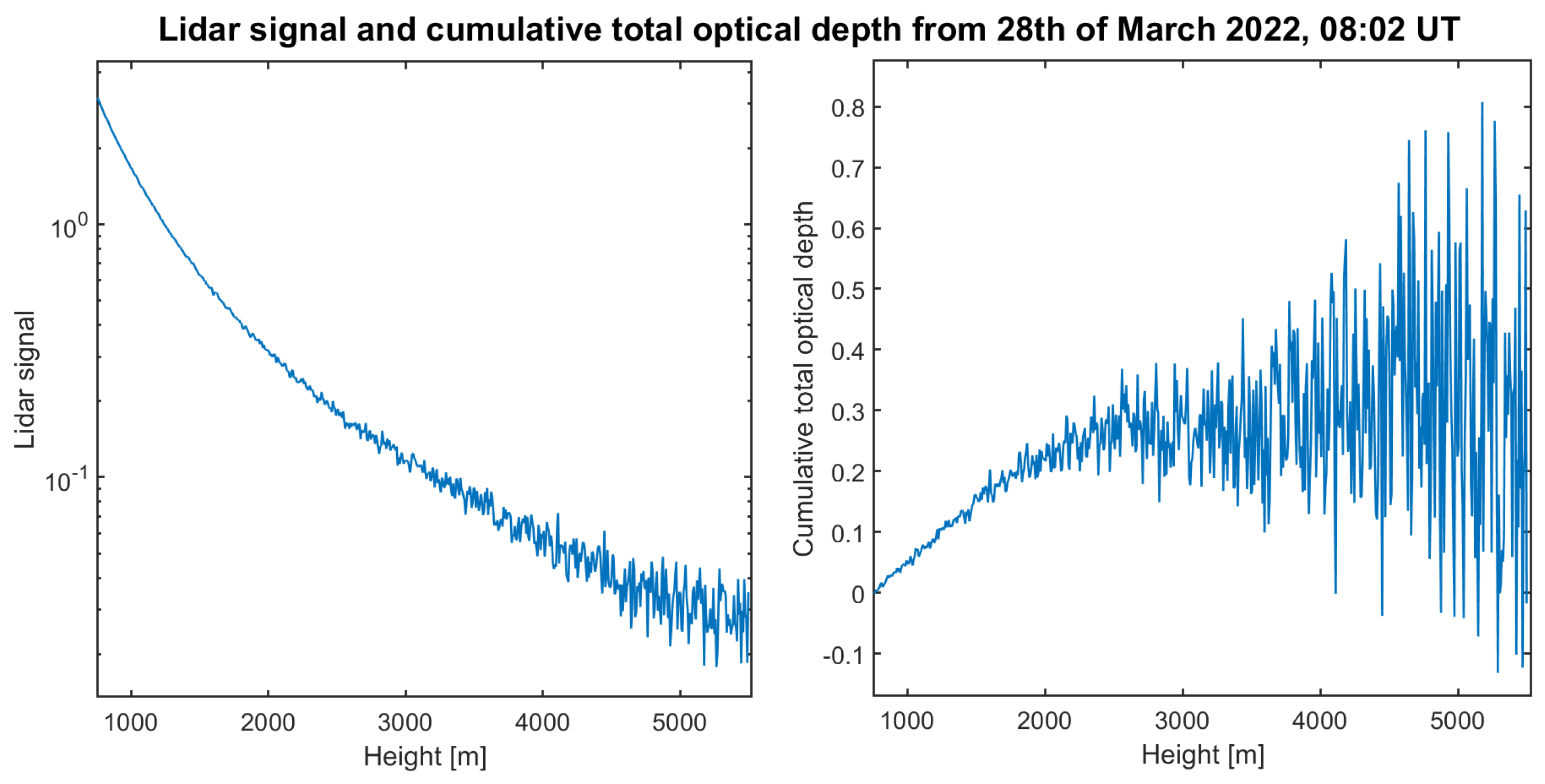
- Clearly, the cumulative AOD over an extended interval is a quality that is much easier to obtain. In theory, it can be obtained directly by smoothing the Lidar signal (without the need of a derivative). However, the cumulative AOD can also be computed by the regularized solutions, as it is the integral (cumulative sum) of the extinction profile. This is another good approach that comes without any smoothing.
6. Outlook
- In future work, one should work on an automated choice of the multiple parameters that can be chosen in the presented methods. This could make the algorithms more accessible to other researchers, since these regularization techniques are not only applicable for determination of Arctic extinction coefficient profiles from Raman Lidar but also at other places. In Figure 17 and Figure 18, a relation between the SNR of the Lidar data and the expected accuracy of the extinction profile is given, which should be valid for other sites as well.
- Another aspect that one might consider in future work is the application of a multiple parameter choice rules. When using the L-curve method, we rely on a correlation between the solution norm and the data error. However, this correlation is sometimes not ideal. Especially for very smooth solutions, the solution norm tends to increase very late, which leads to a smaller regularization parameter at the L-corner. Hence, the solution might be too noisy (Hansen [32], Chapter 8.1). In this case, Hansen [32] recommends using a combination of multiple parameter choice rules. He encountered that using both the L-curve method and a generalized cross-validation (GCV) gives in many cases at least one of two good results. According to (Hansen [32], Chapter 7), the L-curve method is more stable, while the GCV, if it works, tends to give a more accurate regularization parameter. Considering the GCV method, especially if the solution from the L-curve parameter choice rule seems too noisy, is something worth studying in future work. More about GCV can be read in Wahba [33].
- Non-heuristic parameter choice rules, like the principle of Morzorov, are not suitable for our studies due to the uncertainty about the noise level in our signal. When using the Levenberg–Marquardt and Tikhonov–Phillips regularization during this paper, we came to another interesting assumption. No matter which regularized solution was chosen, it always seems like it fits perfectly to a certain constant noise level. Since the noise level of the provided signal is increasing with height, this means that, especially over large intervals, a regularized solution can only fit well to a certain part of the interval. This also explains why separating the intervals mostly results in better solutions.
- Our assumption can be underlined at least for the Tikhonov–Phillips method. As shown in Kaipio and Somersalo [34], the Tikhonov–Phillips regularization is equivalent to a Bayesian Inversion method, which models the true signal as well as the noise as a Gaussian distributed random variable with zero mean and a constant variance. Another idea for future work could be to apply other Bayesian models in Ansmann’s algorithm instead of the Tikhonov–Phillips methods. One could choose different models for the noise distribution that may fit better to the given signals. A suitable family of models could be the family of Lévy--processes [35], which could be capable of modeling an increasing noise level of the signal. Recent work from Suuronen et al. [35] showed the practical usability of those processes as prior assumptions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AOD | aerosol optical depth |
| BSR | backscatter ratio |
| SSA | single scattering albedo |
| SI | splitting of interval |
| SNR | signal-to-noise ratio |
Appendix A. Mathematical Preliminaries
Appendix B. Discretization
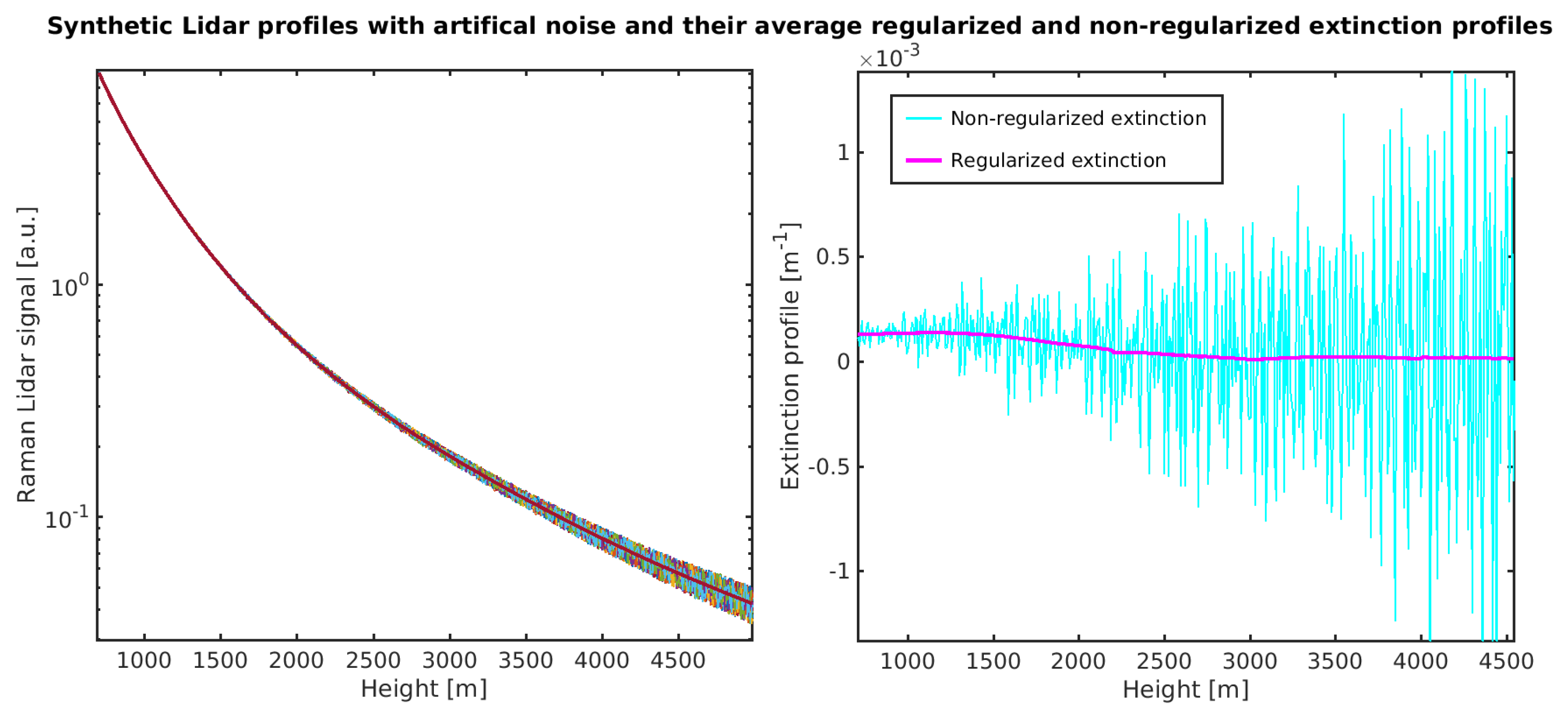
Appendix C. Simple Example with Gaussian Noise
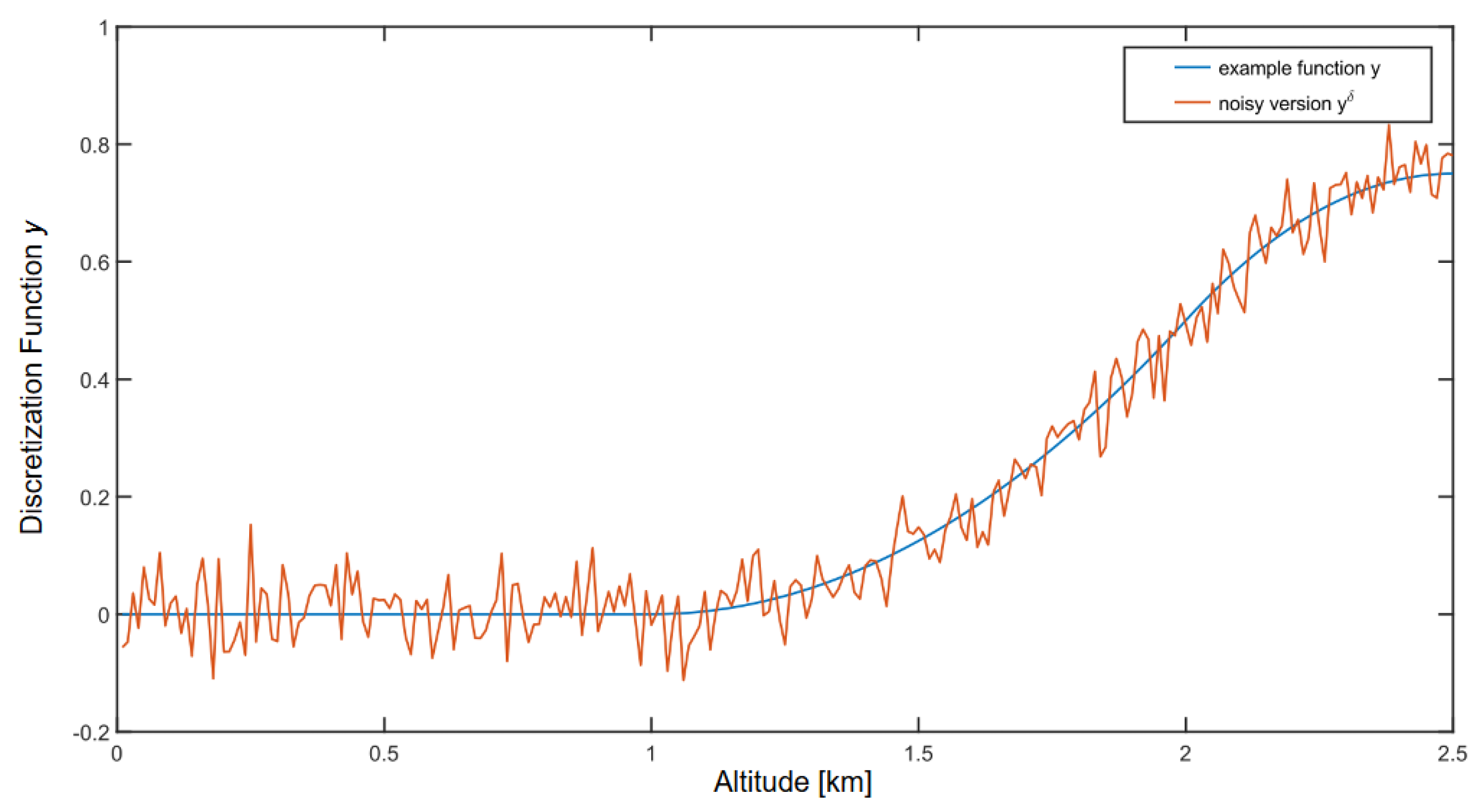
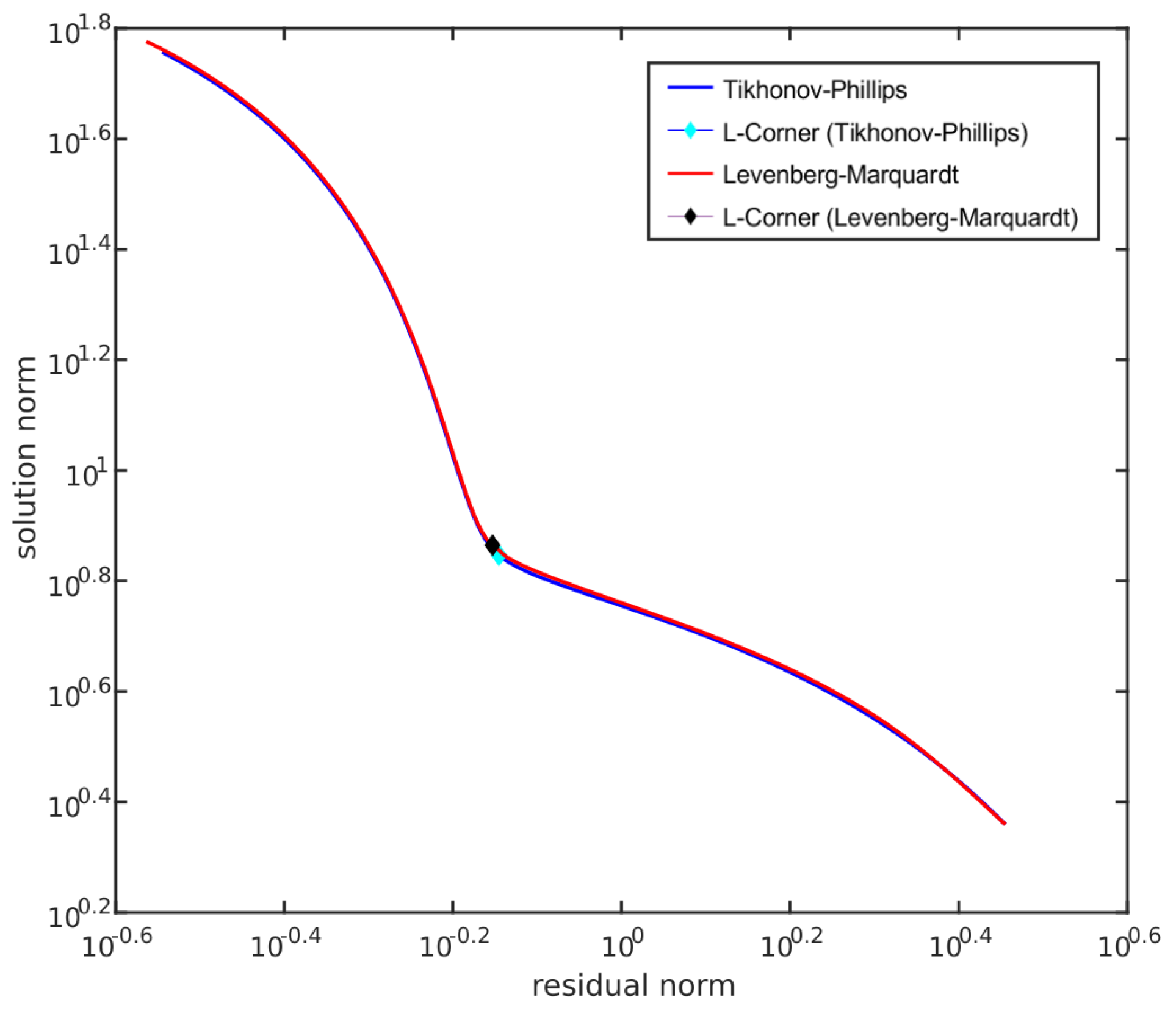

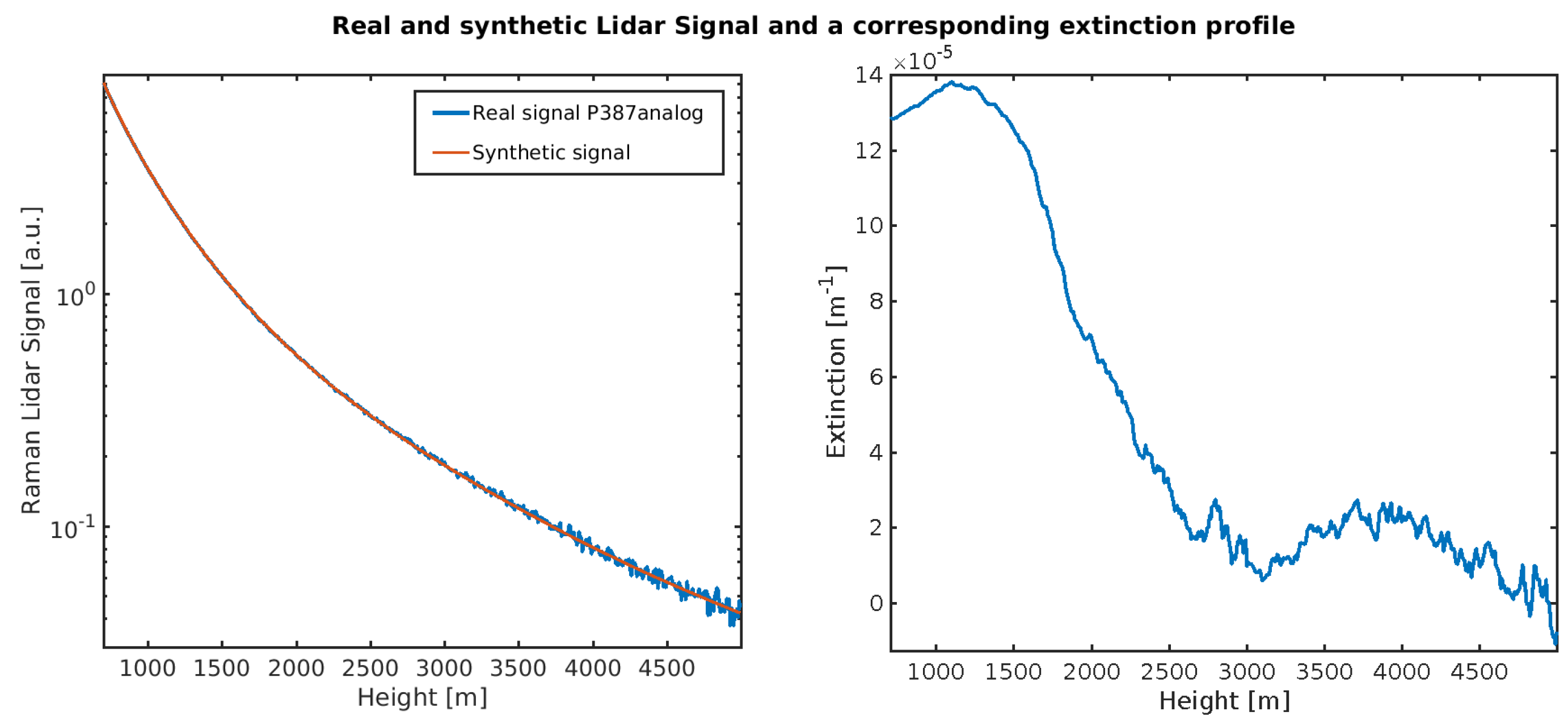
Appendix D. Additional Lidar Application Figures and Tables

| Step Sizes | Iterations per Step Size | ||
|---|---|---|---|
| 10 | 100 | 1 × 10−6, 1 × 10−5, 1 × 10−4 | 10 |
| 10 | 30 | 1 × 10−7, 1 × 10−6, 1 × 10−5, 1 × 10−4 | 20 |
| Exponents x of Reg. Param. | ||
|---|---|---|
| 10 | 100 | 40 equidistant values from |
| 10 | 30 | 100 equidistant values from |
| Interval [m] | Regularization Parameter (Number of Iterations) | Curvature at L-Corner |
|---|---|---|
| 19 | ||
| 10 | ||
| 8 | ||
| 4 | ||
| 6 | ||
| [8661, 10,220] | 3 |
| Interval [m] | Regularization Parameter | Curvature at L-Corner |
|---|---|---|
| × 10+3 | ||
| × 10+4 | ||
| × 10+5 | ||
| × 10+5 | ||
| × 10+7 |
| Interval [m] | Regularization Parameter (Number of Iterations) |
|---|---|
| 12 | |
| 10 | |
| 15 | |
| 10 |
References
- Lohmann, U.; Feichter, J. Global indirect aerosol effects: A review. Atmos. Chem. Phys. 2005, 5, 715–737. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.; et al. Climate change 2021: The physical science basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021; Volume 2, p. 2391. [Google Scholar] [CrossRef]
- Li, J.; Carlson, B.E.; Yung, Y.L.; Lv, D.; Hansen, J.; Penner, J.E.; Liao, H.; Ramaswamy, V.; Kahn, R.A.; Zhang, P.; et al. Scattering and absorbing aerosols in the climate system. Nat. Rev. Earth Environ. 2022, 3, 363–379. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of Absorption and Optical Properties of Key Aerosol Types Observed in Worldwide Locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Nakoudi, K.; Ritter, C.; Böckmann, C.; Kunkel, D.; Eppers, O.; Rozanov, V.; Mei, L.; Pefanis, V.; Jäkel, E.; Herber, A.; et al. Does the intra-Arctic modification of long-range transported aerosol affect the local radiative budget? (a case study). Remote Sens. 2020, 12, 2112. [Google Scholar] [CrossRef]
- Myhre, G.; Myhre, C.; Samset, B.; Storelvmo, T. Aerosols and their relation to global climate and climate sensitivity. Nat. Educ. Knowl. 2013, 4, 7. [Google Scholar]
- Weitkamp, C. Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Foken, T. Springer Handbook of Atmospheric Measurements; Springer Nature: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Böckmann, C. Hybrid regularization method for the ill-posed inversion of multiwavelength lidar data in the retrieval of aerosol size distributions. Appl. Opt. 2001, 40, 1329–1342. [Google Scholar] [CrossRef]
- Veselovskii, I.; Kolgotin, A.; Griaznov, V.; Müller, D.; Franke, K.; Whiteman, D.N. Inversion of multiwavelength Raman lidar data for retrieval of bimodal aerosol size distribution. Appl. Opt. 2004, 43, 1180–1195. [Google Scholar] [CrossRef]
- Müller, D.; Wandinger, U.; Ansmann, A. Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: Simulation. Appl. Opt. 1999, 38, 2358–2368. [Google Scholar] [CrossRef] [PubMed]
- Böckmann, C.; Ritter, C.; Graßl, S. Improvement of Aerosol Coarse-Mode Detection through Additional Use of Infrared Wavelengths in the Inversion of Arctic Lidar Data. Remote Sens. 2024, 16, 1576. [Google Scholar] [CrossRef]
- Böckmann, C.; Kirsche, A. Iterative regularization method for lidar remote sensing. Comput. Phys. Commun. 2006, 174, 607–615. [Google Scholar] [CrossRef]
- Ansmann, A.; Riebesell, M.; Weitkamp, C. Measurement of atmospheric aerosol extinction profiles with a Raman lidar. Opt. Lett. 1990, 15, 746–748. [Google Scholar] [CrossRef]
- Pornsawad, P.; Böckmann, C.; Ritter, C.; Rafler, M. Ill-posed retrieval of aerosol extinction coefficient profiles from Raman lidar data by regularization. Appl. Opt. 2008, 47, 1649–1661. [Google Scholar] [CrossRef]
- Pornsawad, P.; D’Amico, G.; Böckmann, C.; Amodeo, A.; Pappalardo, G. Retrieval of aerosol extinction coefficient profiles from Raman lidar data by inversion method. Appl. Opt. 2012, 51, 2035–2044. [Google Scholar] [CrossRef] [PubMed]
- Ceolato, R.; Berg, M.J. Aerosol light extinction and backscattering: A review with a lidar perspective. J. Quant. Spectrosc. Radiat. Transf. 2021, 262, 107492. [Google Scholar] [CrossRef]
- Hu, M.; Li, S.; Mao, J.; Li, J.; Wang, Q.; Zhang, Y. Novel Inversion Algorithm for the Atmospheric Aerosol Extinction Coefficient Based on an Improved Genetic Algorithm. Photonics 2022, 9, 554. [Google Scholar] [CrossRef]
- Hoffmann, A. Comparative Aerosol Studies based on Multi-wavelength Raman LIDAR at Ny-Ålesund, Spitsbergen. Ph.D. Thesis, Universität Potsdam, Potsdam, Germany, 2010. [Google Scholar]
- Ritter, C.; Münkel, C. Backscatter lidar for aerosol and cloud profiling. In Springer Handbook of Atmospheric Measurements; Springer: Berlin/Heidelberg, Germany, 2021; pp. 683–717. [Google Scholar]
- Thorsen, T.J.; Fu, Q.; Newsom, R.K.; Turner, D.D.; Comstock, J.M. Automated retrieval of cloud and aerosol properties from the ARM Raman lidar. Part I: Feature detection. J. Atmos. Ocean. Technol. 2015, 32, 1977–1998. [Google Scholar] [CrossRef]
- Ansmann, A.; Wandinger, U.; Riebesell, M.; Weitkamp, C.; Michaelis, W. Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined Raman elastic-backscatter lidar. Appl. Opt. 1992, 31, 7113–7131. [Google Scholar] [CrossRef] [PubMed]
- Bakushinskii, A. Remarks on choosing a regularization parameter using the quasi-optimality and ratio criterion. USSR Comput. Math. Math. Phys. 1984, 24, 181–182. [Google Scholar] [CrossRef]
- Kirsche, A.; Böckmann, C. Padé iteration method for regularization. Appl. Math. Comput. 2006, 180, 648–663. [Google Scholar] [CrossRef]
- Böckmann, C.; Pornsawad, P. Iterative Runge–Kutta-type methods for nonlinear ill-posed problems. Inverse Probl. 2008, 24, 025002. [Google Scholar] [CrossRef]
- Ritter, C.; Burgos, M.A.; Böckmann, C.; Mateos, D.; Lisok, J.; Markowicz, K.; Moroni, B.; Cappelletti, D.; Udisti, R.; Maturilli, M.; et al. Microphysical properties and radiative impact of an intense biomass burning aerosol event measured over Ny-Ãlesund, Spitsbergen in July 2015. Tellus B Chem. Phys. Meteorol. 2018, 70, 1–23. [Google Scholar] [CrossRef]
- Dube, J.; Böckmann, C.; Ritter, C. Lidar-Derived Aerosol Properties from Ny-Ålesund, Svalbard during the MOSAiC Spring 2020. Remote Sens. 2022, 14, 2578. [Google Scholar] [CrossRef]
- Graßl, S.; Ritter, C.; Schulz, A. The Nature of the Ny-Ålesund Wind Field Analysed by High-Resolution Windlidar Data. Remote Sens. 2022, 14, 3771. [Google Scholar] [CrossRef]
- Klett, J.D. Lidar inversion with variable backscatter/extinction ratios. Appl. Opt. 1985, 24, 1638–1643. [Google Scholar] [CrossRef]
- Graßl, S.; Ritter, C. Properties of Arctic Aerosol Based on Sun Photometer Long-Term Measurements in Ny-Ålesund, Svalbard. Remote Sens. 2019, 11, 1362. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Hansen, P.C. The L-Curve and Its Use in the Numerical Treatment of Inverse Problems; WIT Press: Southampton, UK, 2001; Volume 4, pp. 119–142. [Google Scholar]
- Wahba, G. Spline Models for Observational Data. Reg. Conf. Ser. Appl. Math. 1990, 59. [Google Scholar] [CrossRef]
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Applied Mathematical Sciences; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Suuronen, J.; Soto, T.; Chada, N.K.; Roininen, L. Bayesian inversion with α-stable priors. Inverse Probl. 2023, 39, 105007. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]





| Method | Description/Use Cases | Weaknesses/Difficulties |
|---|---|---|
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrmann, R.M.; Ritter, C.; Böckmann, C.; Graßl, S. Improved Method for the Retrieval of Extinction Coefficient Profile by Regularization Techniques. Remote Sens. 2025, 17, 841. https://doi.org/10.3390/rs17050841
Herrmann RM, Ritter C, Böckmann C, Graßl S. Improved Method for the Retrieval of Extinction Coefficient Profile by Regularization Techniques. Remote Sensing. 2025; 17(5):841. https://doi.org/10.3390/rs17050841
Chicago/Turabian StyleHerrmann, Richard Matthias, Christoph Ritter, Christine Böckmann, and Sandra Graßl. 2025. "Improved Method for the Retrieval of Extinction Coefficient Profile by Regularization Techniques" Remote Sensing 17, no. 5: 841. https://doi.org/10.3390/rs17050841
APA StyleHerrmann, R. M., Ritter, C., Böckmann, C., & Graßl, S. (2025). Improved Method for the Retrieval of Extinction Coefficient Profile by Regularization Techniques. Remote Sensing, 17(5), 841. https://doi.org/10.3390/rs17050841








