A Spoofing Detection and Direction-Finding Approach for Global Navigation Satellite System Signals Using Off-the-Shelf Anti-Jamming Antennas
Abstract
1. Introduction
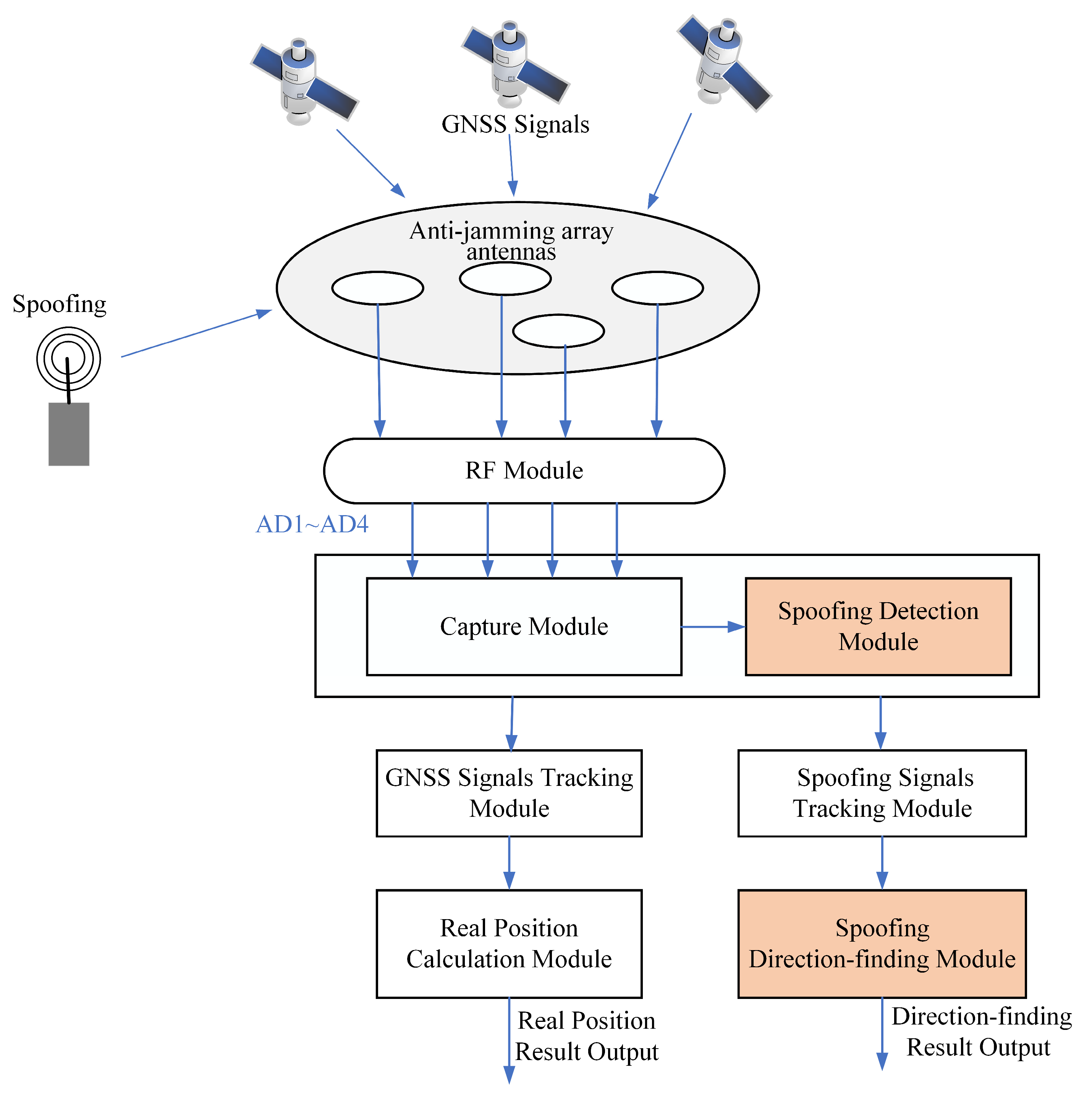
2. Detection and Direction-Finding Framework
3. Spoofing Detection Method Based on LightGBM
3.1. Capturing Phase Signal Model
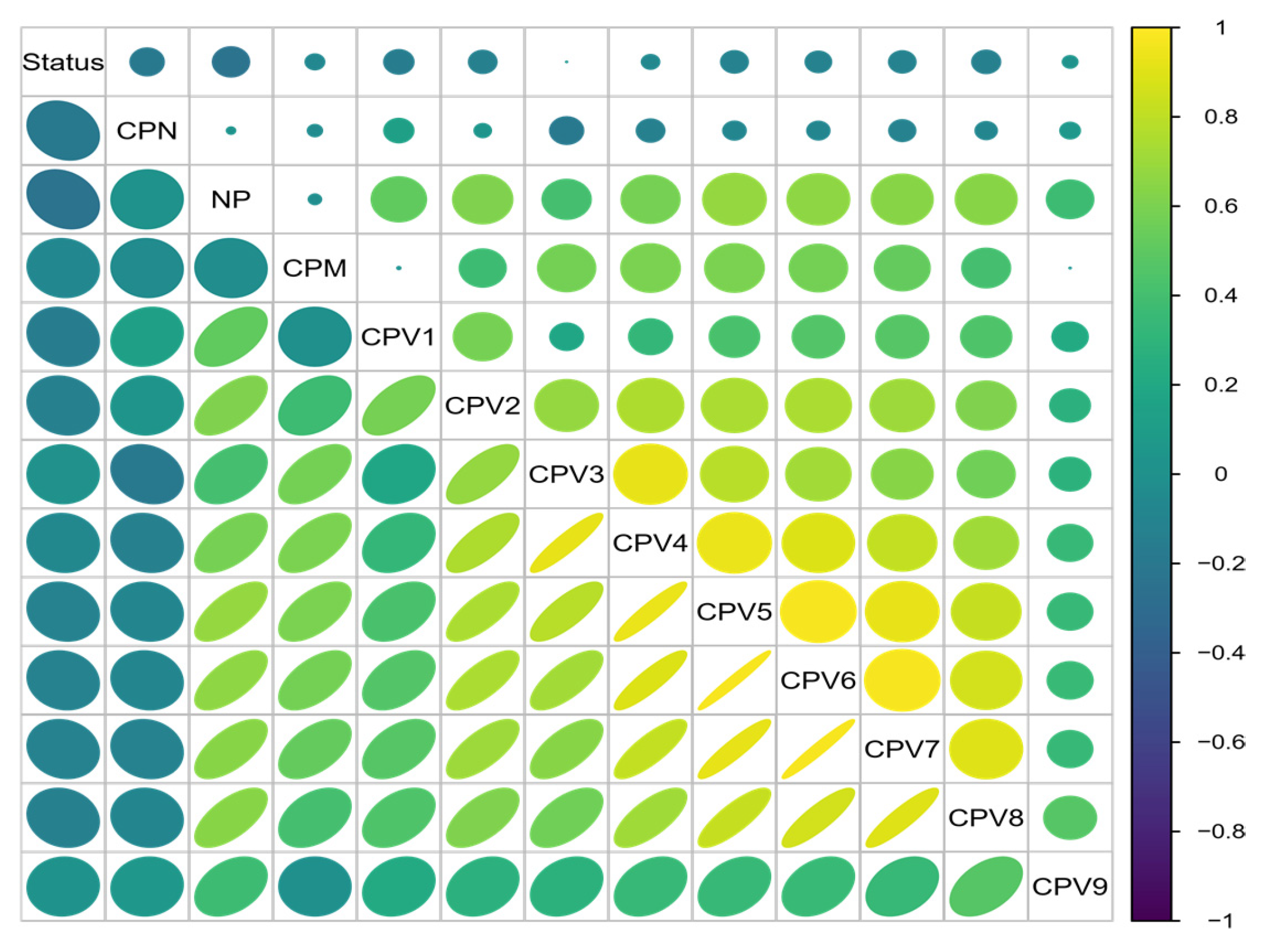
3.2. Feature Extraction
3.2.1. Receiver Status
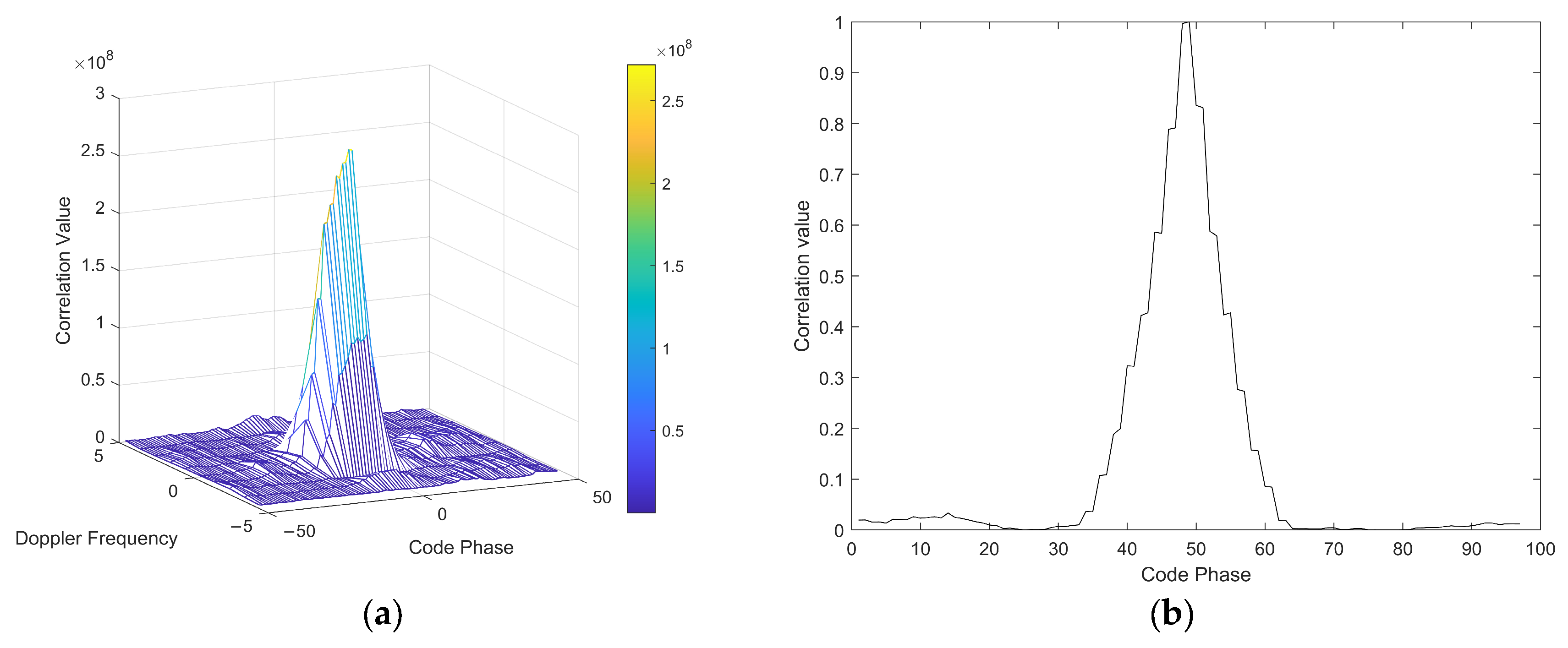
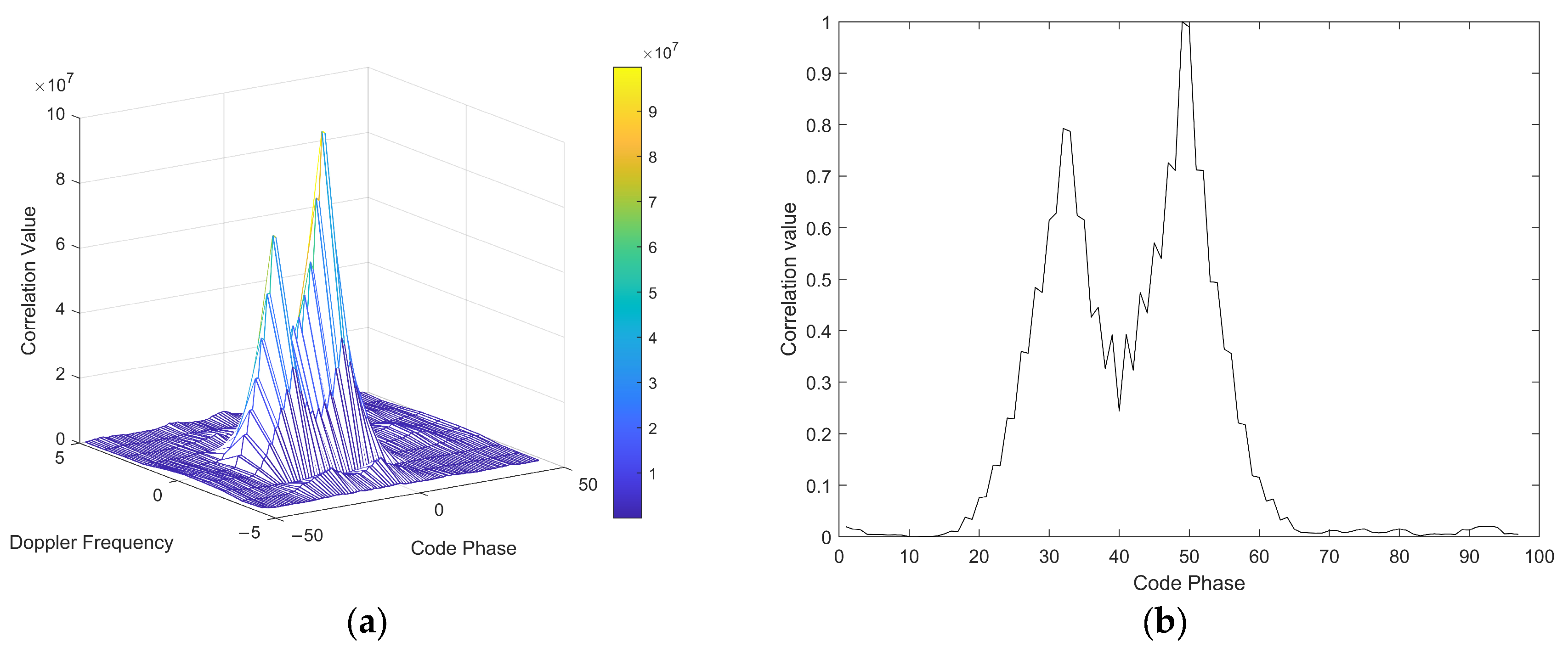
3.2.2. Number of Correlation Peaks
3.2.3. Mean Noise
3.2.4. Capture Parameter
3.2.5. Nine Correlation Peak Sampling Points Within ±1 Chip of the Maximum Correlation Peak Value
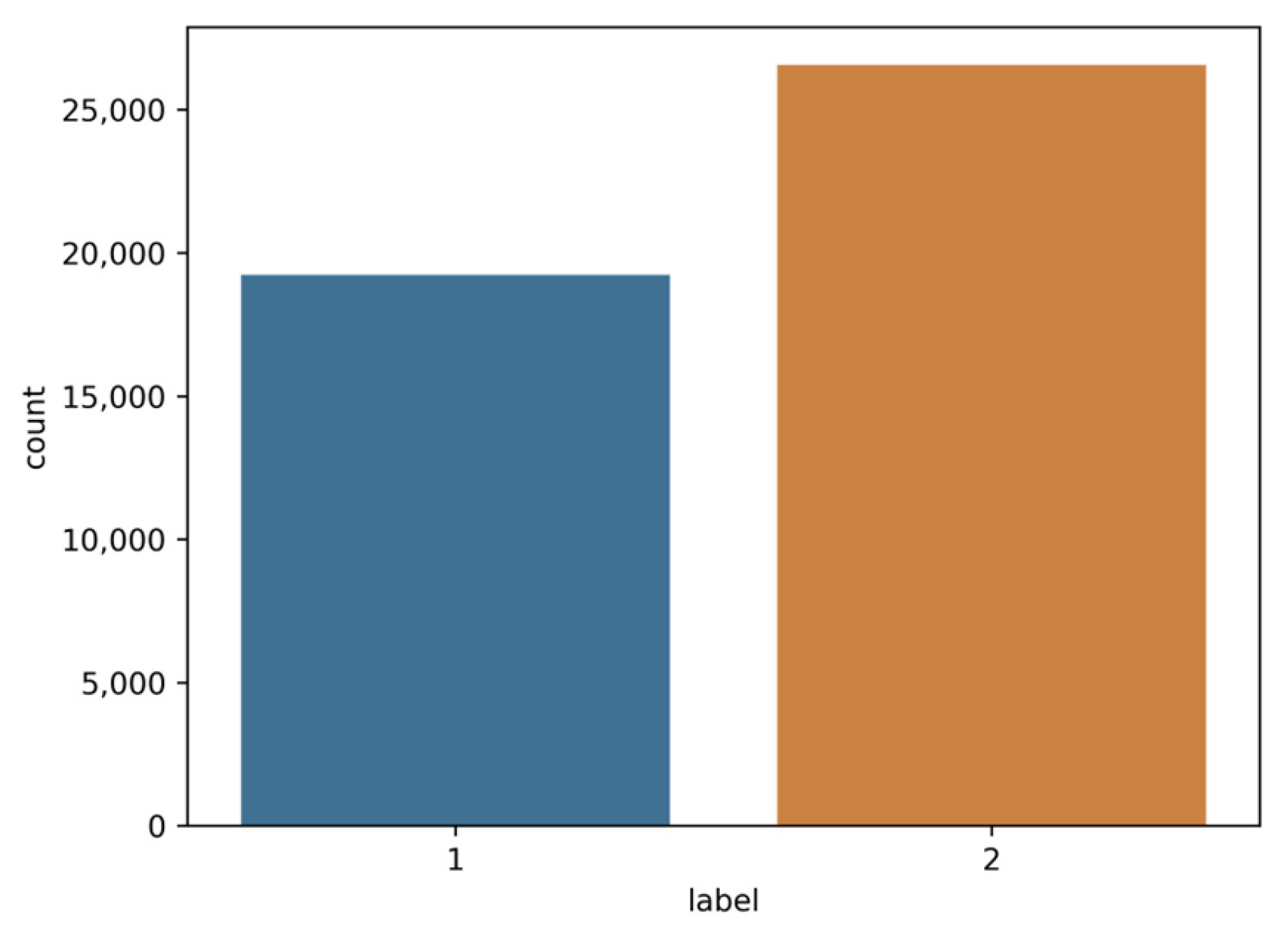
3.3. Machine Learning Classifier and Model Training
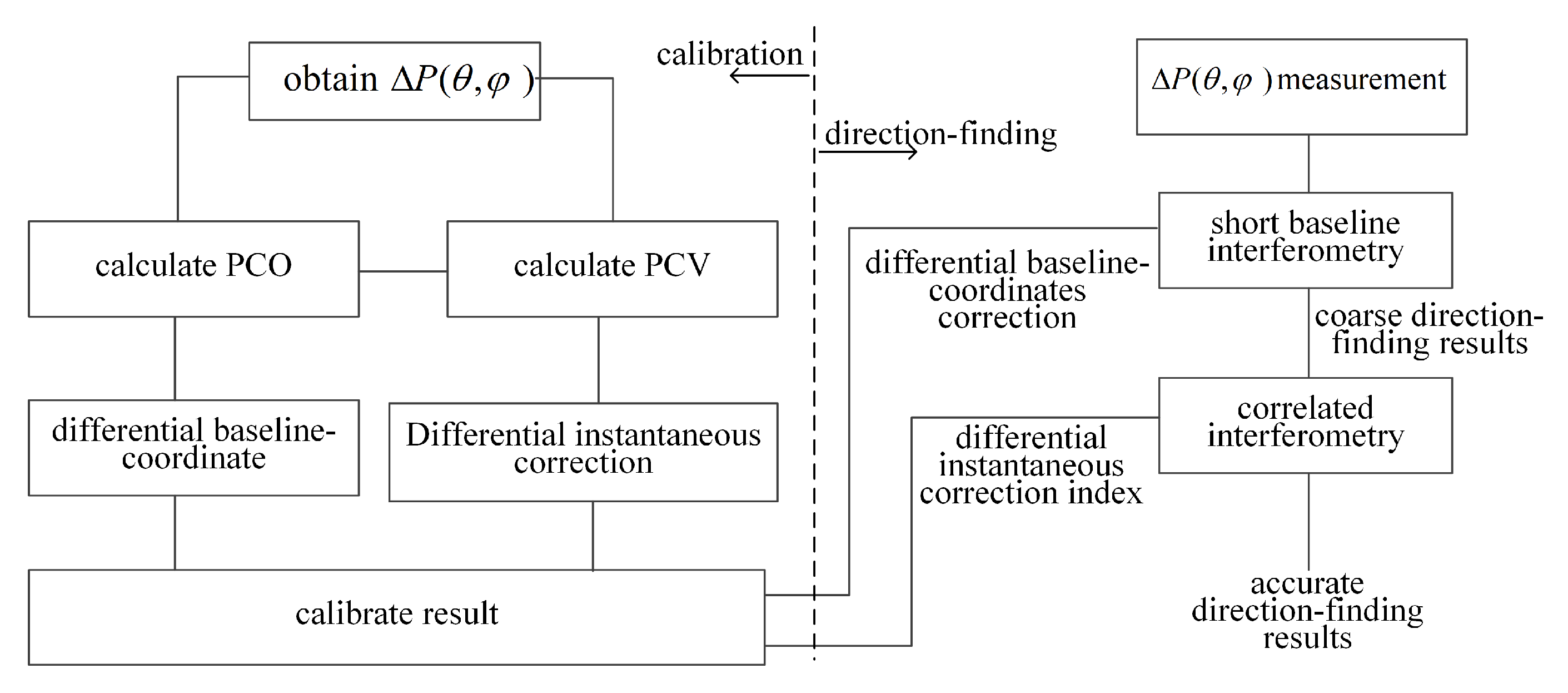
4. Spoofing-Direction-Finding Method Based on Differential Phase-Center Correction
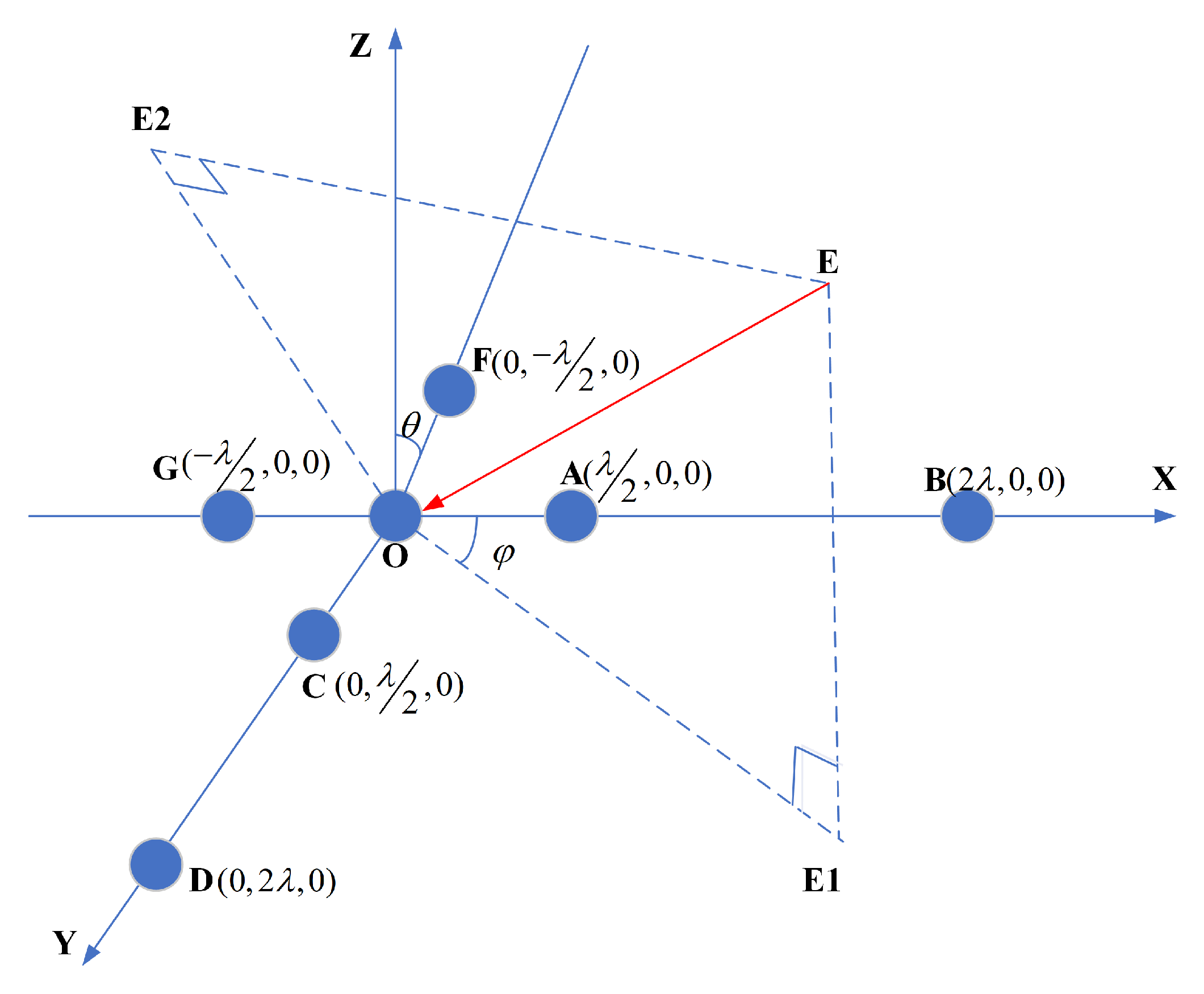
4.1. Analysis of Spoofing-Direction-Finding Errors
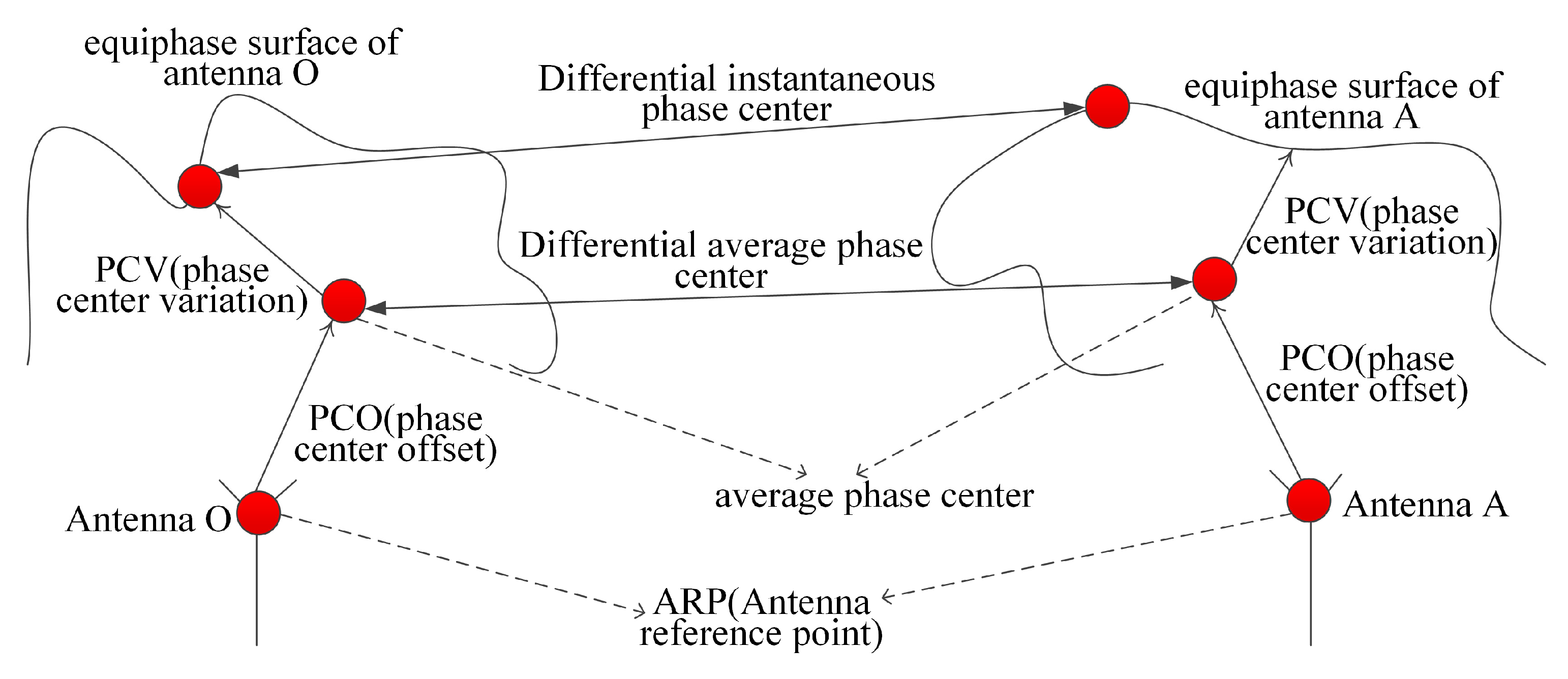
4.2. Array Differential Phase-Center Correction
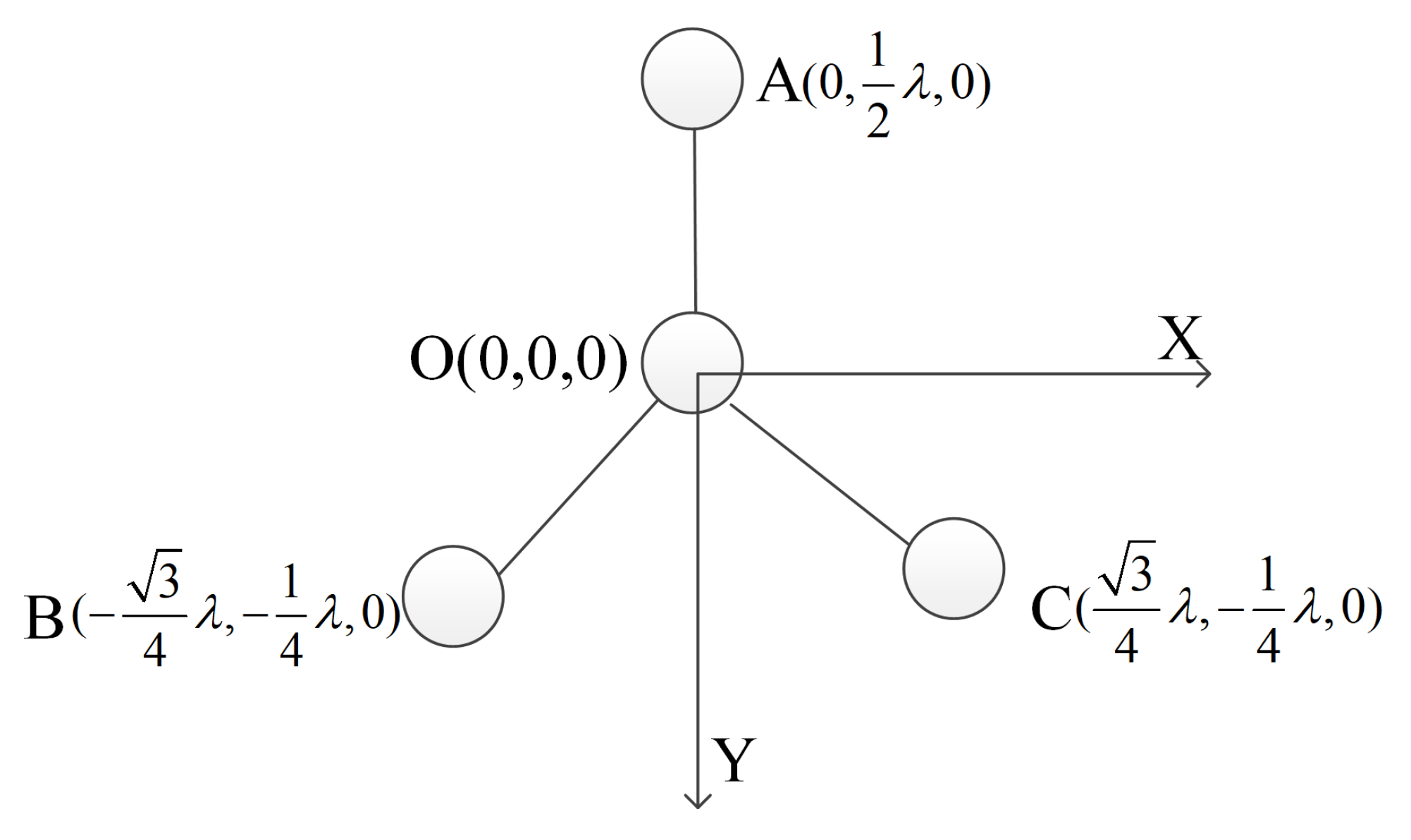
4.3. Spoofing-Direction-Finding: Half-Wavelength Baseline
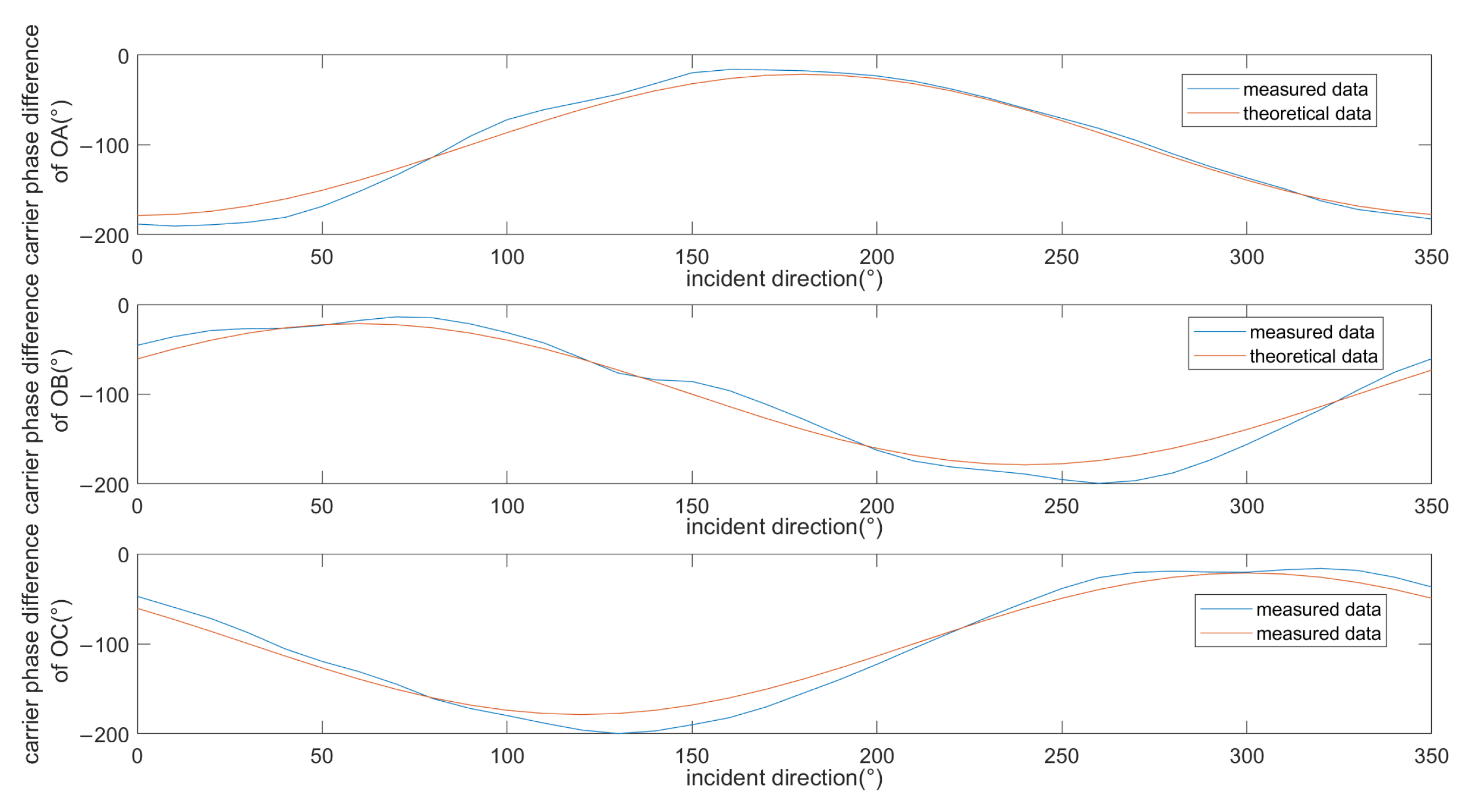
- The spoofing sources are placed in different positions , and the measurement matrix of baselines OA, OB, and OC is measured by the receiver.
- Calculate the differential baseline coordinate values of the stage baselines OA, OB, and OC, and , , and are obtained according to Equation (18).
- Calculate the differential instantaneous corrections and the differential instantaneous correction matrices , , and related to according to Equations (18) and (19).
- Generate the average phase-center coordinate vector of the baselines OA, OB, and OC, and construct a differential instantaneous correction matrix based on .
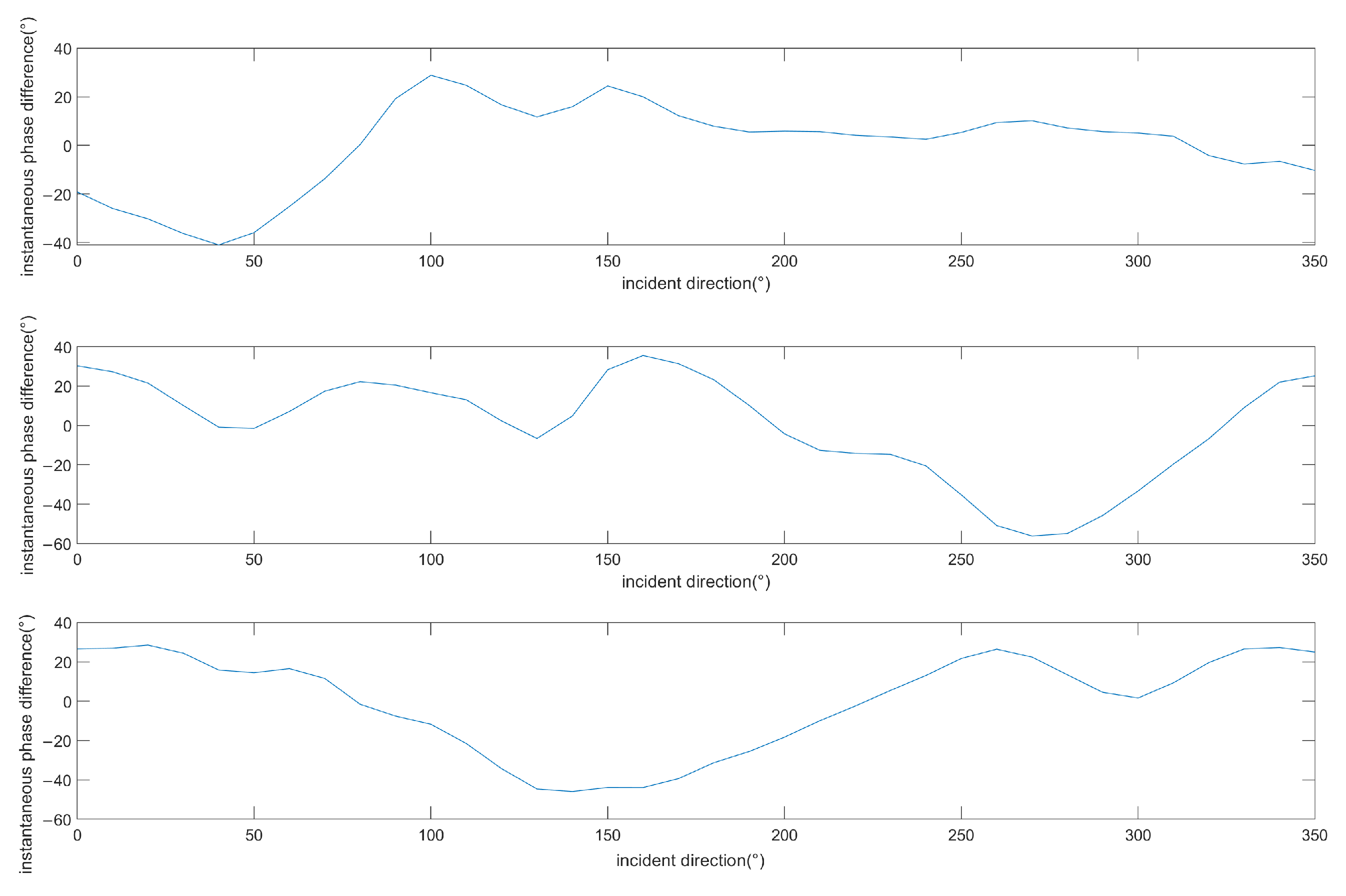
- Complete the preliminary measurement of the direction of the spoofing using the , , data, combined with Equation (11). The measured value includes the instantaneous differential phase error and can only provide a preliminary directional measurement result.
- Set the incoming wave phase error intervals and , discretize the interval with , and calculate the correlation coefficient between the baseline phase difference and the wave path difference of OA/OB/OC using the equation in the next step.Note that n = 1, 2, and 3, respectively, represent baselines OA, OB, and OC.
- Using as the step, search and calculate all the correlation coefficients in the interval , and find the directional value corresponding to the largest correlation coefficient, which is the incident direction of the spoofing signal.
5. Experiments and Results
5.1. Experimental Scenario
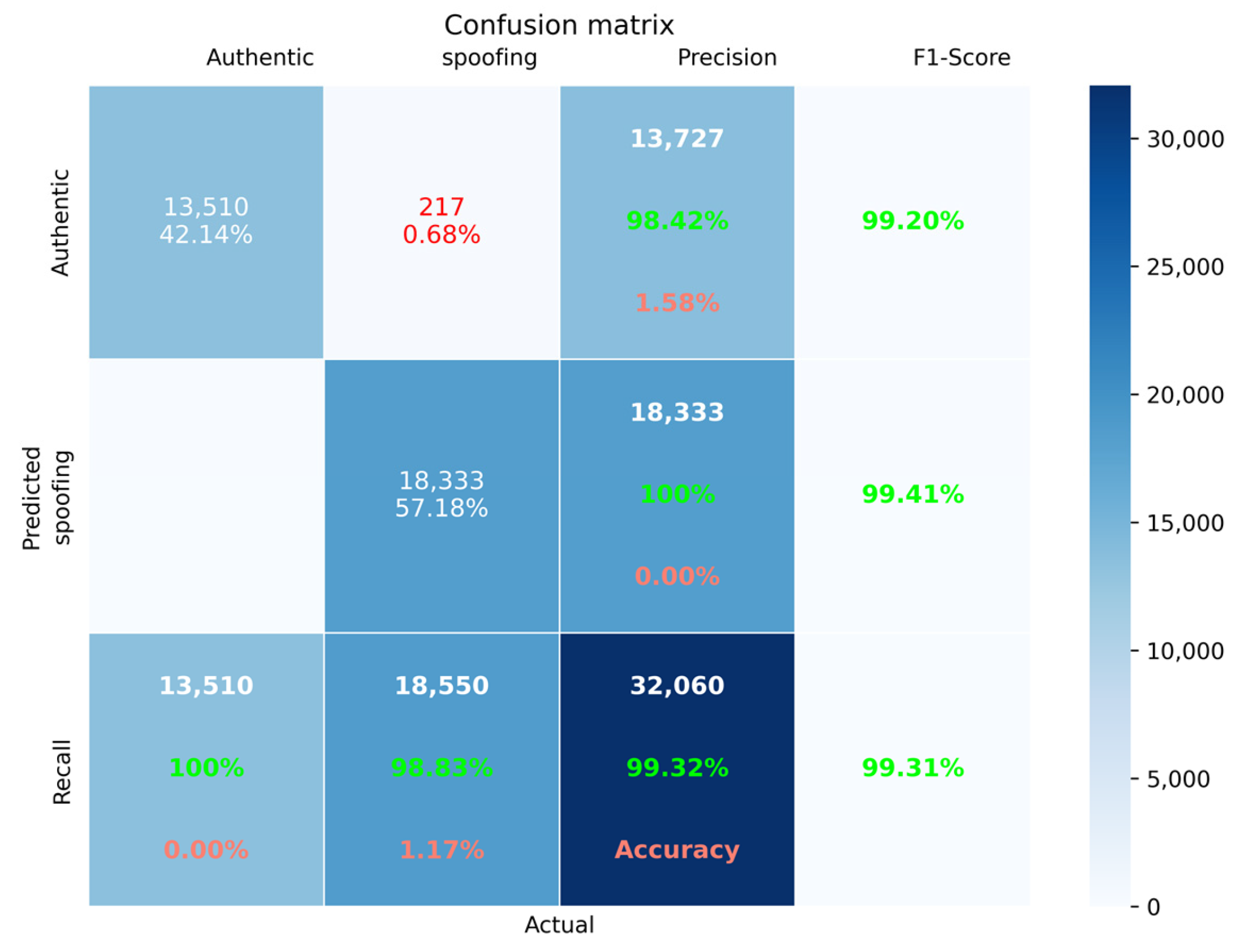
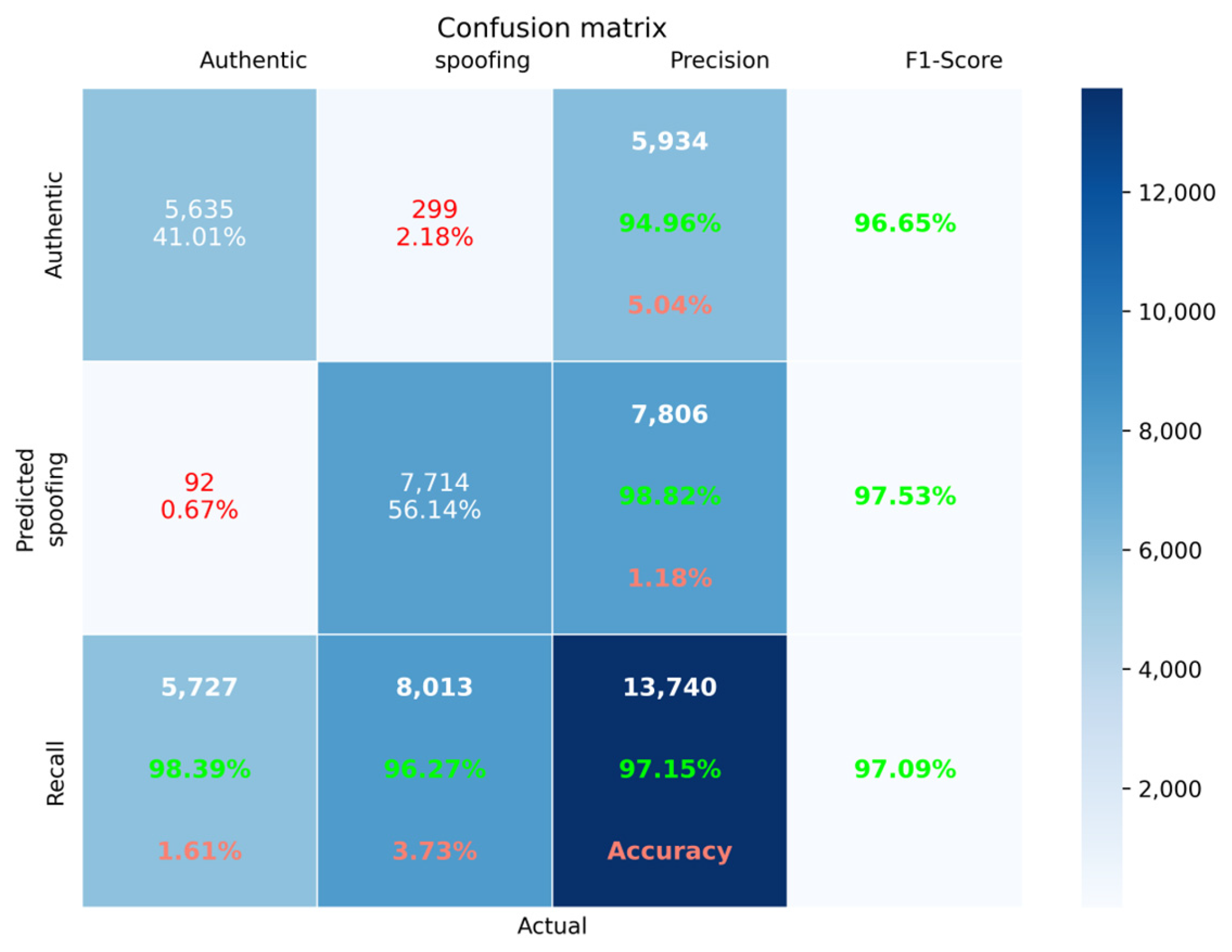
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Humphreys, T. Statement on the Vulnerability of Civil Unmanned Aerial Vehicles and Other Systems to Civil Gps Spoofing; University of Texas at Austin: Austin, TX, USA, 2012; pp. 1–16. [Google Scholar]
- Androjna, A.; Perkovič, M. Impact of spoofing of navigation systems on maritime situational awareness. Trans. Marit. Sci. 2021, 10, 361–373. [Google Scholar] [CrossRef]
- Jones, M. Spoofing in the Black Sea: What really happened? GPS World. 11 October 2017. Available online: https://www.gpsworld.com/spoofing-in-the-black-sea-what-really-happened/ (accessed on 17 February 2025).
- Pany, T.; Falk, N.; Riedl, B.; Stöber, C.; Winkel, J.; Ranner, H.P. GNSS synthetic aperture processing with artificial antenna motion. In Proceedings of the 26th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 3163–3171. [Google Scholar]
- Dampf, J.; Pany, T.; Bär, W.; Winkel, J.; Mervart, L.; Ávila-Rodríguez, J.; Ioannides, R.; Hein, G. Real world spoofing trials and mitigation. Inside GNSS 2017, 12, 55–65. [Google Scholar]
- Mao, P.; Yuan, H.; Chen, X.; Gong, Y.; Li, S.; Li, R.; Luo, R.; Zhao, G.; Fu, C.; Xu, J. A GNSS Spoofing Detection and Direction-Finding Method Based on Low-Cost Commercial Board Components. Remote Sens. 2023, 15, 2781. [Google Scholar] [CrossRef]
- Yang, H.; Jin, R.; Xu, W.; Che, L.; Zhen, W. Satellite Navigation Spoofing Interference Detection and Direction Finding Based on Array Antenna. Sensors 2023, 23, 1604. [Google Scholar] [CrossRef] [PubMed]
- Jahromi, A.J.; Broumandan, A.; Nielsen, J.; Lachapelle, G. GPS spoofer countermeasure effectiveness based on signal strength, noise power, and C/N0 measurements. Int. J. Satell. Commun. Netw. 2012, 30, 181–191. [Google Scholar] [CrossRef]
- Broumandan, A.; Jafarnia-Jahromi, A.; Dehghanian, V.; Nielsen, J.; Lachapelle, G. GNSS spoofing detection in handheld receivers based on signal spatial correlation. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 479–487. [Google Scholar]
- Tu, J.; Zhan, X.; Chen, M.; Gao, H.; Chen, Y. GNSS intermediate spoofing detection via dual-peak in frequency domain and relative velocity residuals. IET Radar Sonar Navig. 2020, 14, 439–447. [Google Scholar] [CrossRef]
- Shang, X.; Sun, F.; Wang, D.; Xiao, K.; Dou, S.; Lu, X.; Sun, J. GNSS spoofing detection based on multicorrelator distortion monitoring. GPS Solut. 2023, 27, 94. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Lu, M. Performance assessment of signal quality monitoring based GNSS spoofing detection techniques. In China Satellite Navigation Conference (CSNC) 2015 Proceedings: Volume I; Springer: Berlin/Heidelberg, Germany, 2015; pp. 783–793. [Google Scholar]
- Meurer, M.; Konovaltsev, A.; Cuntz, M.; Hättich, C. Robust joint multi-antenna spoofing detection and attitude estimation using direction assisted multiple hypotheses RAIM. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 21 September 2012; pp. 3007–3016. [Google Scholar]
- Magiera, J. A multi-antenna scheme for early detection and mitigation of intermediate GNSS spoofing. Sensors 2019, 19, 2411. [Google Scholar] [CrossRef] [PubMed]
- Konovaltsev, A.; Cuntz, M.; Haettich, C.; Meurer, M. Performance analysis of joint multi-antenna spoofing detection and attitude estimation. In Proceedings of the 2013 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 27–29 January 2013; pp. 864–872. [Google Scholar]
- Daneshmand, S.; Jafarnia-Jahromi, A.; Broumandon, A.; Lachapelle, G. A low-complexity GPS anti-spoofing method using a multi-antenna array. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 1233–1243. [Google Scholar]
- Liu, Y.; Li, S.; Fu, Q.; Liu, Z.; Zhou, Q. Analysis of Kalman filter innovation-based GNSS spoofing detection method for INS/GNSS integrated navigation system. IEEE Sens. J. 2019, 19, 5167–5178. [Google Scholar] [CrossRef]
- Tanıl, Ç.; Khanafseh, S.; Joerger, M.; Pervan, B. An INS monitor to detect GNSS spoofers capable of tracking vehicle position. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 131–143. [Google Scholar] [CrossRef]
- Bai, L.; Sun, C.; Dempster, A.G.; Zhao, H.; Feng, W. GNSS Spoofing Detection and Mitigation With a Single 5G Base Station Aiding. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4601–4620. [Google Scholar] [CrossRef]
- Wesson, K.; Rothlisberger, M.; Humphreys, T. Practical cryptographic civil GPS signal authentication. NAVIGATION J. Inst. Navig. 2011, 59, 177–193. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Liu, R. BD-II NMASSI: An scheme of anti-spoofing and open BeiDou II D2 navigation message authentication. IEEE Access 2020, 8, 23759–23775. [Google Scholar] [CrossRef]
- Iqbal, A.; Aman, M.N.; Sikdar, B. Machine and Representation Learning Based GNSS Spoofing Detectors Utilizing Feature Set From Generic GNSS Receivers. IEEE Trans. Consum. Electron. 2023, 70, 574–583. [Google Scholar] [CrossRef]
- Iqbal, A.; Aman, M.N.; Sikdar, B. A Deep Learning based Induced GNSS Spoof Detection Framework. IEEE Trans. Mach. Learn. Commun. Netw. 2024, 2, 457–478. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Li, J.; Zhu, X.; Li, C. GNSS multiparameter spoofing detection method based on support vector machine. IEEE Sens. J. 2022, 22, 17864–17874. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Bhatti, J.A.; Shepard, D.; Wesson, K. The Texas Spoofing Test Battery: Toward a Standard for Evaluating GPS Signal Authentication Techniques; University of Texas at Austin: Austin, TX, USA, 2012. [Google Scholar]
- Kunysz, W. Antenna phase center effects and measurements in GNSS ranging applications. In Proceedings of the 14th International Symposium on Antenna Technology and Applied Electromagnetics & the American Electromagnetics Conference, Ottawa, ON, Canada, 5–8 July 2010; pp. 1–4. [Google Scholar]
- Kumar, A.; Sarma, A.D.; Ansari, E.; Yedukondalu, K. Improved phase center estimation for GNSS patch antenna. IEEE Trans. Antennas Propag. 2013, 61, 1909–1915. [Google Scholar] [CrossRef]
- Schmid, R.; Mader, G.; Herring, T. From relative to absolute antenna phase center corrections. In Proceedings of the IGS Workshop and Symposium 2004, Bern, Switzerland, 1–5 May 2005; pp. 209–219. [Google Scholar]






| Abrv. | Scenario Info | Spoofing Type | Mobility | Power Adv. (dB) | Synchronization | Onset (s) |
|---|---|---|---|---|---|---|
| DS-0 | 0: Clean-Static | N/A | Static | N/A | N/A | N/A |
| DS-1 | 1: Clean-Dynamic | N/A | Dynamic | N/A | N/A | N/A |
| DS-2 | 2: Static Overpowered | Time Push | Static | 10 | Code Phase Prop. | 110 |
| DS-3 | 3: Static Matched-Power | Time Push | Static | 1.3 | Frequency Lock Mode | 120 |
| DS-4 | 4: Static Matched-Power | Position Push | Static | 0.4 | Frequency Lock Mod | 114 |
| DS-5 | 5: Dynamic Overpowered | Time Push | Dynamic | 9.9 | Code Phase Prop. | 102 |
| DS-6 | 6: Dynamic Matched-Power | Position Push | Dynamic | 0.8 | Frequency Lock Mod | 105 |
| DS-7 | 7: Static Matched-Power | Time Push | Static | Matched | Carrier Phase Aligned | 110 |
| DS-8 | 8: Static Matched-Power | Time Push | Static | Matched | Zero-Delay Security Code Estimation and Replay | 110 |
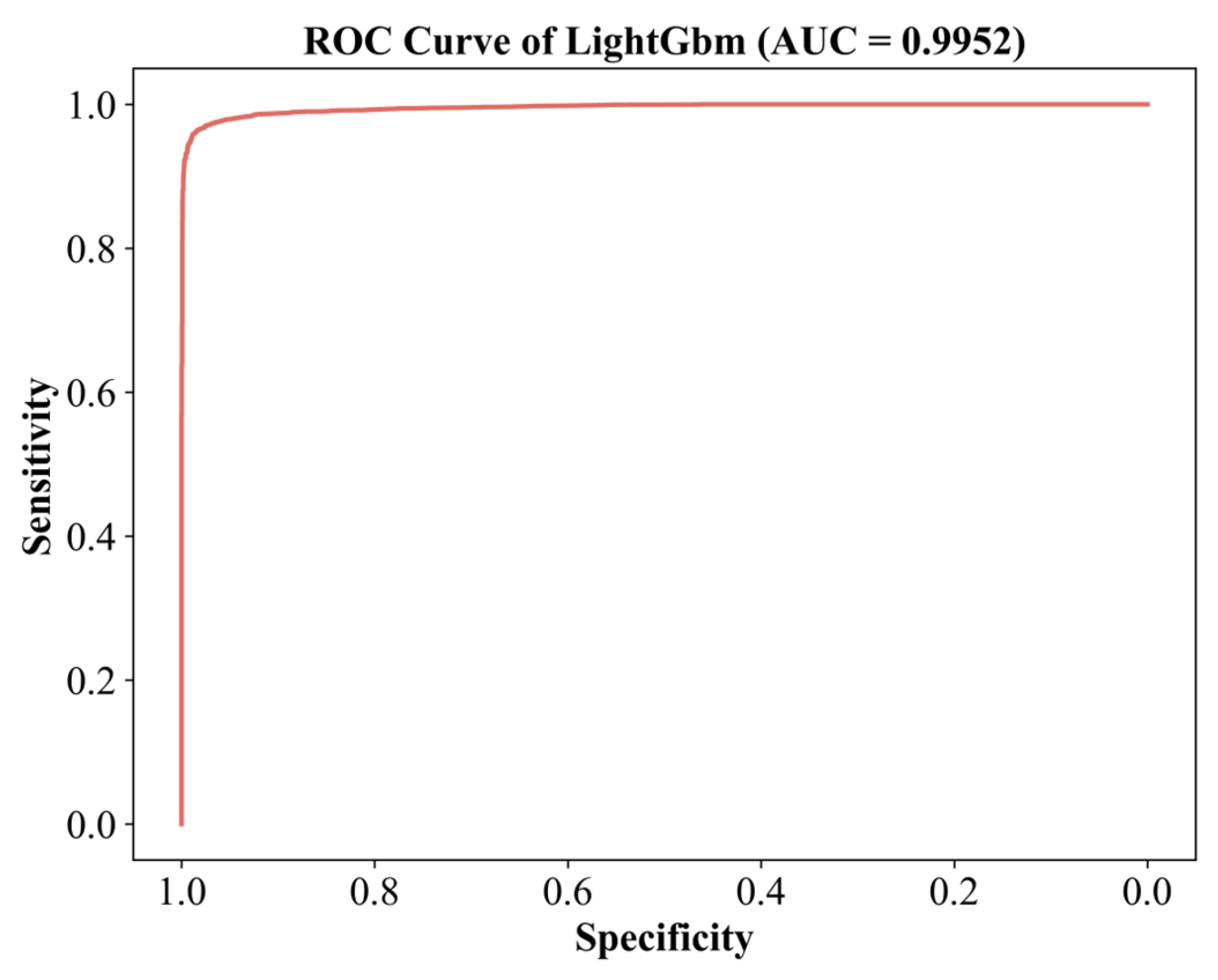
| Method | Feature Extraction Phase | AUC | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|---|---|
| Proposed | Acquisition | 0.9952 | 97.15 | 98.82 | 96.27 | 97.09 |
| Ref. [24] | Tracking and PVT solution | 0.99 | 97.02 | 96.77 | 97.24 | 97.00 |
| Element Number | X Axis (mm) | Y Axis (mm) | Z Axis (mm) | Explain |
|---|---|---|---|---|
| O | 0 | 0 | 0 | Reference origin |
| A | 0 | 84 | 0 | Reference origin |
| B | −72.7 | −42 | 0 | Reference origin |
| C | 72.7 | −42 | 0 | Reference origin |
| OA | 9.538 | 1.25 | 0.0718 | Average differential phase correction |
| OB | −0.8331 | −13.44 | 130.75 | Average differential phase correction |
| OC | −14.94 | 7.04 | −84.12 | Average differential phase correction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, R.; Yan, J.; Cui, X.; Yang, H.; Zhen, W.; Gu, M.; Ji, G.; Chen, L.; Li, H. A Spoofing Detection and Direction-Finding Approach for Global Navigation Satellite System Signals Using Off-the-Shelf Anti-Jamming Antennas. Remote Sens. 2025, 17, 864. https://doi.org/10.3390/rs17050864
Jin R, Yan J, Cui X, Yang H, Zhen W, Gu M, Ji G, Chen L, Li H. A Spoofing Detection and Direction-Finding Approach for Global Navigation Satellite System Signals Using Off-the-Shelf Anti-Jamming Antennas. Remote Sensing. 2025; 17(5):864. https://doi.org/10.3390/rs17050864
Chicago/Turabian StyleJin, Ruimin, Junkun Yan, Xiang Cui, Huiyun Yang, Weimin Zhen, Mingyue Gu, Guangwang Ji, Longjiang Chen, and Haiying Li. 2025. "A Spoofing Detection and Direction-Finding Approach for Global Navigation Satellite System Signals Using Off-the-Shelf Anti-Jamming Antennas" Remote Sensing 17, no. 5: 864. https://doi.org/10.3390/rs17050864
APA StyleJin, R., Yan, J., Cui, X., Yang, H., Zhen, W., Gu, M., Ji, G., Chen, L., & Li, H. (2025). A Spoofing Detection and Direction-Finding Approach for Global Navigation Satellite System Signals Using Off-the-Shelf Anti-Jamming Antennas. Remote Sensing, 17(5), 864. https://doi.org/10.3390/rs17050864





