Kinetic Energy Cascade in the Frequency Domain from Satellite Products
Abstract
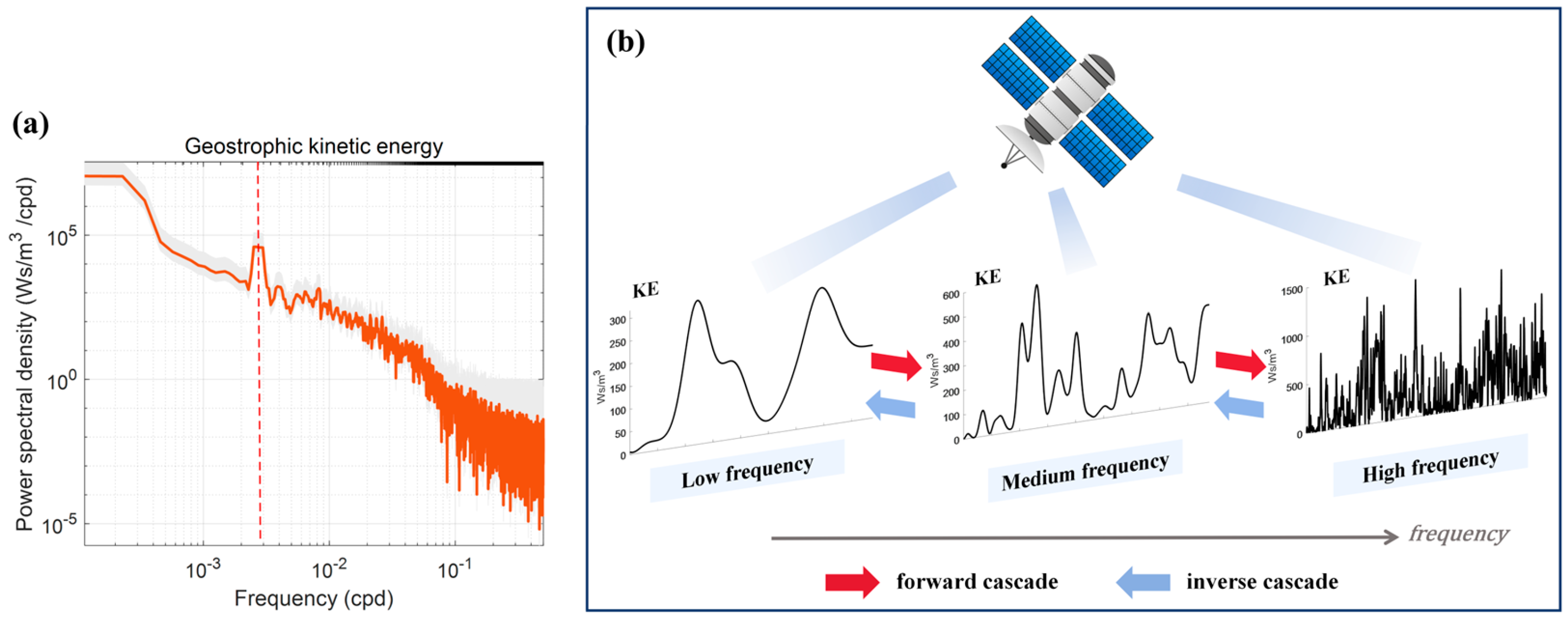
:1. Introduction
2. Formulation of Diagnostic Framework
2.1. Definition of Kinetic Energy Cascade in the Frequency Domain
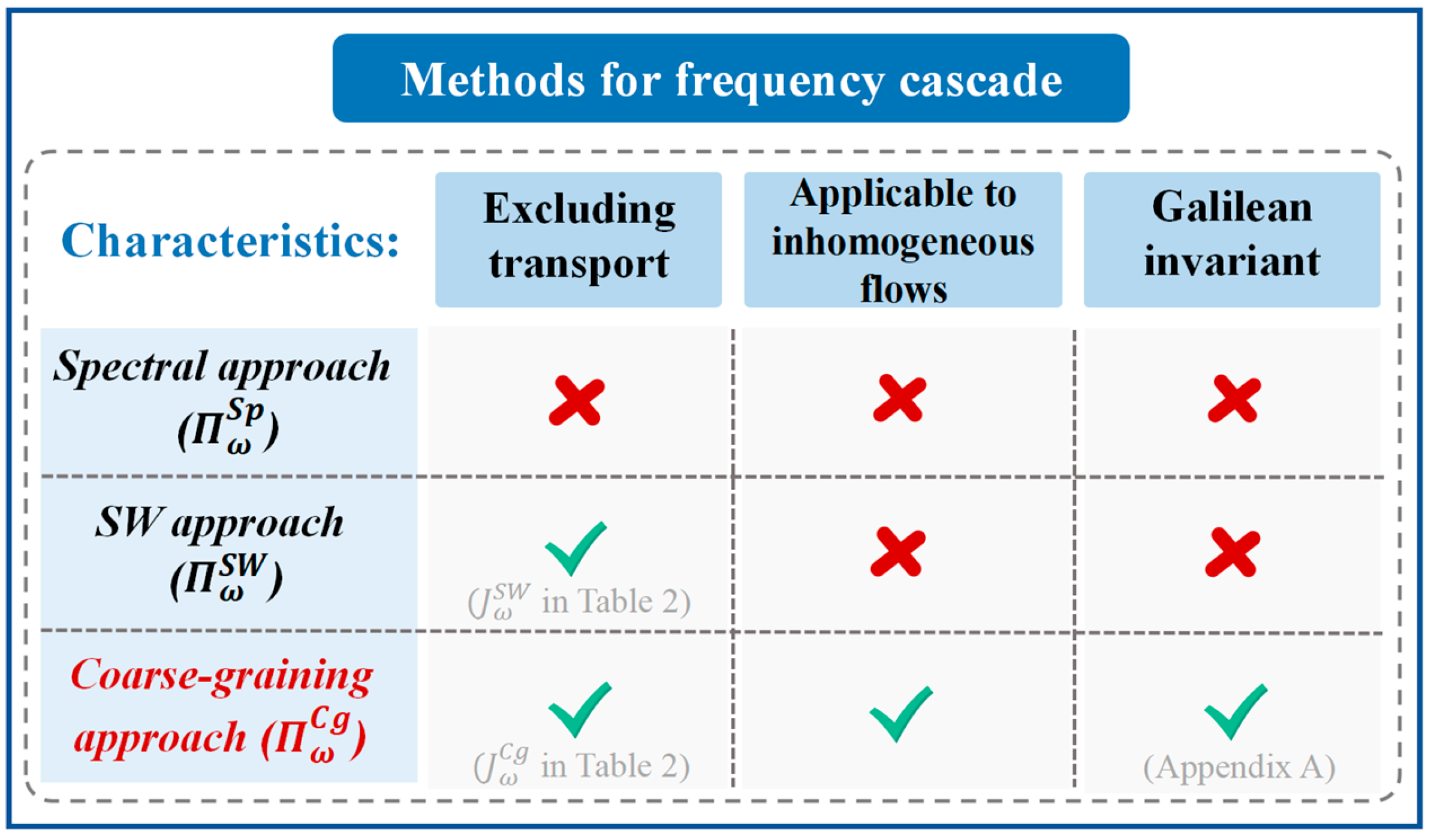
- The spectral approach ( in Table 1): The spectral approach here is developed directly from the primitive equations, instead of from the highly idealized quasi-geostrophic model as that in Arbic et al. [6,18]. It is essentially a natural extension of the spectral approach in the wavenumber domain [10,13] to the frequency domain. Based on the momentum equations (Equation (S1) and (S2) in Supplementary Materials), the spectral KE flux from this approach is obtained through the integration of Fourier-transformed advection term from one specific frequency to the highest available frequency;
- The SW approach ( in Table 1): The SW approach is developed for frequency-domain KE cascade for the first time. It is extended from the method proposed by Frisch [16] and Scott and Wang [2], which has not been applied in the frequency domain. Through applying a low-pass filter to momentum equations, this approach obtains spectral KE flux from the low-frequency KE budget equation. The low-pass filter here is defined as a specific type of filter that allows signals with a frequency lower than the cutoff frequency to pass through, while attenuating signals with frequencies higher than the cutoff frequency. The advection of low-frequency kinetic energy by total velocity ( in Table 2) is excluded from the original advection term due to its small effects to KE budget [16];
- The coarse-graining approach ( in Table 1): Here, the coarse-graining approach is firstly applied to satellite altimetry data and shows its superiority in accurately estimating KE cascade. It was initially introduced by Aluie et al. [14], and was recently extend to the frequency domain [19,20,21] focusing on KE transfer at high frequencies. In situ observations [20] and numerical simulations [19,20,21] were used in these studies. However, previous literature [5,15,21] did not apply this approach to satellite altimetry-based study, and results of low-frequency KE cascade are also yet to be explored from this approach. Here, we apply the coarse-graining approach to the KE cascade study at the whole available frequency range, spanning from monthly to yearly timescales. The KE cascade term from the low-frequency KE budget equation is separated from a transport part ( in Table 2).
2.2. Discussion: Comparison Among the Three Approaches
| Approach | Mathematical Form of Transport Term |
|---|---|
| SW approach | |
| Coarse-graining approach |
2.3. Comparison Between Methods in the Frequency and Wavenumber Domains
3. Data and Methods
3.1. Satellite Products
3.2. Filtering Methods
3.3. Analysis
4. Results
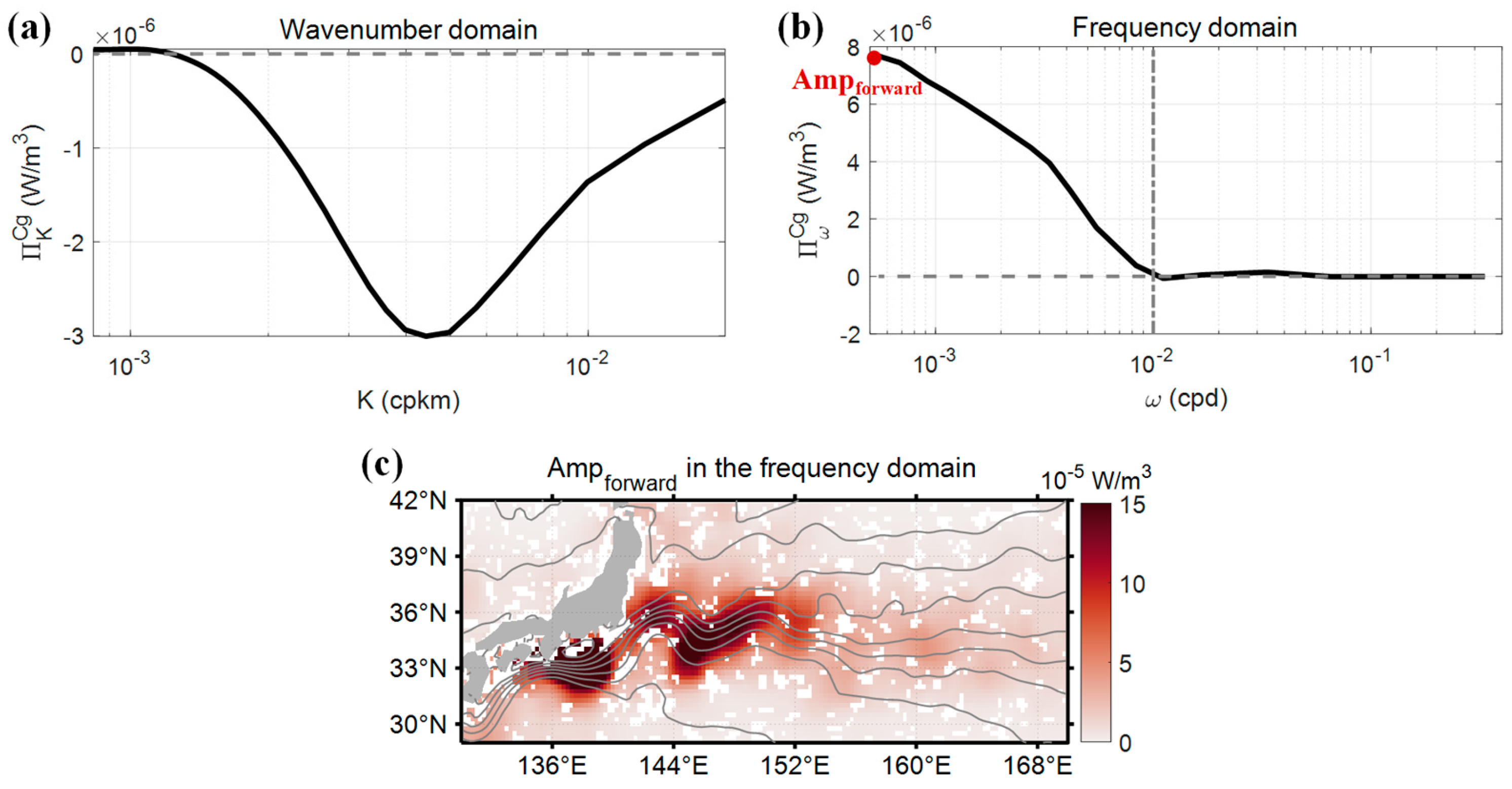
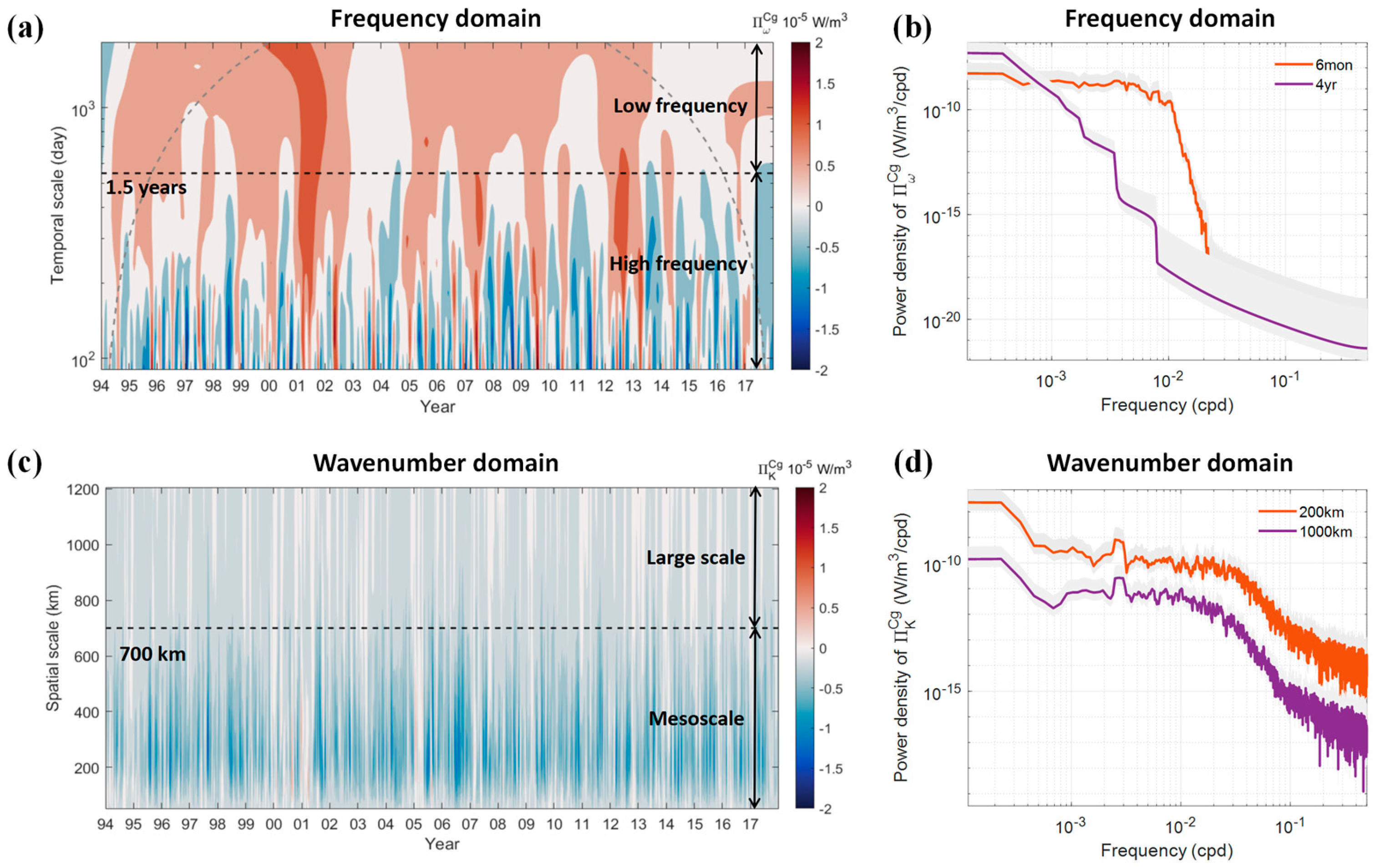
4.1. Forward Energy Cascades: Frequency vs. Wavenumber Domain Results
4.1.1. Phenomenon
4.1.2. Interpretation
4.2. Inverse Energy Cascades: Frequency vs. Wavenumber Domain Results
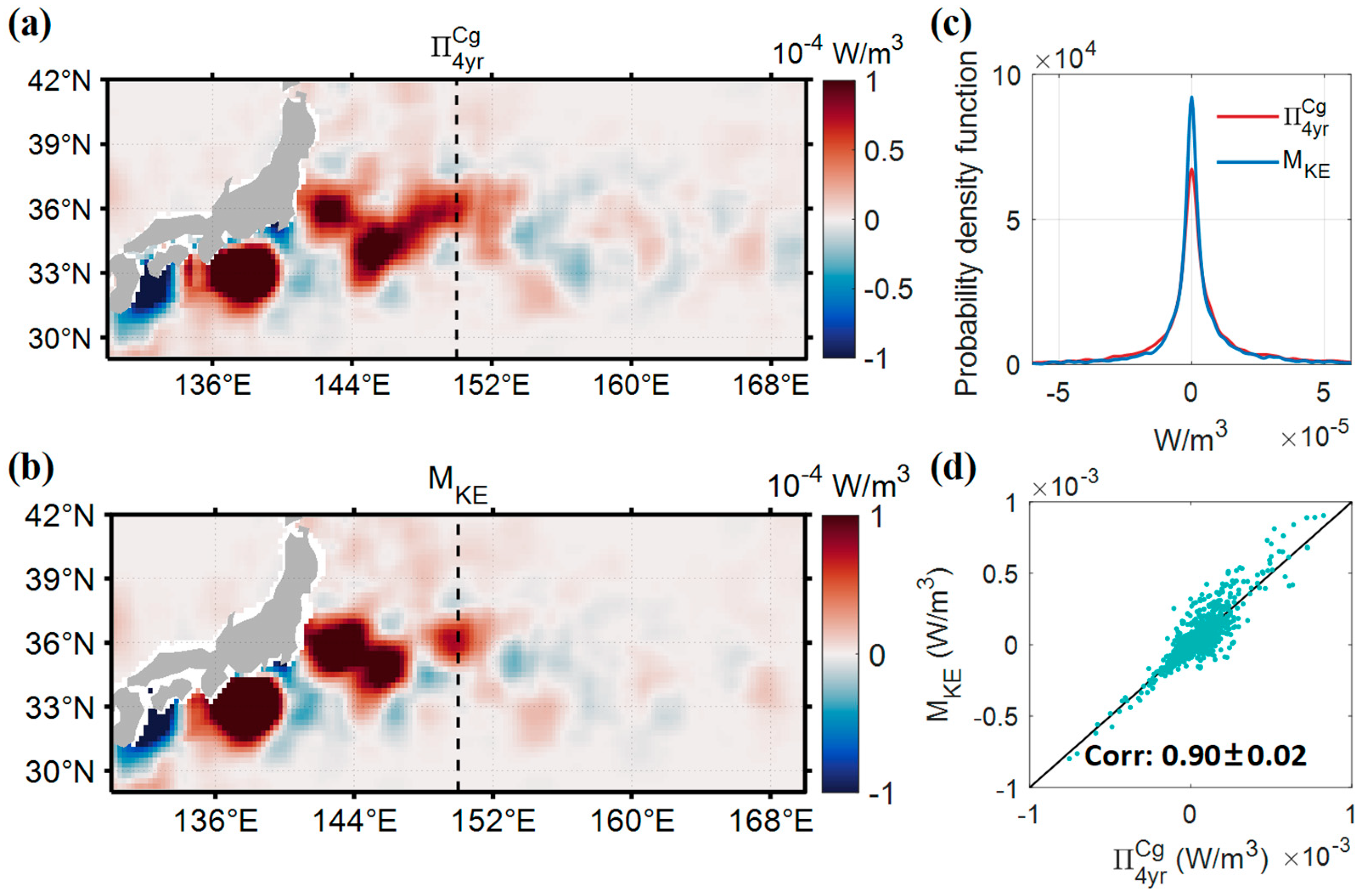
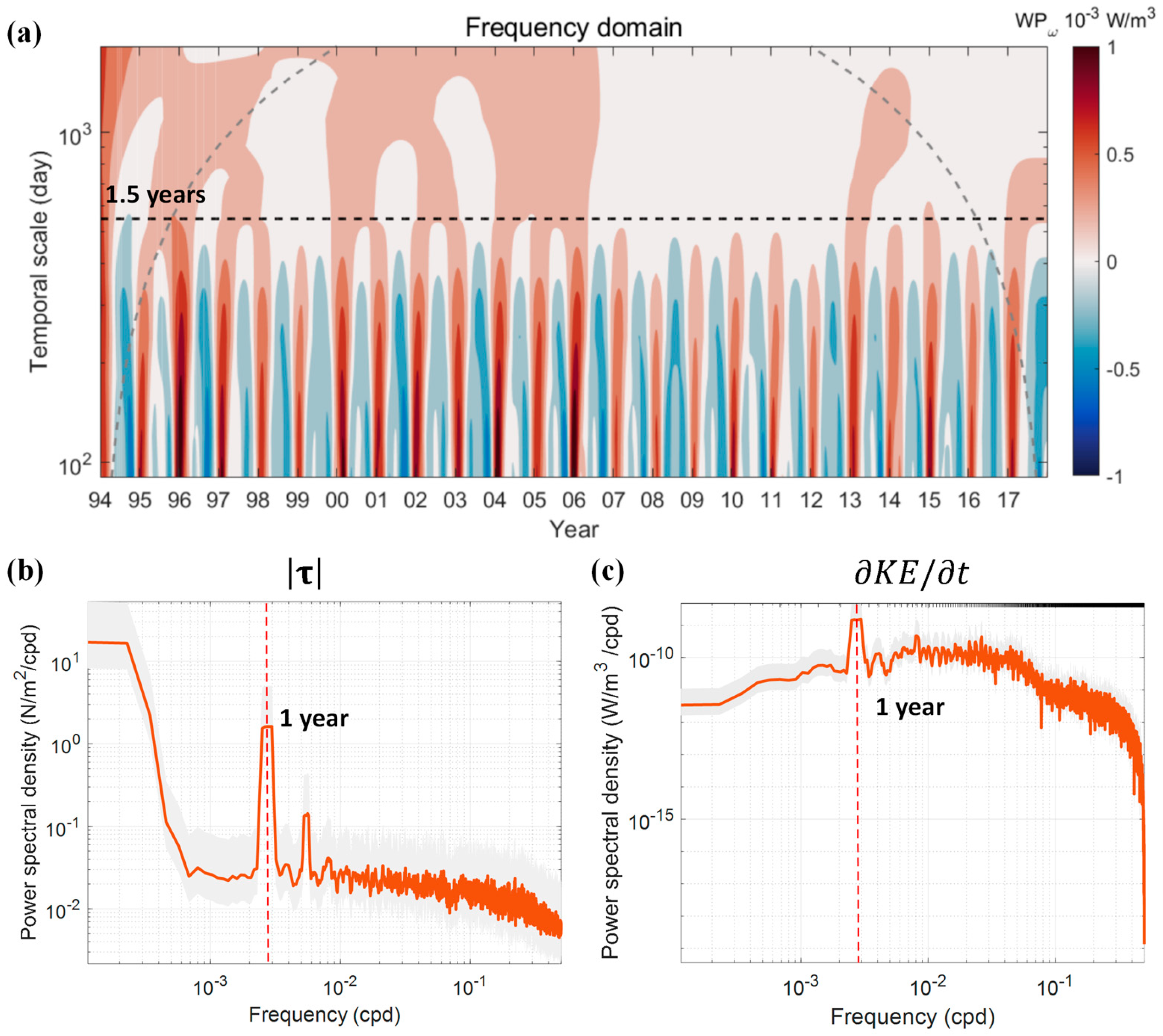
4.3. Temporal Variability of Energy Cascade: Frequency vs. Wavenumber Domain Results
4.4. Linkage Between KE Cascades in the Frequency Domain and Wind Forcing
5. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Confirmation of Galilean Invariance
Appendix B. Spectral Kinetic Energy Fluxes from the Three Approaches

Appendix C. Eddy–Mean Flow Interaction
References
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics, 1st ed.; Cambridge University Press: New York, NY, USA, 2006; p. 995. [Google Scholar]
- Scott, R.B.; Wang, F. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry. J. Phys. Oceanogr. 2005, 35, 1650–1666. [Google Scholar] [CrossRef]
- Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Rep. 2018, 767, 1–101. [Google Scholar] [CrossRef]
- Sérazin, G.; Penduff, T.; Barnier, B.; Molines, J.-M.; Arbic, B.K.; Müller, M.; Terray, L. Inverse cascades of kinetic energy as a source of intrinsic variability: A global OGCM study. J. Phys. Oceanogr. 2018, 48, 1385–1408. [Google Scholar] [CrossRef]
- Storer, B.A.; Buzzicotti, M.; Khatri, H.; Griffies, S.M.; Aluie, H. Global cascade of kinetic energy in the ocean and the atmospheric imprint. Sci. Adv. 2023, 9, eadi7420. [Google Scholar] [CrossRef]
- Arbic, B.K.; Müller, M.; Richman, J.G.; Shriver, J.F.; Morten, A.J.; Scott, R.B.; Sérazin, G.; Penduff, T. Geostrophic turbulence in the frequency–wavenumber domain: Eddy-driven low-frequency variability. J. Phys. Oceanogr. 2014, 44, 2050–2069. [Google Scholar] [CrossRef]
- Arbic, B.K.; Polzin, K.L.; Scott, R.B.; Richman, J.G.; Shriver, J.F. On eddy viscosity, energy cascades, and the horizontal resolution of gridded satellite altimeter products. J. Phys. Oceanogr. 2013, 43, 283–300. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Pang, C. Geographical distribution and anisotropy of the inverse kinetic energy cascade, and its role in the eddy equilibrium processes. J. Geophys. Res. Oceans 2015, 120, 4891–4906. [Google Scholar] [CrossRef]
- Khatri, H.; Sukhatme, J.; Kumar, A.; Verma, M.K. Surface ocean enstrophy, kinetic energy fluxes, and spectra from satellite altimetry. J. Geophys. Res. Oceans 2018, 123, 3875–3892. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current System. Part III: Energy balance and flux. J. Phys. Oceanogr. 2008, 38, 2256–2269. [Google Scholar] [CrossRef]
- Dong, J.; Fox-Kemper, B.; Zhang, H.; Dong, C. The seasonality of submesoscale energy production, content, and cascade. Geophys. Res. Lett. 2020, 47, e2020GL087388. [Google Scholar] [CrossRef]
- Li, H.; Xu, Y. Barotropic and baroclinic inverse kinetic energy cascade in the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2021, 51, 809–824. [Google Scholar] [CrossRef]
- Qiu, B.; Scott, R.B.; Chen, S. Length scales of eddy generation and nonlinear evolution of the seasonally modulated South Pacific Subtropical Countercurrent. J. Phys. Oceanogr. 2008, 38, 1515–1528. [Google Scholar] [CrossRef]
- Aluie, H.; Hecht, M.W.; Maltrud, M.E.; Rai, S.; Sadek, M.; Storer, B.A.; Vallis, G.K. Mapping the energy cascade in the North Atlantic Ocean: The coarse-graining approach. J. Phys. Oceanogr. 2018, 48, 225–244. [Google Scholar] [CrossRef]
- Schubert, R.; Gula, J.; Greatbatch, R.J.; Baschek, B.; Biastoch, A. The submesoscale kinetic energy cascade: Mesoscale absorption of submesoscale mixed layer eddies and frontal downscale fluxes. J. Phys. Oceanogr. 2020, 50, 2573–2589. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: New York, NY, USA, 1995; p. 296. [Google Scholar]
- Yang, Y.; Chen, R. Spectral kinetic-energy fluxes in the North Pacific: Definition comparison and normal- and shear-strain decomposition. J. Mar. Sci. Eng. 2022, 10, 1148. [Google Scholar] [CrossRef]
- Arbic, B.K.; Scott, R.B.; Flierl, G.R.; Morten, A.J.; Richman, J.G.; Shriver, J.F. Nonlinear cascades of surface oceanic geostrophic kinetic energy in the frequency domain. J. Phys. Oceanogr. 2012, 42, 1577–1600. [Google Scholar] [CrossRef]
- Barkan, R.; Srinivasan, K.; Yang, L.; McWilliams, J.C.; Gula, J.; Vic, C. Oceanic mesoscale eddy depletion catalyzed by internal waves. Geophys. Res. Lett. 2021, 48, e2021GL094376. [Google Scholar] [CrossRef]
- Garabato, A.C.N.; Yu, X.; Callies, J.; Barkan, R.; Polzin, K.L.; Frajka-Williams, E.E.; Buckingham, C.E.; Griffies, S.M. Kinetic energy transfers between mesoscale and submesoscale motions in the open ocean’s upper layers. J. Phys. Oceanogr. 2022, 52, 75–97. [Google Scholar] [CrossRef]
- Srinivasan, K.; Barkan, R.; McWilliams, J.C. A forward energy flux at submesoscales driven by fontogenesis. J. Phys. Oceanogr. 2023, 53, 287–305. [Google Scholar] [CrossRef]
- Wortham, C.; Wunsch, C. A multidimensional spectral description of ocean variability. J. Phys. Oceanogr. 2014, 44, 944–966. [Google Scholar] [CrossRef]
- Wunsch, C. The oceanic variability spectrum and transport trends. Atmosphere-Ocean 2009, 47, 281–291. [Google Scholar] [CrossRef]
- Yang, H.; Qiu, B.; Chang, P.; Wu, L.; Wang, S.; Chen, Z.; Yang, Y. Decadal variability of eddy characteristics and energetics in the Kuroshio Extension: Unstable versus stable states. J. Geophys. Res. Oceans 2018, 123, 6653–6669. [Google Scholar] [CrossRef]
- Cao, H.; Fox-Kemper, B.; Jing, Z. Submesoscale eddies in the upper ocean of the Kuroshio Extension from high-resolution simulation: Energy budget. J. Phys. Oceanogr. 2021, 51, 2181–2201. [Google Scholar] [CrossRef]
- Chen, R.; Gille, S.T.; McClean, J.L. Isopycnal eddy mixing across the Kuroshio Extension: Stable versus unstable states in an eddying model. J. Geophys. Res. Oceans 2017, 122, 4329–4345. [Google Scholar] [CrossRef]
- Martin, P.E.; Arbic, B.K.; Hogg, A.M.; Kiss, A.E.; Munroe, J.R.; Blundell, J.R. Frequency-domain analysis of the energy budget in an idealized coupled ocean–atmosphere model. J. Clim. 2020, 33, 707–726. [Google Scholar] [CrossRef]
- Taburet, G.; Sanchez-Roman, A.; Ballarotta, M.; Pujol, M.I.; Legeais, J.F.; Fournier, F.; Faugere, Y.; Dibarboure, G. DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 2019, 15, 1207–1224. [Google Scholar] [CrossRef]
- Butterworth, S. On the theory of filter amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Manal, K.; Rose, W. A general solution for the time delay introduced by a low-pass Butterworth digital filter: An application to musculoskeletal modeling. J. Biomech. 2007, 40, 678–681. [Google Scholar] [CrossRef]
- Shouran, M.; Elgamli, E. Design and implementation of Butterworth filter. Int. J. Innov. Res. Sci. Eng. Technol. 2020, 9, 7975–7983. [Google Scholar]
- Rai, S.; Hecht, M.; Maltrud, M.; Aluie, H. Scale of oceanic eddy killing by wind from global satellite observations. Sci. Adv. 2021, 7, eabf4920. [Google Scholar] [CrossRef]
- Cronin, M. Eddy-mean flow interaction in the Gulf Stream at 68 W. Part II: Eddy forcing on the time-mean flow. J. Phys. Oceanogr. 1996, 26, 2132–2151. [Google Scholar] [CrossRef]
- Chen, R.; Flierl, G.R.; Wunsch, C. A description of local and nonlocal eddy–mean flow interaction in a global eddy-permitting state estimate. J. Phys. Oceanogr. 2014, 44, 2336–2352. [Google Scholar] [CrossRef]
- Kang, D.; Curchitser, E.N. Energetics of eddy–mean flow interactions in the Gulf Stream region. J. Phys. Oceanogr. 2015, 45, 1103–1120. [Google Scholar] [CrossRef]
- Chen, R.; Yang, Y.; Geng, Q.; Stewart, A.; Flierl, G.; Wang, J. Diagnostic framework linking eddy flux ellipse with eddy-mean energy exchange. Ocean-Land-Atmos. Res. 2024, 3, olar.0072. [Google Scholar] [CrossRef]
- Storch, J.-S.V.; Eden, C.; Fast, I.; Haak, H.; Hernández-Deckers, D.; Maier-Reimer, E.; Marotzke, J.; Stammer, D. An estimate of the Lorenz energy cycle for the world ocean based on the STORM/NCEP Simulation. J. Phys. Oceanogr. 2012, 42, 2185–2205. [Google Scholar] [CrossRef]
- Waterman, S.; Jayne, S.R. Eddy-mean flow interactions in the along-stream development of a western boundary current jet: An idealized model study. J. Phys. Oceanogr. 2011, 41, 682–707. [Google Scholar] [CrossRef]
- O’Rourke, A.K.; Arbic, B.K.; Griffies, S.M. Frequency-domain analysis of atmospherically forced versus intrinsic ocean surface kinetic energy variability in GFDL’s CM2-O model hierarchy. J. Clim. 2018, 31, 1789–1810. [Google Scholar] [CrossRef]
- Liang, X.S. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef]
- Liang, X.S. Normalizing the causality between time series. Phys. Rev. E 2015, 92, 022126. [Google Scholar] [CrossRef]
- Yang, H.; Chang, P.; Qiu, B.; Zhang, Q.; Wu, L.; Chen, Z.; Wang, H. Mesoscale air–sea interaction and its role in eddy energy dissipation in the Kuroshio Extension. J. Clim. 2019, 32, 8659–8676. [Google Scholar] [CrossRef]

| Approach | Mathematical Form of Spectral KE Flux |
|---|---|
| where | |
| where |
| Approach | Mathematical Form of Spectral KE Flux |
|---|---|
| where | |
| where |
| Kuroshio Extension | Western Part | Eastern Part | |
|---|---|---|---|
| (10−6 W/m3) | 8.36 | 17.27 | 0.87 |
| (10−6 W/m3) | 6.40 | 11.81 | 0.99 |
| Low Frequency | High Frequency | |||
|---|---|---|---|---|
| With Annual Cycle | Without Annual Cycle | With Annual Cycle | Without Annual Cycle | |
| Correlation coefficients | 0.09 ± 0.03 [√] | 0.09 ± 0.03 [√] | 0.05 ± 0.02 [√] | 0.07 ± 0.02 [√] |
| 0.02 ± 0.06 | 0.02 ± 0.06 | 0.07 ± 0.03 [√] | 0.04 ± 0.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, Q.; Su, X.; Chen, R.; Huang, G.; Shi, W. Kinetic Energy Cascade in the Frequency Domain from Satellite Products. Remote Sens. 2025, 17, 877. https://doi.org/10.3390/rs17050877
Geng Q, Su X, Chen R, Huang G, Shi W. Kinetic Energy Cascade in the Frequency Domain from Satellite Products. Remote Sensing. 2025; 17(5):877. https://doi.org/10.3390/rs17050877
Chicago/Turabian StyleGeng, Qianqian, Xin Su, Ru Chen, Gang Huang, and Wanli Shi. 2025. "Kinetic Energy Cascade in the Frequency Domain from Satellite Products" Remote Sensing 17, no. 5: 877. https://doi.org/10.3390/rs17050877
APA StyleGeng, Q., Su, X., Chen, R., Huang, G., & Shi, W. (2025). Kinetic Energy Cascade in the Frequency Domain from Satellite Products. Remote Sensing, 17(5), 877. https://doi.org/10.3390/rs17050877








