Quantifying the Accuracy of UAS-Lidar Individual Tree Detection Methods Across Height and Diameter at Breast Height Sizes in Complex Temperate Forests
Abstract
:1. Introduction
2. Materials and Methods
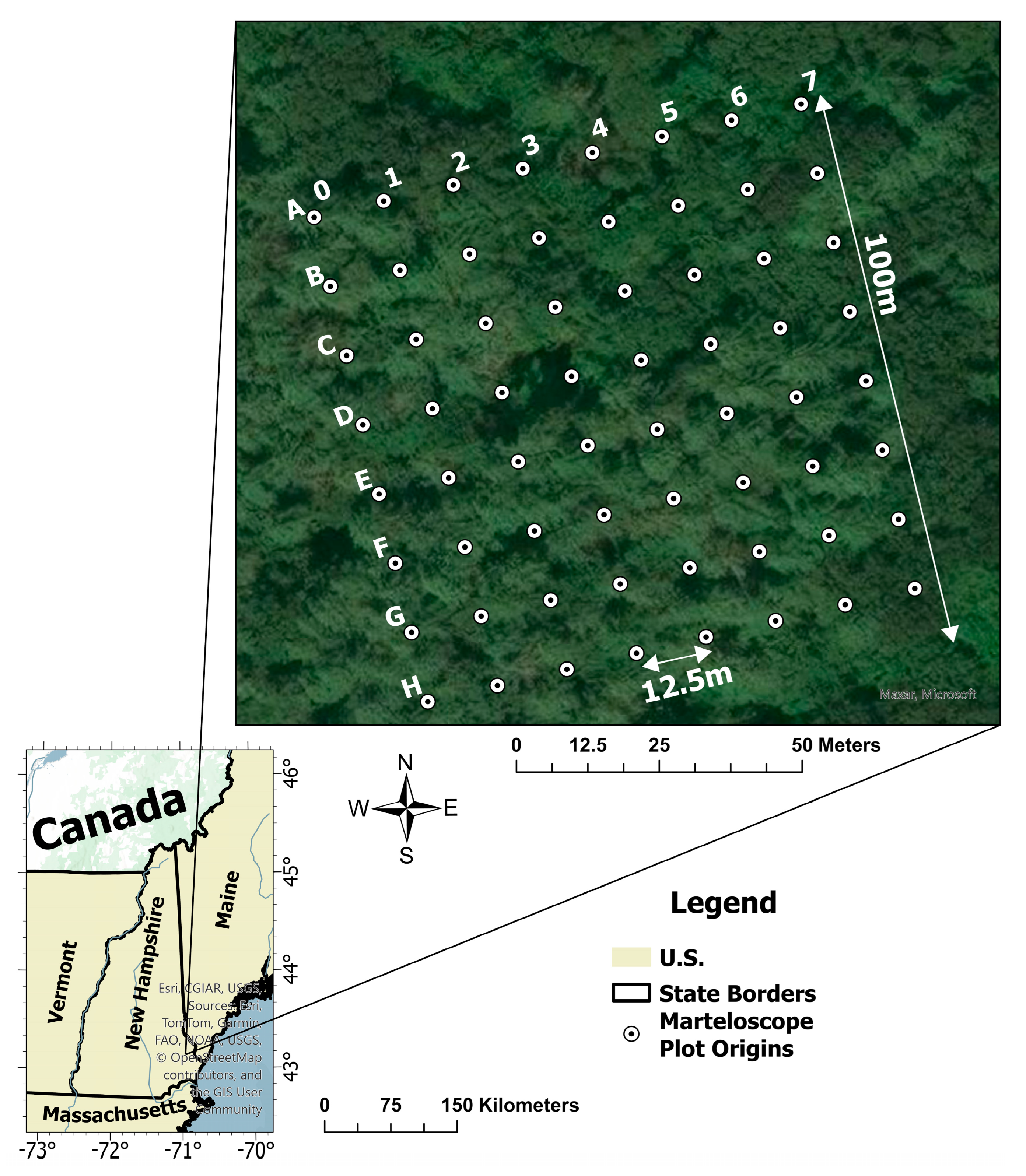
2.1. Study Sites
2.2. Reference Data
2.3. UAS-Lidar Data Collection
2.4. UAS-Lidar Data Pre-Processing
2.5. Tree Detection Methods
2.6. Individual Tree Detection Performance
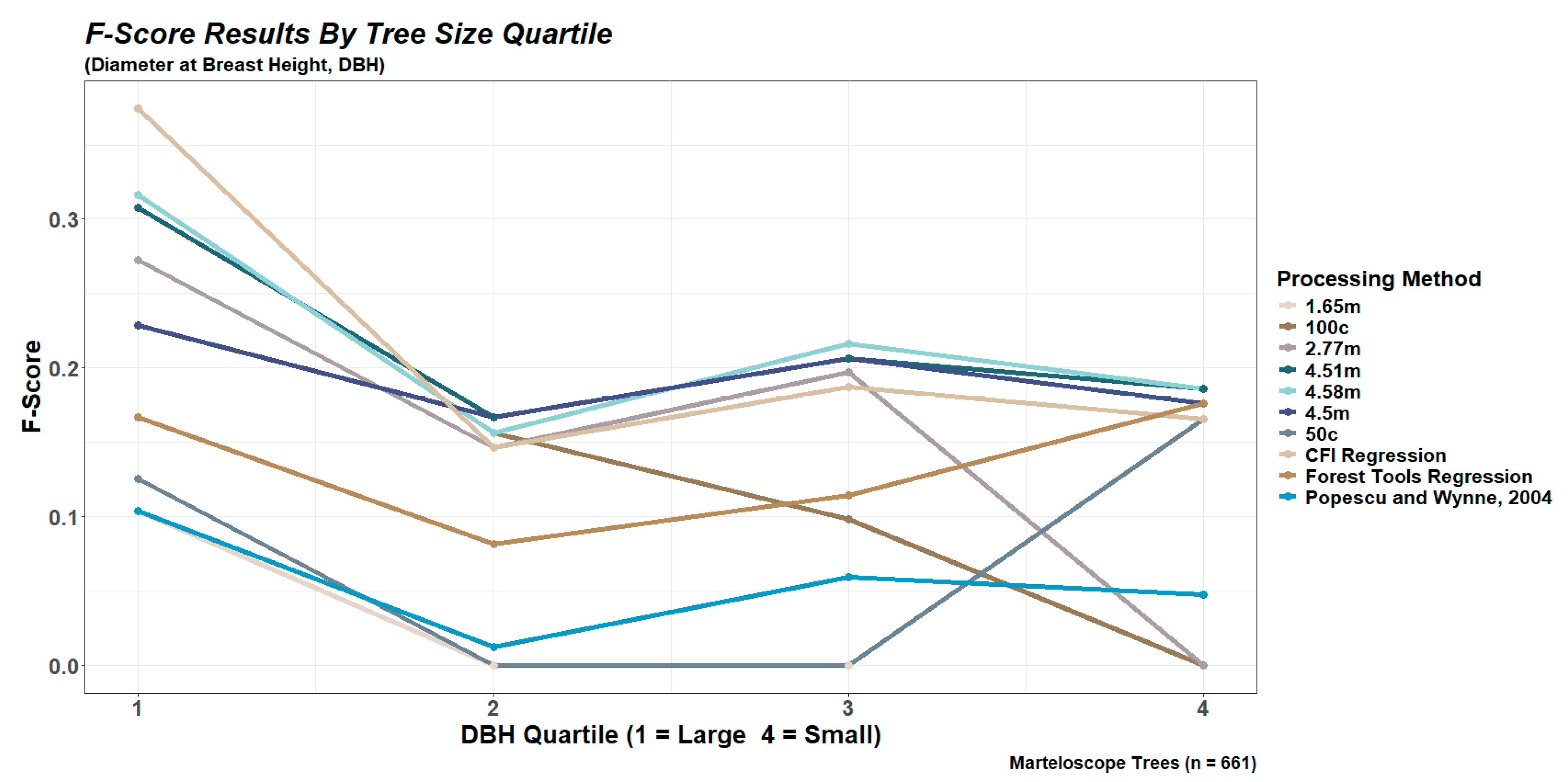
2.6.1. Performance Based on Tree Size Quartiles
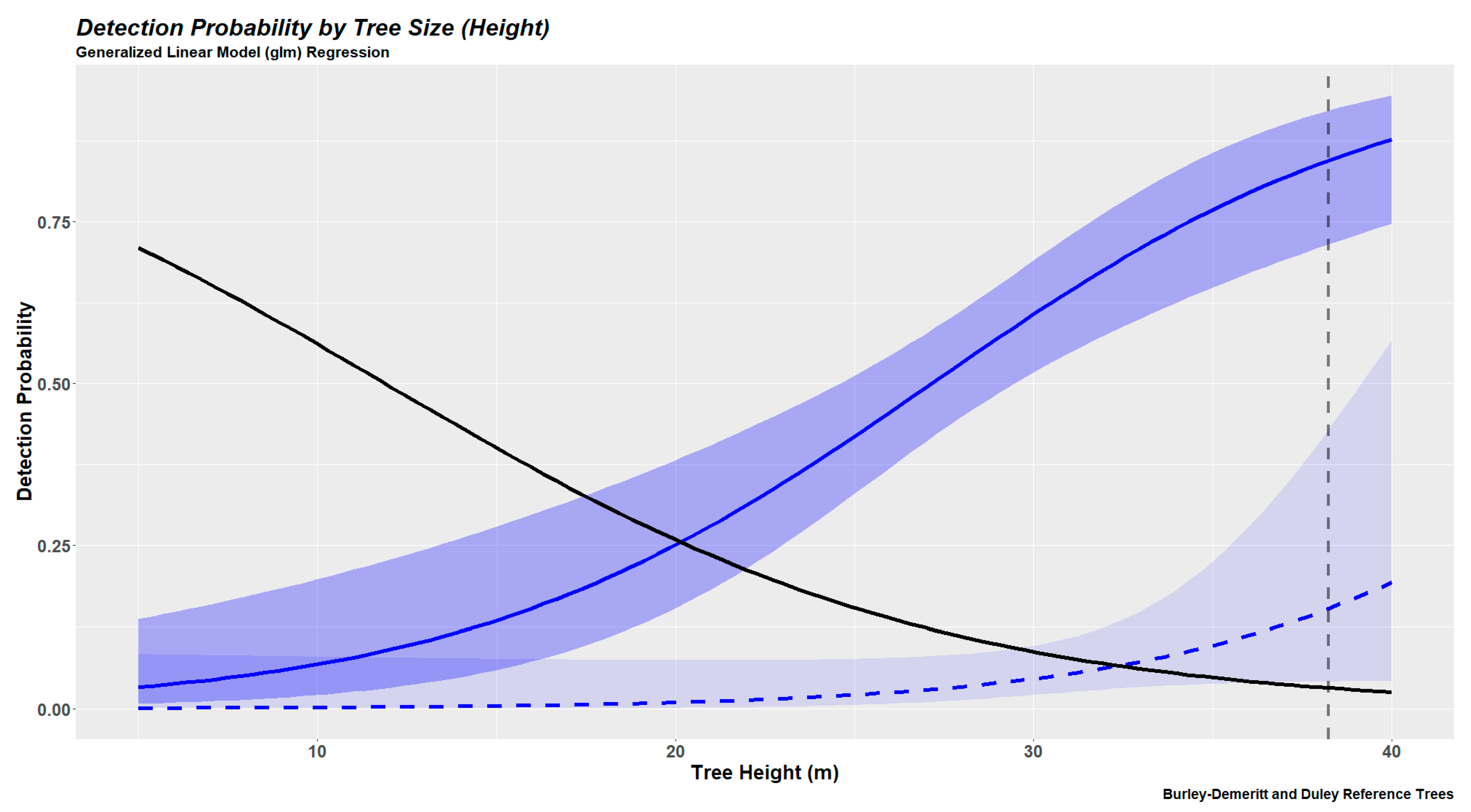
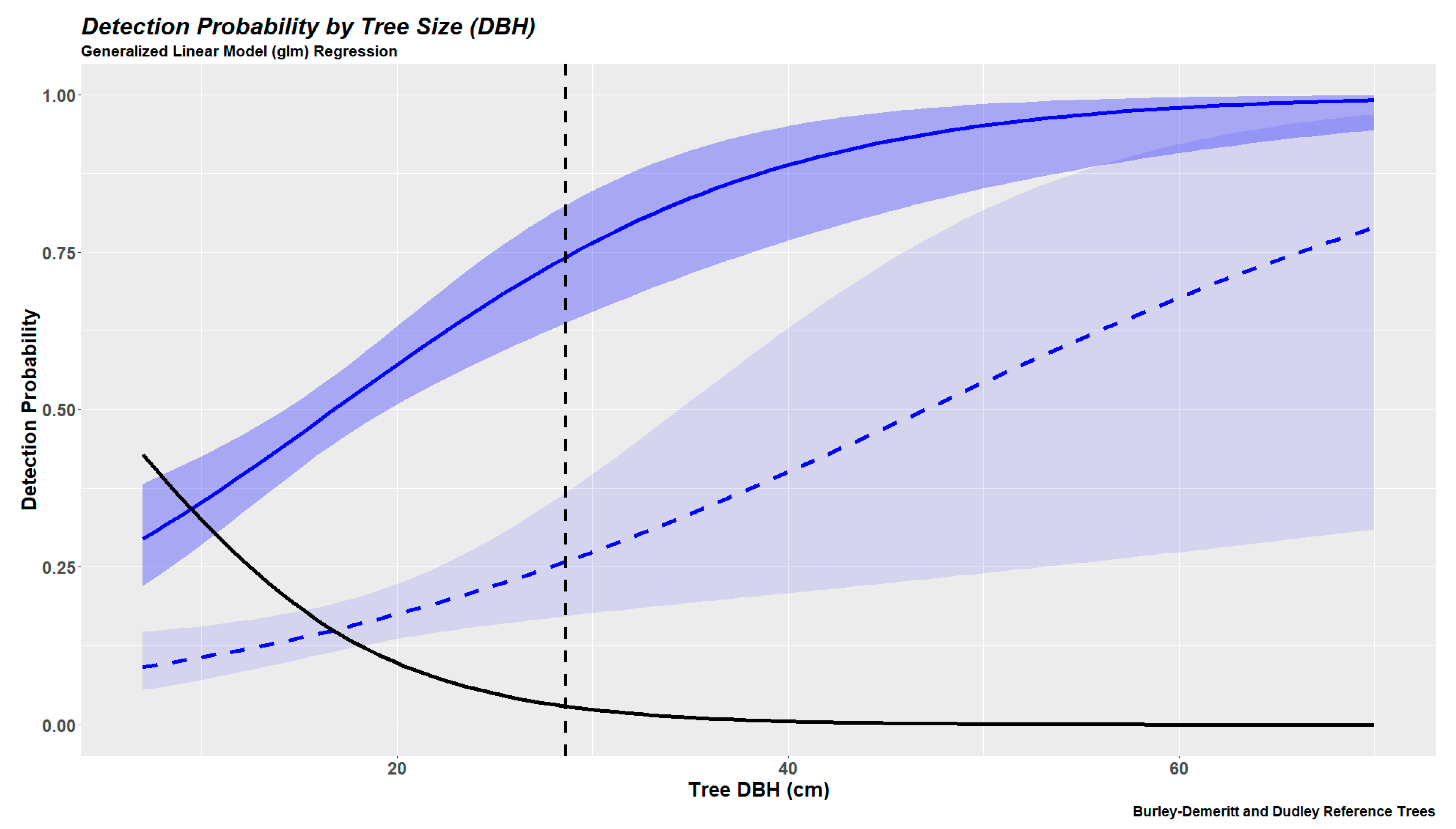
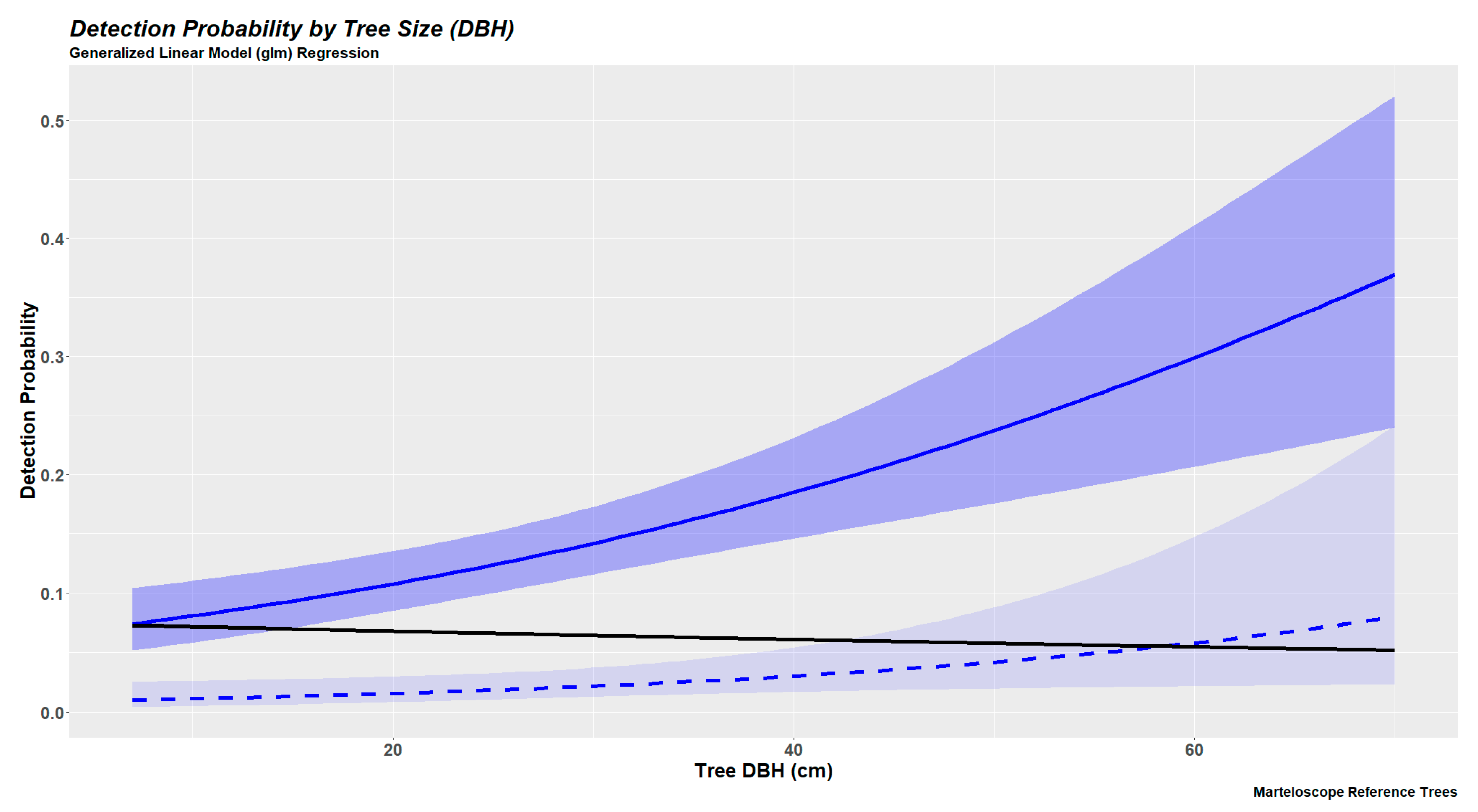
2.6.2. Tree Detection Probabilities Based on Generalized Linear Modeling
3. Results
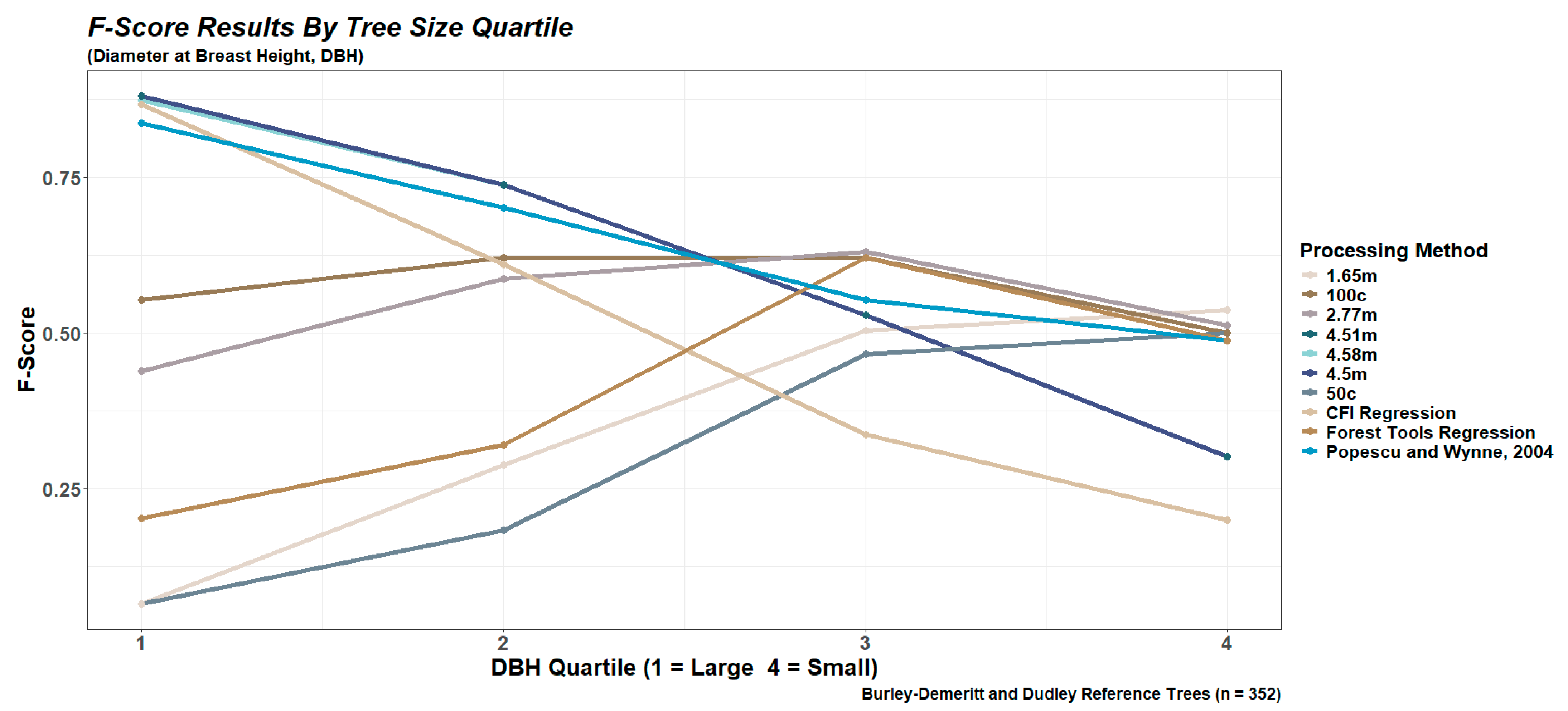
3.1. Tree Detection for the CFI Plots
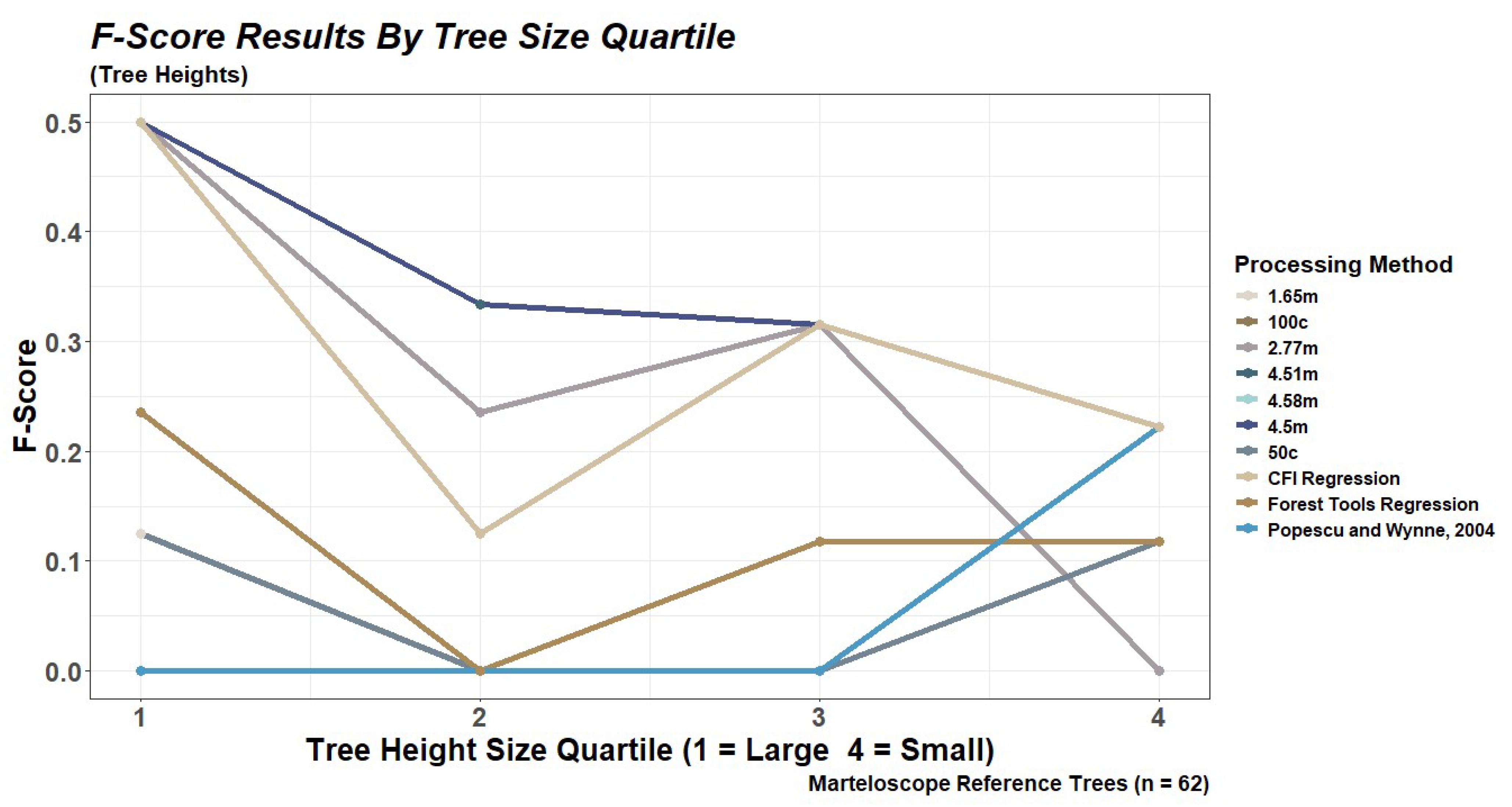
3.2. Tree Detection for the Marteloscope Plot
3.3. Tree Detection as a Continuous Variable (Generalized Linear Models)
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Method | Size 1 | Size 2 | Size 3 | Size 4 | r | p | F-Score |
|---|---|---|---|---|---|---|---|
| FW: 50 cells | 0 39 1 | 5 33 2 | 6 28 7 | 11 24 6 | 0.5789 | 0.1507 | 0.2391 |
| FW: 100 cells | 12 23 5 | 13 17 10 | 18 10 13 | 17 1 23 | 0.5405 | 0.5405 | 0.5405 |
| FW: 1.65 m | 1 38 1 | 7 31 2 | 9 25 7 | 13 21 7 | 0.6383 | 0.2069 | 0.3125 |
| FW: 4.5 m | 30 4 6 | 24 2 14 | 21 0 20 | 19 1 21 | 0.6065 | 0.9307 | 0.7344 |
| FW: 2.77 m | 12 26 2 | 11 20 9 | 17 12 12 | 18 4 19 | 0.5800 | 0.4833 | 0.5273 |
| FW: 4.58 m | 30 4 6 | 24 2 14 | 21 0 20 | 9 1 31 | 0.5419 | 0.9231 | 0.6829 |
| FW: 4.51 m | 30 4 6 | 24 2 14 | 21 0 20 | 9 1 31 | 0.5419 | 0.9231 | 0.6829 |
| Popescu Mixed Forests | 27 9 4 | 21 8 11 | 16 9 16 | 18 5 18 | 0.6260 | 0.7257 | 0.6721 |
| Forest Inventory Regression | 29 0 11 | 18 0 22 | 16 0 25 | 4 0 37 | 0.4136 | 1.00 | 0.5852 |
| ForestTools Regression | 2 37 1 | 9 27 4 | 9 26 6 | 11 24 6 | 0.6458 | 0.2138 | 0.3212 |
| Method | Size 1 | Size 2 | Size 3 | Size 4 | r | p | F-Score |
|---|---|---|---|---|---|---|---|
| FW: 50 cells | 3 84 2 | 9 74 6 | 27 51 113 | 30 38 22 | 0.627 | 0.218 | 0.324 |
| FW: 100 cells | 34 50 5 | 40 27 22 | 40 11 38 | 30 1 59 | 0.537 | 0.618 | 0.575 |
| FW: 1.65 m | 3 84 2 | 15 68 6 | 30 48 11 | 33 31 26 | 0.643 | 0.260 | 0.370 |
| FW: 4.5 m | 70 10 9 | 52 2 35 | 32 1 56 | 16 0 74 | 0.494 | 0.929 | 0.645 |
| FW: 2.77 m | 25 61 3 | 37 34 18 | 41 16 32 | 31 5 54 | 0.556 | 0.536 | 0.546 |
| FW: 4.58 m | 69 10 10 | 52 2 35 | 32 1 56 | 16 0 74 | 0.491 | 0.929 | 0.643 |
| FW: 4.51 m | 70 10 9 | 52 2 35 | 32 1 56 | 16 0 74 | 0.494 | 0.929 | 0.645 |
| Popescu Mixed Forests | 64 20 5 | 48 16 25 | 34 11 44 | 29 8 53 | 0.579 | 0.761 | 0.658 |
| Forest Inventory Regression | 68 0 21 | 39 0 50 | 18 0 71 | 10 0 80 | 0.378 | 1.00 | 0.549 |
| ForestTools Regression | 10 78 1 | 17 64 8 | 40 38 11 | 29 38 23 | 0.691 | 0.306 | 0.424 |
| Method | Size 1 | Size 2 | Size 3 | Size 4 | r | p | F-Score |
|---|---|---|---|---|---|---|---|
| FW: 50 cells | 1 7 7 | 0 3 12 | 0 4 12 | 1 3 12 | 0.044 | 0.105 | 0.063 |
| FW: 100 cells | 5 2 8 | 2 0 13 | 3 0 13 | 0 3 13 | 0.175 | 0.667 | 0.278 |
| FW: 1.65 m | 1 7 7 | 0 3 12 | 0 4 12 | 1 3 12 | 0.044 | 0.105 | 0.063 |
| FW: 4.5 m | 5 1 9 | 3 0 12 | 3 0 13 | 2 1 13 | 0.217 | 0.867 | 0.347 |
| FW: 2.77 m | 5 2 8 | 2 1 12 | 3 1 12 | 2 1 13 | 0.182 | 0.588 | 0.278 |
| FW: 4.58 m | 5 1 9 | 3 0 12 | 3 0 13 | 0 3 13 | 0.217 | 0.867 | 0.347 |
| FW: 4.51 m | 5 1 9 | 3 0 12 | 3 0 13 | 2 1 13 | 0.217 | 0.867 | 0.347 |
| Popescu Mixed Forests | 0 0 0 | 0 0 0 | 0 0 0 | 2 0 14 | 0.125 | 1.000 | 0.222 |
| Forest Inventory Regression | 5 0 10 | 1 0 14 | 3 0 13 | 2 0 14 | 0.177 | 1.000 | 0.301 |
| ForestTools Regression | 2 6 7 | 0 3 12 | 1 4 11 | 1 3 12 | 0.087 | 0.200 | 0.121 |
| Method | Size 1 | Size 2 | Size 3 | Size 4 | r | p | F-Score |
|---|---|---|---|---|---|---|---|
| FW: 50 cells | 11 62 92 | 7 37 121 | 9 35 121 | 15 30 121 | 0.085 | 0.204 | 0.119 |
| FW: 100 cells | 31 29 105 | 14 16 135 | 8 11 136 | 14 12 140 | 0.115 | 0.496 | 0.187 |
| FW: 1.65 m | 9 64 92 | 8 37 120 | 9 35 121 | 15 32 119 | 0.083 | 0.196 | 0.117 |
| FW: 4.5 m | 20 23 112 | 15 10 140 | 19 8 138 | 16 8 142 | 0.116 | 0.588 | 0.194 |
| FW: 2.77 m | 26 36 103 | 13 22 130 | 18 16 131 | 12 18 136 | 0.121 | 0.429 | 0.189 |
| FW: 4.58 m | 31 22 112 | 14 10 141 | 20 7 138 | 17 7 142 | 0.133 | 0.641 | 0.221 |
| FW: 4.51 m | 30 23 112 | 15 10 140 | 19 8 138 | 17 7 142 | 0.132 | 0.628 | 0.218 |
| Popescu Mixed Forests | 9 1 155 | 1 0 164 | 5 0 160 | 4 1 161 | 0.029 | 0.905 | 0.056 |
| Forest Inventory Regression | 38 6 121 | 13 3 149 | 17 1 147 | 15 3 148 | 0.128 | 0.865 | 0.223 |
| ForestTools Regression | 15 57 93 | 7 36 122 | 10 33 122 | 16 28 122 | 0.095 | 0.238 | 0.135 |
References
- Kershaw, J.A.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Burkhart, H.E.; Avery, T.E.; Bullock, B.P. Forest Measurements, 6th ed.; Waveland Press, INC: Long Grove, IL, USA, 2019; ISBN 1-4786-3618-1. [Google Scholar]
- del Río, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N.; et al. Characterization of Mixed Forests. In Dynamics, Silviculture and Management of Mixed Forests; Bravo-Oviedo, A., Pretzsch, H., del Río, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 27–71. ISBN 978-3-319-91953-9. [Google Scholar]
- Corte, A.P.D.; Souza, D.V.; Rex, F.E.; Sanquetta, C.R.; Mohan, M.; Silva, C.A.; Zambrano, A.M.A.; Prata, G.; Alves de Almeida, D.R.; Trautenmüller, J.W.; et al. Forest Inventory with High-Density UAV-Lidar: Machine Learning Approaches for Predicting Individual Tree Attributes. Comput. Electron. Agric. 2020, 179, 105815. [Google Scholar] [CrossRef]
- Spurr, S.H. Aerial Photographs in Forestry, 1st ed.; Ronald Press, Co.: New York, NY, USA, 1948; 340p. [Google Scholar]
- Avery, T.E. Forester’s Guide To Aerial Photo Interpretation; USDA Forest Service: Washington, DC, USA, 1969; 40p. [Google Scholar]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation, 7th ed.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2015; ISBN 978-1-118-34328-9. [Google Scholar]
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A Comparison of Lidar, Radar, and Field Measurements of Canopy Height in Pine and Hardwood Forests of Southeastern North America. For. Ecol. Manag. 2009, 257, 1136–1147. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Karjalainen, M.; Karila, K.; Kaasalainen, S.; Honkavaara, E.; Hyyppä, J. Forest Inventory Attribute Estimation Using Airborne Laser Scanning, Aerial Stereo Imagery, Radargrammetry and Interferometry-Finnish Experiences of the 3d Techniques. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 63–69. [Google Scholar] [CrossRef]
- Chen, Y.; Hakala, T.; Karjalainen, M.; Feng, Z.; Tang, J.; Litkey, P.; Kukko, A.; Jaakkola, A.; Hyyppä, J. UAV -Borne Profiling Radar for Forest Research. Remote Sens. 2017, 9, 58. [Google Scholar] [CrossRef]
- Vierling, K.T.; Vierling, L.A.; Gould, W.A.; Martinuzzi, S.; Clawges, R.M. Lidar: Shedding New Light on Habitat Characterization and Modeling. Front. Ecol. Environ. 2008, 6, 90–98. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using Lidar and Multispectral Data Fusion with Local Filtering and Variable Window Size for Estimating Tree Height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Su, Y.; Ma, Q.; Guo, Q. Fine-Resolution Forest Tree Height Estimation across the Sierra Nevada through the Integration of Spaceborne LiDAR, Airborne LiDAR, and Optical Imagery. Int. J. Digit. Earth 2017, 10, 307–323. [Google Scholar] [CrossRef]
- Rosette, J.; Suarez, J.; North, P.; Los, S. Forestry Applications for Satellite Lidar Remote Sensing. Photogramm. Eng. Remote Sens. 2011, 77, 271–279. [Google Scholar] [CrossRef]
- Renslow, M. Manual of Airborne Topographic Lidar; ASPRS: Bethesda, MD, USA, 2013; ISBN 1-57083-097-5. [Google Scholar]
- Vauhkonen, J.; Maltamo, M.; McRoberts, R.E.; Næsset, E. Introduction to Forestry Applications of Airborne Laser Scanning. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 1–16. ISBN 978-94-017-8663-8. [Google Scholar]
- Donager, J.J.; Sankey, T.T.; Sankey, J.B.; Sanchez Meador, A.J.; Springer, A.E.; Bailey, J.D. Examining Forest Structure with Terrestrial Lidar: Suggestions and Novel Techniques Based on Comparisons Between Scanners and Forest Treatments. Earth Space Sci. 2018, 5, 753–776. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The Use of Terrestrial LiDAR Technology in Forest Science: Application Fields, Benefits and Challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Di Stefano, F.; Chiappini, S.; Gorreja, A.; Balestra, M.; Pierdicca, R. Mobile 3D Scan LiDAR: A Literature Review. Geomat. Nat. Hazards Risk 2021, 12, 2387–2429. [Google Scholar] [CrossRef]
- Heo, H.K.; Lee, D.K.; Park, J.H.; Thorne, J.H. Estimating the Heights and Diameters at Breast Height of Trees in an Urban Park and along a Street Using Mobile LiDAR. Landsc. Ecol. Eng. 2019, 15, 253–263. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR System with Application to Forest Inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2021, 13, 77. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On Promoting the Use of Lidar Systems in Forest Ecosystem Research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Pilarska, M.; Ostrowski, W.; Bakuła, K.; Górski, K.; Kurczyński, Z. The Potential of Light Laser Scanners Developed for Unmanned Aerial Vehicles—The Review and Accuracy. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2016, 42, 87–95. [Google Scholar] [CrossRef]
- Nitoslawski, S.A.; Wong-Stevens, K.; Steenberg, J.W.N.; Witherspoon, K.; Nesbitt, L.; Konijnendijk van den Bosch, C.C. The Digital Forest: Mapping a Decade of Knowledge on Technological Applications for Forest Ecosystems. Earths Future 2021, 9, 1–28. [Google Scholar] [CrossRef]
- Corte, A.P.D.; Rex, F.E.; de Almeida, D.R.A.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Zambrano, A.M.A.; da Cunha Neto, E.M.; Veras, H.F.P.; et al. Measuring Individual Tree Diameter and Height Using Gatoreye High-Density UAV-Lidar in an Integrated Crop-Livestock-Forest System. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR Derived Canopy Height and DBH with Terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Alsadik, B.; Remondino, F. Flight Planning for LiDAR-Based UAS Mapping Applications. ISPRS Int. J. Geoinf. 2020, 9, 378. [Google Scholar] [CrossRef]
- Fraser, B.T.; Bunyon, C.L.; Reny, S.; Lopez, I.S.; Congalton, R.G. Analysis of Unmanned Aerial System (UAS) Sensor Data for Natural Resource Applications: A Review. Geographies 2022, 2, 303–340. [Google Scholar] [CrossRef]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Estimating Forest Structural Attributes Using UAV-LiDAR Data in Ginkgo Plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Zhou, X.; Ma, K.; Sun, H.; Li, C.; Wang, Y. Estimation of Forest Stand Volume in Coniferous Plantation from Individual Tree Segmentation Aspect Using UAV-LiDAR. Remote Sens. 2024, 16, 2736. [Google Scholar] [CrossRef]
- Liu, L.; Lim, S.; Shen, X.; Yebra, M. A Hybrid Method for Segmenting Individual Trees from Airborne Lidar Data. Comput. Electron. Agric. 2019, 163, 104871. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation-Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Fraser, B.T.; Congalton, R.G. Estimating Primary Forest Attributes and Rare Community Characteristics Using Unmanned Aerial Systems (UAS): An Enrichment of Conventional Forest Inventories. Remote Sens. 2021, 13, 2971. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual Mangrove Tree Measurement Using UAV-Based LiDAR Data: Possibilities and Challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- You, H.; Liu, Y.; Lei, P.; Qin, Z.; You, Q. Segmentation of Individual Mangrove Trees Using UAV-Based LiDAR Data. Ecol. Inform. 2023, 77, 102200. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Pyörälä, J.; Lehtomäki, M.; Yu, X.; Kaartinen, H.; Kukko, A.; Honkavaara, E.; Issaoui, A.E.I.; Nevalainen, O.; et al. Forest in Situ Observations Using Unmanned Aerial Vehicle as an Alternative of Terrestrial Measurements. For. Ecosyst. 2019, 6, 20. [Google Scholar] [CrossRef]
- Braun, E.L. Deciduous Forests of Eastern North America, 1st ed.; Echo Point Books & Media, LLC: Brattleboro, VT, USA, 2023; ISBN 1648373119. [Google Scholar]
- Yahner, R.H. Eastern Deciduous Forest, 2nd ed.; Univ of Minnesota Press: Minneapolis, MN, USA, 2000; ISBN 9780816633609. [Google Scholar]
- Puliti, S.; Granhus, A. Drone Data for Decision Making in Regeneration Forests: From Raw Data to Actionable Insights. J. Unmanned Veh. Syst. 2021, 9, 45–58. [Google Scholar] [CrossRef]
- Zaforemska, A.; Xiao, W.; Gaulton, R. Individual Tree Detection from Uav Lidar Data in a Mixed Species Woodland. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2019, 42, 657–663. [Google Scholar] [CrossRef]
- Gu, J.; Grybas, H.; Congalton, R.G. A Comparison of Forest Tree Crown Delineation from Unmanned Aerial Imagery Using Canopy Height Models vs. Spectral Lightness. Forests 2020, 11, 605. [Google Scholar] [CrossRef]
- Reny, S.A. The Estimation of Forest Inventory Biometrics Using UAS-Lidar. Master’s Thesis, University of New Hampshire, Durham, NH, USA, 2023. [Google Scholar]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating Tree Detection and Segmentation Routines on Very High Resolution UAV LiDAR Ata. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Iheaturu, C.J.; Hepner, S.; Batchelor, J.L.; Agonvonon, G.A.; Akinyemi, F.O.; Wingate, V.R.; Ifejika Speranza, C. Integrating UAV LiDAR and Multispectral Data to Assess Forest Status and Map Disturbance Severity in a West African Forest Patch. Ecol. Inform. 2024, 84, 102876. [Google Scholar] [CrossRef]
- Deng, S.; Jing, S.; Zhao, H. A Hybrid Method for Individual Tree Detection in Broadleaf Forests Based on UAV-LiDAR Data and Multistage 3D Structure Analysis. Forests 2024, 15, 1043. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Martins, G.B.; de Almeida, T.M.H.; da Silva Ribeiro, R.; da Veiga Júnior, V.F.; da Silva Rocha Paz, I.; de Siqueira, M.F.; Kurtz, B.C. Estimating Aboveground Biomass of Tropical Urban Forests with UAV-Borne Hyperspectral and LiDAR Data. Urban. For. Urban. Green. 2024, 96, 128362. [Google Scholar] [CrossRef]
- Kanaskie, C.R.; Routhier, M.R.; Fraser, B.T.; Congalton, R.G.; Ayres, M.P.; Garnas, J.R. Early Detection of Southern Pine Beetle Attack by UAV-Collected 2 Multispectral Imagery. Remote Sens. 2024, 16, 2608. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.N.; et al. Individual Tree Detection and Classification with UAV-Based Photogrammetric Point Clouds and Hyperspectral Imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Hirschmugl, M.; Ofner, M.; Raggam, J.; Schardt, M. Single Tree Detection in Very High Resolution Remote Sensing Data. Remote Sens. Environ. 2007, 110, 533–544. [Google Scholar] [CrossRef]
- Liu, Y.; You, H.; Tang, X.; You, Q.; Huang, Y.; Chen, J. Study on Individual Tree Segmentation of Different Tree Species Using Different Segmentation Algorithms Based on 3D UAV Data. Forests 2023, 14, 1327. [Google Scholar] [CrossRef]
- Rollinson, C.R.; Alexander, M.R.; Dye, A.W.; Moore, D.J.P.; Pederson, N.; Trouet, V. Climate Sensitivity of Understory Trees Differs from Overstory Trees in Temperate Mesic Forests. Ecology 2021, 102, e03264. [Google Scholar] [CrossRef] [PubMed]
- Fraser, B.; Congalton, R.G. A Comparison of Methods for Determining Forest Composition from High-Spatial Resolution Remotely Sensed Imagery. Forests 2021, 12, 1290. [Google Scholar] [CrossRef]
- de Oliveira, L.F.R.; Lassiter, H.A.; Wilkinson, B.; Whitley, T.; Ifju, P.; Logan, S.R.; Peter, G.F.; Vogel, J.G.; Martin, T.A. Moving to Automated Tree Inventory: Comparison of Uas-Derived Lidar and Photogrammetric Data with Manual Ground Estimates. Remote Sens. 2021, 13, 72. [Google Scholar] [CrossRef]
- Eisenhaure, S. Burley-Demeritt and Dudley Lot Management and Operations Plan Original 2010—Update 2016; Office of Woodlands and Natural Areas, Univeristy of New Hampshire: Durham, NH, USA, 2016. [Google Scholar]
- Eisenhaure, S. Assessment of Natural Resources and Uses at the Woodman Horticultural Farm; Office of Woodlands and Natural Areas, Univeristy of New Hampshire: Durham, NH, USA, 2013. [Google Scholar]
- EOS Arrow 100 RTK GNSS. Available online: https://eos-gnss.com/product/arrow-series/arrow-200/?gclid=Cj0KCQjw2tCGBhCLARIsABJGmZ47-nIPNrAuu7Xobgf3P0HGlV4mMLHHWZz25lyHM6UuI_pPCu7b2gMaAukeEALw_wcB (accessed on 10 March 2025).
- Marshall, D.D.; Iles, K.; Bell, J.F. Using a Large-Angle Gauge to Select Trees for Measurement in Variable Plot Sampling. Can. J. For. Res. 2004, 34, 840–845. [Google Scholar] [CrossRef]
- Derks, J.; Krumm, F.; Krau, D. GUIDELINES FOR ESTABLISHING I+ Marteloscopes; European Forest Institue: Joensuu, Finland, 2020. [Google Scholar]
- Cosyns, H.; Joa, B.; Mikoleit, R.; Krumm, F.; Schuck, A.; Winkel, G.; Schulz, T. Resolving the Trade-off between Production and Biodiversity in Integrated Forest Management: Comparing Selection Practices of Foresters and Conservationists. Biodivers. Conserv. 2020, 29, 3717–3737. [Google Scholar] [CrossRef]
- O’Brien, L.; Derks, J.; Schuck, A. The Use of Marteloscopes in Science; A Review of Past Research and Suggestions for Further Application; European Forest Institue: Joensuu, Finland, 2022. [Google Scholar]
- Derks, J.; Schuck, A.; O’Brien, L. Forestry Training WITH I+ MARTELOSCOPES; Integrate Network; European Forest Institue: Joensuu, Finland, 2022. [Google Scholar]
- Schuck, A.; Krumm, F.; Kraus, D. Integrate+ Marteloscopes Description of Parameters and Assessment Procedures; European Forest Institue: Joensuu, Finland, 2015. [Google Scholar]
- Stroner, M.; Urban, R.; Linkova, L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUS L1 Scanner. Remote Sens. 2021, 13, 4811. [Google Scholar] [CrossRef]
- Fraser, B.T.; Congalton, R.G. Issues in Unmanned Aerial Systems (UAS) Data Collection of Complex Forest Environments. Remote Sens. 2018, 10, 908. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Goodbody, T.R.H.; Tompalski, P. The LidR Package. Available online: https://r-lidar.github.io/lidRbook/ (accessed on 12 June 2024).
- Roussel, J.; Auty, D. Airborne LiDAR Data Manipulation and Visualization for Forestry Applications; R Package Version 4.2.0. 2024. Available online: https://cran.r-project.org/package=lidR (accessed on 5 January 2025).
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Olea, R.A. Optimal Contour Mapping Using Universal Kriging. J. Geophys. Res. 1974, 79, 695–702. [Google Scholar] [CrossRef]
- Plowright, A.; Roussel, J.-R. ForestTools: Tools for Analyzing Remote Sensing Forest Data. 2024. Available online: https://cran.r-project.org/web/packages/ForestTools/index.html (accessed on 5 January 2025).
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual Tree Detection from Unmanned Aerial Vehicle (UAV) Derived Canopy Height Model in an Open Canopy Mixed Conifer Forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A Review of Methods for Automatic Individual Tree-Crown Detection and Delineation from Passive Remote Sensing. Int. J. Remote Sens. 2011, 32, 4725–4747. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Goos, G.; Hartmanis, J.; Van, J.; Board, L.E.; Hutchison, D.; Kanade, T.; Kittler, J.; Kleinberg, J.M.; Mattern, F.; Zurich, E.; et al. LNCS 3408—Advances in Information Retrieval. In Proceedings of the Advances in Information Retrieval; Losada, D.E., Fernandez-Luna, J.M., Eds.; Springer: Santiago de Compostela, Spain, 2005; pp. 1–571. [Google Scholar]
- Beucher, S.; Meyer, F. The Morphological Approach to Segmentation: The Watershed Transformation. In Mathematical Morphology in Image Processing; CRC Press: Boca Raton, FL, USA, 1992; p. 552. ISBN 9781315214610. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, Wiley Series in Probability and Statistics; 2nd ed.; Wiley-Interscience Publication: New York, NY, USA, 2000; ISBN 978-0471356325. [Google Scholar]
- Everitt, B.S.; Hothorn, T. A Handbook of Statistical Analyses Using R, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010; ISBN 978-1-4200-7933-3. [Google Scholar]
- UCLA: Statistical Consulting Group Logit Regression|R Data Analysis Examples. Available online: https://stats.oarc.ucla.edu/r/dae/logit-regression/ (accessed on 5 January 2025).
- Kashian, D.M.; Zak, D.R.; Barnes, B.V.; Spurr, S.H. Forest Ecology, 5th ed.; Wiley: Hoboken, NJ, USA, 2023; ISBN 978-1119476085. [Google Scholar]
- Goodbody, T.R.H.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned Aerial Systems for Precision Forest Inventory Purposes: A Review and Case Study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef]
- Taylor, S.E.; McDonald, T.P.; Veal, M.W.; Corley, F.W.; Grift, T.E. Precision Forestry: Operational Tactics for Today and Tomorrow. In Proceedings of the 25th Annual Meeting of the Council of Forest Engineers, Auburn, AL, USA, 16–20 June 2002; Volume 6. [Google Scholar]
- Ehbrecht, M.; Seidel, D.; Annighöfer, P.; Kreft, H.; Köhler, M.; Zemp, D.C.; Puettmann, K.; Nilus, R.; Babweteera, F.; Willim, K.; et al. Global Patterns and Climatic Controls of Forest Structural Complexity. Nat. Commun. 2021, 12, 519. [Google Scholar] [CrossRef]
- Xu, W.; Deng, S.; Liang, D.; Cheng, X. A Crown Morphology-Based Approach to Individual Tree Detection in Subtropical Mixed Broadleaf Urban Forests Using UAV Lidar Data. Remote Sens. 2021, 13, 1278. [Google Scholar] [CrossRef]
- Goldbergs, G.; Maier, S.W.; Levick, S.R.; Edwards, A. Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas. Remote Sens. 2018, 10, 161. [Google Scholar] [CrossRef]
- Torresan, C.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Individual Tree Crown Segmentation in Two-Layered Dense Mixed Forests from Uav Lidar Data. Drones 2020, 4, 10. [Google Scholar] [CrossRef]
- Wielgosz, M.; Puliti, S.; Xiang, B.; Schindler, K.; Astrup, R. SegmentAnyTree: A Sensor and Platform Agnostic Deep Learning Model for Tree Segmentation Using Laser Scanning Data. Remote Sens. Environ. 2024, 313, 114367. [Google Scholar] [CrossRef]
- Minor, C.O. Stem-Crown Diameter Relations in Southern Pine. J. For. 1951, 59, 490–493. [Google Scholar]
- Bonnor, G.M. A Tree Volume Table for Red Pine by Crown Width and Height. For. Chron. 1964, 40, 339–346. [Google Scholar] [CrossRef]
- Wang, C.; Luo, S.; Xi, X.; Nie, S.; Ma, D.; Huang, Y. Influence of Voxel Size on Forest Canopy Height Estimates Using Full-Waveform Airborne LiDAR Data. For. Ecosyst. 2020, 7, 31. [Google Scholar] [CrossRef]
- Pearse, G.D.; Watt, M.S.; Dash, J.P.; Stone, C.; Caccamo, G. Comparison of Models Describing Forest Inventory Attributes Using Standard and Voxel-Based Lidar Predictors across a Range of Pulse Densities. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 341–351. [Google Scholar] [CrossRef]
- Zhang, C.; Song, C.; Zaforemska, A.; Zhang, J.; Gaulton, R.; Dai, W.; Xiao, W. Individual Tree Segmentation from UAS Lidar Data Based on Hierarchical Filtering and Clustering. Int. J. Digit. Earth 2024, 17, 2356124. [Google Scholar] [CrossRef]
- Comba, L.; Biglia, A.; Ricauda Aimonino, D.; Gay, P. Unsupervised Detection of Vineyards by 3D Point-Cloud UAV Photogrammetry for Precision Agriculture. Comput. Electron. Agric. 2018, 155, 84–95. [Google Scholar] [CrossRef]
- Changsalak, P.; Tiansawat, P. Comparison of Seedling Detection and Height Measurement Using 3D Point Cloud Models from Three Software Tools: Applications in Forest Restoration. Environ. Asia 2022, 15, 100–105. [Google Scholar] [CrossRef]
- Tian, J.; Dai, T.; Li, H.; Liao, C.; Teng, W.; Hu, Q.; Ma, W.; Xu, Y. A Novel Tree Height Extraction Approach for Individual Trees by Combining TLS and UAV Image-Based Point Cloud Integration. Forests 2019, 10, 537. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Forest Understory Trees Can Be Segmented Accurately within Sufficiently Dense Airborne Laser Scanning Point Clouds. Sci. Rep. 2017, 7, 6770. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Nemmaoui, A.; Aguilar, M.A.; Peñalver, A. Fusion of Terrestrial Laser Scanning and RPAS Image-Based Point Clouds in Mediterranean Forest Inventories. Dyna 2019, 94, 131–136. [Google Scholar] [CrossRef]
- Prošek, J.; Šímová, P. UAV for Mapping Shrubland Vegetation: Does Fusion of Spectral and Vertical Information Derived from a Single Sensor Increase the Classification Accuracy? Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 151–162. [Google Scholar] [CrossRef]
- Karunaratne, S.; Thomson, A.; Morse-McNabb, E.; Wijesingha, J.; Stayches, D.; Copland, A.; Jacobs, J. The Fusion of Spectral and Structural Datasets Derived from an Airborne Multispectral Sensor for Estimation of Pasture Dry Matter Yield at Paddock Scale with Time. Remote Sens. 2020, 12, 2017. [Google Scholar] [CrossRef]
- Pretzsch, H.; Forrester, D.I.; Bauhaus, J. Mixed-Species Forests: Ecology and Management, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; 653p. [Google Scholar] [CrossRef]




| 4 | 3 | 2 | 1 | |
|---|---|---|---|---|
| Height (m) | 12.22 to 23.74 | 23.84 to 28.16 | 28.19 to 32.25 | 32.31 to 39.04 |
| DBH (cm) | 11.43 to 28.45 | 28.96 to 40.64 | 40.89 to 52.83 | 52.83 to 114.3 |
| 4 | 3 | 2 | 1 | |
|---|---|---|---|---|
| Height (m) | 1.9 to 11.9 | 12.1 to 19.0 | 19.3 to 25.2 | 25.8 to 37.7 |
| DBH (cm) | 7.0 to 10.7 | 10.7 to 17.3 | 17.3 to 30.8 | 31.0 to 69.7 |
| Window Function | Description | Method | Citation |
|---|---|---|---|
| Fixed | Generic FW size. | 50 cells (~1.5 m) | |
| Fixed | Generic FW size. | 100 cells (~3 m) | |
| Fixed | Minimizing under-segmentation, to support individual tree classification. | 1.65 m | [54] |
| Fixed | Reference tree crown size average for recent study in this region. | 4.5 m | [37] |
| Fixed | Reference tree crown size average for a deciduous plot for recent study in this region. | 4.51 m | [45] |
| Fixed | Reference tree crown size average for a coniferous plot for recent study in this region. | 4.58 m | [45] |
| Fixed | Average tree crown radius of digitized crowns from previous study at Lee sites | 2.767727 m | [44] |
| Variable | Mixed forest equation from Popescu and Wynne [12] | [12] | |
| Variable | R: ForestTools default parameters | [12,74] | |
| Variable | Forest inventory data (2015) regression | [37,56] |
| Height | |||||||
|---|---|---|---|---|---|---|---|
| Method | Size 1 | Size 2 | Size 3 | Size 4 | R | p | F-score |
| FW: 4.5 m | 30 4 6 | 24 2 14 | 21 0 20 | 19 1 21 | 0.6065 | 0.9307 | 0.7344 |
| FW: 4.58 m | 30 4 6 | 24 2 14 | 21 0 20 | 9 1 31 | 0.5419 | 0.9231 | 0.6829 |
| FW: 4.51 m | 30 4 6 | 24 2 14 | 21 0 20 | 9 1 31 | 0.5419 | 0.9231 | 0.6829 |
| DBH | |||||||
| Method | Size 1 | Size 2 | Size 3 | Size 4 | R | p | F-score |
| Popescu Mixed Forests | 64 20 5 | 48 16 25 | 34 11 44 | 29 8 53 | 0.579 | 0.761 | 0.658 |
| FW: 4.5 m | 70 10 9 | 52 2 35 | 32 1 56 | 16 0 74 | 0.494 | 0.929 | 0.645 |
| FW: 4.51 m | 70 10 9 | 52 2 35 | 32 1 56 | 16 0 74 | 0.494 | 0.929 | 0.645 |
| Height | |||||||
|---|---|---|---|---|---|---|---|
| Method | Size 1 | Size 2 | Size 3 | Size 4 | r | p | F-score |
| FW: 4.5 m | 5 1 9 | 3 0 12 | 3 0 13 | 2 1 13 | 0.217 | 0.867 | 0.347 |
| FW: 4.58 m | 5 1 9 | 3 0 12 | 3 0 13 | 0 3 13 | 0.217 | 0.867 | 0.347 |
| FW: 4.51 m | 5 1 9 | 3 0 12 | 3 0 13 | 2 1 13 | 0.217 | 0.867 | 0.347 |
| DBH | |||||||
| Method | Size 1 | Size 2 | Size 3 | Size 4 | r | p | F-score |
| Forest Inventory Regression | 38 6 121 | 13 3 149 | 17 1 147 | 15 3 148 | 0.128 | 0.865 | 0.223 |
| FW: 4.58 m | 31 22 112 | 14 10 141 | 20 7 138 | 17 7 142 | 0.133 | 0.641 | 0.221 |
| FW: 4.51 m | 30 23 112 | 15 10 140 | 19 8 138 | 17 7 142 | 0.132 | 0.628 | 0.218 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fraser, B.T.; Congalton, R.G.; Ducey, M.J. Quantifying the Accuracy of UAS-Lidar Individual Tree Detection Methods Across Height and Diameter at Breast Height Sizes in Complex Temperate Forests. Remote Sens. 2025, 17, 1010. https://doi.org/10.3390/rs17061010
Fraser BT, Congalton RG, Ducey MJ. Quantifying the Accuracy of UAS-Lidar Individual Tree Detection Methods Across Height and Diameter at Breast Height Sizes in Complex Temperate Forests. Remote Sensing. 2025; 17(6):1010. https://doi.org/10.3390/rs17061010
Chicago/Turabian StyleFraser, Benjamin T., Russell G. Congalton, and Mark J. Ducey. 2025. "Quantifying the Accuracy of UAS-Lidar Individual Tree Detection Methods Across Height and Diameter at Breast Height Sizes in Complex Temperate Forests" Remote Sensing 17, no. 6: 1010. https://doi.org/10.3390/rs17061010
APA StyleFraser, B. T., Congalton, R. G., & Ducey, M. J. (2025). Quantifying the Accuracy of UAS-Lidar Individual Tree Detection Methods Across Height and Diameter at Breast Height Sizes in Complex Temperate Forests. Remote Sensing, 17(6), 1010. https://doi.org/10.3390/rs17061010








