Forest Aboveground Biomass Estimation in Küre Mountains National Park Using Multifrequency SAR and Multispectral Optical Data with Machine-Learning Regression Models
Abstract
:1. Introduction
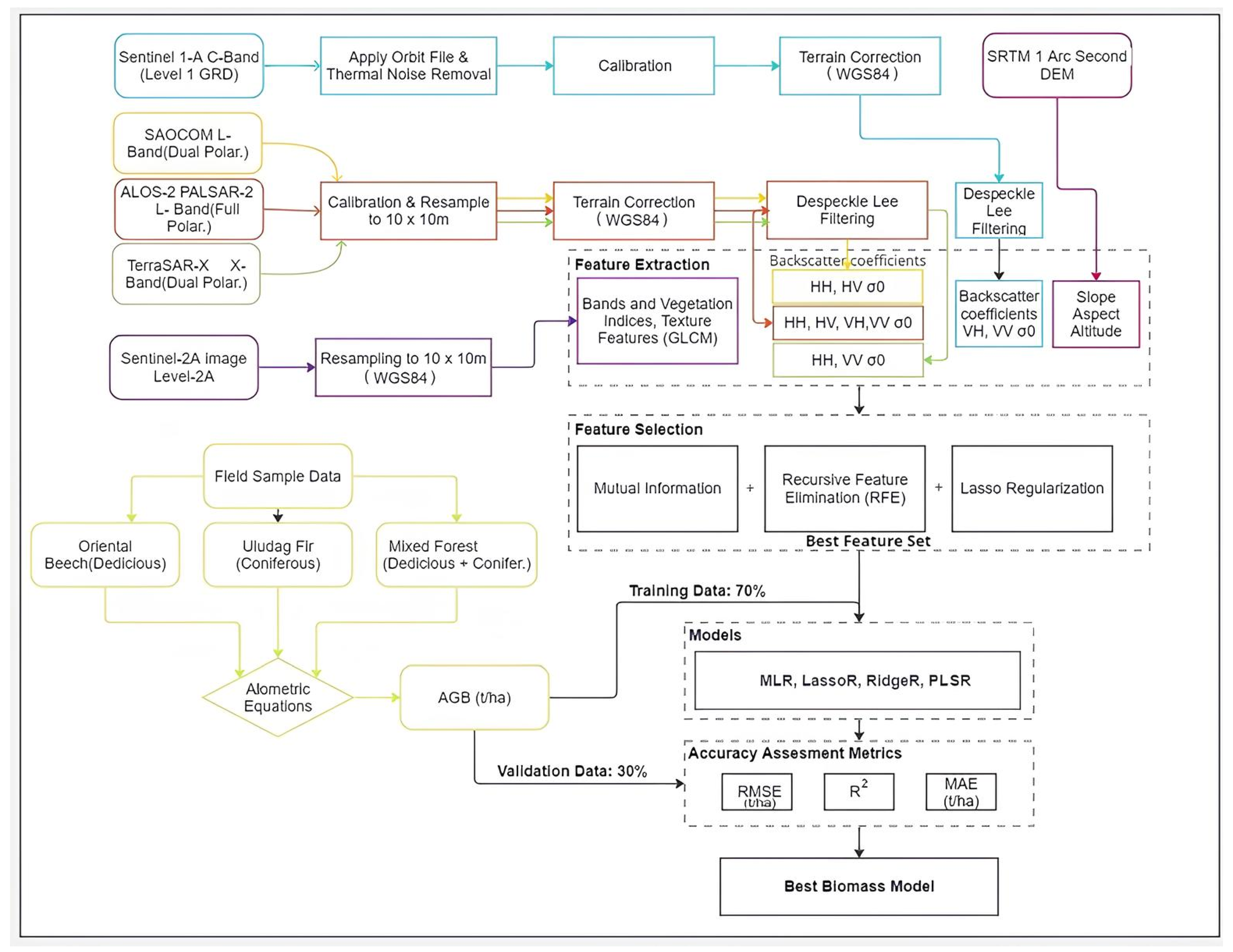
2. Materials and Methods
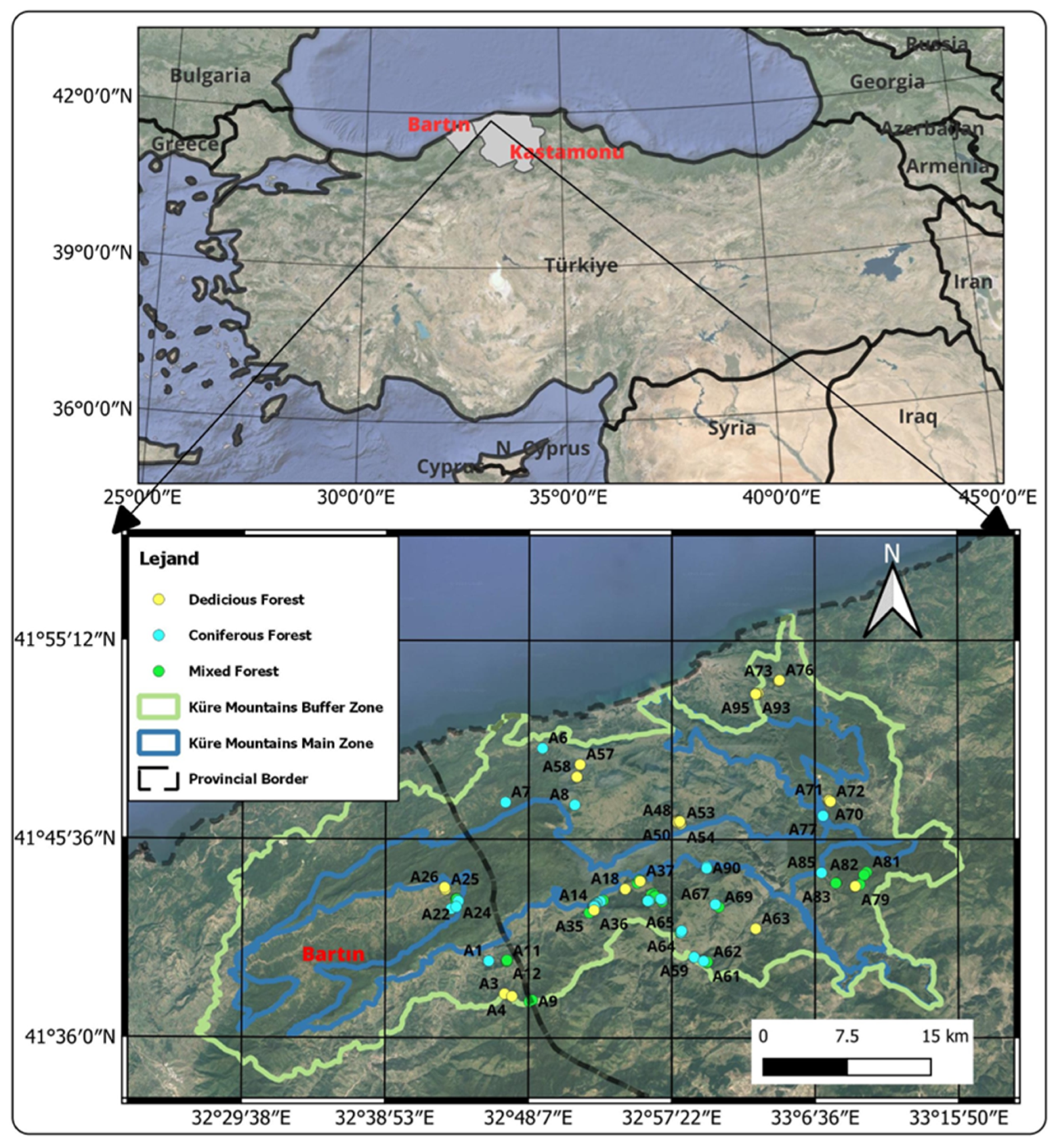
2.1. Study Area
2.2. In-Situ Plot Survey
2.3. Allometric Growth Equation
2.4. Data Pre-Processing and Variables
2.5. Feature Selection Methods
2.5.1. Mutual Information
2.5.2. Recursive Feature Elimination
2.5.3. LASSO Regularization
2.6. Regression Models
2.6.1. Multivariate Linear Regression
2.6.2. LASSO Regression
2.6.3. Ridge Regression
2.6.4. PLS Regression
2.7. Model Accuracy and Statistical Analysis
3. Results
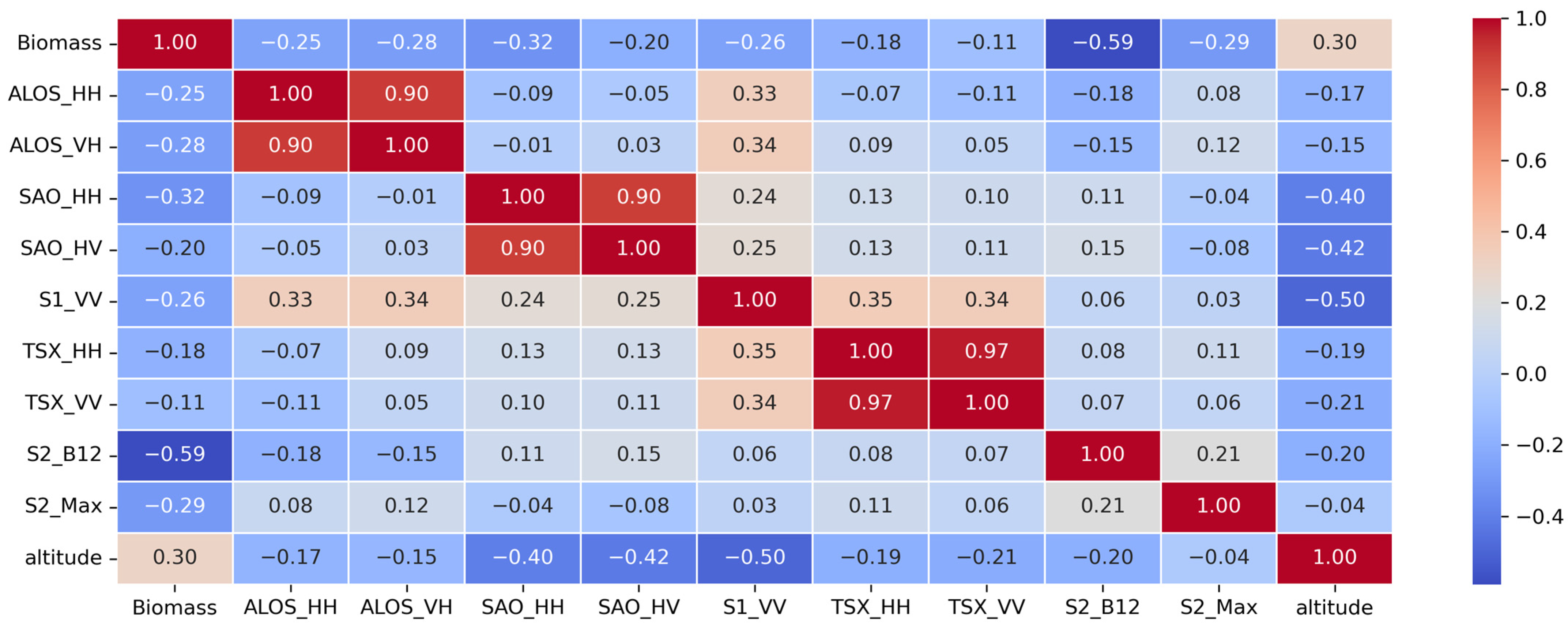
3.1. Statistical Analysis
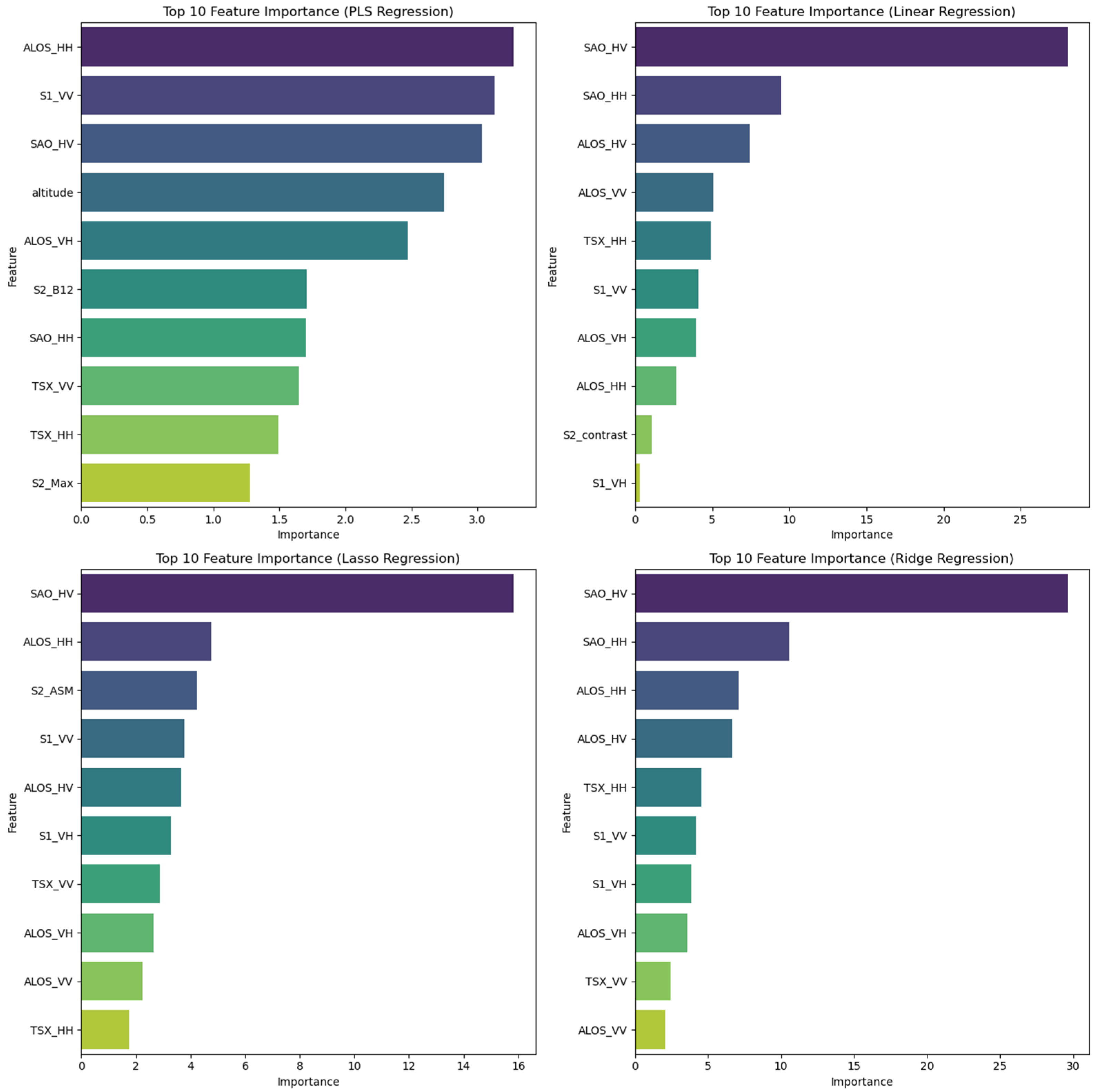
3.2. Analyzing Selecting and Important Predictors for AGB Estimation
3.3. Mapping AGB and Regression Analysis
4. Discussion
4.1. Feature Selection Methods and Impact on AGB Estimation
4.2. Performance of Machine-Learning Regression Models
4.3. Role of Multifrequency Bands and Polarizations in Biomass Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1

Appendix A.2
Appendix A.3
Appendix A.4

References
- Luyssaert, S.; Schulze, E.D.; Börner, A.; Knohl, A.; Hessenmöller, D.; Law, B.E.; Ciais, P.; Grace, J. Old-Growth Forests as Global Carbon Sinks. Nature 2008, 455, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Dixon, R.K.; Brown, S.; Houghton, R.A.; Solomon, A.M.; Trexler, M.C.; Wisniewski, J. Carbon Pools and Flux of Global Forest Ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, X.L.; Han, H.; Shi, Z.J.; Yang, X.H. Biomass Accumulation and Carbon Sequestration in an Age-Sequence of Mongolian Pine Plantations in Horqin Sandy Land, China. Forests 2019, 10, 197. [Google Scholar] [CrossRef]
- Fang, J.Y.; Wang, Z.M. Forest Biomass Estimation at Regional and Global Levels, with Special Reference to China’s Forest Biomass. Ecol. Res. 2001, 16, 587–592. [Google Scholar] [CrossRef]
- Ramachandra, T.V.; Bharath, S. Carbon Sequestration Potential of the Forest Ecosystems in the Western Ghats, a Global Biodiversity Hotspot. Nat. Resour. Res. 2020, 29, 2753–2771. [Google Scholar] [CrossRef]
- Vafaei, S.; Sohrabi, H.; Abdi, E.; Johansen, K.; Darvishsefat, A.A.; Saatchi, S.S. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Lu, D.S.; Chen, Q.; Wang, G.X.; Liu, L.J.; Li, G.Y.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E.J. Predictive Relations of Tropical Forest Biomass from Landsat TM Data and Their Transferability Between Regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Ghasemi, N.; Sahebi, M.R.; Mohammadzadeh, A. Biomass Estimation of a Temperate Deciduous Forest Using Wavelet Analysis. IEEE Trans. Geosci. Remote Sens. 2013, 51, 765–776. [Google Scholar] [CrossRef]
- Letoan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating Forest Biomass to SAR Data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Lu, D.S. The Potential and Challenge of Remote Sensing-Based Biomass Estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Lucas, R.; Cronin, N.; Moghaddam, M.; Lee, A.; Armston, J.; Bunting, P.; Witte, C. An Evaluation of the ALOS PALSAR L-Band Backscatter-Above Ground Biomass Relationship Queensland, Australia: Impacts of Surface Moisture Condition and Vegetation Structure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 576–593. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping Forest Aboveground Biomass in the Northeastern United States with ALOS PALSAR Dual-Polarization L-Band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Li, Y.C.; Li, M.Y.; Li, C.; Liu, Z.Z. Forest Aboveground Biomass Estimation Using Landsat 8 and Sentinel-1A Data with Machine Learning Algorithms. Sci. Rep. 2020, 10, 67024. [Google Scholar] [CrossRef]
- Ji, Y.J.; Wang, L.; Zhang, W.F.; Marino, A.; Wang, M.J.; Ma, J.M.; Shi, J.M.; Jing, Q.; Zhang, F.X.; Zhao, H.; et al. Forest Aboveground Biomass Estimation Using X, C, L, and P Band SAR Polarimetric Observations and Different Inversion Models. Int. J. Digit. Earth 2024, 17, 2310730. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Le Toan, T. L- and P-Band Backscatter Intensity for Biomass Retrieval in Hemiboreal Forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
- Symeonakis, E.; Higginbottom, T.P.; Petroulaki, K.; Rabe, A. Optimisation of Savannah Land Cover Characterisation with Optical and SAR Data. Remote Sens. 2018, 10, 499. [Google Scholar] [CrossRef]
- Bhavsar, D.; Das, A.K.; Chakraborty, K.; Patnaik, C.; Sarma, K.K.; Aggrawal, S.P. Above Ground Biomass Mapping of Tropical Forest of Tripura Using EOS-04 and ALOS-2 PALSAR-2 SAR Data. J. Indian Soc. Remote Sens. 2024, 52, 801–811. [Google Scholar] [CrossRef]
- Wittke, S.; Yu, X.W.; Karjalainen, M.; Hyyppä, J.; Puttonen, E. Comparison of Two-Dimensional Multitemporal Sentinel-2 Data with Three-Dimensional Remote Sensing Data Sources for Forest Inventory Parameter Estimation over a Boreal Forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 167–178. [Google Scholar] [CrossRef]
- Ha, N.T.; Manley-Harris, M.; Pham, T.D.; Hawes, I. The Use of Radar and Optical Satellite Imagery Combined with Advanced Machine Learning and Metaheuristic Optimization Techniques to Detect and Quantify Above Ground Biomass of Intertidal Seagrass in a New Zealand Estuary. Int. J. Remote Sens. 2021, 42, 4716–4742. [Google Scholar] [CrossRef]
- Theofanous, N.; Chrysafis, I.; Mallinis, G.; Domakinis, C.; Verde, N.; Siahalou, S. Aboveground Biomass Estimation in Short Rotation Forest Plantations in Northern Greece Using ESA’s Sentinel Medium-High Resolution Multispectral and Radar Imaging Missions. Forests 2021, 12, 902. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D.; Jagadish, B.; Das, A.K.; Mishra, D.R. A Novel Approach for Estimation of Aboveground Biomass of a Carbon-Rich Mangrove Site in India. J. Environ. Manag. 2021, 292, 112816. [Google Scholar] [CrossRef] [PubMed]
- David, R.M.; Rosser, N.J.; Donoghue, D.N.M. Improving Above-Ground Biomass Estimates of Southern Africa Dryland Forests by Combining Sentinel-1 SAR and Sentinel-2 Multispectral Imagery. Remote Sens. Environ. 2022, 282, 113232. [Google Scholar] [CrossRef]
- Ayushi, K.; Babu, K.N.; Ayyappan, N.; Nair, J.R.; Kakkara, A.; Reddy, C.S. A comparative analysis of machine learning techniques for aboveground biomass estimation: A case study of the Western Ghats, India. Ecol. Inform. 2024, 80, 102479. [Google Scholar] [CrossRef]
- Özdemir, E.G.; Demiralay, A.; Şahin, B. Bartın’daki sahil çamı (Pinus pinaster Ait.) ağaçlandırma alanlarında Sentinel-1 ve Sentinel-2 uydu görüntüleri kullanılarak toprak üstü biyokütlenin kestirilmesi. Türk Uzak. Algılama CBS Derg. 2024, 5, 15–27. [Google Scholar] [CrossRef]
- Singh, R.K.; Biradar, C.M.; Behera, M.D.; Prakash, A.J.; Das, P.; Mohanta, M.R.; Krishna, G.; Dogra, A.; Dhyani, S.K.; Rizvi, J. Optimising carbon fixation through agroforestry: Estimation of aboveground biomass using multi-sensor data synergy and machine learning. Ecol. Inform. 2024, 79, 102408. [Google Scholar] [CrossRef]
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating Mangrove Above-Ground Biomass Using Extreme Gradient Boosting Decision Trees Algorithm with Fused Sentinel-2 and ALOS-2 PALSAR-2 Data in Can Gio Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Li, H.T.; Kato, T.; Hayashi, M.; Wu, L. Estimation of forest aboveground biomass of two major conifers in Ibaraki Prefecture, Japan, from PALSAR-2 and Sentinel-2 data. Remote Sens. 2022, 14, 468. [Google Scholar] [CrossRef]
- Laurin, G.V.; Balling, J.; Corona, P.; Mattioli, W.; Papale, D.; Puletti, N.; Rizzo, M.; Truckenbrodt, J.; Urban, M. Above-ground biomass prediction by Sentinel-1 multitemporal data in central Italy with integration of ALOS2 and Sentinel-2 data. J. Appl. Remote Sens. 2018, 12, 016008. [Google Scholar] [CrossRef]
- Tavasoli, N.; Arefi, H. Comparison of capability of SAR and optical data in mapping forest above ground biomass based on machine learning. Environ. Sci. Proc. 2020, 5, 13. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.C.; Li, M.Y. Improving forest aboveground biomass (AGB) estimation by incorporating crown density and using Landsat 8 OLI images of a subtropical forest in Western Hunan in Central China. Forests 2019, 10, 104. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 2000, 42, 80–86. [Google Scholar] [CrossRef]
- Wold, S.; Martens, H.; Wold, H. The multivariate calibration-problem in chemistry solved by the PLS method. Lect. Notes Math. 1983, 973, 286–293. [Google Scholar]
- Kumar, S.; Pandey, U.; Kushwaha, S.P.; Chatterjee, R.S.; Bijker, W. Aboveground biomass estimation of tropical forest from Envisat advanced synthetic aperture radar data using modeling approach. J. Appl. Remote Sens. 2012, 6, 063588. [Google Scholar] [CrossRef]
- Liu, Z.H.; Michel, O.O.; Wu, G.M.; Mao, Y.; Hu, Y.F.; Fan, W.Y. The potential of fully polarized ALOS-2 data for estimating forest above-ground biomass. Remote Sens. 2022, 14, 669. [Google Scholar] [CrossRef]
- Liu, M.; Popescu, S. Estimation of biomass burning emissions by integrating ICESat-2, Landsat 8, and Sentinel-1 data. Remote Sens. Environ. 2022, 280, 113172. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, Z.B.; Zhang, H.Q.; Zhang, H.C.; Qiu, H.Q. Aboveground Forest Biomass Estimation Using Tent Mapping Atom Search Optimized Backpropagation Neural Network with Landsat 8 and Sentinel-1A Data. Remote Sens. 2023, 15, 5653. [Google Scholar] [CrossRef]
- Nelson, R.; Ranson, K.J.; Sun, G.; Kimes, D.S.; Kharuk, V.; Montesano, P. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
- Monnet, J.M.; Chanussot, J.; Berger, F. Support vector regression for the estimation of forest stand parameters using airborne laser scanning. IEEE Geosci. Remote Sens. Lett. 2011, 8, 580–584. [Google Scholar] [CrossRef]
- Dong, L.; Du, H.; Han, N.; Li, X.; Zhu, D.E.; Mao, F.; Zhang, M.; Zheng, J.; Liu, H.; Huang, Z.; et al. Application of Convolutional Neural Network on Lei Bamboo Above-Ground-Biomass (AGB) Estimation Using Worldview-2. Remote Sens. 2020, 12, 958. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Gitas, I.; Tsakiri-Strati, M. Estimating Mediterranean Forest parameters using multi-seasonal Landsat 8 OLI imagery and an ensemble learning method. Remote Sens. Environ. 2017, 199, 154–166. [Google Scholar] [CrossRef]
- Khan, P.W.; Byun, Y.C.; Lee, S.J.; Park, N. Machine learning based hybrid system for imputation and efficient energy demand forecasting. Energies 2020, 13, 2681. [Google Scholar] [CrossRef]
- Fan, J.L.; Wang, X.K.; Zhang, F.C.; Ma, X.; Wu, L.F. Predicting daily diffuse horizontal solar radiation in various climatic regions of China using support vector machine and tree-based soft computing models with local and extrinsic climatic data. J. Clean. Prod. 2020, 248, 119264. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground mangrove biomass estimation in Beibu Gulf using machine learning and UAV remote sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Huang, T.B.; Ou, G.L.; Xu, H.; Zhang, X.L.; Wu, Y.; Liu, Z.H.; Zou, F.Y.; Zhang, C.; Xu, C. Comparing Algorithms for Estimation of Aboveground Biomass. Forests 2023, 14, 1742. [Google Scholar] [CrossRef]
- Eken, G.; Bozdoğan, M.; İsfendiyaroğlu, S.; Kılıç, D.T.; Lise, Y. Türkiye’nin Önemli Doğa Alanları; Doğa Derneği: Ankara, Turkey, 2006; Volume II. [Google Scholar]
- Erol, O. Batı Küre Dağları ile Ilgarini Dolayının Jeomorfolojisi ve İklim Koşulları. Orman Av Derg. 1998, 77, 10–13. [Google Scholar]
- Köse, N.; Güner, H.T. The Effect of Temperature and Precipitation on the Intra-Annual Radial Growth of Fagus orientalis Lipsky in Artvin, Turkey. Turk. J. Agric. For. 2012, 36, 12. [Google Scholar] [CrossRef]
- Akdeniz, N.S.; Yener, D.Y. Bursa, Uludağ and Fir. Kastamonu Univ. J. For. Fac. 2012, 12, 256–258. [Google Scholar]
- Güner, Ş.T.; Diamantopoulou, M.J.; Poudel, K.P.; Çömez, A.; Özçelik, R. Employing Artificial Neural Network for Effective Biomass Prediction: An Alternative Approach. Comput. Electron. Agric. 2022, 192, 106596. [Google Scholar] [CrossRef]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Ambagau, Y.; Palm, C.A. Reducing Uncertainty in the Use of Allometric Biomass Equations for Predicting Above-Ground Tree Biomass in Mixed Secondary Forests. For. Ecol. Manag. 2001, 146, 199–207. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Improved Allometric Models to Estimate the Aboveground Biomass of Tropical Trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Saraçoğlu, N. Biomass Tables of Beech (Fagus orientalis Lipsky). Turk. J. Agric. For. 1998, 22, 14. [Google Scholar]
- Karabürk, T. Bartın İli Göknar Meşcerelerinin Biyokütle Tablolarının Düzenlenmesi. M.Sc. Thesis, Bartın University, Graduate School of Natural and Applied Sciences, Bartın, Turkey, 2011. [Google Scholar]
- Vincini, M.; Frazzi, E.; D’Alessio, P. A Broad-Band Leaf Chlorophyll Vegetation Index at the Canopy Scale. Precis. Agric. 2008, 9, 303–319. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral Indices for Estimating Photosynthetic Pigment Concentrations: A Test Using Senescent Tree Leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Melillos, G.; Hadjimitsis, D. Using Simple Ratio (SR) Vegetation Index to Detect Deep Man-Made Infrastructures in Cyprus. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXV; SPIE: Bellingham, WA, USA, 2020; Volume 11418, pp. 105–113. [Google Scholar]
- Wang, Z.; Li, M.; Li, J. A Multi-Objective Evolutionary Algorithm for Feature Selection Based on Mutual Information with a New Redundancy Measure. Inf. Sci. 2015, 307, 35–52. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Zhu, R. Feature Selection Based on Mutual Information with Correlation Coefficient. Appl. Intell. 2022, 52, 5457–5474. [Google Scholar] [CrossRef]
- Battiti, R. Using Mutual Information for Selecting Features in Supervised Neural Net Learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef]
- Kinney, J.B.; Atwal, G.S. Equitability, Mutual Information, and the Maximal Information Coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef] [PubMed]
- Belghazi, M.I.; Baratin, A.; Rajeshwar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. MINE: Mutual Information Neural Estimation. arXiv 2018. [Google Scholar] [CrossRef]
- Granitto, P.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive Feature Elimination with Random Forest for PTR-MS Analysis of Agroindustrial Products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A Review of Supervised Object-Based Land-Cover Image Classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Lockhart, R.; Taylor, J.; Tibshirani, R.J.; Tibshirani, R. A Significance Test for the Lasso. Ann. Stat. 2014, 42, 413–468. [Google Scholar] [CrossRef] [PubMed]
- Heiberger, R.M.; Neuwirth, E. Multiple Regression—Three or More X-Variables. In R Through Excel; Use, R., Ed.; Springer: New York, NY, USA, 2009; pp. 183–197. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Yan, X.; Li, J.; Smith, A.R.; Yang, D.; Ma, T.; Su, Y.; Shao, J. Evaluation of Machine Learning Methods and Multi-Source Remote Sensing Data Combinations to Construct Forest Above-Ground Biomass Models. Int. J. Digit. Earth 2023, 16, 4471–4491. [Google Scholar] [CrossRef]
- Fang, K.T.; Jin, H.Y.; Chen, Q.Y. Practical Regression Analysis; Science Press: Beijing, China, 1988. [Google Scholar]
- Zhou, L.; Wang, H.; Xu, Q. Survival forest with partial least squares for high dimensional censored data. Chemom. Intell. Lab. Syst. 2018, 179, 12–21. [Google Scholar] [CrossRef]
- Corrales, D.C.; Santillan, J.; Pola, D.; Aubert, M.; Goudet, M.; Rakotomalala, R.; Ribstein, P. A surrogate model based on feature selection techniques and regression learners to improve soybean yield prediction in southern France. Comput. Electron. Agric. 2022, 192, 106578. [Google Scholar] [CrossRef]
- Gholamrezaie, H.; Hasanlou, M.; Amani, M.; Mirmazloumi, S.M. Automatic Mapping of Burned Areas Using Landsat 8 Time-Series Images in Google Earth Engine: A Case Study from Iran. Remote Sens. 2022, 14, 6376. [Google Scholar] [CrossRef]
- Huang, T.; Ou, G.; Wu, Y.; Zhang, X.; Liu, Z.; Xu, H.; Xu, X.; Wang, Z.; Xu, C. Estimating the Aboveground Biomass of Various Forest Types with High Heterogeneity at the Provincial Scale Based on Multi-Source Data. Remote Sens. 2023, 15, 3550. [Google Scholar] [CrossRef]
- Sanam, H.; Thomas, A.A.; Kumar, A.P.; Lakshmanan, G. Multi-sensor approach for the estimation of above-ground biomass of mangroves. J. Indian Soc. Remote Sens. 2024, 52, 903–916. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, R.; Guo, J.; Dai, J.; Zhang, J.; Zhang, L.; Miao, Y. Estimation of aboveground biomass of senescence grassland in China’s arid region using multi-source data. Sci. Total Environ. 2024, 918, 170602. [Google Scholar] [CrossRef]
- Wang, P.; Tan, S.; Zhang, G.; Wang, S.; Wu, X. Remote Sensing Estimation of Forest Aboveground Biomass Based on Lasso-SVR. Forests 2022, 13, 1597. [Google Scholar] [CrossRef]
- Ge, S.; Tomppo, E.; Rauste, Y.; McRoberts, R.E.; Praks, J.; Gu, H.; Su, W.; Antropov, O. Sentinel-1 Time Series for Predicting Growing Stock Volume of Boreal Forest: Multitemporal Analysis and Feature Selection. Remote Sens. 2023, 15, 3489. [Google Scholar] [CrossRef]
- Görgens, E.B.; Montaghi, A.; Rodriguez, L.C.E. A performance comparison of machine learning methods to estimate the fast-growing forest plantation yield based on laser scanning metrics. Comput. Electron. Agric. 2015, 116, 221–227. [Google Scholar] [CrossRef]
- Cai, T.; Ju, C.; Yang, X. Comparison of Ridge Regression and Partial Least Squares Regression for Estimating Above-Ground Biomass with Landsat Images and Terrain Data in Mu Us Sandy Land, China. Arid. Land Res. Manag. 2009, 23, 248–261. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least squares regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Askari, M.S.; McCarthy, T.; Magee, A.; Murphy, D.J. Evaluation of Grass Quality under Different Soil Management Scenarios Using Remote Sensing Techniques. Remote Sens. 2019, 11, 1835. [Google Scholar] [CrossRef]
- Quegan, S.; Le Toan, T.; Chave, J.; Dall, J.; Exbrayat, J.-F.; Tong Minh, D.H.; Lomas, M.; Mariotti D’Alessandro, M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An Evaluation of Eight Machine Learning Regression Algorithms for Forest Aboveground Biomass Estimation from Multiple Satellite Data Products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
- Sakici, O.E.; Günlü, A. Artificial intelligence applications for predicting some stand attributes using Landsat 8 OLI satellite data: A case study from Turkey. Appl. Ecol. Environ. Res. 2018, 16, 5269–5285. [Google Scholar] [CrossRef]
- Morais, T.G.; Jongen, M.; Tufik, C.; Rodrigues, N.R.; Gama, I.; Fangueiro, D.; Serrano, J.; Vieira, S.; Domingos, T.; Teixeira, R.F. Characterization of Portuguese Sown Rainfed Grasslands Using Remote Sensing and Machine Learning. Precis. Agric. 2023, 24, 161–186. [Google Scholar] [CrossRef]
- Keleş, S.; Günlü, A.; Ercanlı, İ. Estimating aboveground stand carbon by combining Sentinel-1 and Sentinel-2 satellite data: A case study from Turkey. In Forest Resources Resilience and Conflicts; Elsevier: Amsterdam, The Netherlands, 2021; pp. 117–126. [Google Scholar]
- Turgut, R.; Günlü, A. Estimating aboveground biomass using Landsat 8 OLI satellite image in pure Crimean pine (Pinus nigra J.F. Arnold subsp. pallasiana (Lamb.) Holmboe) stands: A case from Turkey. Geocarto Int. 2022, 37, 1737971. [Google Scholar] [CrossRef]
- Günlü, A.; Ercanlı, İ. Artificial neural network models by ALOS PALSAR data for aboveground stand carbon predictions of pure beech stands: A case study from northern of Turkey. Geocarto Int. 2020, 35, 17–28. [Google Scholar] [CrossRef]
- Ningthoujam, R.K.; Balzter, H.; Tansey, K.; Feldpausch, T.R.; Mitchard, E.T.A.; Wani, A.A.; Joshi, P.K. Relationships of S-Band Radar Backscatter and Forest Aboveground Biomass in Different Forest Types. Remote Sens. 2017, 9, 1116. [Google Scholar] [CrossRef]
- Babiy, I.A.; Im, S.T.; Kharuk, V.I. Estimating Aboveground Forest Biomass Using Radar Methods. Contemp. Probl. Ecol. 2022, 15, 433–448. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests—The potential of combined X- and L-band SAR data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Blomberg, E.; Ferro-Famil, L.; Soja, M.J.; Ulander, L.M.H.; Tebaldini, S. Forest Biomass Retrieval From L-Band SAR Using Tomographic Ground Backscatter Removal. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1030–1034. [Google Scholar] [CrossRef]
- Bao, N.; Li, W.; Gu, X.; Liu, Y. Biomass Estimation for Semiarid Vegetation and Mine Rehabilitation Using Worldview-3 and Sentinel-1 SAR Imagery. Remote Sens. 2019, 11, 2855. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Askar, A.; Stratoulias, D.; Wicaksono, P. Combined use of Sentinel-1 and Sentinel-2 data for improving above-ground biomass estimation. Geocarto Int. 2022, 37, 366–376. [Google Scholar] [CrossRef]
- Morin, D.; Planells, M.; Guyon, D.; Villard, L.; Mermoz, S.; Bouvet, A.; Thevenon, H.; Dejoux, J.-F.; Le Toan, T.; Dedieu, G. Estimation and Mapping of Forest Structure Parameters from Open Access Satellite Images: Development of a Generic Method with a Study Case on Coniferous Plantation. Remote Sens. 2019, 11, 1275. [Google Scholar] [CrossRef]
- Vatandaslar, C.; Abdikan, S. Carbon stock estimation by dual-polarized synthetic aperture radar (SAR) and forest inventory data in a Mediterranean forest landscape. J. For. Res. 2022, 33, 827–838. [Google Scholar] [CrossRef]
- Georgopoulos, N.; Sotiropoulos, C.; Stefanidou, A.; Gitas, I.Z. Total Stem Biomass Estimation Using Sentinel-1 and -2 Data in a Dense Coniferous Forest of Complex Structure and Terrain. Forests 2022, 13, 2157. [Google Scholar] [CrossRef]
- Khati, U.; Singh, G. Combining L-band Synthetic Aperture Radar backscatter and TanDEM-X canopy height for forest aboveground biomass estimation. Front. For. Glob. Change 2022, 5, 918408. [Google Scholar] [CrossRef]



| Forest Type | Plots No | Min (t/ha) | Max (t/ha) | Mean (t/ha) | Standard Deviation |
|---|---|---|---|---|---|
| Coniferous forest (Uludağ fir) | 29 | 171.274 | 422.974 | 323.344 | 57.022 |
| Deciduous forest (oriental beech) | 33 | 192.650 | 339.355 | 253.966 | 40.528 |
| Mixed forests (Uludağ fir and oriental beech) | 33 | 234.201 | 391.392 | 315.421 | 38.139 |
| Parameter | Unit | Measurement Method | Validation Method | Accuracy |
|---|---|---|---|---|
| Tree Diameter | cm | Measuring Tape, Digital Caliper | Repeated measurement, cross-checking | ±0.1–0.5 cm |
| Tree Height (h) | m | Haglöf EC II Electronic Clino/Height Meter (Långsele, Sweden) | Repeated measurement, cross-checking | ±0.2–1.0 m |
| Central Coordinates | Degrees | Garmin Oregon GPS (WGS84) (Kansas, USA) | Repeated measurement, cross-checking | ±3–10 m |
| Filed Elevation | m | GPS, DEM | Comparison with DEM (SRTM) | ±5–10 m (GPS) |
| Slope (%) | % | DEM, Clinometer | Validation with DEM data, manual measurement | ±2–5% |
| Aspect (°) | ° | Magnetic Compass, DEM | Comparison with DEM analysis | ±5° |
| Sensor | Band | Pass | Polarization | Range Resolution (m) | Azimuth Resolution (m) | Acquired Date |
|---|---|---|---|---|---|---|
| TerraSAR-X | X | Ascending | HH, VV | 0.91 | 2.42 | 28 July 2023, 8 August 2023, 19 August 2023 (3 frames), |
| Sentinel-1A (GRD) | C | Descending | VH, VV | 20 | 22 | 12 August 2023 |
| SAOCOM 1A | L | Descending | HH, HV | 4.75 | 4.99 | 20 August 2023 (2 frames), 23 August 2023 (2 frames) |
| ALOS-2 PALSAR-2 | L | Descending | HH, HV, VH, VV | 2.86 | 3.12 | 10 August 2023 |
| Variable Types | Variable Number | Variable Names | Description | References |
|---|---|---|---|---|
| Sentinel-2A | 12 | Bands | B1, B2 (Blue), B3 (Green), B4 (Red), B5, B6, B7 (Vegetation Red Edge), B8 (NIR), B8a, B9, B11, B12 | - |
| Vegetation Indices | CVI | Chlorophyll vegetation indices (B4 × B8)/(B3 × B3) | [56] | |
| EVI | Enhanced Vegetation Indices 2.5*(B8 − B4)/(B8 + 6 ×B4 − 7.5*B2 + 1) | [57] | ||
| 5 | PSSRA | The Pigment Specific Simple Ratio a (B7/B4) | [58] | |
| TNDVI | Transformed Normalized Difference Vegetation Indices ([(B8 − B4)/(B8 + B4)] + 0.5)0.5 | [59] | ||
| MSR | Modified Simple Ratio [B4/(B8/B4 + 1)0.5] | [60] | ||
| Texture Measures | 10 | “TjMea, TjVar, TjHom, TjCon, TjM TjDis, TjEn,TjEnt, TjASM, TjCor” | TjXXX represents a texture image developed in the S2 band using the texture measure XXX with a j × j (j = 5) pixel window, where XXX is Mea (Mean), Var (Variance), Hom (Homogeneity), Con (Contrast), M(Max), Dis (Dissimilarity), En (Energy), Ent (Entropy), ASM (Angular Second Moment), or Cor (Correlation). | |
| Topographic Variables | 3 | slope, aspect, altitude | Shuttle Radar Topography Mission (SRTM) 1 Arc Second DEM |
| Regression Statistics | |||||
| Multiple R | 0.847 | ||||
| R squared | 0.717 | ||||
| Adj. R squared | 0.683 | ||||
| Standard Error | 30.857 | ||||
| Observation | 95 | ||||
| ANOVA | |||||
| df | SS | MS | F | Sig. | |
| Regression | 10 | 202,584.479 | 20,258.448 | 21.276 | 4.258 × 10⁻¹⁹ |
| Differences | 84 | 79,981.354 | 952.159 | ||
| Total | 94 | 282,565.833 | |||
| PLSR | LASSO Regression | MLR | Ridge Regression | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Features | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE |
| 1 | [‘S2_B12’, ‘S2_Max’] | 0.24 | 52.73 | 45.24 | 0.26 | 51.97 | 44.71 | 0.25 | 52.46 | 44.75 | 0.13 | 56.26 | 45.13 |
| 2 | [‘ALOS_HH’, ‘SAO_HH’, ‘S1_VV’] | 0.26 | 51.90 | 43.29 | 0.27 | 51.75 | 43.27 | 0.27 | 51.78 | 43.27 | 0.25 | 52.26 | 43.30 |
| 3 | [‘ALOS_HH’, ‘SAO_HH’, ‘TSX_HH’, ‘S1_VV’] | 0.29 | 50.83 | 42.84 | 0.29 | 50.79 | 42.73 | 0.29 | 51.06 | 42.84 | 0.28 | 51.26 | 42.93 |
| 4 | [‘ALOS_HH’, ‘ALOS_VH’, ‘TSX_HH’, ‘S1_VV’, ‘S2_Max’, ‘altitude’] | 0.33 | 49.57 | 39.38 | 0.28 | 51.36 | 40.30 | 0.18 | 54.83 | 45.62 | 0.28 | 51.24 | 40.90 |
| 5 | [‘ALOS_VH’, ‘TSX_HH’, ‘TSX_VV’, ‘S1_VV’, ‘S2_B12’, ‘S2_Max’, ‘altitude’] | 0.44 | 45.03 | 36.60 | 0.54 | 41.12 | 33.76 | 0.51 | 42.08 | 34.70 | 0.38 | 47.70 | 39.86 |
| 6 | [‘ALOS_HH’, ‘ALOS_VH’, ‘TSX_HH’, ‘TSX_VV’, ‘S1_VV’, ‘S2_B12’, ‘altitude’] | 0.51 | 42.34 | 34.12 | 0.55 | 40.57 | 33.24 | 0.53 | 41.59 | 34.52 | 0.35 | 48.76 | 42.40 |
| 7 | [‘SAO_HH’, ‘SAO_HV’, ‘TSX_HH’, ‘S1_VV’, ‘S2_B12’] | 0.53 | 41.31 | 35.13 | 0.53 | 41.31 | 35.13 | 0.52 | 42.04 | 35.67 | 0.37 | 47.79 | 39.81 |
| 8 | [‘ALOS_HH’, ‘SAO_HH’, ‘TSX_VV’, ‘S1_VV’, ‘S2_B12’, ‘S2_Max’, ‘altitude’] | 0.61 | 37.96 | 30.89 | 0.61 | 37.96 | 30.84 | 0.58 | 38.95 | 31.37 | 0.44 | 45.16 | 35.80 |
| 9 | [‘ALOS_HH’, ‘ALOS_VH’, ‘SAO_HH’, ‘TSX_HH’, ‘TSX_VV’, ‘S2_B12’, ‘S2_Max’, ‘altitude’] | 0.63 | 36.74 | 30.56 | 0.61 | 37.71 | 31.72 | 0.59 | 38.65 | 32.56 | 0.44 | 45.14 | 35.89 |
| 10 | [‘ALOS_HH’, ‘ALOS_VH’, ‘SAO_HH’, ‘SAO_HV’, ‘TSX_HH’, ‘S2_B12’, ‘altitude’] | 0.70 | 32.87 | 28.35 | 0.69 | 33.41 | 28.72 | 0.68 | 33.91 | 29.05 | 0.49 | 43.02 | 36.80 |
| 11 | [‘ALOS_HH’, ‘ALOS_VH’, ‘SAO_HH’, ‘SAO_HV’, ‘TSX_HH’, ‘TSX_VV’, ‘S2_B12’, ‘S2_Max’, ‘altitude’] | 0.72 | 31.84 | 28.04 | 0.69 | 33.38 | 28.70 | 0.69 | 33.75 | 29.84 | 0.51 | 42.47 | 36.99 |
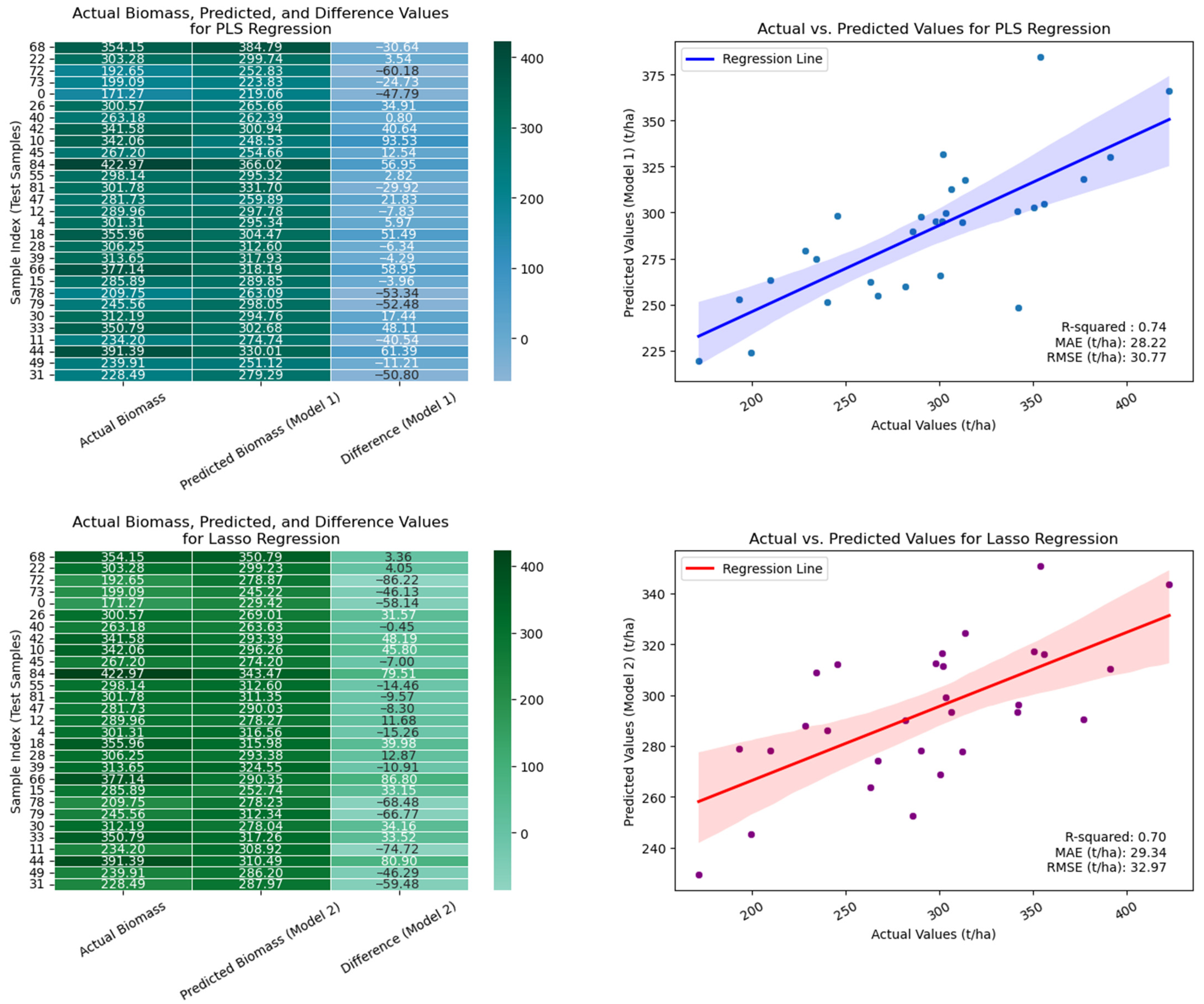
| 12 | [‘ALOS_HH’, ‘ALOS_VH’, ‘SAO_HH’, ‘SAO_HV’, ‘TSX_HH’, ‘TSX_VV’, ‘S1_VV’, ‘S2_B12’, ‘S2_Max’, ‘altitude’] | 0.74 | 30.77 | 28.22 | 0.70 | 32.97 | 29.34 | 0.69 | 33.37 | 29.43 | 0.53 | 36.04 | 35.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozdemir, E.G.; Abdikan, S. Forest Aboveground Biomass Estimation in Küre Mountains National Park Using Multifrequency SAR and Multispectral Optical Data with Machine-Learning Regression Models. Remote Sens. 2025, 17, 1063. https://doi.org/10.3390/rs17061063
Ozdemir EG, Abdikan S. Forest Aboveground Biomass Estimation in Küre Mountains National Park Using Multifrequency SAR and Multispectral Optical Data with Machine-Learning Regression Models. Remote Sensing. 2025; 17(6):1063. https://doi.org/10.3390/rs17061063
Chicago/Turabian StyleOzdemir, Eren Gursoy, and Saygin Abdikan. 2025. "Forest Aboveground Biomass Estimation in Küre Mountains National Park Using Multifrequency SAR and Multispectral Optical Data with Machine-Learning Regression Models" Remote Sensing 17, no. 6: 1063. https://doi.org/10.3390/rs17061063
APA StyleOzdemir, E. G., & Abdikan, S. (2025). Forest Aboveground Biomass Estimation in Küre Mountains National Park Using Multifrequency SAR and Multispectral Optical Data with Machine-Learning Regression Models. Remote Sensing, 17(6), 1063. https://doi.org/10.3390/rs17061063









