Solar Radiation Pressure Modeling and Validation for BDS-3 MEO Satellites
Abstract
1. Introduction
2. Analytical SRP Modeling of BDS Satellites
2.1. Satellite Body-Fixed Frame
2.2. Satellite Engineering Data of BDS-3 MEOs
2.3. Theorical Foundations for the Modeling of the SRP
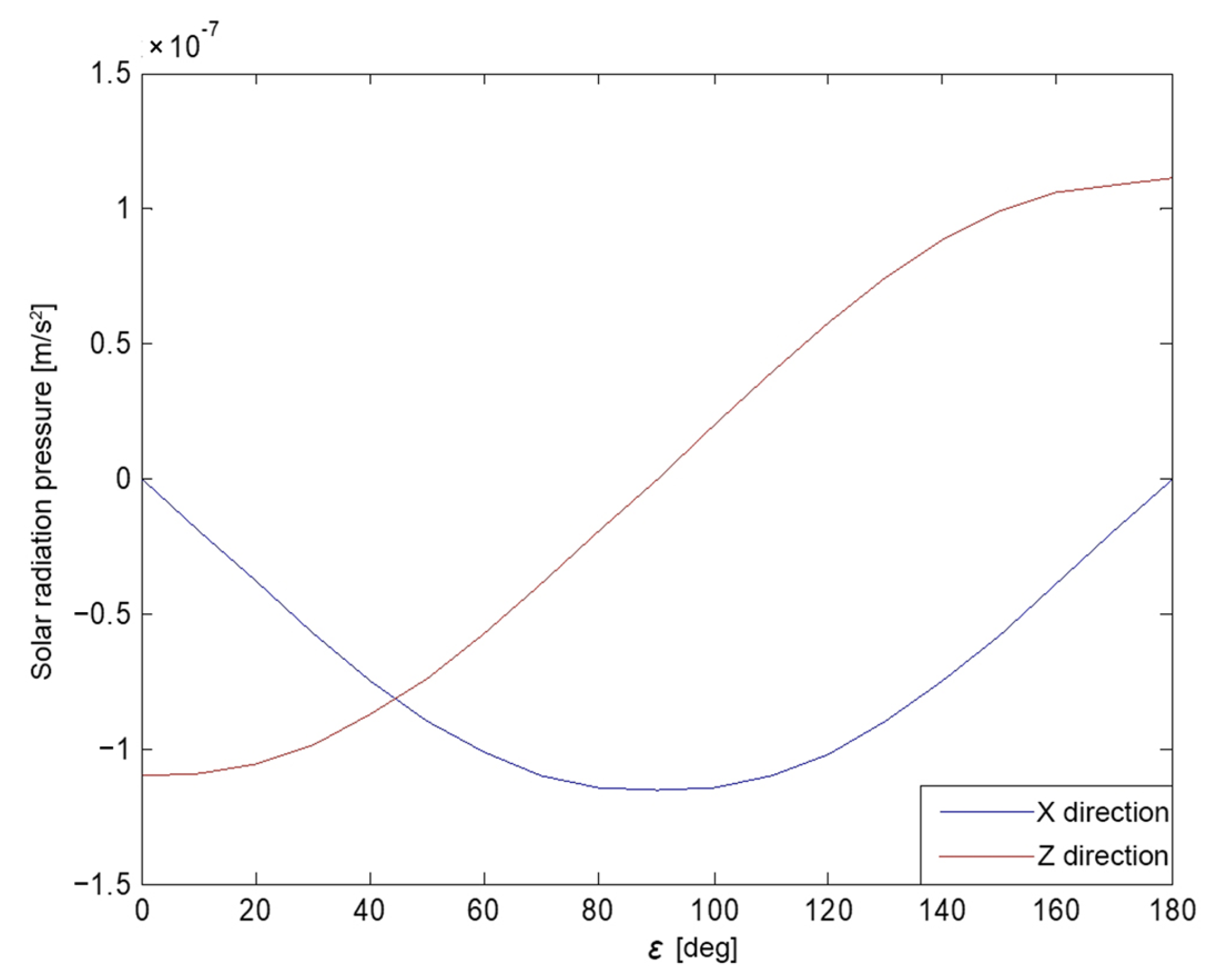
2.4. The Analytical SRP Model with Model Parameterization
3. SRP Model Analysis and Validations
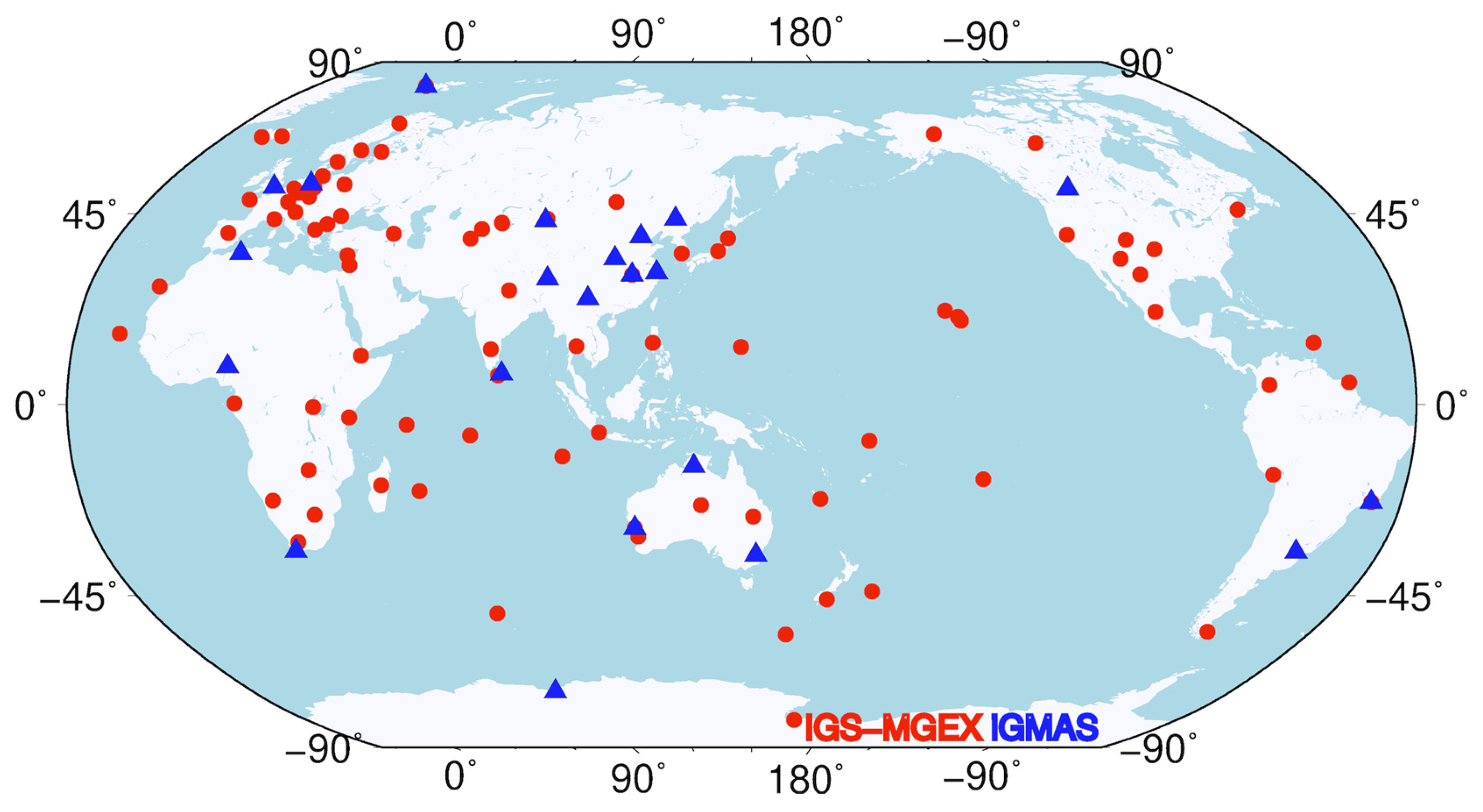
3.1. Strategies of Precise Orbit Determination
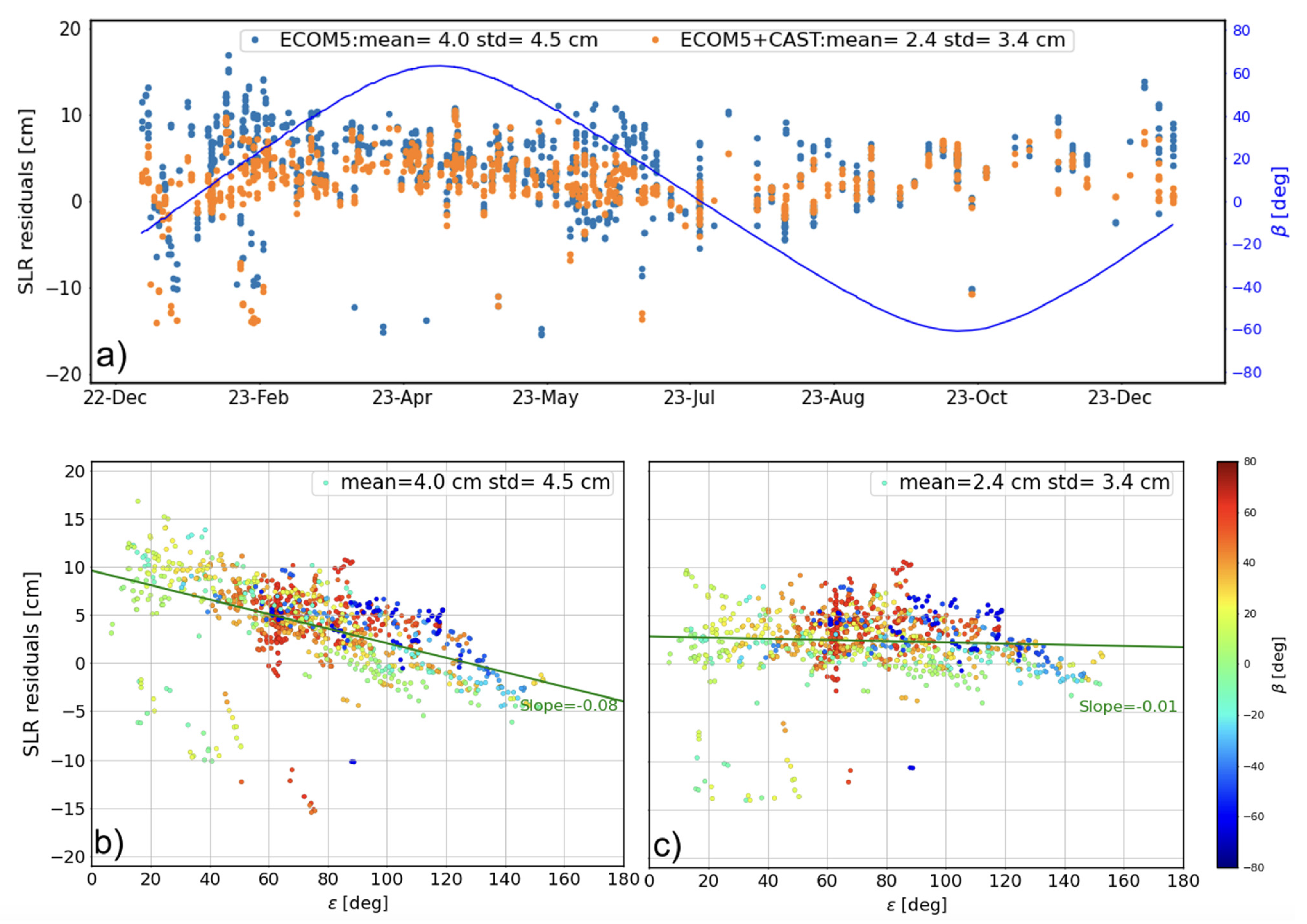
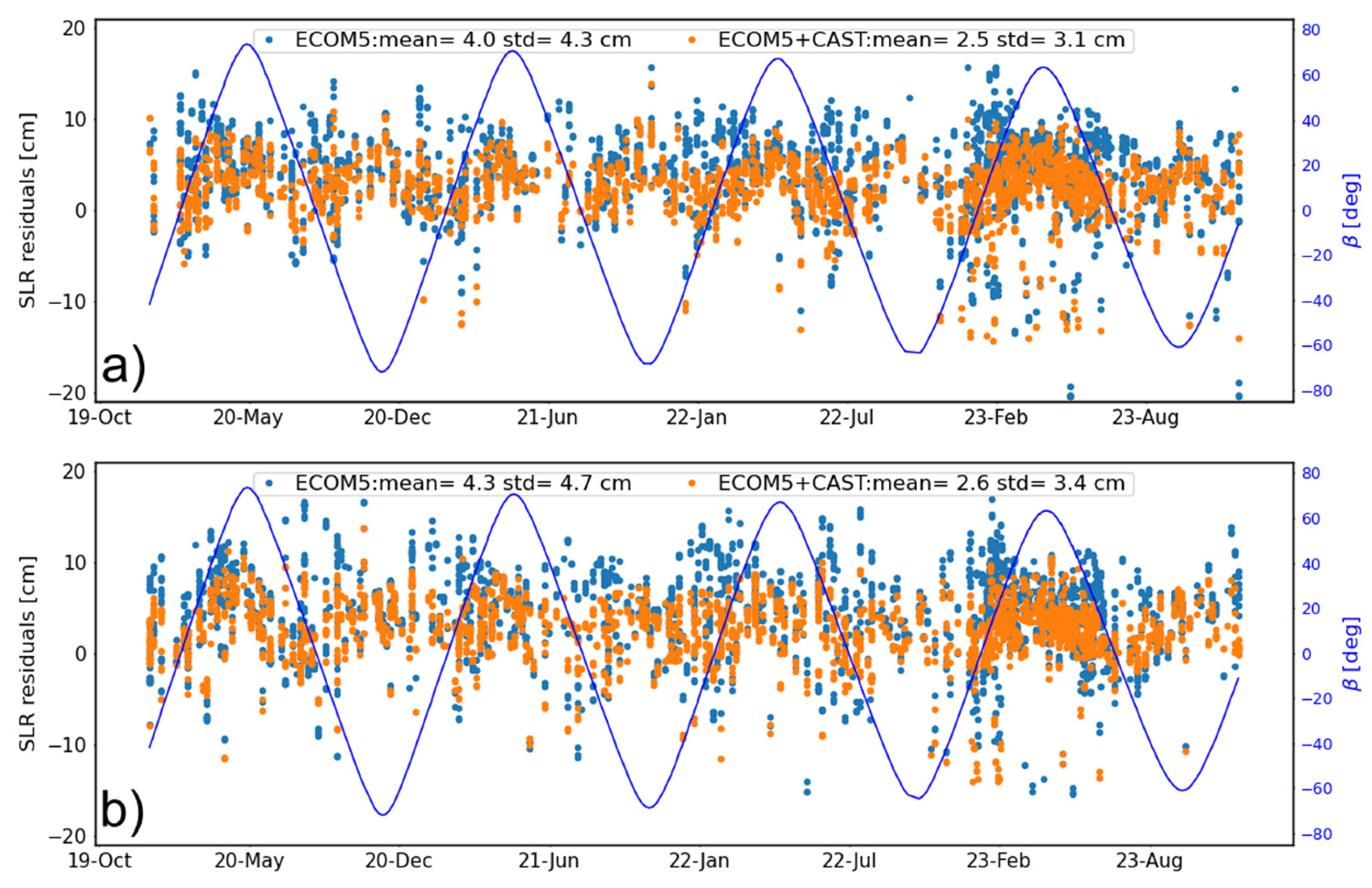
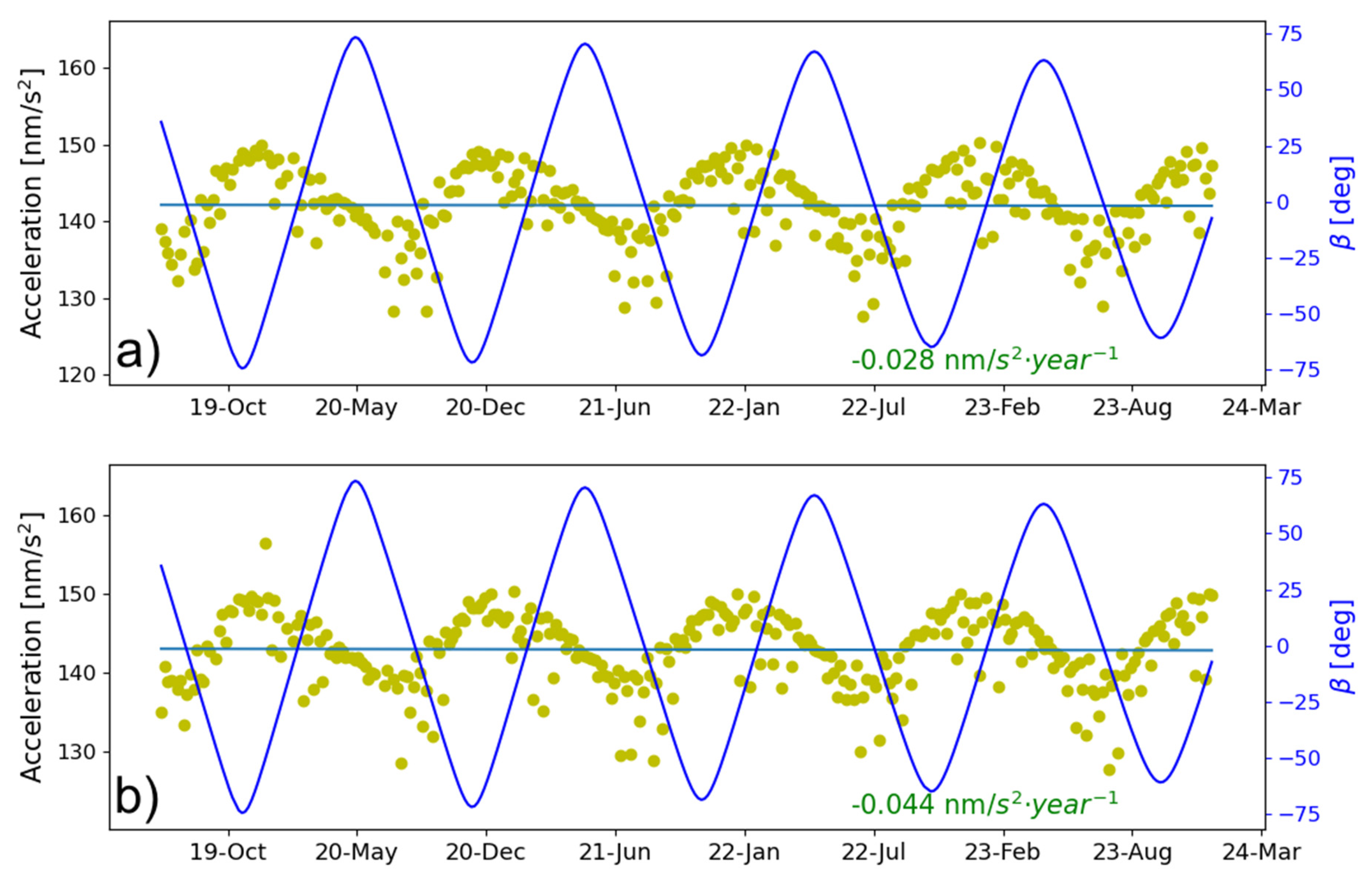
3.2. Model Validations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABW | Adjustable Box-Wing model |
| CAST | China Academy of Space Technology |
| CSNO | China Satellite Navigation Office |
| GNSS | Global Satellite Navigation System |
| iGMAS | International GNSS Monitoring and Assessment System |
| IGS | The International GNSS service |
| ILRS | International laser ranging service |
| LRA | Laser Ranging Array |
| MEO | medium earth orbit |
| POD | Precise orbit determination |
| SAR | Search and Rescue |
| SLR | Satellite laser ranging |
| SRP | Solar radiation pressure |
| SECM | Shanghai Engineering Center for Microsatellites |
References
- Yang, Y.; Mao, Y.; Sun, B. Basic performance and future developments of BeiDou global navigation satellite system. Satell. Navig. 2020, 1, 1. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Wang, C.; Lyu, Y.; Xu, X.; Yang, C.; Li, J. Precise orbit determination for BDS satellites. Satell. Navig. 2022, 3, 2. [Google Scholar] [CrossRef]
- Fligel, H.F.; Gallini, T.E.; Swift, E.R. Global positioning system radial force model for geodetic applications. J. Geophys. Res. 1992, 97, 559–568. [Google Scholar] [CrossRef]
- Fliegel, H.F.; Gallini, T.E. Solar force modeling of block IIR Global Positioning System satellites. J. Spacecr. Rocket. 1996, 33, 863–866. [Google Scholar] [CrossRef]
- Ziebart, M. High Precision Analytical Solar Radiation Pressure Modelling for GNSS Spacecraft. Ph.D. Thesis, University College London (UCL), London, UK, 2001. [Google Scholar]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Verdun, A. Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): Theory and initial results. Eur. Respir. J. 1994, 7, 1350–1364. [Google Scholar] [CrossRef]
- Springer, T.A.; Beulter, G.; Rothacher, M. A new solar radiation pressure model for GPS satellites. GPS Solut. 1999, 2, 50–62. [Google Scholar] [CrossRef]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P. Adjustable box-wing model for solar radiation pressure impacting GPS satellites. Adv. Space Res. 2012, 49, 1113–1128. [Google Scholar] [CrossRef]
- Guo, J. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites. Ph.D. Thesis, GNSS Research Center, Wuhan University, Wuhan, China, 2014. (In Chinese). [Google Scholar]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Yaw attitude modeling for BeiDou I06 and BeiDou-3 satellites. GPS Solut. 2018, 22, 117. [Google Scholar] [CrossRef]
- Yan, X.; Liu, C.; Huang, G.; Zhang, Q.; Wang, L.; Qin, Z.; Xie, S. A priori solar radiation pressure model for BeiDou-3 MEO satellites. Remote Sens. 2019, 11, 1605. [Google Scholar] [CrossRef]
- Sosnica, K.; Zajdel, R.; Bury, G.; Bosy, J.; Moore, M.; Masoumi, S. Assessment of experimental IGS multi-GNSS combined orbits. GPS Solut. 2020, 24, 54. [Google Scholar] [CrossRef]
- Guo, J.; Wang, L.; Yang, C.; Li, J.; Xu, X.; Zhao, Q. Modeling and comparison of solar radiation pressure for two BDS-3 MEO satellites (C45 and C46) with SAR payload. Adv. Space Res. 2024, 75, 1163–1176. [Google Scholar] [CrossRef]
- Wang, C. Solar Radiation Pressure Modelling for BeiDou Navigation Satellites. Ph.D. Thesis, Wuhan University, Wuhan, China, 2019. (In Chinese). [Google Scholar]
- Li, X.; Yuan, Y.; Zhu, Y.; Jiao, W.; Bian, L.; Li, X.; Zhang, K. Improving BDS-3 precise orbit determination for medium earth orbit satellites. GPS Solut. 2020, 24, 53. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I.; Marz, S.; Killian, M.; Rott, M. BeiDou Satellite Radiation Force Models for Precise Orbit Determination and Geodetic Applications. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2823–2836. [Google Scholar] [CrossRef]
- Liu, J.; Gu, D.; Ju, B.; Shen, Z.; Lai, Y.; Yi, D. A new empirical solar radiation pressure model for BeiDou GEO satellites. Adv. Space Res. 2016, 57, 234–244. [Google Scholar] [CrossRef]
- Chen, X.; Ge, M.; Liu, Y.; He, L.; Schuh, H. Adapting empirical solar radiation pressure model for BDS-3 medium Earth orbit satellites. GPS Solut. 2023, 27, 183. [Google Scholar] [CrossRef]
- Prange, L.; Villiger, A.; Sidorov, D.; Schaer, S.; Beutler, G.; Dach, R.; Jäggi, A. Overview of CODE’s MGEX solution with the focus on Galileo. Adv. Space Res. 2020, 66, 2786–2798. [Google Scholar] [CrossRef]
- Tan, B.; Yuan, Y.; Zhang, B.; Hsu, H.; Ou, J. A new analytical solar radiation pressure model for current BeiDou satellites: IGGBSPM. Sci. Rep. 2016, 6, 32967. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I. The Adjusted Optical Properties for Galileo/BeiDou-2/QZS-1 Satellites and Initial Results on BeiDou-3e and QZS-2 satellites. Adv. Space Res. 2018, 63, 1803–1812. [Google Scholar] [CrossRef]
- Shi, C.; Xiao, Y.; Fan, L.; Zheng, F.; Wang, C.; Huang, Z.; Li, Z. Research progress of radiation pressure modelling for navigation satellites. Acta Aeronaut. Astronaut. Sin. 2022, 43, 527389. [Google Scholar]
- Chen, Q.; Chen, Z.; Wang, H. Modeling and Analysis of Solar Radiation Pressure for GPS Satellites. Spacecr. Eng. 2013, 22, 27–32. [Google Scholar] [CrossRef]
- China Satellite Navigation Office. Satellite Information of BDS. 2019. Available online: http://en.beidou.gov.cn/SYSTEMS/Officialdocument/ (accessed on 1 February 2025).
- Montenbruck, O.; Schmid, R.; Steigenberger, P. GNSS Satellite Geometry and Attitude Models. Adv. Space Res. 2015, 56, 1015–1029. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar]
- Huang, W. Effect of Earth Infrared Radiation on Infrared Temperature Measurement for Exoatmospheric Objects. Opto-Electron. Eng. 2009, 36, 34. [Google Scholar]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Lutz, S. Impact of Earth radiation pressure on GPS position estimates. J. Geod. 2011, 86, 309–317. [Google Scholar] [CrossRef]
- Flett, R.M. Passive Temperature Control in Space Environment; National Defense Industry Press: Beijing, China, 1975; pp. 42–43. [Google Scholar]
- Rim, H.; Webb, C.E.; Yoon, S.; Schutz, B.E. Radiation Pressure Modeling for ICESat Precision Orbit Determination. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; pp. 21–24. [Google Scholar]
- Jiao, W.; Ding, Q.; Li, J.; Lu, X.; Feng, L.; Ma, J.; Chen, G. Monitoring and assessment of GNSS open services. J. Navig. 2011, 64 (Suppl. S1), S19–S29. [Google Scholar] [CrossRef]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar] [CrossRef]
- Standish, E.M. JPL Planetary and Lunar Ephemerides. DE405/LE405, JPL IOM 312.F-98-048. 1998. Available online: https://ssd.jpl.nasa.gov/planets/eph_export.html (accessed on 1 February 2025).
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Wu, J.; Wu, S.; Hajj, G.; Bertiger, W.; Lichten, S. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P. Improving carrier-phase ambiguity resolution in global GPS network solutions. J. Geod. 2005, 79, 103–110. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Noll, C.E.; Pavlis, E.C.; Lemoine, F.G.; Combrink, L.; Degnan, J.J.; Kirchner, G.; Schreiber, U. The ILRS: Approaching 20 years and planning for the future. J. Geod. 2019, 93, 2161–2180. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hugentobler, U. Enhanced solar radiation pressure modeling for Galileo satellites. J. Geod. 2015, 89, 283–297. [Google Scholar] [CrossRef]
- Bar-Sever, Y.; Kuang, D. New Empirically-Derived Solar Radiation Pressure Model for GPS Satellites; Technical Report; IPN Progress Report; JPL: La Cañada Flintridge, CA, USA, 2004; pp. 42–159. Available online: https://ipnpr.jpl.nasa.gov/progress_report/42-159/159I.pdf (accessed on 1 February 2025).
- Sibois, A.; Selle, C.; Desai, S.; Sibthorpe, A.; Weiss, J. GSPM13: An updated empirical model for solar radiation pressure forces acting on GPS satellites. In Proceedings of the IGS Workshop 2014, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]


| Manufacturer | Without SAR | With SAR |
|---|---|---|
| CAST | C19–C24 C36–C37 C41–C42 | C32-C33 C45-C46 |
| SECM | C25–C30 C34–C35 | C43-C44 |
| Components | Normal Direction | Area (m2) | The Early Ages of the Satellite | ||
|---|---|---|---|---|---|
| Reflectivity Coefficient () | Specularity Coefficient () | ||||
| Body | Surface component 1 | +X | 2.78 | 0.65 | 0 |
| Surface component 2 | −X | 1.75 | 0.08 | 0 | |
| Surface component 3 | −X | 1.03 | 0.87 | 1 | |
| Surface component 4 | +Y | 3.60 | 0.87 | 1 | |
| Surface component 5 | −Y | 3.60 | 0.87 | 1 | |
| Surface component 6 | +Z | 2.18 | 0.50 | 0 | |
| Surface component 7 | −Z | 2.18 | 0.65 | 0 | |
| Solar panels | Solar panels | 10.22 | 0.08 | 1 | |
| Solar panels | 10.22 | 0.08 | 1 | ||
| Models | Notes |
|---|---|
| Time span | 2023 |
| Observations | Undifferenced ionosphere-free code and phase combination of B1I and B3I |
| Elevation angle cutoff | 10° |
| Observation sampling | 300 s |
| Arc length | 24 h |
| Satellite attitude model | Continuous yaw model [15] |
| Geopotential | EGM2008 |
| N-body gravitation | Sun, Moon, Jupiter, Venus, Mars, Mercury, Uranus, Neptune, Saturn, Pluto, Charon as point mass, JPL DE405 [34] ephemeris used. |
| Solar radiation pressure | Different for solutions |
| Ionospheric delay | Eliminating first-order Ionospheric Errors with ionosphere-free combination |
| Tropospheric delay | Saastamoinen model with GMF mapping function and Zenith Tropospheric Delays are estimated as a piece-wise constant [35] |
| Phase wind-up | Corrected [36] |
| Satellite antenna | IGS20_2022.atx |
| Receiver antenna | IGS20_2022.atx |
| Parameters estimated | Six orbital elements, ECOM5 terms, station coordinates, satellite and receive clocks, zenith tropospheric delay, Earth rotation parameters, etc. |
| Ambiguity | Fixed double-difference ambiguity [37] |
| PRN | ECOM5 | ECOM5+CAST | ||
|---|---|---|---|---|
| Mean | STD Values | Mean | STD Values | |
| C19 | 2.9 | 5.3 | 2.7 | 3.6 |
| C20 | 3.7 | 4.9 | 2.3 | 3.4 |
| C21 | 4.0 | 4.5 | 2.4 | 3.4 |
| C22 | 3.6 | 4.6 | 3.6 | 3.7 |
| C23 | 3.2 | 5.8 | 3.2 | 4.2 |
| C24 | 4.5 | 4.6 | 4.0 | 3.9 |
| C32 | −2.1 | 5.8 | −1.1 | 4.1 |
| C33 | −1.8 | 6.0 | −0.4 | 3.7 |
| C36 | 2.7 | 4.0 | 2.3 | 3.7 |
| C37 | 1.8 | 5.4 | 2.1 | 4.4 |
| C41 | 3.5 | 5.5 | 3.3 | 4.3 |
| C42 | 3.2 | 4.6 | 3.1 | 3.4 |
| C45 | 5.9 | 9.0 | 5.3 | 9.1 |
| C46 | 6.2 | 8.7 | 6.1 | 8.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Zhang, X.; Wang, C.; Wang, H.; Ren, C.; Ma, F.; Zhao, X. Solar Radiation Pressure Modeling and Validation for BDS-3 MEO Satellites. Remote Sens. 2025, 17, 1068. https://doi.org/10.3390/rs17061068
Chen Q, Zhang X, Wang C, Wang H, Ren C, Ma F, Zhao X. Solar Radiation Pressure Modeling and Validation for BDS-3 MEO Satellites. Remote Sensing. 2025; 17(6):1068. https://doi.org/10.3390/rs17061068
Chicago/Turabian StyleChen, Qiuli, Xu Zhang, Chen Wang, Haihong Wang, Chen Ren, Fujian Ma, and Xinglong Zhao. 2025. "Solar Radiation Pressure Modeling and Validation for BDS-3 MEO Satellites" Remote Sensing 17, no. 6: 1068. https://doi.org/10.3390/rs17061068
APA StyleChen, Q., Zhang, X., Wang, C., Wang, H., Ren, C., Ma, F., & Zhao, X. (2025). Solar Radiation Pressure Modeling and Validation for BDS-3 MEO Satellites. Remote Sensing, 17(6), 1068. https://doi.org/10.3390/rs17061068








