Mapping Tropical Forested Wetlands Biomass with LiDAR: A Machine Learning Comparison
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Data
2.2.1. Sampling Method
2.2.2. Biomass Calculation
2.2.3. LiDAR Data
2.3. Modeling
2.3.1. Datasets
2.3.2. Algorithms Training
2.3.3. Correlation Analyses
2.3.4. Prediction of the Complete Study Area
3. Results
3.1. Forest Structure
3.2. Models
3.3. Uncertainty Analyses
3.4. AGB Prediction for the Complete Study Area
4. Discussion
4.1. Models
4.2. Spatial Patterns of AGB
4.3. Uncertainty Analyses
4.4. Potential Limitations of the Study
4.5. Future Monitoring Proposals
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LiDAR | Light Detection and Ranging |
| AGB | Aboveground Biomass |
| DBH | Diameter at Breast Height |
| RMSE | Root Mean Squared Error |
| SD | Standard Deviation |
| CoV | Coefficient of Variation |
| SAR | Synthetic Aperture Radar |
| InSAR | Interferometric Synthetic Aperture Radar |
| GEDI | Global Ecosystem Dynamics Investigation |
References
- Donato, D.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves Among the Most Carbon-Rich Forests in the Tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Alongi, D.M. Carbon Cycling and Storage in Mangrove Forests. Annu. Rev. Mar. Sci. 2014, 6, 195–219. [Google Scholar] [CrossRef] [PubMed]
- Lugo, A.E.; Brown, S.; Brinson, M. Ecosystems of the World, 15. Forested Wetlands; Elsevier Science Publishers: Amsterdam, The Netherlands, 1990; Volume 2, p. 527. ISBN 0444428127. [Google Scholar]
- Ainslie, W.B. Forested Wetlands. In Southern Forest Resource Assessment; Wear, D.N., Greis, J.G., Eds.; General Technical Report; U.S. Department of Agriculture, Forest Service: Washington, DC, USA, 2002; pp. 479–499. [Google Scholar]
- Hutchison, J.; Manica, A.; Swetnam, R.; Balmford, A.; Spalding, M. Predicting Global Patterns in Mangrove Forest Biomass. Conserv. Lett. 2014, 7, 233–240. [Google Scholar] [CrossRef]
- FAO. The World’s Mangroves 2000–2020; FAO: Rome, Italy, 2023. [Google Scholar]
- Murdiyarso, D.; Purbopuspito, J.; Kauffman, J.B.; Warren, M.W.; Sasmito, S.D.; Donato, D.C.; Manuri, S.; Krisnawati, H.; Taberima, S.; Kurnianto, S. The Potential of Indonesian Mangrove Forests for Global Climate Change Mitigation. Nat. Clim. Change 2015, 5, 1089–1092. [Google Scholar] [CrossRef]
- Sjögersten, S.; Barreda-Bautista, B.d.l.; Brown, C.; Boyd, D.; Lopez-Rosas, H.; Hernandez, M.E.; Monroy, R.; Rincon, M.; Vane, C.; Moss-Hayes, V.; et al. Coastal Wetland Ecosystems Deliver Large Carbon Stocks in Tropical Mexico. Geoderma 2021, 403, 115173. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Trejo, H.H.; Carmen Jesus Garcia, M.d.; Heider, C.; Contreras, W.M. Carbon Stocks of Mangroves and Losses Arising from Their Conversion to Cattle Pastures in the Pantanos de Centla, Mexico. Wetl. Ecol. Manag. 2016, 24, 203–216. [Google Scholar] [CrossRef]
- Giri, C. Chandra Observation and Monitoring of Mangrove Forests Using Remote Sensing: Opportunities and Challenges. Remote Sens. 2016, 8, 783. [Google Scholar] [CrossRef]
- Gao, G.; Beardall, J.; Jin, P.; Gao, L.; Xie, S.; Gao, K. A Review of Existing and Potential Blue Carbon Contributions to Climate Change Mitigation in the Anthropocene. J. Appl. Ecol. 2022, 59, 1686–1699. [Google Scholar] [CrossRef]
- Ribeiro, K.; Pacheco, F.S.; Ferreira, J.W.; Sousa-Neto, E.R.d.; Hastie, A.; Krieger Filho, G.C.; Alvalá, P.C.; Forti, M.C.; Ometto, J.P. Tropical Peatlands and Their Contribution to the Global Carbon Cycle and Climate Change. Glob. Change Biol. 2021, 27, 489–505. [Google Scholar] [CrossRef]
- Hilmi, N.; Chami, R.; Sutherland, M.D.; Hall-Spencer, J.M.; Lebleu, L.; Benitez, M.B.; Levin, L.A. The Role of Blue Carbon in Climate Change Mitigation and Carbon Stock Conservation. Front. Clim. 2021, 3, 710546. [Google Scholar] [CrossRef]
- Larrazábal, A.; McCall, M.K.; Mwampamba, T.H.; Skutsch, M. The Role of Community Carbon Monitoring for REDD+: A Review of Experiences. Curr. Opin. Environ. Sustain. 2012, 4, 707–716. [Google Scholar] [CrossRef]
- Theilade, I.; Rutishauser, E.; Poulsen, M.K. Community Assessment of Tropical Tree Biomass: Challenges and Opportunities for REDD+. Carbon Balance Manag. 2015, 10, 17. [Google Scholar] [CrossRef] [PubMed]
- Tokola, T. Remote Sensing Concepts and Their Applicability in REDD+ Monitoring. Curr. For. Rep. 2015, 1, 252–260. [Google Scholar] [CrossRef]
- Choudhary, B.; Dhar, V.; Pawase, A.S. Blue Carbon and the Role of Mangroves in Carbon Sequestration: Its Mechanisms, Estimation, Human Impacts and Conservation Strategies for Economic Incentives. J. Sea Res. 2024, 199, 102504. [Google Scholar] [CrossRef]
- Rahman; Lokollo, F.F.; Manuputty, G.D.; Hukubun, R.D.; Krisye; Maryono; Wawo, M.; Wardiatno, Y. A Review on the Biodiversity and Conservation of Mangrove Ecosystems in Indonesia. Biodivers. Conserv. 2024, 33, 875–903. [Google Scholar] [CrossRef]
- Manuri, S.; Andersen, H.-E.; McGaughey, R.J.; Brack, C. Assessing the Influence of Return Density on Estimation of Lidar-Based Aboveground Biomass in Tropical Peat Swamp Forests of Kalimantan, Indonesia. Int. J. Appl. Earth Obs. Geoinf. 2017, 56, 24–35. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved Allometric Models to Estimate the Aboveground Biomass of Tropical Trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Banin, L.; Phillips, O.L.; Baker, T.R.; Lewis, S.L.; Quesada, C.A.; Affum-Baffoe, K.; Arets, E.J.M.M.; Berry, N.J.; Bird, M.; et al. Height-Diameter Allometry of Tropical Forest Trees. Biogeosciences 2011, 8, 1081–1106. [Google Scholar] [CrossRef]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, Biomass, and Productivity of Mangrove Forests: A Review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Vorster, A.G.; Evangelista, P.H.; Stovall, A.E.L.; Ex, S. Variability and Uncertainty in Forest Biomass Estimates from the Tree to Landscape Scale: The Role of Allometric Equations. Carbon Balance Manag. 2020, 15, 8. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote Sensing of Mangrove Ecosystems: A Review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Simard, M.; Fatoyinbo, L.; Smetanka, C.; Rivera-Monroy, V.H.; Castañeda-Moya, E.; Thomas, N.; Van der Stocken, T. Mangrove Canopy Height Globally Related to Precipitation, Temperature and Cyclone Frequency. Nat. Geosci. 2019, 12, 40–45. [Google Scholar] [CrossRef]
- Saatchi, S. SAR Methods for Mapping and Monitoring Forest Biomass. In The Synthetic Aperture Radar (SAR) Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; Flores-Anderson, A.I., Herndon, K.E., Thapa, R.B., Cherrington, E., Eds.; NASA: Washington, DC, USA, 2019; pp. 207–247. [Google Scholar]
- Feyisa, S.; Soromessa, T.; Bekele, T.; Bereta, A.; Hailemariam, F. Above Ground Biomass Estimation Methods and Challenges: A Review. Int. J. Energy Technol. Policy 2020, 9, 12–25. [Google Scholar] [CrossRef]
- Singh, A.; Mahajan, S. A Review of SAR Image Processing for Mangrove Above Ground Biomass Estimation. J. Plant Sci. Res. 2023, 38, 779–789. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Barbier, N.; Couteron, P.; Ploton, P.; Vincent, G.; Herold, M.; Mermoz, S.; Saatchi, S.; Chave, J.; de Boissieu, F.; et al. Upscaling Forest Biomass from Field to Satellite Measurements: Sources of Errors and Ways to Reduce Them. Surv. Geophys. 2019, 40, 881–911. [Google Scholar] [CrossRef]
- Rodda, S.R.; Fararoda, R.; Gopalakrishnan, R.; Jha, N.; Réjou-Méchain, M.; Couteron, P.; Barbier, N.; Alfonso, A.; Bako, O.; Bassama, P.; et al. LiDAR-Based Reference Aboveground Biomass Maps for Tropical Forests of South Asia and Central Africa. Sci. Data 2024, 11, 334. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Feliciano, E.A.; Lagomasino, D.; Lee, S.K.; Trettin, C. Estimating Mangrove Aboveground Biomass from Airborne LiDAR Data: A Case Study from the Zambezi River Delta. Environ. Res. Lett. 2018, 13, 025012. [Google Scholar] [CrossRef]
- Stovall, A.E.L.; Fatoyinbo, T.; Thomas, N.M.; Armston, J.; Ebanega, M.O.; Simard, M.; Trettin, C.; Zogo, R.V.O.; Aken, I.A.; Debina, M.; et al. Comprehensive Comparison of Airborne and Spaceborne SAR and LiDAR Estimates of Forest Structure in the Tallest Mangrove Forest on Earth. Sci. Remote Sens. 2021, 4, 100034. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Castillo-Santiago, M.Á.; Mas, J.F.; Wheeler, C.E.; Andres-Mauricio, J.; Tun-Dzul, F.; George-Chacón, S.P.; Reyes-Palomeque, G.; Castellanos-Basto, B.; Vaca, R.; et al. Improving Aboveground Biomass Maps of Tropical Dry Forests by Integrating LiDAR, ALOS PALSAR, Climate and Field Data. Carbon Balance Manag. 2020, 15, 15. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground Biomass Density Models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) Lidar Mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Souza Pereira, F.R.d.; Kampel, M.; Soares, M.L.G.; Estrada, G.C.D.; Bentz, C.; Vincent, G. Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data. Remote Sens. 2018, 10, 637. [Google Scholar] [CrossRef]
- Heumann, B.W. Satellite Remote Sensing of Mangrove Forests: Recent Advances and Future Opportunities. Prog. Phys. Geogr. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Nie, S.; Fan, X.; Chen, H.; Ma, D.; Liu, J.; Zou, J.; Lin, Y.; et al. Estimating Forest Aboveground Biomass Using Small-Footprint Full-Waveform Airborne LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101922. [Google Scholar] [CrossRef]
- Garcia, M.; Saatchi, S.; Ferraz, A.; Silva, C.A.; Ustin, S.; Koltunov, A.; Balzter, H. Impact of Data Model and Point Density on Aboveground Forest Biomass Estimation from Airborne LiDAR. Carbon Balance Manag. 2017, 12, 4. [Google Scholar] [CrossRef] [PubMed]
- Zaki, N.A.M.; Latif, Z.A. Carbon Sinks and Tropical Forest Biomass Estimation: A Review on Role of Remote Sensing in Aboveground-Biomass Modelling. Geocarto Int. 2017, 32, 701–716. [Google Scholar] [CrossRef]
- Abbas, S.; Wong, M.S.; Wu, J.; Shahzad, N.; Irteza, S.M. Approaches of Satellite Remote Sensing for the Assessment of Above-Ground Biomass Across Tropical Forests: Pan-Tropical to National Scales. Remote Sens. 2020, 12, 3351. [Google Scholar] [CrossRef]
- Tran, T.V.; Reef, R.; Zhu, X. A Review of Spectral Indices for Mangrove Remote Sensing. Remote Sens. 2022, 14, 4868. [Google Scholar] [CrossRef]
- Solórzano, J.V.; Gallardo-Cruz, J.A.; González, E.J.; Peralta-Carreta, C.; Hernández-Gómez, M.; Oca, A.F.-M.d.; Cervantes-Jiménez, L.G. Contrasting the Potential of Fourier Transformed Ordination and Gray Level Co-Occurrence Matrix Textures to Model a Tropical Swamp Forest’s Structural and Diversity Attributes. J. Appl. Remote Sens. 2018, 12, 036006. [Google Scholar] [CrossRef]
- Bastin, J.-F.F.; Barbier, N.; Couteron, P.; Adams, B.; Shapiro, A.; Bogaert, J.; Cannière, C.D. Aboveground Biomass Mapping of African Forest Mosaics Using Canopy Texture Analysis: Towards a Regional Approach. Ecol. Appl. 2014, 24, 1984–2001. [Google Scholar] [CrossRef]
- Ballhorn, U.; Jubanski, J.; Kronseder, K.; Siegert, F. Airborne LiDAR Measurements to Estimate Tropical Peat Swamp Forest Above Ground Biomass. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1660–1663. [Google Scholar]
- Schlund, M.; Erasmi, S.; Scipal, K. Comparison of Aboveground Biomass Estimation from InSAR and LiDAR Canopy Height Models in Tropical Forests. IEEE Geo-Sci. Remote Sens. Lett. 2020, 17, 367–371. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote Sensing of Above-Ground Biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Englhart, S.; Jubanski, J.; Siegert, F. Quantifying Dynamics in Tropical Peat Swamp Forest Biomass with Multi-Temporal LiDAR Datasets. Remote Sens. 2013, 5, 2368–2388. [Google Scholar] [CrossRef]
- Salum, R.B.; Souza-Filho, P.W.M.; Simard, M.; Silva, C.A.; Fernandes, M.E.B.; Cougo, M.F.; Nascimento, W.d.; Rogers, K. Improving Mangrove Above-Ground Biomass Estimates Using LiDAR. Estuar. Coast. Shelf Sci. 2020, 236, 106585. [Google Scholar] [CrossRef]
- Zadbagher, E.; Marangoz, A.M.; Becek, K. Estimation of Above-Ground Biomass Using Machine Learning Approaches with InSAR and LiDAR Data in Tropical Peat Swamp Forest of Brunei Darussalam. IForest 2024, 17, 172–179. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine Learning in Geosciences and Remote Sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Johnson, L.K.; Mahoney, M.J.; Bevilacqua, E.; Stehman, S.V.; Domke, G.M.; Beier, C.M. Fine-Resolution Landscape-Scale Biomass Mapping Using a Spatiotemporal Patchwork of LiDAR Coverages. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103059. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Q.; Huang, H.; Huang, Y.; Tao, J.; Zhou, G.; Zhang, Y.; Yang, Y.; Lin, J. Aboveground Biomass of Typical Invasive Mangroves and Its Distribution Patterns Using UAV-LiDAR Data in a Subtropical Estuary: Maoling River Estuary, Guangxi, China. Ecol. Indic. 2022, 136, 108694. [Google Scholar] [CrossRef]
- Chen, M.; Qiu, X.; Zeng, W.; Peng, D. Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data. Remote Sens. 2022, 14, 1477. [Google Scholar] [CrossRef]
- Schuh, M.S.; Favarin, J.A.S.; Marchesan, J.; Alba, E.; Berra, E.F.; Pereira, R.S. Machine Learning and Generalized Linear Model Techniques to Predict Aboveground Biomass in Amazon Rainforest Using LiDAR Data. J. Appl. Remote Sens. 2020, 14, 034518. [Google Scholar] [CrossRef]
- Rajput, D.; Wang, W.J.; Chen, C.C. Evaluation of a Decided Sample Size in Machine Learning Applications. BMC Bioinform. 2023, 24, 48. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Réjou-Méchain, M.; Tanguy, A.; Piponiot, C.; Chave, J.; Hérault, B. Biomass: An r Package for Estimating Above-Ground Biomass and Its Uncertainty in Tropical Forests. Methods Ecol. Evol. 2017, 8, 1163–1167. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An r Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Kuhn, M.; Wickham, H. Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles. 2020. Available online: https://cran.r-project.org/web/packages/tidymodels/index.html (accessed on 10 March 2025).
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Xgboost: Extreme Gradient Boosting. 2024. Available online: https://cran.r-project.org/web/packages/xgboost/index.html (accessed on 10 March 2025).
- Kuhn, M.; Vaughan, D.; Hvitfeldt, E. Yardstick: Tidy Characterizations of Model Performance. 2024. Available online: https://cran.r-project.org/web/packages/yardstick/index.html (accessed on 10 March 2025).
- Dancho, M. Modeltime: The Tidymodels Extension for Time Series Modeling. 2024. Available online: https://cran.r-project.org/web/packages/modeltime/index.html (accessed on 10 March 2025).
- Solórzano, J.V.; Gallardo-Cruz, J.A.; Peralta-Carreta, C.; Martínez-Camilo, R.; Oca, A.F.-M. de Plant Community Composition Patterns in Relation to Microtopography and Distance to Water Bodies in a Tropical Forested Wetland. Aquat. Bot. 2020, 167, 103295. [Google Scholar] [CrossRef]
- Zanne, A.E.; Lopez-Gonzalez, G.; Coomes, D.A.; Ilic, J.; Jansen, S.; Lewis, S.L.; Miller, R.B.; Swenson, N.G.; Wiemann, M.C.; Chave, J. Towards a Worldwide Wood Economics Spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error Propagation and Scaling for Tropical Forest Biomass Estimates. Philosophical transactions of the Royal Society of London. Ser. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef]
- Woods, M.; Lim, K.; Treitz, P. Predicting Forest Stand Variables from LiDAR Data in the Great Lakes—St. Lawrence Forest of Ontario. For. Chron. 2008, 84, 827–839. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, W.; Ji, Y.; Huang, J.; Huang, G.; Wang, L. Total and Component Forest Aboveground Biomass Inversion via LiDAR-Derived Features and Machine Learning Algorithms. Front. Plant Sci. 2023, 14, 1258521. [Google Scholar] [CrossRef]
- Salas, E.A.L. Waveform LiDAR Concepts and Applications for Potential Vegetation Phenology Monitoring and Modeling: A Comprehensive Review. Geo-Spat. Inf. Sci. 2021, 24, 179–200. [Google Scholar] [CrossRef]
- Cushman, K.C.; Armston, J.; Dubayah, R.; Duncanson, L.; Hancock, S.; Janík, D.; Král, K.; Krůček, M.; Minor, D.M.; Tang, H.; et al. Impact of Leaf Phenology on Estimates of Aboveground Biomass Density in a Deciduous Broadleaf Forest from Simulated GEDI Lidar. Environ. Res. Lett. 2023, 18, 065009. [Google Scholar] [CrossRef]
- Borsah, A.A.; Nazeer, M.; Wong, M.S. LIDAR-Based Forest Biomass Remote Sensing: A Review of Metrics, Methods, and Assessment Criteria for the Selection of Allometric Equations. Forests 2023, 14, 2095. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Korpela, I.; Polvivaara, A.; Hovi, A.; Junttila, S.; Holopainen, M. Influence of Phenology on Waveform Features in Deciduous and Coniferous Trees in Airborne LiDAR. Remote Sens. Environ. 2023, 293, 113618. [Google Scholar] [CrossRef]
- Simonson, W.; Allen, H.; Coomes, D. Effect of Tree Phenology on Lidar Measurement of Mediterranean Forest Structure. Remote Sens. 2018, 10, 659. [Google Scholar] [CrossRef]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Guerra-Santos, J.J.; Cerón-Bretón, R.M.; Cerón-Bretón, J.G.; Damián-Hernández, D.L.; Sánchez-Junco, R.C.; Carmen Guevara Carrió, E. del Estimation of the Carbon Pool in Soil and Above-Ground Biomass Within Mangrove Forests in Southeast Mexico Using Allometric Equations. J. For. Res. 2014, 25, 129–134. [Google Scholar] [CrossRef]
- Adame, M.F.; Gamboa, J.N.; Torres, O.; Kauffman, J.B.; Reza, M.; Caamal, J.P.; Herrera-Silveira, J.A.; Medina, I. Carbon Stocks of Tropical Coastal Wetlands Within the Karstic Landscape of the Mexican Caribbean. PLoS ONE 2013, 8, e56569. [Google Scholar] [CrossRef]
- Troche-Souza, C.; Priego-Santander, A.; Equihua, J.; Vázquez-Balderas, B. Spatial Distribution of Carbon Stocks Along Protected and Non-Protected Coastal Wetland Ecosystems in the Gulf of Mexico. Ecosystems 2024, 72, 724–738. [Google Scholar] [CrossRef]
- Ávila-Acosta, C.R.; Domínguez-Domínguez, M.; Vázquez-Navarrete, C.J.; Acosta-Pech, R.G.; Martínez-Zurimendi, P. Aboveground Biomass and Carbon Storage in Mangrove Forests in Southeastern Mexico. Resources 2024, 13, 41. [Google Scholar] [CrossRef]
- Velázquez-Pérez, C.; Hernández, C.; Romero-Berny, E.; Jesús-Navarrete, A. Estructura del manglar y su influencia en el almacén de carbono en la Reserva La Encrucijada, Chiapas, México. Madera Bosques 2023, 25, e2531885. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N.C. Status and Distribution of Mangrove Forests of the World Using Earth Observation Satellite Data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Trettin, C.C.; Dai, Z.; Tang, W.; Lagomasino, D.; Thomas, N.; Lee, S.K.; Simard, M.; Ebanega, M.O.; Stoval, A.; Fatoyinbo, T.E. Mangrove Carbon Stocks in Pongara National Park, Gabon. Estuar. Coast. Shelf Sci. 2021, 259, 107432. [Google Scholar] [CrossRef]
- Rahman, M.S.; Donoghue, D.N.M.; Bracken, L.J.; Mahmood, H. Biomass Estimation in Mangrove Forests: A Comparison of Allometric Models Incorporating Species and Structural Information. Environ. Res. Lett. 2021, 16, 124002. [Google Scholar] [CrossRef]
- Zhao, F.; Guo, Q.; Kelly, M. Allometric Equation Choice Impacts Lidar-Based Forest Biomass Estimates: A Case Study from the Sierra National Forest, CA. Agric. For. Meteorol. 2012, 165, 64–72. [Google Scholar] [CrossRef]
- Price, C.A.; Branoff, B.; Cummins, K.; Kakaï, R.G.; Ogurcak, D.; Papeș, M.; Ross, M.; Whelan, K.R.T.; Schroeder, T.A. Global Data Compilation Across Climate Gradients Supports the Use of Common Allometric Equations for Three Transatlantic Mangrove Species. Ecol. Evol. 2024, 14, e70577. [Google Scholar] [CrossRef]
- Rutishauser, E.; Noor’an, F.; Laumonier, Y.; Halperin, J.; Rufi’ie; Hergoualch, K.; Verchot, L. Generic Allometric Models Including Height Best Estimate Forest Biomass and Carbon Stocks in Indonesia. For. Ecol. Manag. 2013, 307, 219–225. [Google Scholar] [CrossRef]
- Day, J.W.; Conner, W.H.; Ley-Lou, F.; Day, R.H.; Navarro, A.M. The Productivity and Composition of Mangrove Forests, Laguna de Términos, Mexico. Aquat. Bot. 1987, 27, 267–284. [Google Scholar] [CrossRef]
- Chavez, S.; Wdowinski, S.; Lagomasino, D.; Castañeda-Moya, E.; Fatoyinbo, T.; Moyer, R.P.; Smoak, J.M. Estimating Structural Damage to Mangrove Forests Using Airborne Lidar Imagery: Case Study of Damage Induced by the 2017 Hurricane Irma to Mangroves in the Florida Everglades, USA. Sensors 2023, 23, 6669. [Google Scholar] [CrossRef]
- Picard, N.; Bosela, F.B.; Rossi, V. Reducing the Error in Biomass Estimates Strongly Depends on Model Selection. Ann. For. Sci. 2015, 72, 811–823. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Muller-Landau, H.C.; Detto, M.; Thomas, S.C.; Toan, T.L.; Saatchi, S.S.; Barreto-Silva, J.S.; Bourg, N.A.; Bunyavejchewin, S.; Butt, N.; et al. Local Spatial Structure of Forest Biomass and Its Consequences for Remote Sensing of Carbon Stocks. Biogeosciences 2014, 11, 6827–6840. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Reyes-Palomeque, G.; Castillo-Santiago, M.Á.; George-Chacón, S.P.; Huechacona-Ruiz, A.H.; Tun-Dzul, F.; Rondon-Rivera, D.; Dupuy, J.M. Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests. Remote Sens. 2018, 10, 1586. [Google Scholar] [CrossRef]
- Dubayah, R.; Armston, J.; Healey, S.P.; Bruening, J.M.; Patterson, P.L.; Kellner, J.R.; Duncanson, L.; Saarela, S.; Ståhl, G.; Yang, Z.; et al. GEDI Launches a New Era of Biomass Inference from Space. Environ. Res. Lett. 2022, 17, 095001. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Healey, S.P.; Patterson, P.L.; Yang, Z.; Andersen, H.-E.; Dubayah, R.O.; Qi, W.; Duncanson, L.I.; Armston, J.D.; et al. Comparing Frameworks for Biomass Prediction for the Global Ecosystem Dynamics Investigation. Remote Sens. Environ. 2022, 278, 113074. [Google Scholar] [CrossRef]
- Tommaso, S.D.; Wang, S.; Lobell, D.B. Combining GEDI and Sentinel-2 for Wall-to-Wall Mapping of Tall and Short Crops. Environ. Res. Lett. 2021, 16, 125002. [Google Scholar] [CrossRef]
- Adrah, E.; Wong, J.P.; Yin, H. Integrating GEDI, Sentinel-2, and Sentinel-1 Imagery for Tree Crops Mapping. Remote Sens. Environ. 2025, 319, 114644. [Google Scholar] [CrossRef]
- Doyog, N.D.; Lin, C. Generating Wall-to-Wall Canopy Height Information from Discrete Data Provided by Spaceborne LiDAR System. Forests 2024, 15, 482. [Google Scholar] [CrossRef]
- Wang, C.; Elmore, A.J.; Numata, I.; Cochrane, M.A.; Lei, S.; Hakkenberg, C.R.; Li, Y.; Zhao, Y.; Tian, Y. A Framework for Improving Wall-to-Wall Canopy Height Mapping by Integrating GEDI LiDAR. Remote Sens. 2022, 14, 3618. [Google Scholar] [CrossRef]



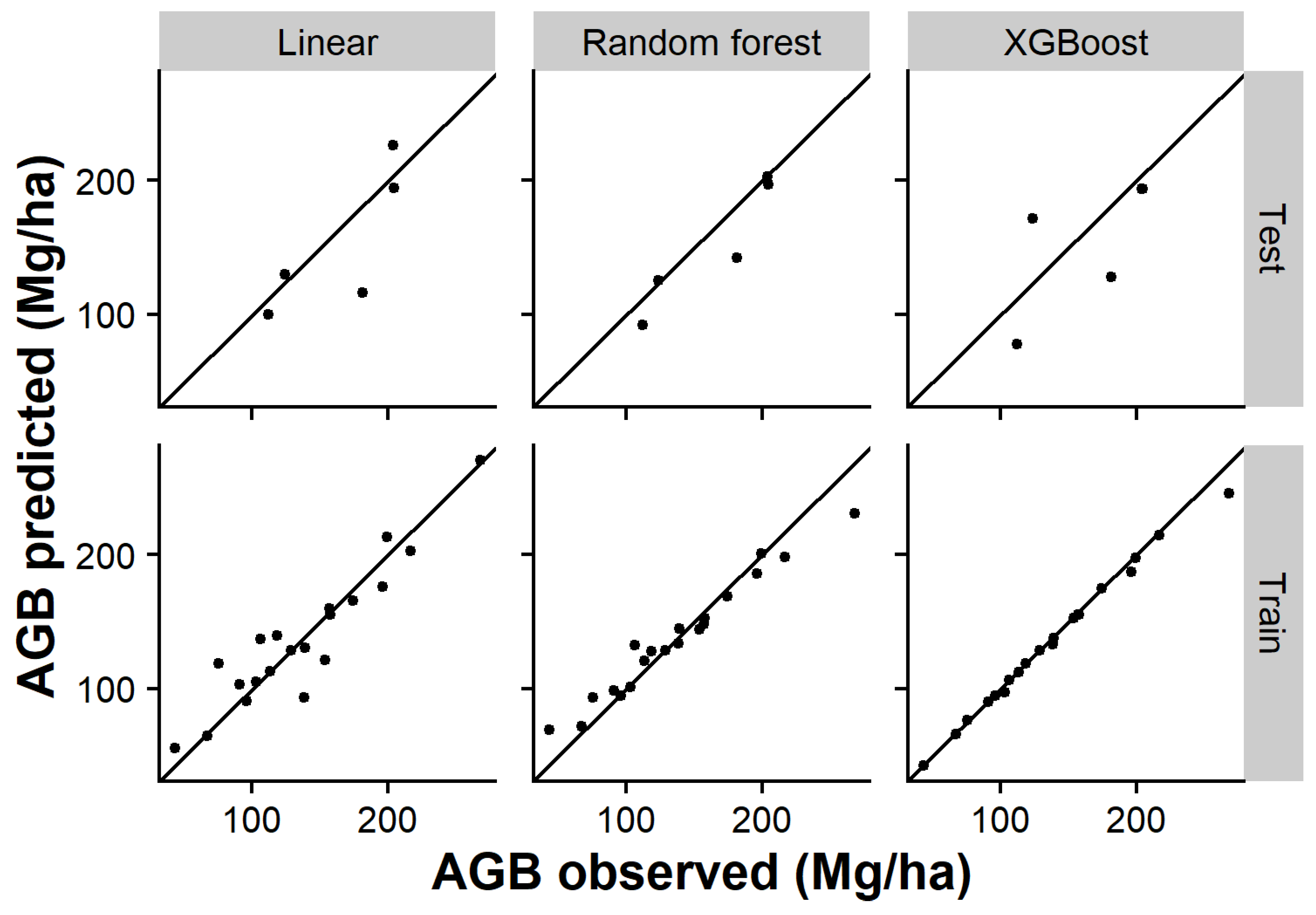
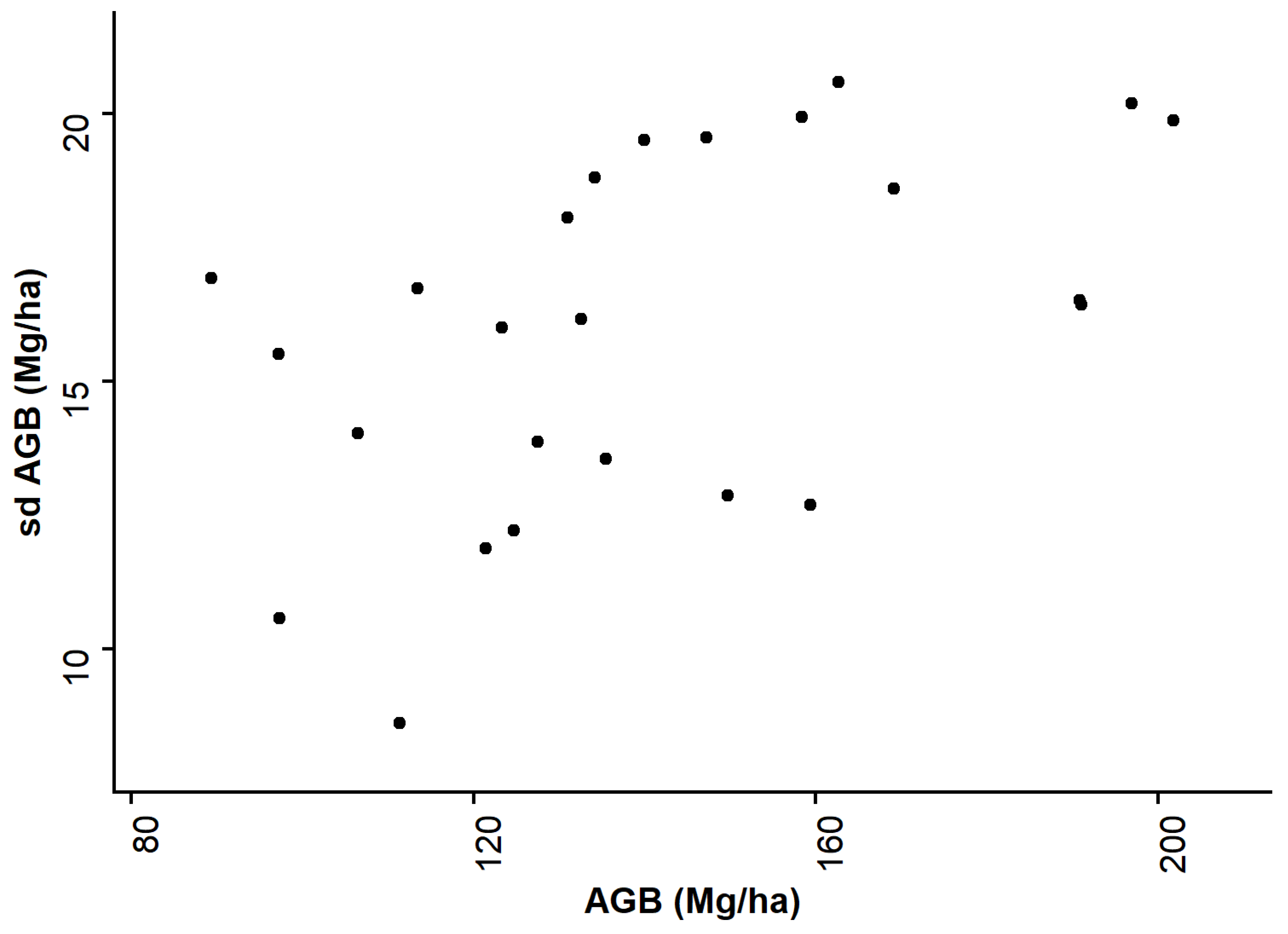

| Dataset | Model | Var 1 | Var 2 | Var 3 | RMSE | rRMSE (%) | R2 | MAE | MAPE |
|---|---|---|---|---|---|---|---|---|---|
| Training | Random forest | zmean | zq35 | p4th | 14.31 | 10.43 | 0.97 | 10.58 | 9.91 |
| XGBoost | zq55 | p4th | zq95 | 5.80 | 4.23 | 0.99 | 2.94 | 1.76 | |
| Linear | zmean | p5th | p2th | 19.60 | 14.29 | 0.87 | 14.02 | 12.54 | |
| Test | Random forest | zmean | zq35 | p4th | 20.24 | 12.25 | 0.88 | 14.25 | 9.19 |
| XGBoost | zq55 | p4th | zq95 | 36.22 | 21.91 | 0.46 | 31.46 | 21.83 | |
| Linear | zmean | p5th | p2th | 31.80 | 19.24 | 0.63 | 23.34 | 13.63 |
| Var 1 | Var 2 | Variable Importance | Pearson Coeff | p |
|---|---|---|---|---|
| AGB | zmean | 100 | 0.85 | <0.001 |
| AGB | zq35 | 93.7 | 0.87 | <0.001 |
| AGB | p4th | 73.7 | 0.53 | 0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solórzano, J.V.; Peralta-Carreta, C.; Gallardo-Cruz, J.A. Mapping Tropical Forested Wetlands Biomass with LiDAR: A Machine Learning Comparison. Remote Sens. 2025, 17, 1076. https://doi.org/10.3390/rs17061076
Solórzano JV, Peralta-Carreta C, Gallardo-Cruz JA. Mapping Tropical Forested Wetlands Biomass with LiDAR: A Machine Learning Comparison. Remote Sensing. 2025; 17(6):1076. https://doi.org/10.3390/rs17061076
Chicago/Turabian StyleSolórzano, Jonathan V., Candelario Peralta-Carreta, and J. Alberto Gallardo-Cruz. 2025. "Mapping Tropical Forested Wetlands Biomass with LiDAR: A Machine Learning Comparison" Remote Sensing 17, no. 6: 1076. https://doi.org/10.3390/rs17061076
APA StyleSolórzano, J. V., Peralta-Carreta, C., & Gallardo-Cruz, J. A. (2025). Mapping Tropical Forested Wetlands Biomass with LiDAR: A Machine Learning Comparison. Remote Sensing, 17(6), 1076. https://doi.org/10.3390/rs17061076







