Prediction of Vegetation Indices Series Based on SWAT-ML: A Case Study in the Jinsha River Basin
Abstract
:1. Introduction
2. Materials and Methods
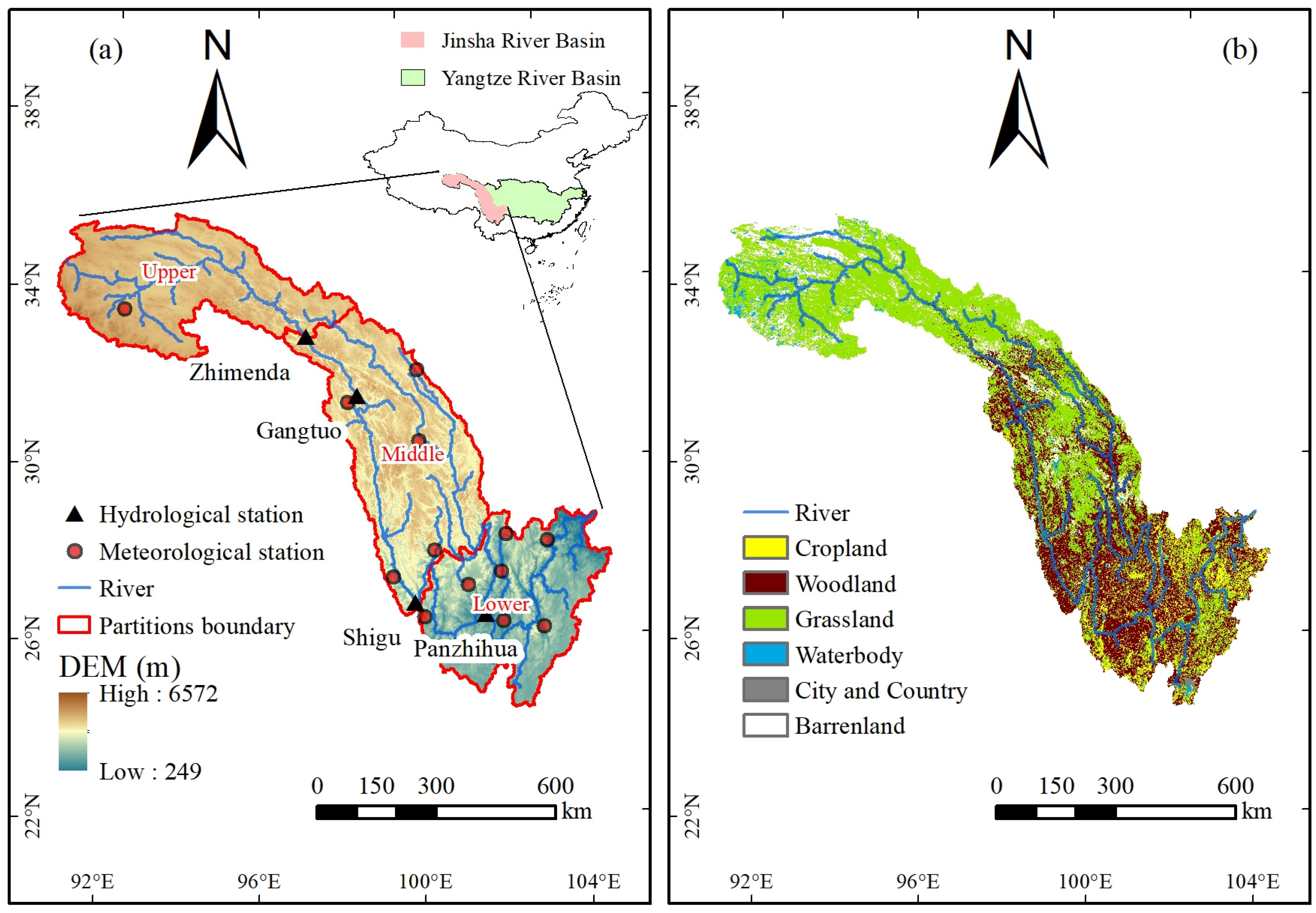
2.1. Study Area and Data
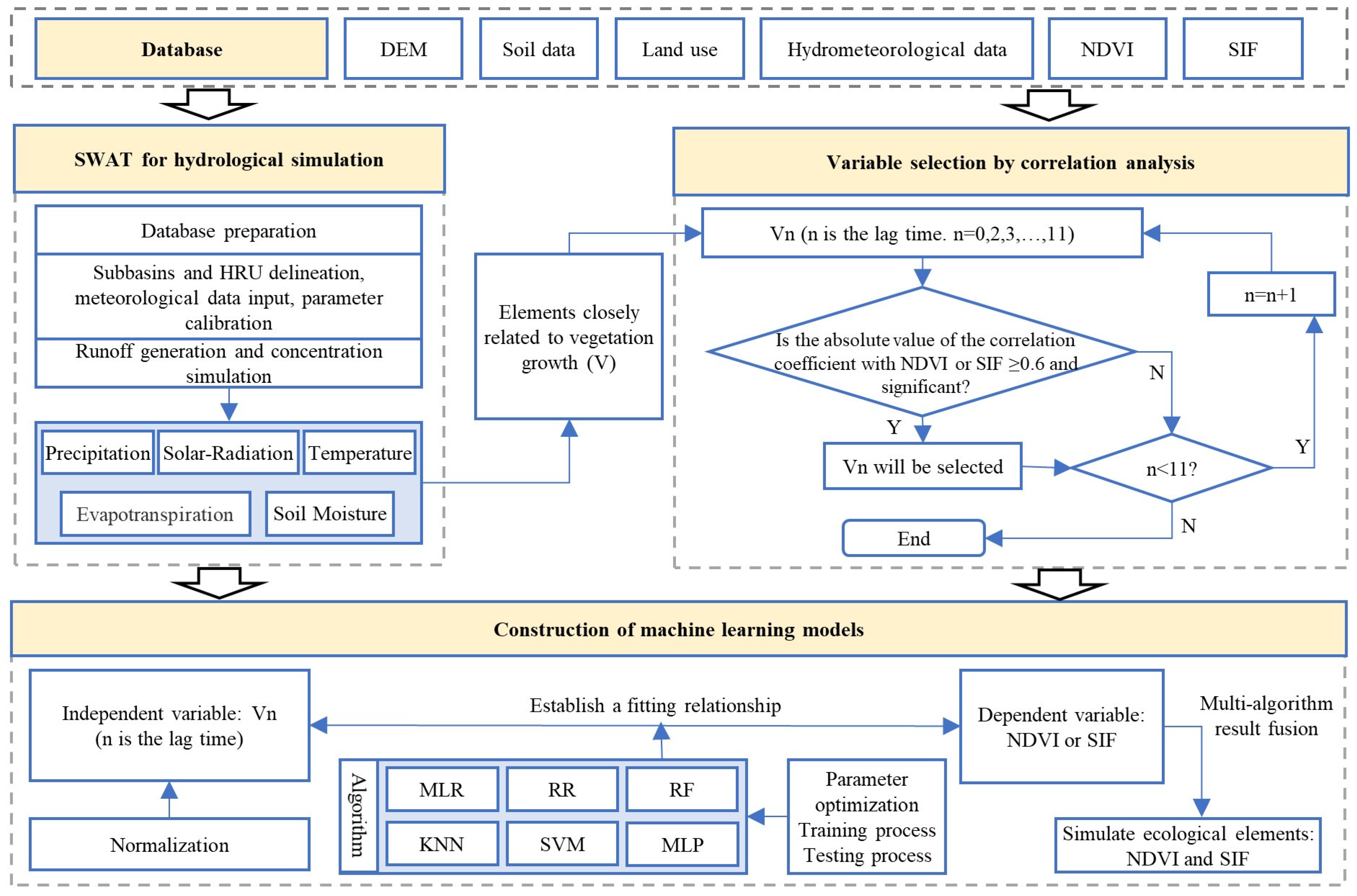
2.2. Framework
2.3. SWAT Model for Hydrological Simulation
2.4. Machine Learning Method for Vegetation Simulation
2.5. Ecohydrological Trend Analysis
3. Results
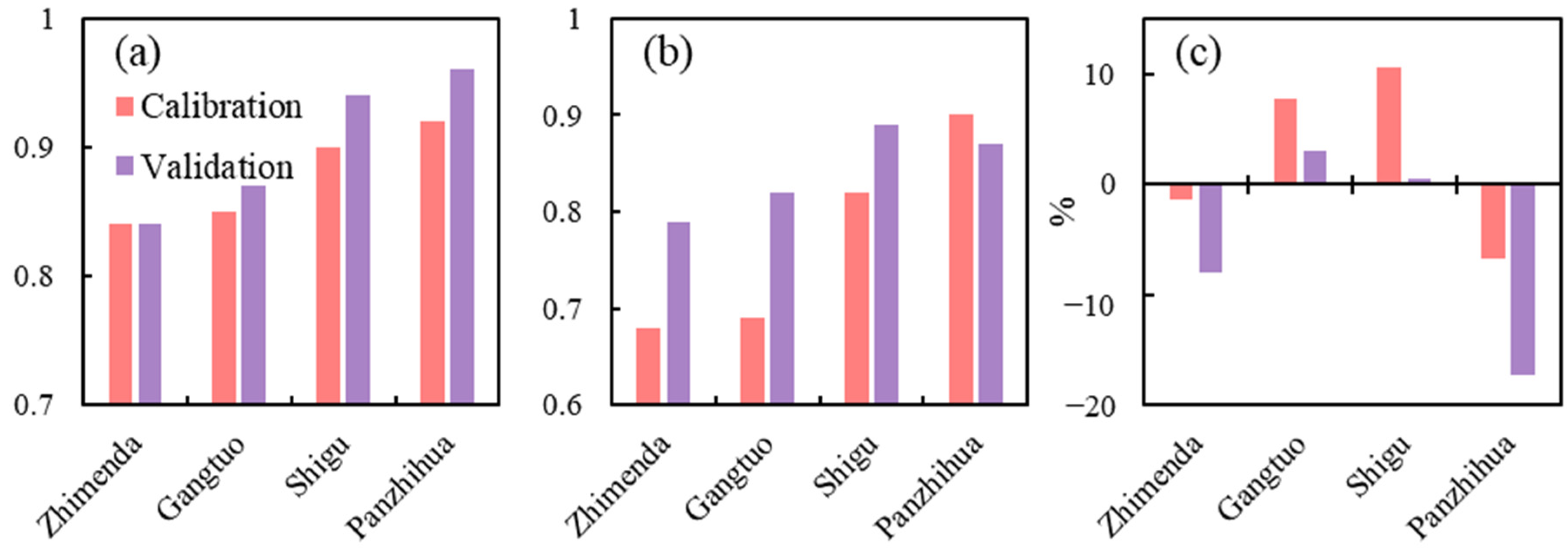
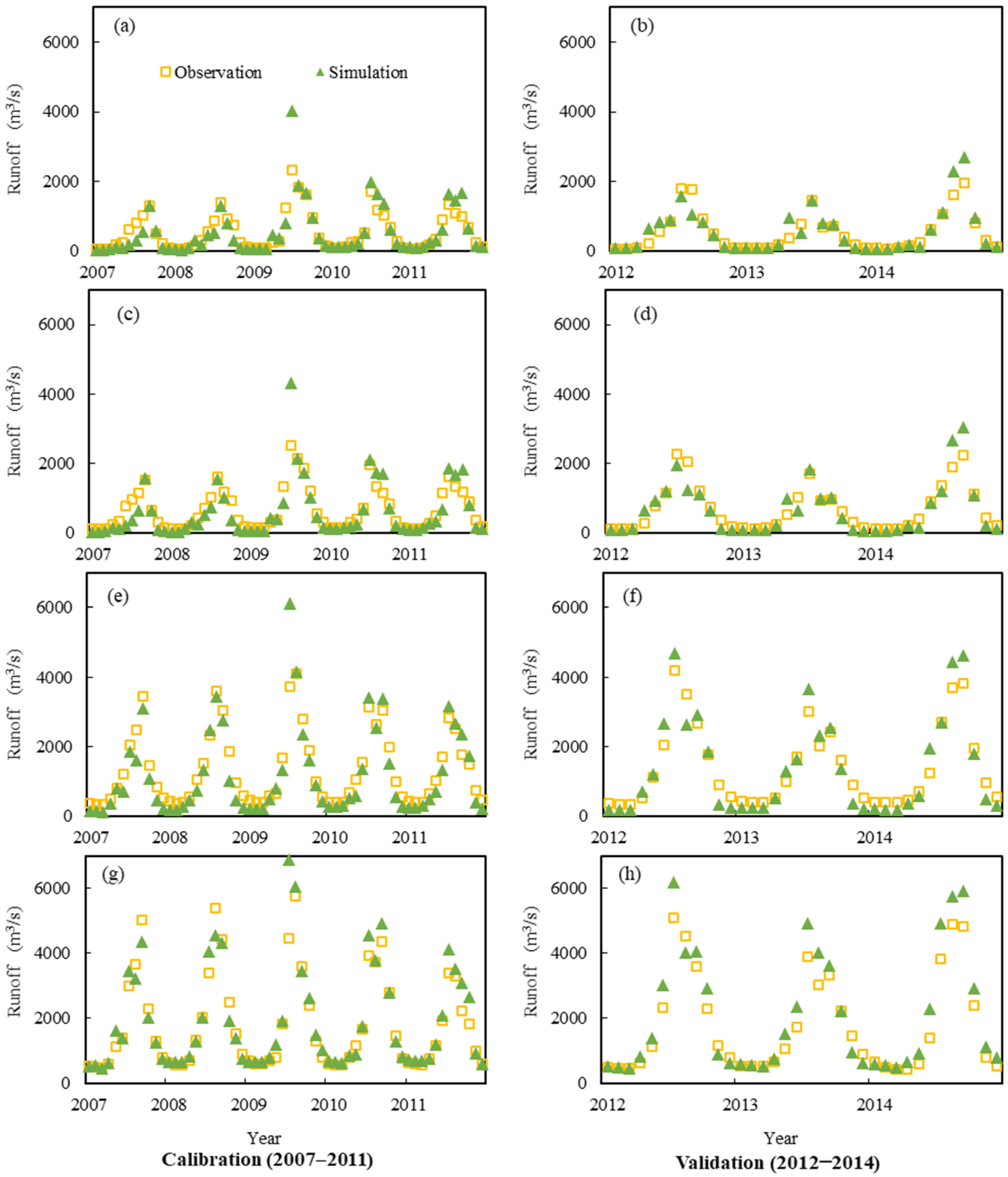
3.1. SWAT Model Calibration and Validation
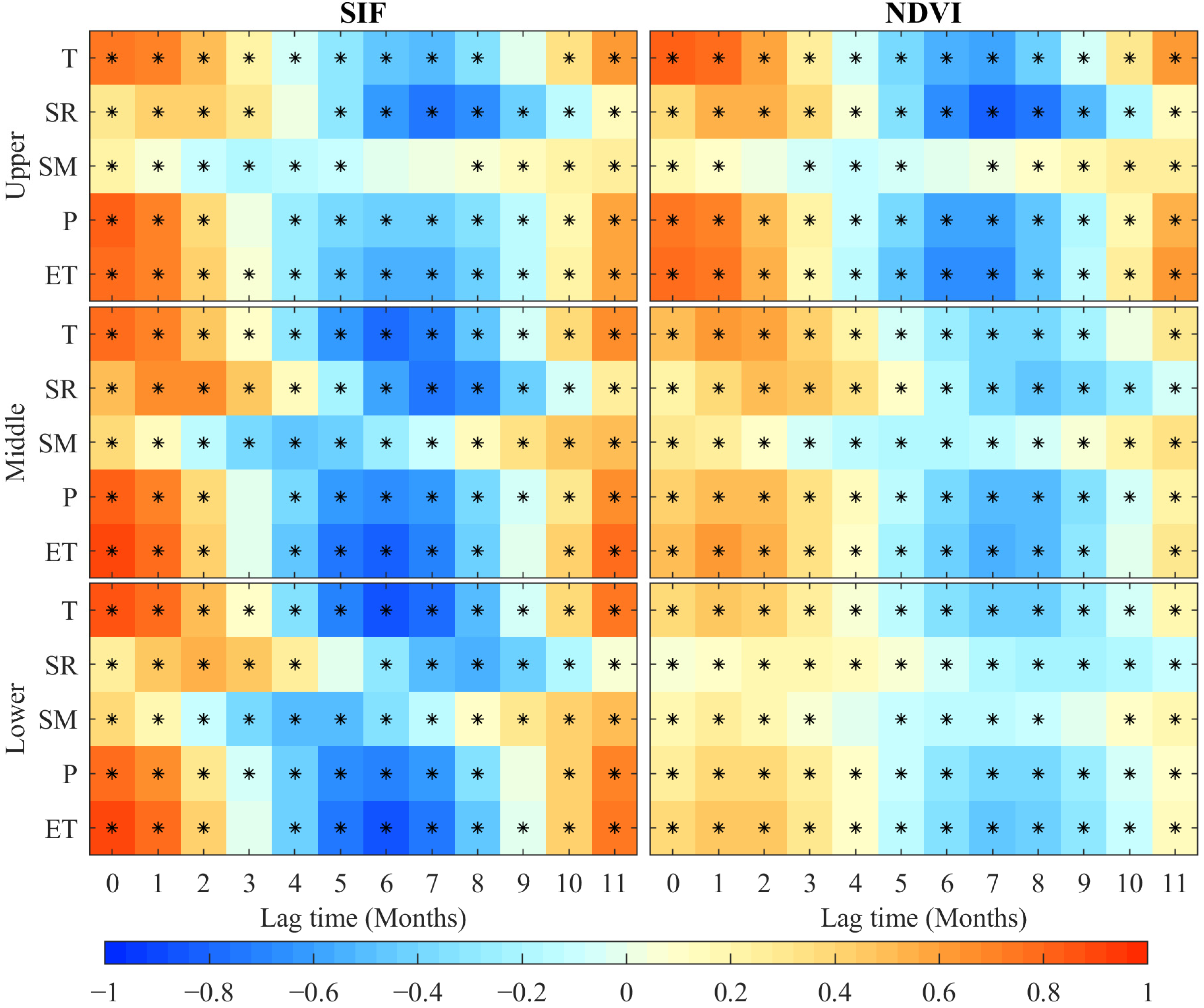
3.2. Correlation Between Vegetation Indicators and Hydrometeorological Elements
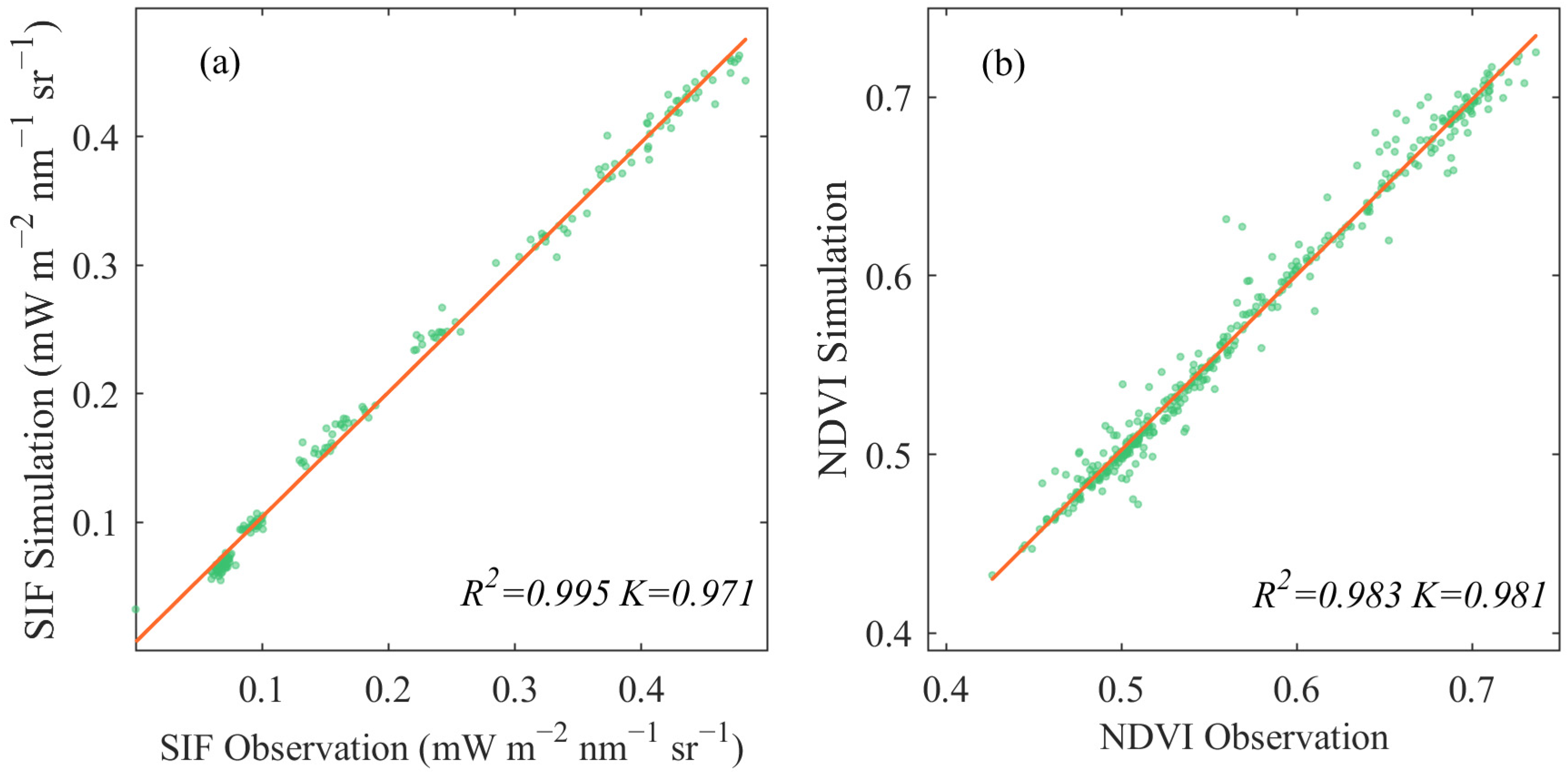
3.3. Vegetation Dynamic Simulation Performance
3.4. Spatial and Temporal Evolution of Vegetation
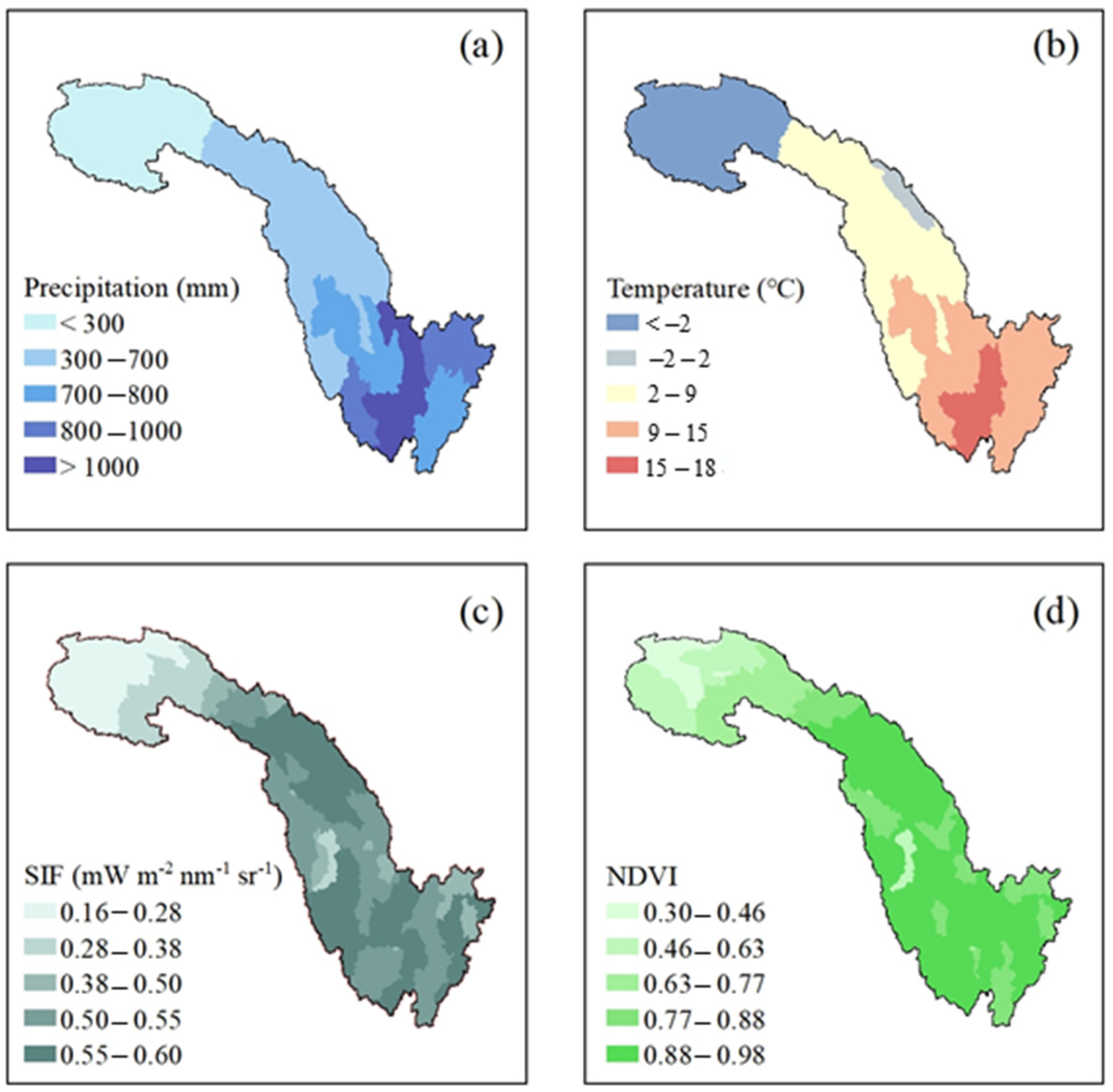
3.4.1. Multiyear Average Vegetation and Meteorological Conditions
3.4.2. Regional Interannual Vegetation and Climate Change
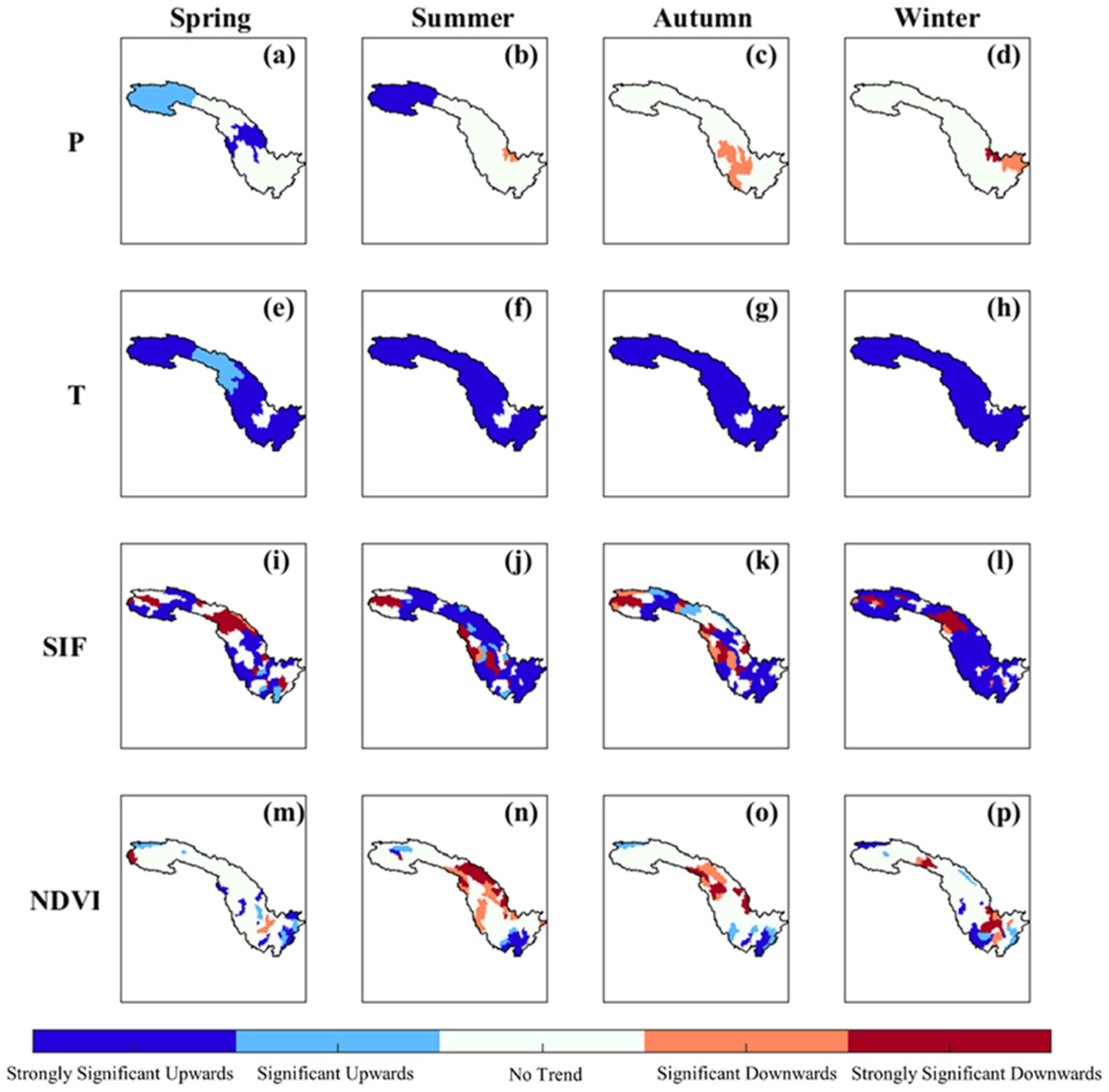
3.4.3. Seasonal Vegetation and Climate Change in Spatial Distribution
4. Discussion
4.1. Performance of the SWAT-ML in the JRB
4.2. Applicability and Potential of the SWAT-ML
4.3. Limitations and Prospects
5. Conclusions
- (1)
- The SWAT-ML framework can simulate the hydrological process, performing well at each hydrological station satisfactorily (R2 > 0.84, NS > 0.68 in the training set; R2 > 0.79, NS > 0.79 in the test set), and establishing the regression relationship between hydrometeorological elements and SIF (NS > 0.98, MSE < 0.001 in the training set; NS > 0.77, MSE < 0.004 in the test set).
- (2)
- NDVI is more sensitive to temperature than precipitation in the whole basin, while SIF is more sensitive to precipitation than temperature in the upper and middle reaches. Compared with NDVI, SIF shows a closer correlation with ecohydrological elements in the middle and lower reaches and is a more suitable indicator to characterize the vegetation in the middle and lower reaches of the Jinsha River Basin.
- (3)
- In the context of climate warming, the annual mean values of SIF and NDVI increased, and the annual maximum values of SIF and NDVI decreased in the upper reaches. The midstream showed a decreasing trend in greenness and an increasing physiological activity in summer, autumn, and throughout the year. The intensity of physiological activity and greenness increased downstream.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiao, Y.; Lei, H.; Yang, D.; Huang, M.; Liu, D.; Yuan, X. Impact of vegetation dynamics on hydrological processes in a semi-arid basin by using a land surface-hydrology coupled model. J. Hydrol. 2017, 551, 116–131. [Google Scholar] [CrossRef]
- Lin, H. Earth’s Critical Zone and hydropedology: Concepts, characteristics, and advances. Hydrol. Earth Syst. Sci. 2010, 14, 25–45. [Google Scholar] [CrossRef]
- Song, X.; Zhou, H.; Liu, G. Assessment of vegetation conservation status in plateau areas based on multi-view and difference identification. Concurr. Comput. Pract. Exp. 2022, e7223. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Cao, L.; Feng, R.; Pan, Y. Response of NDVI of Natural Vegetation to Climate Changes and Drought in China. Land 2021, 10, 966. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, S.; Luo, P.; Xie, D.; Zhu, W. Watershed Ecohydrological Processes in a Changing Environment: Opportunities and Challenges. Water 2022, 14, 1502. [Google Scholar] [CrossRef]
- Gu, X.; Jamshidi, S.; Gu, L.; Nadi, S.; Wang, D.; Cammarano, D.; Sun, H. Drought dynamics in California and Mississippi: A wavelet analysis of meteorological to agricultural drought transition. J. Environ. Manag. 2024, 370, 122883. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhu, X.; Gao, X.; Zhao, X. An Evaluation of Future Climate Change Impacts on Key Elements of the Water–Carbon Cycle Using a Physics-Based Ecohydrological Model in Sanchuan River Basin, Loess Plateau. Remote Sens. 2024, 16, 3581. [Google Scholar] [CrossRef]
- Ding, Y.; He, X.; Zhou, Z.; Hu, J.; Cai, H.; Wang, X.; Li, L.; Xu, J.; Shi, H. Response of vegetation to drought and yield monitoring based on NDVI and SIF. CATENA 2022, 219, 106328. [Google Scholar] [CrossRef]
- Fu, B.; Lan, F.; Xie, S.; Liu, M.; He, H.; Li, Y.; Liu, L.; Huang, L.; Fan, D.; Gao, E.; et al. Spatio-temporal coupling coordination analysis between marsh vegetation and hydrology change from 1985 to 2019 using LandTrendr algorithm and Google Earth Engine. Ecol. Indic. 2022, 137, 108763. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, L.; He, Y.; Cao, S.; Li, H.; Ran, L.; Ding, Y.; Filonchyk, M. LSTM time series NDVI prediction method incorporating climate elements: A case study of Yellow River Basin, China. J. Hydrol. 2024, 629, 130518. [Google Scholar] [CrossRef]
- Zhang, X. Reconstruction of a complete global time series of daily vegetation index trajectory from long-term AVHRR data. Remote Sens. Environ. 2015, 156, 457–472. [Google Scholar] [CrossRef]
- Zheng, K.; Tan, L.; Sun, Y.; Wu, Y.; Duan, Z.; Xu, Y.; Gao, C. Impacts of climate change and anthropogenic activities on vegetation change: Evidence from typical areas in China. Ecol. Indic. 2021, 126, 107648. [Google Scholar] [CrossRef]
- Qu, S.; Wang, L.; Lin, A.; Yu, D.; Yuan, M.; Li, C. Distinguishing the impacts of climate change and anthropogenic factors on vegetation dynamics in the Yangtze River Basin, China. Ecol. Indic. 2020, 108, 105724. [Google Scholar] [CrossRef]
- Shi, Y.; Jin, N.; Ma, X.; Wu, B.; He, Q.; Yue, C.; Yu, Q. Attribution of climate and human activities to vegetation change in China using machine learning techniques. Agric. For. Meteorol. 2020, 294, 108146. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Li, M.; Cao, S.; Zhu, Z.; Wang, Z.; Myneni, R.B.; Piao, S. Spatiotemporally consistent global dataset of the GIMMS Normalized Difference Vegetation Index (PKU GIMMS NDVI) from 1982 to 2022. Earth Syst. Sci. Data 2023, 15, 4181–4203. [Google Scholar] [CrossRef]
- Zhang, Y.; Joiner, J.; Alemohammad, S.H.; Zhou, S.; Gentine, P. A global spatially contiguous solar-induced fluorescence (CSIF) dataset using neural networks. Biogeosciences 2018, 15, 5779–5800. [Google Scholar] [CrossRef]
- Xue, J.; Huete, A.; Liu, Z.; Wang, Y.; Lu, X. Estimation of global ecosystem isohydricity from solar-induced chlorophyll fluorescence and meteorological datasets. Remote Sens. Environ. 2024, 307, 114168. [Google Scholar] [CrossRef]
- Feldman, A.F.; Konings, A.G.; Gentine, P.; Cattry, M.; Wang, L.; Smith, W.K.; Biederman, J.A.; Chatterjee, A.; Joiner, J.; Poulter, B. Large global-scale vegetation sensitivity to daily rainfall variability. Nature 2024, 636, 380–384. [Google Scholar] [CrossRef]
- Crow, W.T.; Koster, R.D.; Reichle, R.H.; Sharif, H.O. Relevance of time-varying and time-invariant retrieval error sources on the utility of spaceborne soil moisture products. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Chaney, N.; Guan, K.; Sadri, S.; Yuan, X.; Olang, L.; Amani, A.; Ali, A.; Demuth, S.; et al. A Drought Monitoring and Forecasting System for Sub-Sahara African Water Resources and Food Security. Bull. Am. Meteorol. Soc. 2014, 95, 861–882. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mishra, A.; Trenberth, K.E. Climate Change and Drought: A Perspective on Drought Indices. Curr. Clim. Change Rep. 2018, 4, 145–163. [Google Scholar] [CrossRef]
- Tapas, M.R.; Etheridge, R.; Tran, T.-N.-D.; Le, M.-H.; Hinckley, B.; van Nguyen, T.; Lakshmi, V. Evaluating combinations of rainfall datasets and optimization techniques for improved hydrological predictions using the SWAT+ model. J. Hydrol. Reg. Stud. 2025, 57, 102134. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Zhang, J.; Hou, Y.; Shen, M.; Chen, J.; Xu, C. Impacts of climate change and LULC change on runoff in the Jinsha River Basin. J. Geogr. Sci. 2020, 30, 85–102. [Google Scholar] [CrossRef]
- Benos, L.; Tagarakis, A.C.; Dolias, G.; Berruto, R.; Kateris, D.; Bochtis, D. Machine Learning in Agriculture: A Comprehensive Updated Review. Sensors 2021, 21, 3758. [Google Scholar] [CrossRef]
- Saleem, M.H.; Potgieter, J.; Arif, K.M. Automation in Agriculture by Machine and Deep Learning Techniques: A Review of Recent Developments. Precis. Agric. 2021, 22, 2053–2091. [Google Scholar] [CrossRef]
- Naghdyzadegan Jahromi, M.; Zand-Parsa, S.; Razzaghi, F.; Jamshidi, S.; Didari, S.; Doosthosseini, A.; Pourghasemi, H.R. Developing machine learning models for wheat yield prediction using ground-based data, satellite-based actual evapotranspiration and vegetation indices. Eur. J. Agron. 2023, 146, 126820. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H.; Hu, Q.; Jiang, M. Analysis of runoff generation driving factors based on hydrological model and interpretable machine learning method. J. Hydrol. Reg. Stud. 2022, 42, 101139. [Google Scholar] [CrossRef]
- Li, W.; Xin, Q.; Zhou, X.; Zhang, Z.; Ruan, Y. Comparisons of numerical phenology models and machine learning methods on predicting the spring onset of natural vegetation across the Northern Hemisphere. Ecol. Indic. 2021, 131, 108126. [Google Scholar] [CrossRef]
- He, N.; Guo, W.; Lan, J.; Yu, Z.; Wang, H. The impact of human activities and climate change on the eco-hydrological processes in the Yangtze River basin. J. Hydrol. Reg. Stud. 2024, 53, 101753. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Tang, Z.-Y.; Jiang, Z.-Q.; Xu, Y.; Liu, Y.; Zhang, H.-R. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Zhang, X.-F.; Yan, H.-C.; Yue, Y.; Xu, Q.-X. Quantifying natural and anthropogenic impacts on runoff and sediment load: An investigation on the middle and lower reaches of the Jinsha River Basin. J. Hydrol. Reg. Stud. 2019, 25, 100617. [Google Scholar] [CrossRef]
- Ju, X.; Wang, Y.; Wang, D.; Singh, V.P.; Xu, P.; Wu, J.; Ma, T.; Liu, J.; Zhang, J. A time-varying drought identification and frequency analyzation method: A case study of Jinsha River Basin. J. Hydrol. 2021, 603, 126864. [Google Scholar] [CrossRef]
- Liu, X.; Peng, D.; Xu, Z. Identification of the Impacts of Climate Changes and Human Activities on Runoff in the Jinsha River Basin, China. Adv. Meteorol. 2017, 2017, 4631831. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Wang, J.; Zhao, Y.; Chen, J.; Xu, C. Impacts of Climate Change and Land-Use Change on Hydrological Extremes in the Jinsha River Basin. Water 2019, 11, 1398. [Google Scholar] [CrossRef]
- Sun, G.; Hu, Z.; Wang, J.; Ma, W.; Gu, L.; Sun, F.; Xie, Z.; Yan, X. The spatial heterogeneity of land surface conditions and its influence on surface fluxes over a typical underlying surface in the Tibetan Plateau. Theor. Appl. Clim. 2019, 135, 221–235. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, Y.; Liu, S.; Wang, Y.; Fu, Q.; Shi, H. Estimating the Applicability of NDVI and SIF to Gross Primary Productivity and Grain-Yield Monitoring in China. Remote Sens. 2022, 14, 3237. [Google Scholar] [CrossRef]
- Wei, Y.; Sun, S.; Liang, D.; Jia, Z. Spatial–temporal variations of NDVI and its response to climate in China from 2001 to 2020. Int. J. Digit. Earth 2022, 15, 1463–1484. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, H.; Huang, L.; Ouyang, W. Changing runoff due to temperature and precipitation variations in the dammed Jinsha River. J. Hydrol. 2020, 582, 124500. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment Part I: Model development1. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large RWER basin with point and nonpoint sources1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Le Gates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ge, W.; Deng, L.; Wang, F.; Han, J. Quantifying the contributions of human activities and climate change to vegetation net primary productivity dynamics in China from 2001 to 2016. Sci. Total Environ. 2021, 773, 145648. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Glob. Change Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef]
- Huang, W.; Henderson, M.; Liu, B.; Su, Y.; Zhou, W.; Ma, R.; Chen, M.; Zhang, Z. Cumulative and Lagged Effects: Seasonal Characteristics of Drought Effects on East Asian Grasslands. Remote Sens. 2024, 16, 3478. [Google Scholar] [CrossRef]
- Pearson, K. VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Sousa, S.I.V.; Martins, F.G.; Alvim-Ferraz, M.C.M.; Pereira, M.C. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ. Model. Softw. 2007, 22, 97–103. [Google Scholar] [CrossRef]
- Walker, E.; Birch, J.B. Influence Measures in Ridge Regression. Technometrics 1988, 30, 221–227. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Peterson, L. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP). Geomat. Approaches Model. Land Change Scenar. 2018, 451–455. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Hao, F.; Wu, Y.; Li, C.; Xu, Y. Evaluating the contributions of climate change and human activities to runoff in typical semi-arid area, China. J. Hydrol. 2020, 590, 125555. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Sun, R.; Chen, S.; Su, H. Climate Dynamics of the Spatiotemporal Changes of Vegetation NDVI in Northern China from 1982 to 2015. Remote Sens. 2021, 13, 187. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Lin, H.; Montenegro, A.; Zhu, X. NDVI and vegetation phenology dynamics under the influence of sunshine duration on the Tibetan plateau. Int. J. Climatol. 2015, 35, 687–698. [Google Scholar] [CrossRef]
- Niu, J.; Chen, J.; Sun, L.; Sivakumar, B. Time-lag effects of vegetation responses to soil moisture evolution: A case study in the Xijiang basin in South China. Stoch. Environ. Res. Risk Assess. 2018, 32, 2423–2432. [Google Scholar] [CrossRef]
- Ma, M.; Wang, Q.; Liu, R.; Zhao, Y.; Zhang, D. Effects of climate change and human activities on vegetation coverage change in northern China considering extreme climate and time-lag and -accumulation effects. Sci. Total Environ. 2023, 860, 160527. [Google Scholar] [CrossRef]
- Liu, L.; Yang, X.; Zhou, H.; Liu, S.; Zhou, L.; Li, X.; Yang, J.; Han, X.; Wu, J. Evaluating the utility of solar-induced chlorophyll fluorescence for drought monitoring by comparison with NDVI derived from wheat canopy. Sci. Total Environ. 2018, 625, 1208–1217. [Google Scholar] [CrossRef]
- Liu, F.; Qin, Q.; Zhan, Z. A novel dynamic stretching solution to eliminate saturation effect in NDVI and its application in drought monitoring. Chin. Geogr. Sci. 2012, 22, 683–694. [Google Scholar] [CrossRef]
- Peng, B.; Guan, K.; Zhou, W.; Jiang, C.; Frankenberg, C.; Sun, Y.; He, L.; Köhler, P. Assessing the benefit of satellite-based Solar-Induced Chlorophyll Fluorescence in crop yield prediction. Int. J. Appl. Earth Obs. Geoinf. 2020, 90, 102126. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Leng, P.; Shang, G.-F.; Zhang, X.; Li, Z.-L. Sun-induced chlorophyll fluorescence is superior to satellite vegetation indices for predicting summer maize yield under drought conditions. Comput. Electron. Agric. 2023, 205, 107615. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, Y.; Ata-Ul-Karim, S.T.; Ge, Q.; Li, X.; Xiao, J. Integrating climate and satellite remote sensing data for predicting county-level wheat yield in China using machine learning methods. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102861. [Google Scholar] [CrossRef]
- Dong, Z.; Jia, W.; Sarukkalige, R.; Fu, G.; Meng, Q.; Wang, Q. Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China. Water 2020, 12, 3293. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X. Long-term trend analysis for temperature in the Jinsha River Basin in China. Theor. Appl. Clim. 2012, 109, 591–603. [Google Scholar] [CrossRef]
- Krishnaswamy, J.; John, R.; Joseph, S. Consistent response of vegetation dynamics to recent climate change in tropical mountain regions. Glob. Change Biol. 2014, 20, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Wahid, A.; Gelani, S.; Ashraf, M.; Foolad, M.R. Heat tolerance in plants: An overview. Environ. Exp. Bot. 2007, 61, 199–223. [Google Scholar] [CrossRef]
- Toledo, M.; Poorter, L.; Peña-Claros, M.; Alarcón, A.; Balcázar, J.; Leaño, C.; Licona, J.C.; Llanque, O.; Vroomans, V.; Zuidema, P.; et al. Climate is a stronger driver of tree and forest growth rates than soil and disturbance. J. Ecol. 2011, 99, 254–264. [Google Scholar] [CrossRef]
- Qu, S.; Wang, L.; Lin, A.; Zhu, H.; Yuan, M. What drives the vegetation restoration in Yangtze River basin, China: Climate change or anthropogenic factors? Ecol. Indic. 2018, 90, 438–450. [Google Scholar] [CrossRef]
- Qiu, R.; Li, X.; Han, G.; Xiao, J.; Ma, X.; Gong, W. Monitoring drought impacts on crop productivity of the U.S. Midwest with solar-induced fluorescence: GOSIF outperforms GOME-2 SIF and MODIS NDVI, EVI, and NIRv. Agric. For. Meteorol. 2022, 323, 109038. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Xu, C.; Jiang, Y.; Su, Z.; Liu, Y.; Lyu, J. Assessing the impacts of Grain-for-Green Programme on ecosystem services in Jinghe River basin, China. Ecol. Indic. 2022, 137, 108757. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Wu, D.; Chen, W.; Zhao, X.; Hou, M.; Li, A.; Zhu, Y. LAI-indicated vegetation dynamic in ecologically fragile region: A case study in the Three-North Shelter Forest program region of China. Ecol. Indic. 2021, 120, 106932. [Google Scholar] [CrossRef]

| Parameters | Definition | Value Range for Calibration | Best Value |
|---|---|---|---|
| CN2 | Initial SCS runoff curve number for moisture condition II | [−0.2, 0.2] | −0.19 |
| ALPHA_BF | Baseflow alpha factor (days) | [−0.5, 0.6] | 0.56 |
| GW_DELAY | Groundwater delay (days) | [0.8, 1] | 242.57 |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur (mm) | [−0.8, 0.8] | 43.01 |
| ALPHA_BNK | Baseflow alpha factor for bank storage | [0, 1] | 0.44 |
| ESCO | Soil evaporation compensation factor | [−0.2, 0.4] | 0.80 |
| SOL_AWC | Available water capacity of the soil layer | [30, 450] | 0.31 |
| SOL_BD | Moist bulk density | [0, 0.2] | −0.15 |
| GW_REVAP | Groundwater "revap" coefficient | [0, 0.3] | 0.05 |
| SFTMP | Snowfall temperature | [0, 500] | −0.56 |
| SOL_K | Saturated hydraulic conductivity | [5, 130] | 0.39 |
| CH_N2 | Manning’s "n" value for the main channel | [−5, 5] | 0.18 |
| CH_K2 | Effective hydraulic conductivity in main channel alluvium | [0, 1] | 44.62 |
| No. | Dependent Variable | Independent Variable | Machine Learning Algorithms | Regions | Training Period | Testing Period |
|---|---|---|---|---|---|---|
| 1 | SIF | Tn, SRn, SMn, Pn and ETn (n was the selected lag time by correlation analysis) | MLR, RR, RF, KNN, SVM and MLP | Upper, middle, and lower reaches | 2000–2012 | 2013–2014 |
| 2 | NDVI | 1982–2006 | 2007–2014 |
| District | Method | SIF | NDVI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | ||||||
| NS | MSE | NS | MSE | NS | MSE | NS | MSE | ||
| Upper | MLR | 0.711 | 0.005 | 0.723 | 0.005 | 0.721 | 0.007 | 0.702 | 0.007 |
| RR | 0.677 | 0.005 | 0.699 | 0.005 | 0.709 | 0.007 | 0.710 | 0.007 | |
| RF | 0.977 | 0.000 | 0.775 | 0.004 | 0.978 | 0.001 | 0.780 | 0.005 | |
| KNN | 0.896 | 0.002 | 0.701 | 0.005 | 0.895 | 0.003 | 0.687 | 0.007 | |
| SVM | 0.821 | 0.003 | 0.817 | 0.003 | 0.806 | 0.005 | 0.801 | 0.005 | |
| MLP | 0.759 | 0.004 | 0.766 | 0.004 | 0.791 | 0.005 | 0.800 | 0.005 | |
| Middle | MLR | 0.880 | 0.004 | 0.868 | 0.005 | 0.409 | 0.009 | 0.320 | 0.009 |
| RR | 0.850 | 0.005 | 0.845 | 0.005 | 0.392 | 0.009 | 0.316 | 0.009 | |
| RF | 0.985 | 0.001 | 0.887 | 0.004 | 0.938 | 0.001 | 0.426 | 0.007 | |
| KNN | 0.928 | 0.002 | 0.897 | 0.004 | 0.670 | 0.005 | 0.318 | 0.009 | |
| SVM | 0.913 | 0.003 | 0.895 | 0.004 | 0.518 | 0.007 | 0.405 | 0.008 | |
| MLP | 0.892 | 0.004 | 0.890 | 0.004 | 0.413 | 0.008 | 0.312 | 0.009 | |
| Lower | MLR | 0.892 | 0.003 | 0.860 | 0.005 | 0.244 | 0.007 | 0.227 | 0.007 |
| RR | 0.884 | 0.003 | 0.855 | 0.005 | 0.235 | 0.007 | 0.240 | 0.007 | |
| RF | 0.989 | 0.000 | 0.862 | 0.005 | 0.923 | 0.001 | 0.303 | 0.006 | |
| KNN | 0.946 | 0.002 | 0.865 | 0.005 | 0.590 | 0.004 | 0.182 | 0.007 | |
| SVM | 0.928 | 0.002 | 0.882 | 0.004 | 0.375 | 0.006 | 0.328 | 0.006 | |
| MLP | 0.886 | 0.003 | 0.831 | 0.006 | 0.178 | 0.007 | 0.126 | 0.008 |
| District | Climate Factors | Z Value | Slope | Trend |
|---|---|---|---|---|
| Upper | Precipitation | 2.83 | 4.08 | Strongly significant upwards |
| Temperature | 4.94 | 0.06 | Strongly significant upwards | |
| Middle | Precipitation | −0.45 | −0.69 | Insignificant downwards |
| Temperature | 5.09 | 0.05 | Strongly Significant upwards | |
| Lower | Precipitation | −1.50 | −2.91 | Insignificant downwards |
| Temperature | 5.50 | 0.06 | Strongly significant upwards |
| District | Climate Factors | Z Value | Slope | Trend |
|---|---|---|---|---|
| Upper | SIFmax | −0.20 | −1.91 × 10−4 | Insignificant downwards |
| SIFave | 1.29 | 2.17 × 10−4 | Insignificant upwards | |
| NDVImax | −0.42 | −1.81 × 10−4 | Insignificant downwards | |
| NDVIave | 0.11 | 2.32 × 10−5 | Insignificant upwards | |
| Middle | SIFmax | 3.70 | 1.25 × 10−3 | Strongly significantly upwards |
| SIFave | 2.46 | 3.12 × 10−4 | Strongly significantly upwards | |
| NDVImax | −2.93 | −7.40 × 10−4 | Strongly significantly downwards | |
| NDVIave | −0.67 | −1.75 × 10−4 | Insignificant downwards | |
| Lower | SIFmax | 3.24 | 9.21 × 10−4 | Strongly significantly upwards |
| SIFave | 2.68 | 3.97 × 10−4 | Strongly significantly upwards | |
| NDVImax | 2.68 | 1.04 × 10−3 | Strongly significantly upwards | |
| NDVIave | 1.84 | 4.67 × 10−4 | Insignificant upwards |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhao, Q.; Fei, J.; Cui, L.; Zhang, X.; Yin, G. Prediction of Vegetation Indices Series Based on SWAT-ML: A Case Study in the Jinsha River Basin. Remote Sens. 2025, 17, 958. https://doi.org/10.3390/rs17060958
Li C, Zhao Q, Fei J, Cui L, Zhang X, Yin G. Prediction of Vegetation Indices Series Based on SWAT-ML: A Case Study in the Jinsha River Basin. Remote Sensing. 2025; 17(6):958. https://doi.org/10.3390/rs17060958
Chicago/Turabian StyleLi, Chong, Qianzuo Zhao, Junyuan Fei, Lei Cui, Xiu Zhang, and Guodong Yin. 2025. "Prediction of Vegetation Indices Series Based on SWAT-ML: A Case Study in the Jinsha River Basin" Remote Sensing 17, no. 6: 958. https://doi.org/10.3390/rs17060958
APA StyleLi, C., Zhao, Q., Fei, J., Cui, L., Zhang, X., & Yin, G. (2025). Prediction of Vegetation Indices Series Based on SWAT-ML: A Case Study in the Jinsha River Basin. Remote Sensing, 17(6), 958. https://doi.org/10.3390/rs17060958





