Comparison of the Reflectivities from Precipitation Measurement Radar Onboard the FY-3G Satellite and Ground-Based S-Band Dual-Polarization Radars

Abstract

Fengyun-3G (FY-3G), successfully launched on 16 April 2023, is China’s first and the third in the world satellite dedicated to precipitation measurement. In this study, the reflectivity factors of the FY-3G satellite Precipitation Measurement Radar (PMR) are analyzed and compared with ground-based S-band dual-polarized radar (GR) data for typical precipitation events in parts of southern China during April–August 2024. By performing preprocessing and spatiotemporal matching, 169,657 matched pairs of FY-3G PMR and GR datasets are obtained, from which the agreement of reflectivity between FY-3G PMR and GR and the sensitivities to different precipitation types and phase states are evaluated. The results show that the reflectivity factors of FY-3G PMR and GR have a strong positive correlation, with an overall correlation coefficient of 0.82, especially in the stratiform precipitation. In addition, FY-3G PMR agrees with GR well in moderate precipitation, but systematically underestimates reflectivity in heavy rain rates and overestimates in light rain rates. Furthermore, FY-3G PMR has high accuracy in detecting liquid precipitation below the bright band, although with some underestimation of reflectivity for ice-phase precipitation above the bright band. Nevertheless, FY-3G PMR still provides valuable information on ice-phase precipitation. Overall, PMR has great potential for application in the monitoring of stratiform and liquid precipitation, but more complete processing is needed when applying PMR observations to heavy precipitation and complex meteorological conditions.

1. Introduction

Precipitation is a crucial component of the global hydrometeorological cycle, and its spatial and temporal variations have a significant impact on human life and economic activities. Accurate measurement of precipitation is essential for both social and scientific needs.

Unlike the traditional observation instruments, such as rain gauges and ground-based Doppler radars (GRs), which have a limited detection range and are available over land only, spaceborne radars (SRs) have a wider detection range and are able to provide data over the sea. Therefore, SRs have a great advantage in detecting sea surface precipitation and are capable of obtaining high-resolution information on the vertical structure of precipitation [1]. The Tropical Rainfall Measurement Mission (TRMM) satellite carried the first spaceborne precipitation radar (PR) operating at Ku-band and provided a lot of important information on rainfall in tropical and sub-tropical regions [2]. Building upon the success of TRMM, the Global Precipitation Measurement (GPM) mission carrying an advanced dual-frequency precipitation radar (DPR) was launched by the National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA) in February 2014. It covered a wider range of latitudes from 65°S to 65°N and was more sensitive to light rain rates and snowfall than TRMM [3].

As the successor of GPM, the Fengyun-3G (FY-3G) satellite, China’s first low-inclination-orbit precipitation measurement satellite, was launched on 16 April 2023. It successfully completed over six months of trial operations on 23 October 2023, and was officially put into operation on 1 May 2024. Similar to GPM DPR, the Precipitation Measuring Radar (PMR), as a key sensor onboard FY-3G satellite, consisting of Ku (13.6 GHz) and Ka (35.5 GHz) dual-frequency-band radars, detects precipitation actively and is capable of providing three-dimensional precipitation structure from top to bottom. It enhances the capability of spaceborne precipitation measurement and improves understanding of storm structures, cloud microphysics and dynamics of mesoscale weather systems, leading to more accurate weather forecasts [4,5]. A detailed comparison of TRMM PR, GPM DPR and FY-3G PMR is provided in

Table 1. Comparison of FY-3G PMR with TRMM PR and GPM DPR.

Radar Systems	FY-3G PMR	GPM-DPR	TRMM PR
Frequency band	Ku (13.6 GHz), Ka (35.5 GHz)		Ku (13.6 GHz)
Vertical resolution (m)	250	250 (Ku), 250/500 (Ka)	250
Horizontal resolution (km)	5	5	5
Orbital periods (min)	93	91	91.3
Swath width (km)	303	245 (Ku), 115 (Ka)	215
Vertical detectable range (km)	18~−5 ASL	18~−5 ASL(Ku), 18~−3 ASL (Ka)	15~−5 ASL
Minimum detectable precipitation rate (mm/h)	0.5 (18 dBZ, Ku), 0.2 (12 dBZ, Ka)	0.5 (18 dBZ, Ku), 0.2 (12 dBZ, Ka)	0.7
Coverage	50°N–50°S	65°N–65°S	35°N~35°S
Antenna peak sidelobe (dB)	≤−30	≤−25	≤−25

.

Validating data accuracy is the first and critical step for the future application of FY-3G PMR. Direct comparison with satellite-based measurements such as GPM DPR would be the best and clearest way to examine the performance of FY-3G PMR since they have similar properties. However, up to the beginning of this study, only one warm-season set of data of FY-3G were available. If comparing to GPM DPR, the matched sample size would be too small to obtain statistically significant results since these two satellites have different orbits and trajectories, and the time separations are different when their trajectories cross, creating a challenge for finding more events that the two satellites simultaneously detect in the same precipitation region. Instead, comparing FY-3G PMR with the ground-based system, especially with GRs, which have a denser network coverage and higher time resolution (6 min) and avoid the variables retrieval compared to disdrometers [6], seems to be a feasible approach to achieve more matched samples and robust results.

Actually, space–ground radar comparison tests have been widely used in TRMM PR (e.g., Liao and Meneghini, 2009 [7]) and GPM DPR (e.g., Seto, 2024 [8]). To compare the satellite-based radar (SR) and ground-based radar (GR), Schwaller and Morris [9] proposed a Volume Matching Method (VMM) for cross-validation between SR and GR, which avoids introducing additional errors from interpolation methods. Warren et al. [10] further improved this method by analyzing the different factors affecting the matching results. Using the VMM method, the correlation coefficient between GPM-DPR’s reflectivity factors after attenuation correction and ground-based radars’ reflectivity factors is greater than 0.8 [8,11,12,13,14].

To our limited knowledge, few studies have been conducted on FY-3G PMR data since FY-3G was launched quite recently. In this paper, we choose ground-based radar systems to assess the performance of FY-3G PMR, which will help establish a foundation for its application in operational forecasting, space–ground radar integration and data assimilation. To evaluate the performance of FY-3G PMR under different precipitation conditions, multiple types and phases of precipitation are included to compare the radar reflectivity factors between the FY-3G PMR and ground-based S-band dual-polarization radar data. Section 2 provides details about the data and methodology used in this paper. In Section 3, two typical precipitation cases in China are analyzed to assess FY-3G PMR’s accuracy. Then, we combine all samples and compare observations of FY-3G PMR and ground-based radars for different rain types and droplet phases. Conclusions and discussions are provided in Section 4.

2. Materials and Methods

This section introduces the data and methods utilized in this study. Section 2.1 and Section 2.2 introduce the properties and quality control methods of FY-3G PMR and ground-based radars (GRs), respectively. Section 2.3 compares the differences of FY-3G PMR and GR and details the data preprocessing and the spatiotemporal methods, especially for the spatial matching method called the volume matching method (VMM). Section 2.4 presents the methods of the statistics and analysis employed in this paper.

2.1. FY-3G PMR

As the key sensor of the FY-3G satellite, PMR operates with two frequency bands, Ku (13.35 ± 0.01 GHz) and Ka (35.55 ± 0.01 GHz), both in single-polarization and one-dimension phase array radar [4]. FY-3G PMR scans perpendicularly to the satellite orientation with a scanning angle of 20° and has an observation range between 50°S and 50°N. Figure 1 displays the scan mode of Ku/Ka band radar. The swath width of FY-3G PMR is 303 km, with a horizontal resolution 5 km at the sub-satellite point, and each scan row consists of 59 beams. FY-3G PMR completes a full orbit scan in about 93 min. The vertical detection range is from the ground surface up to a height of about 18 km, with a high-range resolution of 250 m and a vertical sampling interval of 50 m and 400 vertical bins. The minimum detectable precipitation rates are 0.5 mm/h (18 dBZ) for the Ku-band radar and 0.2 mm/h (12 dBZ) for the Ka-band radar [15,16]. In April 2024, the China Meteorological Administration (CMA) National Satellite Meteorological Centre (NSMC) released the Level 2 Ku-band precipitation products (KuRs), including variables related to bright-band detection, rain type classification, 3D raindrop profiles, etc. Since the Ka-band product is not yet available online, this paper focuses on the validation of Ku-band radar only. FY-3G PMR Ku-band data were collected for 65 typical precipitation events in the region of 110°E–125°E, 15°N–35°N, during the period from April to August 2024.

In order to exclude the nonprecipitation echoes and low-quality data, only the precipitation pixels with good-quality flags in KuR production are utilized. Since the minimum detectable precipitation rate of FY-3G PMR Ku-band radar is 18 dBZ, data with reflectivity factors greater than 18 dBZ only are used. Meanwhile, in order to reduce the effect of non-uniform beam filling and retain more data, a threshold is set to retain those bins that have more than 70% of data in each bin with reflectivity greater than 18 dBZ, following Warren et al. [10].

2.2. Ground-Based Radar

For cross-validation of the FY-3G PMR measurements and products, observations from S-band dual-polarization radars (CINRAD/SAD, hereafter referred to as GR) deployed in the region of (110–123°E, 15–35°N) are utilized. Figure 2 shows the location of these radar stations and the number of detection events for each station. The gate spacing and beamwidth of GR are 250 m and about 1°, respectively. The maximum detection range of GR is 460 km, with a 6 min time resolution of the volume scans.

In this study, the elevation angles used for validation are 1.5°, 2.4°, 3.4°, 4.3°, 6.0° and 10°. In order to minimize the ground clutter interference, we exclude the data from the lowest elevation (0.5°). Due to the influence of the GR’s cone of silence, caused by its scan mode, storms closer to the GR are scanned at lower levels than those farther away [17]. Hence, we set the minimum detection range to 15 km from the center of the GR site. Moreover, as the distance from the GR site increases, the radar sampling resolution decreases, with the beam broadening. Therefore, the maximum range is set to 115 km. Before validation, GR data have been preprocessed with the copolar correlation coefficient (${\mathsf{\rho }}_{\mathrm{hv}}\ge 0.85$) to remove nonprecipitation echoes and other contamination. Further, to match the limitation of FY-3G PMR’s minimum detectable precipitation rate, the minimum reflectivity factor for GR is limited to 15 dBZ.

2.3. Volume Matching Methods for Comparison

In addition to the quality control methods mentioned above, considering the large differences in the detection modes, frequency bands and resolutions between FY-3G PMR and GR (as listed in

Table 2. Comparison of FY-3G PMR with ground-based radars (GRs).

Radar Systems	FY-3G PMR	GR
Frequency band	Ku (13.6 GHz), Ka (35.5 GHz)	S (3 GHz)
Resolution (km)	5 (Horizontal), 0.25 (Vertical)	0.25
Cycle for one track (min)	93 min	6 min
Scan mode	Vertical scan	Cone scan
Minimum detectable precipitation rate (mm/h)	0.5 mm/h (18 dBZ, Ku), 0.2 mm/h (12 dBZ, Ka)	N/A
Coverage	50°N–50°S	460 km
Beam width ($°$)	0.7	≈1.0

), it is necessary to carry out attenuation correction, band conversion and sampling volumes matching in both the time and space domains for the two radars before validation [7].

For attenuation correction, the relevant variable (attenuation-corrected reflectivity factor) has been processed in the KuR product. To keep the validation less sensitive to the scattering differences of the two types of radars, an equivalent reflectivity factor in the Ku-band (Z_Ku) is calculated from the S-band radar observations, including the reflectivity factor Z_h (in mm⁻⁶ m⁻³) and the differential reflectivity Z_dr (unitless), as follows:

$${\mathrm{Z}}_{\mathrm{Ku}}=0.582\times {\mathrm{Z}}_{\mathrm{h}}^{1.5}\times {\mathrm{Z}}_{\mathrm{dr}}^{1.19}$$

(1)

The relationship is obtained using least square fitting from simulated radar variables, using the raindrop size distribution data in [18]. The calculation of the radar variables follows [19], with the S-band and Ku-band scattering amplitudes calculated using a T-matrix method, as in [20]. It can avoid redundant additional errors introduced by using the dual-polarization parameter directly to replace the bright-band identification and phase classification process in other methods [7,21]. After that, the GR’s reflectivity is converted from the S-band to the Ku-band, which is the same as FY-3G PMR.

For temporal matching, the closest scanning moment of each GR station corresponding to the FY-3G PMR transit was selected for each precipitation event. As for spatial matching, we project FY-3G PMR and GR into the same coordinate system and then use a method called volume matching method (VMM), proposed by Schwaller and Morris [9] and further improved by Warren et al. [10]. VMM utilizes the intersection of the GR and FY-3G PMR beams to find a common scanning volume (the red column in Figure 3a) and averages the data within that volume horizontally and vertically, respectively. Specifically, for FY-3G PMR, averaging is along the vertical direction at the top and bottom of each GR scanning elevation angle, meaning that the PMR data within the red box in Figure 3c are vertically averaged; for GR, weighted averaging is along the horizontal direction within the half-power point of the PMR beam, meaning that the GR data within the red circle in Figure 3b are horizontally averaged. As a result, the matching pairs have the same horizontal resolution as FY-3G PMR (5 km) and the same vertical resolution as GR’s beam width. This method does not require interpolation, extrapolation or oversampling of data, and its matching results are closer to the original observation data.

After the series of data preprocessing steps mentioned above, 65 typical precipitation events detected by FY-3G PMR in the study area (110–123°E, 15–35°N) from April to August 2024 were selected. A total of 169,657 matched pairs were saved for further analysis.

2.4. Methods of Statistics and Analysis

We first select two typical precipitation events, one Mei-yu case and one typhoon case, for qualitative analysis. Then, we perform a quantitative comparison of the FY-3G PMR and GR performances using all 169,657 samples, through statistical methods, including calculating Pearson correlation coefficients (CCs), the root mean square error (RMSE) and the mean bias (MB). The formulas of these statistical indices are as follows:

$$\mathrm{C}\mathrm{C}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{Z}}_{\mathrm{P}\mathrm{M}\mathrm{R}}-\overline{{\mathrm{Z}}_{\mathrm{P}\mathrm{M}\mathrm{R}}}\right)\left({\mathrm{Z}}_{\mathrm{G}\mathrm{R}}-\overline{{\mathrm{Z}}_{\mathrm{G}\mathrm{R}}}\right)}{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{Z}}_{\mathrm{P}\mathrm{M}\mathrm{R}}-\overline{{\mathrm{Z}}_{\mathrm{P}\mathrm{M}\mathrm{R}}}\right){\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{Z}}_{\mathrm{G}\mathrm{R}}-\overline{{\mathrm{Z}}_{\mathrm{G}\mathrm{R}}}\right)}}}$$

(2)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{\mathrm{n}}}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{Z}}_{\mathrm{P}\mathrm{M}\mathrm{R}}-{\mathrm{Z}}_{\mathrm{G}\mathrm{R}}\right)}^2}$$

(3)

$$\mathrm{M}\mathrm{B}={\displaystyle \frac{1}{\mathrm{n}}}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{Z}}_{\mathrm{P}\mathrm{M}\mathrm{R}}-{\mathrm{Z}}_{\mathrm{G}\mathrm{R}}\right)$$

(4)

Furthermore, we classify precipitation into convective precipitation and stratiform precipitation, according to the variable (named TypePrecip) from the KuR products, and each is compared with GR data to evaluate FY-3G PMR’s detection accuracy for different rainfall types. Meanwhile, we compare FY-3G PMR with GR at different heights, especially for different precipitation phases above and below the bright band. Events with less than two matching pairs after filtering are excluded.

3. Results

This section presents the results of the comparison of reflectivity factors obtained from FY-3G PMR and GR. Section 3.1 primarily provides a qualitative and quantitative comparison between FY-3G PMR and GR for two typical precipitation events. Section 3.2 conducts the quantitative comparisons for all matched samples from April to August in 2024, offering a statistical assessment of the agreement between the two datasets. In Section 3.3, a sensitivity analysis is conducted to investigate the influence of rain type and droplet phase on the observed differences, aiming to identify potential sources of bias and uncertainty in FY-3G PMR measurements.

3.1. Comparison of FY-3G PMR and GR for Two Typical Precipitation Events

Firstly, we compare FY-3G PMR and GR for two typical precipitation events in China: a Mei-yu case (Figure 4 and Figure 5) and a typhoon case (Figure 6 and Figure 7). The comparison includes spatial horizontal and vertical distributions using raw data (Figure 4 and Figure 6) and statistical analyses using matched samples (Figure 5 and Figure 7) to assess the agreement and potential biases between the two radar systems.

3.1.1. Mei-Yu Case

Mei-yu is a unique precipitation event in East Asia, mainly occurring in June and July. In China, Mei-yu predominately happens in the Yangtze River Delta, from Yichang in Hubei Province to the coastal regions of East China, and 28°N near the South Ridge, while the northern edge extends to around 34°N [23]. In 2024, the Mei-yu season in Nantong City was from 19 June to 16 July. At about 08:34 UTC on 21 June 2024, FY-3G PMR captured a heavy precipitation event during the Mei-yu period. Therefore, we compared the FY-3G PMR raw data with the GR detection at Nantong station (120.98°E, 32.08°E), Jiangsu Province (Figure 4).

Figure 4. Radar reflectivity factors (shaded) for Mei-yu case at 08:34 UTC on 21 June 2024. (a) is the distribution of attenuation-corrected Ku-band radar reflectivity factors at about 3 km from FY-3G PMR, while (b) is for GR at 1.5° elevation angle at Nantong station. (b) and (d) are vertical cross sections along the brown line in (a) and (c), respectively. The red stars and black circles in (a,c) indicate the positions and 115 km detection ranges and the location of the radars at the Nantong stations, respectively. The dashed lines in (a) represent the detection track of FY-3G PMR.

Figure 4. Radar reflectivity factors (shaded) for Mei-yu case at 08:34 UTC on 21 June 2024. (a) is the distribution of attenuation-corrected Ku-band radar reflectivity factors at about 3 km from FY-3G PMR, while (b) is for GR at 1.5° elevation angle at Nantong station. (b) and (d) are vertical cross sections along the brown line in (a) and (c), respectively. The red stars and black circles in (a,c) indicate the positions and 115 km detection ranges and the location of the radars at the Nantong stations, respectively. The dashed lines in (a) represent the detection track of FY-3G PMR.

Figure 4a displays the distribution of attenuation-corrected Ku-band radar reflectivity factors at about 3 km, measured by the FY-3G PMR detection, and Figure 4c are S-band radar reflectivity factors measured by ground-based radar in Nantong City, Jiangsu Province at a 1.5-degree elevation angle. Clearly, before spatiotemporal matching and frequency conversion, the shape and intensity of radar echoes from FY-3G PMR (Figure 4a) and GR (Figure 4c) are very similar. Additionally, the vertical cross sections of the two radars (Figure 4b,d) also show good consistency. The strongest echo heights are both near 6 km, and the strong echo positions correspond well to each other, showing a triple-peak shape.

Then, we carry out a series of data processing, including quality control, attenuation correction, band conversion and spatiotemporal matching for the two radars. Figure 5 shows the distribution of reflectivity and its differences between the matched FY-3G PMR and GR at 1.5° elevation. The echoes of the matched FY-3G PMR are concentrated in the western part of the center of the GR (Figure 5a). By comparing with the distributions of the reflectivity of GR (Figure 5b), it is clear that the spatial distribution patterns of their reflectivity are similar; FY-3G PMR and GR reflectivity factors are basically distributed along the one-to-one line, and the correlation coefficient (CC) between FY-3G PMR and GR is 0.88 (Figure 5d), indicating a strong correlation between FY-3G PMR and GR measurement. Figure 5e shows the histogram of the reflectivity distributions for FY-3G PMR (orange) and GR (blue) (bin size = 2 dB). Again, the two reflectivity distributions are quite similar, but the FY-3G PMR distribution is slightly shifted to the right compared to that of GR, indicating a slight overestimation of the FY-3G PMR reflectivity. The differences between the FY-3G PMR and GR reflectivity factors are relatively small in the different regions (Figure 5c), and are mainly centered in the range of −5 to 5 dBZ, with a mean and median of differences of 1.08 dBZ and 1.12 dBZ, respectively (Figure 5f). In summary, all the results indicate a good relationship between the reflectivity of FY-3G PMR and GR, though a slight overestimation of FY-3G PMR reflectivity is found when compared to GR.

Figure 5. Comparison between FY-3G PMR and GR (located in Nantong, Jiangsu Province) for a Mei-yu case at about 08:34 UTC on 21 June 2024. (a,b) Horizontal distribution of FY-3G PMR reflectivity and GR reflectivity at 1.5° elevation, respectively. (c) Difference between FY-3G PMR and GR (PMR-GR). Dashed rings show the detection ranges. (d) Scatter plot of FY-3G PMR and GR reflectivity, with a correlation coefficient (corr) and the number of matched pairs (n). Solid line in (d) shows one-to-one line. (e) Histogram of reflectivity distributions for FY-3G PMR (orange) and GR (blue) (bin = 2 dB). Dashed lines in (d,e) indicate the minimum FY-3G PMR reflectivity. (f) Histogram of PMR-GR reflectivity, the values of its mean and median indicated in top left.

Figure 5. Comparison between FY-3G PMR and GR (located in Nantong, Jiangsu Province) for a Mei-yu case at about 08:34 UTC on 21 June 2024. (a,b) Horizontal distribution of FY-3G PMR reflectivity and GR reflectivity at 1.5° elevation, respectively. (c) Difference between FY-3G PMR and GR (PMR-GR). Dashed rings show the detection ranges. (d) Scatter plot of FY-3G PMR and GR reflectivity, with a correlation coefficient (corr) and the number of matched pairs (n). Solid line in (d) shows one-to-one line. (e) Histogram of reflectivity distributions for FY-3G PMR (orange) and GR (blue) (bin = 2 dB). Dashed lines in (d,e) indicate the minimum FY-3G PMR reflectivity. (f) Histogram of PMR-GR reflectivity, the values of its mean and median indicated in top left.

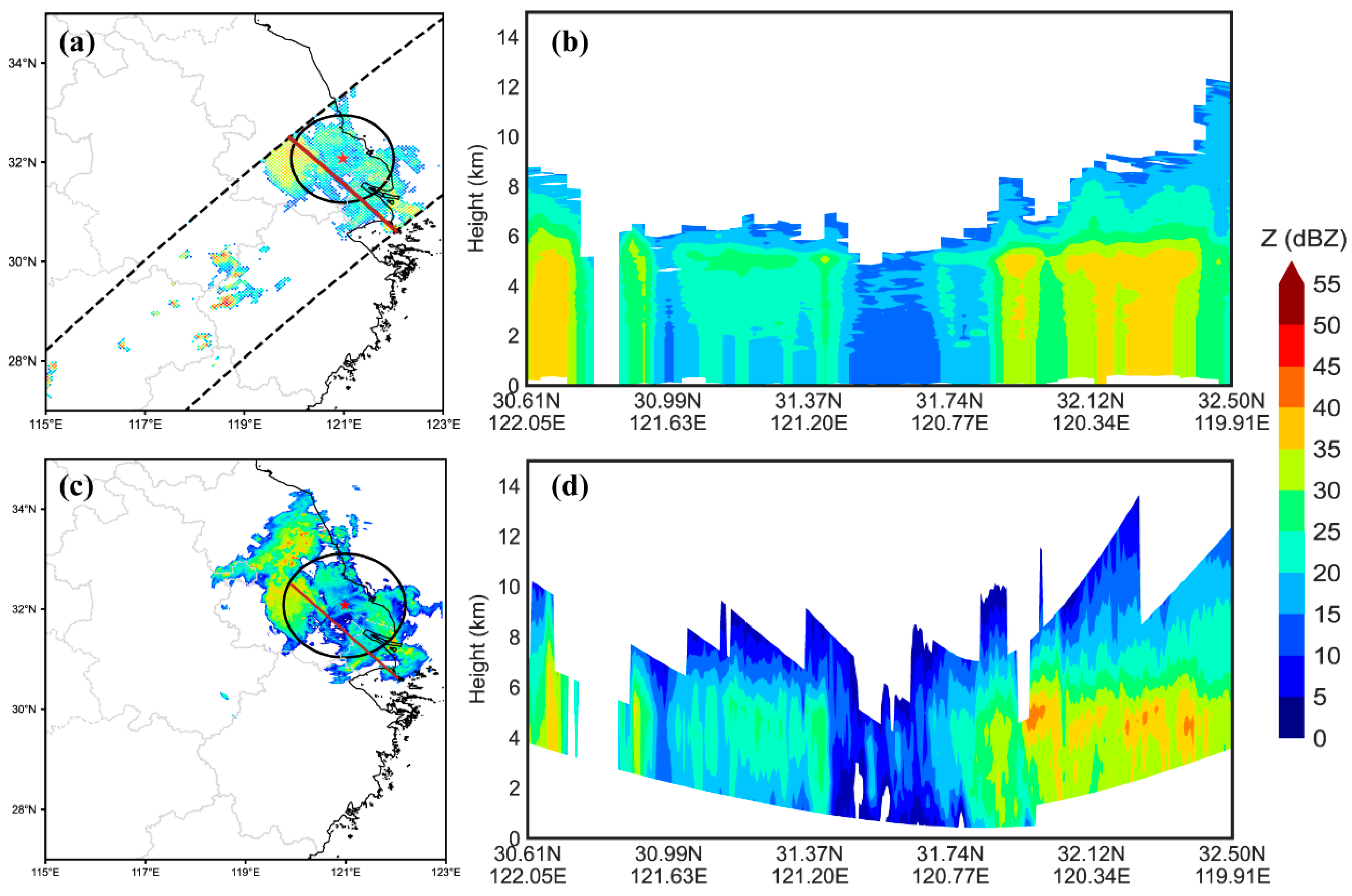
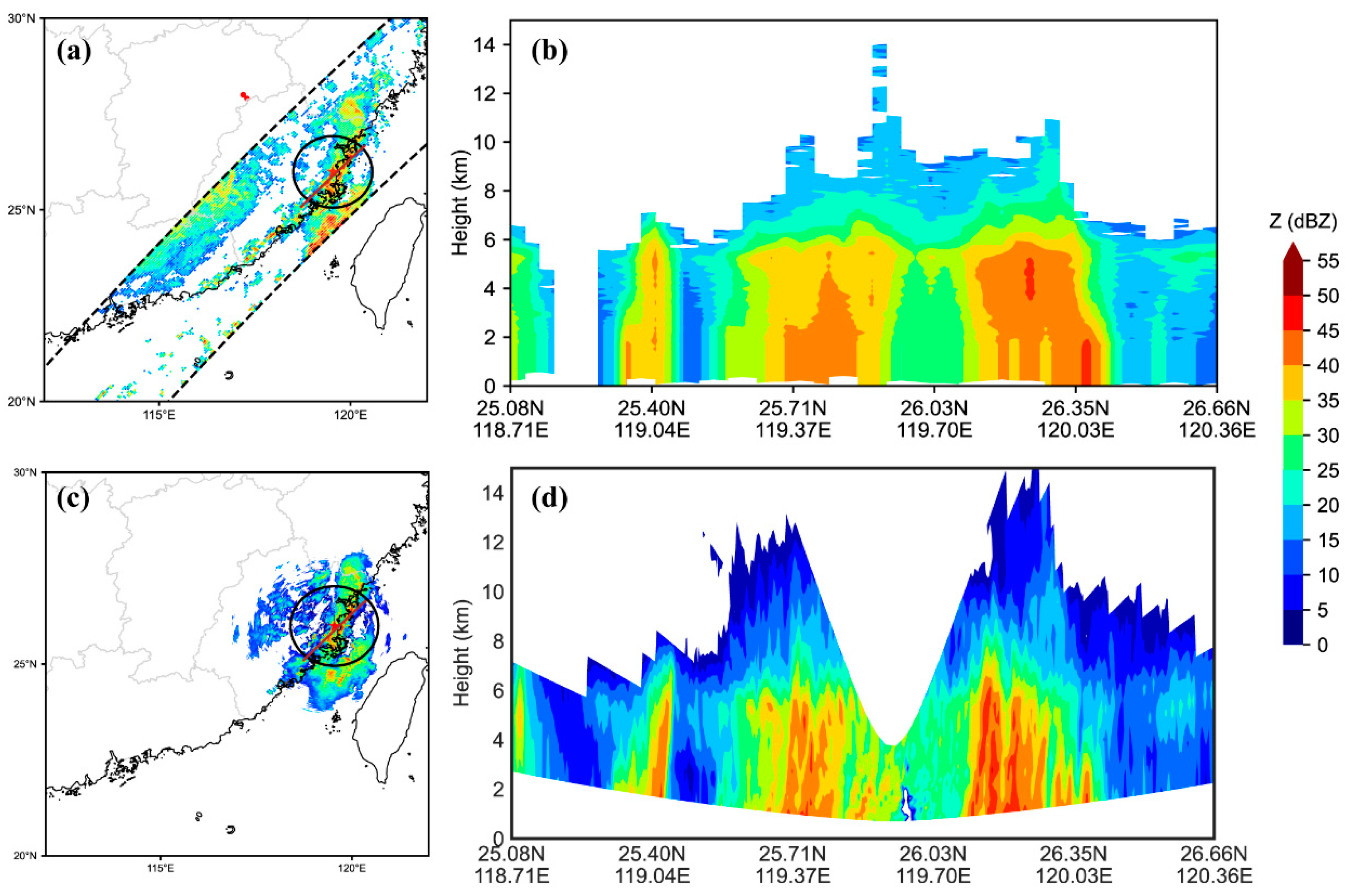
3.1.2. Typhoon Case

Typhoon rainfall is also one of the most important weather events in China; therefore, a typhoon rainfall case is chosen for detailed comparison. Typhoon Gaemi (2403), the first super typhoon in the year of 2024, generated east of the Philippines on 20 July 2024. By about 17:47 UTC on 26 July 2024, it entered Jiangxi Province with typhoon intensity. At that time, the FY-3G PMR crossed Fujian Province and captured the heavy precipitation produced by the western part of the typhoon’s spiral rain band in Fujian Province (Figure 6a). Similar to the Mei-yu case (Figure 4), FY-3G PMR also shows a good consistency with GR (Figure 6) before spatiotemporal matching and the frequency switch. FY-3G PMR successfully captures the north–south-oriented strong rain band (Figure 6a), and both the location and intensity correspond well with GR in Fuzhou City (Figure 6c). Compared to the vertical cross section (Figure 6b,d), the strongest echo heights, location and intensity are very similar between the two radars.

Figure 6. Radar reflectivity factors (shaded) for Typhoon Gaemi (2304) at 17:47 (UTC) on 26 July 2024. (a) is the distribution of attenuation-corrected Ku-band radar reflectivity factors at about 3 km from FY-3G PMR, while (b) is for GR at 1.5° elevation angle at Fuzhou station. (b) and (d) are vertical cross sections along the brown line in (a) and (c), respectively. The red stars and black circles in (a,c) indicate the positions and 115 km detection ranges and the location of the radars at the Nantong stations, respectively. The dashed lines in (a) represent the detection track of FY-3G PMR.

Figure 6. Radar reflectivity factors (shaded) for Typhoon Gaemi (2304) at 17:47 (UTC) on 26 July 2024. (a) is the distribution of attenuation-corrected Ku-band radar reflectivity factors at about 3 km from FY-3G PMR, while (b) is for GR at 1.5° elevation angle at Fuzhou station. (b) and (d) are vertical cross sections along the brown line in (a) and (c), respectively. The red stars and black circles in (a,c) indicate the positions and 115 km detection ranges and the location of the radars at the Nantong stations, respectively. The dashed lines in (a) represent the detection track of FY-3G PMR.

At 1.5° elevation, we compared FY-3G PMR observations with GR located at Fuzhou (119.54°E, 25.99°N), Fujian Province, at the corresponding time (Figure 7). The echo structure distribution of FY-3G PMR is almost the same as that of GR, and the location of the strongest echoes are successfully detected, showing a similar rain band pattern (Figure 7a,b), and the correlation coefficient between the reflectivity of the two radars is 0.84 (Figure 7d). The reflectivity values are slightly biased, with FY-3G PMR showing a positive bias for the detection of the moderately intense rain zone in the south, and a negative bias for the detection of the strongest rain bands in the central and northern parts of the region (Figure 7c,d). And the bias is roughly distributed in the range −5–10 dBZ (Figure 7f).

Figure 7. Comparison of FY-3G PMR reflectivity and GR reflectivity (located in Fuzhou, Fujian Province) at an elevation angle of 1.5° for Typhoon Gaemi (2403) at about UTC 17:47 on 26 July 2024. (a,b) Horizontal distribution of FY-3G PMR reflectivity and GR reflectivity at 1.5° elevation, respectively. (c) Difference between FY-3G PMR and GR (PMR-GR). Dashed rings in (a–c) show the detection ranges. (d) Scatter plot of FY-3G PMR and GR reflectivity, with a correlation coefficient (corr) and the number of matched pairs (n). Solid line in (d) shows one-to-one line. (e) Histogram of reflectivity distributions for FY-3G PMR (orange) and GR (blue) (bin = 2 dB). Dashed lines in (d,e) indicate the minimum FY-3G PMR reflectivity. (f) Histogram of PMR-GR reflectivity, the values of its mean and median indicated in top left.

Figure 7. Comparison of FY-3G PMR reflectivity and GR reflectivity (located in Fuzhou, Fujian Province) at an elevation angle of 1.5° for Typhoon Gaemi (2403) at about UTC 17:47 on 26 July 2024. (a,b) Horizontal distribution of FY-3G PMR reflectivity and GR reflectivity at 1.5° elevation, respectively. (c) Difference between FY-3G PMR and GR (PMR-GR). Dashed rings in (a–c) show the detection ranges. (d) Scatter plot of FY-3G PMR and GR reflectivity, with a correlation coefficient (corr) and the number of matched pairs (n). Solid line in (d) shows one-to-one line. (e) Histogram of reflectivity distributions for FY-3G PMR (orange) and GR (blue) (bin = 2 dB). Dashed lines in (d,e) indicate the minimum FY-3G PMR reflectivity. (f) Histogram of PMR-GR reflectivity, the values of its mean and median indicated in top left.

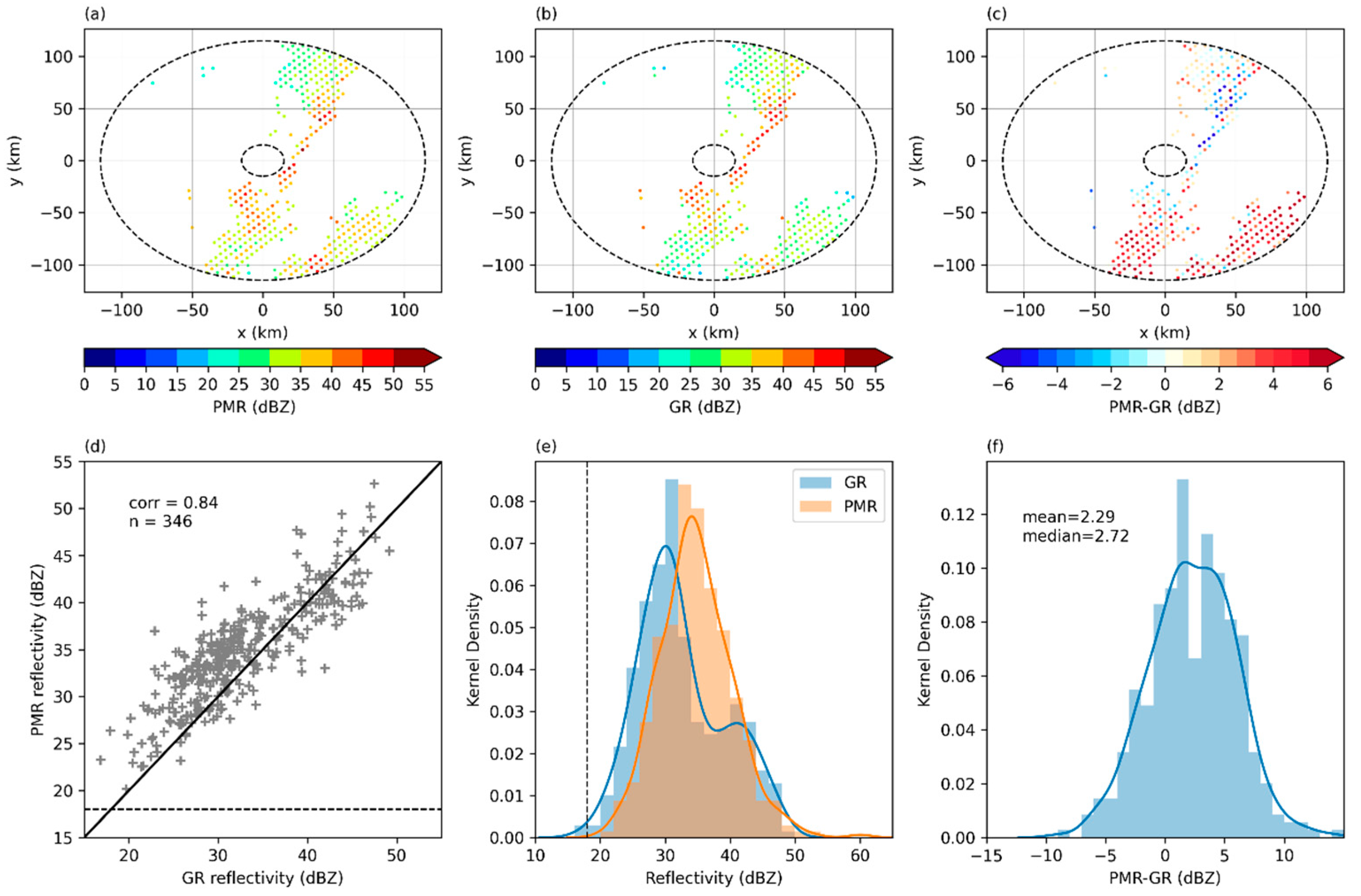
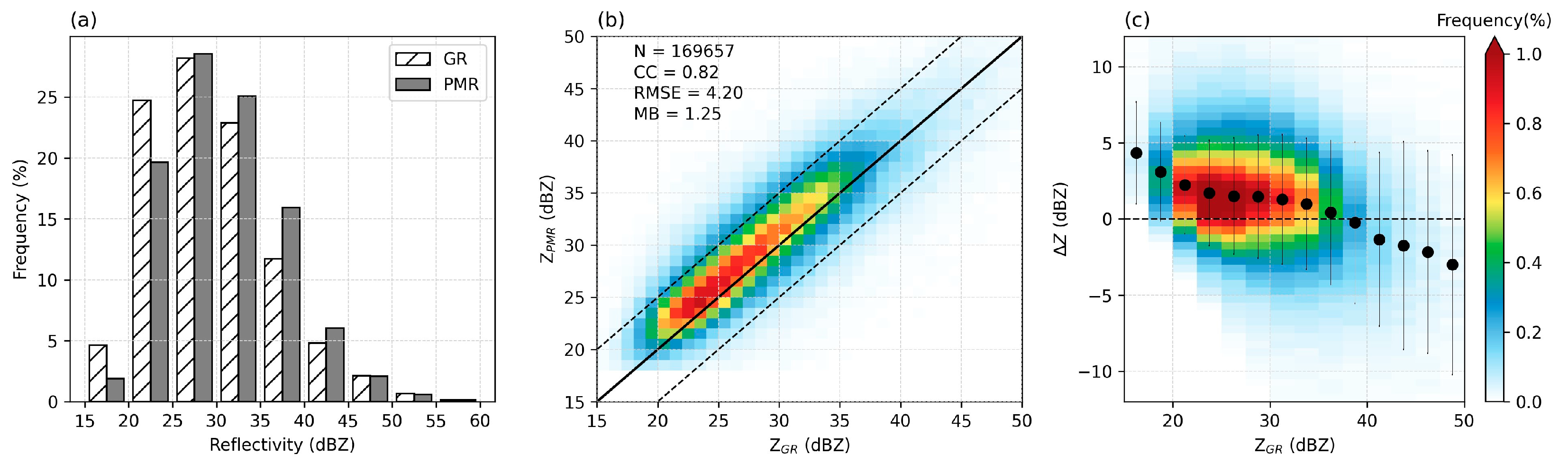
3.2. Characteristics of All Matching Samples

After data processing of the data quality control and spatial–temporal matching mentioned in Section 2.3, 169,657 matched pairs of reflectivity data of FY-3G PMR and GR for 65 typical precipitation events from April to August 2024 are selected. Figure 8a illustrates the frequency distribution of the reflectivity factor of GR (slanted-line column) and FY-3G PMR (solid column) in different reflectivity bins. The reflectivity ranges for both radars are from 15 dBZ to 60 dBZ, with a concentration primarily between 20 and 40 dBZ. In the reflectivity range of 15 to 30 dBZ, GR displays a notably higher frequency than FY-3G PMR. In contrast, for reflectivity values exceeding 30 dBZ, FY-3G PMR shows a higher frequency compared to GR.

Figure 8b presents the bivariate histograms of the reflectivity for GR (Z_GR) and FY-3G PMR (Z_PMR), with the red areas indicating higher frequencies. Most of the data fall within the error range of ±5 dBZ (dashed lines), and the matched samples are basically distributed along the one-to-one line (solid line), meaning that the two radars are well matched. The overall CC is 0.82, indicating a strong positive correlation between the two radars. Additionally, the root mean square error (RMSE) and mean bias (MB) are 4.20 dB and 1.25 dB, respectively, indicating that the FY-3G PMR’s reflectivity is slightly higher than GR’s. Liao and Meneghini found that the CC and MB of TRMM PR were 0.81 and 0.8 dB relative to the WSR at Melbourne, Florida, for the period 1998–2007 [7]. And Li et al. systematically compared GPM DPR and 136 WSR-88D from 2014 to 2020 and found that the averaged biases are 2.4 dB and 1.0 dB for DPR version 6 and version 7, respectively [24]. FY-3G PMR’s performance is comparable to TRMM PR and GPM DPR.

Figure 8c shows the bias between FY-3G PMR and GR reflectivity (ΔZ = Z_PMR − Z_GR) relative to the reflectivity of GR. The black dots represent the median value, and the solid lines indicate the interquartile ranges (IQRs). When GR reflectivity values are below 40 dBZ, the reflectivity from FY-3G PMR is slightly higher than GR (ΔZ > 0), with ΔZ showing a decreasing trend as GR reflectivity increases. At a moderate intensity of reflectivity (20–40 dBZ), the bias between the two radars is small (the median is close to 0), revealing the good agreement between FY-3G PMR and GR at moderate precipitation. However, as the GR reflectivity exceeds 40 dBZ, the FY-3G PMR reflectivity is significantly lower than GR (ΔZ < 0), displaying a wider distribution and more obvious deviation. It suggests a systematic underestimation of FY-3G PMR for heavy precipitation. Combined with the results of all samples (denoted by “ALL”) in

Table 3. The performance of FY-3G PMR reflectivity compared to GR’s in different elevations (1.5°, 2.4°, 3.4°, 4.3°, 6.0°, 10°) and rain types (stratiform and convective precipitation).

Elevation		1.5°	2.4°	3.4°	4.3°	6.0°	10.0°	Total
Stratiform	N	46,916	35,704	26,881	16,932	6887	1262	134,582
	CC	0.80	0.77	0.79	0.80	0.79	0.76	0.80
	MB	1.60	0.93	0.96	1.05	1.063	0.93	1.19
	RMSE	3.66	3.70	3.61	3.59	3.65	3.61	3.65
Convective	N	10,127	8692	7377	5617	2555	697	35,065
	CC	0.68	0.68	0.77	0.77	0.76	0.76	0.75
	MB	1.57	1.17	1.47	1.66	1.72	0.79	1.46
	RMSE	5.73	5.83	5.86	5.98	6.22	6.01	5.86
All	N	57,043	44,396	34,268	22,548	9443	1959	169,657
	CC	0.83	0.81	0.82	0.82	0.81	0.80	0.82
	MB	1.59	0.98	1.07	1.20	1.24	0.88	1.25
	RMSE	4.10	4.20	4.19	4.31	4.49	4.61	4.20

, the performances of FY-3G PMR among different elevations are consistent, and all display a strong linear relationship and small deviations. Overall, FY-3G PMR reflectivity agrees well with GR for moderate-intensity precipitation, but tends to underestimate reflectivity for heavy precipitation events.

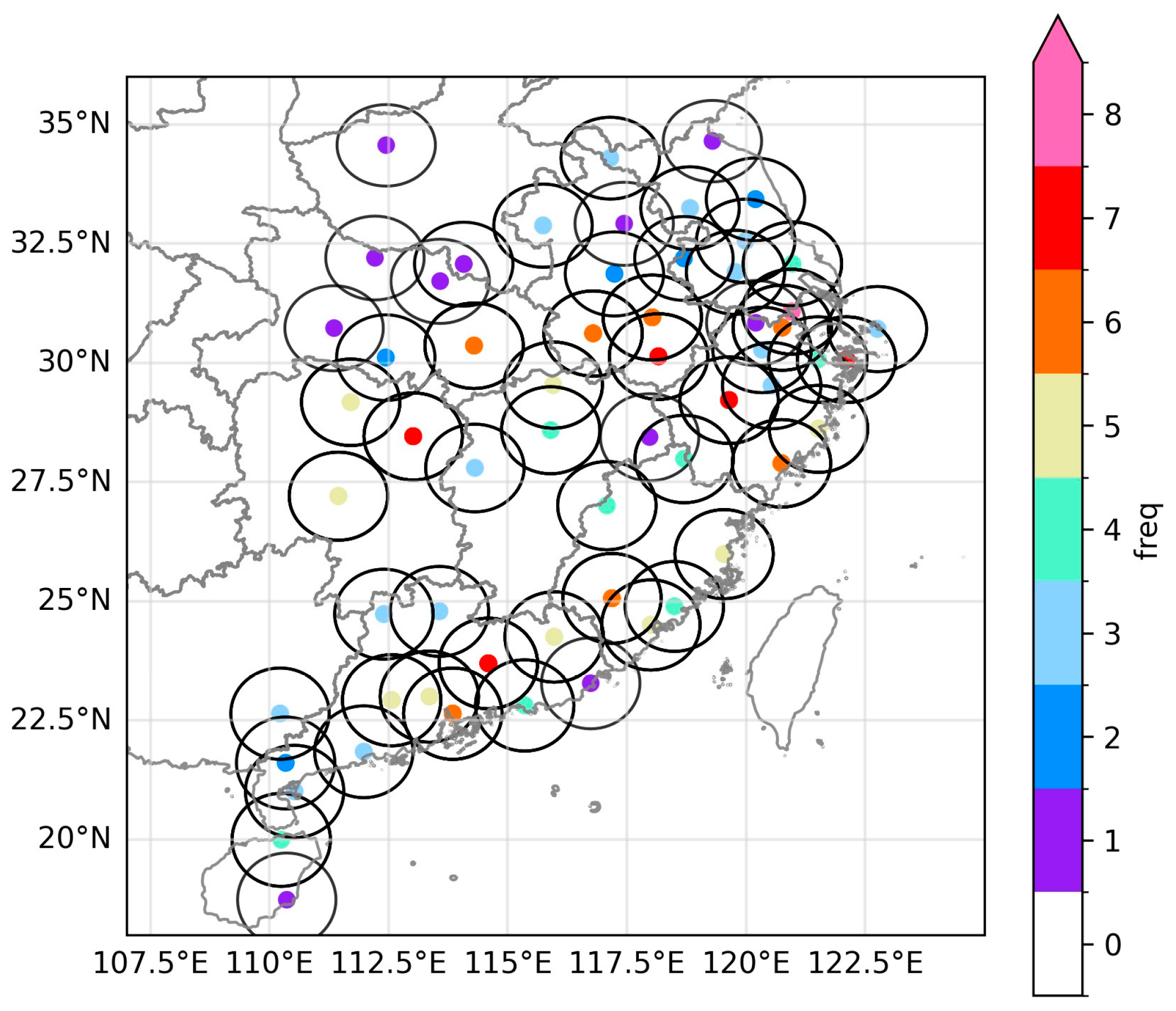
3.3. Sensitivity Analysis

This section presents a sensitivity analysis of FY-3G PMR’s performance under different precipitation conditions, focusing on rain type and droplet phase. We evaluate FY-3G PMR’s accuracy in stratiform and convective precipitation (in Section 3.3.1), as well as its ability to detect liquid and ice-phase precipitation (in Section 3.3.2) relative to ground-based radar (GR).

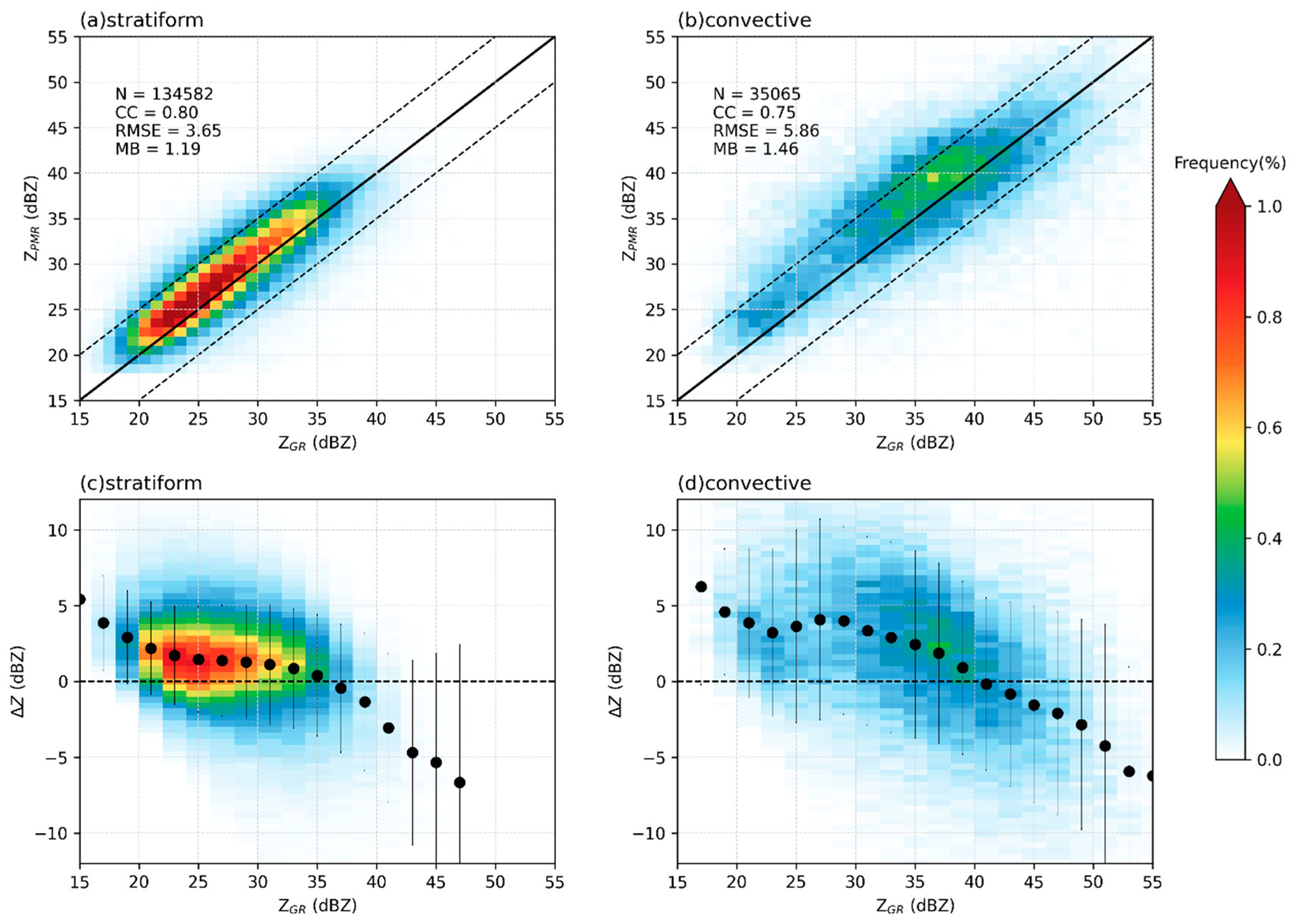
3.3.1. Rain Type

In order to understand the accuracy of FY-3G PMR in different precipitation types in details, we classify the precipitation into stratiform and convection by using the rain-type identification variable in the KuR product, and analyze the FY-3G PMR measurements in the two different rain types in comparison with GR, respectively.

Figure 9 illustrates the distribution of the reflectivity factors and differences between FY-3G PMR and GR under stratiform and convective precipitation conditions. For stratiform precipitation, a total of 134,582 matched sample pairs were analyzed. Similar to Figure 8, the reflectivity data are primarily centered between 20 and 35 dBZ, with most data points falling within a ±5 dB error range (Figure 8a). This indicates a strong linear relationship between the two types of radar (CC = 0.80). The reflectivity errors are relatively small, with RMSE = 3.65 dB and MB = 1.19 dB, demonstrating FY-3G PMR’s high accuracy in measuring stratiform precipitation (compared to GPM DPR version 6 with CC = 0.84, MB = 1.31 dB and RMSE = 3.54 dB [24]). The differences in reflectivity (ΔZ) are centered around zero, particularly in the medium reflectivity range (approximately 20–40 dBZ), further confirming good agreement between FY-3G PMR and GR. However, for GR reflectivity values exceeding 40 dBZ, ΔZ indicates FY-3G PMR’s systematic underestimation of GR for stratiform precipitation.

In contrast, for convective precipitation, 35,065 matched pairs of samples are used for analysis. It is found that the reflectivity factors of GR and FY-3G PMR for convective precipitation have a more dispersed distribution (Figure 9b) compared to those of stratiform precipitation (Figure 9a), with a slightly lower correlation coefficient (CC = 0.75) and increased RMSE (5.86 dB) and MB (1.46 dB). It suggests the slightly weaker agreement between the two instruments for convective precipitation. The distribution of ΔZ (Figure 9d) is broader than that of stratiform precipitation (Figure 9c). While the median ΔZ value remains near zero in higher reflectivity ranges, its fluctuations are more pronounced compared to stratiform precipitation, indicating higher variability in FY-3G PMR’s measurement for convective events.

Table 3 further presents the performance of FY-3G PMR versus GR across different elevation angles in stratiform conditions (Stratiform). FY-3G PMR shows strong agreement with GR at almost every elevation angle, where the CC is relatively high (CC ~ 0.80), and the RMSE and MB values are very stable. This indicates that FY-3G PMR is highly reliable at capturing stratiform precipitation. However, FY-3G PMR’s performance under the convective precipitation condition becomes more inconsistent across elevation angles (Table 3). At lower elevation angles (ele ≤ 2.4°), the correlation coefficient (CC) is slightly smaller (about 0.68), but the RMSE and MB values are not significant compared to the high elevation angles in convective precipitation. At higher elevation angles (ele > 2.4°), though the CC is increased (0.76~0.77), the deviations between the FY-3G PMR and GR reflectivity factors are larger, as shown by the increasing RMSE and MB values. This highlights the challenges FY-3G PMR faces in accurately capturing convective precipitation.

In conclusion, FY-3G PMR demonstrates high accuracy and consistency in measuring stratiform precipitation, especially at lower elevation angles and medium reflectivity ranges. However, its performance decreases significantly under convective precipitation conditions, with greater variability and bias, particularly in higher reflectivity ranges and at higher elevation angles. These results emphasize that although FY-3G PMR performs well for stratiform precipitation, further calibration and improvement are needed for more accurate detection of convective precipitation, particularly at high elevations.

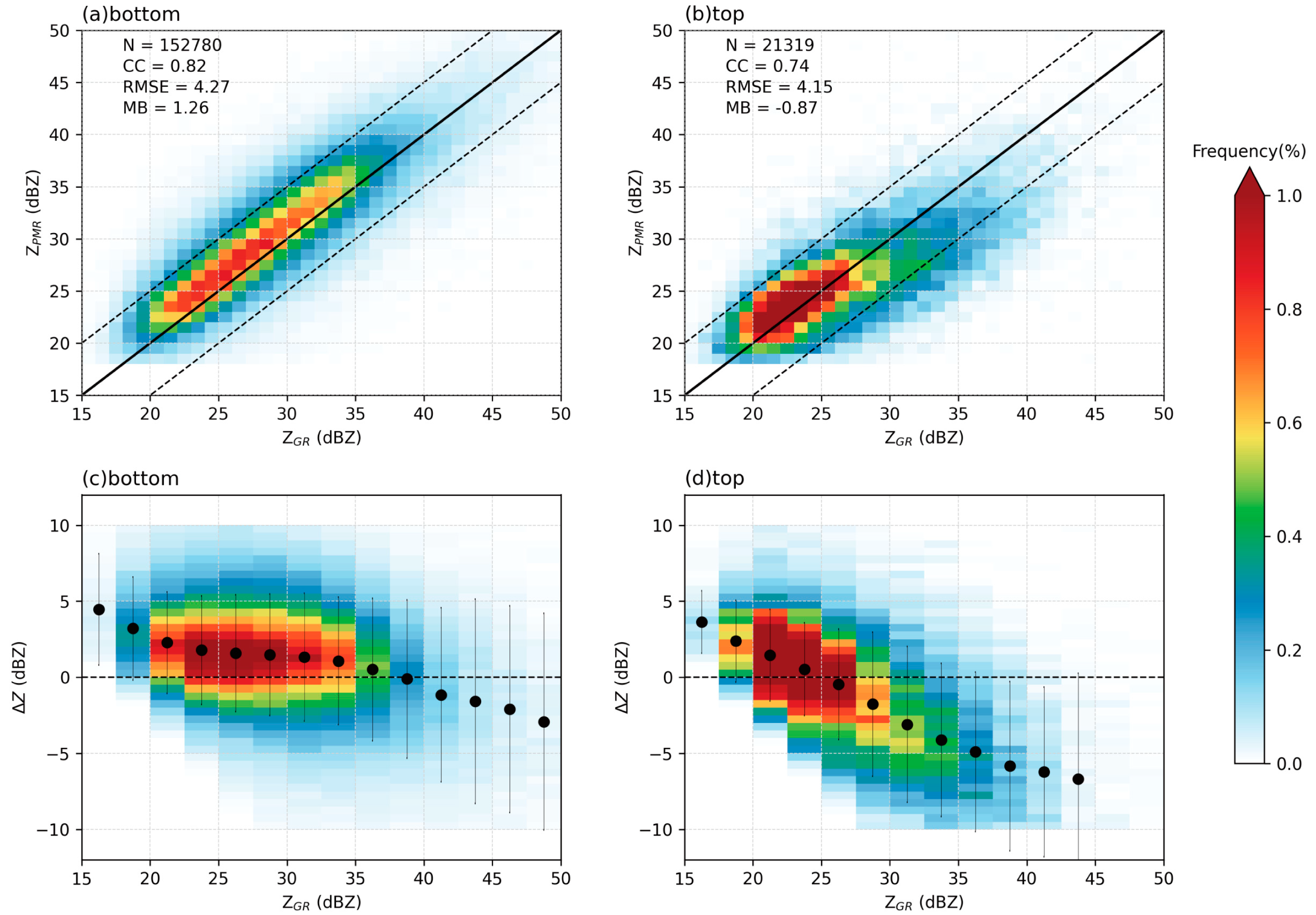
3.3.2. Droplet Phases

Bright bands (BBs) often complicate radar reflectivity measurements due to the phase changes of snow and rain, resulting in reflectivity above and below the BB exhibiting different characteristics: below the BB, droplets are predominantly in the liquid phase, whereas above the bright zone, they are predominantly in the ice phase. To further illustrate the performance of FY-3G PMR in detecting precipitation in different phases, we matched and averaged the precipitation pixels above and below the BB, respectively, using the variables of the bins of bright-band identification in KuR production. More details about the method of bright-band identification can be found in the official document of KuR production [15]. Due to the small number of sample points inside the bright band, we only discuss the bright band above and below.

Figure 10 shows a comparison of the distribution of FY-3G PMR and GR radar reflectivity factors in the region below (Figure 10a,c) and above the BB (Figure 10b,d). In the region below the BB, there are 152,780 sample points, with CC = 0.82, RMSE = 4.27 dB and MB = 1.26 dBZ. The Z_PMR and the Z_GR show a strong positive correlation, with the data points mainly concentrated in the ZGR range of 25 to 35 dBZ, and with the sample points distributed near the one-to-one line (Figure 10a). It shows that below the BB, FY-3G PMR and GR are in good linear agreement, and although there is systematic overestimation of FY-3G PMR at lower reflectivity and underestimation at higher reflectivity intervals (Figure 10c), the overall deviation is within a reasonable range, which indicates that FY-3G PMR has high accuracy in detecting liquid precipitation.

In contrast, in the ice-phase precipitation region above the BB, the matched pairs (20,433) show a weaker correlation (CC = 0.74), and although the error (RMSE = 4.15 dB) is slightly smaller than that below the BB, its mean bias (MB = −0.87 dB) suggests that there is a certain underestimation of the reflectivity factor of ice-phase precipitation by FY-3G PMR. This error is more remarkable in the range of 20 to 30 dBZ, and the data points deviate more significantly from the one-to-one line as GR reflectivity increases (Figure 10b,d). Nevertheless, the correlation coefficient remains at 0.74, indicating that the detection accuracy of FY-3G PMR above the bright band is still informative, especially when the intensity of ice-phase precipitation is small, and FY-3G PMR is still able to provide some reflectivity information.

In summary, FY-3G PMR shows high detection accuracy in the detection of liquid precipitation, especially in the region below the BB, and the correlation and consistency between FY-3G PMR and GR are better. As for the ice-phase precipitation detection above the bright band, the overall detection results of FY-3G PMR are still highly informative, despite some underestimation of FY-3G PMR. Therefore, the detection accuracy of FY-3G PMR is sufficient to play an important role in precipitation monitoring, especially in providing reliable data for large-scale precipitation situations in meteorological monitoring and forecasting. Meanwhile, to address the limitations of FY-3G PMR in ice-phase precipitation, future research is needed to improve its detection accuracy under complex weather conditions.

4. Discussion

This study provides a systematic comparison of reflectivity factors measured by FY-3G PMR (Ku-band) and ground-based dual-polarization S-band radar (GR). Overall, the strong correlation (CC = 0.82) across 169,657 matched samples confirms FY-3G PMR’s ability to capture precipitation structures and highlights its potential for diverse precipitation monitoring. However, the data used in this study are limited to one warm season (April–August in the year of 2024) in southern China; it is essential to extend the data period to achieve more statistically significant results. Furthermore, it would be valuable to examine the performance of FY-3G PMR by comparing it directly to satellite-based systems (such as GPM DPR) when more FY-3G PMR data are available. On top of that, the validation variable is also a point of concern. So far, the calibration is solely for reflectivity factors. More variables, such as the rain rate and the parameters of the raindrop spectrum, in FY-3G PMR Level 2 products should be checked.

This study proves the potential of FY-3G PMR in monitoring various precipitation processes, and offers robust support and valuable reference for the future application of FY-3G PMR, especially in the fields of data assimilation and microphysics parameterization schemes in typhoon numerical forecasting. Future research could focus more on how to effectively combine FY-3G PMR with ground-based observational systems to complement each other’s strengths for their applications in various research areas.

5. Conclusions

This study utilizes ground-based S-band dual-polarization radar (GR) data, along with band conversion techniques and spatial–temporal matching, to analyze the observations of FY-3G Precipitation Measurement Radar (PMR) for typical precipitation cases, such as the Mei-yu season and typhoons. Furthermore, a large dataset of precipitation matching samples (a total of 169,657 pairs) from southern China (110°–125°E, 15°–35°N) between April and August 2024 was used to validate the performance of FY-3G PMR. The main conclusions are as follows:

(1)

Whether the study is based on two individual cases (Mei-yu and Typhoon) or entire samples, the reflectivity of FY-3G PMR and GR shows a strong positive correlation, with an overall correlation coefficient of 0.82. For moderate precipitation (e.g., during the Mei-yu season in 2024), the two radars show good consistency, with FY-3G PMR successfully detecting a strong echo location, and with the same echo pattern and intensity distribution compared to GR. However, there is general overestimation of reflectivity for FY-3G PMR compared to GR, with an average deviation of 1 to 3 dBZ. As for heavy precipitation events, FY-3G PMR shows slight underestimation.

(2)

The analysis of stratiform versus convective precipitation shows that FY-3G PMR performs better in stratiform precipitation, especially at moderate precipitation, in which measurement biases are small. In contrast, the performance of FY-3G PMR in convective precipitation is less stable with relatively larger uncertainty. However, the CC of 0.75 in convective precipitation still remains a relatively high level.

(3)

FY-3G PMR demonstrates high accuracy in detecting liquid precipitation below the bright band, with a strong correlation to GR and small errors. However, in ice-phase precipitation above the bright band, FY-3G PMR shows a tendency to underestimate reflectivity, particularly in regions with intense ice-phase precipitation. Nevertheless, FY-3G PMR still provides valuable information for ice-phase precipitation (CC = 0.74).

To summarize, FY-3G PMR radar has shown good performance in monitoring various precipitation events, making it a useful tool to obtain high-resolution vertical observations and to fill a gap in prior observation, especially in detecting typhoons at their early generation stage over the ocean.