Evapotranspiration Disaggregation Using an Integrated Indicating Factor Based on Slope Units
Abstract
1. Introduction
2. Materials and Methods
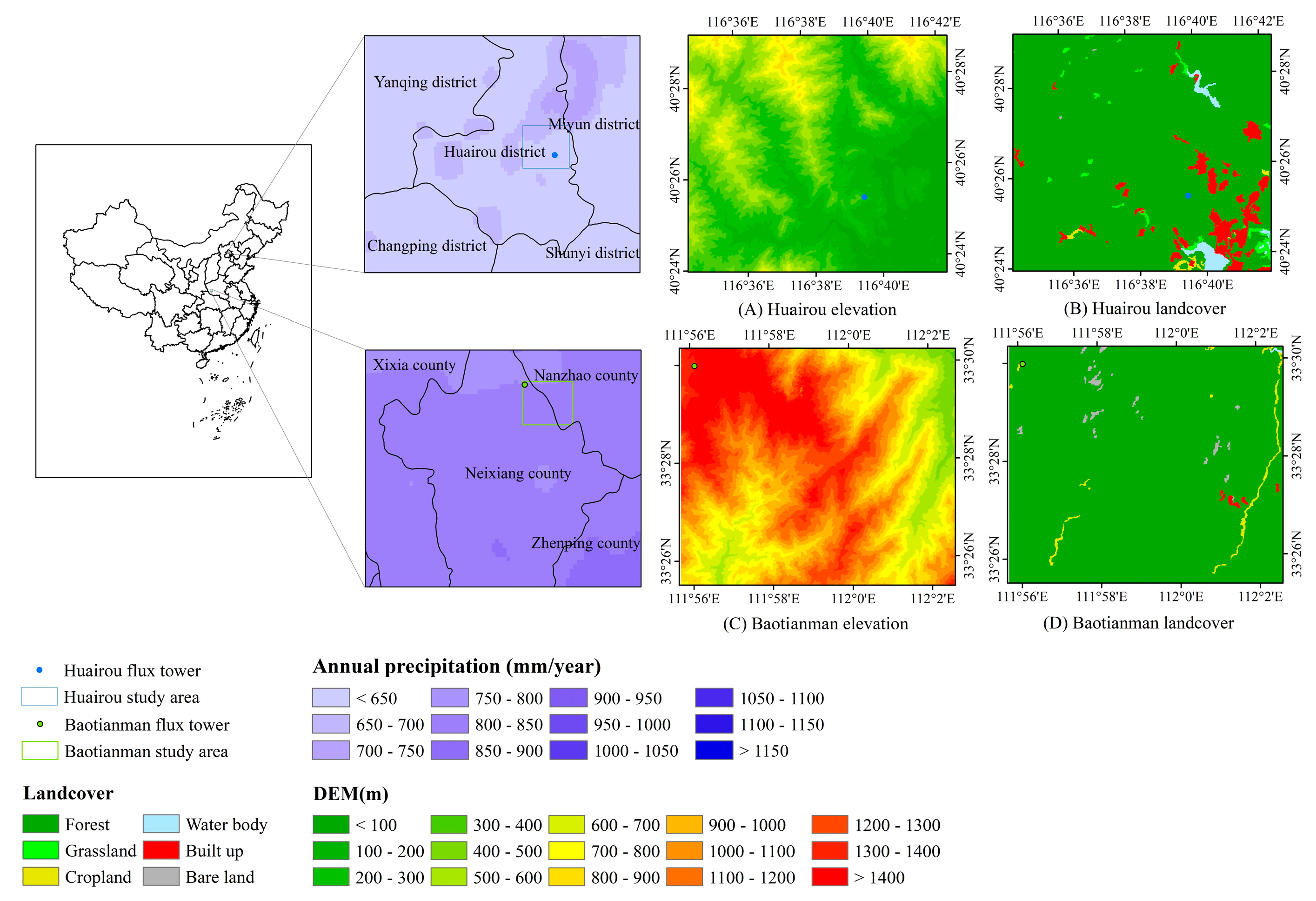
2.1. Study Area
2.2. Data Sources
2.2.1. Remote Sensing Data
2.2.2. In Situ Tower Observation Data
2.2.3. Meteorological Data
2.2.4. ETWatch ET Data
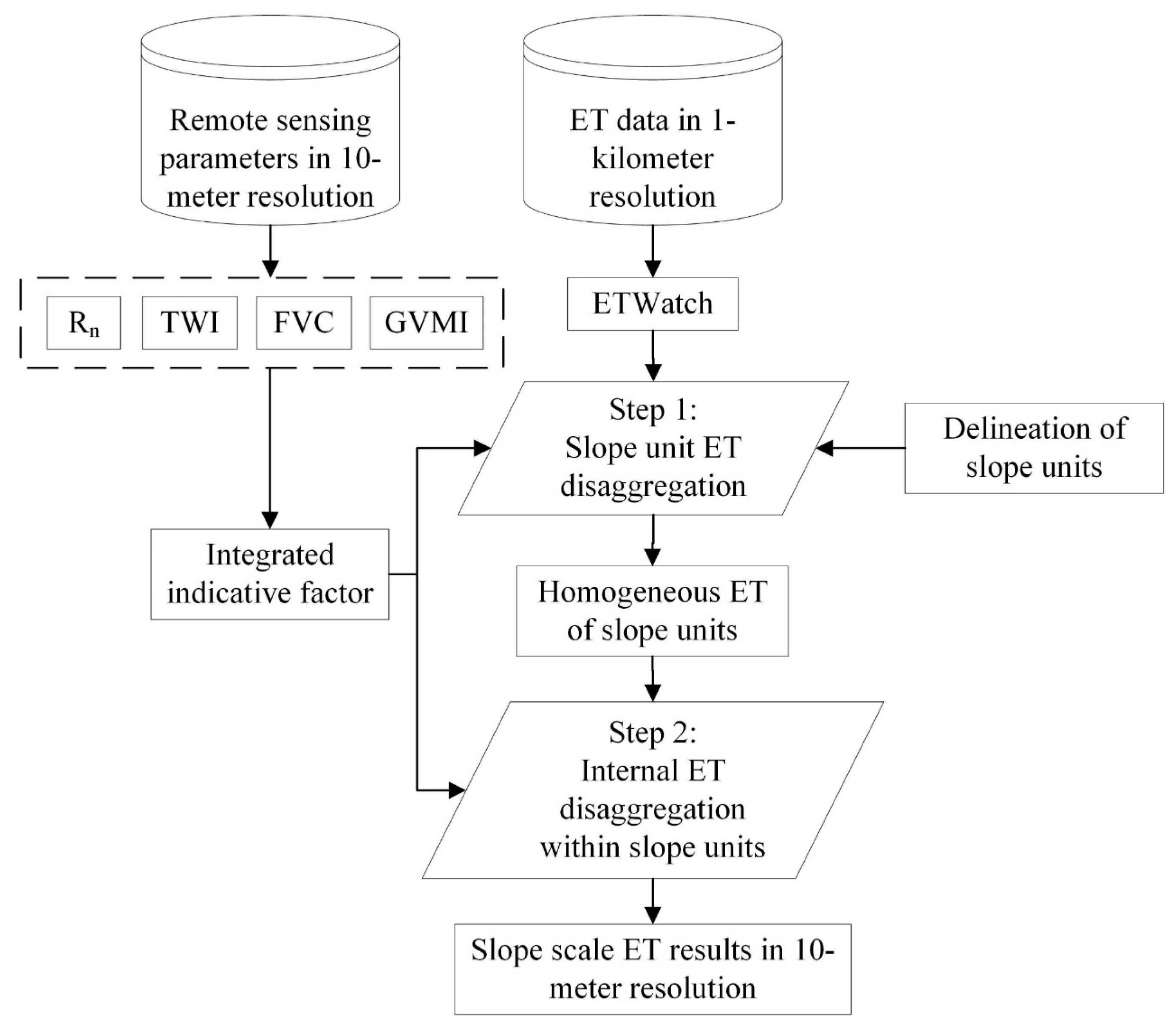
2.3. Methods
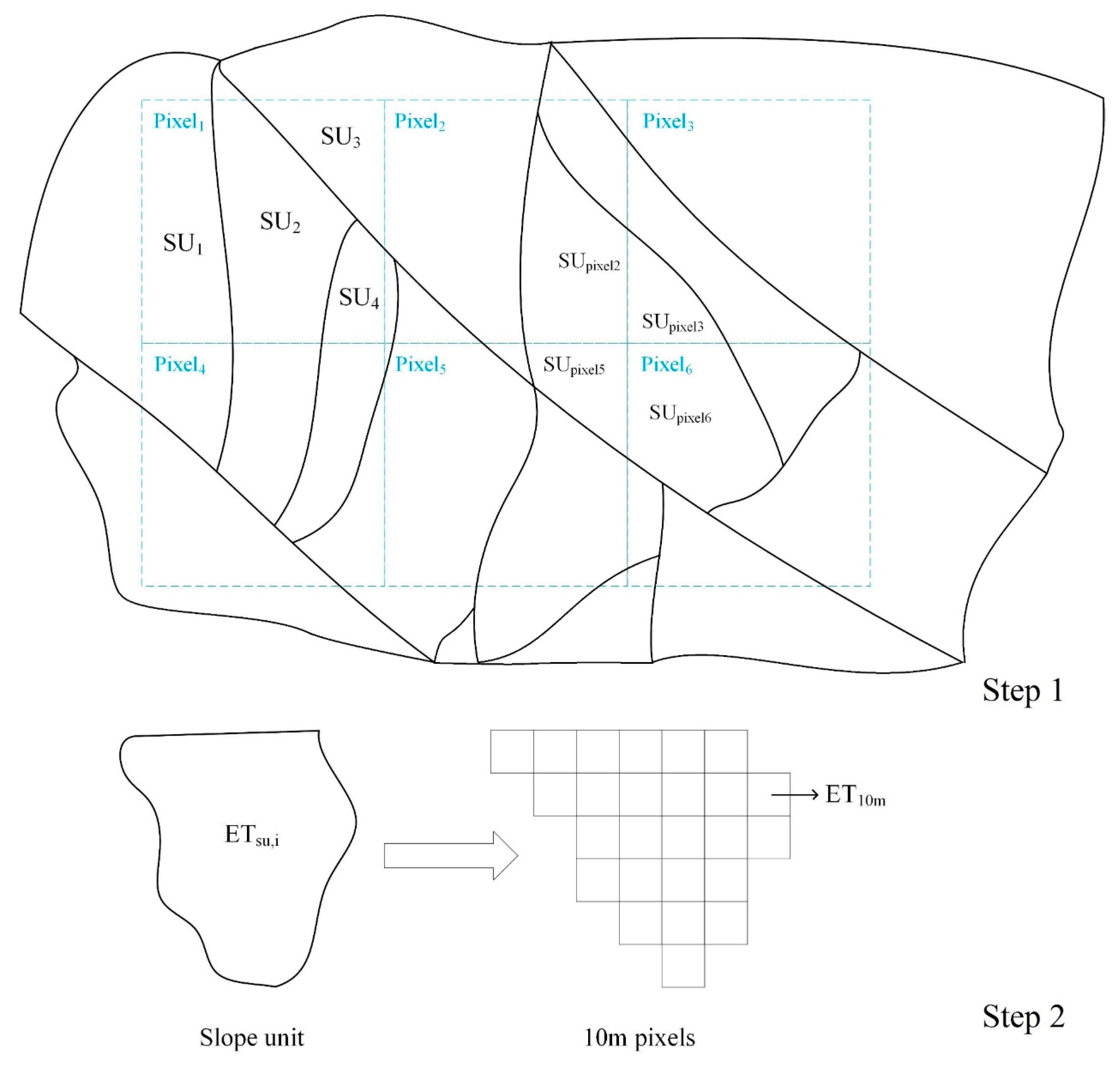
2.3.1. Delineation of Slope Units
2.3.2. Development of the Integrated Indicating Factor
2.3.3. ET Disaggregation Method
3. Results
3.1. Results of Slope Unit Delineation
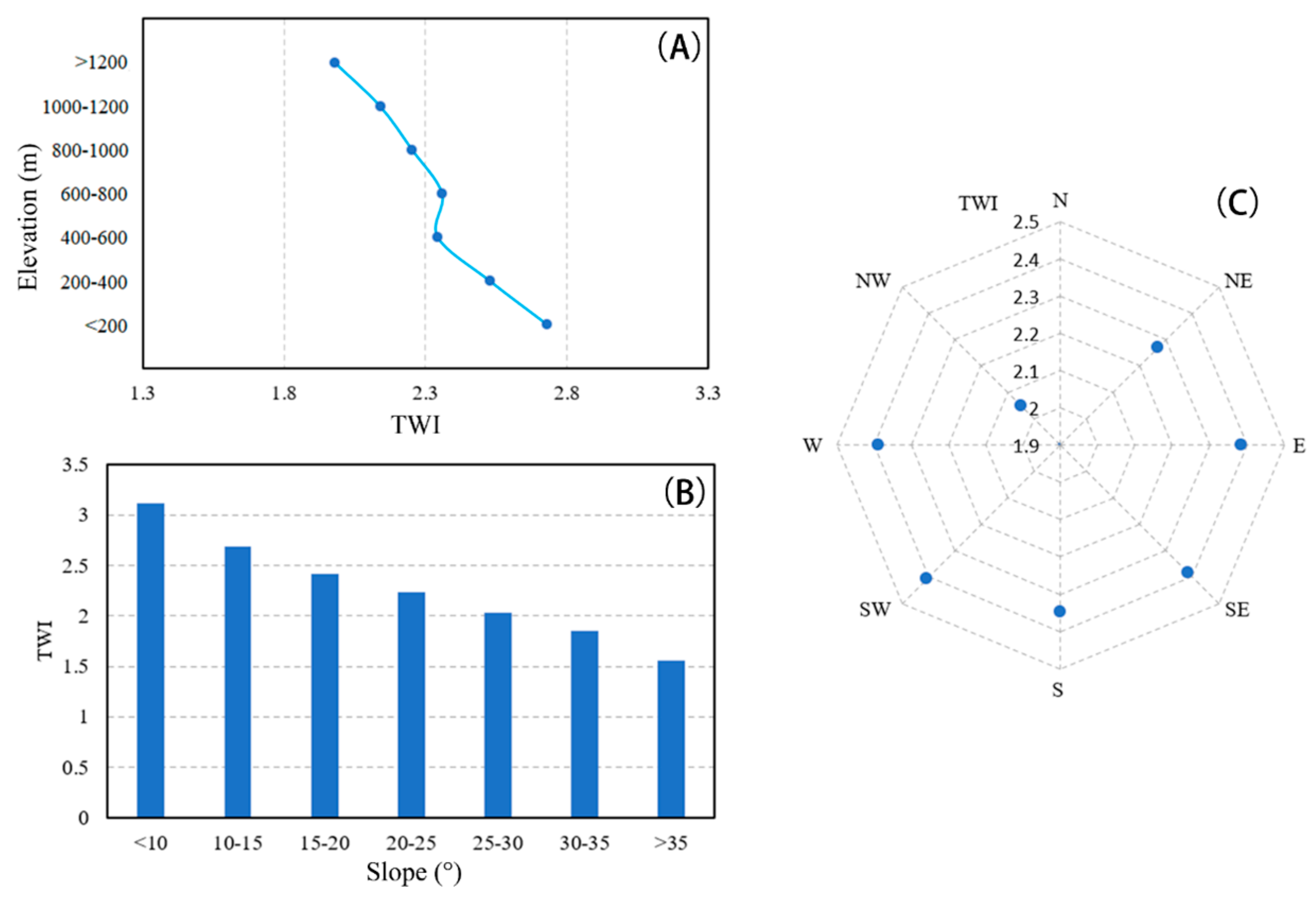
3.2. Factors Reflecting the Differences in Slope-Scale ET
3.3. Results of the Integrated Indicating Factor
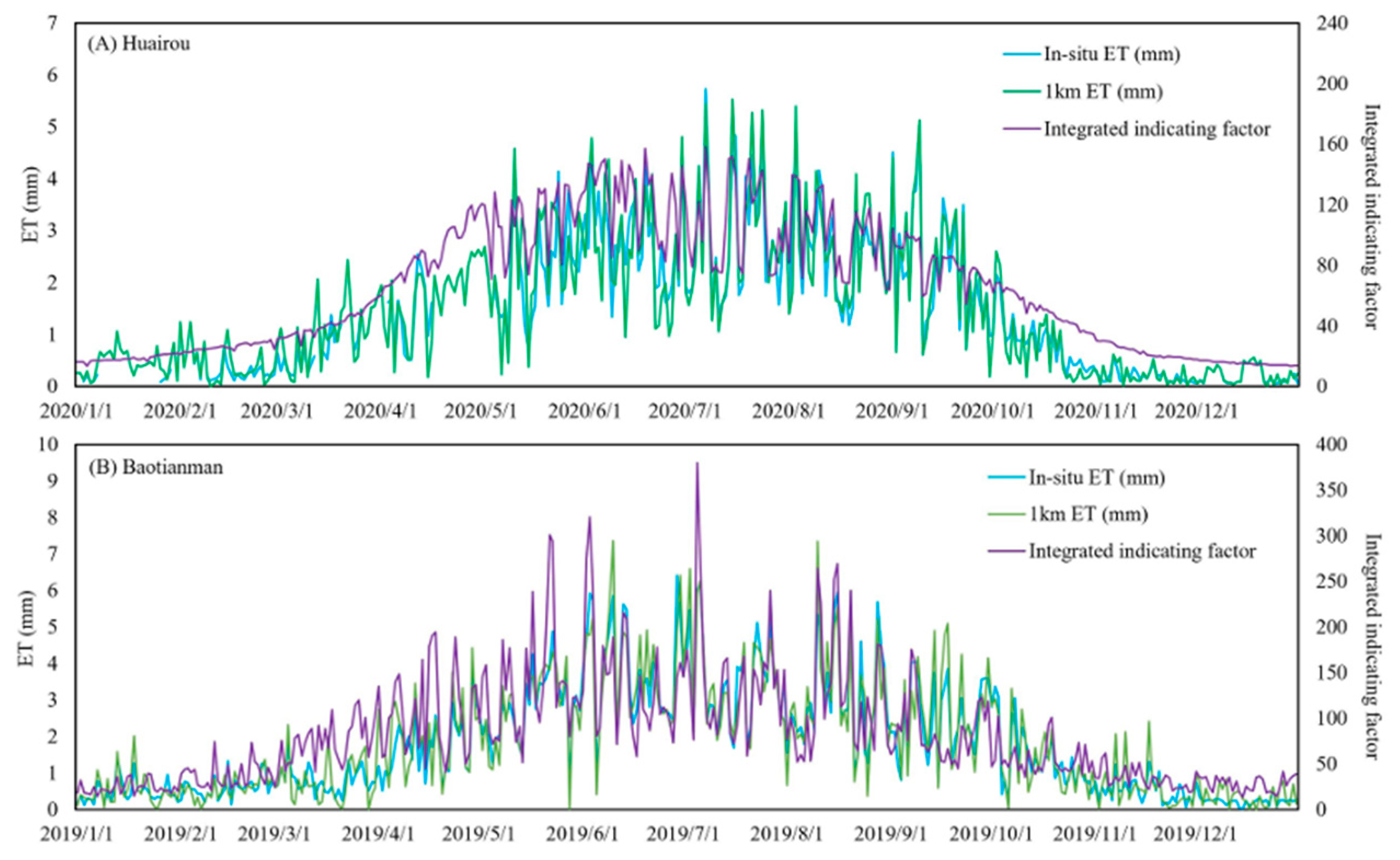
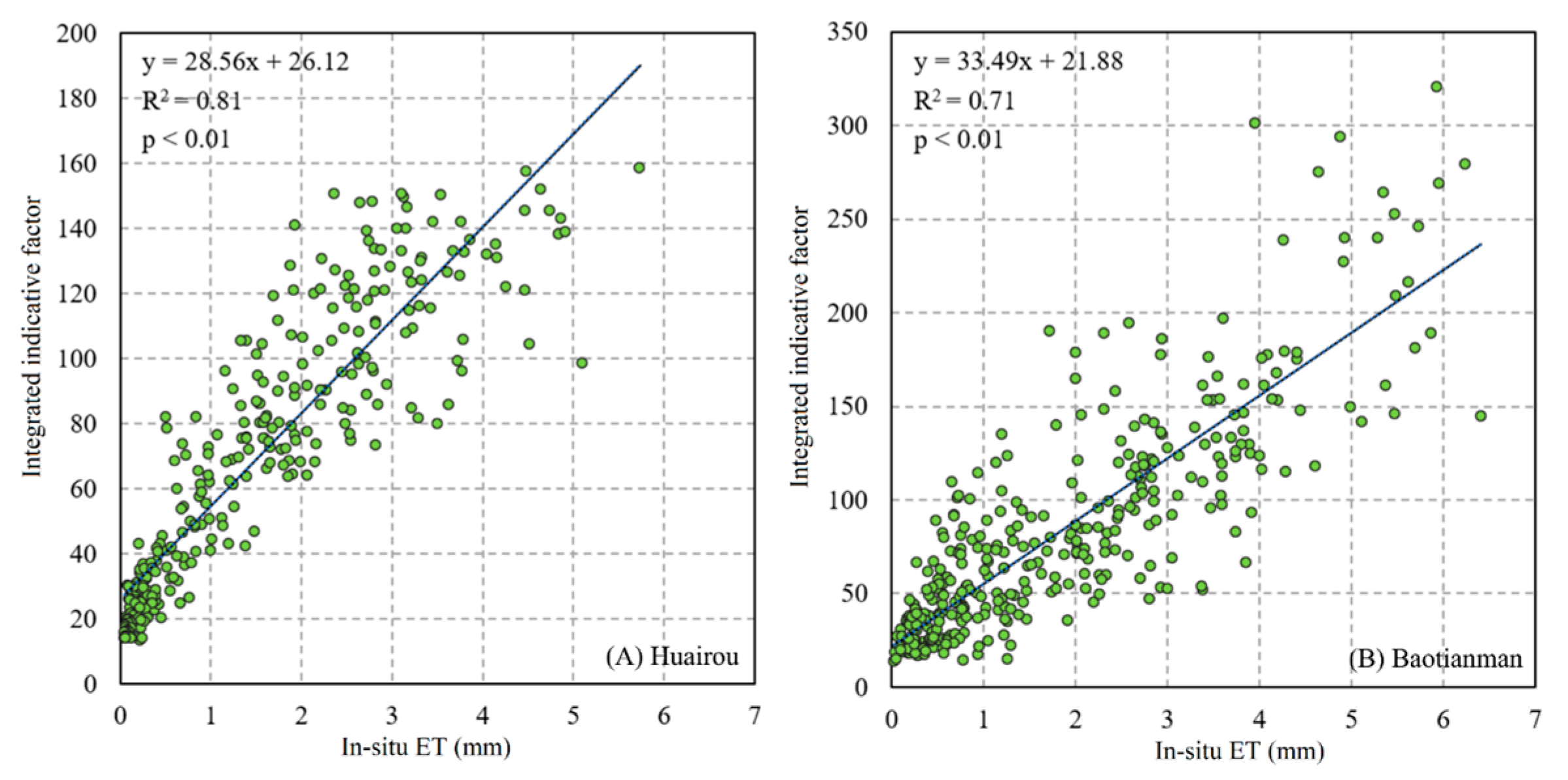
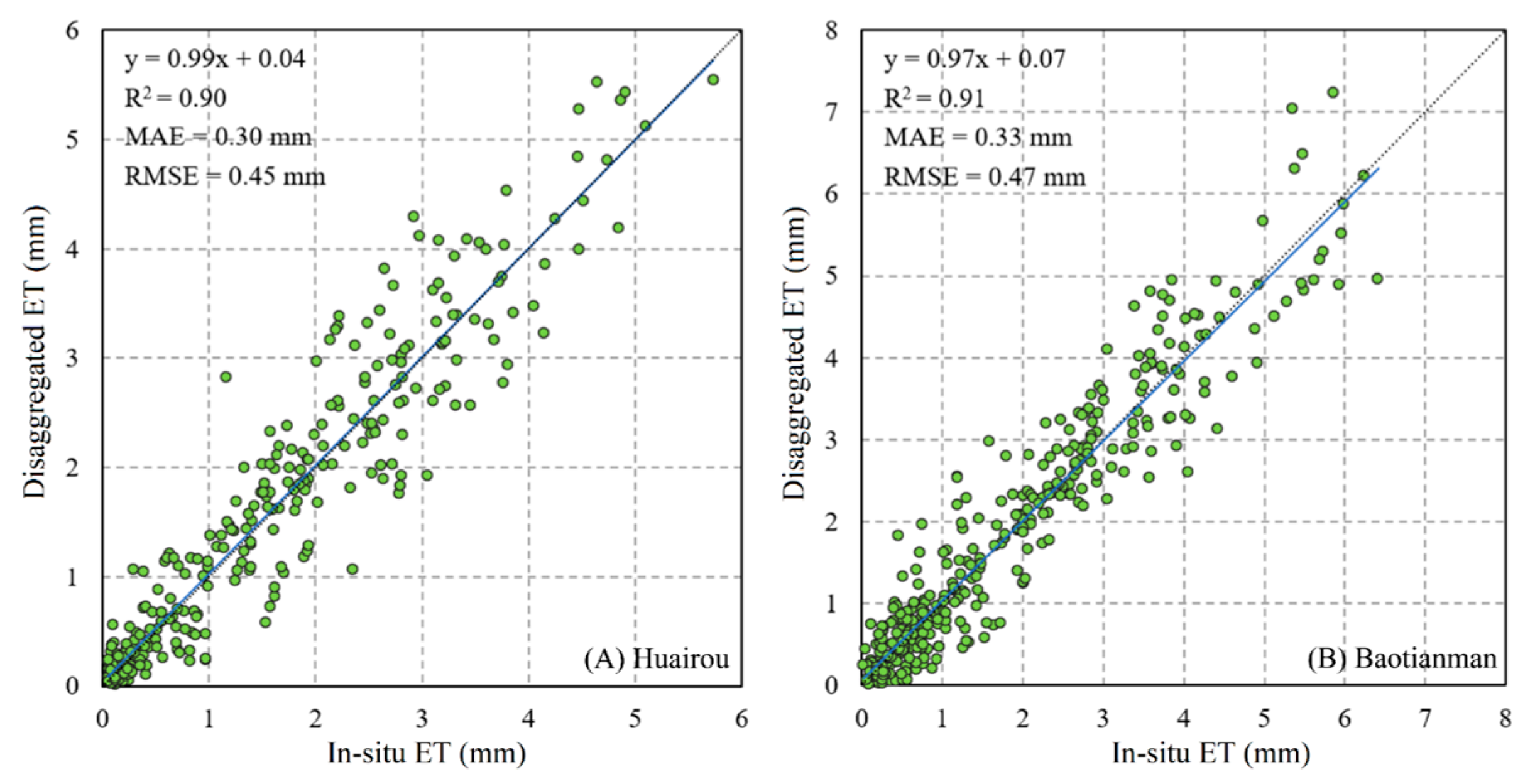
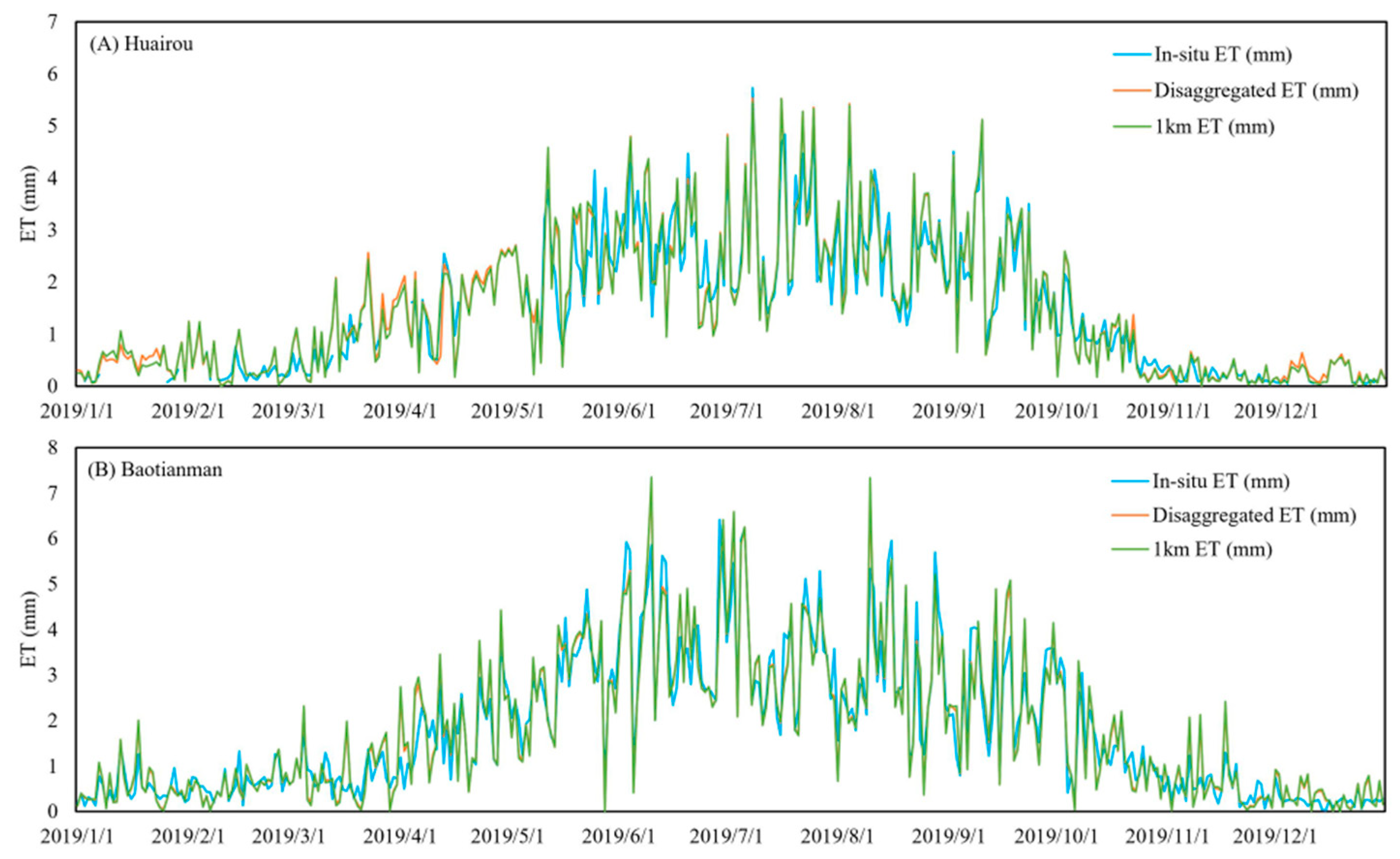
3.4. Results of ET Disaggregation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Funnell, D.C.; Price, M.F. Mountain geography: A review. Geogr. J. 2003, 169, 183–190. [Google Scholar] [CrossRef]
- Ives, J.D.; Messerli, B. The Himalayan Dilemma: Reconciling Development and Conservation; Routledge: London, UK, 2003. [Google Scholar]
- Gaertner, B.A.; Zegre, N.; Warner, T.; Fernandez, R.; He, Y.; Merriam, E.R. Climate, forest growing season, and evapotranspiration changes in the central Appalachian Mountains, USA. Sci. Total Environ. 2019, 650, 1371–1381. [Google Scholar] [CrossRef] [PubMed]
- Grêt-Regamey, A.; Brunner, S.H.; Kienast, F. Mountain ecosystem services: Who cares? Mt. Res. Dev. 2012, 32. [Google Scholar] [CrossRef]
- Briner, S.; Huber, R.; Bebi, P.; Elkin, C.; Schmatz, D.R.; Grêt-Regamey, A. Trade-offs between ecosystem services in a mountain region. Ecol. Soc. 2013, 18, 35. [Google Scholar] [CrossRef]
- Gret-Regamey, A.; Weibel, B. Global assessment of mountain ecosystem services using earth observation data. Ecosyst. Serv. 2020, 46, 101213. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef]
- Vinukollu, R.; Sheffield, J.; Ferguson, C.; Pan, M.; Wood, E. Developing Evapotranspiration Data Records for the Global Terrestrial Water Cycle. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2009; p. N43C-1159. [Google Scholar]
- Elnashar, A.; Shojaeezadeh, S.A.; Weber, T.K.D. A Multi-Model approach for remote Sensing-Based actual evapotranspiration mapping using Google Earth Engine (ETMapper-GEE). J. Hydrol. 2025, 657, 133062. [Google Scholar] [CrossRef]
- Ma, Z.; Yan, N.; Wu, B.; Stein, A.; Zhu, W.; Zeng, H. Variation in actual evapotranspiration following changes in climate and vegetation cover during an ecological restoration period (2000–2015) in the Loess Plateau, China. Sci. Total Environ. 2019, 689, 534–545. [Google Scholar] [CrossRef]
- Elnashar, A.; Zeng, H.; Wu, B.; Gebremicael, T.G.; Marie, K. Assessment of environmentally sensitive areas to desertification in the Blue Nile Basin driven by the MEDALUS-GEE framework. Sci. Total Environ. 2022, 815, 152925. [Google Scholar] [CrossRef]
- Zeng, H.; Elnashar, A.; Wu, B.; Zhang, M.; Zhu, W.; Tian, F.; Ma, Z. A framework for separating natural and anthropogenic contributions to evapotranspiration of human-managed land covers in watersheds based on machine learning. Sci. Total Environ. 2022, 823, 153726. [Google Scholar] [CrossRef]
- Nagler, P.L.; Glenn, E.P.; Hinojosa-Huerta, O. Synthesis of ground and remote sensing data for monitoring ecosystem functions in the Colorado River Delta, Mexico. Remote Sens. Environ. 2009, 113, 1473–1485. [Google Scholar]
- Peng, H.; Jia, Y.; Zhan, C.; Xu, W. Topographic controls on ecosystem evapotranspiration and net primary productivity under climate warming in the Taihang Mountains, China. J. Hydrol. 2020, 581, 124394. [Google Scholar]
- Ma, Z.; Wu, B.; Yan, N.; Zhu, W.; Xu, J. Coupling water and carbon processes to estimate field-scale maize evapotranspiration with Sentinel-2 data. Agric. For. Meteorol. 2021, 306, 108421. [Google Scholar]
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to 2019. Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar]
- Wang, L.; Wu, B.; Elnashar, A.; Zeng, H.; Zhu, W.; Yan, N. Synthesizing a regional territorial evapotranspiration dataset for Northern China. Remote Sens. 2021, 13, 1076. [Google Scholar] [CrossRef]
- Dile, Y.T.; Ayana, E.K.; Worqlul, A.W.; Xie, H.; Srinivasan, R.; Lefore, N.; You, L.; Clarke, N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Total Environ. 2020, 743, 140702. [Google Scholar]
- Wang, L.; Wu, B.; Elnashar, A.; Zhu, W.; Yan, N.; Ma, Z.; Liu, S.; Niu, X. Incorporation of net radiation model considering complex terrain in evapotranspiration determination with Sentinel-2 data. Remote Sens. 2022, 14, 1191. [Google Scholar] [CrossRef]
- Abiodun, O.O.; Guan, H.; Post, V.E.; Batelaan, O. Comparison of MODIS and SWAT evapotranspiration over a complex terrain at different spatial scales. Hydrol. Earth Syst. Sci. 2018, 22, 2775–2794. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Song, Y.; Han, C.; Liu, J.; Liu, Z. Sensitivity of potential evapotranspiration to meteorological factors and their elevational gradients in the Qilian Mountains, northwestern China. J. Hydrol. 2019, 568, 147–159. [Google Scholar]
- Cristóbal, J.; Poyatos, R.; Ninyerola, M.; Llorens, P.; Pons, X. Combining remote sensing and GIS climate modelling to estimate daily forest evapotranspiration in a Mediterranean mountain area. Hydrol. Earth Syst. Sci. 2011, 15, 1563–1575. [Google Scholar]
- Minderlein, S.; Menzel, L. Evapotranspiration and energy balance dynamics of a semi-arid mountainous steppe and shrubland site in Northern Mongolia. Environ. Earth Sci. 2015, 73, 593–609. [Google Scholar] [CrossRef]
- Atchley, A.L.; Maxwell, R.M. Influences of subsurface heterogeneity and vegetation cover on soil moisture, surface temperature and evapotranspiration at hillslope scales. Hydrogeol. J. 2011, 19, 289. [Google Scholar]
- Chen, X.; Su, Z.; Ma, Y.; Yang, K.; Wang, B. Estimation of surface energy fluxes under complex terrain of Mt. Qomolangma over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 1607–1618. [Google Scholar]
- Liu, X.; Shen, Y.; Li, H.; Guo, Y.; Pei, H.; Dong, W. Estimation of land surface evapotranspiration over complex terrain based on multi-spectral remote sensing data. Hydrol. Process. 2017, 31, 446–461. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y. Relative contribution of the topographic influence on the triangle approach for evapotranspiration estimation over mountainous areas. Adv. Meteorol. 2014, 2014, 584040. [Google Scholar]
- Lima, R.N.d.S.; Ribeiro, C.B.d.M. Spatial variability of daily evapotranspiration in a mountainous watershed by coupling surface energy balance and solar radiation model with gridded weather dataset. In Proceedings of the 2nd International Electronic Conference on Remote Sensing, Online, 22 March–5 April 2018; p. 342. [Google Scholar]
- Wang, D.; Zhan, Y.; Yu, T.; Liu, Y.; Jin, X.; Ren, X.; Chen, X.; Liu, Q. Improving meteorological input for surface energy balance system utilizing mesoscale weather research and forecasting model for estimating daily actual evapotranspiration. Water 2019, 12, 9. [Google Scholar] [CrossRef]
- Cherif, I.; Alexandridis, T.; Jauch, E.; Chambel-Leitao, P.; Almeida, C. Improving remotely sensed actual evapotranspiration estimation with raster meteorological data. Int. J. Remote Sens. 2015, 36, 4606–4620. [Google Scholar]
- Qian, Q.; Wu, B.; Xiong, J. Interpolation system for generating meteorological surfaces using to compute evapotranspiration in Haihe River Basin. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Republic of Korea, 25–29 July 2005; IGARSS’05; p. 4. [Google Scholar]
- Goulden, M.; Anderson, R.; Bales, R.; Kelly, A.; Meadows, M.; Winston, G. Evapotranspiration along an elevation gradient in California’s Sierra Nevada. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Li, S.; Tarboton, D.G.; McKee, M. GIS-Based Temperature Interpolation for Distributed Modelling of Reference Evapotranspiration. 2003. Available online: https://digitalcommons.usu.edu/cee_facpub/2218/ (accessed on 16 January 2025).
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Sun, R.; Zhang, B. Topographic effects on spatial pattern of surface air temperature in complex mountain environment. Environ. Earth Sci. 2016, 75, 1–12. [Google Scholar] [CrossRef]
- Mahour, M.; Tolpekin, V.; Stein, A.; Sharifi, A. A comparison of two downscaling procedures to increase the spatial resolution of mapping actual evapotranspiration. Isprs J. Photogramm. Remote Sens. 2017, 126, 56–67. [Google Scholar] [CrossRef]
- Shen, T.; Wu, B.; Yan, N.; Zhu, W. An NDVI-Based Statistical ET Downscaling Method. Water 2017, 9, 995. [Google Scholar] [CrossRef]
- Jiang, C.; Guan, K.; Pan, M.; Ryu, Y.; Wang, S. BESS-STAIR: A framework to estimate daily, 30-meter, and allweather crop evapotranspiration using multi-source satellite data for the U.S. Corn Belt. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–36. [Google Scholar] [CrossRef]
- Tan, S.; Wu, B.; Yan, N. A method for downscaling daily evapotranspiration based on 30-m surface resistance. J. Hydrol. 2019, 577, 123882. [Google Scholar] [CrossRef]
- Carrara, A. Drainage and divide networks derived from high-fidelity digital terrain models. In Quantitative Analysis of Mineral and Energy Resources; Springer: Berlin/Heidelberg, Germany, 1988; pp. 581–597. [Google Scholar]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Xie, M.; Esaki, T.; Zhou, G. GIS-based probabilistic mapping of landslide hazard using a three-dimensional deterministic model. Nat. Hazards 2004, 33, 265–282. [Google Scholar] [CrossRef]
- Holland, P.; Steyn, D. Vegetational responses to latitudinal variations in slope angle and aspect. J. Biogeogr. 1975, 2, 179–183. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Zha, T.; Barr, A.G.; van der Kamp, G.; Black, T.A.; McCaughey, J.H.; Flanagan, L.B. Interannual variation of evapotranspiration from forest and grassland ecosystems in western Canada in relation to drought. Agric. For. Meteorol. 2010, 150, 1476–1484. [Google Scholar]
- Metzen, D.; Sheridan, G.J.; Benyon, R.G.; Bolstad, P.V.; Griebel, A.; Lane, P.N. Spatio-temporal transpiration patterns reflect vegetation structure in complex upland terrain. Sci. Total Environ. 2019, 694, 133551. [Google Scholar] [CrossRef]
- Ward, A.D.; Trimble, S.W. Environmental Hydrology; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Williams, C.; McNamara, J.; Chandler, D. Controls on the temporal and spatial variability of soil moisture in a mountainous landscape: The signature of snow and complex terrain. Hydrol. Earth Syst. Sci. 2009, 13, 1325–1336. [Google Scholar]
- Cao, B.; Yu, L.; Naipal, V.; Ciais, P.; Li, W.; Zhao, Y.; Wei, W.; Chen, D.; Liu, Z.; Gong, P. A 30 m terrace mapping in China using Landsat 8 imagery and digital elevation model based on the Google Earth Engine. Earth Syst. Sci. Data 2021, 13, 2437–2456. [Google Scholar]
- Farwell, L.S.; Gudex-Cross, D.; Anise, I.E.; Bosch, M.J.; Olah, A.M.; Radeloff, V.C.; Razenkova, E.; Rogova, N.; Silveira, E.M.; Smith, M.M. Satellite image texture captures vegetation heterogeneity and explains patterns of bird richness. Remote Sens. Environ. 2021, 253, 112175. [Google Scholar]
- Vrieling, A.; Meroni, M.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Zurita-Milla, R.; Oosterbeek, K.; O’Connor, B.; Paganini, M. Vegetation phenology from Sentinel-2 and field cameras for a Dutch barrier island. Remote Sens. Environ. 2018, 215, 517–529. [Google Scholar] [CrossRef]
- Sun, Y.; Qin, Q.; Ren, H.; Zhang, T.; Chen, S. Red-edge band vegetation indices for leaf area index estimation from Sentinel-2/MSI imagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 826–840. [Google Scholar]
- Akbar, M.; Arisanto, P.; Sukirno, B.; Merdeka, P.; Priadhi, M.; Zallesa, S. Mangrove vegetation health index analysis by implementing NDVI (normalized difference vegetation index) classification method on sentinel-2 image data case study: Segara Anakan, Kabupaten Cilacap. IOP Conf. Ser. Earth Environ. Sci. 2020, 584, 012069. [Google Scholar] [CrossRef]
- Rujoiu-Mare, M.-R.; Olariu, B.; Mihai, B.-A.; Nistor, C.; Săvulescu, I. Land cover classification in Romanian Carpathians and Subcarpathians using multi-date Sentinel-2 remote sensing imagery. Eur. J. Remote Sens. 2017, 50, 496–508. [Google Scholar]
- Gašparović, M.; Jogun, T. The effect of fusing Sentinel-2 bands on land-cover classification. Int. J. Remote Sens. 2018, 39, 822–841. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 data for land cover/use mapping: A review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Saleem, A.; Awange, J. Coastline shift analysis in data deficient regions: Exploiting the high spatio-temporal resolution Sentinel-2 products. Catena 2019, 179, 6–19. [Google Scholar]
- Li, J.; Peng, B.; Wei, Y.; Ye, H. Accurate extraction of surface water in complex environment based on Google Earth Engine and Sentinel-2. PLoS ONE 2021, 16, e0253209. [Google Scholar] [CrossRef]
- Puletti, N.; Mattioli, W.; Bussotti, F.; Pollastrini, M. Monitoring the effects of extreme drought events on forest health by Sentinel-2 imagery. J. Appl. Remote Sens. 2019, 13, 020501. [Google Scholar]
- Haghighian, F.; Yousefi, S.; Keesstra, S. Identifying tree health using sentinel-2 images: A case study on Tortrix viridana L. infected oak trees in Western Iran. Geocarto Int. 2022, 37, 304–314. [Google Scholar]
- Wu, B.; Liu, S.; Zhu, W.; Yu, M.; Yan, N.; Xing, Q. A method to estimate sunshine duration using cloud classification data from a geostationary meteorological satellite (FY-2D) over the Heihe River Basin. Sensors 2016, 16, 1859. [Google Scholar] [CrossRef]
- Rossi, C.; Gonzalez, F.R.; Fritz, T.; Yague-Martinez, N.; Eineder, M. TanDEM-X calibrated raw DEM generation. ISPRS J. Photogramm. Remote Sens. 2012, 73, 12–20. [Google Scholar]
- Kljun, N.; Calanca, P.; Rotach, M.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar]
- Babel, W.; Charuchittipan, D.; Zhao, P.; Biermann, T.; Gatzsche, K.; Foken, T. Application of an energy balance correction method for turbulent flux measurements based on buoyancy. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; p. 6936. [Google Scholar]
- Liu, S.; Xu, Z.; Zhu, Z.; Jia, Z.; Zhu, M. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar]
- Wu, B.; Zhu, W.; Yan, N.; Xing, Q.; Wang, L. Regional Actual Evapotranspiration Estimation with Land and Meteorological Variables Derived from Multi-Source Satellite Data. Remote Sens. 2020, 12, 332. [Google Scholar] [CrossRef]
- Dodson, R.; Marks, D. Daily air temperature interpolated at high spatial resolution over a large mountainous region. Clim. Res. 1997, 8, 1–20. [Google Scholar] [CrossRef]
- Wu, B.; Yan, N.; Xiong, J.; Bastiaanssen, W.; Zhu, W.; Stein, A. Validation of ETWatch using field measurements at diverse landscapes: A case study in Hai Basin of China. J. Hydrol. 2012, 436, 67–80. [Google Scholar] [CrossRef]
- Tan, S.; Wu, B.; Yan, N.; Zeng, H. Satellite-based water consumption dynamics monitoring in an extremely arid area. Remote Sens. 2018, 10, 1399. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar]
- Leuning, R.; Zhang, Y.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar]
- Yao, Y.; Liang, S.; Cheng, J.; Liu, S.; Fisher, J.B.; Zhang, X.; Jia, K.; Zhao, X.; Qin, Q.; Zhao, B. MODIS-driven estimation of terrestrial latent heat flux in China based on a modified Priestley–Taylor algorithm. Agric. For. Meteorol. 2013, 171, 187–202. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Gregoire, J.-M. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 2. Validation and applications. Remote Sens. Environ. 2002, 82, 198–207. [Google Scholar] [CrossRef]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1: Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar]
- Cao, R.; Chen, Y.; Shen, M.; Chen, J.; Zhou, J.; Wang, C.; Yang, W. A simple method to improve the quality of NDVI time-series data by integrating spatiotemporal information with the Savitzky-Golay filter. Remote Sens. Environ. 2018, 217, 244–257. [Google Scholar]
- Shwetha, H.R.; Nagesh Kumar, D. Estimation of daily vegetation coefficients using MODIS data for clear and cloudy sky conditions. Int. J. Remote Sens. 2018, 39, 3776–3800. [Google Scholar]
- Western, A.W.; Grayson, R.B.; Blöschl, G.; Willgoose, G.R.; McMahon, T.A. Observed spatial organization of soil moisture and its relation to terrain indices. Water Resour. Res. 1999, 35, 797–810. [Google Scholar]
- Kopecký, M.; Macek, M.; Wild, J. Topographic Wetness Index calculation guidelines based on measured soil moisture and plant species composition. Sci. Total Environ. 2021, 757, 143785. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 1–19. [Google Scholar]
- Yang, X.; Zuo, X.; Xie, W.; Li, Y.; Guo, S.; Zhang, H. A correction method of NDVI topographic shadow effect for rugged terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8456–8472. [Google Scholar] [CrossRef]
- Mutiibwa, D.; Strachan, S.; Albright, T. Land surface temperature and surface air temperature in complex terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4762–4774. [Google Scholar]
- Wen, J.; Zhao, X.; Liu, Q.; Tang, Y.; Dou, B. An improved land-surface albedo algorithm with DEM in rugged terrain. IEEE Geosci. Remote Sens. Lett. 2013, 11, 883–887. [Google Scholar]
- Tran, B.N.; Van Der Kwast, J.; Seyoum, S.; Uijlenhoet, R.; Jewitt, G.; Mul, M. Uncertainty assessment of satellite remote-sensing-based evapotranspiration estimates: A systematic review of methods and gaps. Hydrol. Earth Syst. Sci. 2023, 27, 4505–4528. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R. On uncertainty in global terrestrial evapotranspiration estimates from choice of input forcing datasets. J. Hydrometeorol. 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Yang, Z.; Pan, X.; Liu, Y.; Tansey, K.; Yuan, J.; Wang, Z.; Liu, S.; Yang, Y. Evaluation of spatial downscaling for satellite retrieval of evapotranspiration from the nonparametric approach in an arid area. J. Hydrol. 2024, 628, 130538. [Google Scholar]
- Bisquert, M.; Sánchez, J.; López-Urrea, R.; Caselles, V. Estimating high resolution evapotranspiration from disaggregated thermal images. Remote Sens. Environ. 2016, 187, 423–433. [Google Scholar] [CrossRef]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar]
- Youssef, A.M. Landslide susceptibility delineation in the Ar-Rayth area, Jizan, Kingdom of Saudi Arabia, using analytical hierarchy process, frequency ratio, and logistic regression models. Environ. Earth Sci. 2015, 73, 8499–8518. [Google Scholar]




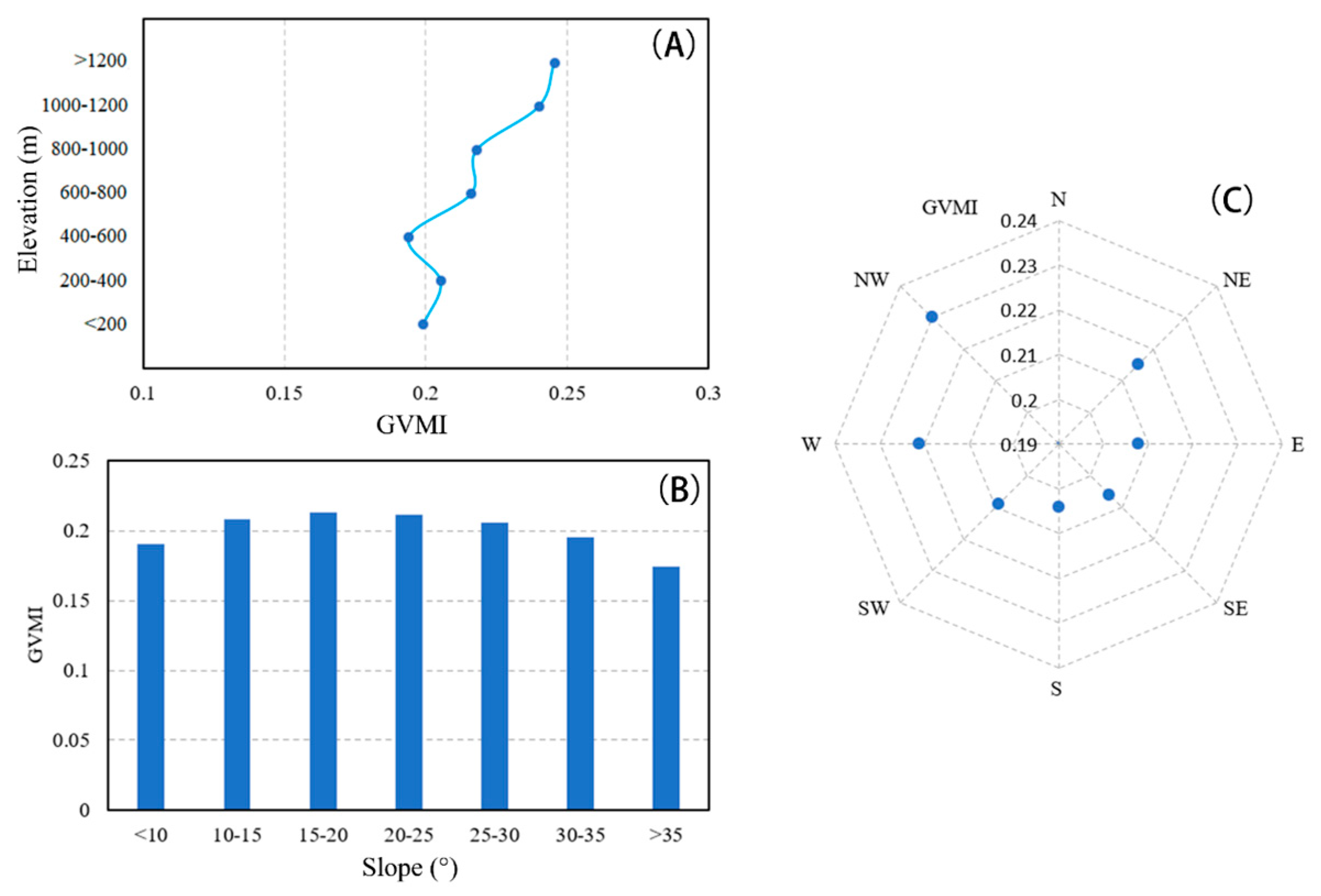
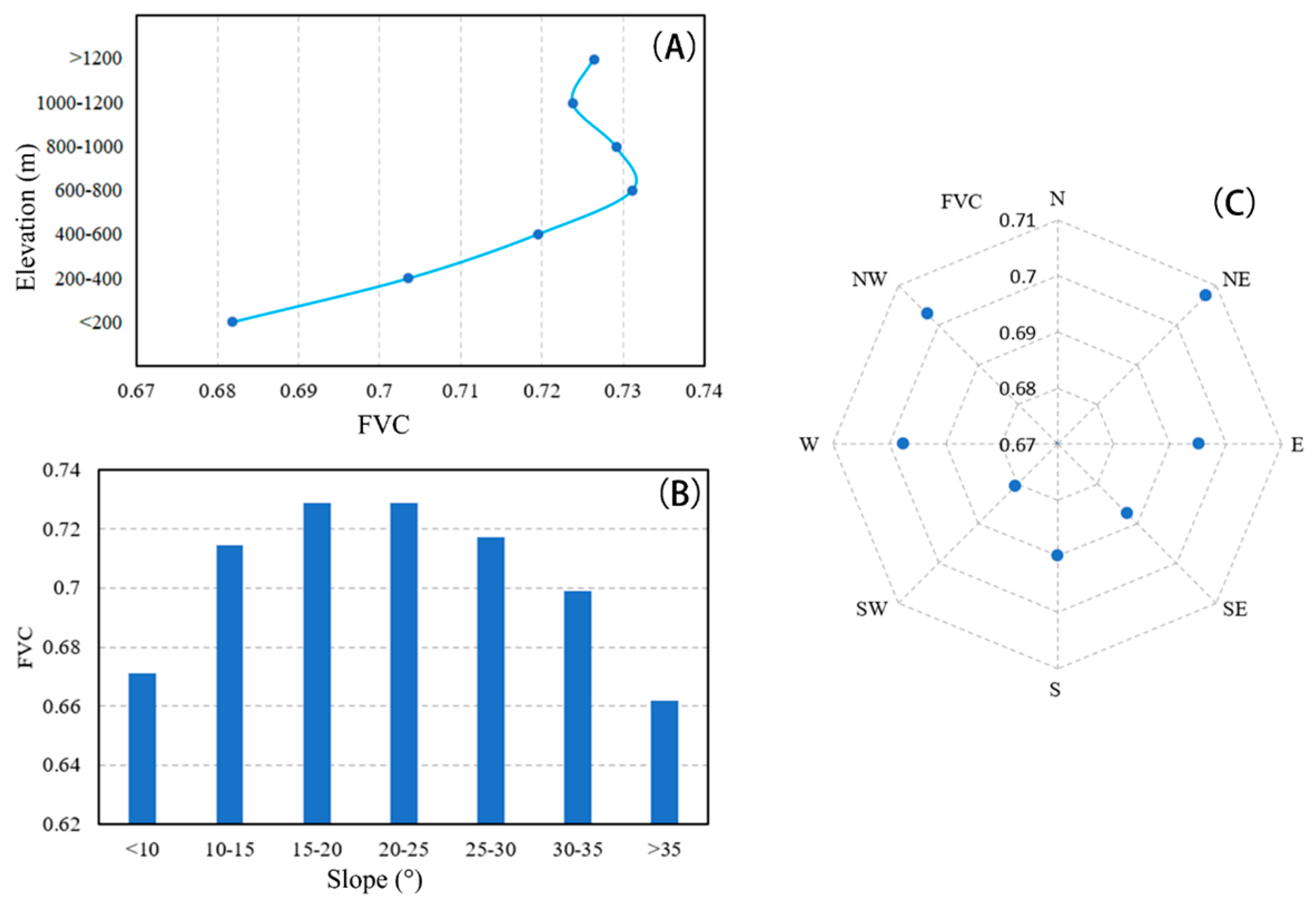

| Site | Elevation (m) | Slope (°) | Aspect | Proportions of Slopes with Different Aspect Within the Flux Tower Footprint Area (%) | ||
|---|---|---|---|---|---|---|
| Sunny Slope | Shady Slope | Others | ||||
| Huairou | 328 | 22 | Southeast | 27.1 | 38.7 | 34.2 |
| Baotianman | 1410.7 | 18.1 | West | 22.6 | 47.5 | 29.9 |
| Assessment Indicator | ETWatch ET with 1 km Resolution | Disaggregated Results Based on ETWatch ET | |
|---|---|---|---|
| Huairou | R2 | 0.89 | 0.90 |
| RMSE | 0.57 | 0.45 | |
| Baotianman | R2 | 0.89 | 0.91 |
| RMSE | 0.54 | 0.47 |
| R2 | RMSE | |
|---|---|---|
| ETWatch ET with 1 km resolution | 0.89 | 0.54 |
| Disaggregated results based on ETWatch ET | 0.91 | 0.47 |
| SSEBop ET with 1 km resolution | 0.83 | 0.67 |
| Disaggregated results based on SSEBop ET | 0.85 | 0.58 |
| FLDAS ET with 10 km resolution | 0.81 | 0.62 |
| Disaggregated results based on FLDAS ET | 0.82 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wu, B.; Zhu, W.; Elnashar, A.; Yan, N.; Ma, Z. Evapotranspiration Disaggregation Using an Integrated Indicating Factor Based on Slope Units. Remote Sens. 2025, 17, 1201. https://doi.org/10.3390/rs17071201
Wang L, Wu B, Zhu W, Elnashar A, Yan N, Ma Z. Evapotranspiration Disaggregation Using an Integrated Indicating Factor Based on Slope Units. Remote Sensing. 2025; 17(7):1201. https://doi.org/10.3390/rs17071201
Chicago/Turabian StyleWang, Linjiang, Bingfang Wu, Weiwei Zhu, Abdelrazek Elnashar, Nana Yan, and Zonghan Ma. 2025. "Evapotranspiration Disaggregation Using an Integrated Indicating Factor Based on Slope Units" Remote Sensing 17, no. 7: 1201. https://doi.org/10.3390/rs17071201
APA StyleWang, L., Wu, B., Zhu, W., Elnashar, A., Yan, N., & Ma, Z. (2025). Evapotranspiration Disaggregation Using an Integrated Indicating Factor Based on Slope Units. Remote Sensing, 17(7), 1201. https://doi.org/10.3390/rs17071201










