Embedding Moving Baseline RTK for High-Precision Spatiotemporal Synchronization in Virtual Coupling Applications
Abstract
1. Introduction
2. System Architecture and Principles
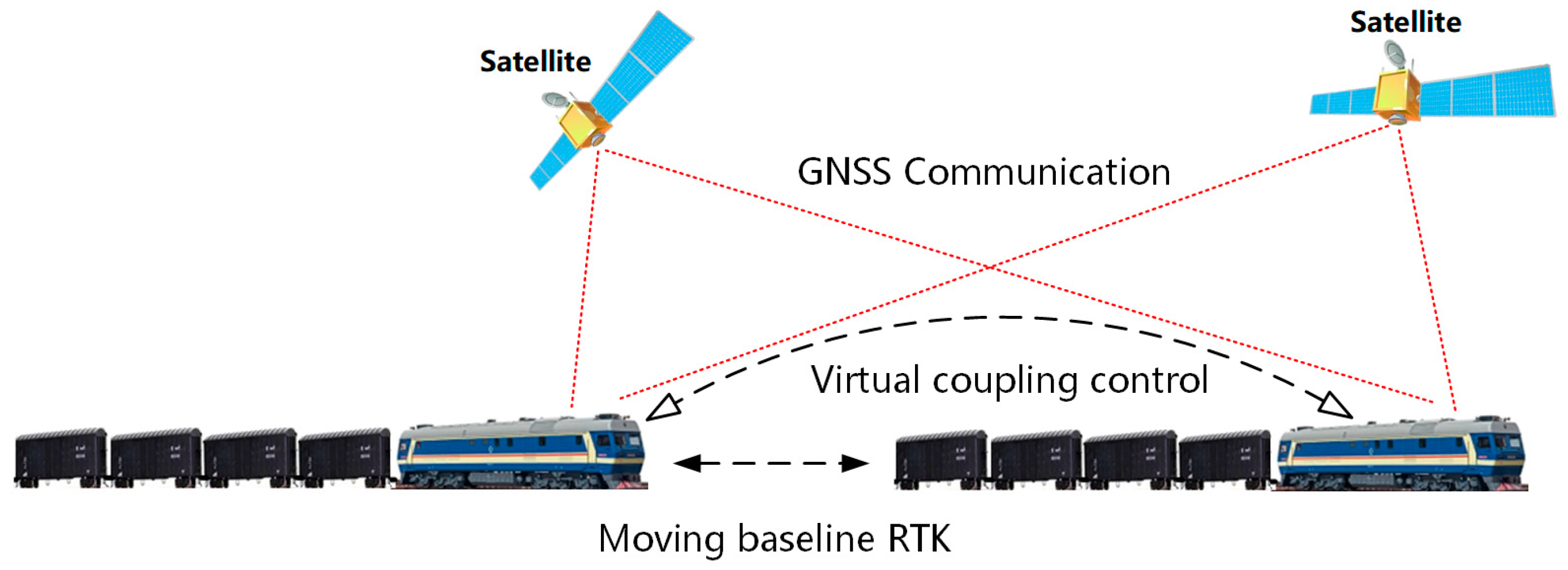
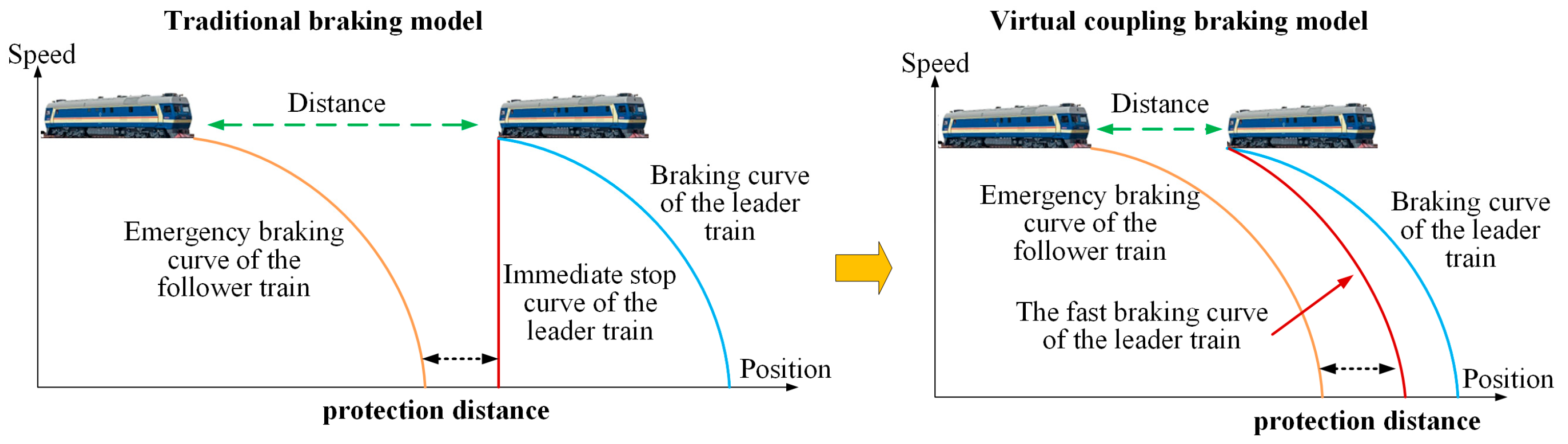
2.1. Virtual Coupling Fundamentals
2.2. Moving Baseline RTK Technology
2.2.1. Differential GNSS Processing for High Accuracy
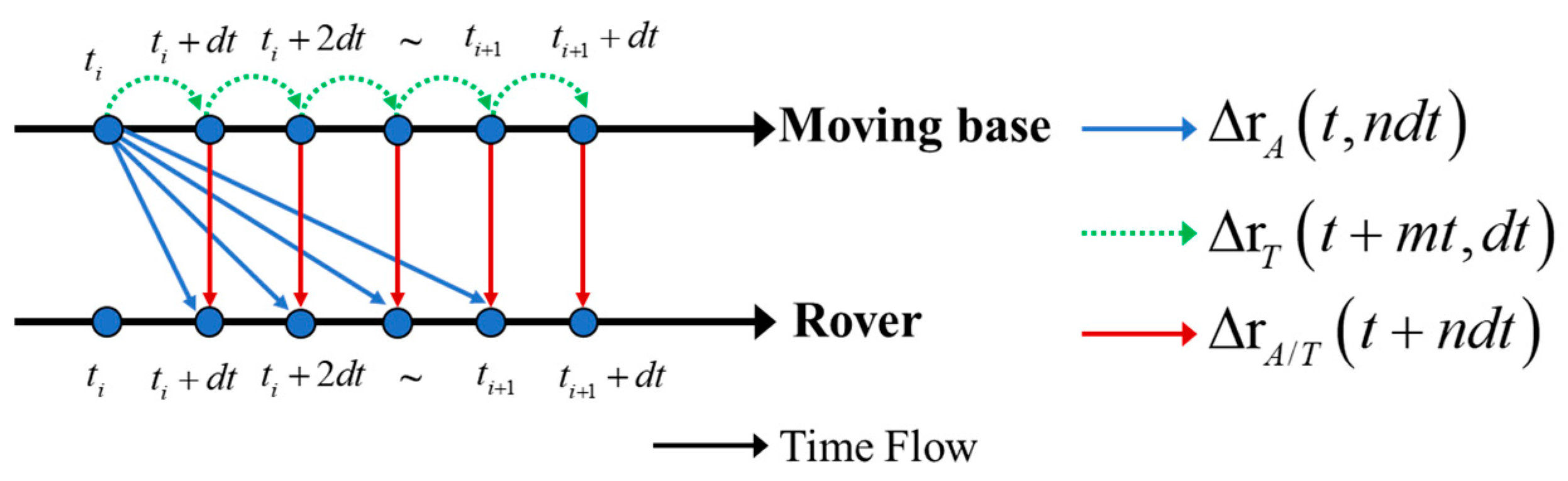
2.2.2. Dynamic Baseline Estimation
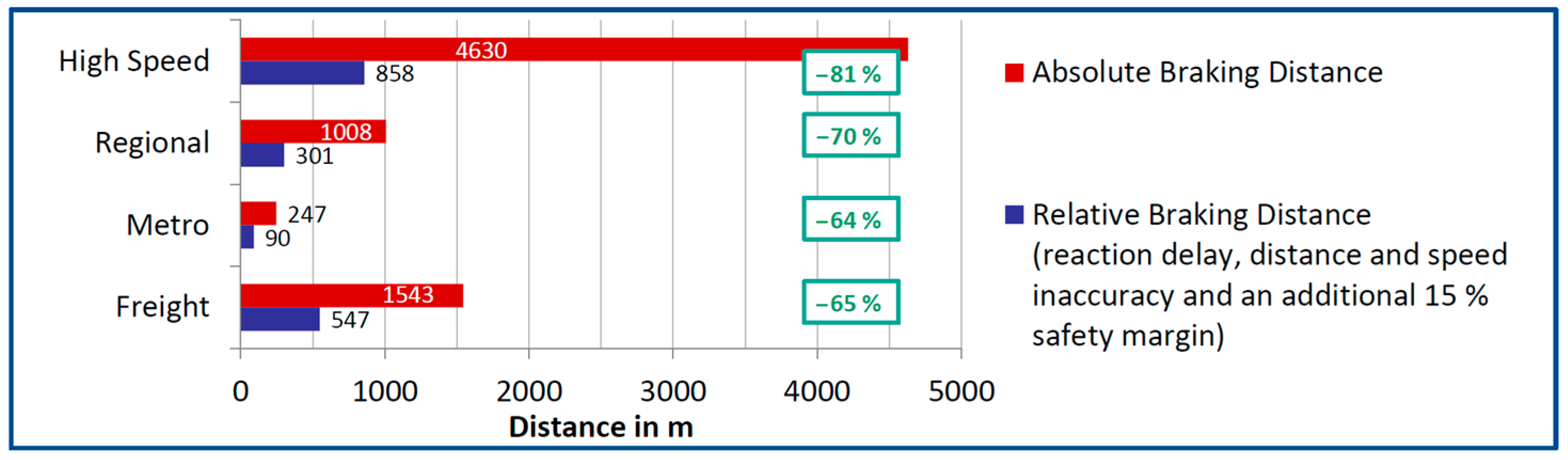
2.3. Spatiotemporal Synchronization Requirements
3. System Implementation
3.1. Dynamic Model of Virtual Coupling
3.2. Spatiotemporal Synchronization and Communication
3.2.1. Spatiotemporal Synchronization Mechanism
3.2.2. Decentralized Synchronization Algorithm
4. Experimental Results
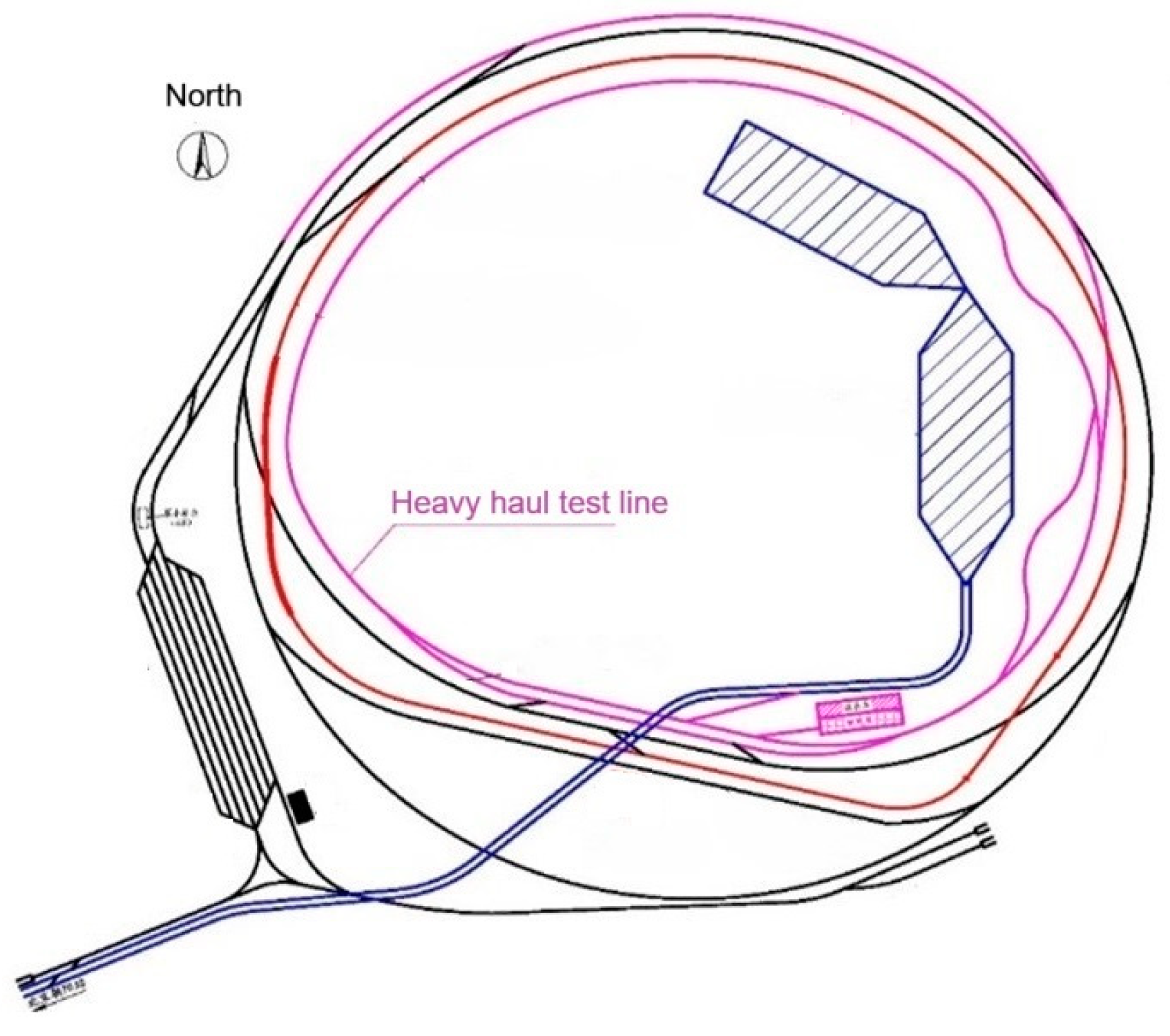
4.1. Experimental Environment and Setup
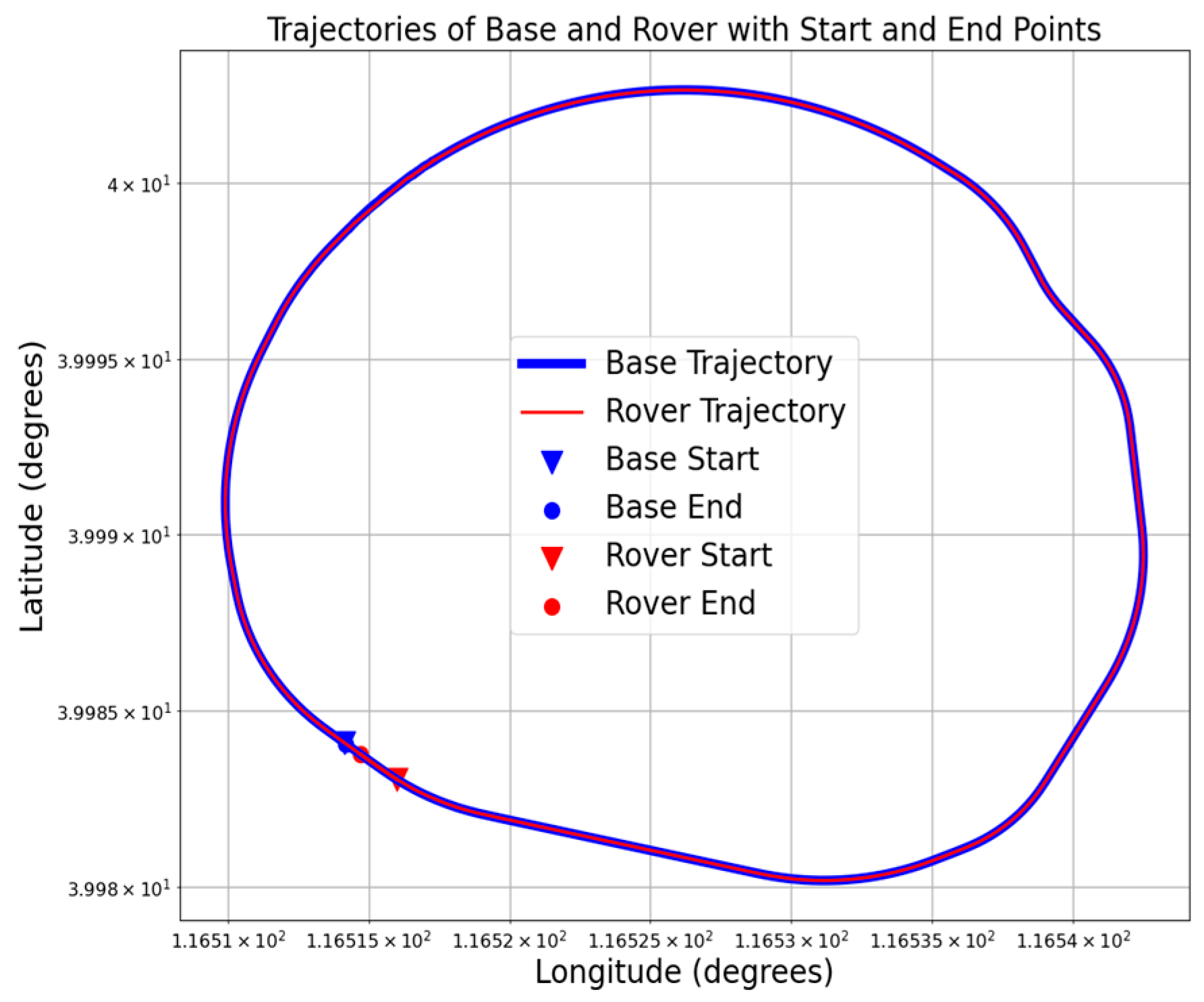
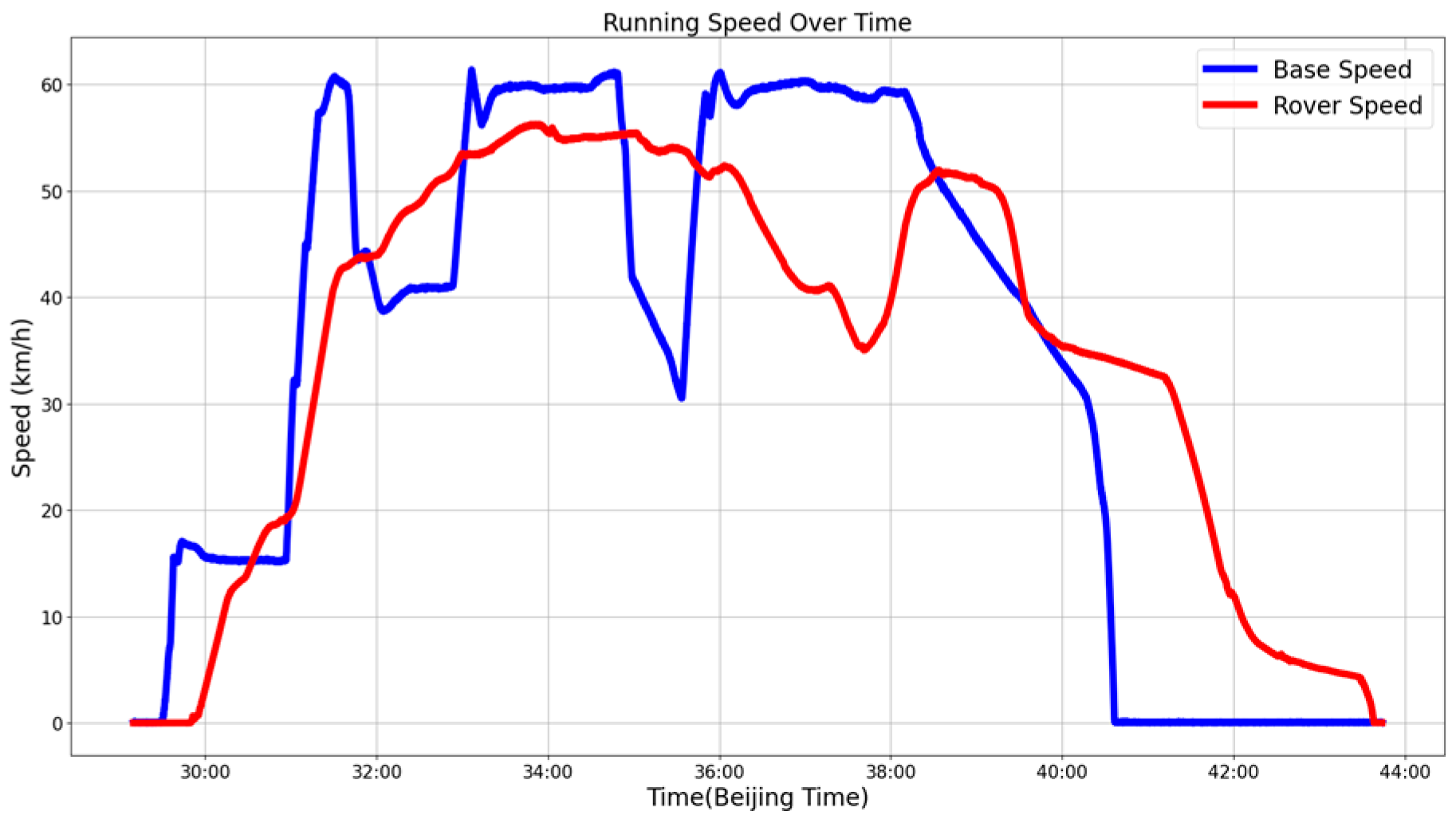
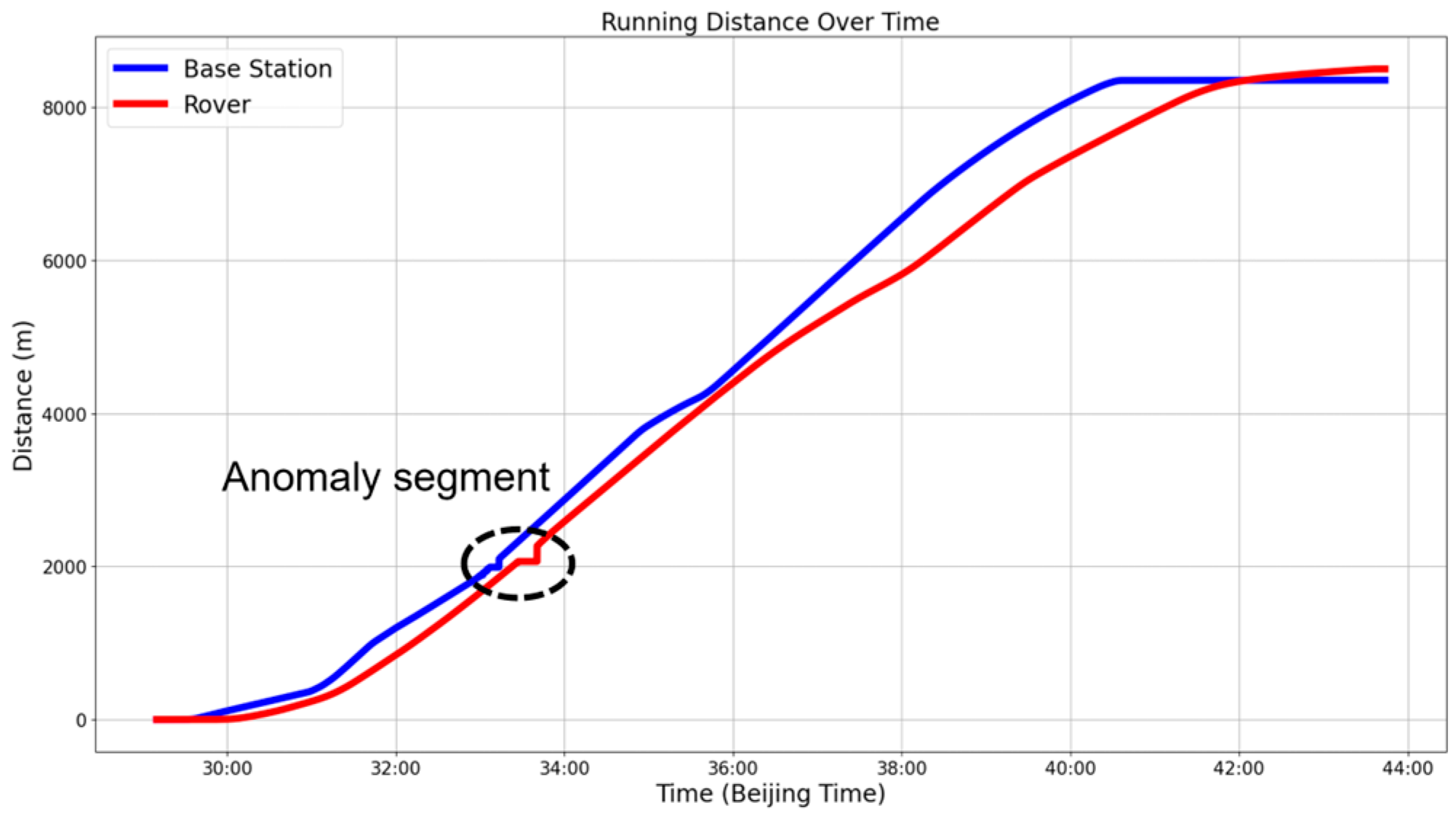
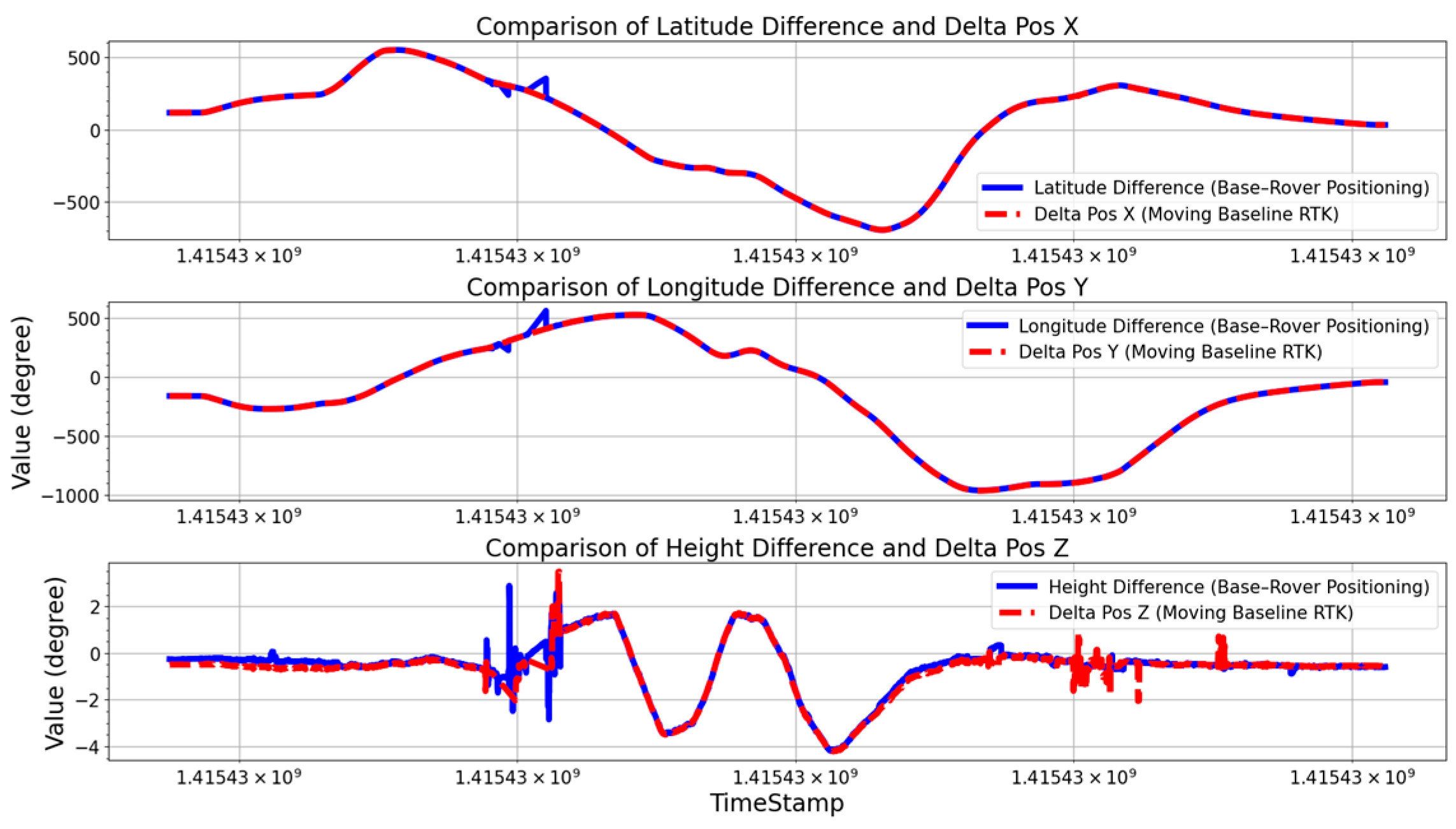
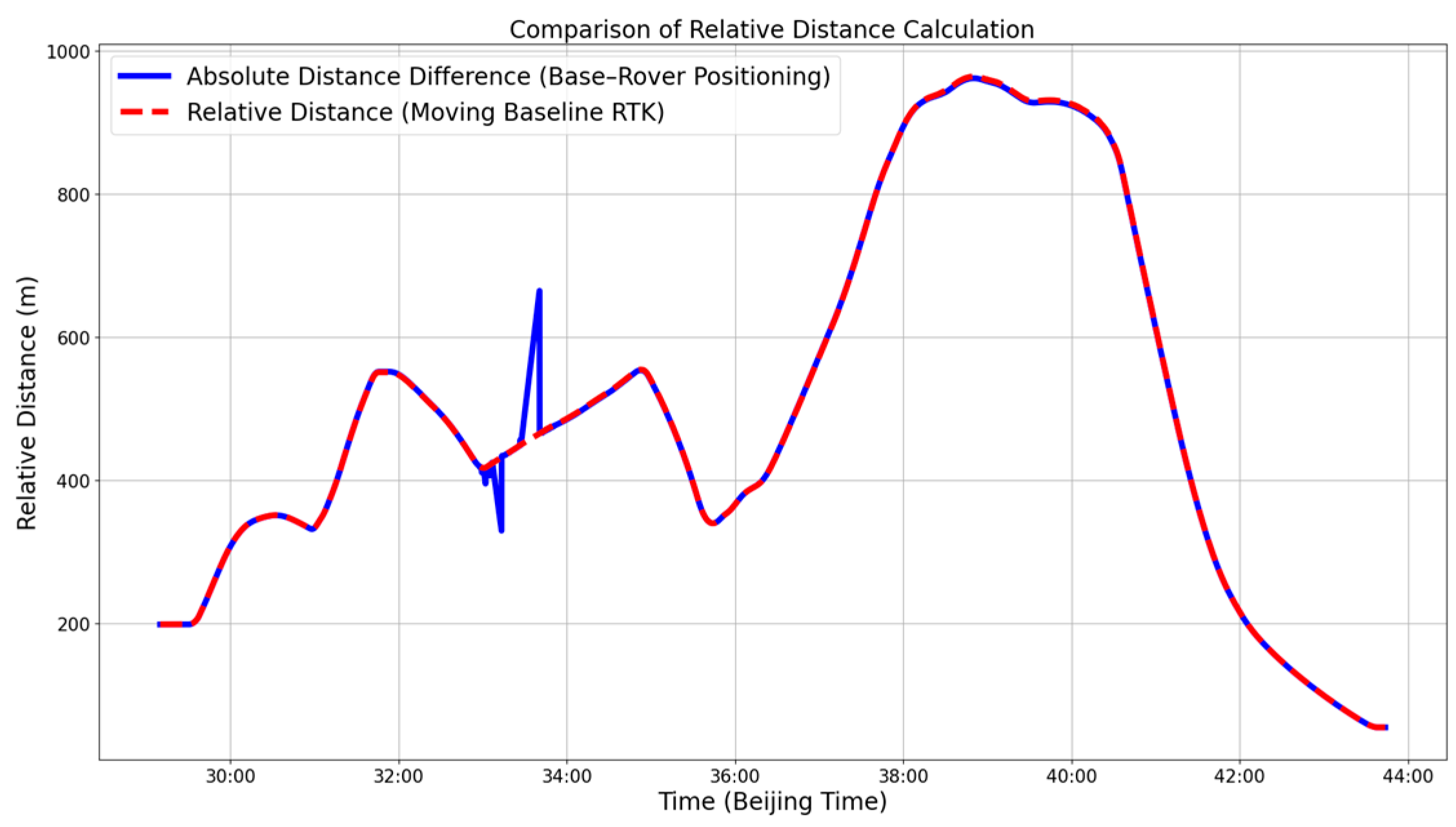
4.2. Overall Tracking Performance
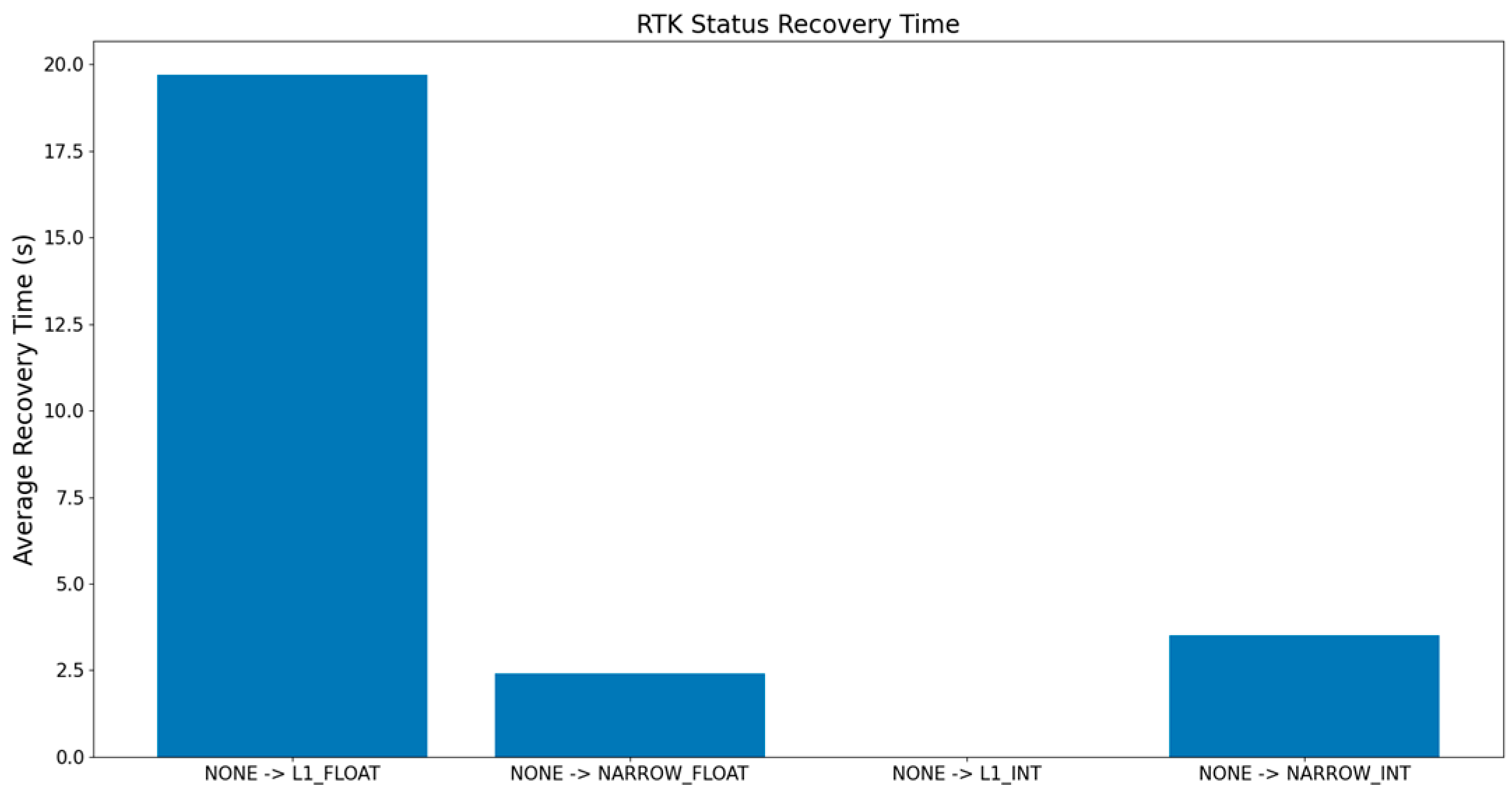
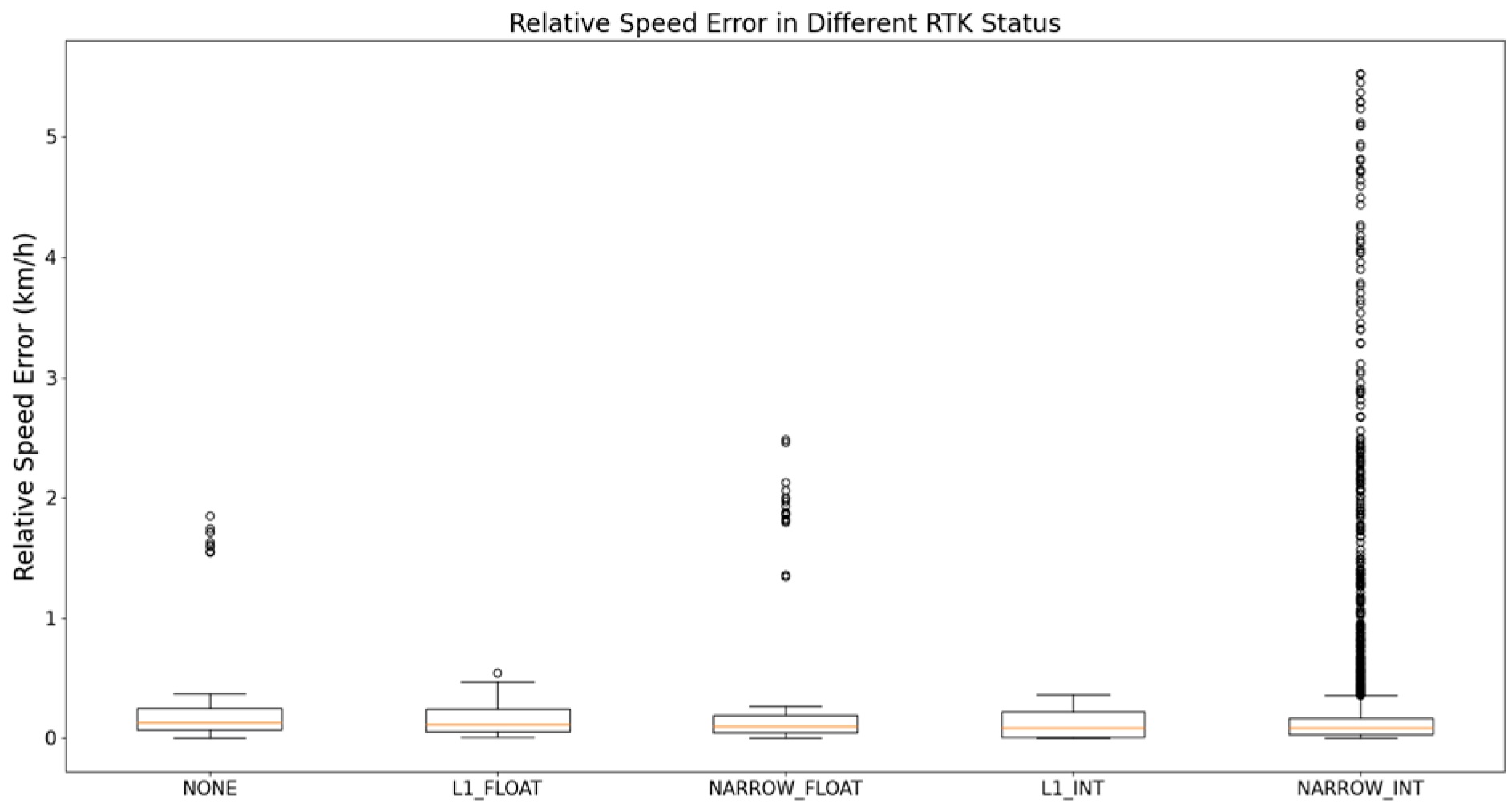
4.3. RTK Status Analysis
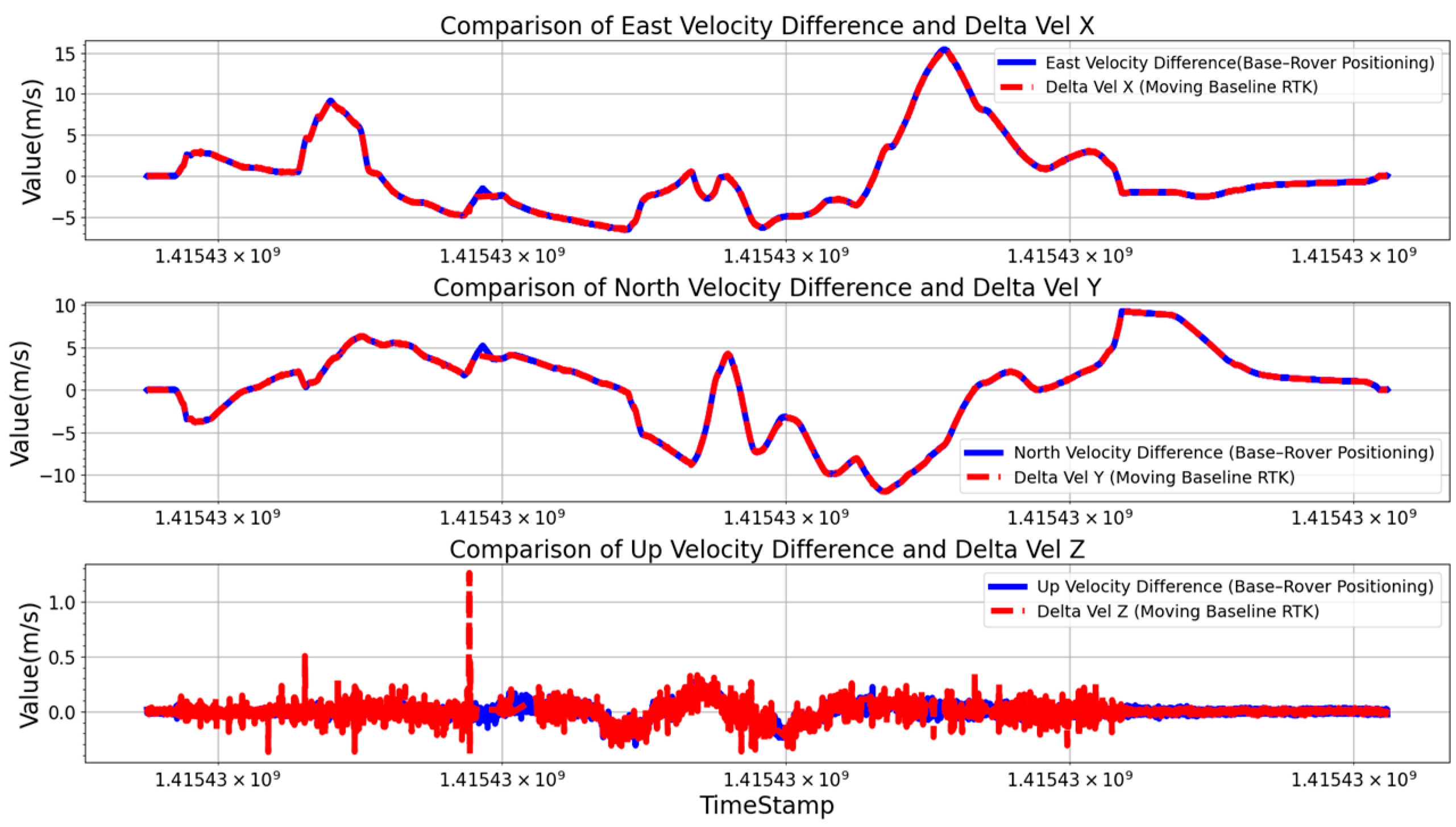
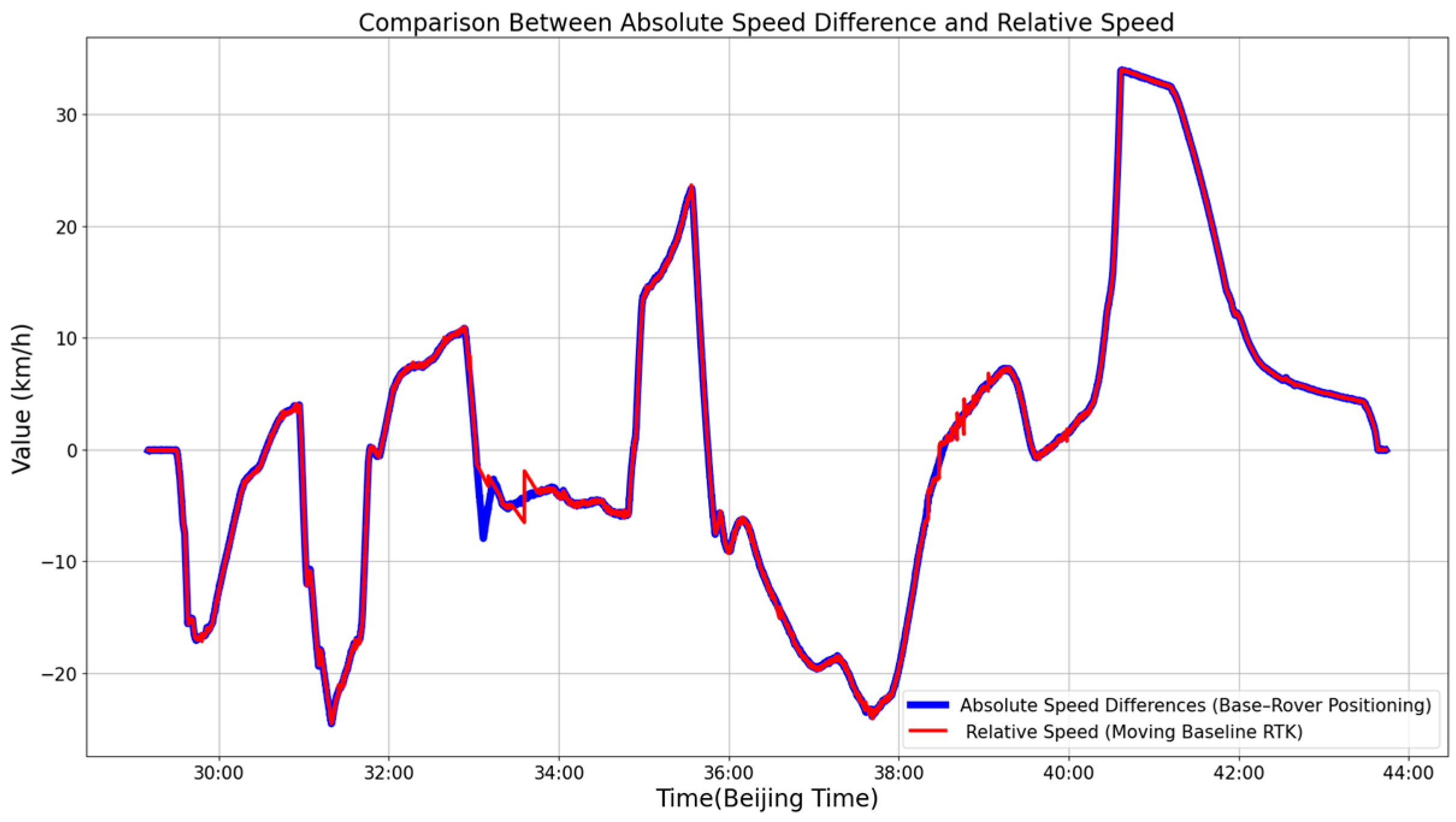
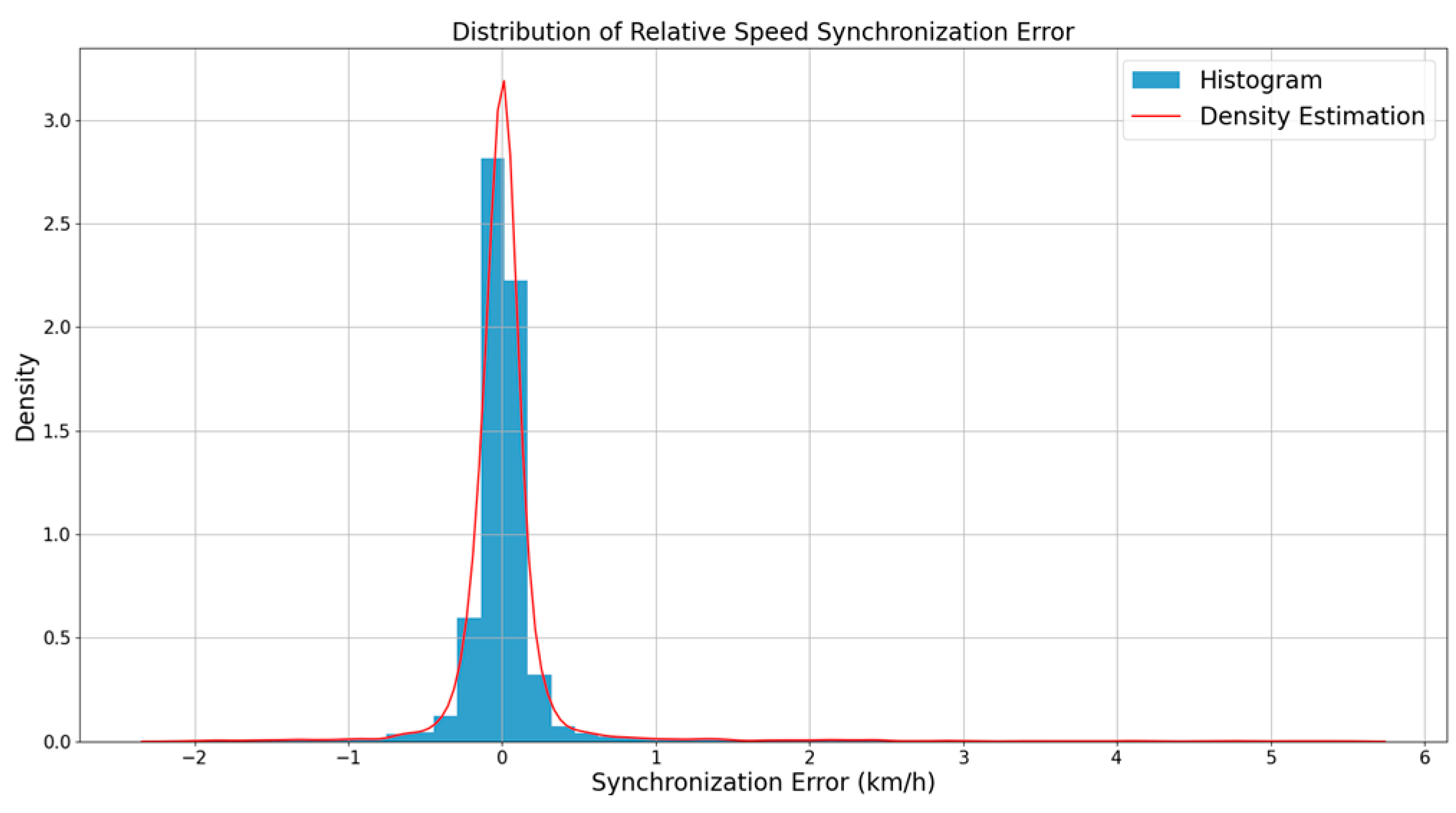
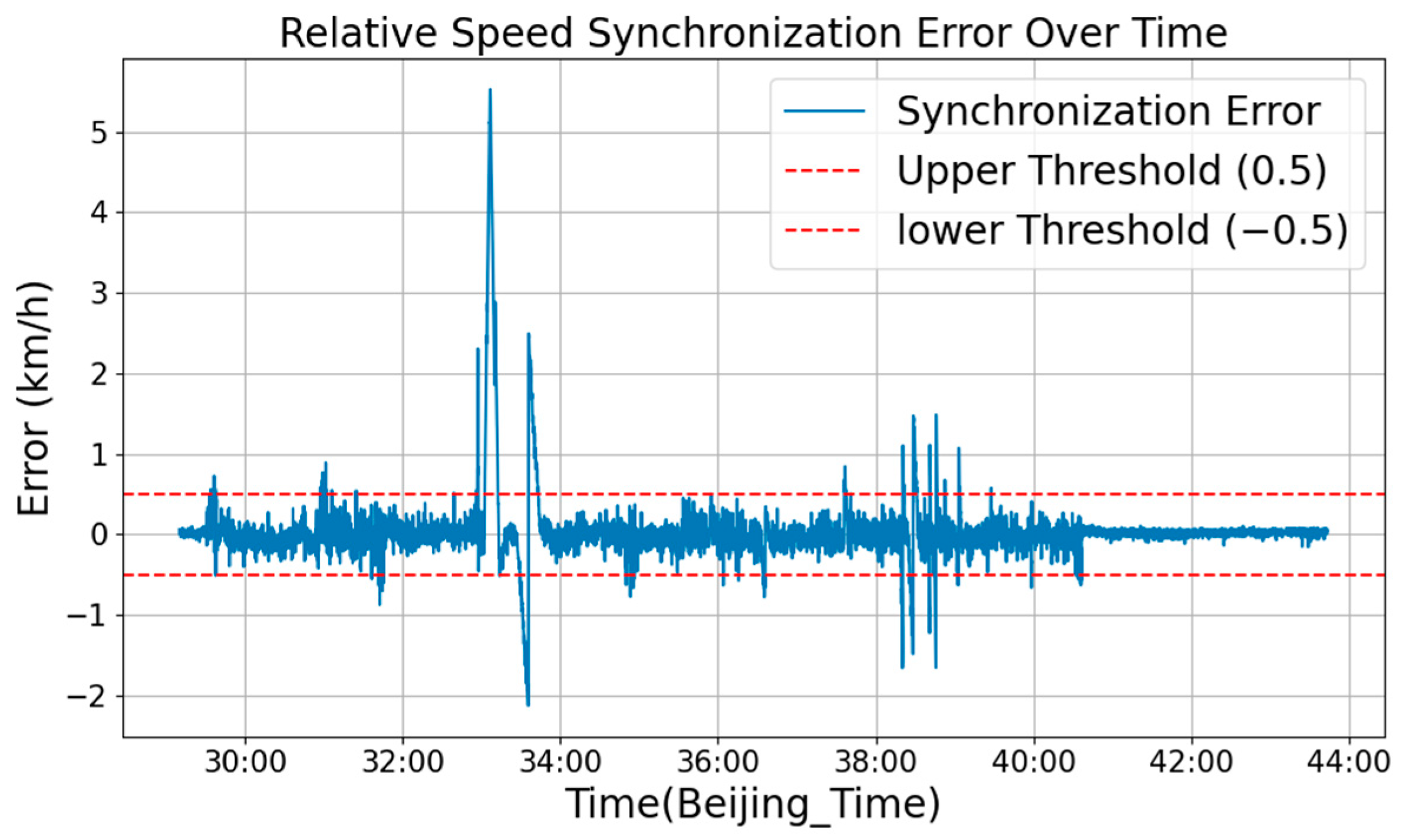
4.4. Spatiotemporal Synchronization Metrics
4.5. Summary
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Félez, J.; Vaquero-Serrano, M.A. Virtual Coupling in Railways: A Comprehensive Review. Machines 2023, 11, 521. [Google Scholar] [CrossRef]
- X2Rail-3. Advanced Signalling, Automation and Communication System (IP2 and IP5)—Prototyping the Future by Means of Capacity Increase, Autonomy and Flexible Communication. Cordis Database. Available online: https://cordis.europa.eu/project/id/826141 (accessed on 7 October 2022).
- Aoun, J.; Quaglietta, E.; Goverde, M.P. Roadmap Development for the Deployment of Virtual Coupling in Railway Signalling. Technol. Forecast. Soc. Chang. 2023, 189, 122263. [Google Scholar] [CrossRef]
- Schumann, T. Increase of capacity on the shinkansen high-speed line using virtual coupling. Int. J. Transp. Dev. Integr. 2017, 1, 666–676. [Google Scholar] [CrossRef]
- Liu, C.; Xu, Z. Multi-Agent System Based Cooperative Control for Speed Convergence of Virtually Coupled Train Formation. Sensors 2024, 24, 4231. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Q.; Wang, R.; Jia, G.; Niu, X. Onboard train localization based on railway track irregularity matching. IEEE Trans. Instrum. Meas. 2022, 71, 9501013. [Google Scholar] [CrossRef]
- Li, G.; Zou, J.; Ma, W.; Lan, M. Research on virtual coupling technology in rail transit train collision protection. Transp. Saf. Environ. 2024, 6, tdad012. [Google Scholar] [CrossRef]
- Park, J.; Lee, B.-H.; Eun, Y. Virtual Coupling of Railway Vehicles: Gap Reference for Merge and Separation, Robust Control, and Position Measurement. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1085–1096. [Google Scholar] [CrossRef]
- Quaglietta, E.; Spartalis, P.; Wang, M.; Goverde, R.M.; van Koningsbruggen, P. Modelling and analysis of Virtual Coupling with dynamic safety margin considering risk factors in railway operations. J. Rail Transp. Plan. Manag. 2022, 22, 100313. [Google Scholar] [CrossRef]
- Tian, S.; Yan, F.; Shang, W.-L.; Majumdar, A.; Chen, H.; Chen, M.; Zeinab, M.; Tian, Y. Energy consumption analysis of trains based on multi-mode virtual coupling operation control strategies. Appl. Energy 2025, 377, 124684. [Google Scholar] [CrossRef]
- Basile, G.; Lui, D.G.; Petrillo, A.; Santini, S. Deep deterministic policy gradient virtual coupling control for the coordination and manoeuvring of heterogeneous uncertain nonlinear high-speed trains. Eng. Appl. Artif. Intell. 2024, 133, 108120. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Zhang, Y.; Chai, M.; Ma, S. An adaptive safety control approach for virtual coupling system with model parametric uncertainties. Transp. Res. Part C Emerg. Technol. 2023, 154, 104235. [Google Scholar] [CrossRef]
- Cai, B.; Liu, J.; Dong, X.; Liu, J. Study on key technologies of GNSS-based train state perception for train-centric railway signaling. High-Speed Railw. 2023, 1, 47–55. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, L.; Wang, D.; Li, Q.; Wu, J.; Wu, M. Low-latency, high-rate, high-precision relative positioning with moving base in real time. GPS Solut. 2020, 24, 56. [Google Scholar] [CrossRef]
- Amatetti, C.; Polonelli, T.; Masina, E.; Moatti, C.; Mikhaylov, D.; Amato, D.; Vanelli-Coralli, A.; Magno, M.; Benini, L. Towards the Future Generation of Railway Localization and Signaling Exploiting sub-meter RTK GNSS. In Proceedings of the 2022 IEEE Sensors Applications Symposium (SAS), Sundsvall, Sweden, 1–3 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, H.; Dong, S.-Q.; Xie, C.-H. High-speed train positioning based on a combination of Beidou navigation, inertial navigation and an electronic map. Sci. China Inf. Sci. 2023, 66, 172207. [Google Scholar] [CrossRef]
- Mikhaylov, D.; Amatetti, C.; Polonelli, T.; Masina, E.; Campana, R.; Berszin, K.; Moatti, C.; Amato, D.; Vanelli-Coralli, A.; Magno, M.; et al. Toward the Future Generation of Railway Localization Exploiting RTK and GNSS. IEEE Trans. Instrum. Meas. 2023, 72, 8502610. [Google Scholar] [CrossRef]
- Specht, M.; Specht, C.; Stateczny, A.; Burdziakowski, P.; Dąbrowski, P.; Lewicka, O. Study on the positioning accuracy of the GNSS/INS system supported by the RTK receiver for railway measurements. Energies 2022, 15, 4094. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Li, J.; Wang, J.; Rizos, C.; Cai, B. Robust train length calculation and monitoring method using GNSS multi-constellation moving-baseline positioning resolution. GPS Solut. 2024, 28, 114. [Google Scholar] [CrossRef]
- Wang, S.; Dai, P.; Xu, T.; Nie, W.; Cong, Y.; Xing, J.; Gao, F. Maximum Mixture Correntropy Criterion-Based Variational Bayesian Adaptive Kalman Filter for INS/UWB/GNSS-RTK Integrated Positioning. Remote Sens. 2025, 17, 207. [Google Scholar] [CrossRef]
- Schutz, A.; Sanchez-Morales, D.E.; Pany, T. Precise positioning through a loosely-coupled sensor fusion of GNSS-RTK, INS and LiDAR for autonomous driving. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 219–225. [Google Scholar] [CrossRef]
- Ji, S.; Wang, J.; Weng, D.; Chen, W. Detailed Investigation on Ambiguity Validation of Long-Distance RTK. Remote Sens. 2024, 16, 2982. [Google Scholar] [CrossRef]
- Huang, W.; Zhao, Z.; Zhu, X. An Effective Scheme for Modeling and Compensating Differential Age Errors in Real-Time Kinematic Positioning. Remote Sens. 2024, 16, 2662. [Google Scholar] [CrossRef]
- Elsayed, H.; El-Mowafy, A.; Allahvirdi-Zadeh, A.; Wang, K.; Mi, X. A Combination of Classification Robust Adaptive Kalman Filter with PPP-RTK to Improve Fault Detection for Integrity Monitoring of Autonomous Vehicles. Remote Sens. 2025, 17, 284. [Google Scholar] [CrossRef]
- Han, J.-H.; Park, C.-H.; Jang, Y.Y. Development of a Moving Baseline RTK/Motion Sensor-Integrated Positioning-Based Autonomous Driving Algorithm for a Speed Sprayer. Sensors 2022, 22, 9881. [Google Scholar] [CrossRef] [PubMed]
- Kazim, S.A.; Tmazirte, N.A.; Marais, J. Realistic position error models for GNSS simulation in railway environments. In Proceedings of the European Navigation Conference (ENC), Dresden, Germany, 23–24 November 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Shehata, A.G.; Zarzoura, F.H.; El-Mewafi, M. Assessing the influence of differential code bias and satellite geometry on GNSS ambiguity resolution through MANS-PPP software package. J. Appl. Geodesy 2023, 18, 1–20. [Google Scholar] [CrossRef]
- Jia, M.; Khalife, J.; Kassas, Z.M. Performance analysis of opportunistic ARAIM or navigation with GNSS signals fused with terrestrial signals of opportunity. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10587–10602. [Google Scholar] [CrossRef]
- Guo, W.; Li, L.; Zhao, D.; Zhu, F.; Lai, L. Enhancing BDS-3 PPP-B2b real-time positioning performance by tightly integrating MEMS IMU and LiDAR in GNSS-degraded environment. Measurement 2025, 242, 116015. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Wu, Q.; Ding, L. Co-design of bandwidth-aware communication scheduler and cruise controller for multiple high-speed trains. IEEE Trans. Veh. Technol. 2024, 73, 4993–5004. [Google Scholar] [CrossRef]
- Zeng, P.; Zhang, Y.; Xia, X.; Zhang, J.; Du, P.; Hua, Z.; Li, S. Research on sea clutter simulation method based on deep cognition of characteristic parameters. Remote Sens. 2024, 16, 4741. [Google Scholar] [CrossRef]
- Wu, Q.; Ge, X.; Zhu, S.; Cole, C.; Spiryagin, M. Physical coupling and decoupling of railway trains at cruising speeds: Train control and dynamics. Int. J. Rail Transp. 2023, 12, 217–232. [Google Scholar] [CrossRef]
- Schenker, M. S2R Innovation Days Presentation X2R3-TD2.8 Virtually Coupled Train Sets. In Proceedings of the S2R Innovation Days Presentation X2R3-TD2.8 Virtually Coupled Train Sets, Stuttgart, Germany, 22–23 October 2020. [Google Scholar]







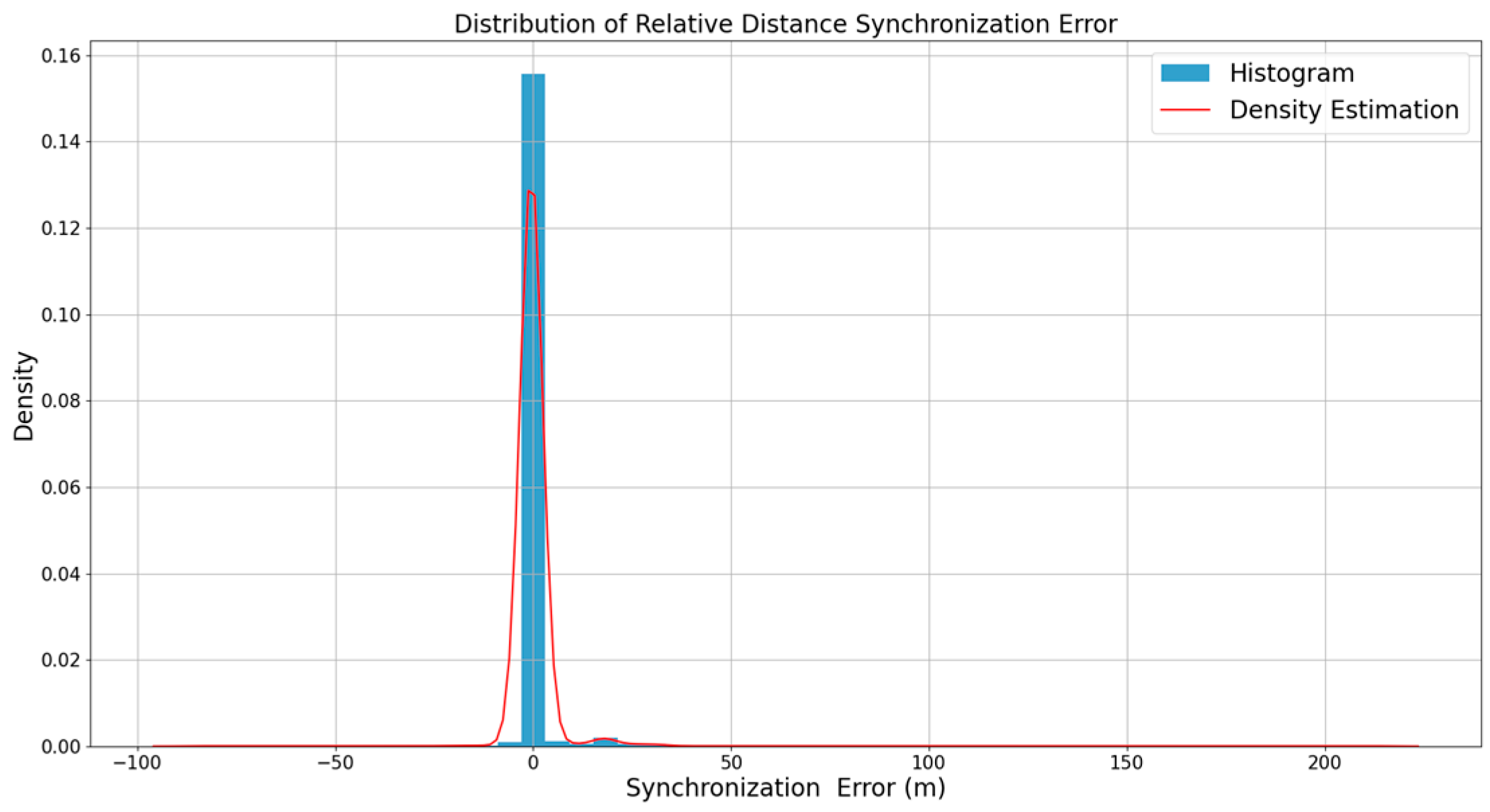

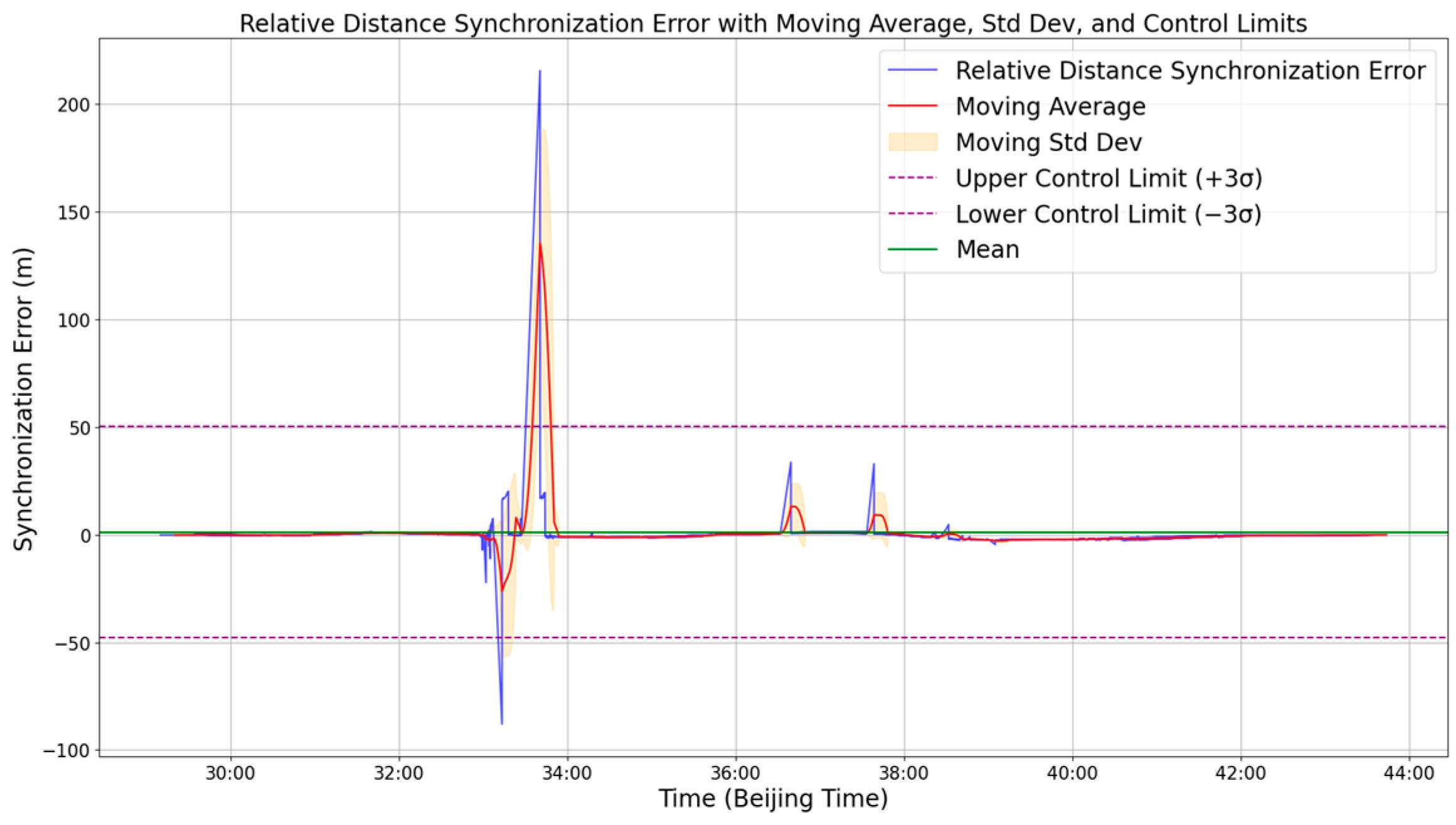
| Aspect | Centralized Synchronization | Distributed Synchronization |
|---|---|---|
| Communication load | High: All state vectors sent to a central node, requiring high bandwidth. | Low: Only relative states (position, velocity) with neighbors are exchanged. Communication reduced by ~60%. |
| Latency sensitivity | High: Single-point failure or delay affects the entire system. | Low: Local calculations reduce reliance on network latency. Tolerates delays up to with minimal errors. |
| Scalability | Limited: Bandwidth and computation grow quadratically with the number of trains . | High: Communication scales linearly with local neighborhood size. Consensus algorithm complexity is . |
| Robustness | Vulnerable: Central node failure can disrupt the entire system. | Resilient: Localized corrections and fault-tolerant consensus ensure operation during interruptions. |
| Implementation complexity | Moderate: Requires a centralized controller with high computational power. | Moderate-High: Requires onboard processing but eliminates the need for a central node. |
| Error tolerance | Low: Sensitive to synchronization errors under high latency or packet loss. | High: Distributed error correction and predictive algorithms ensure accurate state estimation. |
| RTK Status | Recovery Time (s) | Distance Error (m) | Speed Error (km/h) |
|---|---|---|---|
| NONE | ~20.0 | >100 | >1.0 |
| L1_FLOAT | >10 | 50–100 | 0.5–1.0 |
| NARROW_FLOAT | 3–5 | 400–600 | 0.2–0.5 |
| L1_INT | ~5 | 10–50 | 0.1–0.3 |
| NARROW_INT | 5–8 | <10 | <0.1 |
| Metric | GNSS Absolute Methods | MB-RTK Relative Methods |
|---|---|---|
| Relative speed accuracy | Highly affected by GNSS errors, leading to larger deviations | Lower errors, more stable speed fluctuations |
| Relative position accuracy | Higher errors, especially in long-span measurements | More stable, with errors concentrated near zero |
| Noise resistance | Prone to GNSS signal jumps and variations | Stronger resistance to noise and fluctuations |
| Adaptability to complex environments | Heavily influenced by multipath effects and signal loss | More robust against multipath interference and signal degradation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Cai, B.; Lu, D.; Zhao, Y.; Zhang, M.; Shang, L. Embedding Moving Baseline RTK for High-Precision Spatiotemporal Synchronization in Virtual Coupling Applications. Remote Sens. 2025, 17, 1238. https://doi.org/10.3390/rs17071238
Huang S, Cai B, Lu D, Zhao Y, Zhang M, Shang L. Embedding Moving Baseline RTK for High-Precision Spatiotemporal Synchronization in Virtual Coupling Applications. Remote Sensing. 2025; 17(7):1238. https://doi.org/10.3390/rs17071238
Chicago/Turabian StyleHuang, Susu, Baigen Cai, Debiao Lu, Yang Zhao, Miao Zhang, and Linyu Shang. 2025. "Embedding Moving Baseline RTK for High-Precision Spatiotemporal Synchronization in Virtual Coupling Applications" Remote Sensing 17, no. 7: 1238. https://doi.org/10.3390/rs17071238
APA StyleHuang, S., Cai, B., Lu, D., Zhao, Y., Zhang, M., & Shang, L. (2025). Embedding Moving Baseline RTK for High-Precision Spatiotemporal Synchronization in Virtual Coupling Applications. Remote Sensing, 17(7), 1238. https://doi.org/10.3390/rs17071238







