Two-Dimensional Spatial Variation Analysis and Correction Method for High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar (SAR) Imaging
Abstract
:1. Introduction
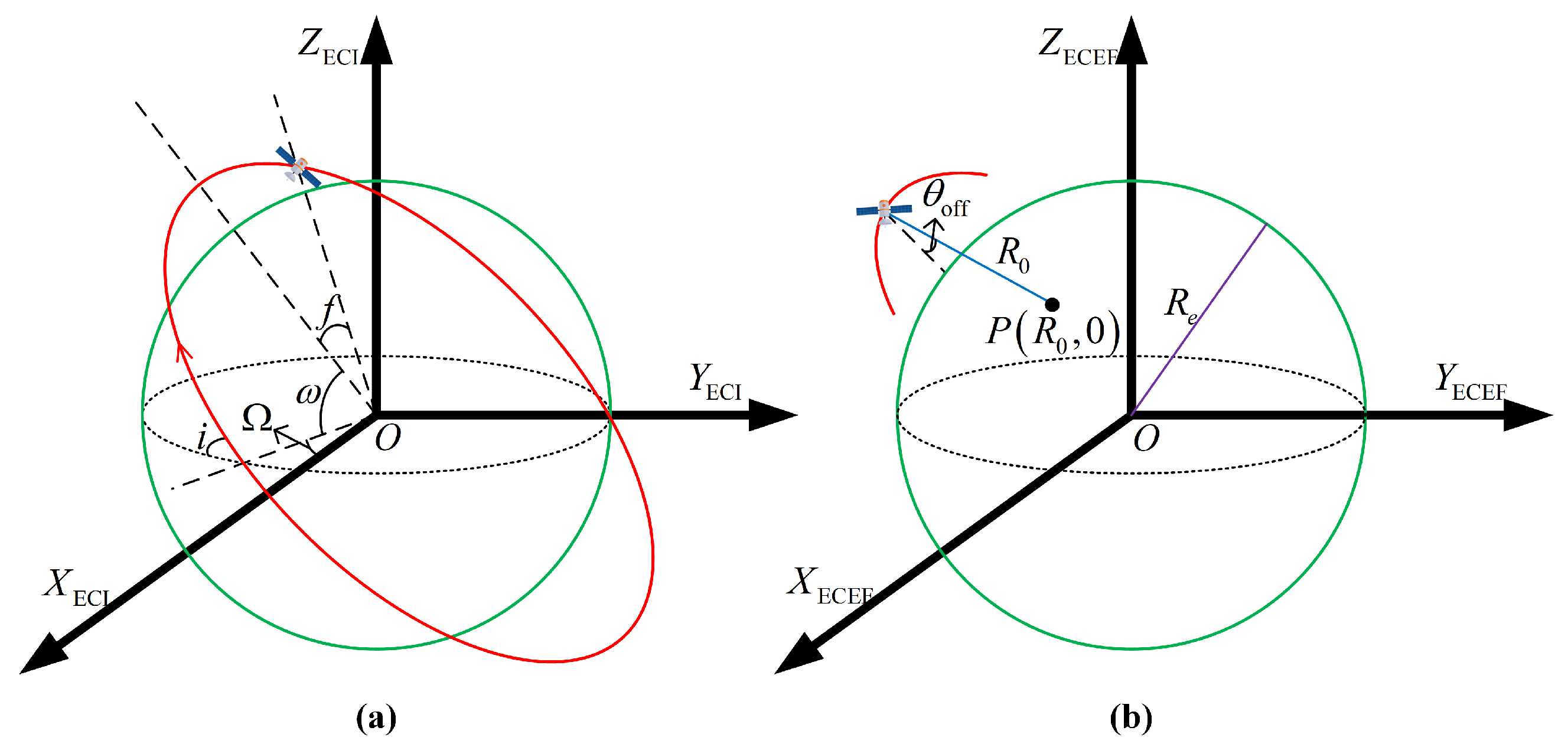
2. Geometric and Signal Models of Spaceborne SAR
3. Theoretical Analysis of Two-Dimensional Spatial Variation
3.1. Curve-Sphere Model
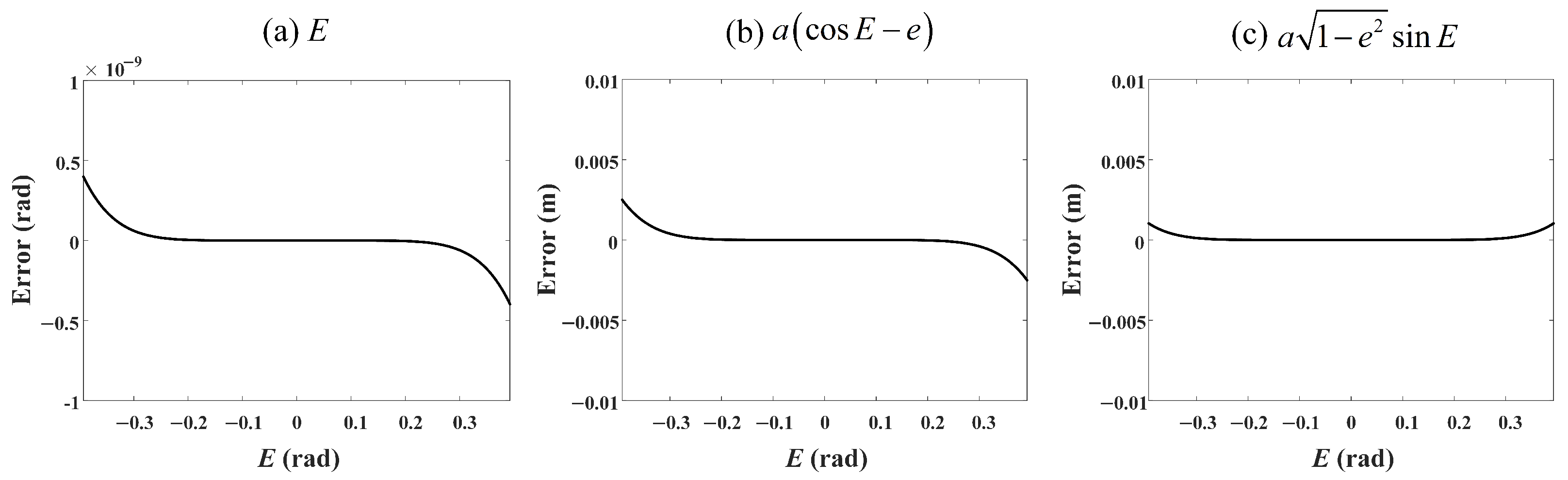
3.2. Satellite Trajectory
3.2.1. Slant Range History
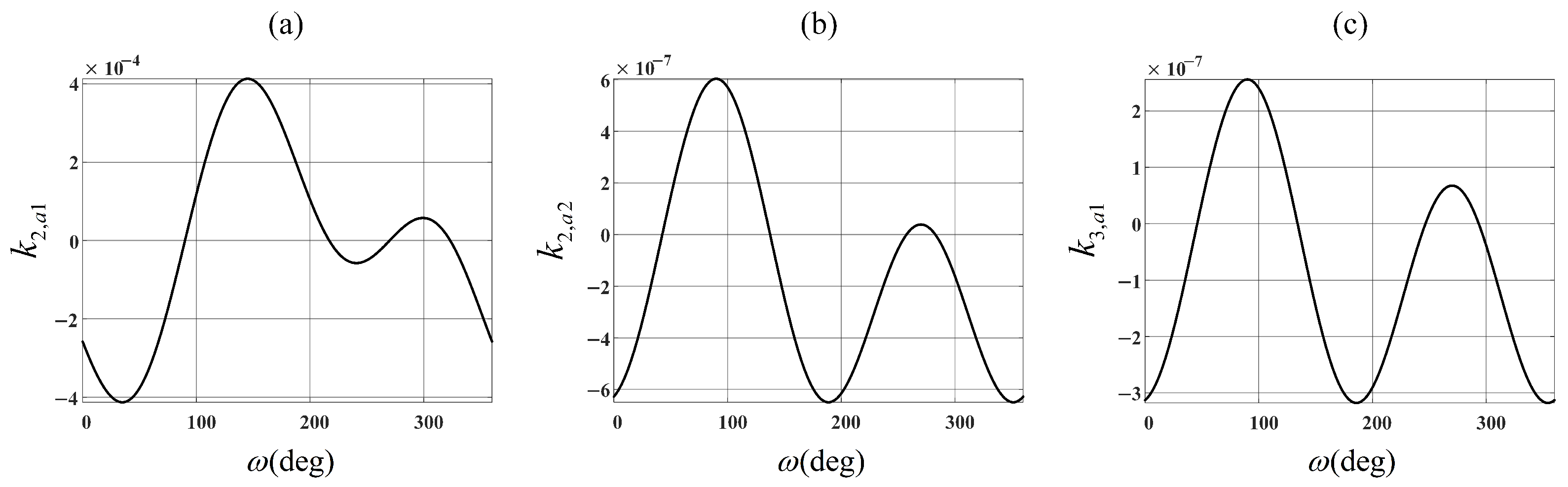
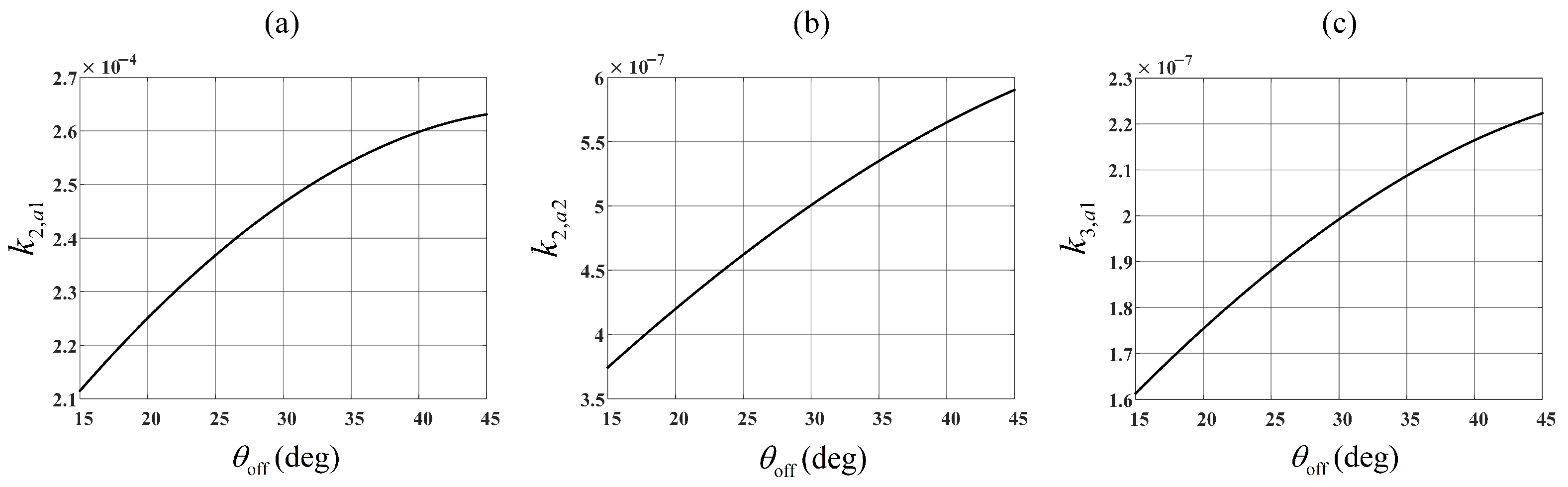
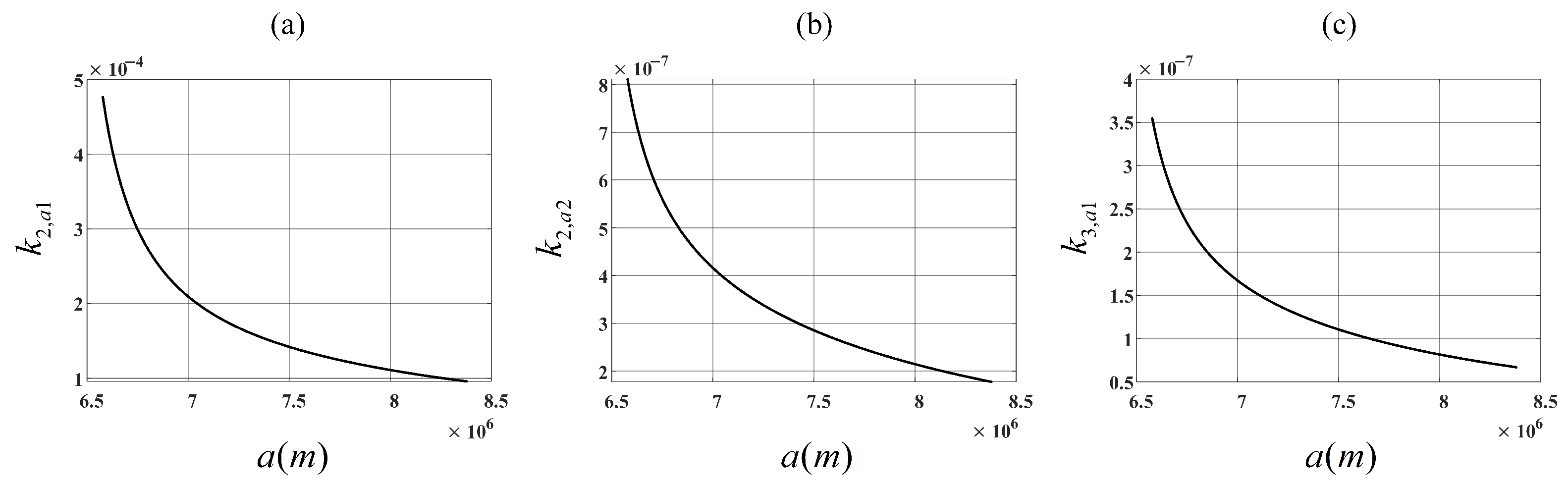
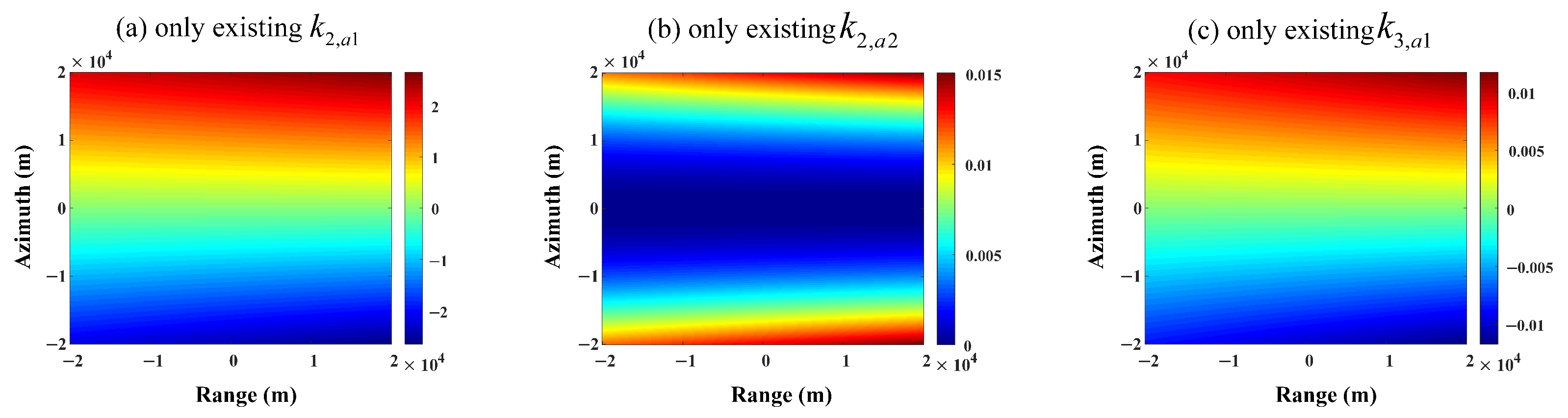
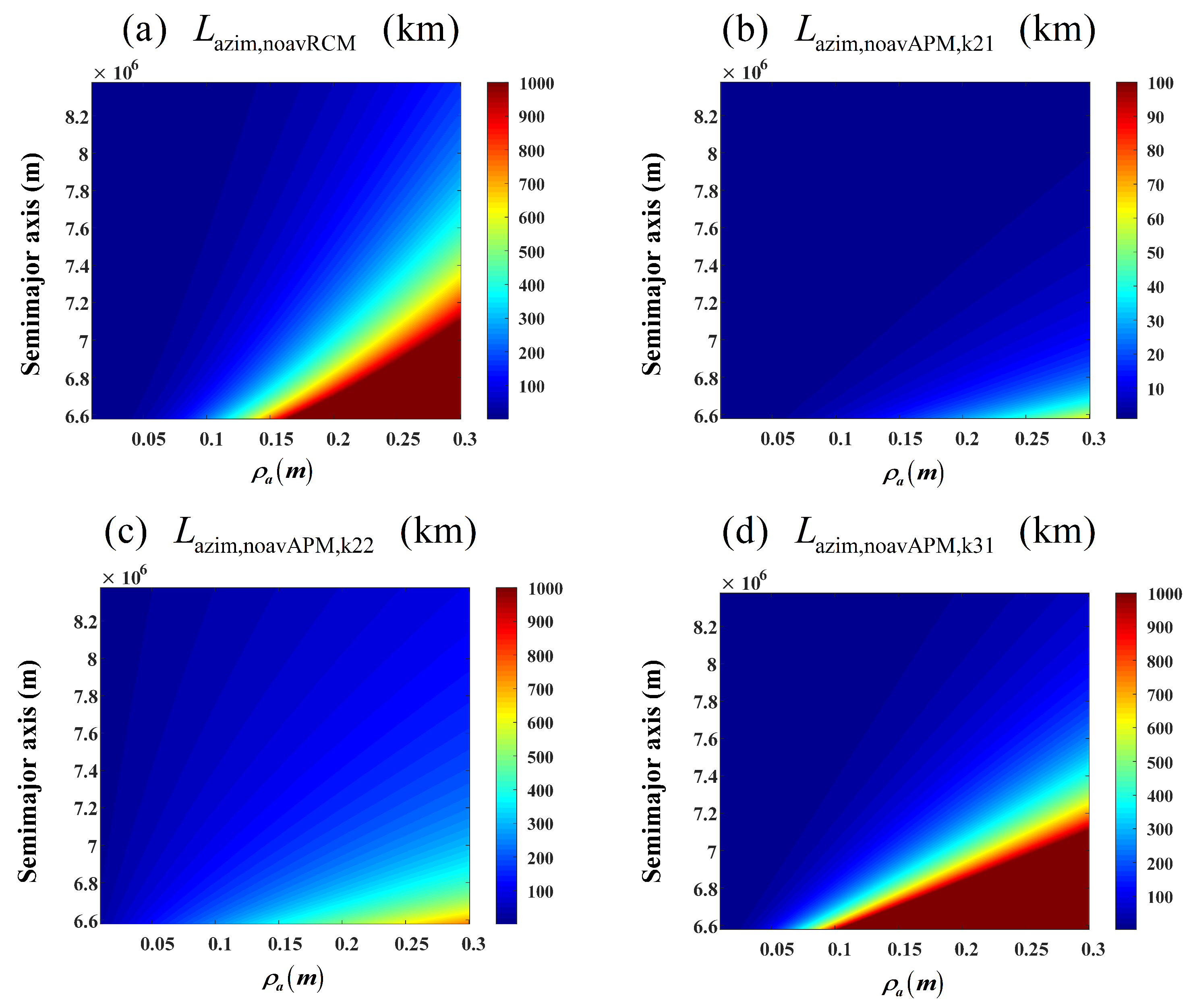
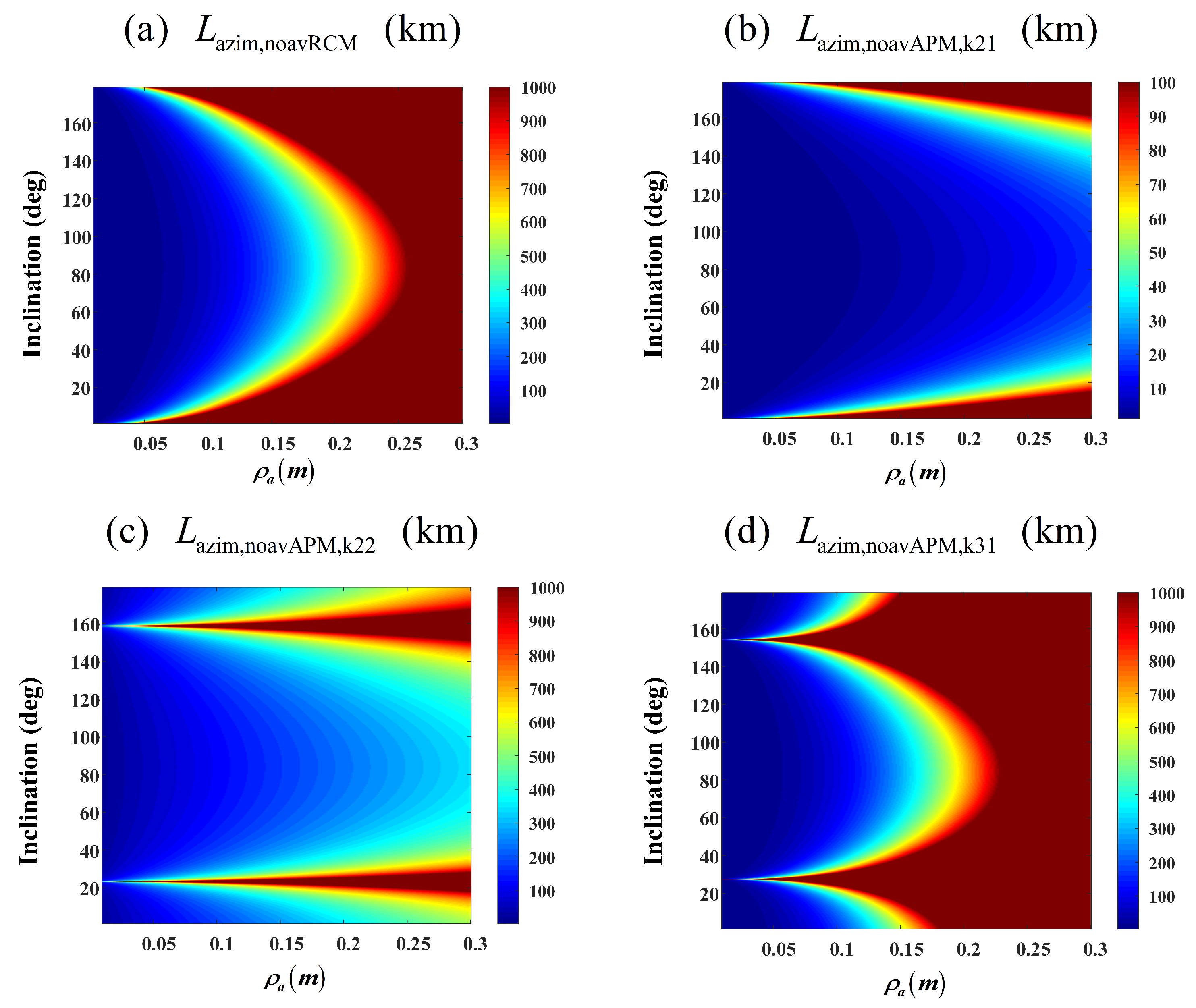
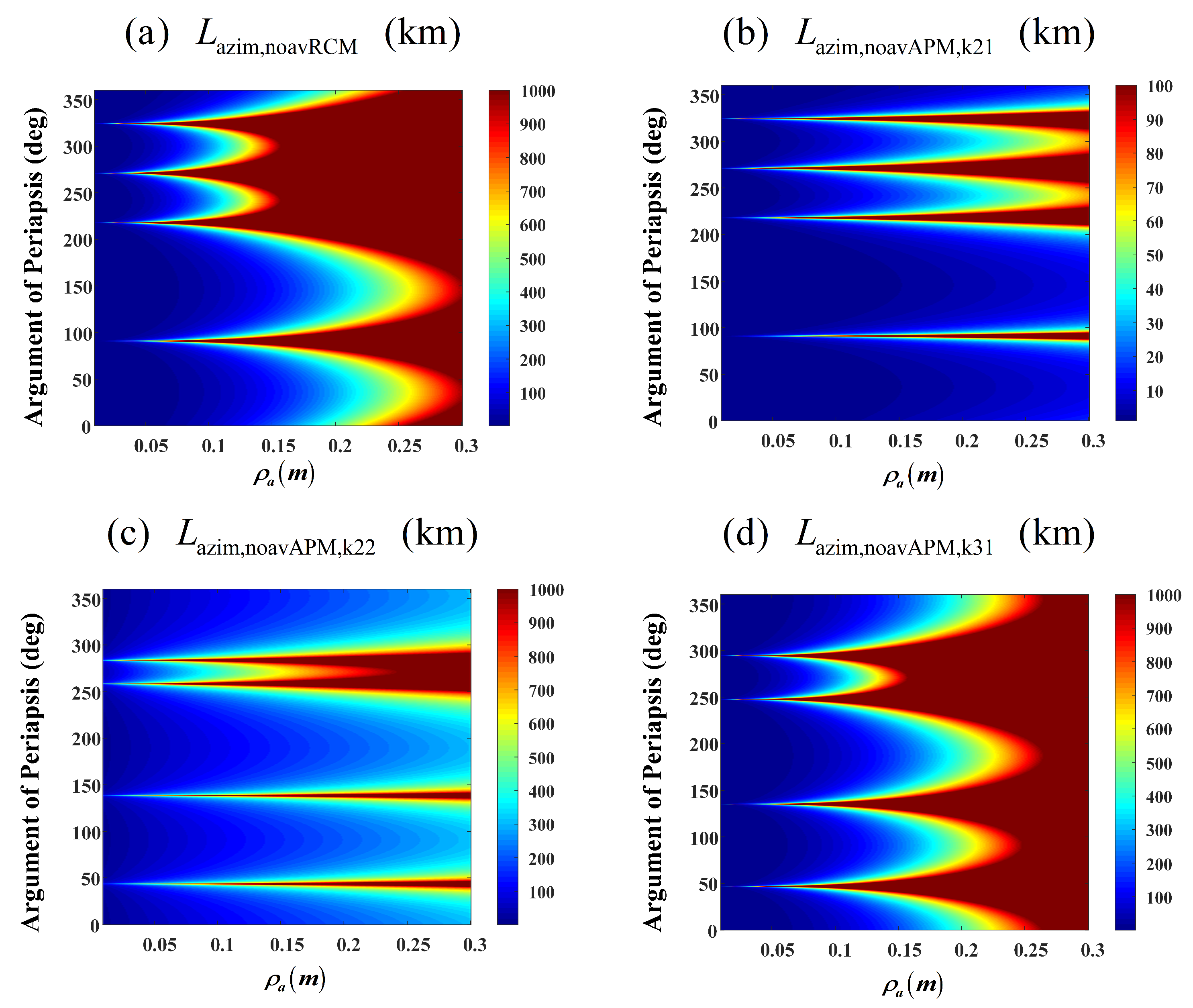
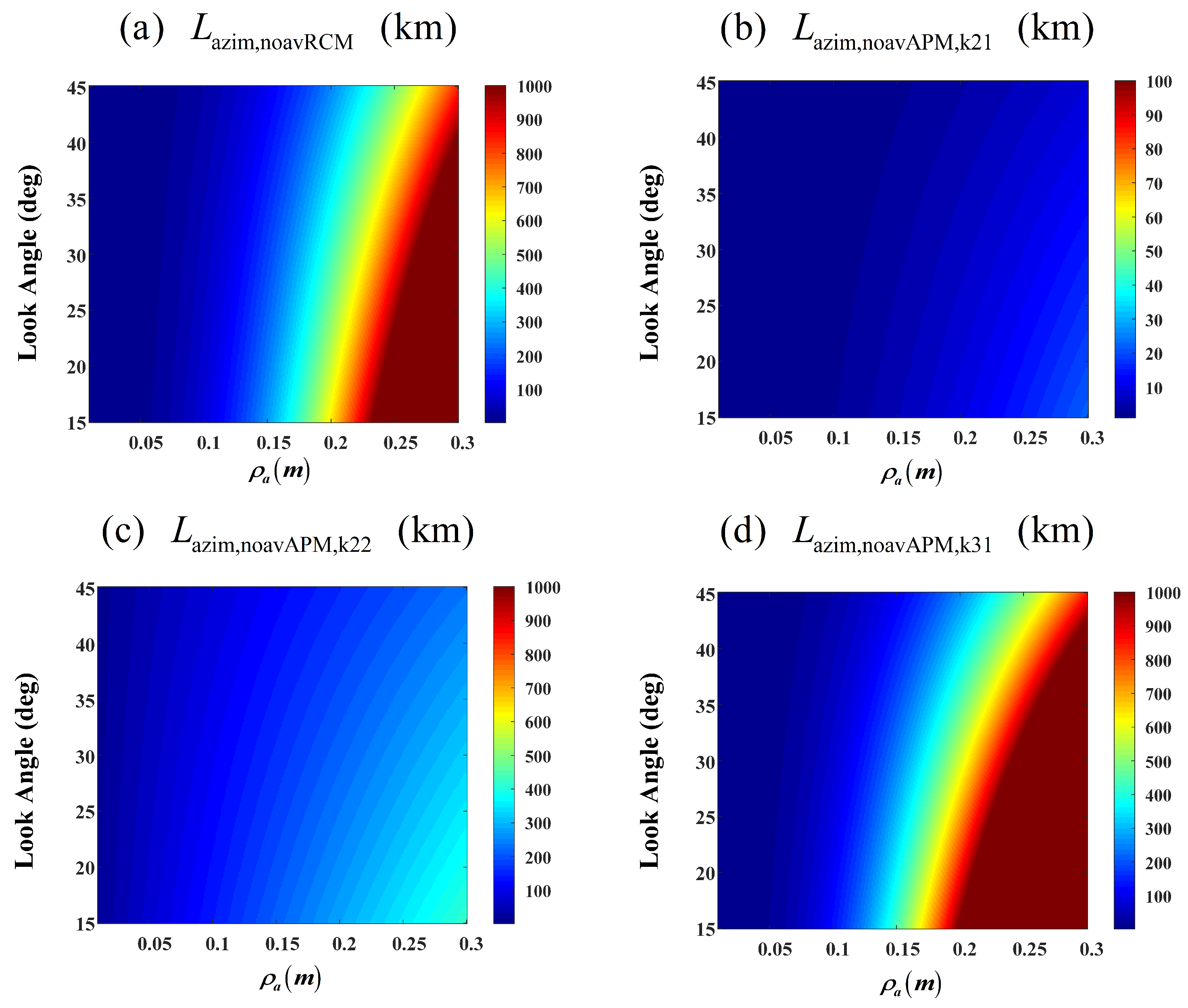
3.2.2. Two-Dimensional Spatial Variation
- (1)
- The variation trends of and are nearly identical, being approximately three orders of magnitude smaller than .
- (2)
- The spatial variation appears most severe in polar orbits (with orbital inclination of 90°).
- (3)
- Spatial variation intensifies with decreasing orbital altitude.
- (4)
- Larger look angles (which correspond to greater under identical orbital elements) result in more pronounced spatial variation.
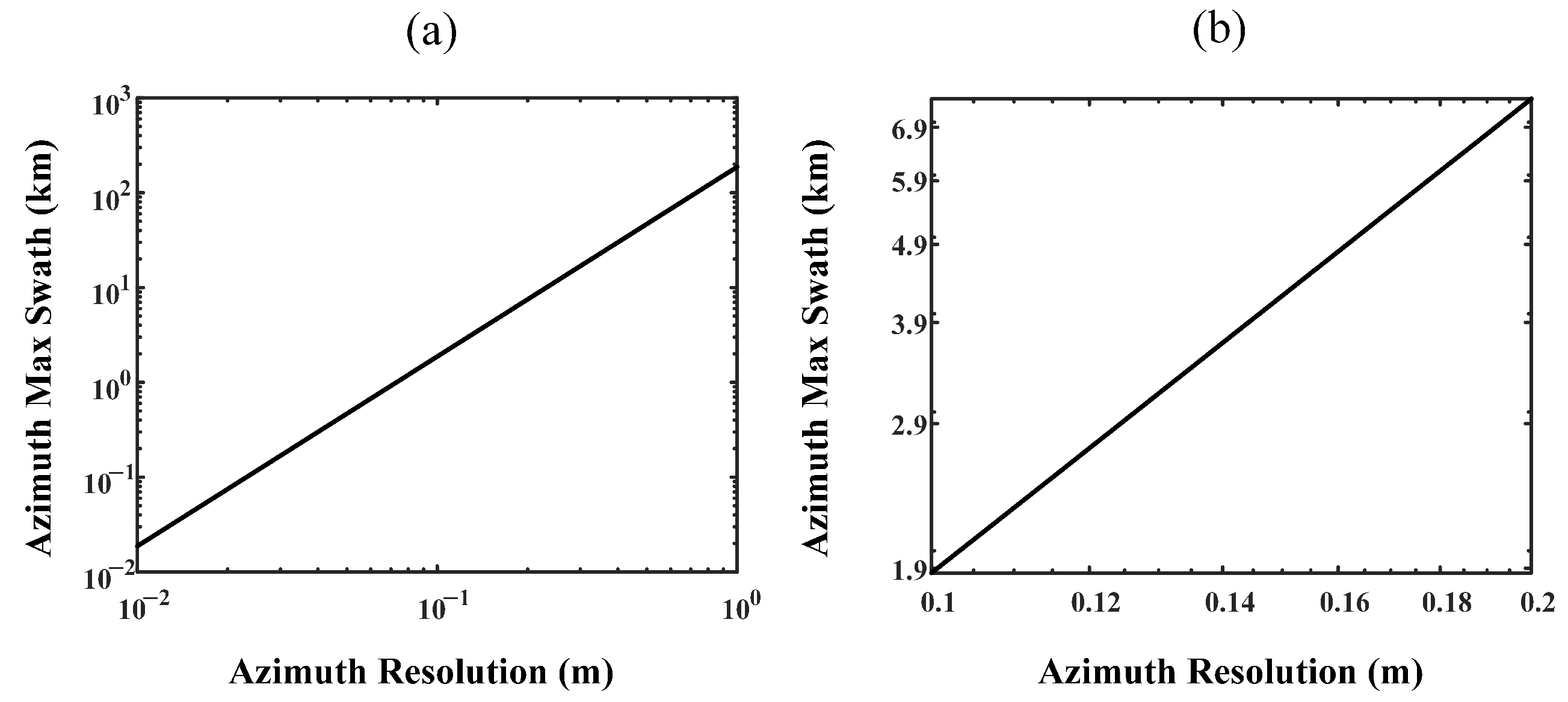
4. Analysis of Two-Dimensional Spatial Variation Effects
4.1. Impact on RCM
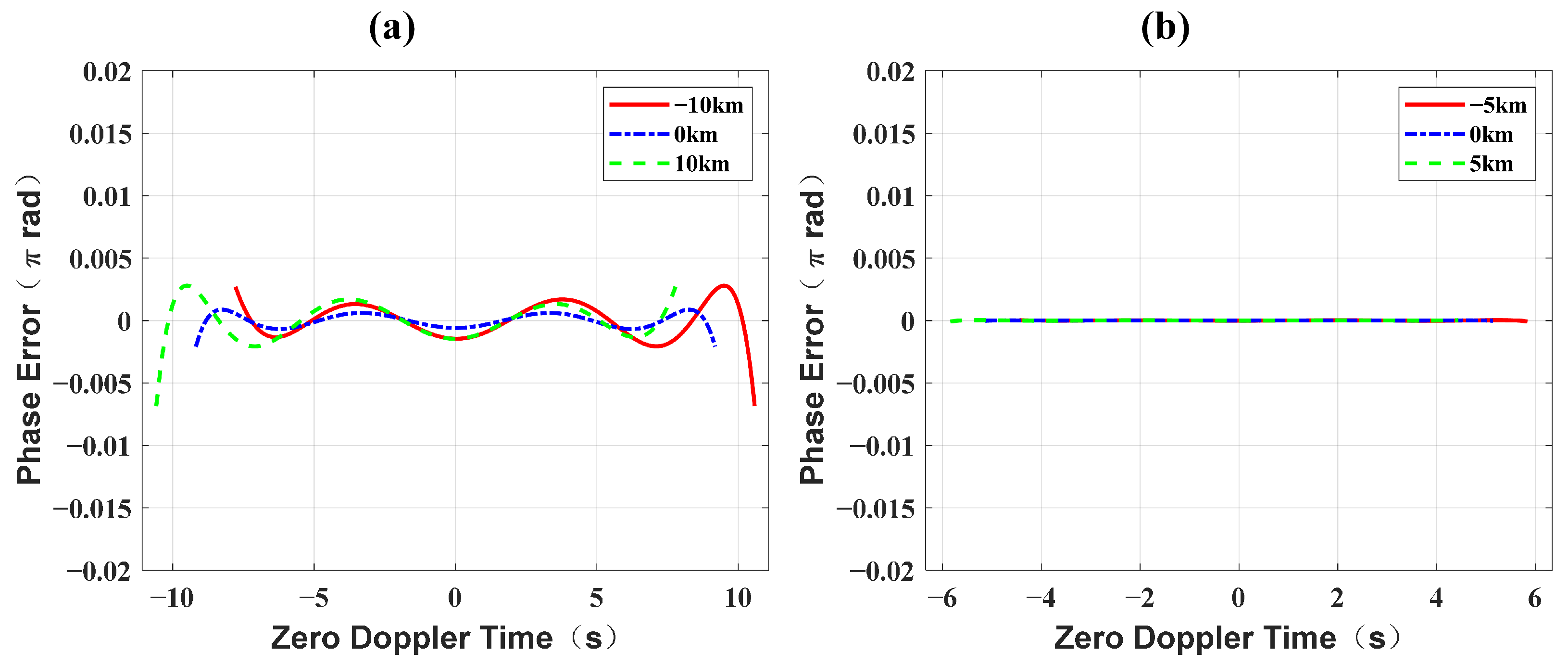
4.2. Impact of Azimuth Modulation on Phase Characteristics
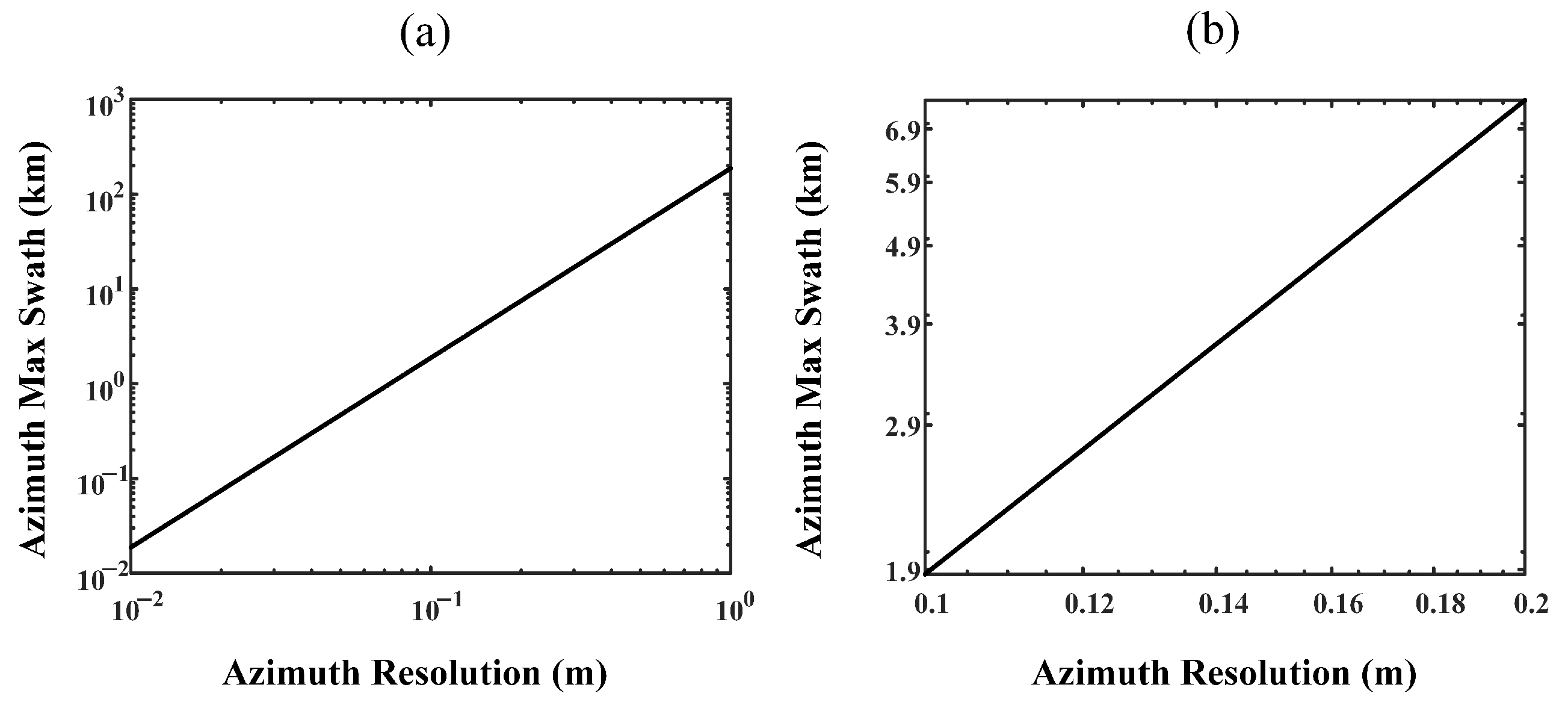
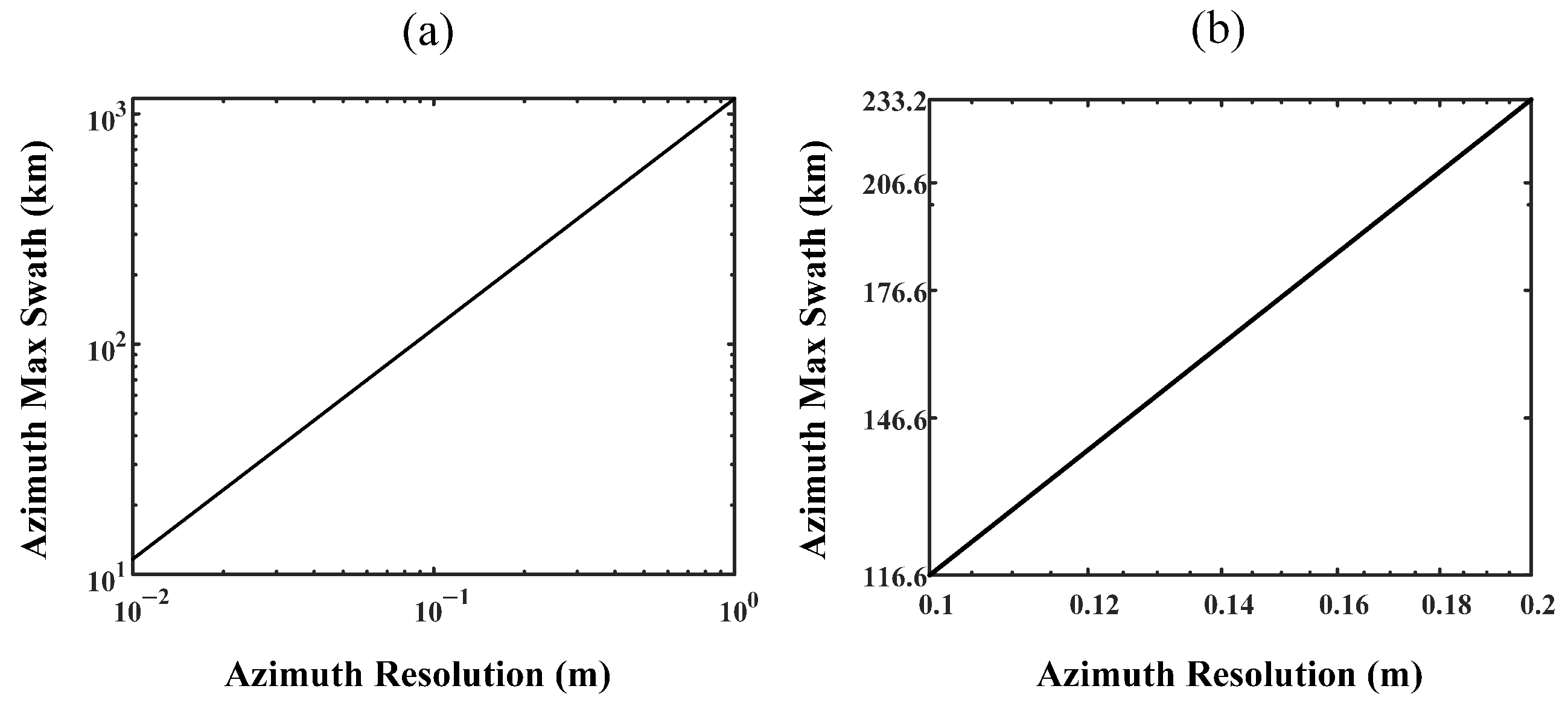
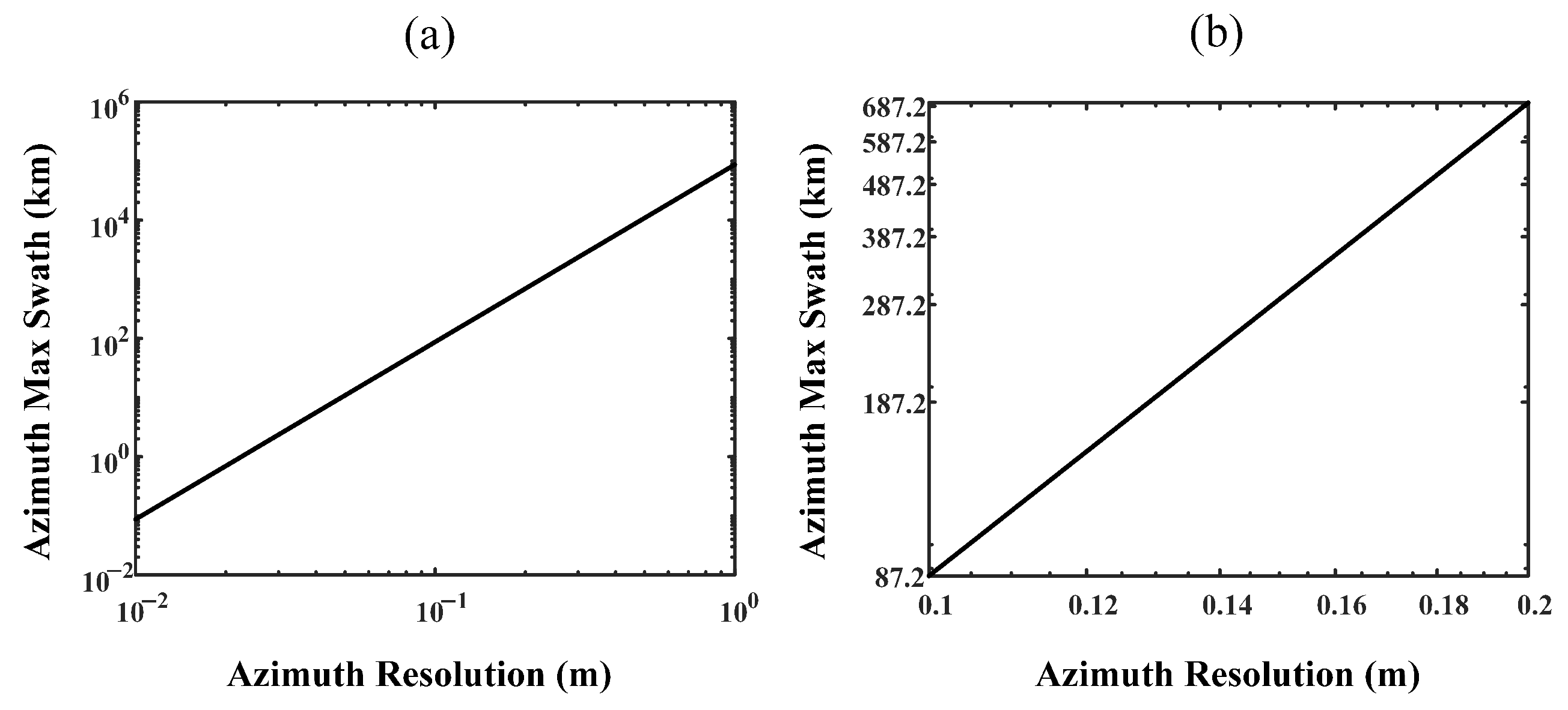
5. Two-Dimensional Spatial Variation Processing Methods
5.1. Azimuth Nonlinear Chirp Scaling Processing
5.2. Algorithm Extensions
6. Experiments and Results
6.1. Simulation
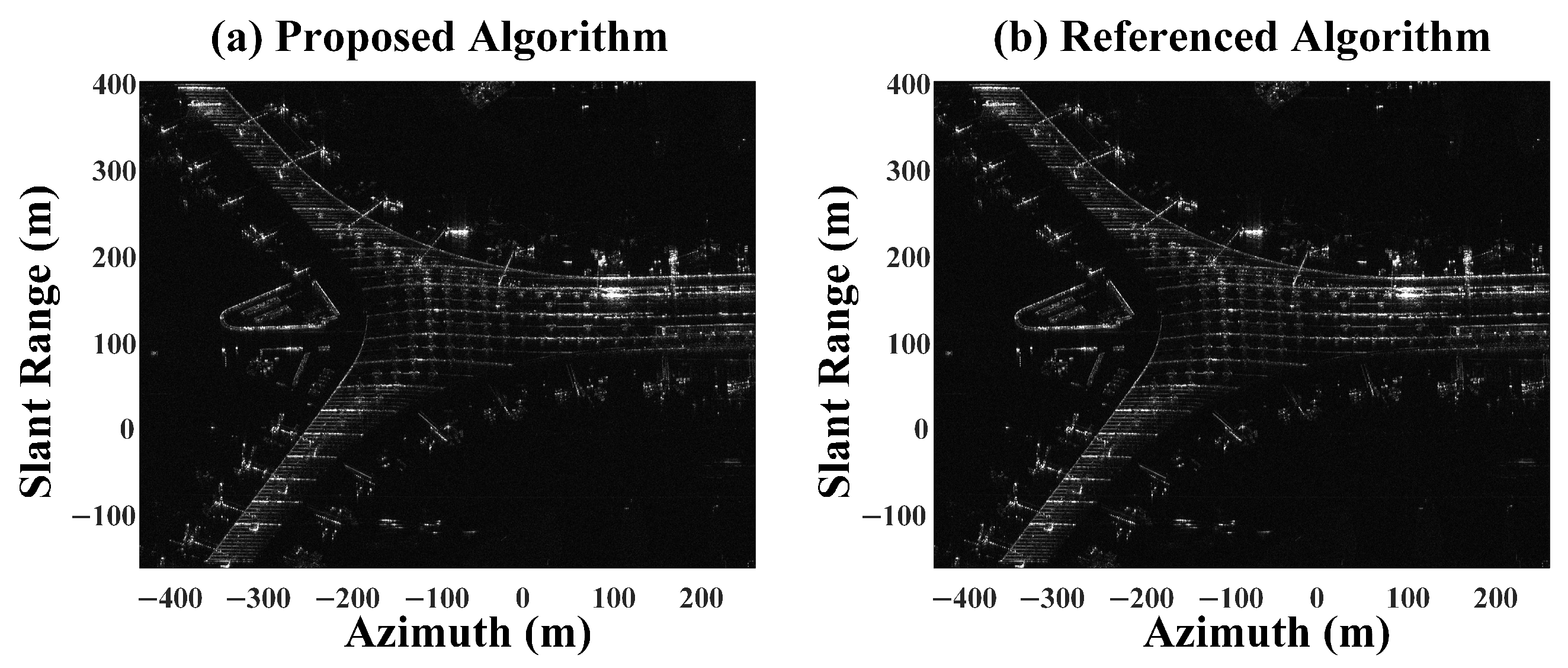
6.2. Processing of Real Data
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Liu, K.Y.; Jin, M. Modeling and a Correlation Algorithm for Spaceborne SAR Signals. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 563–575. [Google Scholar] [CrossRef]
- Eldhuset, K. A New Fourth-Order Processing Algorithm for Spaceborne SAR. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 824–835. [Google Scholar]
- Eldhuset, K. Ultra High Resolution Spaceborne SAR Processing. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 370–378. [Google Scholar]
- Kim, J.-H.; Younis, M.; Prats-Iraola, P.; Gabele, M.; Krieger, G. First Spaceborne Demonstration of Digital Beamforming for Azimuth Ambiguity Suppression. IEEE Trans. Geosci. Remote Sens. 2012, 51, 579–590. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; De Zan, F.; Bräutigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the Processing of Very High Resolution Spaceborne SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar]
- Xiang, T.; Zhu, D.; Xu, F. Processing of Ultra-High Resolution Spaceborne Spotlight SAR Data Based on One-Step Motion Compensation. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8933–8936. [Google Scholar]
- Liang, D.; Zhang, H.; Fang, T.; Deng, Y.; Yu, W.; Zhang, L.; Fan, H. Processing of Very High Resolution GF-3 SAR Spotlight Data with Non-Start–Stop Model and Correction of Curved Orbit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2112–2122. [Google Scholar]
- Sun, G.-C.; Liu, Y.; Xiang, J.; Liu, W.; Xing, M.; Chen, J. Spaceborne Synthetic Aperture Radar Imaging Algorithms: An Overview. IEEE Geosci. Remote Sens. Mag. 2021, 10, 161–184. [Google Scholar]
- Meng, D.; Huang, L.; Qiu, X.; Li, G.; Hu, Y.; Han, B.; Hu, D. A Novel Approach to Processing Very-High-Resolution Spaceborne SAR Data With Severe Spatial Dependence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7472–7482. [Google Scholar]
- Mao, X. Spherical Geometry Algorithm for Space-Borne Synthetic Aperture Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar]
- Hernández-Burgos, S.; Gibert, F.; Broquetas, A.; Kleinherenbrink, M.; De la Cruz, A.F.; Gómez-Olivé, A.; García-Mondéjar, A.; i Aparici, M.R. A Fully Focused SAR Omega-K Closed-Form Algorithm for the Sentinel-6 Radar Altimeter: Methodology and Applications. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar]
- Shibata, M.; Kuriyama, T.; Hoshino, T.; Nakamura, S.; Kankaku, Y.; Motohka, T.; Suzuki, S. SAR Techniques and SAR Processing Algorithm for ALOS-4. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7449–7451. [Google Scholar]
- Farquharson, G.; Castelletti, D.; De, S.; Stringham, C.; Yague, N.; Bes, V.C.; Ryu, J.; Goncharenko, Y. The New Capella Space Satellite Generation: Acadia. In Proceedings of the IGARSS 2023–2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 1513–1516. [Google Scholar]
- He, F.; Chen, Q.; Dong, Z.; Sun, Z. Processing of Ultrahigh-Resolution Spaceborne Sliding Spotlight SAR Data on Curved Orbit. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 819–839. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A High-Order Imaging Algorithm for High-Resolution Spaceborne SAR Based on a Modified Equivalent Squint Range Model. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1225–1235. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, G.-C.; Yang, C.; Yang, J.; Xing, M.; Bao, Z. Processing of Very High Resolution Spaceborne Sliding Spotlight SAR Data Using Velocity Scaling. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1505–1518. [Google Scholar] [CrossRef]
- Tang, S.; Lin, C.; Zhou, Y.; So, H.C.; Zhang, L.; Liu, Z. Processing of Long Integration Time Spaceborne SAR Data with Curved Orbit. IEEE Trans. Geosci. Remote Sens. 2017, 56, 888–904. [Google Scholar]
- Liu, W.; Sun, G.-C.; Xia, X.-G.; Chen, J.; Guo, L.; Xing, M. A Modified CSA Based on Joint Time-Doppler Resampling for MEO SAR Stripmap Mode. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3573–3586. [Google Scholar]
- Guo, Y.; Wang, P.; Chen, J.; Men, Z.; Cui, L.; Zhuang, L. A Novel Imaging Algorithm for High-Resolution Wide-Swath Space-Borne SAR Based on a Spatial-Variant Equivalent Squint Range Model. Remote Sens. 2022, 14, 368. [Google Scholar] [CrossRef]
- Ding, Z.; Zheng, P.; Li, H.; Zhang, T.; Li, Z. Spaceborne High-Squint High-Resolution SAR Imaging Based on Two-Dimensional Spatial-Variant Range Cell Migration Correction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Chen, X.; Hou, Z.; Dong, Z.; He, Z. Performance Analysis of Wavenumber Domain Algorithms for Highly Squinted SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1563–1575. [Google Scholar]
- Hou, Z.; Zhang, Z.; Li, P.; Yun, Z.; He, F.; Dong, Z. Range-Dependent Variance Correction Method for High-Resolution and Wide-Swath Spaceborne Synthetic Aperture Radar Imaging Based on Block Processing in Range Dimension. Remote Sens. 2024, 17, 50. [Google Scholar] [CrossRef]
- Zhang, Q. System Design and Key Technologies of the GF-3 Satellite. Acta Geod. Cartogr. Sin. 2017, 46, 269–277. [Google Scholar]













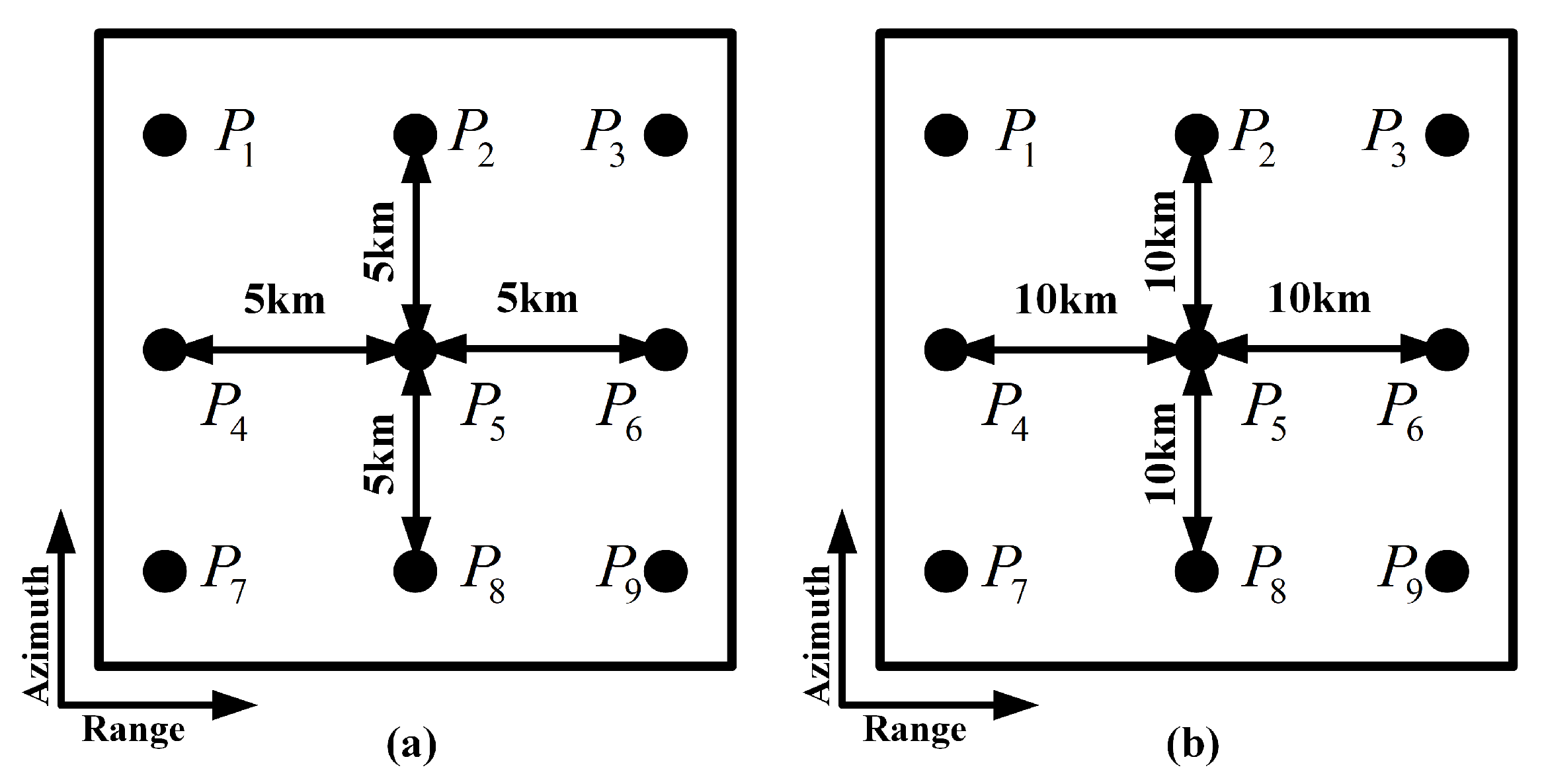
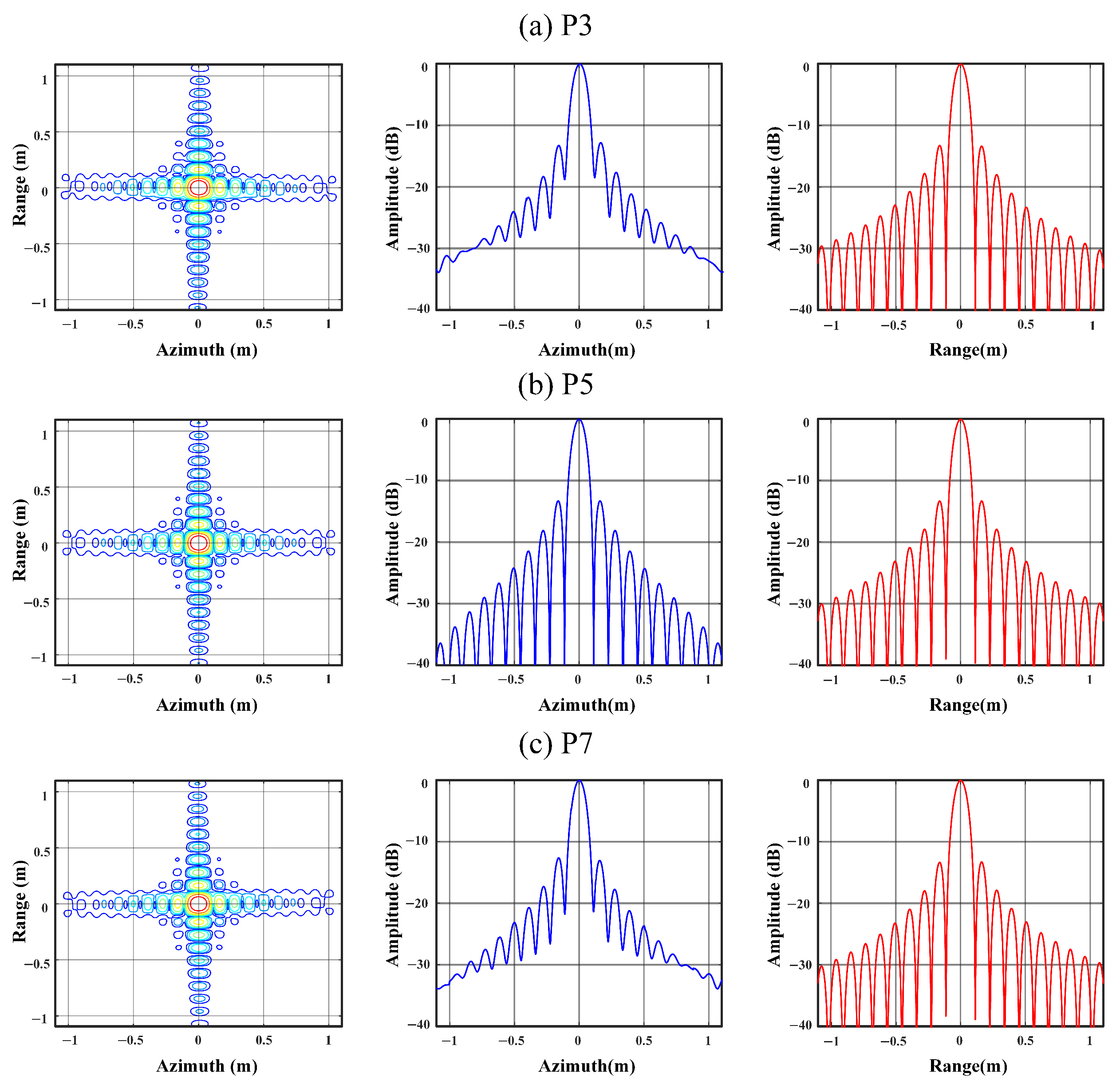
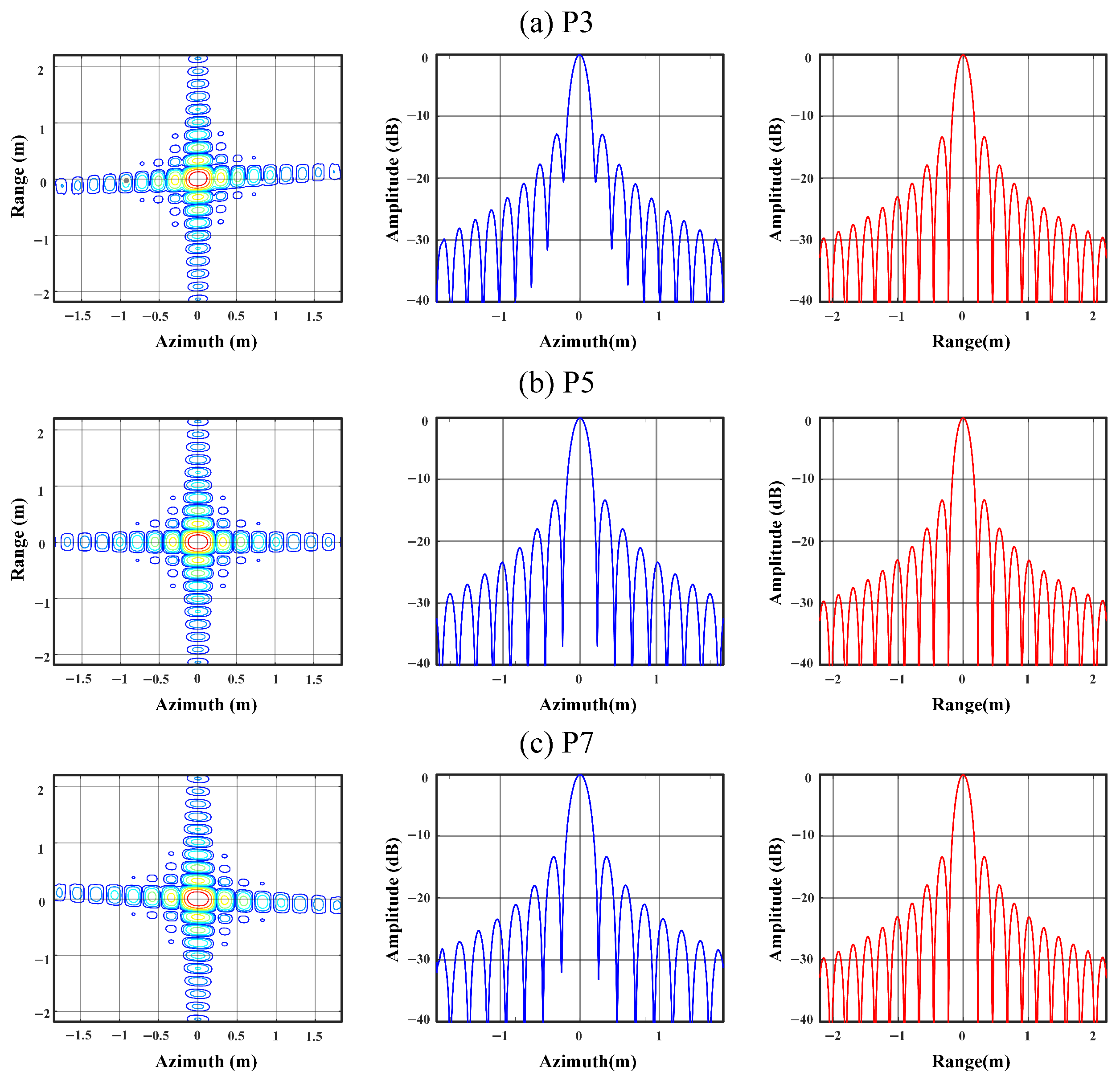
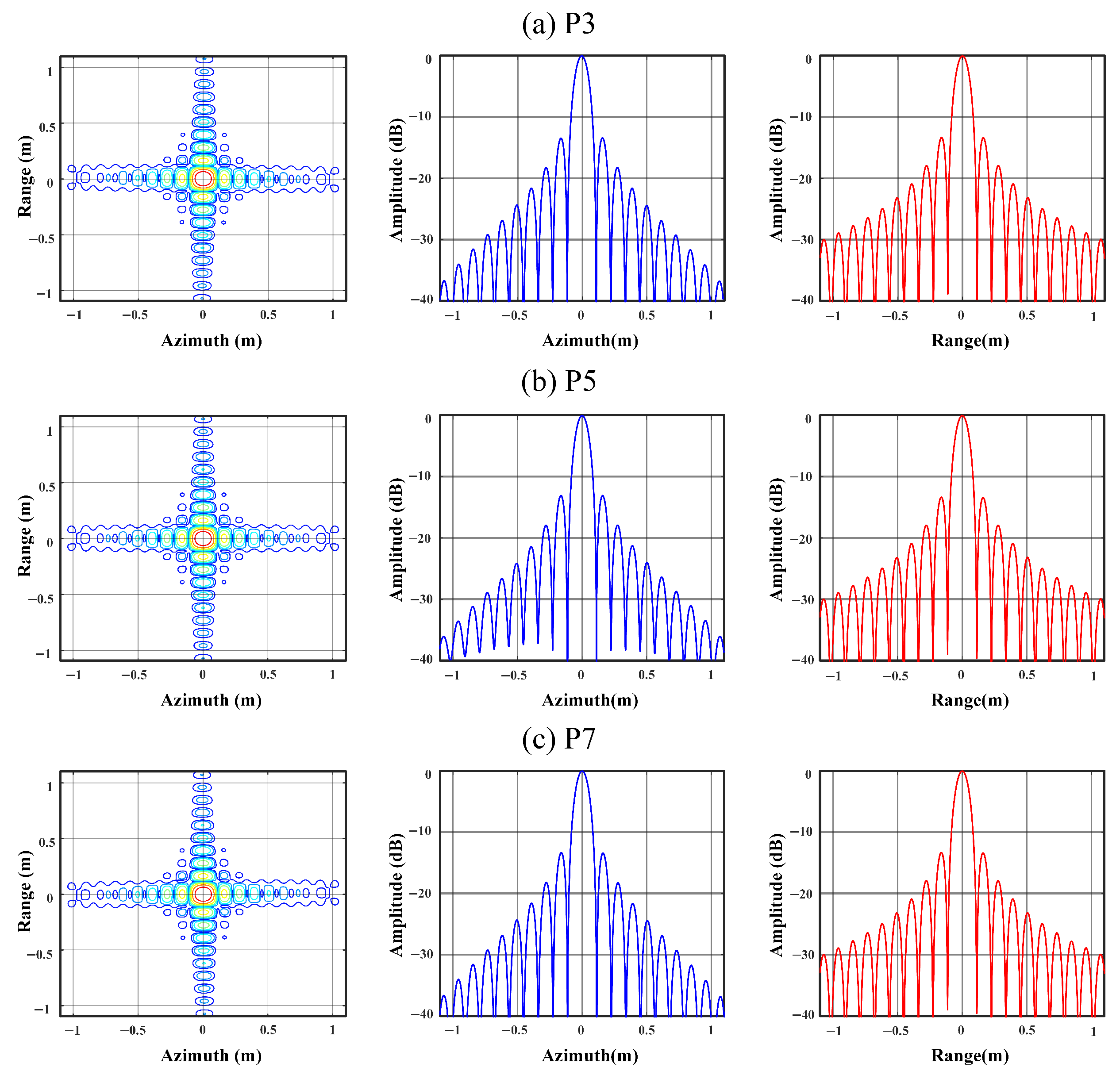

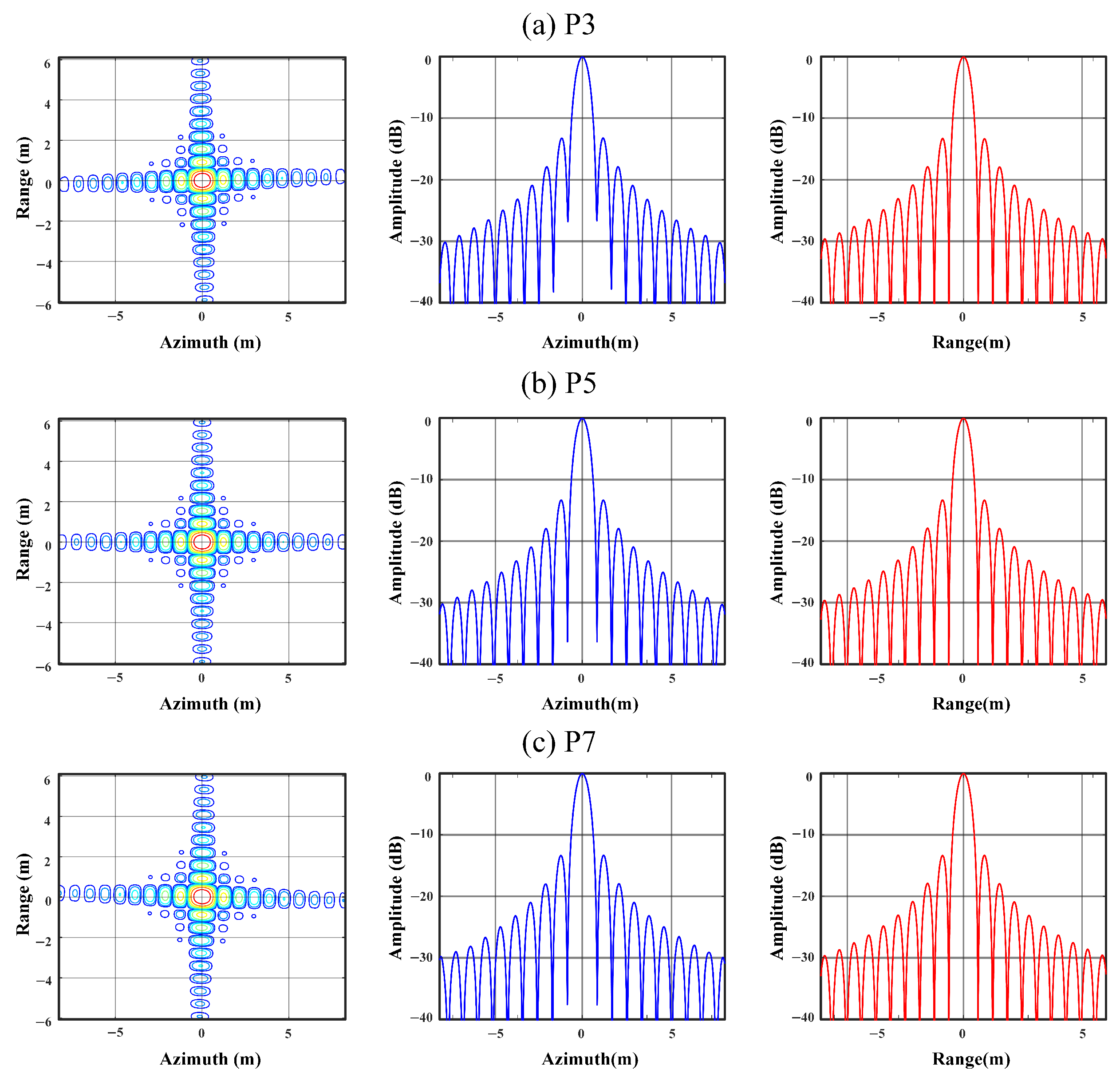
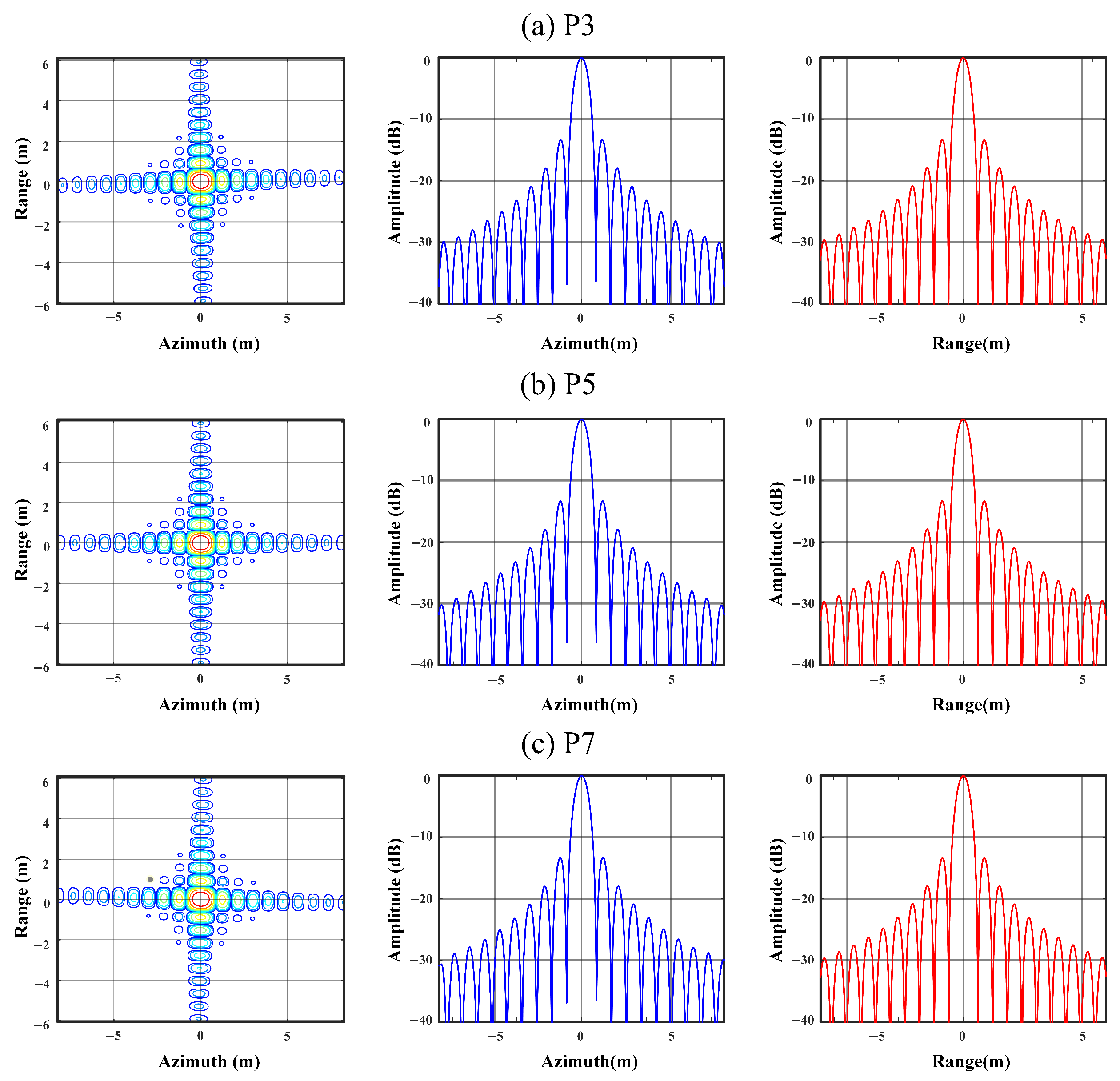


| Parameter | Value |
|---|---|
| Semi-major axis | 6897.56 km |
| Orbital inclination | 97.46° |
| Eccentricity | 0.0013 |
| Longitude of the ascending node | 0° |
| Argument of periapsis | 111.11° |
| True anomaly | 0° |
| Look angle | 25° |
| Wavelength | 0.031 m |
| Parameter | Simulation 1 | Simulation 2 |
|---|---|---|
| () | 1328.08 | 664.04 |
| () | 62,768.00 | 31,384.00 |
| () | 7084.42 | 7084.42 |
| () | 588.76 | 588.76 |
| () | 29.90 | 241.50 |
| () | 1.86 | 7.49 |
| () | 164.27 | 329.56 |
| () | 344.08 | 2778.22 |
| Parameter | Value |
|---|---|
| () | 177.08 |
| () | 7984.61 |
| () | 6756.13 |
| () | 8270.36 |
| () | 3705.14 |
| () | 54.80 |
| () | 652.91 |
| () | 16,683.69 |
| Algorithm | Target | Azimuth | Range | ||||
|---|---|---|---|---|---|---|---|
| IRW | PSLR | ISLR | IRW | PSLR | ISLR | ||
| Reference Algorithm | 0.7446 | 13.1567 | 10.056 | 0.5526 | 13.2506 | 9.8105 | |
| 0.7540 | 13.2642 | 10.1049 | 0.5526 | 13.2524 | 9.8135 | ||
| 0.7629 | 13.2586 | 10.1210 | 0.5515 | 13.2773 | 9.8024 | ||
| Proposed Algorithm | 0.7429 | 13.2658 | 10.1177 | 0.5526 | 13.2593 | 9.8146 | |
| 0.7540 | 13.2642 | 10.1049 | 0.5526 | 13.2554 | 9.8136 | ||
| 0.7656 | 13.2416 | 10.0972 | 0.5526 | 13.2770 | 9.8010 | ||
| Algorithm | Target | Azimuth | Range | ||||
|---|---|---|---|---|---|---|---|
| IRW | PSLR | ISLR | IRW | PSLR | ISLR | ||
| Reference Algorithm | 0.1021 | 12.7699 | 9.1658 | 0.1000 | 13.2288 | 10.0081 | |
| 0.0997 | 13.3532 | 10.6065 | 0.1000 | 13.2621 | 9.9797 | ||
| 0.0977 | 12.5516 | 9.2375 | 0.1000 | 13.2482 | 9.8236 | ||
| Proposed Algorithm | 0.0992 | 13.3422 | 10.5922 | 0.1000 | 13.2705 | 9.9382 | |
| 0.0997 | 13.2634 | 10.4491 | 0.1000 | 13.2790 | 9.9282 | ||
| 0.1000 | 13.2904 | 10.6456 | 0.1000 | 13.2727 | 9.9384 | ||
| Algorithm | Target | Azimuth | Range | ||||
|---|---|---|---|---|---|---|---|
| IRW | PSLR | ISLR | IRW | PSLR | ISLR | ||
| Reference Algorithm | 0.1844 | 12.8206 | 9.7908 | 0.1996 | 13.2570 | 9.7928 | |
| 0.1998 | 13.2848 | 10.3101 | 0.1996 | 13.2536 | 9.7913 | ||
| 0.2108 | 13.2212 | 10.3475 | 0.2000 | 13.2479 | 9.7831 | ||
| Proposed Algorithm | 0.1840 | 13.2188 | 10.2805 | 0.1996 | 13.2545 | 9.7910 | |
| 0.1998 | 13.2853 | 10.3105 | 0.1996 | 13.2544 | 9.7916 | ||
| 0.2099 | 13.2951 | 10.2949 | 0.2000 | 13.2554 | 9.7868 | ||
| Region | Algorithm | Contrast | Entropy |
|---|---|---|---|
| Region 1 | Reference Algorithm | 7.1272 | 1.6524 |
| Proposed Algorithm | 7.1274 | 1.6518 | |
| Region 2 | Reference Algorithm | 7.3634 | 1.6062 |
| Proposed Algorithm | 7.4450 | 1.5920 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Z.; Li, P.; Zhang, Z.; Yun, Z.; He, F.; Dong, Z. Two-Dimensional Spatial Variation Analysis and Correction Method for High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar (SAR) Imaging. Remote Sens. 2025, 17, 1262. https://doi.org/10.3390/rs17071262
Hou Z, Li P, Zhang Z, Yun Z, He F, Dong Z. Two-Dimensional Spatial Variation Analysis and Correction Method for High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar (SAR) Imaging. Remote Sensing. 2025; 17(7):1262. https://doi.org/10.3390/rs17071262
Chicago/Turabian StyleHou, Zhenyu, Pin Li, Zehua Zhang, Zhuo Yun, Feng He, and Zhen Dong. 2025. "Two-Dimensional Spatial Variation Analysis and Correction Method for High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar (SAR) Imaging" Remote Sensing 17, no. 7: 1262. https://doi.org/10.3390/rs17071262
APA StyleHou, Z., Li, P., Zhang, Z., Yun, Z., He, F., & Dong, Z. (2025). Two-Dimensional Spatial Variation Analysis and Correction Method for High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar (SAR) Imaging. Remote Sensing, 17(7), 1262. https://doi.org/10.3390/rs17071262








