Extensive Feature-Inferring Deep Network for Hyperspectral and Multispectral Image Fusion
Abstract
1. Introduction
- We introduce a novel deep framework architecture called EFINet for HS-MS image fusion that is capable of interactively merging multi-scale characteristics and utilizing global details for reconstructing HRHSIs with minimum spatial detail corruption and spectral distortion;
- The ESFI unit based on dynamic self-attention (DSA) is proposed. The DSA process is designed to efficiently and effectively model the local information by scheming a network of Transformers in an efficient time. This module overcomes the restriction of the traditional Transformer in recreating the local features;
- We design a practical correlation refinement network (GCR) to adequately produce lightweight self-attention for global characteristic discovery. The suggested GCR collects multi-receptive-field attributes and reinforces the most prosperous characteristics to reconstruct the desired HRHSIs progressively;
- Detailed experiments are performed to prove the effectiveness of the devised EFINet techniques by utilizing two well-known remote sensing datasets, the Houston and Chikusei datasets. The performance is compared with state-of-the-art HS-MS image fusion strategies.
2. Related Works
2.1. Model-Driven Strategies
2.2. Data-Driven Strategies
3. Materials and Methods
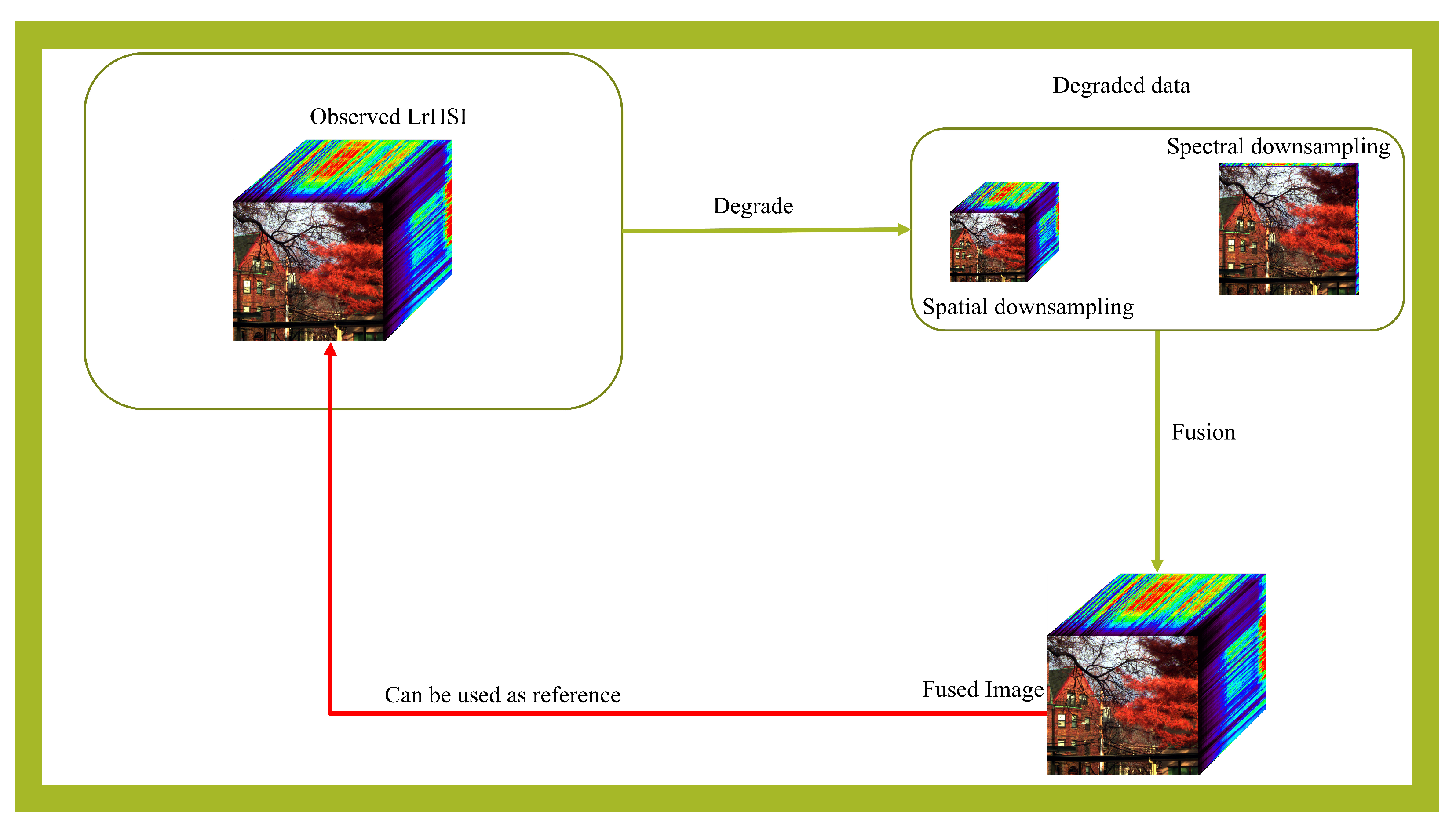
3.1. Problem Formulation
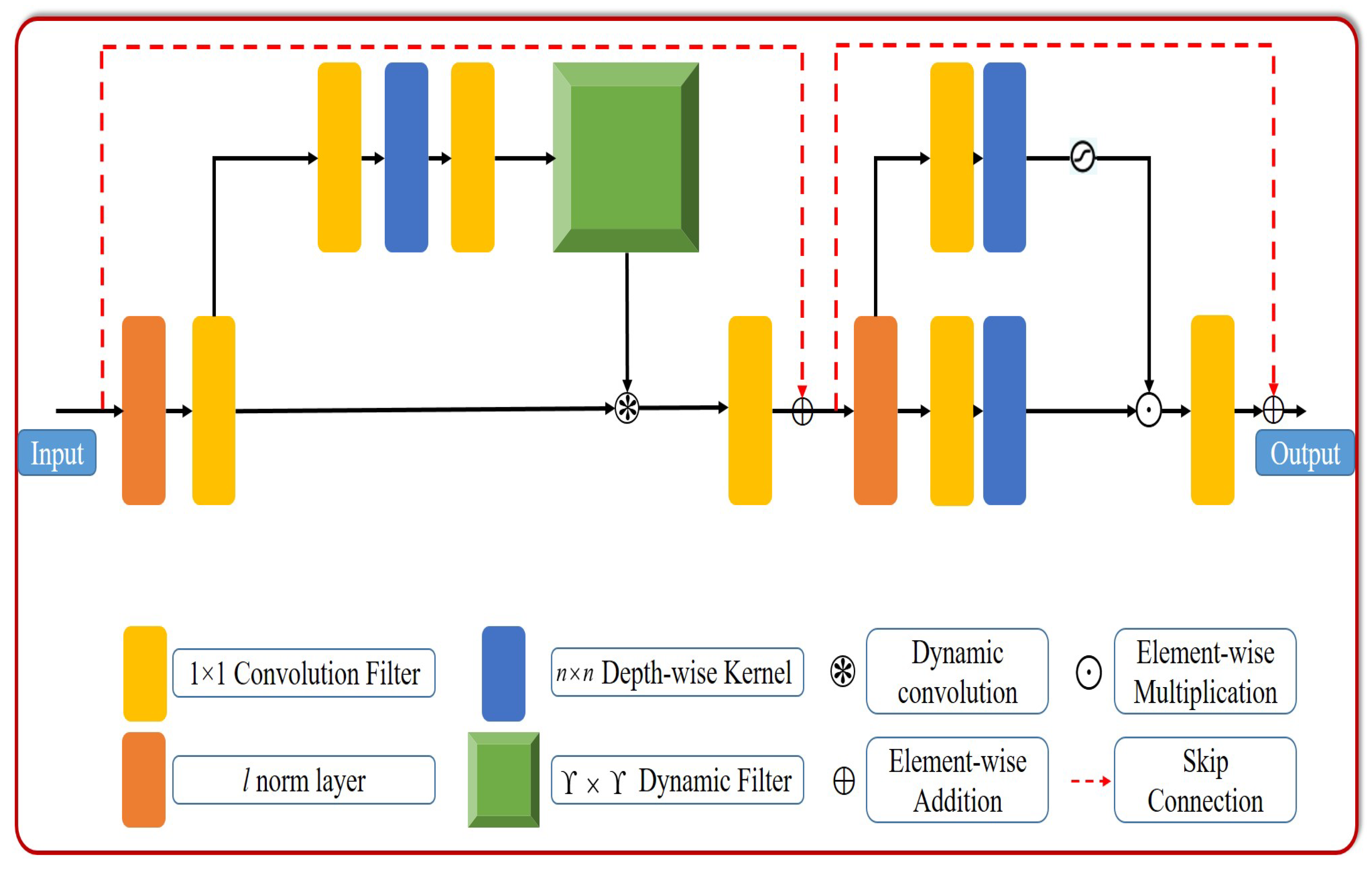
3.2. The Proposed Extensive Feature-Inferring Deep Network
3.2.1. Outline of the Proposed Framework Architecture
| Algorithm 1 Extensive Feature-Inferring Deep Network. |
Input: Two feature maps of LRHSI and HRMSI, and .
Output: Return the fused image in step 7. |
3.2.2. Multi-Scale Feature Extraction
3.2.3. Extensive-Scale Feature-Interacting Module
3.2.4. Global Correlation Refinement Module
3.3. The Loss Function
4. Experimental Outcomes and Discussion
4.1. Empirical Databases
- (1)
- Houston dataset: The Houston 2018 image is a remote sensing hyperspectral image captured over the University of Houston campus in February 2017. It was taken from the 2018 IEEE GRSS Data Fusion Challenge. The Houston hyperspectral image was acquired by utilizing the ITRES CASI-1500 hyperspectral imaging device and the Optech Titam multiwave (MW) (14SEN/CON340) sensor’s LiDAR information as well, with a spatial size of pixels. Spanning from the 380 to 1050 nm range, the Houston dataset contains 50 spectral channels, where spectral bands with low SNR are discarded, and 46 bands remain for our experiment.
- (2)
- Chikusei dataset: The remote sensing Chikusei hyperspectral dataset was collected over metropolitan and farming regions of Chikusei, Ibaraki, Japan, on 29 July 2014, operating a visible and near-infrared (NIR) hyperspectral imaging instrument. The spectral resolution of the Chikusei dataset is 128 spectral bands covering the spectrum range from 363 to 1018 nm, while the spatial resolution has a size of pixels. For convenience, the central region covering pixels is extracted for the experimentation, where the black boundaries in the geometric resolution are discarded.
4.2. The State-of-the-Art HS-MS Image Fusion Techniques for Comparison
4.3. Quantitative Assessment Indices
4.3.1. Structural Similarity Index (SSIM)
4.3.2. Peak Signal-to-Noise Ratio (PSNR)
4.3.3. Spectral Angle Mapper (SAM)
4.3.4. Relative Dimension Global Error in Synthesis (ERGAS)
4.4. Implementation Details
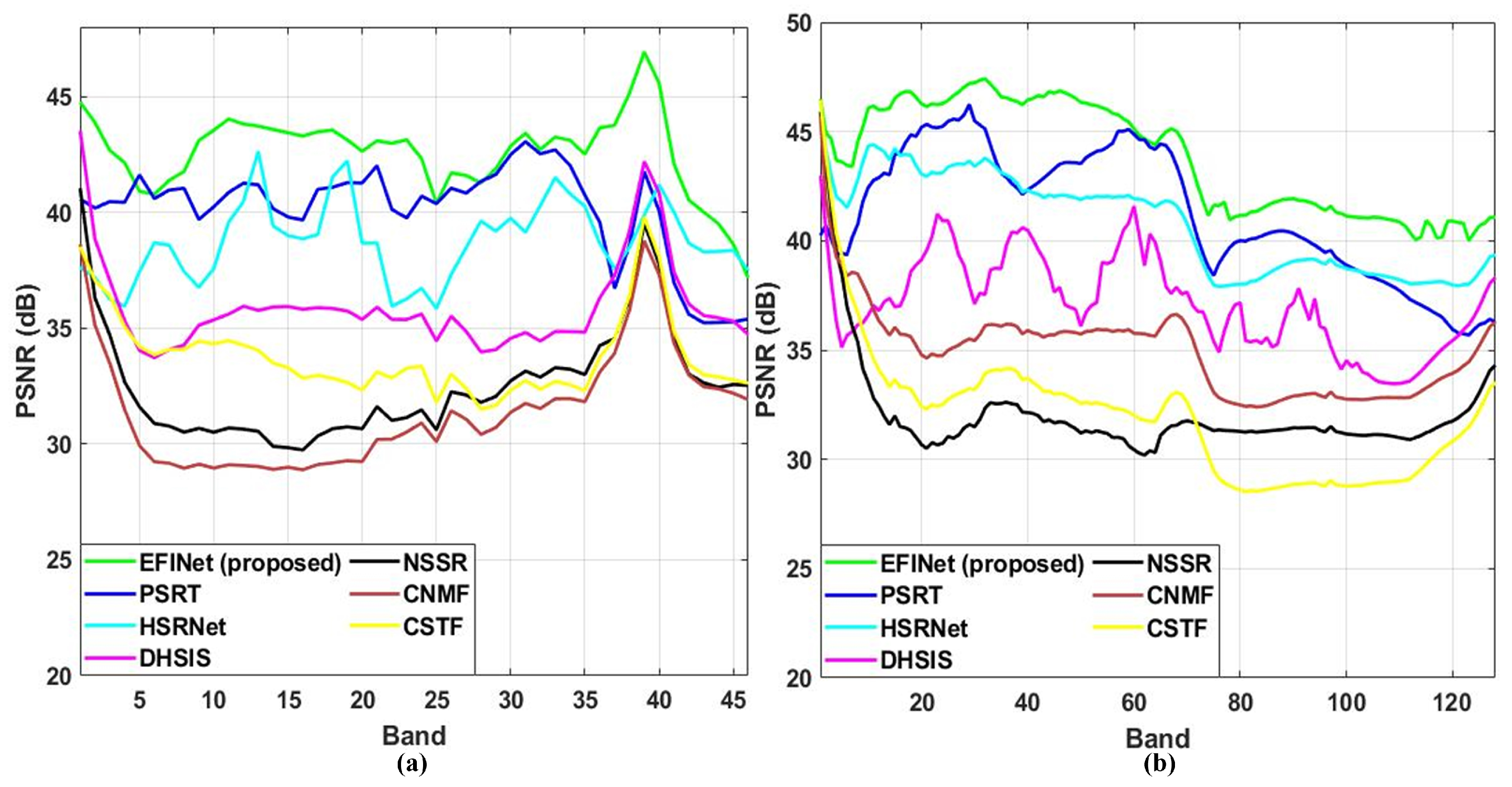
4.5. Experimental Outcomes and Discussion
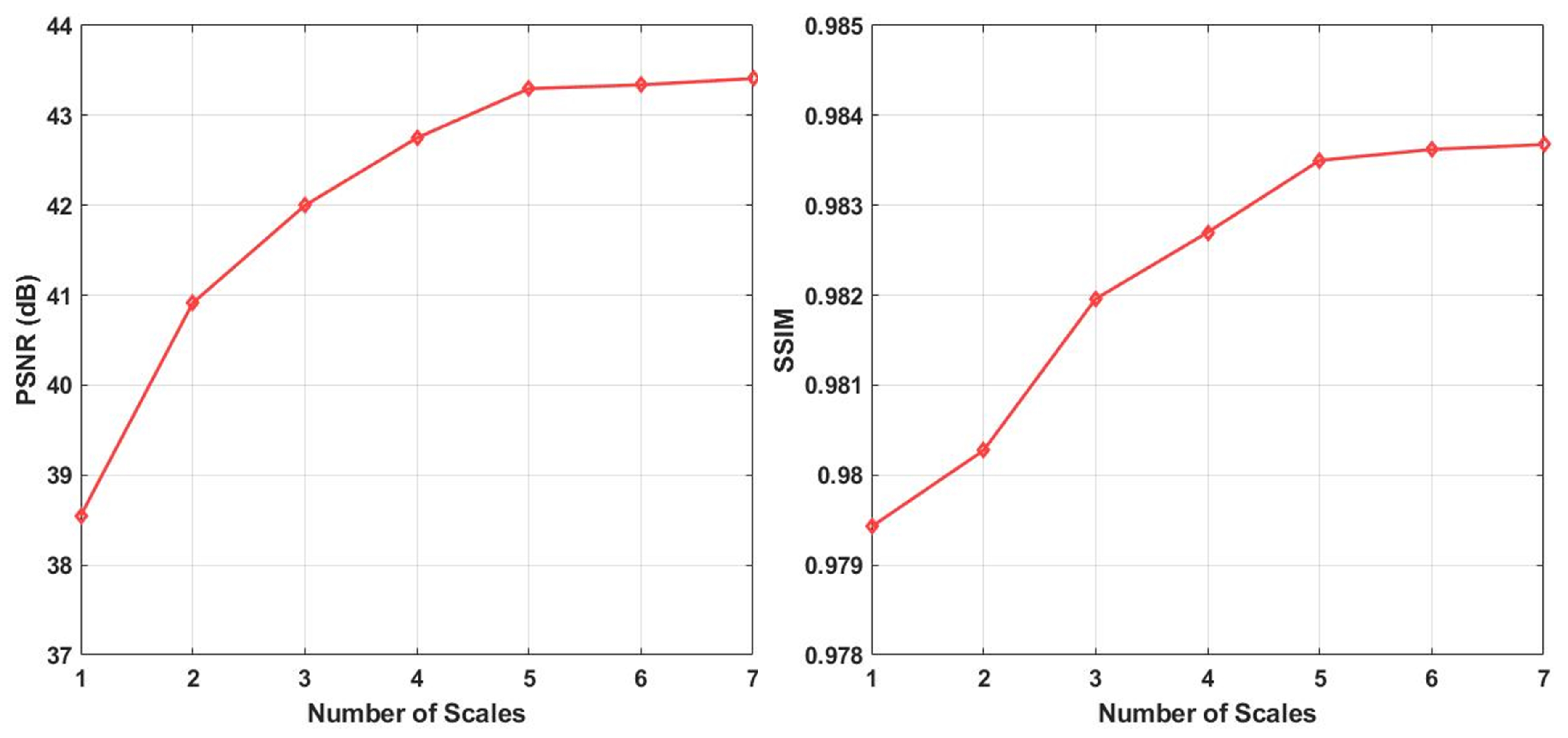
4.6. Ablation Study
4.7. Comparative Experiments Under Different Noise Levels
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Vali, A.; Comai, S.; Matteucci, M. Deep learning for land use and land cover classification based on hyperspectral and multispectral earth observation data: A review. Remote Sens. 2020, 12, 2495. [Google Scholar] [CrossRef]
- Hill, P.R.; Kumar, A.; Temimi, M.; Bull, D.R. HABNet: Machine learning, remote sensing-based detection of harmful algal blooms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3229–3239. [Google Scholar]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Avtar, R.; Komolafe, A.A.; Kouser, A.; Singh, D.; Yunus, A.P.; Dou, J.; Kumar, P.; Gupta, R.D.; Johnson, B.A.; Minh, H.V.T.; et al. Assessing sustainable development prospects through remote sensing: A review. Remote Sens. Appl. Soc. Environ. 2020, 20, 100402. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Hu, Q.; Cheng, Y.; Ma, J. Hyperspectral image super-resolution meets deep learning: A survey and perspective. IEEE/CAA J. Autom. Sin. 2023, 10, 1668–1691. [Google Scholar]
- Li, Y.; Zhang, L.; Dingl, C.; Wei, W.; Zhang, Y. Single hyperspectral image super-resolution with grouped deep recursive residual network. In Proceedings of the 2018 IEEE Fourth International Conference on Multimedia Big Data (BigMM), Xi’an, China, 13–16 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]
- Dian, R.; Li, S.; Sun, B.; Guo, A. Recent advances and new guidelines on hyperspectral and multispectral image fusion. Inf. Fusion 2021, 69, 40–51. [Google Scholar]
- Alparone, L.; Arienzo, A.; Garzelli, A. Spatial Resolution Enhancement of Satellite Hyperspectral Data Via Nested Hyper-Sharpening with Sentinel-2 Multispectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10956–10966. [Google Scholar]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature extraction of hyperspectral images with image fusion and recursive filtering. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3742–3752. [Google Scholar]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Model-based fusion of multi-and hyperspectral images using PCA and wavelets. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2652–2663. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Wang, Z.; Wang, Z.J.; Ward, R.K.; Wang, X. Deep learning for pixel-level image fusion: Recent advances and future prospects. Inf. Fusion 2018, 42, 158–173. [Google Scholar]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2011, 50, 528–537. [Google Scholar] [CrossRef]
- Peng, J.; Sun, W.; Li, H.C.; Li, W.; Meng, X.; Ge, C.; Du, Q. Low-rank and sparse representation for hyperspectral image processing: A review. IEEE Geosci. Remote Sens. Mag. 2021, 10, 10–43. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Zhao, X.L.; Chan, J.C.W.; Xu, Z.; Meng, D. Hyperspectral and multispectral image fusion via nonlocal low-rank tensor decomposition and spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7654–7671. [Google Scholar] [CrossRef]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing hyperspectral and multispectral images via coupled sparse tensor factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef] [PubMed]
- Ciotola, M.; Guarino, G.; Vivone, G.; Poggi, G.; Chanussot, J.; Plaza, A.; Scarpa, G. Hyperspectral Pansharpening: Critical review, tools, and future perspectives. IEEE Geosci. Remote Sens. Mag. 2024, 13, 311–338. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, T.; Qu, J.; Li, Y.; Xia, H. A spatial–spectral dual-optimization model-driven deep network for hyperspectral and multispectral image fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Shen, H.; Jiang, M.; Li, J.; Yuan, Q.; Wei, Y.; Zhang, L. Spatial–spectral fusion by combining deep learning and variational model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6169–6181. [Google Scholar] [CrossRef]
- Vivone, G.; Deng, L.J.; Deng, S.; Hong, D.; Jiang, M.; Li, C.; Li, W.; Shen, H.; Wu, X.; Xiao, J.L.; et al. Deep Learning in Remote Sensing Image Fusion: Methods, protocols, data, and future perspectives. IEEE Geosci. Remote Sens. Mag. 2024, 13, 269–310. [Google Scholar] [CrossRef]
- Khader, A.; Xiao, L.; Yang, J. A model-guided deep convolutional sparse coding network for hyperspectral and multispectral image fusion. Int. J. Remote Sens. 2022, 43, 2268–2295. [Google Scholar] [CrossRef]
- Xu, S.; Amira, O.; Liu, J.; Zhang, C.X.; Zhang, J.; Li, G. HAM-MFN: Hyperspectral and multispectral image multiscale fusion network with RAP loss. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4618–4628. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and multispectral image fusion via deep two-branches convolutional neural network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Chernyavskiy, A.; Ilvovsky, D.; Nakov, P. Transformers:“The end of history” for natural language processing? In Proceedings of the Machine Learning and Knowledge Discovery in Databases. Research Track: European Conference, ECML PKDD 2021, Bilbao, Spain, 13–17 September 2021; Proceedings, Part III 21. Springer: Berlin/Heidelberg, Germany, 2021; pp. 677–693. [Google Scholar]
- Tang, B.; Matteson, D.S. Probabilistic transformer for time series analysis. Adv. Neural Inf. Process. Syst. 2021, 34, 23592–23608. [Google Scholar]
- Chen, L.; Vivone, G.; Qin, J.; Chanussot, J.; Yang, X. Spectral–spatial transformer for hyperspectral image sharpening. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 16733–16747. [Google Scholar] [CrossRef]
- Ma, Q.; Jiang, J.; Liu, X.; Ma, J. Learning a 3D-CNN and transformer prior for hyperspectral image super-resolution. Inf. Fusion 2023, 100, 101907. [Google Scholar] [CrossRef]
- Zhuo, Y.W.; Zhang, T.J.; Hu, J.F.; Dou, H.X.; Huang, T.Z.; Deng, L.J. A deep-shallow fusion network with multidetail extractor and spectral attention for hyperspectral pansharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7539–7555. [Google Scholar] [CrossRef]
- Hu, J.F.; Huang, T.Z.; Deng, L.J.; Dou, H.X.; Hong, D.; Vivone, G. Fusformer: A transformer-based fusion network for hyperspectral image super-resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral image super-resolution via non-negative structured sparse representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Ge, Z.; Cao, G.; Shi, H.; Fu, P. Adaptive nonnegative sparse representation for hyperspectral image super-resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4267–4283. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, L.; Hou, C.; Kung, S.Y. Hyperspectral and multispectral image fusion based on local low rank and coupled spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5997–6009. [Google Scholar] [CrossRef]
- Peng, Y.; Li, W.; Luo, X.; Du, J.; Gan, Y.; Gao, X. Integrated fusion framework based on semicoupled sparse tensor factorization for spatio-temporal–spectral fusion of remote sensing images. Inf. Fusion 2021, 65, 21–36. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Prévost, C.; Usevich, K.; Brie, D.; Bermudez, J.C.; Richard, C. Coupled tensor decomposition for hyperspectral and multispectral image fusion with inter-image variability. IEEE J. Sel. Top. Signal Process. 2021, 15, 702–717. [Google Scholar] [CrossRef]
- Liu, N.; Li, W.; Tao, R. Geometric low-rank tensor approximation for remotely sensed hyperspectral and multispectral imagery fusion. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2819–2823. [Google Scholar]
- Dian, R.; Li, S. Hyperspectral image super-resolution via subspace-based low tensor multi-rank regularization. IEEE Trans. Image Process. 2019, 28, 5135–5146. [Google Scholar] [CrossRef]
- Tian, X.; Li, K.; Zhang, W.; Wang, Z.; Ma, J. Interpretable model-driven deep network for hyperspectral, multispectral, and panchromatic image fusion. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 14382–14395. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Wang, M.; Wang, W.; Yang, G. FS-Net: Four-stream Network with Spatial-spectral Representation Learning for Hyperspectral and Multispecral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8845–8857. [Google Scholar] [CrossRef]
- Cao, X.; Lian, Y.; Wang, K.; Ma, C.; Xu, X. Unsupervised hybrid network of transformer and CNN for blind hyperspectral and multispectral image fusion. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Li, W.; Li, L.; Peng, M.; Tao, R. KANDiff: Kolmogorov–Arnold Network and Diffusion Model-Based Network for Hyperspectral and Multispectral Image Fusion. Remote Sens. 2025, 17, 145. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part IV 13. Springer: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Zhou, F.; Hang, R.; Liu, Q.; Yuan, X. Pyramid fully convolutional network for hyperspectral and multispectral image fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1549–1558. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Guo, A.; Fang, L. Deep hyperspectral image sharpening. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5345–5355. [Google Scholar] [PubMed]
- Zheng, Y.; Li, J.; Li, Y.; Guo, J.; Wu, X.; Chanussot, J. Hyperspectral pansharpening using deep prior and dual attention residual network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8059–8076. [Google Scholar]
- Wang, K.; Liao, X.; Li, J.; Meng, D.; Wang, Y. Hyperspectral image super-resolution via knowledge-driven deep unrolling and transformer embedded convolutional recurrent neural network. IEEE Trans. Image Process. 2023, 32, 4581–4594. [Google Scholar] [PubMed]
- Liu, S.; Liu, S.; Zhang, S.; Li, B.; Hu, W.; Zhang, Y.D. SSAU-Net: A spectral–spatial attention-based U-Net for hyperspectral image fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Hu, J.F.; Huang, T.Z.; Deng, L.J.; Jiang, T.X.; Vivone, G.; Chanussot, J. Hyperspectral image super-resolution via deep spatiospectral attention convolutional neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7251–7265. [Google Scholar]
- Jha, A.; Bose, S.; Banerjee, B. GAF-Net: Improving the performance of remote sensing image fusion using novel global self and cross attention learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 6354–6363. [Google Scholar]
- Deng, S.Q.; Deng, L.J.; Wu, X.; Ran, R.; Hong, D.; Vivone, G. PSRT: Pyramid shuffle-and-reshuffle transformer for multispectral and hyperspectral image fusion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Zhang, X.; Zeng, H.; Guo, S.; Zhang, L. Efficient long-range attention network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 649–667. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Xu, Y.; Du, B.; Zhang, L.; Cerra, D.; Pato, M.; Carmona, E.; Prasad, S.; Yokoya, N.; Hänsch, R.; Le Saux, B. Advanced multi-sensor optical remote sensing for urban land use and land cover classification: Outcome of the 2018 IEEE GRSS data fusion contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1709–1724. [Google Scholar]
- Yokoya, N.; Iwasaki, A. Airborne hyperspectral data over Chikusei. Space Appl. Lab. Univ. Tokyo Tokyo Japan Tech. Rep. SAL-2016-05-27 2016, 5, 5. [Google Scholar]








| Method | Houston [58] | ||||
|---|---|---|---|---|---|
| PSNR (dB) | SAM | ERGAS | SSIM | Time (S) | |
| Best value | ∞ | 0 | 0 | 1 | 0 |
| CSTF [17] | 33.81 | 4.01 | 4.3228 | 0.9572 | 94.20 |
| CNMF [14] | 31.43 | 4.94 | 5.1622 | 0.9325 | 26.85 |
| NSSR [31] | 32.52 | 4.18 | 4.2579 | 0.9508 | 117.53 |
| DHSIS [46] | 35.93 | 3.47 | 3.1758 | 0.9720 | 8.34 |
| HSRNet [50] | 38.73 | 3.22 | 2.9024 | 0.9779 | 0.63 |
| PSRT [52] | 40.11 | 2.95 | 2.0298 | 0.9844 | 5.81 |
| EFINet | 42.58 | 2.64 | 1.8774 | 0.9893 | 0.52 |
| Method | Chikusei [59] | ||||
|---|---|---|---|---|---|
| PSNR (dB) | SAM | ERGAS | SSIM | Time (S) | |
| Best value | ∞ | 0 | 0 | 1 | 0 |
| CSTF [17] | 31.97 | 6.14 | 3.4681 | 0.9529 | 116.43 |
| CNMF [14] | 34.96 | 4.58 | 2.9272 | 0.9601 | 31.10 |
| NSSR [31] | 32.04 | 5.83 | 3.3590 | 0.9558 | 213.25 |
| DHSIS [46] | 37.15 | 4.26 | 2.6231 | 0.9623 | 21.68 |
| HSRNet [50] | 40.82 | 3.69 | 2.1735 | 0.9784 | 1.29 |
| PSRT [52] | 41.26 | 3.02 | 1.9038 | 0.9801 | 9.57 |
| EFINet | 43.79 | 2.43 | 1.7861 | 0.9838 | 0.84 |
| ESFI | GCR | Chikusei [59] | |||
|---|---|---|---|---|---|
| PSNR (dB) | SAM | ERGAS | SSIM | ||
| Best value | ∞ | 0 | 0 | 1 | |
| ✓ | × | 41.58 | 2.90 | 2.3609 | 0.9801 |
| × | ✓ | 43.06 | 2.64 | 1.9729 | 0.9809 |
| ✓ | ✓ | 43.79 | 2.43 | 1.7861 | 0.9838 |
| Method | Houston [58] | |||
|---|---|---|---|---|
| PSNR (dB) | SAM | ERGAS | SSIM | |
| Best value | ∞ | 0 | 0 | 1 |
| Noise level | SNR = 10/15 | |||
| CSTF [17] | 24.62 | 10.23 | 7.0454 | 0.8692 |
| CNMF [14] | 23.15 | 9.88 | 7.7836 | 0.8561 |
| NSSR [31] | 24.39 | 11.62 | 6.9013 | 0.8759 |
| DHSIS [46] | 28.60 | 8.55 | 5.8501 | 0.9046 |
| HSRNet [50] | 33.47 | 6.89 | 3.5273 | 0.9385 |
| PSRT [52] | 36.01 | 5.27 | 2.5905 | 0.9493 |
| EFINet | 38.94 | 4.59 | 1.9681 | 0.9624 |
| Noise level | SNR = 30/35 | |||
| CSTF [17] | 33.81 | 4.01 | 4.3228 | 0.9572 |
| CNMF [14] | 31.43 | 4.94 | 5.1622 | 0.9325 |
| NSSR [31] | 32.52 | 4.18 | 4.2579 | 0.9508 |
| DHSIS [46] | 35.93 | 3.47 | 3.1758 | 0.9720 |
| HSRNet [50] | 38.73 | 3.22 | 2.9024 | 0.9779 |
| PSRT [52] | 40.11 | 2.95 | 2.0298 | 0.9844 |
| EFINet | 42.58 | 2.64 | 1.8774 | 0.9893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khader, A.; Yang, J.; Ghorashi, S.A.; Ahmed, A.; Dehghan, Z.; Xiao, L. Extensive Feature-Inferring Deep Network for Hyperspectral and Multispectral Image Fusion. Remote Sens. 2025, 17, 1308. https://doi.org/10.3390/rs17071308
Khader A, Yang J, Ghorashi SA, Ahmed A, Dehghan Z, Xiao L. Extensive Feature-Inferring Deep Network for Hyperspectral and Multispectral Image Fusion. Remote Sensing. 2025; 17(7):1308. https://doi.org/10.3390/rs17071308
Chicago/Turabian StyleKhader, Abdolraheem, Jingxiang Yang, Sara Abdelwahab Ghorashi, Ali Ahmed, Zeinab Dehghan, and Liang Xiao. 2025. "Extensive Feature-Inferring Deep Network for Hyperspectral and Multispectral Image Fusion" Remote Sensing 17, no. 7: 1308. https://doi.org/10.3390/rs17071308
APA StyleKhader, A., Yang, J., Ghorashi, S. A., Ahmed, A., Dehghan, Z., & Xiao, L. (2025). Extensive Feature-Inferring Deep Network for Hyperspectral and Multispectral Image Fusion. Remote Sensing, 17(7), 1308. https://doi.org/10.3390/rs17071308






