Spatio-Temporal Patterns and Drivers of the Urban Heat Island Effect in Arid and Semi-Arid Regions of Northern China
Abstract
:1. Introduction
2. Materials and Methods
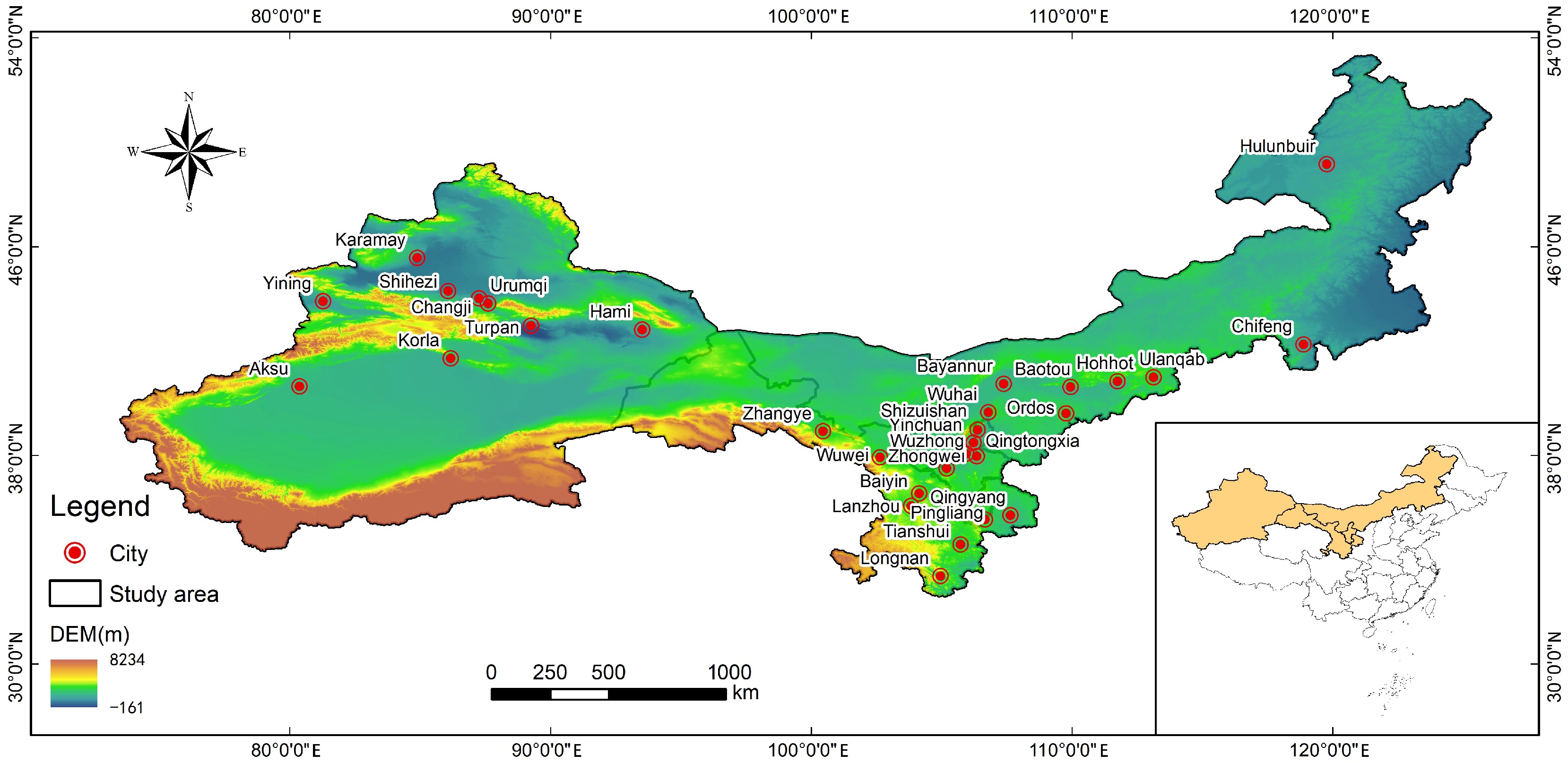
2.1. Study Area
2.2. Materials
2.3. Quantification of SUHII
2.4. Methods to Analyze Trends of SUHII and Driving Mechanisms
3. Results
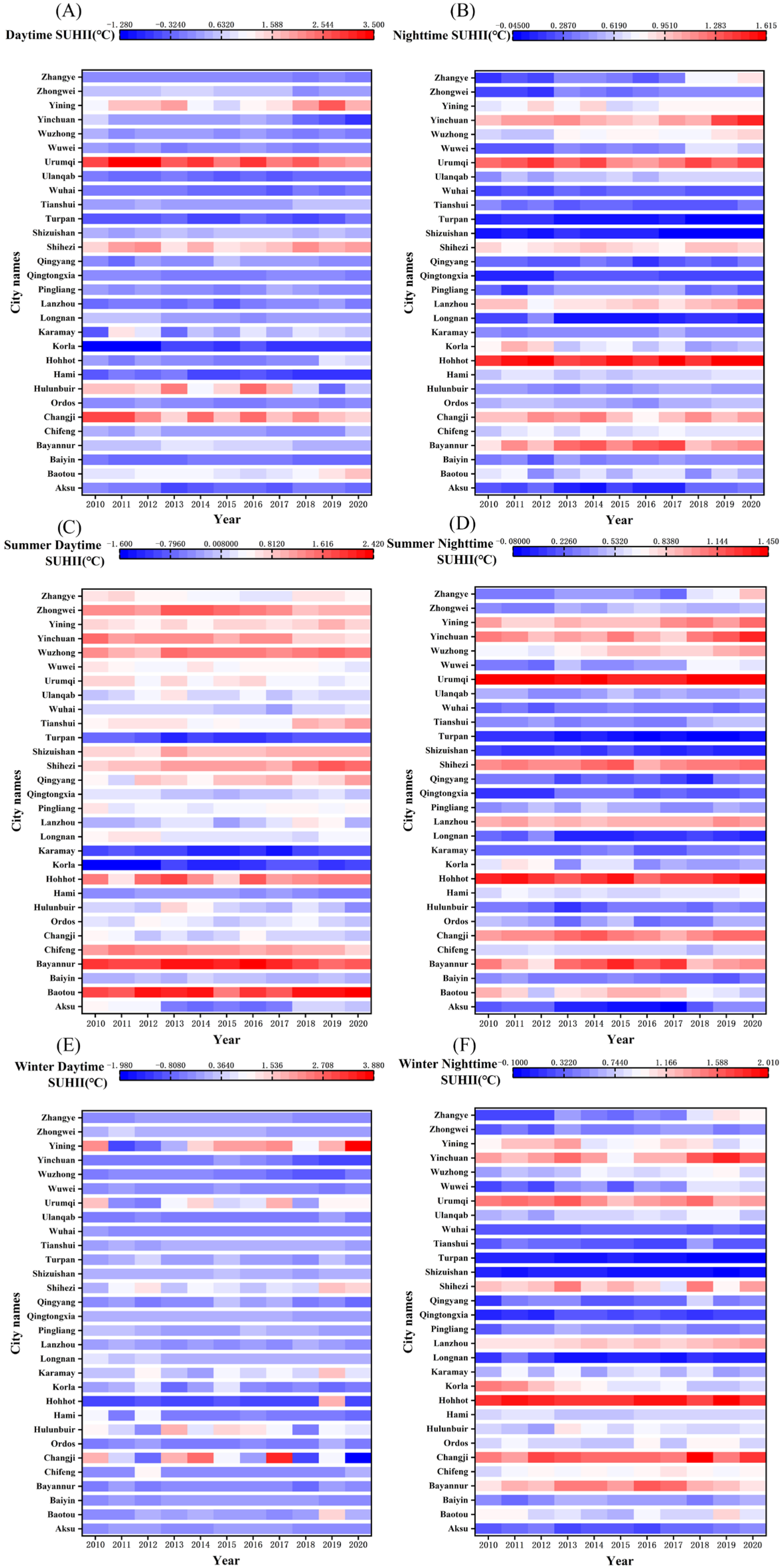
3.1. Temporal Trends of SUHII
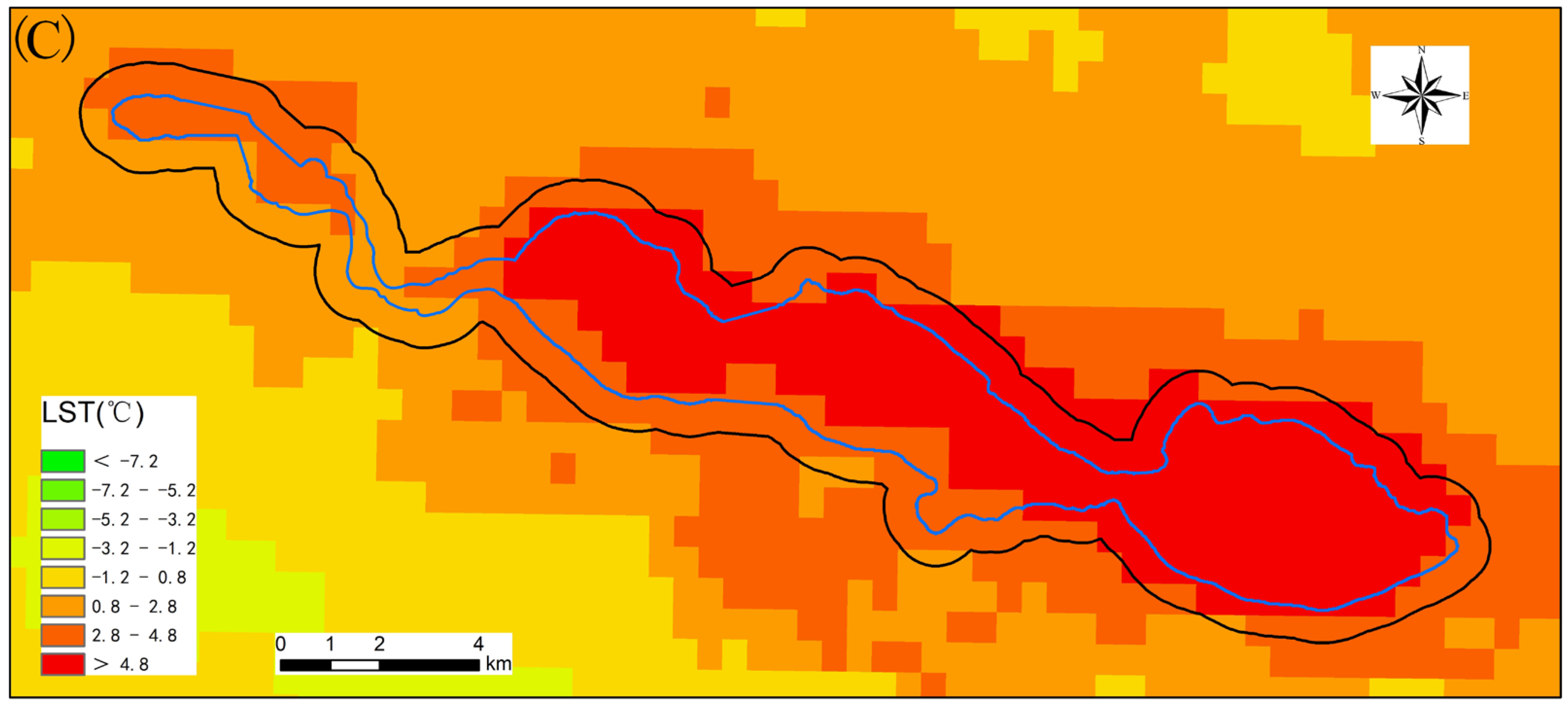
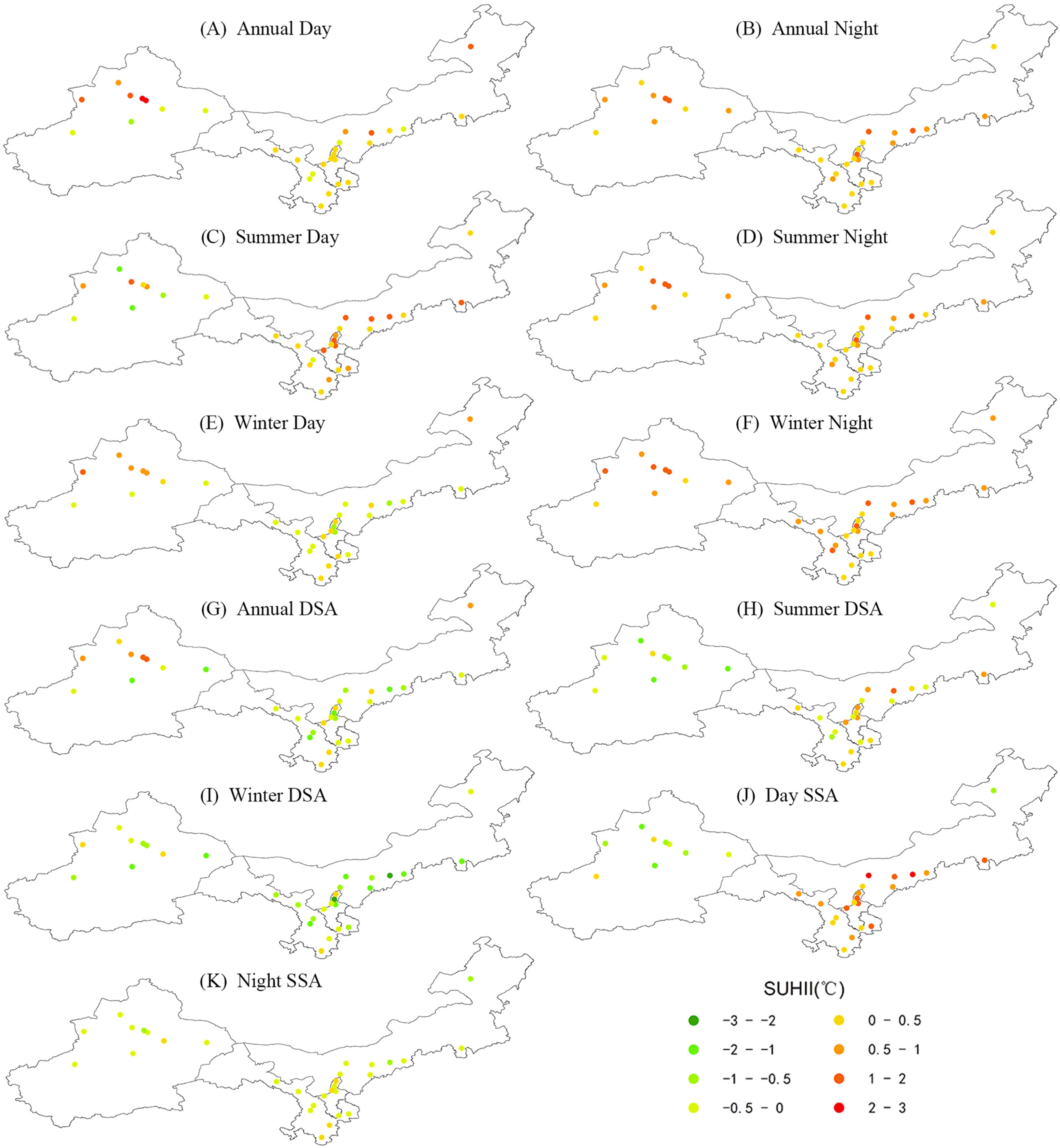
3.2. Spatial Patterns of SUHII
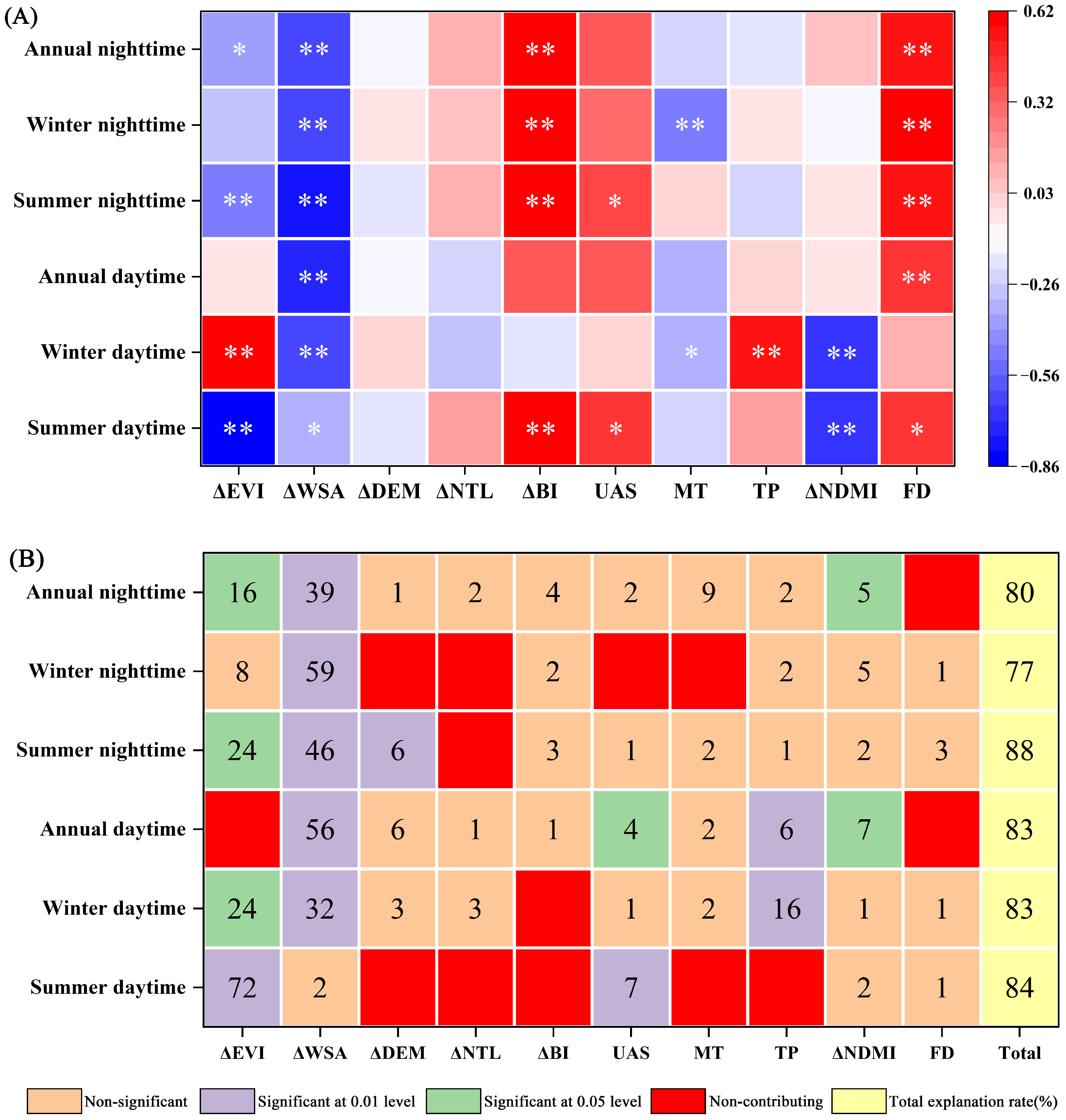
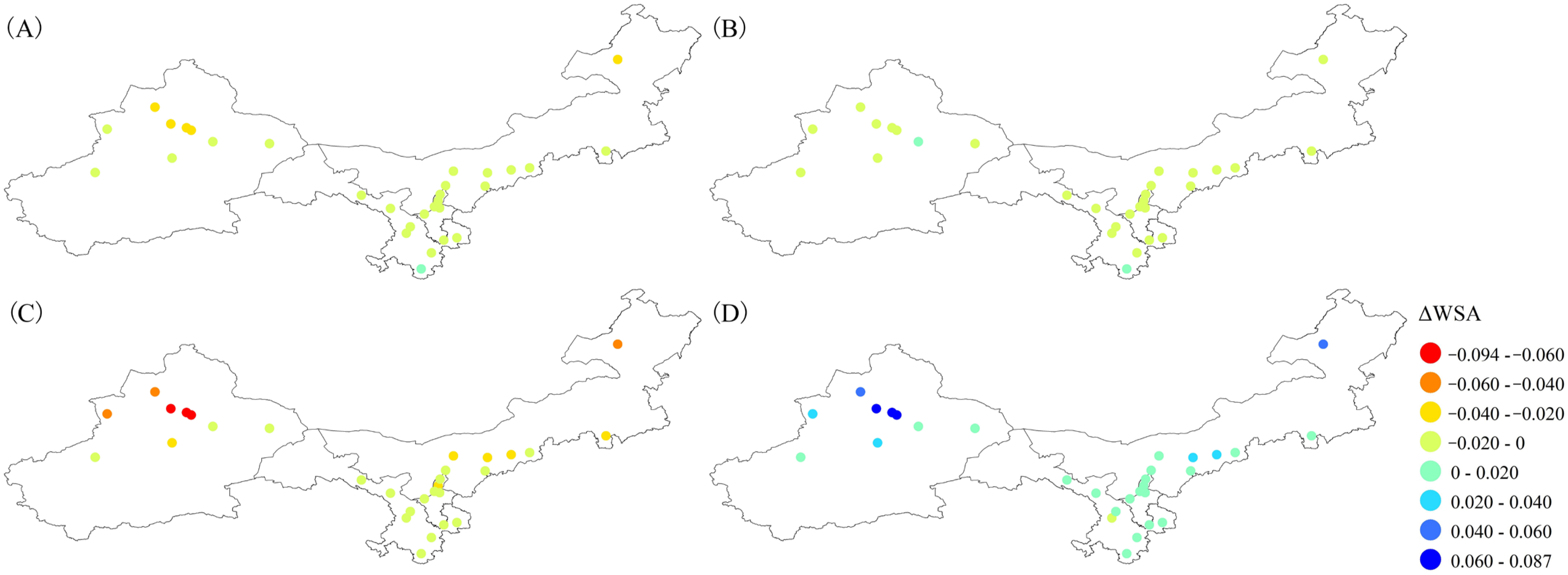
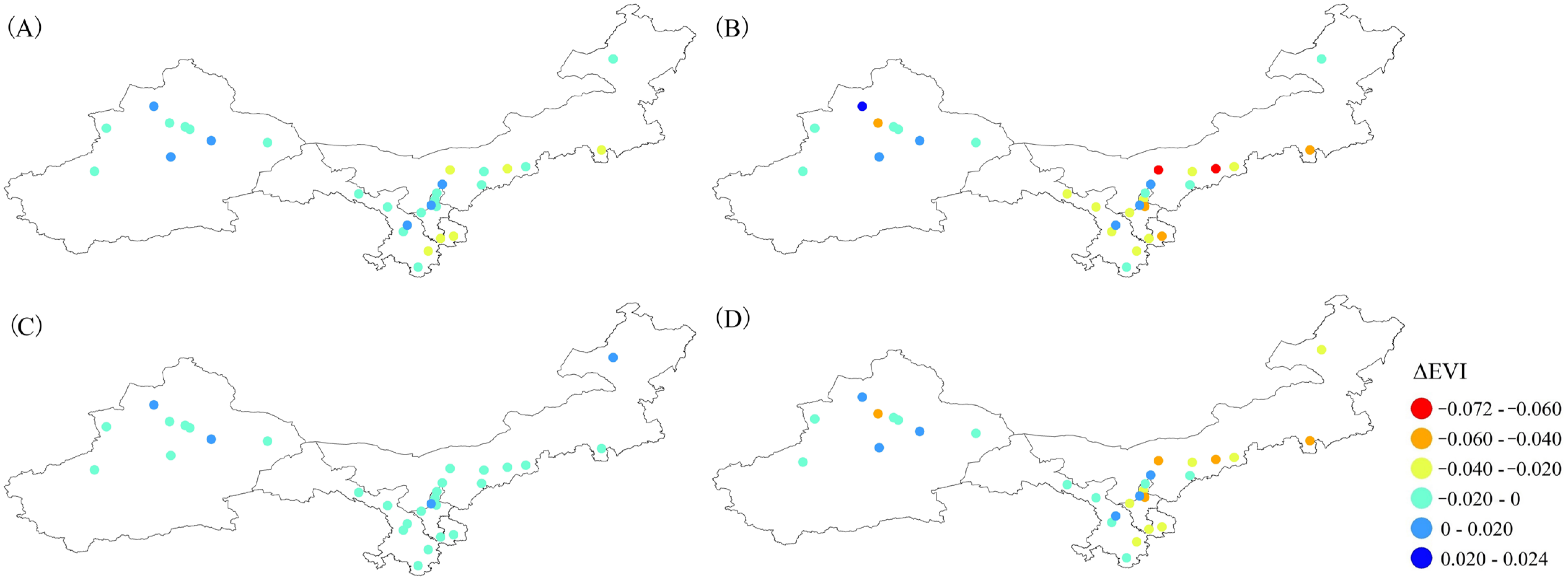
3.3. Analysis of Potential Driving Factors
4. Discussion
4.1. UHI Effects in Arid and Semi-Arid Regions
4.2. Drivers and Underlying Mechanisms of SUHII
4.3. Implications and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Zhang, X.; Shen, L. The impact of urbanization policy on land use change: A scenario analysis. Cities 2011, 28, 147–159. [Google Scholar] [CrossRef]
- Mohajerani, A.; Bakaric, J.; Jeffrey-Bailey, T. The urban heat island effect, its causes, and mitigation, with reference to the thermal properties of asphalt concrete. J. Environ. Manag. 2017, 197, 522–538. [Google Scholar] [CrossRef]
- Rossi, F.; Pisello, A.L.; Nicolini, A.; Filipponi, M.; Palombo, M. Analysis of retro-reflective surfaces for urban heat island mitigation: A new analytical model. Appl. Energy 2014, 114, 621–631. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Susca, T.; Pomponi, F. Heat island effects in urban life cycle assessment: Novel insights to include the effects of the urban heat island and UHI-mitigation measures in LCA for effective policy making. J. Ind. Ecol. 2020, 24, 410–423. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S.; Mall, R.K. Urban ecology and human health: Implications of urban heat island, air pollution and climate change nexus. In Urban Ecology; Elsevier: Amsterdam, The Netherlands, 2020; pp. 317–334. [Google Scholar] [CrossRef]
- Vargas, N.; Magaña, V. Climatic risk in the Mexico city metropolitan area due to urbanization. Urban Clim. 2020, 33, 100644. [Google Scholar] [CrossRef]
- Huang, H.; Deng, X.; Yang, H.; Zhou, X.; Jia, Q. Spatio-Temporal Mechanism Underlying the Effect of Urban Heat Island on Cardiovascular Diseases. Iran. J. Public Health 2020, 49, 1455. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Hu, L.; Brunsell, N.A. A new perspective to assess the urban heat island through remotely sensed atmospheric profiles. Remote Sens. Environ. 2015, 158, 393–406. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2018, 11, 48. [Google Scholar] [CrossRef]
- Clay, R.; Guan, H.; Wild, N.; Bennett, J.; Vinodkumar; Ewenz, C. Urban Heat Island traverses in the City of Adelaide, South Australia. Urban Clim. 2016, 17, 89–101. [Google Scholar] [CrossRef]
- Chen, L.; Wang, X.; Cai, X.; Yang, C.; Lu, X. Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China. Remote Sens. 2021, 13, 323. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. Approaches to study Urban Heat Island—Abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Wang, K.; Jiang, S.; Wang, J.; Zhou, C.; Wang, X.; Lee, X. Comparing the diurnal and seasonal variabilities of atmospheric and surface urban heat islands based on the Beijing urban meteorological network. J. Geophys. Res. Atmos. 2017, 122, 2131–2154. [Google Scholar] [CrossRef]
- Dewan, A.; Kiselev, G.; Botje, D.; Mahmud, G.I.; Bhuian, M.H.; Hassan, Q.K. Surface urban heat island intensity in five major cities of Bangladesh: Patterns, drivers and trends. Sustain. Cities Soc. 2021, 71, 102926. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface Urban Heat Island Across 419 Global Big Cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef]
- Gohain, K.J.; Mohammad, P.; Goswami, A. Assessing the impact of land use land cover changes on land surface temperature over Pune city, India. Quat. Int. 2021, 575, 259–269. [Google Scholar] [CrossRef]
- Rizvi, S.H.; Fatima, H.; Iqbal, M.J.; Alam, K. The effect of urbanization on the intensification of SUHIs: Analysis by LULC on Karachi. J. Atmos. Sol.-Terr. Phys. 2020, 207, 105374. [Google Scholar] [CrossRef]
- Shao, L.; Liao, W.; Li, P.; Luo, M.; Xiong, X.; Liu, X. Drivers of global surface urban heat islands: Surface property, climate background, and 2D/3D urban morphologies. Build. Environ. 2023, 242, 110581. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, Y.; Tong, X.; Hu, T.; Liu, Y.; Chakraborty, T.C.; Yao, R.; Xiao, C.; Chen, S.; Ma, Z. Influence of urban extent discrepancy on the estimation of surface urban heat island intensity: A global-scale assessment in 892 cities. J. Clean. Prod. 2023, 426, 139032. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Niu, Z.; Liu, F.; Wang, Q. Temporal trends of surface urban heat islands and associated determinants in major Chinese cities. Sci. Total Environ. 2017, 609, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Xie, M.; Chen, B.; Wang, H.; Teng, Y. Surface Regional Heat (Cool) Island Effect and Its Diurnal Differences in Arid and Semiarid Resource-based Urban Agglomerations. Chin. Geogr. Sci. 2023, 33, 131–143. [Google Scholar] [CrossRef]
- Rasul, A.; Balzter, H.; Smith, C. Diurnal and Seasonal Variation of Surface Urban Cool and Heat Islands in the Semi-Arid City of Erbil, Iraq. Climate 2016, 4, 42. [Google Scholar] [CrossRef]
- Chakraborty, T.; Hsu, A.; Manya, D.; Sheriff, G. A spatially explicit surface urban heat island database for the United States: Characterization, uncertainties, and possible applications. ISPRS J. Photogramm. Remote Sens. 2020, 168, 74–88. [Google Scholar] [CrossRef]
- Bhanage, V.; Kulkarni, S.; Sharma, R.; Lee, H.; Gedam, S. Enumerating and Modelling the Seasonal alterations of Surface Urban Heat and Cool Island: A Case Study over Indian Cities. Urban Sci. 2023, 7, 38. [Google Scholar] [CrossRef]
- Haashemi, S.; Weng, Q.; Darvishi, A.; Alavipanah, S. Seasonal Variations of the Surface Urban Heat Island in a Semi-Arid City. Remote Sens. 2016, 8, 352. [Google Scholar] [CrossRef]
- Masoodian, S.A.; Montazeri, M. Quantifying of surface urban cool island in arid environments case study: Isfahan metropolis. Landsc. Ecol. Eng. 2021, 17, 147–156. [Google Scholar] [CrossRef]
- Gherraz, H.; Guechi, I.; Alkama, D. Quantifying the effects of spatial patterns of green spaces on urban climate and urban heat island in a semi-arid climate. Bull. Société R. Sci. Liège 2020, 89, 164–185. [Google Scholar] [CrossRef]
- Gong, P.; Li, X.; Zhang, W. 40-Year (1978–2017) human settlement changes in China reflected by impervious surfaces from satellite remote sensing. Sci. Bull. 2019, 64, 756–763. [Google Scholar] [CrossRef]
- Miao, S.; Jiang, W.; Liang, P.; Liu, H.; Wang, X.; Tan, J.; Zhang, N.; Li, J.; Du, W.; Pei, L. Advances in Urban Meteorological Research in China. J. Meteorol. Res. 2020, 34, 218–242. [Google Scholar] [CrossRef]
- Zhou, D.; Sun, S.; Li, Y.; Zhang, L.; Huang, L. A multi-perspective study of atmospheric urban heat island effect in China based on national meteorological observations: Facts and uncertainties. Sci. Total Environ. 2023, 854, 158638. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Guangrong, S.; Chen, Z.; Hao, S.; Zhouyiling, Z.; Shan, Y. Quantitative analysis and prediction of urban heat island intensity on urban-rural gradient: A case study of Shanghai. Sci. Total Environ. 2022, 829, 154264. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Hu, C.; Wang, Y.; Wang, Z.; Zhang, J. Examining Spatio-Temporal Characteristics of Urban Heat Islands and Factors Driving Them in Hangzhou, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8316–8325. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Wang, R.; Liu, J. Evaluating urban heat island intensity and its associated determinants of towns and cities continuum in the Yangtze River Delta Urban Agglomerations. Sustain. Cities Soc. 2019, 50, 101659. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, Q.; Allam, M.; Hu, D.; Zhang, L.; Menenti, M. Environmental and anthropogenic drivers of surface urban heat island intensity: A case-study in the Yangtze River Delta, China. Ecol. Indic. 2021, 128, 107845. [Google Scholar] [CrossRef]
- Fu, X.; Yao, L.; Xu, W.; Wang, Y.; Sun, S. Exploring the multitemporal surface urban heat island effect and its driving relation in the Beijing-Tianjin-Hebei urban agglomeration. Appl. Geogr. 2022, 144, 102714. [Google Scholar] [CrossRef]
- Hou, L.; Yue, W.; Liu, X. Spatiotemporal patterns and drivers of summer heat island in Beijing-Tianjin-Hebei Urban Agglomeration, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7516–7527. [Google Scholar] [CrossRef]
- Geng, S.; Yang, L.; Sun, Z.; Wang, Z.; Qian, J.; Jiang, C.; Wen, M. Spatiotemporal patterns and driving forces of remotely sensed urban agglomeration heat islands in South China. Sci. Total Environ. 2021, 800, 149499. [Google Scholar] [CrossRef]
- Shahfahad, A.A.; Bindajam, A.A.; Naikoo, M.W.; Horo, J.P.; Mallick, J.; Rihan, M.; Malcoti, M.D.; Talukdar, S.; Rahman, R.; Rahman, A. Response of soil moisture and vegetation conditions in seasonal variation of land surface temperature and surface urban heat island intensity in sub-tropical semi-arid cities. Theor. Appl. Clim. 2023, 153, 367–395. [Google Scholar] [CrossRef]
- Zhou, B.; Rybski, D.; Kropp, J.P. The role of city size and urban form in the surface urban heat island. Sci. Rep. 2017, 7, 4791. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Crosson, W.L.; Al-Hamdan, M.Z.; Hemmings, S.N.; Wade, G.M. A daily merged MODIS Aqua–Terra land surface temperature data set for the conterminous United States. Remote Sens. Environ. 2012, 119, 315–324. [Google Scholar] [CrossRef]
- Zhou, D.; Bonafoni, S.; Zhang, L.; Wang, R. Remote sensing of the urban heat island effect in a highly populated urban agglomeration area in East China. Sci. Total Environ. 2018, 628–629, 415–429. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30 m annual land cover datasets and its dynamics in China from 1985 to 2022. Earth Syst. Sci. Data 2023, 13, 3907–3925. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.S.; Belz, J.E.; Chapin, E.C.; Martin, J.M.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products; Technical Report JPL D-31639; Jet Propulsion Laboratory: Pasadena, CA, USA, 2005; p. 143. [Google Scholar]
- Wu, Y.; Shi, K.; Chen, Z.; Liu, S.; Chang, Z. Developing Improved Time-Series DMSP-OLS-Like Data (1992–2019) in China by Integrating DMSP-OLS and SNPP-VIIRS. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4407714. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Use of impervious surface in urban land-use classification. Remote Sens. Environ. 2006, 102, 146–160. [Google Scholar] [CrossRef]
- Peng, S.; Feng, Z.; Liao, H.; Huang, B.; Peng, S.; Zhou, T. Spatial-temporal pattern of, and driving forces for, urban heat island in China. Ecol. Indic. 2019, 96, 127–132. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Liu, Y.; Niu, Z.; Wang, S.; Wang, L. Long-term trends of surface and canopy layer urban heat island intensity in 272 cities in the mainland of China. Sci. Total Environ. 2021, 772, 145607. [Google Scholar] [CrossRef]
- Reisi, M.; Ahmadi Nadoushan, M.; Aye, L. Remote sensing for urban heat and cool islands evaluation in semi-arid areas. Glob. J. Environ. Sci. Manag. 2019, 5, 319–330. [Google Scholar] [CrossRef]
- Karimi, A.; Mohammad, P.; Gachkar, S.; Gachkar, D.; García-Martínez, A.; Moreno-Rangel, D.; Brown, R.D. Surface Urban Heat Island Assessment of a Cold Desert City: A Case Study over the Isfahan Metropolitan Area of Iran. Atmosphere 2021, 12, 1368. [Google Scholar] [CrossRef]
- Fryd, O.; Pauleit, S.; Bühler, O. The role of urban green space and trees in relation to climate change. CABI Rev. 2012, 6, 1–18. [Google Scholar] [CrossRef]
- He, K.; Huo, H.; Zhang, Q. Urban air pollution in China: Current status, characteristics, and progress. Annu. Rev. Energy Environ. 2002, 27, 397–431. [Google Scholar] [CrossRef]
- Sang, J.; Liu, H.; Liu, H.; Zhang, Z. Observational and numerical studies of wintertime urban boundary layer. J. Wind Eng. Ind. Aerodyn. 2000, 87, 243–258. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E. Synergistic interactions between urban heat islands and heat waves: The impact in cities is larger than the sum of its parts. J. Appl. Meteorol. Climatol. 2013, 52, 2051–2064. [Google Scholar] [CrossRef]
- Montazeri, M.; Masoodian, S.A. Tempo-spatial behavior of surface urban heat island of Isfahan metropolitan area. J. Indian Soc. Remote Sens. 2020, 48, 263–270. [Google Scholar] [CrossRef]
- Lazzarini, M.; Marpu, P.R.; Ghedira, H. Temperature-land cover interactions: The inversion of urban heat island phenomenon in desert city areas. Remote Sens. Environ. 2013, 130, 136–152. [Google Scholar] [CrossRef]
- Georgescu, M.; Moustaoui, M.; Mahalov, A.; Dudhia, J. An alternative explanation of the semiarid urban area “oasis effect”. J. Geophys. Res. Atmos. 2011, 116, D24113. [Google Scholar] [CrossRef]
- Wang, Y.; Berardi, U.; Akbari, H. Comparing the effects of urban heat island mitigation strategies for Toronto, Canada. Energy Build. 2016, 114, 2–19. [Google Scholar] [CrossRef]
- Dutta, K.; Basu, D.; Agrawal, S. Evaluation of seasonal variability in magnitude of urban heat islands using local climate zone classification and surface albedo. Int. J. Environ. Sci. Technol. 2022, 19, 8677–8698. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, L.; Li, D.; Huang, D.; Zhu, C. Climate–vegetation control on the diurnal and seasonal variations of surface urban heat islands in China. Environ. Res. Lett. 2016, 11, 074009. [Google Scholar] [CrossRef]
- Lin, P.; Gou, Z.; Lau, S.; Qin, H. The Impact of Urban Design Descriptors on Outdoor Thermal Environment: A Literature Review. Energies 2017, 10, 2151. [Google Scholar] [CrossRef]
- Wang, J.; Huang, B.; Fu, D.; Atkinson, P. Spatiotemporal Variation in Surface Urban Heat Island Intensity and Associated Determinants across Major Chinese Cities. Remote Sens. 2015, 7, 3670–3689. [Google Scholar] [CrossRef]
- Vujovic, S.; Haddad, B.; Karaky, H.; Sebaibi, N.; Boutouil, M. Urban Heat Island: Causes, Consequences, and Mitigation Measures with Emphasis on Reflective and Permeable Pavements. CivilEng 2021, 2, 459–484. [Google Scholar] [CrossRef]
- Lian, X.; Zeng, Z.; Yao, Y.; Peng, S.; Wang, K.; Piao, S. Spatiotemporal variations in the difference between satellite-observed daily maximum land surface temperature and station-based daily maximum near-surface air temperature. J. Geophys. Res. Atmos. 2017, 122, 2254–2268. [Google Scholar] [CrossRef]
- Deng, X.; Yu, W.; Shi, J.; Huang, Y.; Li, D.; He, X.; Xie, Z. Characteristics of surface urban heat islands in global cities of different scales: Trends and drivers. Sustain. Cities Soc. 2024, 107, 105483. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Schatz, J.; Kucharik, C.J. Seasonality of the urban heat island effect in Madison, Wisconsin. J. Appl. Meteorol. Climatol. 2014, 53, 2371–2386. [Google Scholar] [CrossRef]
- Tabassum, A.; Hong, S.-H.; Park, K.; Baik, J.-J. Impacts of Changes in Soil Moisture on Urban Heat Islands and Urban Breeze Circulations: Idealized Ensemble Simulations. Asia-Pac. J. Atmos. Sci. 2024, 60, 541–553. [Google Scholar] [CrossRef]
- Husain, S.Z.; Bélair, S.; Leroyer, S. Influence of soil moisture on urban microclimate and surface-layer meteorology in Oklahoma City. J. Appl. Meteorol. Climatol. 2014, 53, 83–98. [Google Scholar] [CrossRef]
- Martilli, A. Numerical study of urban impact on boundary layer structure: Sensitivity to wind speed, urban morphology, and rural soil moisture. J. Appl. Meteorol. 2002, 41, 1247–1266. [Google Scholar] [CrossRef]
- Du, H.; Wang, D.; Wang, Y.; Zhao, X.; Qin, F.; Jiang, H.; Cai, Y. Influences of land cover types, meteorological conditions, anthropogenic heat and urban area on surface urban heat island in the Yangtze River Delta Urban Agglomeration. Sci. Total Environ. 2016, 571, 461–470. [Google Scholar] [CrossRef]
- Lambers, H.; Oliveira, R.S. Plant water relations. In Plant Physiological Ecology; Springer International Publishing: Cham, Switzerland, 2019; pp. 187–263. [Google Scholar] [CrossRef]
- Wang, S.; Davidson, A. Impact of climate variations on surface albedo of a temperate grassland. Agric. For. Meteorol. 2007, 142, 133–142. [Google Scholar] [CrossRef]
- Sugathan, N.; Biju, V.; Renuka, G. Influence of soil moisture content on surface albedo and soil thermal parameters at a tropical station. J. Earth Syst. Sci. 2014, 123, 1115–1128. [Google Scholar] [CrossRef]
- Hall, A. The Role of Surface Albedo Feedback in Climate. J. Clim. 2004, 17, 1550–1568. [Google Scholar] [CrossRef]
- Morabito, M.; Crisci, A.; Messeri, A.; Orlandini, S.; Raschi, A.; Maracchi, G.; Munafò, M. The impact of built-up surfaces on land surface temperatures in Italian urban areas. Sci. Total Environ. 2016, 551–552, 317–326. [Google Scholar] [CrossRef]
- Fu, S.; Wang, L.; Khalil, U.; Cheema, A.H.; Ullah, I.; Aslam, B.; Alarifi, S.S. Prediction of surface urban heat island based on predicted consequences of urban sprawl using deep learning: A way forward for a sustainable environment. Phys. Chem. Earth Parts A/B/C 2024, 135, 103682. [Google Scholar] [CrossRef]
- Feng, J.-M.; Wang, Y.-L.; Ma, Z.-G.; Liu, Y.-H. Simulating the Regional Impacts of Urbanization and Anthropogenic Heat Release on Climate across China. J. Clim. 2012, 25, 7187–7203. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Karimimoshaver, M.; Khalvandi, R.; Khalvandi, M. The effect of urban morphology on heat accumulation in urban street canyons and mitigation approach. Sustain. Cities Soc. 2021, 73, 103127. [Google Scholar] [CrossRef]
- Mughal, M.O.; Li, X.X.; Norford, L.K. Urban heat island mitigation in Singapore: Evaluation using WRF/multilayer urban canopy model and local climate zones. Urban Clim. 2020, 34, 100714. [Google Scholar] [CrossRef]
- Levin, N.; Kyba, C.C.M.; Zhang, Q.; Sánchez De Miguel, A.; Román, M.O.; Li, X.; Portnov, B.A.; Molthan, A.L.; Jechow, A.; Miller, S.D.; et al. Remote sensing of night lights: A review and an outlook for the future. Remote Sens. Environ. 2020, 237, 111443. [Google Scholar] [CrossRef]
- Saha, M.; Kafy, A.A.; Bakshi, A.; Faisal, A.A.; Almulhim, A.I.; Rahaman, Z.A.; Al Rakib, A.; Fattah, M.A.; Akter, K.S.; Rahman, M.T.; et al. Modelling microscale impacts assessment of urban expansion on seasonal surface urban heat island intensity using neural network algorithms. Energy Build. 2022, 275, 112452. [Google Scholar] [CrossRef]
- Li, Y.; Schubert, S.; Kropp, J.P.; Rybski, D. On the influence of density and morphology on the Urban Heat Island intensity. Nat. Commun. 2020, 11, 2647. [Google Scholar] [CrossRef]
- Tu, L.; Qin, Z.; Li, W.; Geng, J.; Yang, L.; Zhao, S.; Wang, F. Surface urban heat island effect and its relationship with urban expansion in Nanjing, China. J. Appl. Remote Sens. 2016, 10, 026037. [Google Scholar] [CrossRef]
- Kang, S.; Lee, D.; Park, J.; Jung, J. Exploring Urban Forms Vulnerable to Urban Heat Islands: A Multiscale Analysis. Sustainability 2022, 14, 3603. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, M.; Kang, M.; Xing, K.; Wang, Y.; Xue, F.; Chen, C. Diurnal and seasonal variation of the elevation gradient of air temperature in the northern flank of the western Qinling Mountain range, China. J. Mt. Sci. 2017, 14, 94–105. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Mackey, C.W.; Lee, X.; Smith, R.B. Remotely sensing the cooling effects of city scale efforts to reduce urban heat island. Build. Environ. 2012, 49, 348–358. [Google Scholar] [CrossRef]
- Morabito, M.; Crisci, A.; Guerri, G.; Messeri, A.; Congedo, L.; Munafò, M. Surface urban heat islands in Italian metropolitan cities: Tree cover and impervious surface influences. Sci. Total Environ. 2021, 751, 142334. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhou, D.; Liu, S. Data concurrency is required for estimating urban heat island intensity. Environ. Pollut. 2016, 208, 118–124. [Google Scholar] [CrossRef] [PubMed]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of Southeast Asia. Sci. Total Environ. 2017, 577, 349–359. [Google Scholar] [CrossRef] [PubMed]



| Category | Variable | Abbreviation | Unit | Spatial Resolution | Time Scale | Data Source |
|---|---|---|---|---|---|---|
| Vegetation | Enhanced vegetation index | EVI | - | 1 km | 2010–2020 | MYD13A2 product |
| Soil moisture | Normalized difference moisture index | NDMI | - | 500 m | 2010–2020 | MOD09A1 product |
| City size, urban morphology, terrain, and albedo | Fractal dimension | FD | - | - | 2010–2020 | Urban boundary extracted from CLCD land cover data |
| Urban area size | UAS | km2 | - | 2010–2020 | Derived from CLCD land cover data | |
| Digital elevation model | DEM | m | 30 m | 2015 | SRTM product | |
| White sky albedo | WSA | - | 500 m | 2010–2020 | MCD43A3 product | |
| Socio-economy | Nighttime light | NTL | - | 1 km | 2010–2020 | Combination of DMSP-OLS data and SNPP-VIIRS data released by Wu et al. (2021) [49] |
| Built-up intensity | BI | - | 30 m | 2010–2020 | Derived from CLCD land cover data | |
| Climate | Mean temperature | MT | °C | - | 2010–2020 | Derived from the air temperature provided by the National Meteorological Science Data Center |
| Total precipitation | TP | mm | - | 2010–2020 | Derived from the precipitation provided by the National Meteorological Science Data Center |
| City Name | Trend Slope (°C/year) | Lower Bound at 95% CI of Slope | Upper Bound at 95% CI of Slope | |
|---|---|---|---|---|
| Annual daytime | Tianshui | 0.027 * | −0.025 | 0.029 |
| Hami | −0.052 ** | −0.038 | 0.040 | |
| Urumqi | −0.096 * | −0.091 | 0.088 | |
| Wuzhong | −0.039 * | −0.027 | 0.025 | |
| Yinchuan | −0.089 * | −0.056 | 0.055 | |
| Zhongwei | −0.048 * | −0.035 | 0.034 | |
| Summer daytime | Korla | 0.062 * | −0.041 | 0.042 |
| Qingyang | 0.056 * | −0.054 | 0.047 | |
| Shihezi | 0.080 ** | −0.055 | 0.058 | |
| Shizuishan | 0.036 * | −0.028 | 0.028 | |
| Chifeng | −0.043 ** | −0.029 | 0.028 | |
| Hami | −0.021 * | −0.022 | 0.021 | |
| Yinchuan | −0.084 * | −0.058 | 0.049 | |
| Winter daytime | Yining | 0.349 * | −0.249 | 0.262 |
| Hami | −0.038 * | −0.046 | 0.044 | |
| Longnan | −0.025 * | −0.017 | 0.032 | |
| Wuzhong | −0.048 * | −0.040 | 0.040 | |
| Zhongwei | −0.028 ** | −0.027 | 0.026 |
| City Name | Trend Slope (°C/year) | Lower Bound at 95% CI of Slope | Upper Bound at 95% CI of Slope | |
|---|---|---|---|---|
| Annual nighttime | Hohhot | 0.011 * | −0.016 | 0.015 |
| Lanzhou | 0.024 * | −0.021 | 0.018 | |
| Ulanqab | 0.011 ** | −0.010 | 0.011 | |
| Wuwei | 0.040 ** | −0.030 | 0.031 | |
| Wuzhong | 0.026 ** | −0.022 | 0.020 | |
| Zhangye | 0.065 ** | −0.041 | 0.035 | |
| Korla | −0.036 ** | −0.031 | 0.032 | |
| Turpan | −0.018 * | −0.012 | 0.013 | |
| Summer nighttime | Hulunbuir | 0.004 * | −0.008 | 0.008 |
| Wuwei | 0.030 ** | −0.028 | 0.026 | |
| Wuzhong | 0.032 ** | −0.022 | 0.023 | |
| Yining | 0.018 * | −0.018 | 0.019 | |
| Zhongwei | 0.019 * | −0.018 | 0.015 | |
| Zhangye | 0.042 * | −0.028 | 0.032 | |
| Turpan | −0.014 ** | −0.009 | 0.010 | |
| Winter nighttime | Aksu | 0.020 * | −0.016 | 0.016 |
| Lanzhou | 0.023 ** | −0.016 | 0.016 | |
| Ulanqab | 0.021 * | −0.018 | 0.019 | |
| Wuwei | 0.064 ** | −0.041 | 0.042 | |
| Wuzhong | 0.036 * | −0.026 | 0.023 | |
| Zhongwei | 0.020 * | −0.018 | 0.018 | |
| Zhangye | 0.077 ** | −0.051 | 0.054 | |
| Korla | −0.070 ** | −0.045 | 0.043 | |
| Shizuishan | −0.011 * | −0.009 | 0.009 | |
| Turpan | −0.017 ** | −0.011 | 0.010 |
| Variable | Longitude | Latitude |
|---|---|---|
| Annual daytime SUHII | −0.230 | 0.457 * |
| Summer daytime SUHII | 0.451 * | −0.185 |
| Winter daytime SUHII | −0.503 ** | 0.500 ** |
| Winter nighttime SUHII | −0.076 | 0.398 * |
| Variable | Variance Inflation Factor | |||||
|---|---|---|---|---|---|---|
| Annual Daytime SUHII | Annual Nighttime SUHII | Summer Daytime SUHII | Summer Nighttime SUHII | Winter Daytime SUHII | Winter Nighttime SUHII | |
| ΔEVI | 4.023 | 4.023 | 4.287 | 4.287 | 4.766 | 4.766 |
| ΔWSA | 2.350 | 2.350 | 2.763 | 2.763 | 4.171 | 4.171 |
| ΔDEM | 1.575 | 1.575 | 1.708 | 1.708 | 1.984 | 1.984 |
| ΔNTL | 1.745 | 1.745 | 1.911 | 1.911 | 1.960 | 1.960 |
| ΔBI | 4.733 | 4.733 | 4.458 | 4.458 | 3.182 | 3.182 |
| UAS | 3.063 | 3.063 | 3.503 | 3.503 | 3.921 | 3.921 |
| MT | 2.219 | 2.219 | 3.480 | 3.480 | 2.775 | 2.775 |
| TP | 1.844 | 1.844 | 3.293 | 3.293 | 1.573 | 1.573 |
| ΔNDMI | 2.095 | 2.095 | 4.184 | 4.184 | 3.391 | 3.391 |
| FD | 4.466 | 4.466 | 4.487 | 4.487 | 3.585 | 3.585 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Lu, L.; Zhou, X.; Huang, G.; Chen, Z. Spatio-Temporal Patterns and Drivers of the Urban Heat Island Effect in Arid and Semi-Arid Regions of Northern China. Remote Sens. 2025, 17, 1339. https://doi.org/10.3390/rs17081339
Wang J, Lu L, Zhou X, Huang G, Chen Z. Spatio-Temporal Patterns and Drivers of the Urban Heat Island Effect in Arid and Semi-Arid Regions of Northern China. Remote Sensing. 2025; 17(8):1339. https://doi.org/10.3390/rs17081339
Chicago/Turabian StyleWang, Jingwen, Lei Lu, Xiaoming Zhou, Guanghui Huang, and Zihan Chen. 2025. "Spatio-Temporal Patterns and Drivers of the Urban Heat Island Effect in Arid and Semi-Arid Regions of Northern China" Remote Sensing 17, no. 8: 1339. https://doi.org/10.3390/rs17081339
APA StyleWang, J., Lu, L., Zhou, X., Huang, G., & Chen, Z. (2025). Spatio-Temporal Patterns and Drivers of the Urban Heat Island Effect in Arid and Semi-Arid Regions of Northern China. Remote Sensing, 17(8), 1339. https://doi.org/10.3390/rs17081339







