Hyperspectral Image Reconstruction Based on Blur–Kernel–Prior and Spatial–Spectral Attention
Abstract
:1. Introduction
- We present a novel HSI reconstruction method that leverages a Blur–Kernel–Prior neural network for the denoising and reconstruction of HSIs affected by mixed blur noise, marking the first application of this technique in the field.
- The architecture incorporates two distinct modules: a Blur–Kernel–Prior denoising module-based U-Net backbone and a spatial attention feature-reconstruction module. The module implements an end-to-end encoding-decoding process utilizing a dual U-Net architecture, which effectively isolates the blur kernel from the original image. Meanwhile, the spatial attention feature-reconstruction module employs hybrid 2D–3D convolution provided shallow feature extraction locally and attention mechanisms with multi-head attention to facilitate comprehensive deep feature extraction across both spatial and spectral dimensions globally.
- Experimental evaluations conducted on the Cave, Chikusei, and Pavia University datasets, which include mixed simulated noise, demonstrate that our research surpasses the state-of-the-art of deep-learning-based approaches across different image-quality metrics.
2. Related Work
2.1. Traditional Image Blind Deconvolution Model
2.2. Effective Estimation of Blur Kernels Based on Deep Learning
2.3. Attention Mechanisms for HSIs Reconstruction
3. Methodology
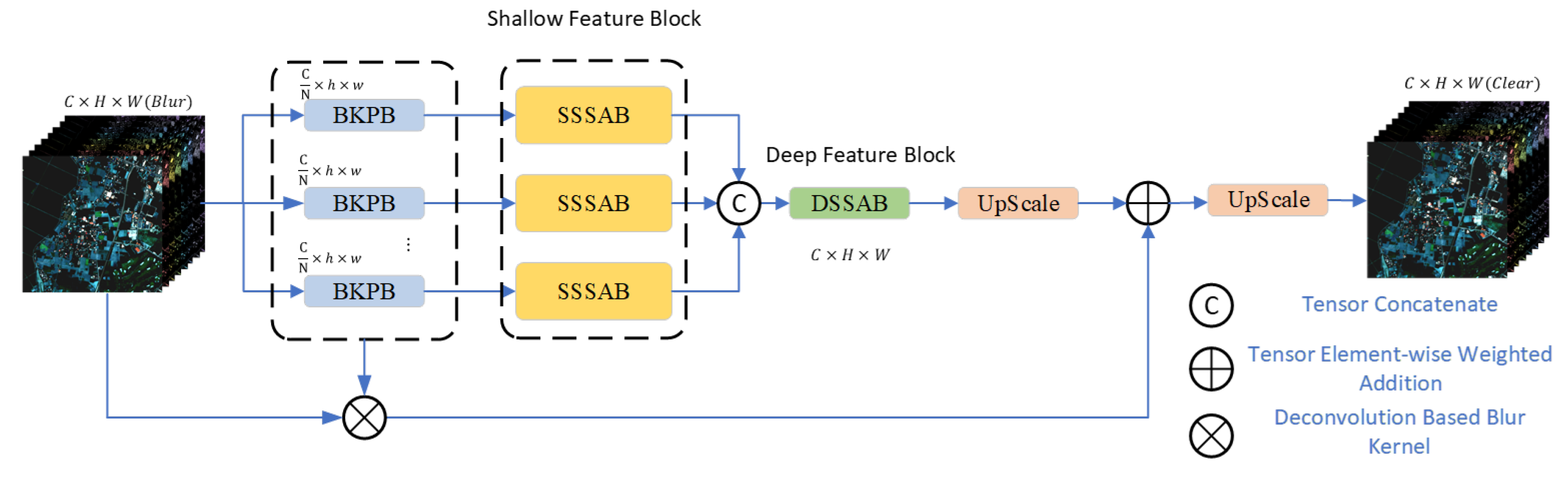
3.1. Overall Architecture
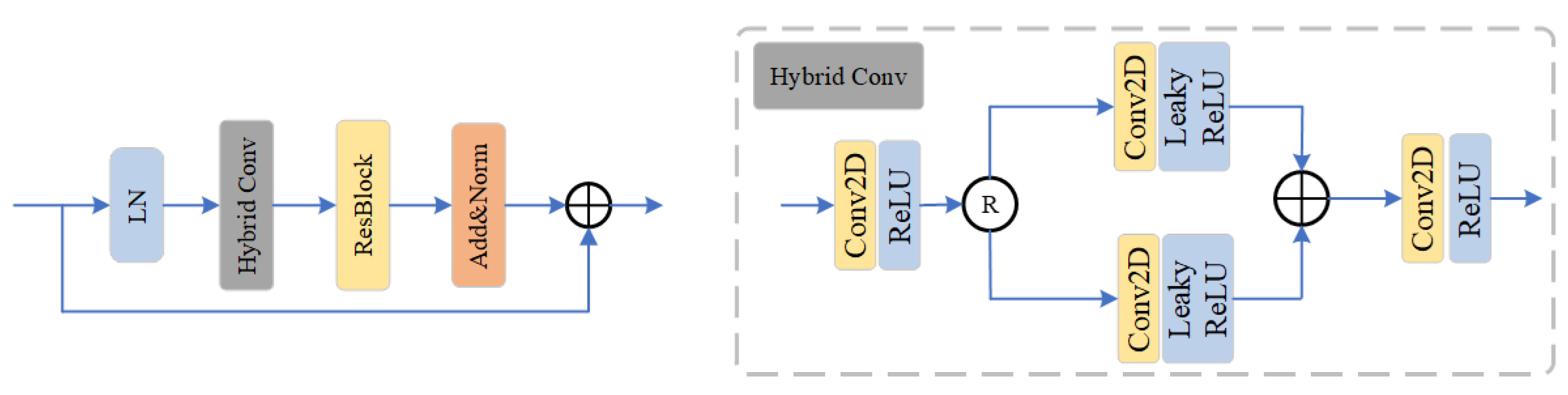
3.2. Blur Kernel Denoise Prior

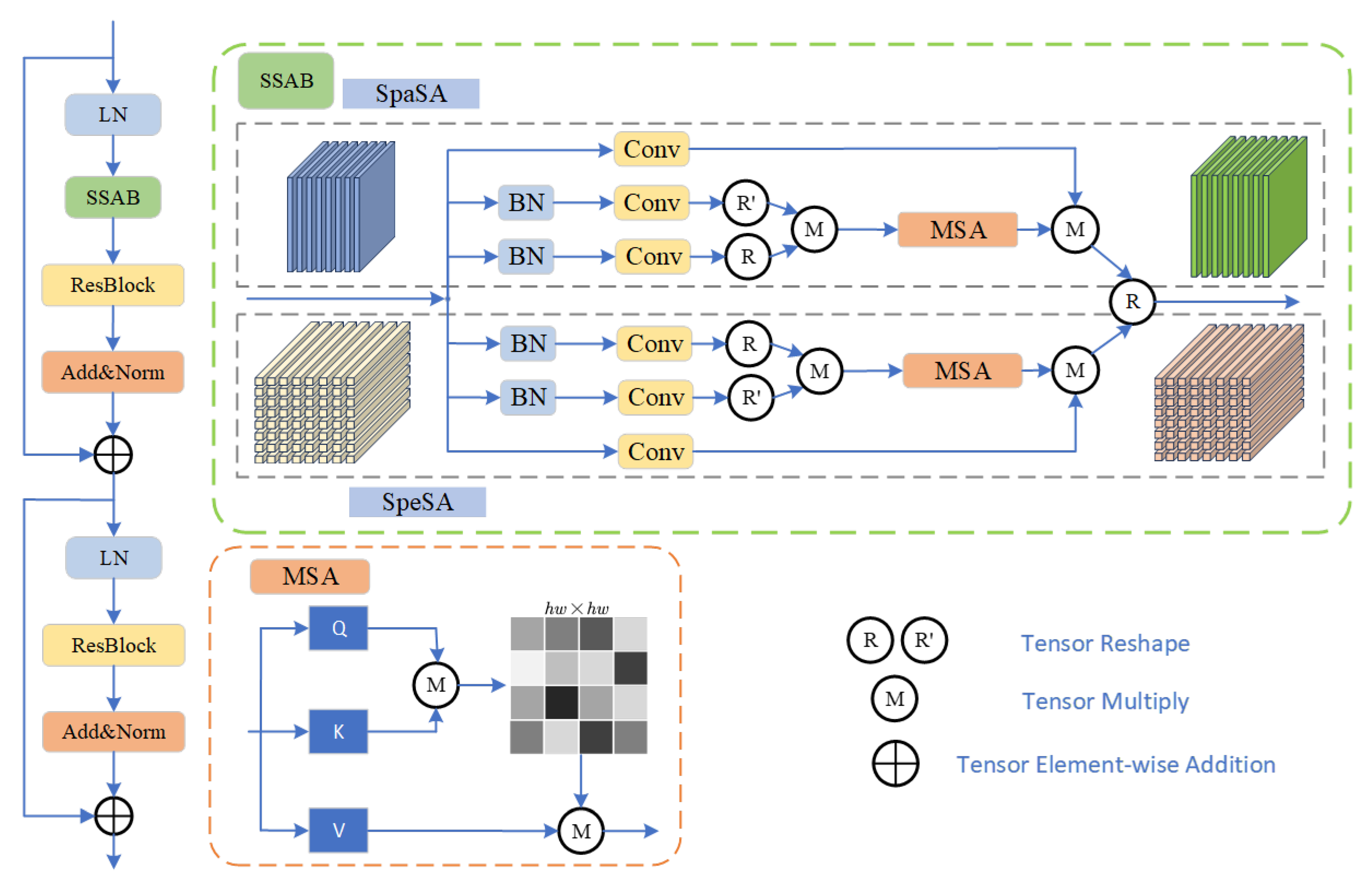
3.3. Spatial–Spectral Attention Feature Rebuild
3.4. Overall Loss Function
4. Results
4.1. Data Description
4.1.1. Cave Dataset
4.1.2. Pavia University Dataset
4.1.3. Chikusei Dataset
4.1.4. XiongAn Dataset
4.2. Evaluation Metrics
4.2.1. Spectral Angle Mapping (SAM)
4.2.2. Root-Mean-Square Error (RMSE)
4.2.3. Peak Signal-to-Noise Ratio (PSNR)
4.2.4. Structural Similarity Index (SSIM)
4.2.5. Erreur Relative Globale Adimensionnelle de Synthèse (ERGAS)
4.2.6. Cross-Correlation (CC)
4.2.7. Model Scale
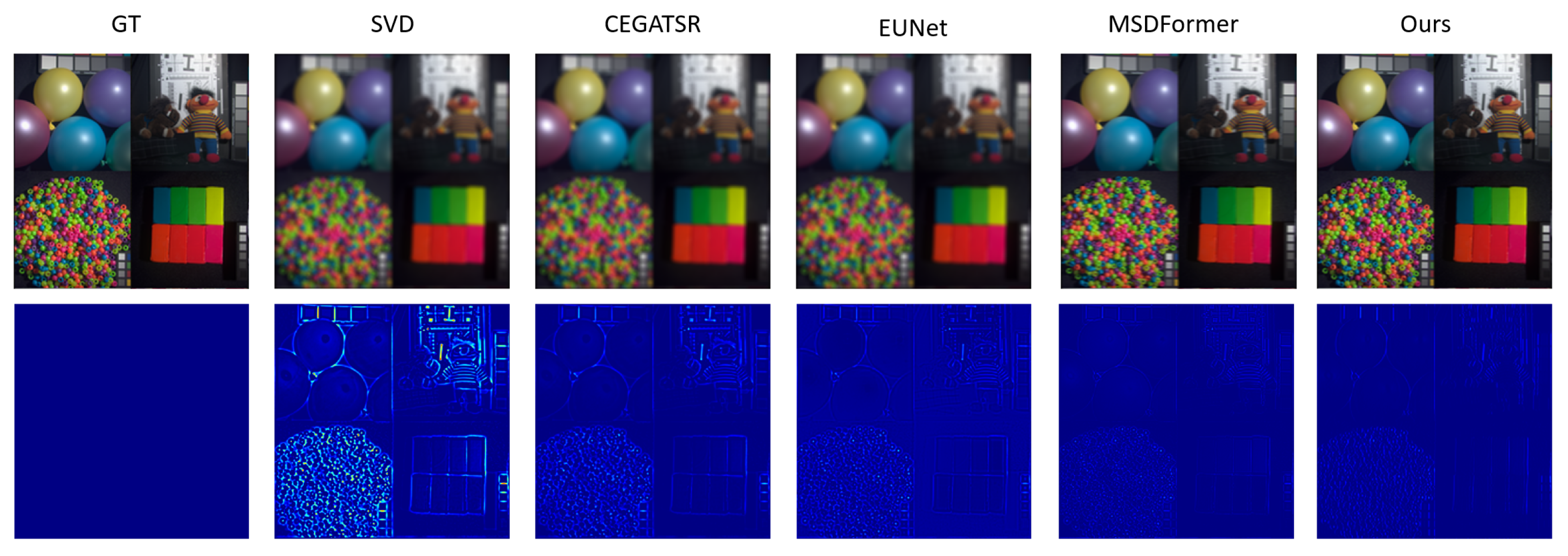
4.3. Comparison with State-of-the-Art HSIs Reconstruction Method
4.3.1. Experiments on the Cave Dataset
4.3.2. Experiments on the Pavia University Dataset
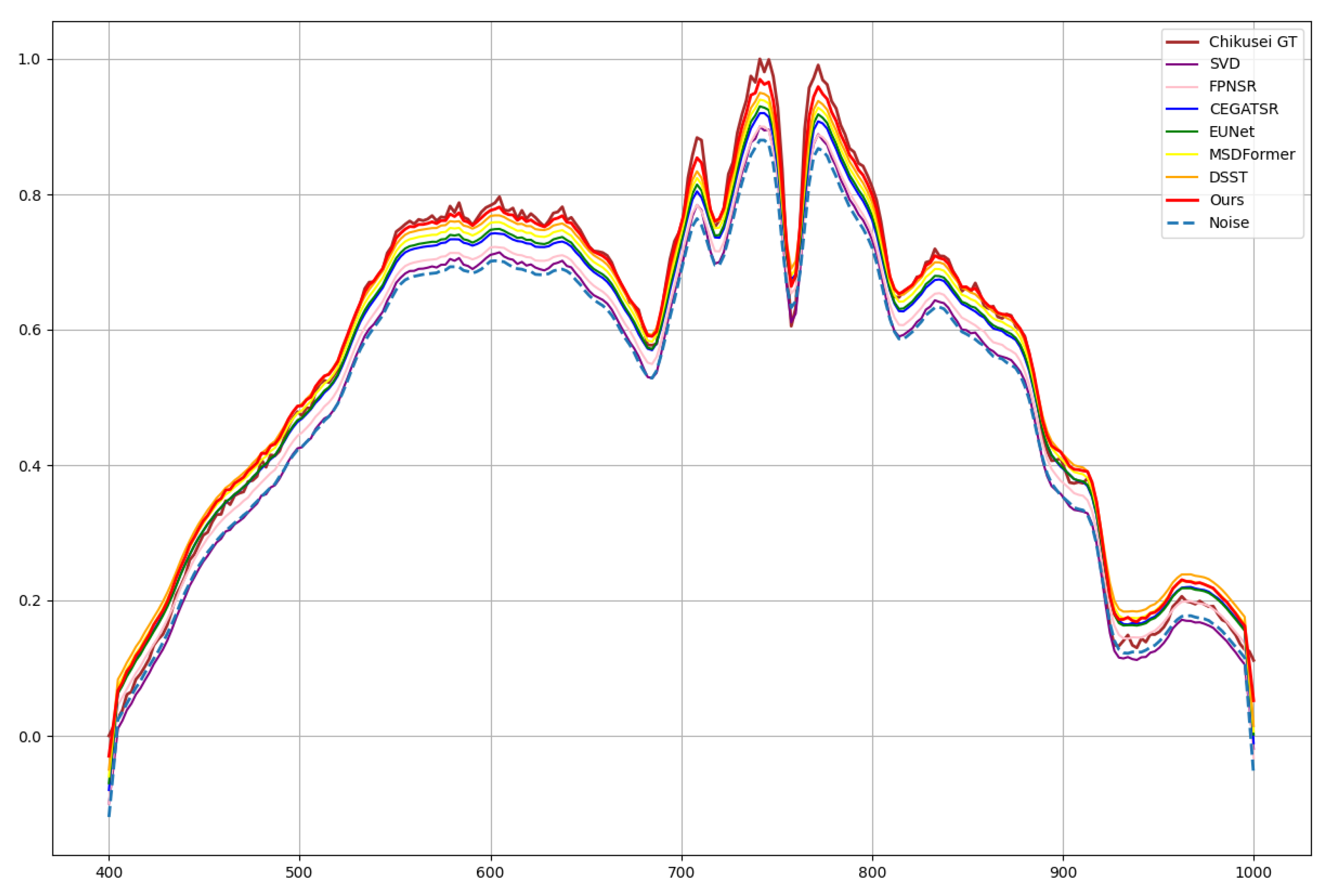
4.3.3. Experiments on the Chikusei Dataset
4.3.4. Comprehensive Evaluation in the XiongAn Database
5. Discussion
5.1. Comparison of Robustness Performance of Different Models at a More Subdivided Noise Scale
5.2. Effectiveness of the Grouping Strategy
5.3. Effectiveness of the BKP Block
5.4. Effectiveness of Spatial and Spectral Attention
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tejasree, G.; Agilandeeswari, L. An extensive review of hyperspectral image classification and prediction: Techniques and challenges. Multimed. Tools Appl. 2024, 83, 80941–81038. [Google Scholar] [CrossRef]
- Nie, X.; Xue, Z.; Lin, C.; Zhang, L.; Su, H. Structure-prior-constrained low-rank and sparse representation with discriminative incremental dictionary for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5506319. [Google Scholar] [CrossRef]
- Shu, Z.; Wang, Y.; Yu, Z. Dual attention transformer network for hyperspectral image classification. Eng. Appl. Artif. Intell. 2024, 127, 107351. [Google Scholar] [CrossRef]
- Namburu, H.; Munipalli, V.N.; Vanga, M.; Pasam, M.; Sikhakolli, S.; Chinnadurai, S. Cholangiocarcinoma Classification using MedisawHSI: A Breakthrough in Medical Imaging. In Proceedings of the 2024 Second International Conference on Emerging Trends in Information Technology and Engineering (ICETITE), Vellore, India, 22–23 February 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Li, S.; Song, Q.; Liu, Y.; Zeng, T.; Liu, S.; Jie, D.; Wei, X. Hyperspectral imaging-based detection of soluble solids content of loquat from a small sample. Postharvest Biol. Technol. 2023, 204, 112454. [Google Scholar] [CrossRef]
- Gong, M.; Jiang, F.; Qin, A.K.; Liu, T.; Zhan, T.; Lu, D.; Zheng, H.; Zhang, M. A spectral and spatial attention network for change detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5521614. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Kalivas, D.P.; Georgopoulou, I.A.; Srivastava, P.K. Urban vegetation cover extraction from hyperspectral imagery and geographic information system spatial analysis techniques: Case of Athens, Greece. J. Appl. Remote Sens. 2015, 9, 096088. [Google Scholar] [CrossRef]
- Zia, A.; Zhou, J.; Gao, Y. Exploring chromatic aberration and defocus blur for relative depth estimation from monocular hyperspectral image. IEEE Trans. Image Process. 2021, 30, 4357–4370. [Google Scholar] [CrossRef]
- Geladi, P.; Burger, J.; Lestander, T. Hyperspectral imaging: Calibration problems and solutions. Chemom. Intell. Lab. Syst. 2004, 72, 209–217. [Google Scholar] [CrossRef]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Jia, J.; Zheng, X.; Guo, S.; Wang, Y.; Chen, J. Removing stripe noise based on improved statistics for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2020, 19, 5501405. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- He, H.; Cao, M.; Gao, Y. Noise learning of instruments for high-contrast, high-resolution and fast hyperspectral microscopy and nanoscopy. Nat. Commun. 2024, 15, 754. [Google Scholar] [CrossRef]
- Jiang, T.X.; Zhuang, L.; Huang, T.Z. Adaptive hyperspectral mixed noise removal. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Peng, J.; Sun, W.; Li, H.C.; Li, W.; Meng, X.; Ge, C.; Du, Q. Low-rank and sparse representation for hyperspectral image processing: A review. IEEE Geosci. Remote Sens. Mag. 2021, 10, 10–43. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, C.; Zhang, Y.; Liu, H. An efficient SVD-based method for image denoising. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 868–880. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Benediktsson, J.A. Hyperspectral mixed Gaussian and sparse noise reduction. IEEE Geosci. Remote Sens. Lett. 2019, 17, 474–478. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Hyperspectral image classification using Gaussian mixture models and Markov random fields. IEEE Geosci. Remote Sens. Lett. 2013, 11, 153–157. [Google Scholar] [CrossRef]
- Wang, X.; Hu, Q.; Cheng, Y.; Ma, J. Hyperspectral image super-resolution meets deep learning: A survey and perspective. IEEE/CAA J. Autom. Sin. 2023, 10, 1668–1691. [Google Scholar] [CrossRef]
- Han, X.H.; Shi, B.; Zheng, Y. SSF-CNN: Spatial and spectral fusion with CNN for hyperspectral image super-resolution. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 2506–2510. [Google Scholar] [CrossRef]
- Wang, L.; Bi, T.; Shi, Y. A frequency-separated 3D-CNN for hyperspectral image super-resolution. IEEE Access 2020, 8, 86367–86379. [Google Scholar] [CrossRef]
- Arun, P.V.; Buddhiraju, K.M.; Porwal, A.; Chanussot, J. CNN-based super-resolution of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6106–6121. [Google Scholar] [CrossRef]
- Dixit, A.; Gupta, A.K.; Gupta, P.; Srivastava, S.; Garg, A. UNFOLD: 3D U-Net, 3D CNN and 3D transformer based hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5529710. [Google Scholar] [CrossRef]
- Wang, Z.; Ng, M.K.; Zhuang, L.; Gao, L.; Zhang, B. Nonlocal self-similarity-based hyperspectral remote sensing image denoising with 3-D convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531617. [Google Scholar] [CrossRef]
- Hou, R.; Li, F. Hyperspectral image denoising via cooperated self-supervised CNN transform and nonconvex regularization. Neurocomputing 2024, 616, 128912. [Google Scholar] [CrossRef]
- Shi, H.; Cao, G.; Zhang, Y.; Ge, Z.; Liu, Y.; Fu, P. H2A2 Net: A hybrid convolution and hybrid resolution network with double attention for hyperspectral image classification. Remote Sens. 2022, 14, 4235. [Google Scholar] [CrossRef]
- Galassi, A.; Lippi, M.; Torroni, P. Attention in natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4291–4308. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Zhang, D.; Zhou, F. Self-supervised image denoising for real-world images with context-aware transformer. IEEE Access 2023, 11, 14340–14349. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhai, D.; Jiang, J.; Liu, X. ADRN: Attention-based deep residual network for hyperspectral image denoising. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 2668–2672. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, L.; Zhang, L. Msdformer: Multi-scale deformable transformer for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5525614. [Google Scholar] [CrossRef]
- Yang, J.; Lin, T.; Liu, F.; Xiao, L. Learning degradation-aware deep prior for hyperspectral image reconstruction. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5531515. [Google Scholar] [CrossRef]
- Zhuang, L.; Ng, M.K.; Gao, L.; Michalski, J.; Wang, Z. Eigenimage2Eigenimage (E2E): A self-supervised deep learning network for hyperspectral image denoising. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 16262–16276. [Google Scholar] [CrossRef]
- Geng, P.; Zhang, M.; Li, X. Hyperspectral image deblurring based on joint utilization of spatial-spectral information. In Proceedings of the 2023 16th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 16–17 December 2023; pp. 156–160. [Google Scholar] [CrossRef]
- Fan, H.; Li, C.; Guo, Y.; Kuang, G.; Ma, J. Spatial–Spectral Total Variation Regularized Low-Rank Tensor Decomposition for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6196–6213. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2015, 54, 178–188. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y.; Yuan, Q.; Song, M.; Yu, H.; Xiao, Y. Hyperspectral image denoising: From model-driven, data-driven, to model-data-driven. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 13143–13163. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhang, X.; Guo, P. Expected patch log likelihood with a prior of mixture of matrix normal distributions for image denoising. In Proceedings of the 2018 Ninth International Conference on Intelligent Control and Information Processing (ICICIP), Wanzhou, China, 9–11 November 2018; pp. 344–348. [Google Scholar] [CrossRef]
- Mildenhall, B.; Barron, J.T.; Chen, J.; Sharlet, D.; Ng, R.; Carroll, R. Burst denoising with kernel prediction networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2502–2510. [Google Scholar] [CrossRef]
- Cai, J.; Zuo, W.; Zhang, L. Dark and bright channel prior embedded network for dynamic scene deblurring. IEEE Trans. Image Process. 2020, 29, 6885–6897. [Google Scholar] [CrossRef]
- Xia, Z.; Perazzi, F.; Gharbi, M.; Sunkavalli, K.; Chakrabarti, A. Basis Prediction Networks for Effective Burst Denoising with Large Kernels. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11841–11850. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, J.; Kang, X.; Luo, J.; Fan, S. Interactformer: Interactive transformer and CNN for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531715. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Y.; Kang, X.; Fan, S. Multilevel progressive network with nonlocal channel attention for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5543714. [Google Scholar] [CrossRef]
- Jiang, J.; Sun, H.; Liu, X.; Ma, J. Learning spatial-spectral prior for super-resolution of hyperspectral imagery. IEEE Trans. Comput. Imaging 2020, 6, 1082–1096. [Google Scholar] [CrossRef]
- Liu, D.; Li, J.; Yuan, Q.; Zheng, L.; He, J.; Zhao, S.; Xiao, Y. An efficient unfolding network with disentangled spatial-spectral representation for hyperspectral image super-resolution. Inf. Fusion 2023, 94, 92–111. [Google Scholar] [CrossRef]
- Cordonnier, J.B.; Loukas, A.; Jaggi, M. Multi-head attention: Collaborate instead of concatenate. arXiv 2020, arXiv:2006.16362. [Google Scholar] [CrossRef]
- Hu, M.; Wu, C.; Zhang, L. GlobalMind: Global multi-head interactive self-attention network for hyperspectral change detection. ISPRS J. Photogramm. Remote Sens. 2024, 211, 465–483. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Sun, H.; Zhong, Z.; Zhai, D.; Liu, X.; Jiang, J. Hyperspectral image super-resolution using multi-scale feature pyramid network. In Proceedings of the Digital TV and Wireless Multimedia Communication: 16th International Forum, IFTC 2019, Shanghai, China, 19–20 September 2019; Revised Selected Papers 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 49–61. [Google Scholar] [CrossRef]
- Liu, C.; Dong, Y. CNN-Enhanced graph attention network for hyperspectral image super-resolution using non-local self-similarity. Int. J. Remote Sens. 2022, 43, 4810–4835. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized assorted pixel camera: Postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhang, L. A comparative study of spatial approaches for urban mapping using hyperspectral ROSIS images over Pavia City, northern Italy. Int. J. Remote Sens. 2009, 30, 3205–3221. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Airborne Hyperspectral Data over Chikusei; SAL-2016-5-27; The University of Tokyo: Tokyo, Japan, 2016. [Google Scholar]
- Sohn, Y.; Rebello, N.S. Supervised and unsupervised spectral angle classifiers. Photogramm. Eng. Remote Sens. 2002, 68, 1271–1282. [Google Scholar] [CrossRef]
- Renza, D.; Martinez, E.; Arquero, A. A new approach to change detection in multispectral images by means of ERGAS index. IEEE Geosci. Remote Sens. Lett. 2012, 10, 76–80. [Google Scholar] [CrossRef]
- Lei, J.; Liu, P.; Xie, W.; Gao, L.; Li, Y.; Du, Q. Spatial–spectral cross-correlation embedded dual-transfer network for object tracking using hyperspectral videos. Remote Sens. 2022, 14, 3512. [Google Scholar] [CrossRef]
- Sun, H.; Wang, L.; Zhang, L.; Gao, L. Hyperbolic space-based autoencoder for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5522115. [Google Scholar] [CrossRef]






| Method | Noise SNR | PSNR↑ | SSIM↑ | SAM↓ | CC↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|---|---|
| SVD | 41.0335 | 0.9126 | 3.8944 | 0.9025 | 0.0308 | 5.3216 | |
| FPNSR | 42.6521 | 0.9207 | 3.6567 | 0.9212 | 0.0238 | 3.1894 | |
| CEGATSR | 45.6018 | 0.9265 | 3.1517 | 0.9304 | 0.0201 | 2.5681 | |
| EUNet | 40 dB | 47.0216 | 0.9480 | 2.8912 | 0.9411 | 0.0156 | 1.9260 |
| MSDformer | 48.0500 | 0.9610 | 2.2365 | 0.9698 | 0.0102 | 1.5724 | |
| DSST | 48.3570 | 0.9660 | 2.0951 | 0.9661 | 0.0098 | 1.5654 | |
| Ours | 49.5379 | 0.9701 | 2.0015 | 0.9764 | 0.0071 | 1.3256 | |
| SVD | 32.5610 | 0.9027 | 3.8691 | 0.8712 | 0.0575 | 4.2561 | |
| FPNSR | 35.4107 | 0.9100 | 3.3568 | 0.8998 | 0.0452 | 3.9430 | |
| CEGATSR | 35.7075 | 0.9271 | 3.0176 | 0.9008 | 0.0399 | 3.6508 | |
| EUNet | 30 dB | 36.5417 | 0.9365 | 2.9315 | 0.9106 | 0.0368 | 3.2654 |
| MSDformer | 40.2125 | 0.9459 | 2.7776 | 0.9170 | 0.0304 | 2.9969 | |
| DSST | 39.8931 | 0.9441 | 3.0014 | 0.9246 | 0.0347 | 2.8469 | |
| Ours | 41.0015 | 0.9503 | 2.8958 | 0.9321 | 0.0211 | 2.3673 | |
| SVD | 31.2659 | 0.8164 | 5.0918 | 0.8565 | 0.0899 | 7.7517 | |
| FPNSR | 33.0023 | 0.8801 | 4.2019 | 0.8797 | 0.0765 | 6.6162 | |
| CEGATSR | 33.3654 | 0.8834 | 4.0025 | 0.8865 | 0.0715 | 5.5681 | |
| EUNet | 20 dB | 34.2611 | 0.9068 | 3.9897 | 0.8944 | 0.0560 | 5.0007 |
| MSDformer | 35.5610 | 0.9227 | 3.6613 | 0.9017 | 0.0454 | 4.2526 | |
| DSST | 36.0021 | 0.9296 | 3.3218 | 0.9065 | 0.0488 | 4.0524 | |
| Ours | 37.0147 | 0.9403 | 3.1994 | 0.9169 | 0.0450 | 3.9367 |
| Method | Noise SNR | PSNR↑ | SSIM↑ | SAM↓ | CC↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|---|---|
| SVD | 32.6901 | 0.9210 | 4.5464 | 0.9201 | 0.0509 | 3.9651 | |
| FPNSR | 33.6158 | 0.9377 | 4.0107 | 0.9447 | 0.0452 | 3.2654 | |
| CEGATSR | 34.4504 | 0.9405 | 3.9790 | 0.9564 | 0.0401 | 3.1145 | |
| EUNet | 40 dB | 35.1123 | 0.9499 | 3.7984 | 0.9650 | 0.0347 | 2.9897 |
| MSDformer | 35.8185 | 0.9511 | 3.6139 | 0.9744 | 0.0266 | 2.7710 | |
| DSST | 35.6089 | 0.9597 | 3.5612 | 0.9781 | 0.0264 | 2.7798 | |
| Ours | 36.0061 | 0.9602 | 3.5721 | 0.9790 | 0.0254 | 2.6066 | |
| SVD | 24.6511 | 0.7677 | 5.2315 | 0.8210 | 0.0552 | 7.0056 | |
| FPNSR | 25.4101 | 0.7758 | 4.9890 | 0.8526 | 0.0508 | 6.8709 | |
| CEGATSR | 26.5140 | 0.7912 | 4.9208 | 0.8670 | 0.0432 | 6.6511 | |
| EUNet | 30 dB | 26.5964 | 0.7829 | 4.9085 | 0.8794 | 0.0401 | 6.1625 |
| MSDformer | 28.7894 | 0.8020 | 4.7797 | 0.8907 | 0.0379 | 5.9773 | |
| DSST | 28.8975 | 0.8089 | 4.5120 | 0.8991 | 0.0397 | 5.7171 | |
| Ours | 29.0017 | 0.8207 | 4.1711 | 0.9024 | 0.0335 | 5.4107 | |
| SVD | 20.6841 | 0.6615 | 7.7978 | 0.7200 | 0.0779 | 9.9841 | |
| FPNSR | 21.0564 | 0.6879 | 7.5009 | 0.7602 | 0.0705 | 9.6759 | |
| CEGATSR | 21.6548 | 0.6977 | 7.2154 | 0.7877 | 0.0674 | 9.1555 | |
| EUNet | 20 dB | 21.8904 | 0.6954 | 7.0256 | 0.7889 | 0.0646 | 9.1606 |
| MSDformer | 22.6424 | 0.7069 | 6.6706 | 0.8001 | 0.0608 | 8.3564 | |
| DSST | 23.1212 | 0.7102 | 6.5132 | 0.8115 | 0.0598 | 8.2356 | |
| Ours | 23.5617 | 0.7256 | 6.0799 | 0.8210 | 0.0501 | 8.1979 |
| Method | Noise SNR | PSNR↑ | SSIM↑ | SAM↓ | CC↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|---|---|
| SVD | 40.2125 | 0.9021 | 1.8880 | 0.9311 | 0.0399 | 6.5613 | |
| FPNSR | 41.9690 | 0.9125 | 1.6510 | 0.9545 | 0.0213 | 5.6556 | |
| CEGATSR | 41.3915 | 0.9360 | 1.2665 | 0.9601 | 0.0117 | 4.9001 | |
| EUNet | 40 dB | 42.8070 | 00.9290 | 1.6105 | 0.9726 | 0.0208 | 4.6324 |
| MSDformer | 47.2824 | 0.9722 | 1.1498 | 0.9800 | 0.0129 | 2.4315 | |
| DSST | 47.5658 | 0.9801 | 1.2056 | 0.9811 | 0.0102 | 2.3001 | |
| Ours | 48.5601 | 0.9821 | 1.1257 | 0.9852 | 0.0097 | 2.1871 | |
| SVD | 30.2501 | 0.8871 | 2.9251 | 0.8210 | 0.0454 | 10.0235 | |
| FPNSR | 32.0024 | 0.9015 | 2.8864 | 0.8599 | 0.0421 | 9.5001 | |
| CEGATSR | 33.3871 | 0.9295 | 2.2665 | 0.8479 | 0.0397 | 8.9802 | |
| EUNet | 30 dB | 32.9207 | 0.9034 | 2.4098 | 0.8325 | 0.0315 | 9.1060 |
| MSDformer | 35.0911 | 0.9310 | 2.2914 | 0.8534 | 0.0256 | 8.9203 | |
| DSST | 36.0091 | 0.9541 | 2.6050 | 0.8736 | 0.0212 | 8.7215 | |
| Ours | 38.6061 | 0.9544 | 2.7281 | 0.8834 | 0.0201 | 7.9957 | |
| SVD | 22.5640 | 0.8012 | 5.4689 | 0.7921 | 0.0932 | 12.0309 | |
| FPNSR | 24.0545 | 0.8211 | 4.6507 | 0.8172 | 0.0804 | 11.8907 | |
| CEGATSR | 25.6849 | 0.8263 | 4.4190 | 0.8410 | 0.0826 | 11.5119 | |
| EUNet | 20 dB | 24.9102 | 0.8362 | 4.5023 | 0.8349 | 0.0751 | 11.0029 |
| MSDformer | 25.5914 | 0.8402 | 4.2531 | 0.8563 | 0.0699 | 10.5203 | |
| DSST | 25.9014 | 0.8415 | 4.1989 | 0.8623 | 0.0665 | 10.4911 | |
| Ours | 28.0651 | 0.8521 | 4.7215 | 0.8590 | 0.0601 | 10.0718 |
| FPNSR | CEGATSR | EUNet | MSDformer | DDST | Ours | ||
|---|---|---|---|---|---|---|---|
| Parameters | 4.42 M | 13.55 M | 12.83 M | 14.90 M | 20.65 M | 12.77 M | |
| FLOPs | 5.762 G | 29.925 G | 16.613 G | 53.915 G | 59.34 G | 38.89 G | |
| PSNR↑ | 33.1614 | 34.0316 | 34.9877 | 35.0235 | 35.6724 | 36.9011 | |
| SSIM↑ | 0.9001 | 0.9102 | 0.9125 | 0.9271 | 0.9235 | 0.9460 | |
| SAM↓ | 3.5652 | 3.4540 | 3.1654 | 3.1027 | 3.0562 | 2.8965 | |
| CC↑ | 0.8985 | 0.9022 | 9.9075 | 0.9108 | 0.9156 | 0.9279 | |
| RMSE↓ | 0.0204 | 0.0299 | 0.0285 | 0.0256 | 0.0244 | 0.0217 | |
| ERGAS↓ | 5.4510 | 5.3021 | 5.3654 | 5.2347 | 5.2194 | 5.2024 | |
| Variant | Params/FLOPs | PSNR↑ | SSIM↑ | SAM↓ | RMSE↓ |
|---|---|---|---|---|---|
| w/o Groups | 8.48 M/26.77 G | 30.0291 | 0.8671 | 3.5689 | 0.0588 |
| w/o AE | 5.56 M/15.02 G | 30.2401 | 0.8823 | 4.0905 | 0.0627 |
| w/o SA1 | 7.81 M/18.65 G | 31.5689 | 0.8564 | 3.6580 | 0.0460 |
| w/o SA2 | 5.56 M/16.52 G | 30.6522 | 0.9088 | 2.6512 | 0.0362 |
| Ours | 12.77 M/38.89 G | 35.0911 | 0.9310 | 2.2914 | 0.0256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.; Yang, M.; Huang, H.; Zhang, M.; Zhang, W.; Jiao, Q.; Xu, L.; Tan, X. Hyperspectral Image Reconstruction Based on Blur–Kernel–Prior and Spatial–Spectral Attention. Remote Sens. 2025, 17, 1401. https://doi.org/10.3390/rs17081401
Xie H, Yang M, Huang H, Zhang M, Zhang W, Jiao Q, Xu L, Tan X. Hyperspectral Image Reconstruction Based on Blur–Kernel–Prior and Spatial–Spectral Attention. Remote Sensing. 2025; 17(8):1401. https://doi.org/10.3390/rs17081401
Chicago/Turabian StyleXie, Hongyu, Mingyu Yang, Huansong Huang, Mingle Zhang, Wei Zhang, Qingbin Jiao, Liang Xu, and Xin Tan. 2025. "Hyperspectral Image Reconstruction Based on Blur–Kernel–Prior and Spatial–Spectral Attention" Remote Sensing 17, no. 8: 1401. https://doi.org/10.3390/rs17081401
APA StyleXie, H., Yang, M., Huang, H., Zhang, M., Zhang, W., Jiao, Q., Xu, L., & Tan, X. (2025). Hyperspectral Image Reconstruction Based on Blur–Kernel–Prior and Spatial–Spectral Attention. Remote Sensing, 17(8), 1401. https://doi.org/10.3390/rs17081401






