Orbital Design Optimization for Large-Scale SAR Constellations: A Hybrid Framework Integrating Fuzzy Rules and Chaotic Sequences
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Related Works
1.3. Contributions
- Hybrid optimization framework with chaos and fuzzy logic: We propose a novel hybrid framework that synergizes chaotic sequence initialization and fuzzy rule-based decision mechanisms to address high-dimensional SAR constellation optimization. The chaotic mapping ensures uniform initial population distribution, mitigating premature convergence, while the fuzzy logic system dynamically adapts crossover strategies based on real-time population diversity, fitness gaps, and convergence trends. This integration enhances both global exploration capabilities and convergence efficiency, addressing the limitations of traditional genetic algorithms in handling complex multi-modal search spaces.
- Multi-objective optimization model with normalized weighting: A comprehensive multi-objective optimization model was developed to balance competing requirements, including revisit time, SAR performance, coverage range, and cost-effectiveness. By integrating a normalized weighted objective function, the model resolves scale discrepancies among heterogeneous metrics (e.g., spatial coverage in square kilometers vs. cost in monetary units). This unified framework enables systematic trade-off analysis and provides a standardized benchmark for evaluating constellation configurations under diverse mission priorities.
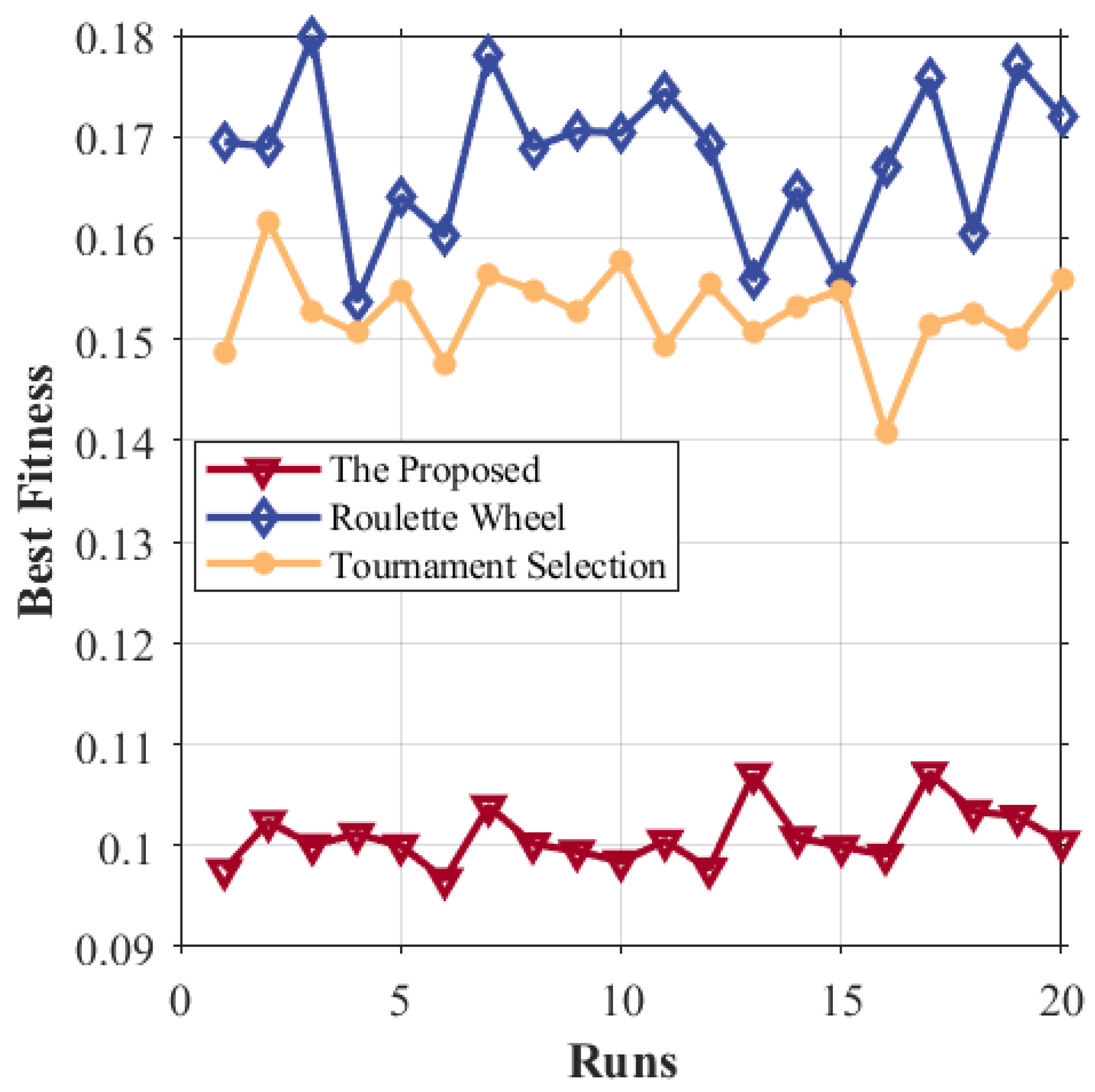
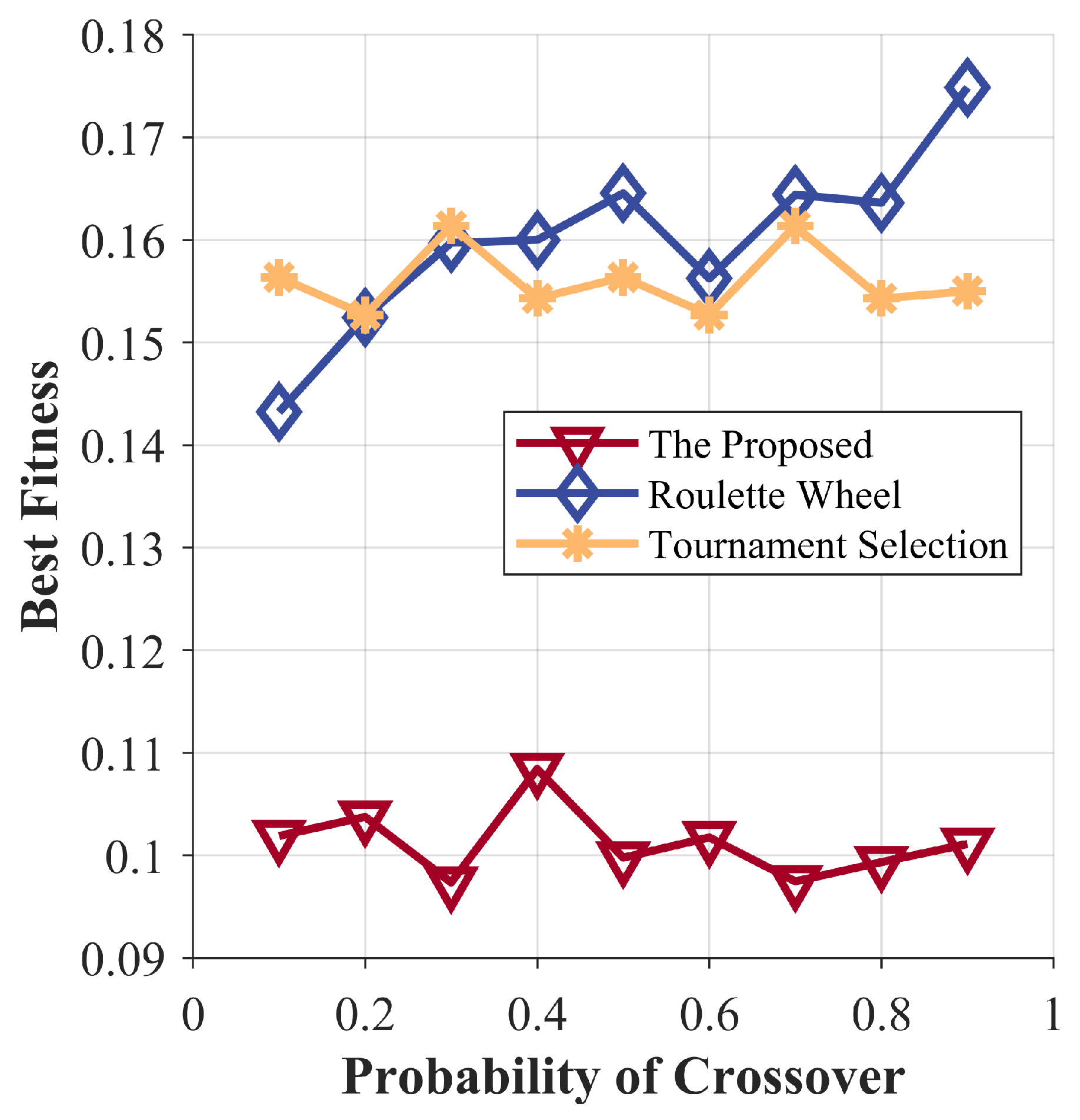
- Fuzzy-adaptive crossover strategy with dynamic parameter control: A fuzzy logic-guided crossover strategy was designed to autonomously adjust crossover patterns and intensities during evolutionary processes. By monitoring real-time metrics (e.g., population diversity index and fitness variance), the strategy adaptively balances exploration and exploitation, aggressively exploring new solutions in low-diversity scenarios while refining high-quality candidates in convergent phases. The experimental results demonstrate that this approach achieves a 40.47% improvement in average fitness over roulette wheel selection and 35.48% over tournament selection, with enhanced robustness across parameter variations.
1.4. Organization
2. Problem Formulation
2.1. Optimization Goals
2.1.1. Revisiting the Period Objective Function
2.1.2. SAR System Payload Capability Objective Function
2.1.3. Cost Objective Function
2.1.4. Coverage Function
2.1.5. Establishing a Comprehensive Objective Function
2.2. Decision Variables
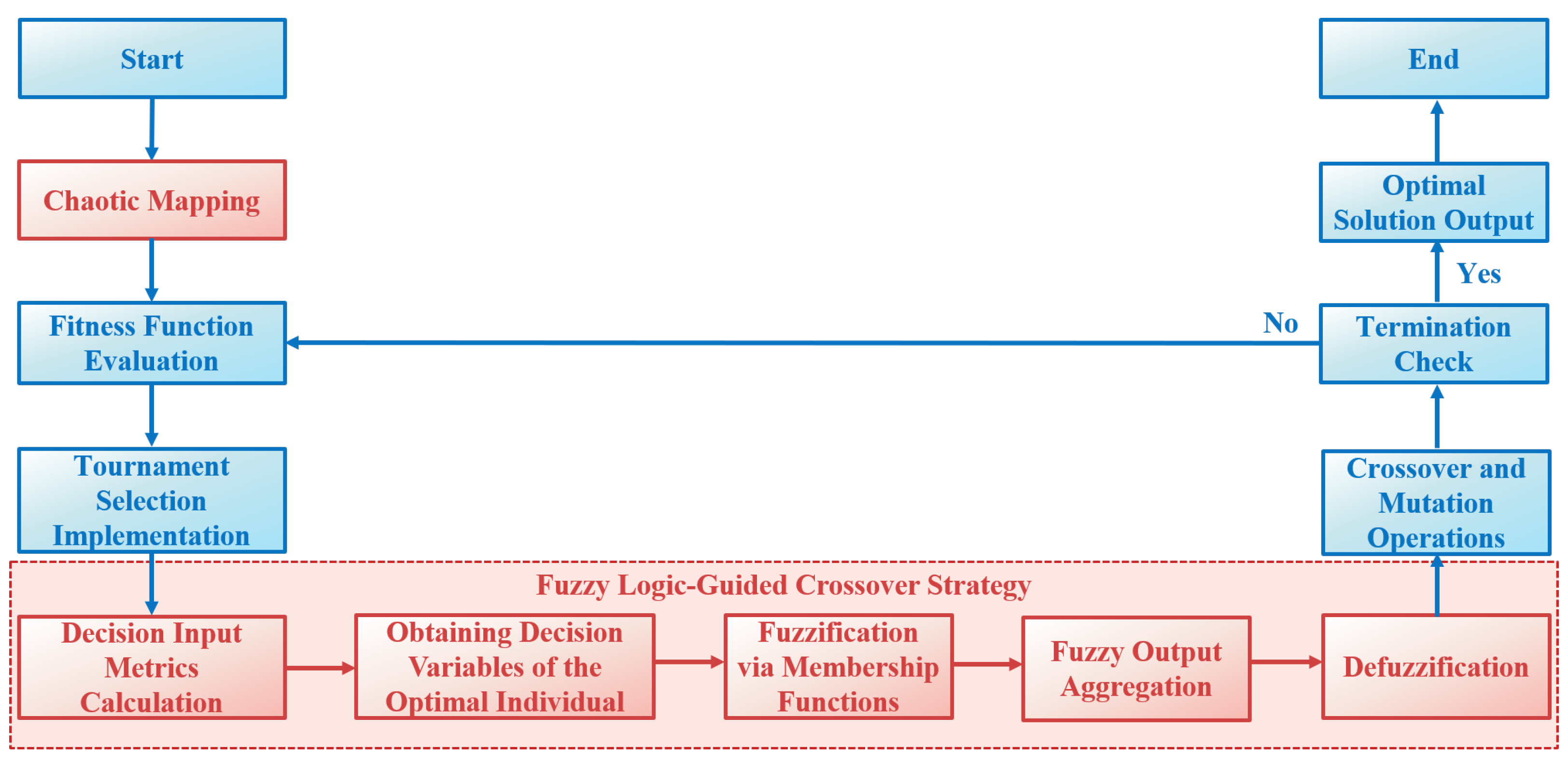
3. The Proposed Method
3.1. Step 1: Initial Population Generation via Chaotic Mapping
3.2. Step 2: Fitness Evaluation for All Individuals in the Population
3.3. Step 3: Tournament Selection Based on Fitness Evaluation Results
- It mitigates premature convergence through stochastic selection pressure;
- It reduces sensitivity to fitness value variations by comparing local subsets;
- It balances exploitation and exploration more effectively in high-dimensional search spaces.
3.4. Step 4: Fuzzy Logic-Guided Crossover Strategy
3.4.1. Decision Input Metrics Calculation
- Population diversity (D): This is measured using the average Euclidean distance between individuals in the solution space;
- Fitness gap (G): Defined as the difference between the maximum and median fitness values in the population;
- Convergence speed (V): Calculated as the slope of the best fitness curve over the last generations.
3.4.2. Obtaining Decision Variables of the Current Optimal Individual
3.4.3. The Input Variables Are Fuzzified Using Predefined Membership Functions
- -
- Low: Indicates high similarity among individuals in the population, implying insufficient diversity;
- -
- Medium: Indicates that diversity is at a moderate level;
- -
- High: Indicates significant differences among individuals, implying rich diversity.
- -
- Low Altitude: Favors low cost but has a small coverage area;
- -
- Medium Altitude: Balances cost and coverage area;
- -
- High Altitude: Has a large coverage area but is costly.
3.4.4. Incorporating Fuzzified Results into Relevant Fuzzy Rules
3.4.5. Aggregate Fuzzy Outputs
3.4.6. Defuzzification
3.5. Step 5: Crossover and Mutation Operations
3.6. Step 6: Termination Check
4. Simulation Results
4.1. Simulation Settings
4.2. Monte Carlo Experiment Results
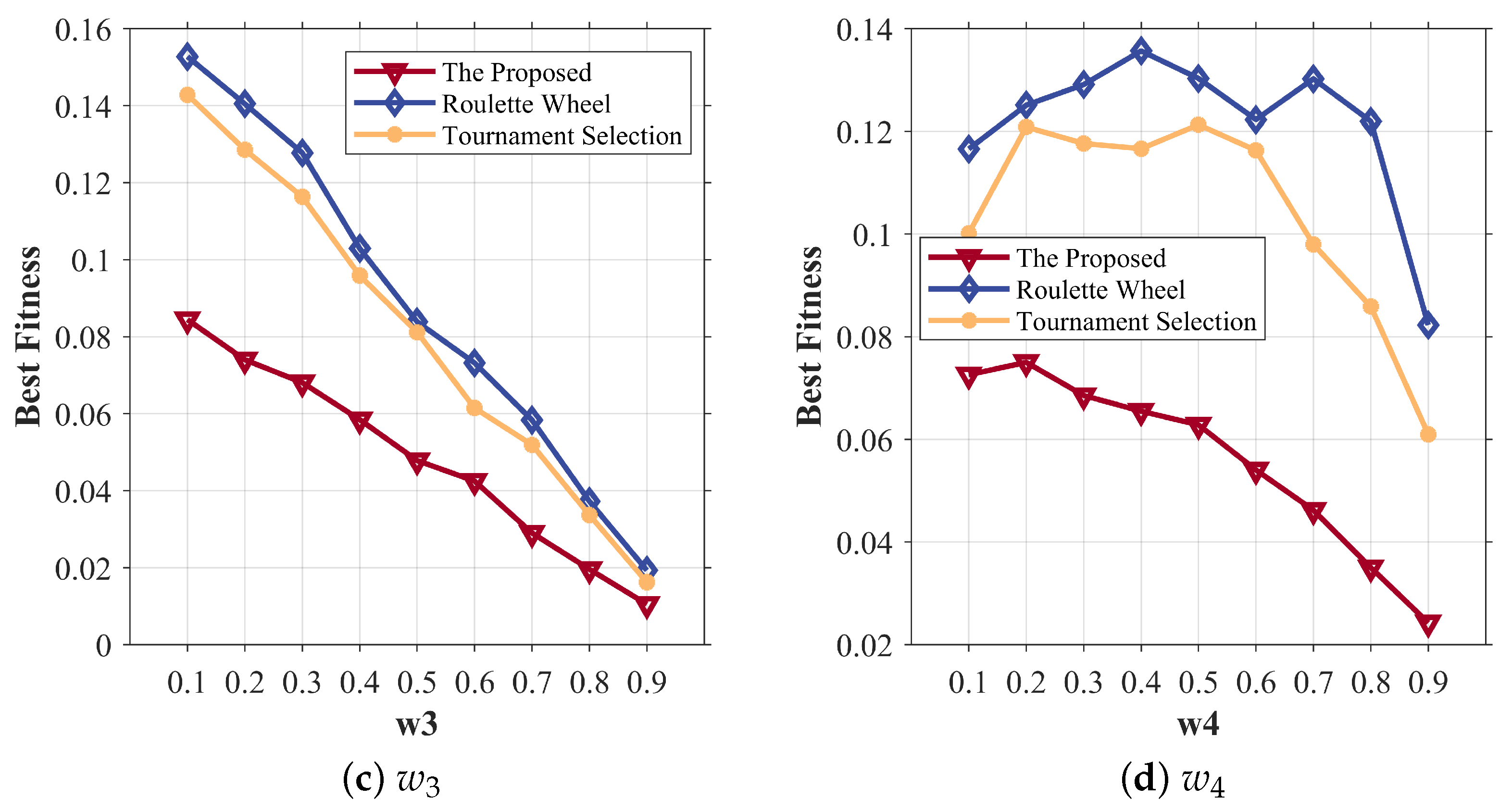
4.3. Parameter Sensitivity Analysis Results
4.4. Robustness Analysis Results
4.5. Time Complexity Analysis
- Fitness evaluation: Let denote the complexity of evaluating the fitness of a single individual. Given a population size of N, the total time complexity for fitness evaluation in one generation is .
- Crossover and mutation:
- −
- Crossover: For single-point or multi-point crossover, the computational complexity per individual is , where L is the chromosome length. The total complexity is: ;
- −
- Mutation: Similarly, bit-flip mutation has complexity , leading to a total complexity of .
- Fuzzy decision module:
- −
- Population diversity calculation: Diversity is calculated by traversing all individuals and extracting features, resulting in a complexity of ;
- −
- Fuzzy rule application: The number of triggered fuzzy rules depends on the dimensionality of the input variables. The complexity is , where rules denotes the number of fuzzy rules.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, Y.; Tang, S.; Chang, S.; Zhang, H.; Liu, D.; Wang, W. A novel scheme for range ambiguity suppression of spaceborne SAR based on underdetermined blind source separation. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–15. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An advanced scheme for range ambiguity suppression of spaceborne SAR based on blind source separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Wang, R.; Qiu, J.; Wang, W.; Zhao, Q.; Liu, D. An advanced echo separation scheme for space-time waveform-encoding SAR based on digital beamforming and blind source separation. Remote Sens. 2022, 14, 3585. [Google Scholar] [CrossRef]
- Liu, D.; Chang, S.; Deng, Y.; He, Z.; Wang, F.; Zhang, Z.; Han, C.; Yu, C. A novel spaceborne SAR constellation scheduling algorithm for sea surface moving target search tasks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 3715–3726. [Google Scholar] [CrossRef]
- Guan, T.; Chang, S.; Wang, C.; Jia, X. SAR Small Ship Detection Based on Enhanced YOLO Network. Remote Sens. 2025, 17, 839. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Zhang, X.; Zhou, Z.; Xiong, B.; Ji, K.; Kuang, G. Arbitrary-direction SAR ship detection method for multi-scale imbalance. IEEE Trans. Geosci. Remote Sens. 2025. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S.; Sun, Z.; Liu, C.; Sun, Y.; Ji, K.; Kuang, G. Cross-sensor SAR image target detection based on dynamic feature discrimination and center-aware calibration. IEEE Trans. Geosci. Remote Sens. 2025. [Google Scholar] [CrossRef]
- Bai, W.; Wang, G.; Huang, F.; Sun, Y.; Du, Q.; Xia, J.; Wang, X.; Meng, X.; Hu, P.; Yin, C.; et al. Review of Assimilating Spaceborne Global Navigation Satellite System Remote Sensing Data for Tropical Cyclone Forecasting. Remote Sens. 2025, 17, 118. [Google Scholar] [CrossRef]
- Chen, W.; Zhi, X.; Hu, J.; Yu, L.; Han, Q.; Zhang, W. Genetic Algorithm-Based Weighted Constraint Target Band Selection for Hyperspectral Target Detection. Remote Sens. 2025, 17, 673. [Google Scholar] [CrossRef]
- Ulybyshev, Y. Satellite constellation design for complex coverage. J. Spacecr. Rocket. 2008, 45, 843–849. [Google Scholar] [CrossRef]
- Ulybyshev, Y.P. Design of satellite constellations with continuous coverage on elliptic orbits of Molniya type. Cosm. Res. 2009, 47, 310–321. [Google Scholar] [CrossRef]
- Cinelli, M.; Ortore, E.; Laneve, G.; Circi, C. Geometrical approach for an optimal inter-satellite visibility. Astrodynamics 2021, 5, 237–248. [Google Scholar] [CrossRef]
- Kim, H.; Song, S.; Chang, Y.K. Design of SAR Satellite Constellation Configuration for ISR Mission. J. Korean Soc. Aeronaut. Space Sci. 2017, 45, 54–62. [Google Scholar] [CrossRef]
- Doody, S.; Cohen, M.; Monchieri, E.; Marquez-Martinez, J. SAR Constellation for Low Cost and Rapid Earth Monitoring. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1879–1881. [Google Scholar]
- Song, Z.; Chen, X.; Luo, X.; Wang, M.; Dai, G. Multi-objective optimization of agile satellite orbit design. Adv. Space Res. 2018, 62, 3053–3064. [Google Scholar] [CrossRef]
- Jiang, Q.; Zheng, L.; Zhou, Y.; Liu, H.; Kong, Q.; Zhang, Y.; Chen, B. Efficient On-Orbit Remote Sensing Imagery Processing via Satellite Edge Computing Resource Scheduling Optimization. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1000519. [Google Scholar] [CrossRef]
- Xue, W.; Hu, M.; Ruan, Y.; Wang, X.; Yu, M. Research on Design and Staged Deployment of LEO Navigation Constellation for MEO Navigation Satellite Failure. Remote Sens. 2024, 16, 3667. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, X.; Wu, C.; Fan, G.; Li, M.; Xu, T.; Zhao, X. Multi-Layer LEO Constellation Optimization Based on D-NSDE Algorithm. Remote Sens. 2025, 17, 994. [Google Scholar] [CrossRef]
- Tang, C.; Ding, J.; Zhang, L. Leo satellite downlink distributed jamming optimization method using a non-dominated sorting genetic algorithm. Remote Sens. 2024, 16, 1006. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.Y.; Kim, J.; Ka, M.H.; Song, Y. Mission design and orbit-attitude control algorithms development of multistatic sar satellites for very-high-resolution stripmap imaging. Aerospace 2022, 10, 33. [Google Scholar] [CrossRef]
- Chen, J.; Chen, S.; Fu, R.; Wang, C.; Li, D.; Peng, Y.; Wang, L.; Jiang, H.; Zheng, Q. Remote sensing estimation of chlorophyll-A in case-II waters of coastal areas: Three-band model versus genetic algorithm–artificial neural networks model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3640–3658. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Metwaly, M.M.; Metwalli, M.R.; AbdelRahman, M.A.; Badreldin, N. Integrating active and passive remote sensing data for mapping soil salinity using machine learning and feature selection approaches in arid regions. Remote Sens. 2023, 15, 1751. [Google Scholar] [CrossRef]
- Melaku, S.D.; Kim, H.D. Optimization of multi-mission CubeSat constellations with a multi-objective genetic algorithm. Remote Sens. 2023, 15, 1572. [Google Scholar] [CrossRef]
- Meziane-Tani, I.; Métris, G.; Lion, G.; Deschamps, A.; Bendimerad, F.T.; Bekhti, M. Optimization of small satellite constellation design for continuous mutual regional coverage with multi-objective genetic algorithm. Int. J. Comput. Intell. Syst. 2016, 9, 627–637. [Google Scholar] [CrossRef]
- Guan, Y.; Liu, H.; Liu, T.; Wang, J. Optimal configuration design of regional observation heterogeneous satellite constellation based on multi-objective genetic algorithm. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 5740–5747. [Google Scholar]
- Paek, S.W.; Kim, S.; de Weck, O. Optimization of reconfigurable satellite constellations using simulated annealing and genetic algorithm. Sensors 2019, 19, 765. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Yu, W.; Wang, P.; Xiao, D.; Wang, W.; Liu, K.; Zhang, H. The High-Resolution Synthetic Aperture Radar System and Signal Processing Techniques: Current Progress and Future Prospects. IEEE Geosci. Remote Sens. Mag. 2024, 12, 169–189. [Google Scholar] [CrossRef]
- Sun, J.; Chen, X.; Jiang, C.; Guo, S. Distributionally Robust Optimization of On-Orbit Resource Scheduling for Remote Sensing in Space-Air-Ground Integrated 6G Networks. IEEE J. Sel. Areas Commun. 2024, 43, 382–395. [Google Scholar] [CrossRef]
- Li, X.; Wang, R.; Liang, G.; Yang, Z. A Multi-Objective Intelligent Optimization Method for Sensor Array Optimization in Distributed SAR-GMTI Radar Systems. Remote Sens. 2024, 16, 3041. [Google Scholar] [CrossRef]
- Suzuki, R.; Hirose, A.; Natsuaki, R. Optimizing PN-Sequences with Genetic Algorithm for SAR Waveform Diversity. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 11161–11164. [Google Scholar]
- Sun, Z.; Sun, H.; An, H.; Li, Z.; Wu, J.; Yang, J. Trajectory optimization for maneuvering platform bistatic SAR with geosynchronous illuminator. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Liang, J.; Yang, Z.; Bi, Y.; Qu, B.; Liu, M.; Xue, B.; Zhang, M. A Multi-Tree Genetic Programming-based Feature Construction Approach to Crop Classification Using Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4410817. [Google Scholar] [CrossRef]
- Lau, H.C.; Chan, T.; Tsui, W. Item-location assignment using fuzzy logic guided genetic algorithms. IEEE Trans. Evol. Comput. 2008, 12, 765–780. [Google Scholar] [CrossRef]
- Lau, H.C.; Chan, T.; Tsui, W. Fuzzy logic guided genetic algorithms for the location assignment of items. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 4281–4288. [Google Scholar]





| Decision Variable | Symbol | Value Range |
|---|---|---|
| Number of Satellites | N | |
| Satellite Altitude | h | [400, 1000] km |
| Orbital Inclination | i | [0°, 180°] |
| Right Ascension of Ascending Node | [0°, 360°) | |
| Argument of Perigee | M | [0°, 360°) |
| Field of View | [3°, 60°] | |
| Quality Factor | Q | [10, 100] |
| Decision Variable | Symbol | Value Range |
|---|---|---|
| Satellite Altitude | h | km |
| Orbital Inclination | i | to |
| Right Ascension of the Ascending Node | ||
| Argument of Perigee | ||
| True Anomaly | M | |
| Visible Range | ||
| Quality Factor | Q |
| Rule | Population Diversity | Fitness Gap | Single-Point Crossover | Multi-Point Crossover | Uniform Crossover |
|---|---|---|---|---|---|
| Rule 1 | High | Large | Low | Medium | High |
| Rule 2 | High | Medium | Medium | Medium | Medium |
| Rule 3 | High | Small | Medium | High | Medium |
| Rule 4 | Medium | Large | Medium | High | Medium |
| Rule 5 | Medium | Medium | Medium | Medium | Medium |
| Rule 6 | Medium | Small | Low | Medium | Medium |
| Rule 7 | Low | High | Medium | Medium | Low |
| Rule 8 | Low | Medium | Medium | Medium | Low |
| Rule 9 | Low | Small | High | Low | Low |
| Rule | Population Diversity | Fitness Gap | Crossover Proportion |
|---|---|---|---|
| Rule 1 | Low | Small | Low (e.g., 0.2) |
| Rule 2 | Low | Large | Medium (e.g., 0.5) |
| Rule 3 | Low | Medium | Medium (e.g., 0.5) |
| Rule 4 | Medium | Large | High (e.g., 0.7) |
| Rule 5 | Medium | Medium | Medium (e.g., 0.5) |
| Rule 6 | Medium | Small | Low (e.g., 0.3) |
| Rule 7 | High | Large | High (e.g., 0.8) |
| Rule 8 | High | Medium | Medium (e.g., 0.5) |
| Rule 9 | High | Small | Medium (e.g., 0.5) |
| Satellite No. | Orbit Altitude (km) | Inclination | Ascending Node Longitude | Argument of Perigee | True Anomaly | Quality Factor | Viewing Angle Range |
|---|---|---|---|---|---|---|---|
| 1 | 558.85 | 180.00 | 246.92 | 346.36 | 12.83 | 70.00 | 47.74 |
| 2 | 657.92 | 37.70 | 360.00 | 360.00 | 360.00 | 100.00 | 50.00 |
| 3 | 673.68 | 152.50 | 360.00 | 360.00 | 341.77 | 100.00 | 38.84 |
| 4 | 569.23 | 144.30 | 268.50 | 34.84 | 227.25 | 70.00 | 50.00 |
| 5 | 741.18 | 44.70 | 360.00 | 16.48 | 246.73 | 30.00 | 50.00 |
| 6 | 669.25 | 141.60 | 360.00 | 360.00 | 360.00 | 90.00 | 50.00 |
| 7 | 534.46 | 99.10 | 360.00 | 360.00 | 283.09 | 100.00 | 24.03 |
| 8 | 744.05 | 142.70 | 360.00 | 64.91 | 252.62 | 60.00 | 39.78 |
| 9 | 405.23 | 145.40 | 360.00 | 360.00 | 300.03 | 80.00 | 50.00 |
| 10 | 959.07 | 135.00 | 360.00 | 299.06 | 283.09 | 60.00 | 50.00 |
| 11 | 1000.00 | 134.50 | 360.00 | 290.66 | 354.61 | 100.00 | 50.00 |
| 12 | 606.55 | 142.10 | 305.23 | 360.00 | 268.08 | 50.00 | 44.76 |
| Satellite No. | Orbit Altitude (km) | Inclination | Ascending Node Longitude | Argument of Perigee | True Anomaly | Quality Factor | Viewing Angle Range |
|---|---|---|---|---|---|---|---|
| 1 | 814.08 | 136.30 | 360.00 | 360.00 | 60.13 | 10.00 | 50.00 |
| 2 | 648.43 | 34.10 | 360.00 | 360.00 | 360.00 | 10.00 | 50.00 |
| 3 | 623.78 | 39.00 | 360.00 | 317.73 | 360.00 | 10.00 | 50.00 |
| 4 | 576.40 | 151.20 | 360.00 | 357.23 | 360.00 | 50.00 | 50.00 |
| 5 | 833.44 | 39.50 | 17.31 | 360.00 | 360.00 | 10.00 | 50.00 |
| 6 | 1000.00 | 121.20 | 186.21 | 360.00 | 55.27 | 10.00 | 50.00 |
| 7 | 750.55 | 136.70 | 360.00 | 360.00 | 360.00 | 20.00 | 50.00 |
| 8 | 615.96 | 142.80 | 241.37 | 195.75 | 172.39 | 90.00 | 50.00 |
| 9 | 712.79 | 105.30 | 170.38 | 349.33 | 313.59 | 60.00 | 50.00 |
| 10 | 804.32 | 142.70 | 360.00 | 254.92 | 360.00 | 100.00 | 47.20 |
| 11 | 972.87 | 26.50 | 133.37 | 37.35 | 295.58 | 10.00 | 50.00 |
| 12 | 890.54 | 31.40 | 317.98 | 171.10 | 118.82 | 70.00 | 50.00 |
| Satellite No. | Orbit Altitude (km) | Inclination | Ascending Node Longitude | Argument of Perigee | True Anomaly | Quality Factor | Viewing Angle Range |
|---|---|---|---|---|---|---|---|
| 1 | 557.41 | 140.00 | 360.00 | 265.82 | 254.98 | 10.00 | 50.00 |
| 2 | 712.18 | 137.80 | 170.60 | 360.00 | 360.00 | 10.00 | 50.00 |
| 3 | 713.92 | 138.40 | 360.00 | 344.90 | 158.40 | 10.00 | 50.00 |
| 4 | 617.40 | 140.80 | 102.87 | 360.00 | 7.65 | 10.00 | 50.00 |
| 5 | 712.09 | 138.00 | 360.00 | 290.36 | 360.00 | 10.00 | 50.00 |
| 6 | 714.99 | 137.30 | 209.72 | 360.00 | 360.00 | 10.00 | 50.00 |
| 7 | 821.12 | 136.00 | 216.03 | 135.09 | 360.00 | 10.00 | 50.00 |
| 8 | 663.38 | 140.80 | 165.83 | 360.00 | 360.00 | 10.00 | 50.00 |
| 9 | 670.80 | 102.90 | 289.62 | 80.39 | 360.00 | 10.00 | 50.00 |
| 10 | 657.99 | 138.40 | 360.00 | 154.14 | 128.01 | 10.00 | 50.00 |
| 11 | 659.12 | 138.40 | 135.52 | 360.00 | 360.00 | 10.00 | 50.00 |
| 12 | 554.00 | 140.50 | 112.46 | 137.74 | 110.03 | 10.00 | 50.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Deng, Y.; Chang, S.; Zhu, M.; Zhang, Y.; Zhang, Z. Orbital Design Optimization for Large-Scale SAR Constellations: A Hybrid Framework Integrating Fuzzy Rules and Chaotic Sequences. Remote Sens. 2025, 17, 1430. https://doi.org/10.3390/rs17081430
Liu D, Deng Y, Chang S, Zhu M, Zhang Y, Zhang Z. Orbital Design Optimization for Large-Scale SAR Constellations: A Hybrid Framework Integrating Fuzzy Rules and Chaotic Sequences. Remote Sensing. 2025; 17(8):1430. https://doi.org/10.3390/rs17081430
Chicago/Turabian StyleLiu, Dacheng, Yunkai Deng, Sheng Chang, Mengxia Zhu, Yusheng Zhang, and Zixuan Zhang. 2025. "Orbital Design Optimization for Large-Scale SAR Constellations: A Hybrid Framework Integrating Fuzzy Rules and Chaotic Sequences" Remote Sensing 17, no. 8: 1430. https://doi.org/10.3390/rs17081430
APA StyleLiu, D., Deng, Y., Chang, S., Zhu, M., Zhang, Y., & Zhang, Z. (2025). Orbital Design Optimization for Large-Scale SAR Constellations: A Hybrid Framework Integrating Fuzzy Rules and Chaotic Sequences. Remote Sensing, 17(8), 1430. https://doi.org/10.3390/rs17081430







